Commute Networks as a Signature of Urban Socioeconomic Performance: Evaluating Mobility Structures with Deep Learning Models
Abstract
Highlights
- Mobility network structures derived from census-based commute data significantly enhance modeling performance for socioeconomic modeling, even without using region-specific features.
- The proposed deep learning framework employing Graph Neural Networks outperforms traditional models using regional-level features across 12 major U.S. cities.
- Network-based representations derived from deep learning methods offer a powerful alternative to traditional location-based approaches for urban analysis and forecasting of population-based metrics.
- The approach provides urban researchers and policymakers with scalable tools to incorporate mobility-driven structural and topological network effects—derived purely from commuting patterns—into socioeconomic planning and decision-making.
Abstract
1. Introduction
- We demonstrate that mobility (commute) networks alone, without reliance on auxiliary contextual data, can provide sufficient structural signal for effective socioeconomic modeling.
- We propose a unified GNN + VNN architecture that jointly learns network embeddings and performs downstream prediction of urban location characteristics in a single end-to-end training pipeline.
2. Materials and Methods
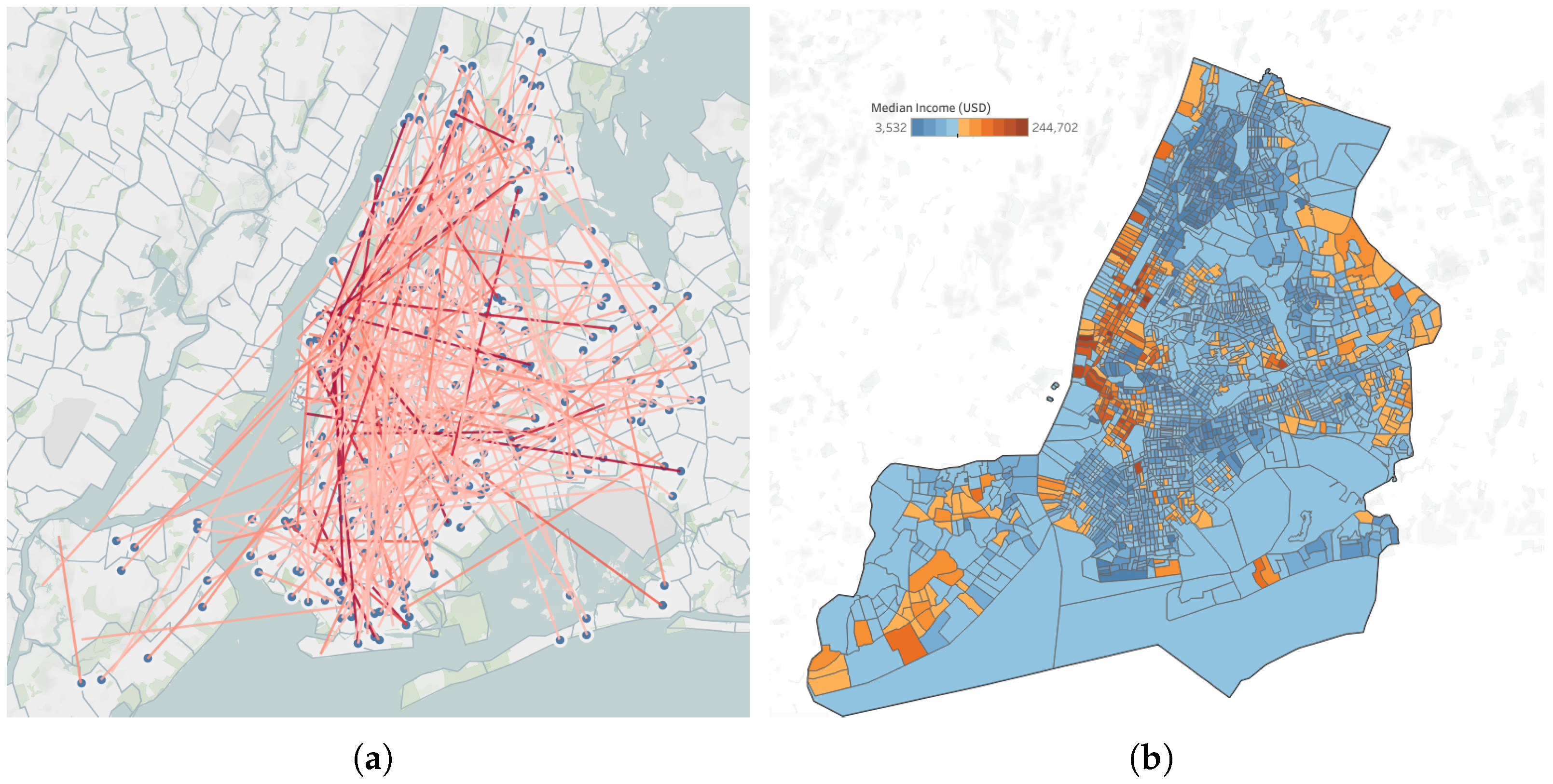
2.1. Data Overview
2.2. Methods
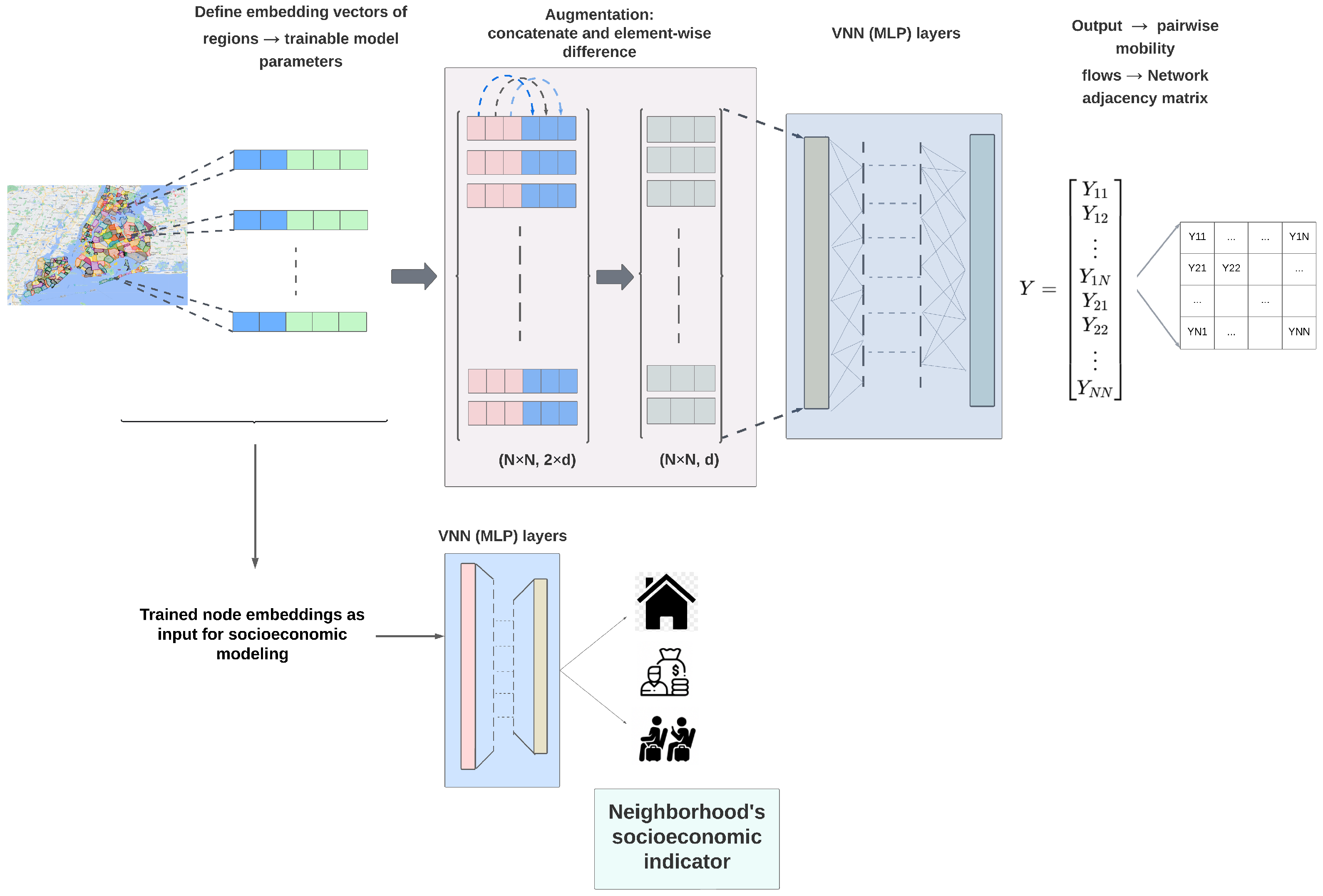
2.2.1. Network Embedding as Model Inputs
2.2.2. Evaluating Mobility Networks—VNN Based Embedding
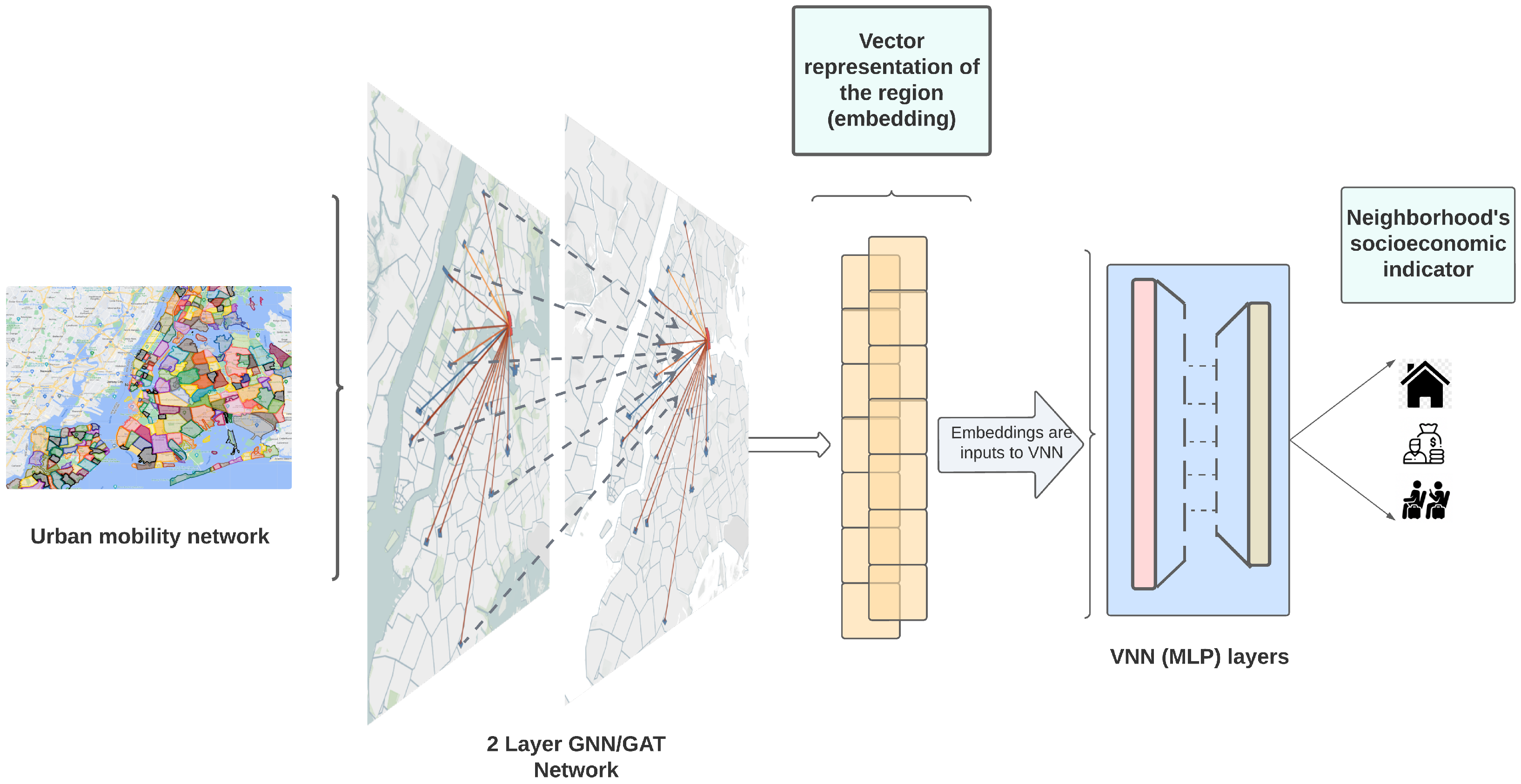
2.2.3. Single-Pipeline Modeling: GNN + VNN Framework
2.3. Experiments
3. Results
4. Discussion
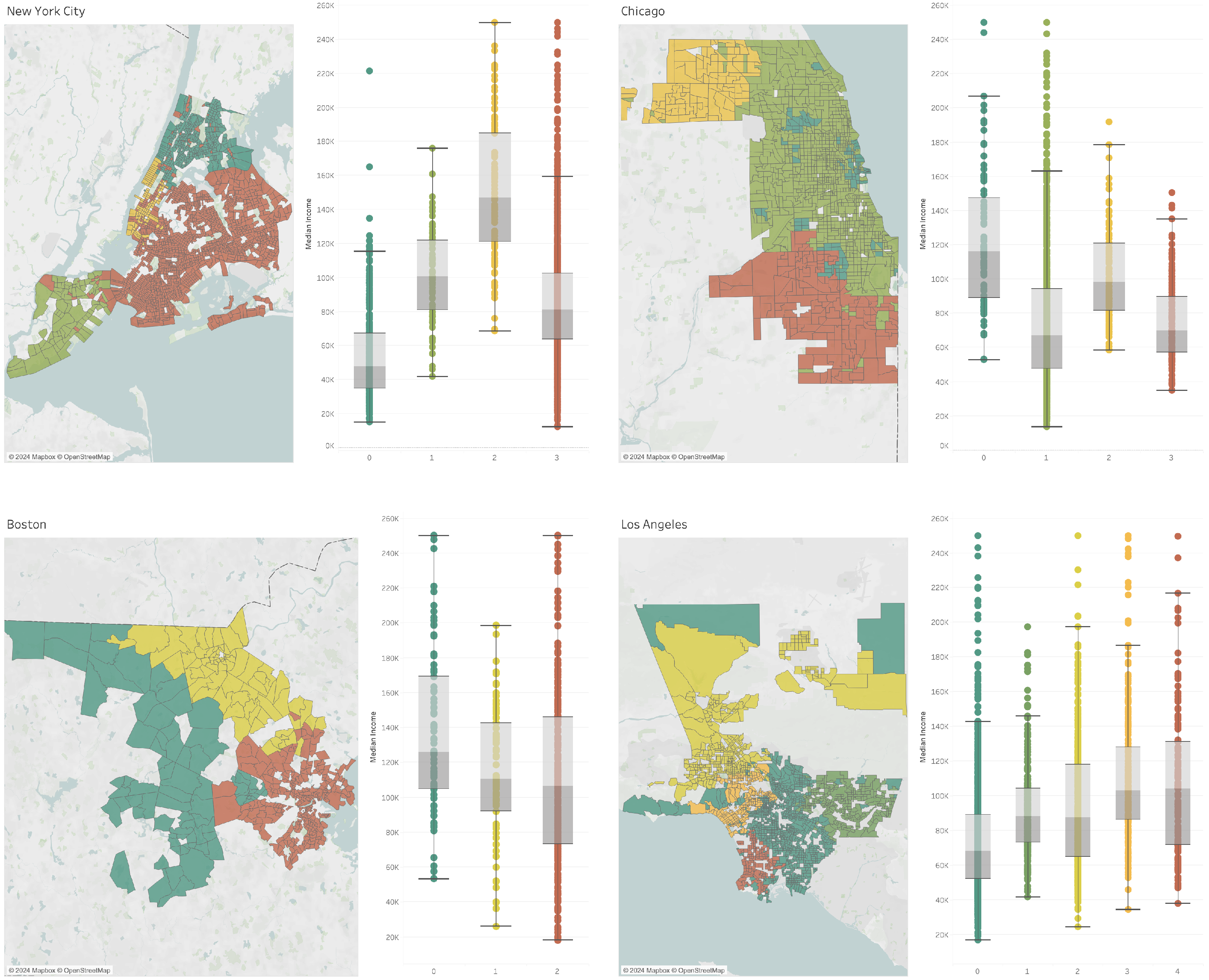
4.1. Interpretation of Embedding Configurations
4.2. Graph vs. Non-Graph Models
4.3. Policy Implications and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GNN | Graph Neural Network |
| LEHD | Longitudinal Employer Household Dynamics |
| SVD | Singular Value Decomposition |
| GAT | Graph Attention Network |
| VNN | Vanilla Neural Network |
| MLP | Multi Layer Perceptron |
| NYC | New York City |
Appendix A
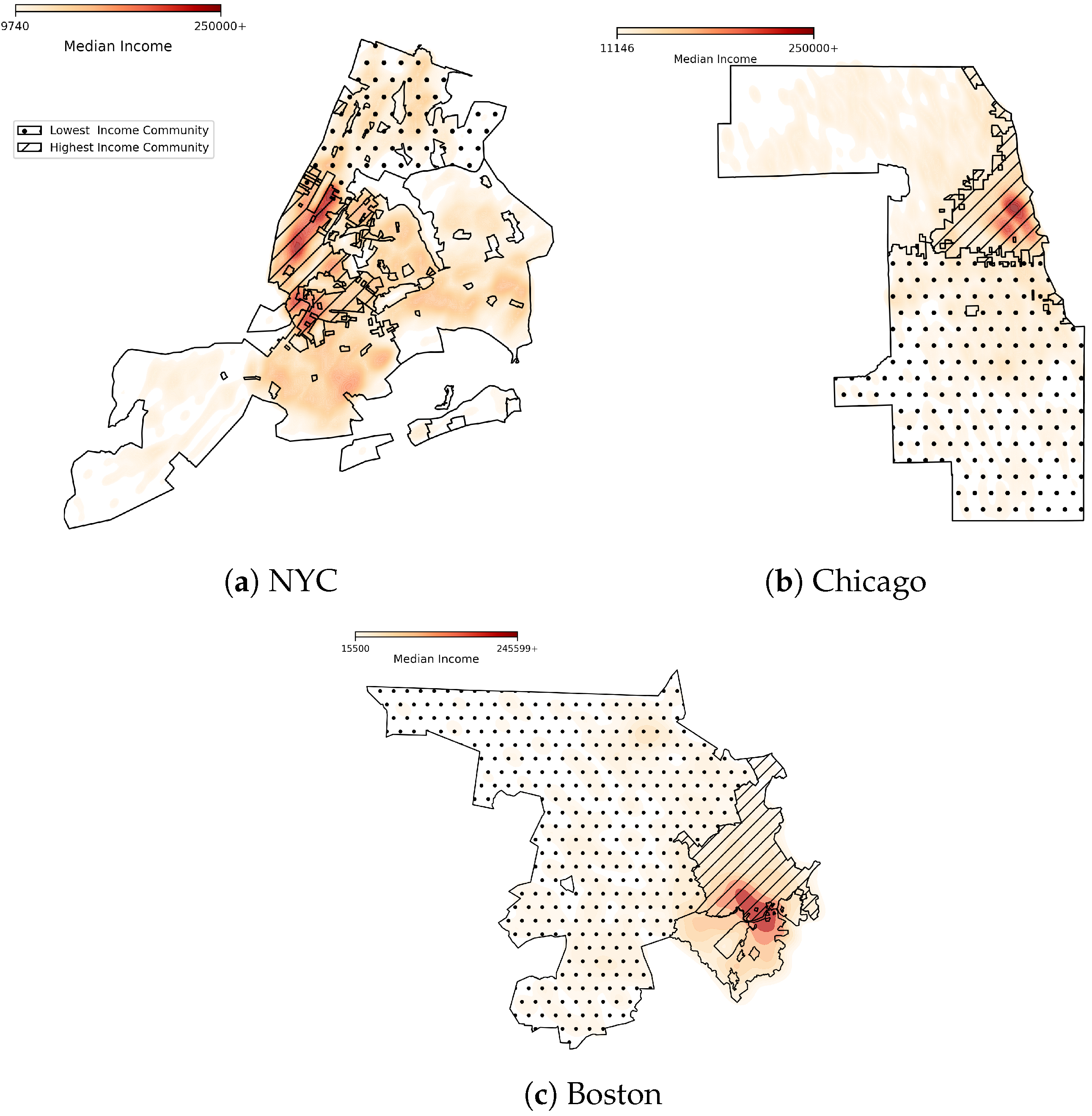
Appendix A.1. Data
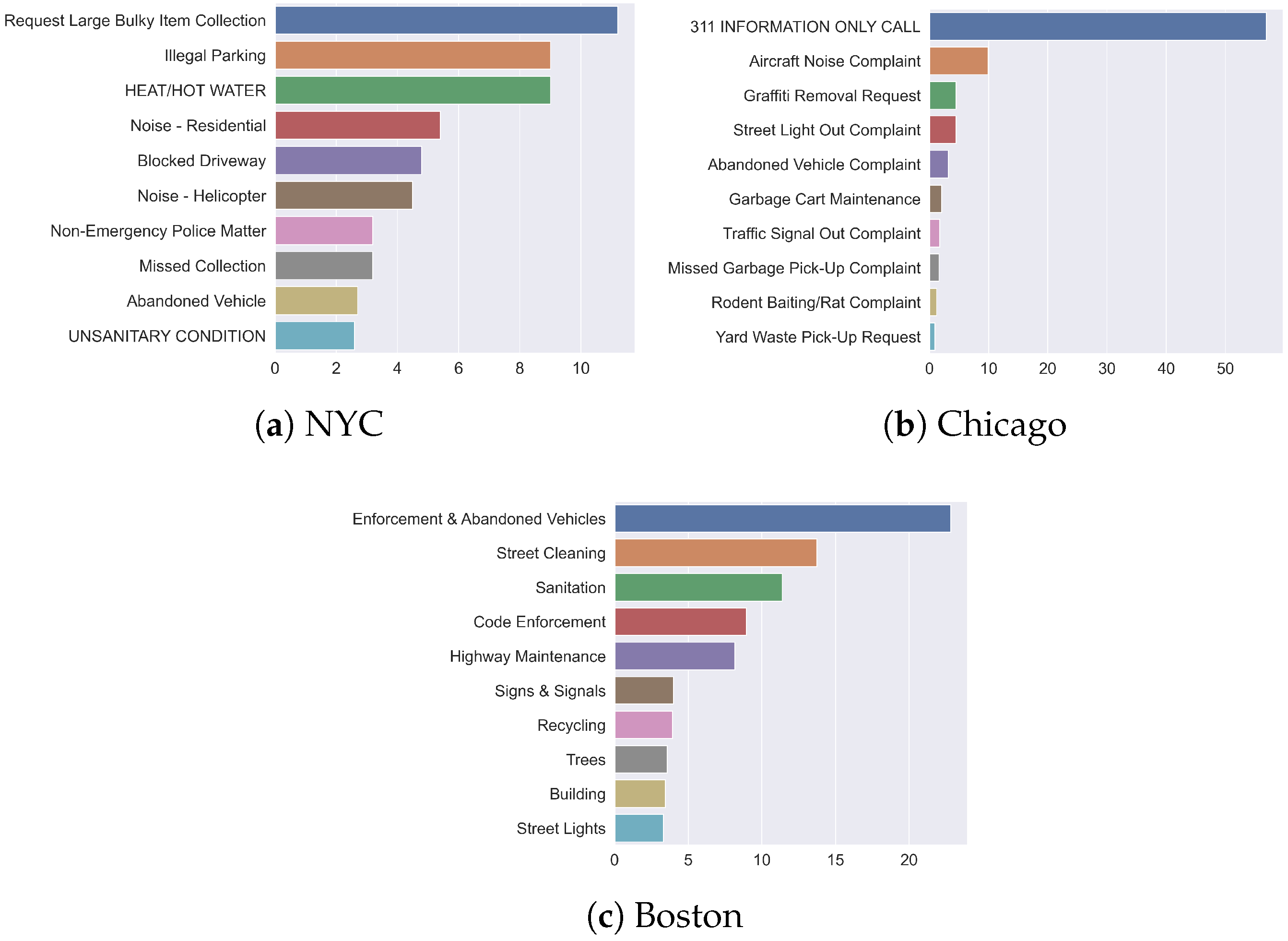
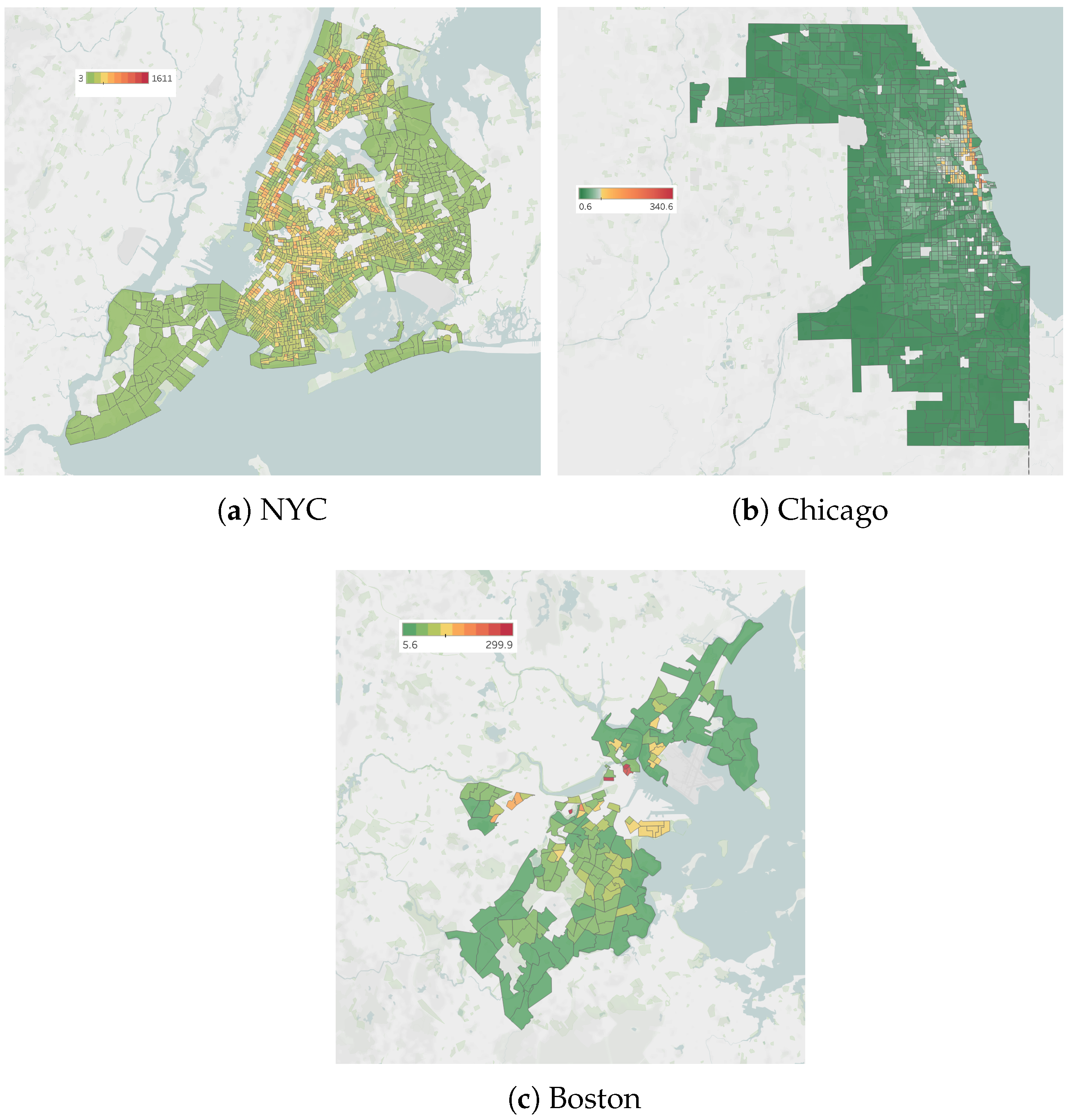
Appendix A.2. Network Embedding Clustering
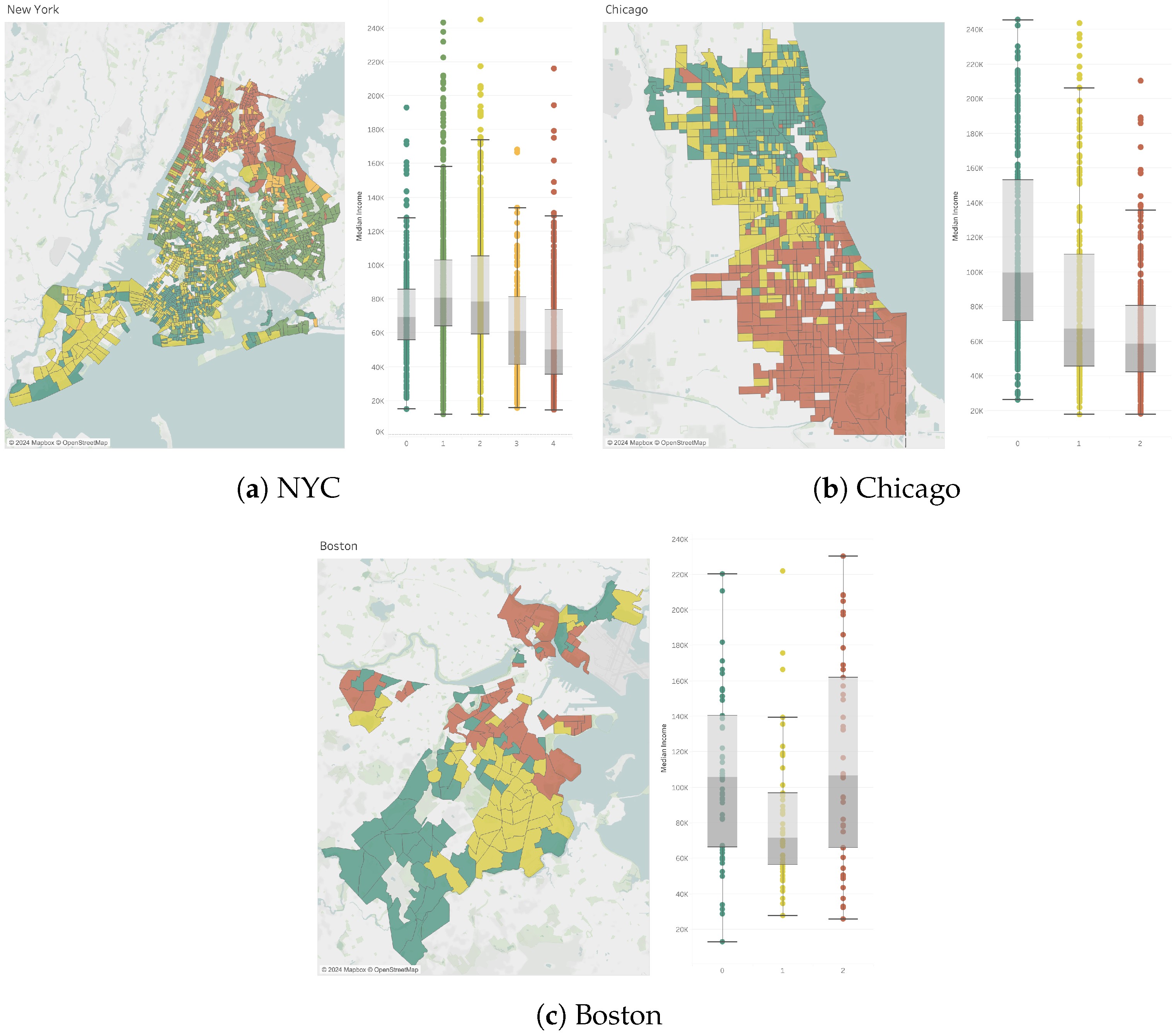
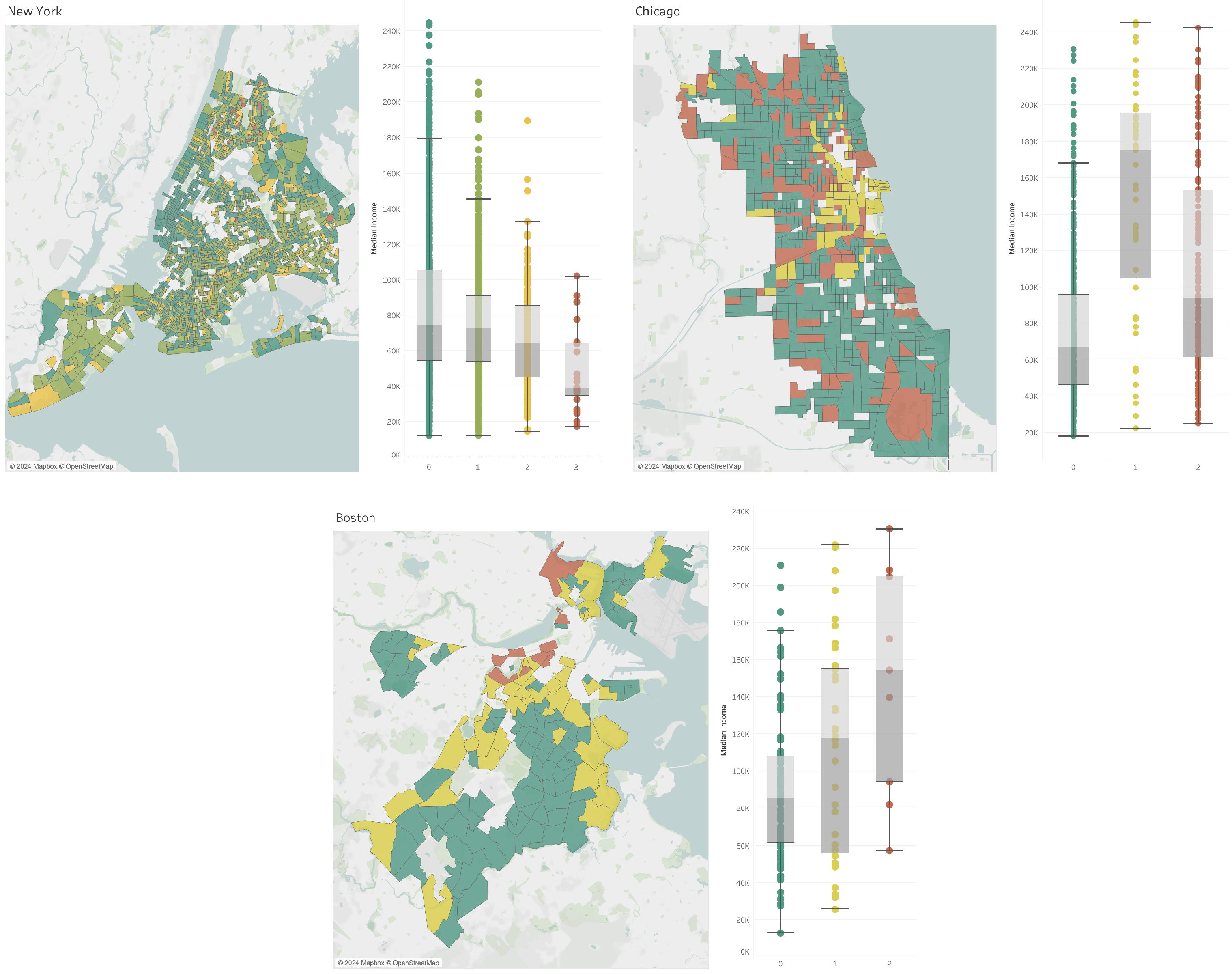
Appendix A.3. Experiments with Embedding: Dimensionality
| VNN Embedding | Cities | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NYC | Boston | Chicago | San Jose | San Diego | Austin | Dallas | LA | San Antonio | Phoenix | |
| d = 2 | ||||||||||
| d = 5 | ||||||||||
| d = 10 | ||||||||||
| d = 15 | ||||||||||
Appendix A.4. Comparison with Classical ML Models
| City | LR | RF | GB | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 311 | Pop.Density | Job.Density | 311 | Pop.Density | Job.Density | 311 | Pop.Density | Job.Density | |
| NYC | |||||||||
| LA | |||||||||
| Chicago | |||||||||
| Boston | |||||||||
| Philadelphia | |||||||||
| Dallas | |||||||||
| Austin | |||||||||
| San Jose | |||||||||
| San Diego | |||||||||
Appendix A.5. Concatenation and Modeling with Neighborhood-Level Features
| Model Inputs | Cities | ||
|---|---|---|---|
| NYC | Boston | Chicago | |
| Population density | 0.02 | 0.01 | 0.16 |
| Job density | 0.07 | 0.08 | 0.12 |
| Embedding + Population density | 0.53 | 0.33 | 0.68 |
| Embedding + Job density | 0.53 | 0.33 | 0.68 |
| Embedding + 311 data | 0.64 | 0.33 | 0.75 |
References
- Rosvall, M.; Trusina, A.; Minnhagen, P.; Sneppen, K. Networks and cities: An information perspective. Phys. Rev. Lett. 2005, 94, 028701. [Google Scholar] [CrossRef]
- Pflieger, G.; Rozenblat, C. Introduction. Urban networks and network theory: The city as the connector of multiple networks. Urban Stud. 2010, 47, 2723–2735. [Google Scholar] [CrossRef]
- Jiang, B.; Claramunt, C. Topological analysis of urban street networks. Environ. Plan. B Plan. Des. 2004, 31, 151–162. [Google Scholar] [CrossRef]
- Li, X.; Lv, Z.; Zheng, Z.; Zhong, C.; Hijazi, I.H.; Cheng, S. Assessment of lively street network based on geographic information system and space syntax. Multimed. Tools Appl. 2017, 76, 17801–17819. [Google Scholar] [CrossRef]
- Shi, G.; Shan, J.; Ding, L.; Ye, P.; Li, Y.; Jiang, N. Urban Road Network Expansion and Its Driving Variables: A Case Study of Nanjing City. Int. J. Environ. Res. Public Health 2019, 16, 2318. [Google Scholar] [CrossRef]
- Xu, Y.; Belyi, A.; Bojic, I.; Ratti, C. Human mobility and socioeconomic status: Analysis of Singapore and Boston. Comput. Environ. Urban Syst. 2018, 72, 51–67. [Google Scholar] [CrossRef]
- Lee, S.; Lin, J. Natural amenities, neighbourhood dynamics, and persistence in the spatial distribution of income. Rev. Econ. Stud. 2018, 85, 663–694. [Google Scholar] [CrossRef]
- Wang, L.; Qian, C.; Kats, P.; Kontokosta, C.; Sobolevsky, S. Structure of 311 service requests as a signature of urban location. PLoS ONE 2017, 12, e0186314. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. LINE: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Sobolevsky, S.; Belyi, A. Graph neural network inspired algorithm for unsupervised network community detection. Appl. Netw. Sci. 2022, 7, 63. [Google Scholar] [CrossRef]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. Stat 2017, 1050, 10–48550. [Google Scholar]
- Kempinska, K.; Murcio, R. Modelling urban networks using Variational Autoencoders. Appl. Netw. Sci. 2019, 4, 114. [Google Scholar] [CrossRef]
- Pagani, A.; Mehrotra, A.; Musolesi, M. Graph input representations for machine learning applications in urban network analysis. Environ. Plan. B Urban Anal. City Sci. 2021, 48, 741–758. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, D.; Mai, G.; Guo, X.; Cui, L. Learning urban region representations with POIs and hierarchical graph infomax. ISPRS J. Photogramm. Remote Sens. 2023, 196, 134–145. [Google Scholar] [CrossRef]
- Kim, N.; Yoon, Y. Effective urban region representation learning using heterogeneous urban graph attention network (hugat). arXiv 2022, arXiv:2202.09021. [Google Scholar]
- Mishina, M.; Sobolevsky, S.; Kovtun, E.; Khrulkov, A.; Belyi, A.; Budennyy, S.; Mityagin, S. Prediction of Urban Population-Facilities Interactions with Graph Neural Network. In Computational Science and Its Applications—ICCSA 2023; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2023; Volume 13956. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M.; Yin, H. A graph convolutional neural network for classification of building patterns using spatial vector data. ISPRS J. Photogramm. Remote. Sens. 2019, 150, 259–273. [Google Scholar] [CrossRef]
- Xu, Y.; Jin, S.; Chen, Z.; Xie, X.; Hu, S.; Xie, Z. Application of a graph convolutional network with visual and semantic features to classify urban scenes. Int. J. Geogr. Inf. Sci. 2022, 36, 2009–2034. [Google Scholar] [CrossRef]
- Natterer, E.; Engelhardt, R.; Hörl, S.; Bogenberger, K. Graph Neural Network Approach to Predict the Effects of Road Capacity Reduction Policies: A Case Study for Paris, France. arXiv 2024, arXiv:2408.06762. [Google Scholar]
- Zhang, Y.; Dong, X.; Shang, L.; Zhang, D.; Wang, D. A multi-modal graph neural network approach to traffic risk forecasting in smart urban sensing. In Proceedings of the 2020 17th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Como, Italy, 22–25 June 2020; pp. 1–9. [Google Scholar]
- Zhai, X.; Jiang, J.; Dejl, A.; Rago, A.; Guo, F.; Toni, F.; Sivakumar, A. Heterogeneous Graph Neural Networks with Post-hoc Explanations for Multi-modal and Explainable Land Use Inference. arXiv 2024, arXiv:2406.13724. [Google Scholar]
- Khulbe, D.; Belyi, A.; Mikeš, O.; Sobolevsky, S. Mobility Networks as a Predictor of Socioeconomic Status in Urban Systems. In Computational Science and Its Applications—ICCSA 2023; Springer: Cham, Switzerland, 2023; pp. 139–157. [Google Scholar]
- Center for Economic Studies at the U.S. Census Bureau. Longitudinal Employer-Household Dynamics. 2023. Available online: https://lehd.ces.census.gov/ (accessed on 9 August 2023).
- U.S. Census Bureau. American Community Survey Data. 2023. Available online: https://www.census.gov/programs-surveys/acs/data.html (accessed on 9 August 2023).
- NYC Open Data. NYC 311 Data. 2023. Available online: https://data.cityofnewyork.us/Social-Services/NYC-311-Data/jrb2-thup (accessed on 9 August 2023).
- Sium, Y.; Kollias, G.; Idé, T.; Das, P.; Abe, N.; Lozano, A.; Li, Q. Direction aware positional and structural encoding for directed graph neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023. [Google Scholar]
- Dwivedi, V.; Bresson, X. A Generalization of Transformer Networks to Graphs. arXiv 2020, arXiv:2012.09699. [Google Scholar]
- Rampášek, L.; Galkin, M.; Dwivedi, V.P.; Luu, A.T.; Wolf, G.; Beaini, D. Recipe for a General, Powerful, Scalable graph transformer. Adv. Neural Inf. Process. Syst. 2022, 35, 14501–14515. [Google Scholar]
- Kreuzer, D.; Beaini, D.; Hamilton, W.; Létourneau, V.; Tossou, P. Rethinking graph transformers with spectral attention. Adv. Neural Inf. Process. Syst. 2021, 34, 21618–21629. [Google Scholar]
- Ying, C.; Cai, T.; Luo, S.; Zheng, S.; Ke, G.; He, D.; Shen, Y.; Liu, T.Y. Do transformers really perform badly for graph representation? In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–14 December 2021. [Google Scholar]
- Li, P.; Wang, Y.; Wang, H.; Leskovec, J. Distance encoding: Design provably more powerful neural networks for graph representation learning. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Volume 33, pp. 4465–4478. [Google Scholar]
- Dwivedi, V.P.; Luu, A.T.; Laurent, T.; Bengio, Y.; Bresson, X. Graph neural networks with learnable structural and positional representations. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Brüel-Gabrielsson, R.; Yurochkin, M.; Solomon, J. Rewiring with positional encodings for graph neural networks. arXiv 2022, arXiv:2201.12674. [Google Scholar]
- Xu, F.; Lin, Z.; Xia, T.; Guo, D.; Li, Y. SUME: Semantic-enhanced Urban Mobility Network Embedding for User Demographic Inference. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2020, 4, 98. [Google Scholar] [CrossRef]
- Chandra, D.K.; Leopold, J.; Fu, Y. NodeSense2Vec: Spatiotemporal Context-Aware Network Embedding for Heterogeneous Urban Mobility Data. In Proceedings of the 2021 IEEE International Conference on Big Data (Big Data), Virtual, 15–18 December 2021; pp. 2884–2893. [Google Scholar] [CrossRef]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Dong, L.; Duarte, F.; Duranton, G.; Santi, P.; Barthelemy, M.; Batty, M.; Bettencourt, L.; Goodchild, M.; Hack, G.; Liu, Y.; et al. Defining a city—Delineating urban areas using cell-phone data. Nat. Cities 2024, 1, 117–125. [Google Scholar] [CrossRef]
- He, M.; Bogomolov, Y.; Khulbe, D.; Sobolevsky, S. Distance deterrence comparison in urban commute among different socioeconomic groups: A normalized linear piece-wise gravity model. J. Transp. Geogr. 2023, 113, 103732. [Google Scholar] [CrossRef]
- Bogomolov, Y.; He, M.; Khulbe, D.; Sobolevsky, S. Impact of income on urban commute across major cities in US. Procedia Comput. Sci. 2021, 193, 325–332. [Google Scholar] [CrossRef]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 1025–1035. [Google Scholar]
- Hicks, N.; Streeten, P. Indicators of development: The search for a basic needs yardstick. World Dev. 1979, 7, 567–580. [Google Scholar] [CrossRef]
- Li, Y.; Hyder, A.; Southerland, L.T.; Hammond, G.; Porr, A.; Miller, H.J. 311 Service Requests as Indicators of Neighborhood Distress and Opioid Use Disorder. Sci. Rep. 2020, 10, 14334. [Google Scholar] [CrossRef] [PubMed]
- Kontokosta, C.; Hong, B.; Korsberg, K. Equity in 311 reporting: Understanding socio-spatial differentials in the propensity to complain. arXiv 2017, arXiv:1710.02452. [Google Scholar]
- Chen, D.T. The Science of Smart Growth. Sci. Am. 2000, 283, 84–91. [Google Scholar] [CrossRef]
- Leslie, T.F.; Ó hUallacháin, B. Polycentric Phoenix. Econ. Geogr. 2006, 82, 167–192. [Google Scholar] [CrossRef]
- Wang, D.; Cui, P.; Zhu, W. Structural Deep Network Embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’16), San Francisco, CA, USA, 13–17 August 2016; pp. 1225–1234. [Google Scholar] [CrossRef]
- Chang, S.; Han, W.; Tang, J.; Qi, G.J.; Aggarwal, C.C.; Huang, T.S. Heterogeneous Network Embedding via Deep Architectures. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’15), Sydney, Australia, 10–13 August 2015; pp. 119–128. [Google Scholar] [CrossRef]
- Yap, W.; Stouffs, R.; Biljecki, F. Urbanity: Automated modelling and analysis of multidimensional networks in cities. npj Urban Sustain. 2023, 3, 45. [Google Scholar] [CrossRef]
- Yap, W.; Biljecki, F. A Global Feature-Rich Network Dataset of Cities and Dashboard for Comprehensive Urban Analyses. Sci. Data 2023, 10, 667. [Google Scholar] [CrossRef]
- Boston 311 Data. 2023. Available online: https://data.boston.gov/dataset/311-service-requests/resource/f53ebccd-bc61-49f9-83db-625f209c95f5 (accessed on 9 August 2023).
- Chicago 311 Data. 2023. Available online: https://data.cityofchicago.org/Service-Requests/311-Service-Requests/v6vf-nfxy (accessed on 9 August 2023).
- Brin, S. The PageRank citation ranking: Bringing order to the web. Proc. ASIS 1998, 98, 161–172. [Google Scholar]
- Jia, C.; Du, Y.; Wang, S.; Bai, T.; Fei, T. Measuring the vibrancy of urban neighborhoods using mobile phone data with an improved PageRank algorithm. Trans. GIS 2019, 23, 241–258. [Google Scholar] [CrossRef]
- Jiang, B. Ranking spaces for predicting human movement in an urban environment. Int. J. Geogr. Inf. Sci. 2009, 23, 823–837. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
| City | Nodes | Non-Zero Edges | Avg. Edge Weight |
|---|---|---|---|
| New York | 2157 | 976,832 | 0.69 |
| Chicago | 1318 | 439,553 | 1.06 |
| Boston | 520 | 127,357 | 3.5 |
| Austin | 218 | 34,777 | 8.63 |
| Dallas | 529 | 129,352 | 2.83 |
| Los Angeles | 2341 | 1,171,362 | 0.65 |
| San Antonio | 366 | 83,192 | 4.77 |
| San Diego | 627 | 180,781 | 2.97 |
| San Jose | 372 | 81,938 | 4.73 |
| Philadelphia | 384 | 68,119 | 2.57 |
| Phoenix | 916 | 349,894 | 2.10 |
| Houston | 786 | 290,496 | 2.50 |
| Comparison Benchmark [8] | VNN | (GNN + VNN) | (GAT + VNN) | ||||
|---|---|---|---|---|---|
| 311 Features | Spatial | SVD | LE | Random Walk | |
| NYC | 0.49 | 0.55 | 0.58 | 0.58 | 0.30 | 0.46 | 0.29 | 0.33 | 0.20 | 0.20 | 0.35 | 0.45 | 0.44 |
| LA | 0.16 | 0.13 | 0.32 | 0.28 | 0.11 | 0.31 | 0.31 | 0.1 | 0.24 |0.24 | 0.1 | 0.21 | 0.20 |
| Chicago | 0.59 | 0.7 | 0.69 | 0.68 | 0.3 | 0.44 | 0.44 | 0.5 | 0.15 | 0.14 | 0.56 | 0.61 | 0.60 |
| Boston | 0.15 | 0.35 | 0.50 | 0.50 | 0.3 | 0.28 | 0.25 | 0.44 | 0.14 | 0.10 | 0.35 | 0.21 | 0.15 |
| Philadelphia | 0.51 | 0.28 | 0.33 | 0.33 | 0.51 | 0.55 | 0.52 | 0.3 | 0.31 | 0.3 | 0.3 | 0.45 | 0.45 |
| Houston | NA | 0.23 | 0.17 | 0.15 | 0.36 | 0.42 | 0.40 | 0.19 | 0.18 | 0.18 | 0.25 | 0.39 | 0.39 |
| Dallas | 0.37 | 0.33 | 0.27 | 0.26 | 0.58 | 0.58 | 0.56 | 0.38 | 0.08 | 0.05 | 0.36 | 0.41 | 0.40 |
| Austin | 0.28 | 0.43 | 0.38 | 0.38 | 0.59 | 0.57 | 0.53 | 0.33 | 0.04 | 0.07 | 0.36 | 0.31 | 0.34 |
| San Jose | 0.46 | 0.21 | 0.4 | 0.4 | 0.75 | 0.42 | 0.4 | 0.21 | 0.21 | 0.24 | 0.36 | 0.03 | 0.09 |
| San Diego | 0.36 | 0.16 | 0.26 | 0.28 | 0.43 | 0.34 | 0.32 | 0.27 | 0.26 | 0.25 | 0.36 | 0.41 | 0.33 |
| San Antonio | NA | 0.3 | 0.48 | 0.41 | 0.52 | 0.52 | 0.33 | 0.3 | 0.04 | 0.03 | 0.14 | 0.34 | 0.3 |
| Phoenix | NA | 0.14 | 0.25 | 0.25 | 0.15 | 0.26 | 0.25 | 0.21 | 0.25 | 0.24 | 0.15 | 0.26 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khulbe, D.; Belyi, A.; Sobolevsky, S. Commute Networks as a Signature of Urban Socioeconomic Performance: Evaluating Mobility Structures with Deep Learning Models. Smart Cities 2025, 8, 125. https://doi.org/10.3390/smartcities8040125
Khulbe D, Belyi A, Sobolevsky S. Commute Networks as a Signature of Urban Socioeconomic Performance: Evaluating Mobility Structures with Deep Learning Models. Smart Cities. 2025; 8(4):125. https://doi.org/10.3390/smartcities8040125
Chicago/Turabian StyleKhulbe, Devashish, Alexander Belyi, and Stanislav Sobolevsky. 2025. "Commute Networks as a Signature of Urban Socioeconomic Performance: Evaluating Mobility Structures with Deep Learning Models" Smart Cities 8, no. 4: 125. https://doi.org/10.3390/smartcities8040125
APA StyleKhulbe, D., Belyi, A., & Sobolevsky, S. (2025). Commute Networks as a Signature of Urban Socioeconomic Performance: Evaluating Mobility Structures with Deep Learning Models. Smart Cities, 8(4), 125. https://doi.org/10.3390/smartcities8040125





