Comparison of Optimisation Techniques for the Electric Vehicle Scheduling Problem

Highlights

What are the main findings?

• Heuristic dominance in large-scale E-VSP instances: The newly developed heuristic consistently outperformed metaheuristics and the exact MILP approach in scalability and computation time, successfully solving large-scale instances (up to 420 trips) in seconds while maintaining feasible, operationally relevant solutions.
• Limited practicality of exact and metaheuristic methods: Although exact MILP methods guarantee optimality and metaheuristics (e.g., genetic algorithms, simulated annealing) achieve better distance optimisation on small problems, both approaches struggle with scalability, rendering them impractical for typical urban transit schedules.

What is the implication of the main finding?

• Scalable heuristics are essential for real-world transport scheduling: Given the computational limitations of exact and metaheuristic methods on large instances, transport agencies should prioritise heuristic-based solutions for operational deployment, especially when managing fleets with hundreds of daily trips.
• Algorithm selection should align with operational priorities: The choice of optimisation technique should depend on the specific context—metaheuristics may be suitable for small fleets prioritising distance savings, while heuristics are better suited for large-scale systems where speed, feasibility, and adaptability to real-world constraints are paramount.

Abstract

The Electric Vehicle Scheduling Problem (E-VSP) addresses the challenge of efficiently assigning predetermined trips to an electric vehicle fleet while accounting for charging infrastructure and battery range constraints. Despite numerous optimisation approaches proposed in the literature, comparative analyses of these methods remain scarce, with researchers typically focusing on developing novel algorithms rather than evaluating existing algorithms. Moreover, studies often employ convenient assumptions tailored to improve the performance of their optimisation technique. This study presents a comprehensive comparison of several optimisation techniques (mixed integer linear programming (MILP) using the branch-and-cut algorithm, metaheuristics, and heuristics) applied to the E-VSP under identical assumptions and constraints. The techniques are evaluated across multiple metrics, including solution quality, computational efficiency, and implementation complexity. Findings reveal that the branch-and-cut algorithm cannot solve instances with more than 10 trips in a reasonable time. Among metaheuristics, only genetic algorithms and simulated annealing demonstrate competitive performance, but both struggle with instances exceeding 100 trips. Our recently developed heuristic algorithm consistently found better solutions in significantly shorter computation times than the metaheuristics due to its ability to efficiently navigate the solution space while respecting the unique constraints of the E-VSP.

1. Introduction

The imperative to reduce greenhouse gas emissions and combat climate change has intensified the search for sustainable transportation solutions in urban environments. Among alternatives, electric public transport has emerged as a promising option for reducing greenhouse gas emissions and urban pollution. Electric buses and other electric transit vehicles offer reduced emissions, lower long-term operating costs, and decreased dependency on fossil fuels, making them increasingly attractive for cities worldwide [1,2]. However, transitioning from conventional to electric vehicles introduces unique operational challenges, particularly in fleet scheduling and management.

Unlike internal combustion engine (ICE) vehicles that can be quickly refuelled, electric buses require more sophisticated scheduling to balance operational efficiency with charging needs. This operational challenge is known as the E-VSP, which extends the classical Vehicle Scheduling Problem (VSP) by incorporating critical constraints related to battery capacity, charging infrastructure availability, and charging time requirements [3]. Insufficient attention to these constraints may result in service disruptions, suboptimal fleet utilisation, or excessive operational costs [4].

The literature offers various optimisation approaches to address the E-VSP, broadly categorised into exact methods, metaheuristic algorithms, and heuristic techniques. Exact methods such as MILP guarantee mathematically optimal solutions but often become computationally prohibitive for large-scale combinatorial instances, as is typical with real-life E-VSP instances [5]. Conversely, metaheuristic and heuristic techniques sacrifice guaranteed optimality for near-optimal solutions and scalability [6]. Metaheuristics such as genetic algorithms and simulated annealing employ general-purpose, problem-independent search strategies to escape local optima and explore the promising regions of the solution space. In contrast, heuristics employ problem-specific rules and logical shortcuts to navigate the solution space efficiently [7].

Despite the growing body of research on optimisation techniques for the E-VSP, a critical gap exists in the current literature: most studies develop and validate specific algorithms without thorough comparisons against alternative approaches. Even comprehensive review studies, such as in [8], often lack critical comparative elements such as processing time, solution quality, and scalability—largely because the original studies rarely include these metrics and it would therefore require reimplementation of all methods for proper comparison. Additionally, many researchers introduce simplifying assumptions that favour their particular optimisation technique [9], potentially obscuring its true comparative performance. This, along with the lack of standardised testing datasets, creates a significant disconnect between academic research and practical implementation needs.

This study addresses these gaps by conducting a comprehensive, systematic comparison of an exact method (MILP formulation solved with the branch-and-cut algorithm (BCA)), metaheuristic, and our heuristic optimisation techniques applied to the E-VSP. We evaluate these methods across the following metrics: processing speed, solution quality, feature set, and implementation complexity. We maintain consistent problem formulations and testing environments to ensure valid cross-method comparisons. Consequently, we provide actionable insights into each optimisation strategy’s strengths, limitations, and trade-offs.

Our research contributes to the literature in several important ways. First, we establish a standardised framework for evaluating E-VSP optimisation techniques that can inform both researchers and practitioners. Second, we provide a novel MILP formulation for the E-VSP. Third, we compare metaheuristic algorithms to determine which demonstrate superior convergence properties for E-VSP instances. Fourth, we provide a comparison of algorithm speed between the BCA, metaheuristic, and heuristic approaches across different problem sizes, highlighting the practical limitations of each method. Fifth, we evaluate solution quality across all approaches, demonstrating that heuristic algorithms often yield superior solutions due to their ability to handle larger problem instances efficiently. Finally, we provide guidelines for selecting appropriate optimisation techniques based on specific operational priorities and constraints in real-world transit operations.

The remainder of this paper is structured as follows: Section 2 reviews the literature on optimisation techniques and related work on the E-VSP. In Section 3, we define the specific E-VSP problem formulation used as the basis for our comparative analysis. Section 4 details the implementation methodology for each optimisation technique we consider. Section 5 outlines the experimental framework, including dataset specifications and testing procedures. Section 6 provides our results and an in-depth discussion. Finally, Section 7 concludes with key findings and future research directions.

2. Literature

Optimisation is finding the best or close-to-best solution to a problem within given constraints, according to some objective function [10]. Efficiently scheduling EVs to meet transportation demand requires optimising vehicle routes and charging schedules while considering factors like charging costs, vehicle availability, and customer service quality. Such optimisation problems have attracted significant research attention, and various solution techniques have been proposed.

When choosing an optimisation algorithm, some are better suited to some types of problems, and the choice of the appropriate method depends on the problem structure and the desired solution properties [11]. The same problem can be formulated in multiple ways, each resulting in distinct characteristics and solution techniques.

2.1. Optimisation Problem Types

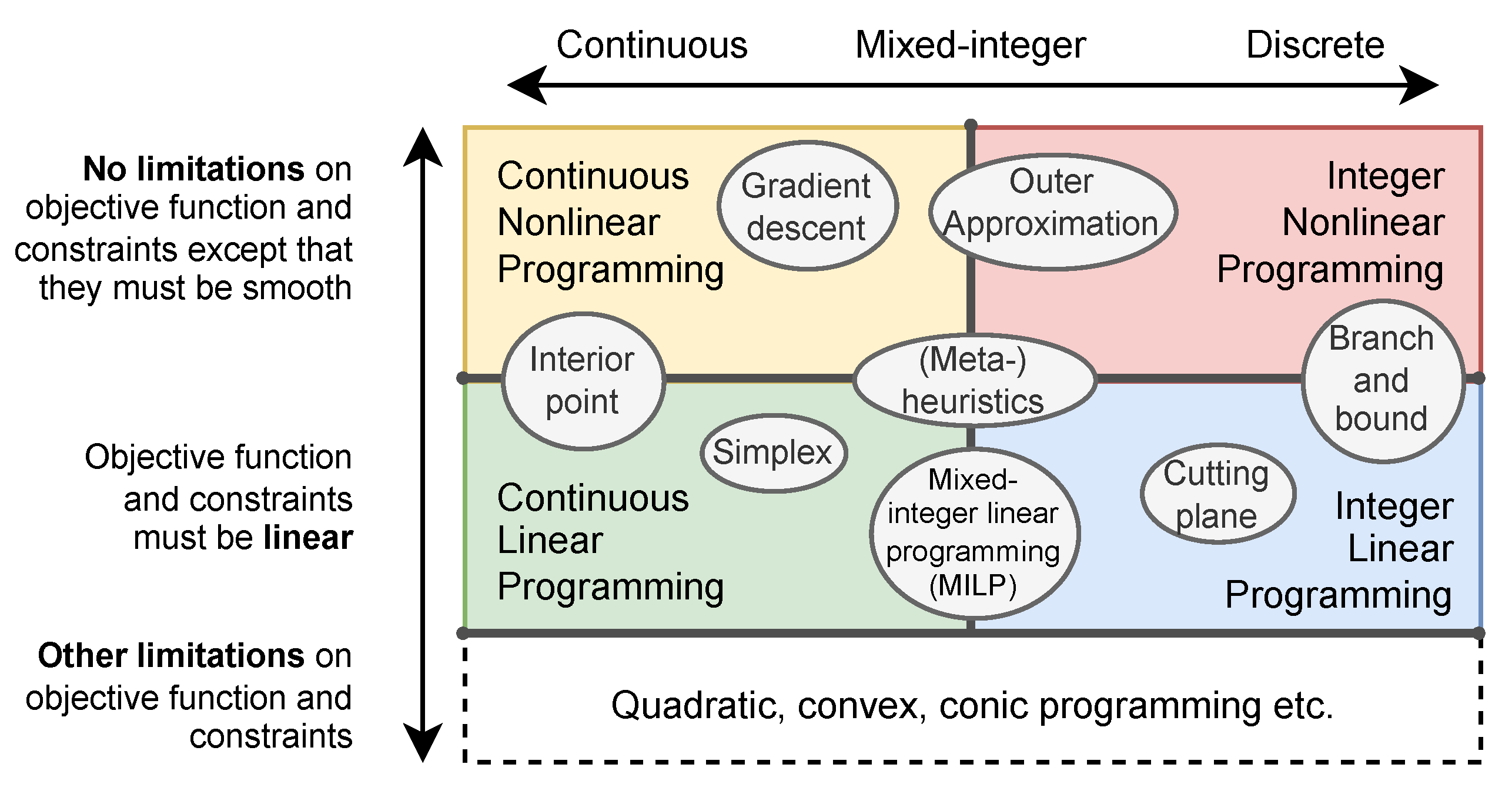
Optimisation problems can be classified based on various characteristics. Generally, optimisation problems can be categorised as being continuous or discrete, and non-linear or linear (see Figure 1). Each category has solution algorithms applicable to the specific type of optimisation problem (shown as grey circles; not exhaustive) [10].

Besides linear problems, other limitations on the objective function and constraints exist, forming additional optimisation branches such as quadratic programming, convex programming, and more.

Furthermore, optimisation problems are usually formulated with a single objective function, but multi-objective optimisation problems are also common. These are dealt with using the weighted sum approach or through analysis of the Pareto set, among others [12].

2.2. Optimisation Method Types

Nearly all optimisation methods can be categorised into exact and approximate methods. Exact methods aim to find provably optimal solutions (it is guaranteed that no other feasible solution exists that performs better according to the objective function value), while approximate methods sacrifice the guarantee of optimality for improved computation times [13]. Exact methods model the problem using precise mathematical formulations, but often become computationally intractable for large, realistic scenarios [14]. In contrast, approximate methods such as heuristics and metaheuristics use simplifications and intelligent search strategies to find high-quality solutions efficiently.

Next, we discuss the three optimisation methods used in this work.

2.2.1. Mixed Integer Linear Program

The formulation of a MILP is an exact optimisation method that guarantees optimal solutions (if feasible) through mathematical formulations with linear objective functions and constraints, where some variables must take integer values. The computational complexity of algorithms solving a MILP stems primarily from integer and binary decision variables, for which the solution algorithms require exploration through branch-and-bound search trees, leading to exponential growth in solution time as the problem size increases [15].

In the E-VSP, MILP solution algorithms face particular challenges when implementing non-linear elements such as min/max functions for battery constraints. These require additional binary variables and constraints, further increasing model complexity [5].

2.2.2. Heuristics

Heuristics are problem-specific techniques that provide good, but not necessarily optimal, solutions in a reasonable amount of time [16]. They are frequently employed when exact methods, such as linear programming, are computationally expensive, infeasible, or too time-consuming, or when near-optimal solutions are adequate for the application.

Heuristic optimisation refers to techniques that follow practical rules or guidelines to find good approximate solutions to complex optimisation problems, rather than pursuing the guaranteed optimal solution. It uses a heuristic or “rule of thumb” to guide the search towards promising areas of the solution space [17].

Heuristics can be classified into several categories. Constructive heuristics generate a complete solution from scratch by iteratively making decisions based on problem-specific criteria. Improvement heuristics start with an initial solution and try to enhance it through local modifications. Matheuristics combine mathematical programming techniques with heuristics to solve optimisation problems [18].

2.2.3. Metaheuristics

While heuristics are tailored to specific problems, metaheuristics are more generalised. In short, a metaheuristic is a higher-level procedure or framework that can be applied to various optimisation problems to guide and control an underlying heuristic or search process, aiming to find good solutions in a reasonable time. Metaheuristics often combine different heuristics and incorporate mechanisms to balance the exploration of new regions and the exploitation of promising areas [19].

Examples include genetic algorithms (GAs), which are evolutionary metaheuristics based on natural selection and genetics, maintaining a population of candidate solutions that evolve through selection, crossover, and mutation operations [20]. Simulated annealing (SA) is a probabilistic technique inspired by the annealing process in metallurgy, which employs controlled cooling to find global optima by accepting worse solutions with decreasing probability as the search progresses [21]. Ant colony optimisation (ACO) is a swarm intelligence metaheuristic inspired by the foraging behaviour of ants that uses artificial ants to construct solutions based on pheromone trails and heuristic information [22].

In contrast to heuristics, which leverage domain-specific knowledge and intuition about the problem structure, metaheuristics, being general-purpose algorithms, do not always take advantage of such problem-specific information. Consequently, metaheuristics may lead to less efficient and effective solutions than well-designed heuristics for a particular problem [17].

2.3. Related Work

Early works, such as Haghani and Banihashemi [23], addressed multiple depot vehicle scheduling problems with route time constraints, introducing heuristics that improved real-world operations by nearly 8% in vehicle numbers and 6% in costs. Reuer et al. [24] later extended traditional scheduling approaches for electric fleets by developing algorithms that intelligently add charging stops through network flow decomposition.

Mixed Integer Programming formulations have been employed to model the E-VSP with precision. Li et al. [9] developed a time–space–energy network that addresses range and refuelling constraints. Meanwhile, Janovec and Kohani [25] presented a linear model accounting for charging infrastructure limitations in urban settings.

As E-VSP instances grow in complexity, particularly with the introduction of partial charging with limited chargers and multiple vehicle types, computational challenges have led researchers toward more flexible solution approaches. Column generation techniques have emerged as a middle ground, with Tang et al. [26] extending branch-and-price frameworks to handle stochastic travel times, and van Kooten Niekerk et al. [27] developing methods that incorporate complex charging models with battery degradation considerations.

Given the NP-hard nature of the problem, heuristic approaches offer practical solutions for realistic instances. Liu et al. [28] developed an effective lexicographic method that minimised vehicle and charger requirements for battery-electric transit scheduling. Olsen et al. [29] introduced a three-phase approach using an aggregated time–space network that handled real-world timetables while optimising charging infrastructure placement. Rinaldi et al. [30] proposed a decomposition scheme that enhanced scalability for mixed fleet management, revealing that careful modelling of mixed-fleet conditions substantially improves operational savings. Wüst et al. [31] developed a fast-executing heuristic that addresses unique challenges, including temporal flexibility, multiple vehicle types, multiple depots, partial charging, and intermittent electricity supply, while achieving multi-objective optimisation of vehicles, charging stations, and trip delays.

Metaheuristic approaches have demonstrated remarkable effectiveness for larger instances. Wang and Shen [32] developed a multiple ant colony algorithm that effectively minimised both vehicle requirements and deadhead times. Genetic algorithms have shown particular promise, with Chao and Xiaohong [33] employing a modified Non-dominated Sorting Genetic Algorithm that successfully balanced capital investment and charging demand for Shanghai’s electric bus project. Liu et al. [34] demonstrated that GA-based solutions could reduce total costs by 19.6% compared with greedy algorithms when applied to Beijing’s bus systems.

Other successful metaheuristics include Wen et al.’s [35] Adaptive Large Neighbourhood Search, which provided quality solutions across instance sizes, and Teng et al.’s [36] particle swarm optimisation algorithm that effectively balanced fleet size, charging costs, and service quality. Zhou et al. [37] developed a simulated annealing approach for collaborative optimisation of vehicle scheduling and charging in mixed bus fleets.

The diverse approaches to solving the E-VSP reflect the complex trade-offs transit operators face when transitioning to electric fleets, balancing operational constraints, infrastructure requirements, and economic considerations.

3. Problem Definition

Several variations of the E-VSP exist. For this study, we investigate a simple form that is still applicable to real-life problems.

Suppose one has a set of trips that need to be completed by a specified set of electric vehicles over a certain time horizon (typically a day). Each trip needs to be completed by exactly one electric vehicle. For every trip, its departure time, departing location, and destination are fixed. In addition, a distance and time matrix must be provided. These matrices should be used to ensure that vehicle time and battery capacity constraints are not violated. In between trips, a vehicle can either travel directly to its next assigned trip or return to the depot to charge.

The optimal solution uses the minimum number of vehicles and travels the minimum total distance, without violating any constraints.

However, the best algorithm also needs to produce the optimal solution in a reasonable time.

3.1. Constraints

The following constraints must be satisfied:

• A vehicle cannot be at more than one location simultaneously.
• The battery state of charge may not be below 0% or higher than 100% at any time.
• One charger can only charge one vehicle at a time.

3.2. Assumptions

In order to simplify the problem to facilitate comparison of the various optimisation techniques, numerous assumptions are made; these are:

• There is no temporal flexibility (some E-VSP solutions provide some time variations to allow for more optimal solutions).
• The number of EVs is provided as an input parameter.
• Vehicles have a fixed efficiency in terms of distance. We choose a conservative consumption figure of 0.5 kWh/km.
• All vehicles have an identical range. For this study, we set the range to 120 km, corresponding to a battery size of 60 kWh. In reality, the battery will have a larger capacity, but by using this number, we can avoid reaching low battery states-of-charge.
• Vehicles start with a full state-of-charge.
• All vehicles’ initial location is the depot (to be provided in the input data).
• All vehicles return to the depot after their last trip.
• There are as many chargers as EVs, always to ensure charger availability.
• Chargers are located at the depot location only.
• The charge rate is fixed at 20 kW; or 0.33 kWh/min; or 0.67 km/min. Since AC chargers are rated for 22 kW, this allows for approximately ten per cent of losses.

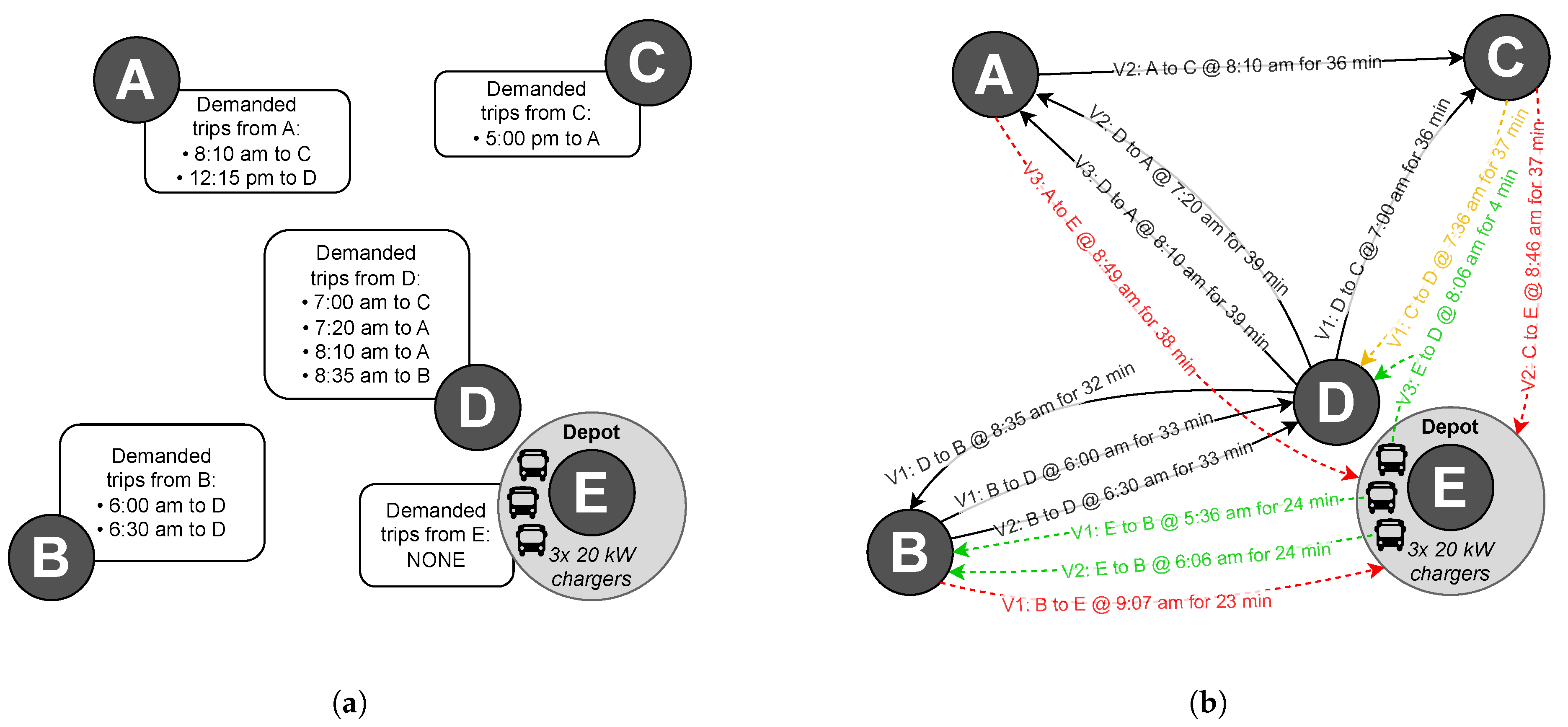
A hypothetical scenario with the problem and a partial solution is given as two maps in Figure 2a,b. Several collection/drop-off locations on these maps are shown as grey circles. Location E is a depot where three chargers are situated. Several demand service trips are departing from some locations throughout the day. At the start of the day, three electric vehicles are situated at location E—the depot. The problem is then, if some set of trips is demanded between the various locations, when should which vehicle travel from some location to another in order to satisfy all the demanded service trips while minimising the total number of vehicles required within the fleet and/or the total distance driven by all vehicles (Figure 2a)? The solution shown in Figure 2b provides the mobility of the three vehicles during the morning period. Although this is not the only solution, it is an optimal solution with minimum distance. In this example, range constraints did not come into play. However, in reality, vehicles often need to return to the depot for charging even if they are ideally located for the next trip because their battery is empty. A proper optimisation algorithm has to account for this.

3.3. Mathematical Notation

Here we present the general mathematical formulation of the problem inputs. With each optimisation technique, these will be used in addition to the technique-specific processing required to model the problem entirely as given in Section 4.

3.3.1. Sets

We define the following sets:

$$\begin{array}{}\mathrm{(1)}& T=\{1,2,\dots ,n_T\}\hfill & \hfill \mathrm{Set} \mathrm{of} \mathrm{trips}\mathrm{(2)}& V=\{1,2,\dots ,n_V\}\hfill & \hfill \mathrm{Set} \mathrm{of} \mathrm{electric} \mathrm{vehicles}\mathrm{(3)}& L=\{1,2,\dots ,n_L\}\hfill & \hfill \mathrm{Set} \mathrm{of} \mathrm{locations}\end{array}$$

3.3.2. Parameters

The following parameters are required:

• $D_{ij}$: Distance from location $i\in L$ to location $j\in L$;
• $T_{ij}$: Traveling time from location $i\in L$ to location $j\in L$;
• $s_i$: Starting time of trip $i\in T$;
• $o_i$: Starting location (origin) of trip $i\in T$, where $o_i\in L$;
• $f_i$: End location of trip $i\in T$, where $d_i\in L$;
• p: Depot location, where $p\in L$;
• $\beta =60$$\mathrm{k}\mathrm{W}\mathrm{h}$: Battery capacity of each vehicle;
• $\eta =0.5$$\mathrm{k}\mathrm{W}\mathrm{h}/\mathrm{k}\mathrm{m}$: vehicle energy consumption rate;
• $r=0.33$$\mathrm{k}\mathrm{W}\mathrm{h}/\min$: charging rate.

4. Optimisation Technique Implementation

We apply several optimisation techniques to the problem explained in Section 3. We use the sets and parameters defined in Section 3.3.1 and Section 3.3.2, respectively, unless noted otherwise.

4.1. Mixed Integer Linear Programming Technique

Formulating the E-VSP linearly presents several challenges. One complicating factor lies in allowing vehicles to return to the depot to charge between two assigned trips. The alternative would be assuming vehicles only visit the depot before their first and after their last trip, with no charging in between any trips. However, this is not a fair assumption, and we therefore allow for intermediate charging. Furthermore, if there are fewer chargers than EVs, chargers must be assigned to vehicles, complicating the problem. This is not always the case, and we therefore assume sufficient chargers to simplify the problem.

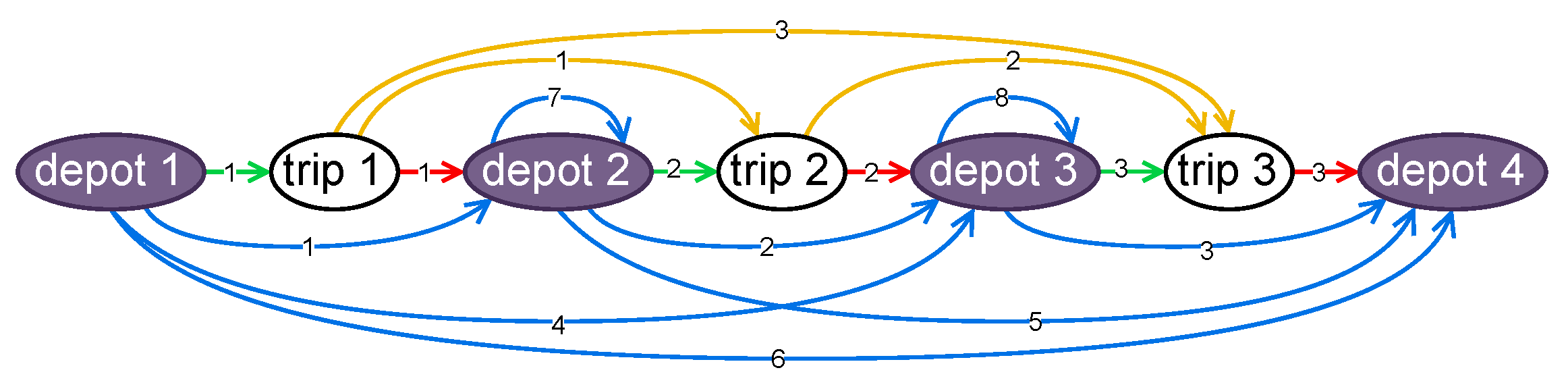
This section presents our novel formulation of an E-VSP MILP model. First, we reduce the problem size by performing preprocessing steps. Instead of using a decision variable that assigns trips to vehicles, node arcs to and from trips and the depot will be assigned to vehicles, as seen in the example in Figure 3. We use the term ‘node’ for a trip or a depot visit. A crucial step is inserting depot nodes between each trip. Then we calculate the feasibility of all node arcs and remove infeasible arcs. Finally, we use an MILP model with a decision variable that describes which vehicles perform which node arcs to solve the problem. An additional decision variable tracks the battery state-of-charge of each vehicle through its respective node arcs. The appropriate constraints will be added to ensure logical flow, that each trip is performed only once, and that the battery limits are adhered to.

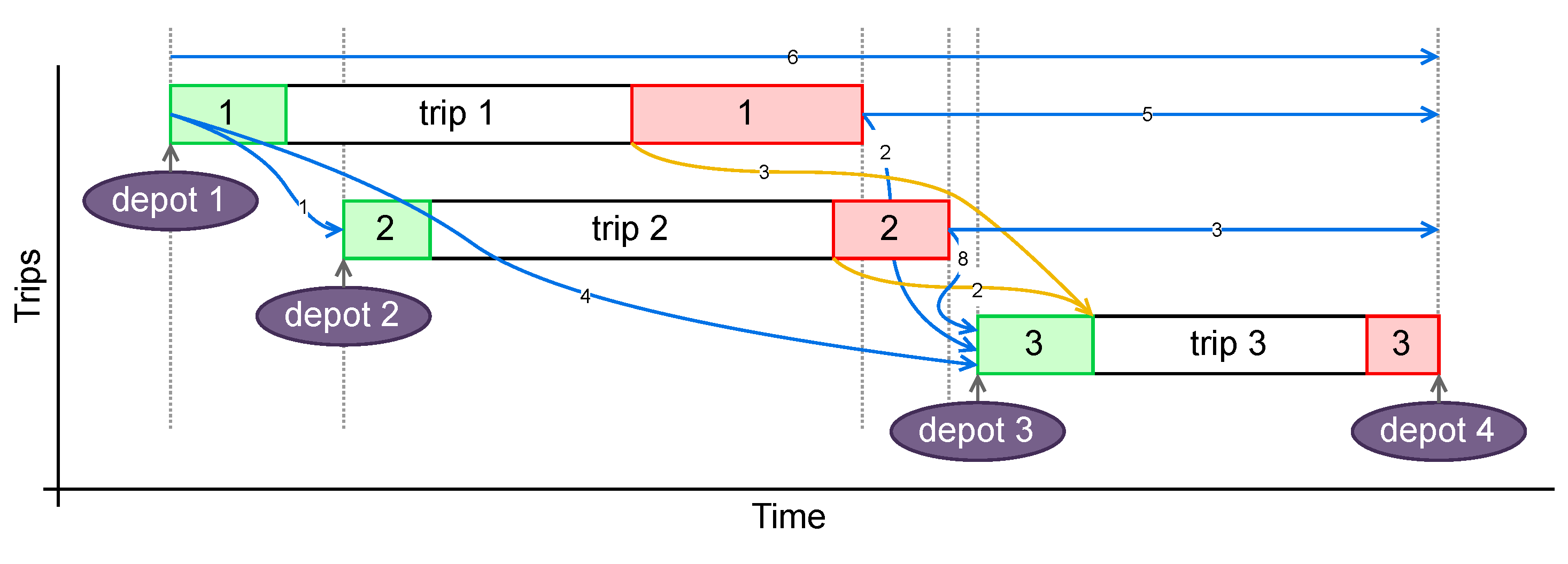
To better illustrate how the graph in Figure 3 relates to time events, we provide an example schedule in Figure 4 with representative times using the same colour scheme. For clarity, we removed node arcs that become infeasible based on the representative deadhead and trip times. This preprocessing step will be crucial to reduce the problem size.

4.1.1. Preprocessing

During the preprocessing of this formulation, several steps are taken:

• Each trip is a node. Between each node, a depot node is inserted.
• Node arcs are created. Charging node arcs are created between depot nodes. Direct deadhead node arcs are created between trip nodes. Normal deadhead node arcs are created between sequential depot-trip nodes and trip-depot nodes.
• Each node arc is processed with a brute-force approach, and if the first node finishes after the second one starts, the node arc is removed.
• If the node arc has not been removed, its energy consumption or absorption (in the case of charging) is calculated. More details regarding this step are given below.
• Optionally, depending on the objective function, the feasible node arcs’ distances are also calculated.
• Then, the decision variables and constraints are set up to allow vehicles to be assigned to the remaining node arcs.

An example of an infeasible node arc being removed (Step 3) is given in Figure 4. Direct deadhead 1 (Figure 3) is not possible since trip 2 starts before trip 1 ends and is therefore excluded in Figure 4.

Step 4 requires calculating each node arc’s energy consumption or absorption. However, this step is non-trivial. A trip consumes energy, but, unlike deadheads, it is not a node arc. To account for this, we include the trip consumption in all node arcs going to the trip. In the example in Figure 3, trip consumption of trip 3 is included in yellow node arcs 2 and 3 and green node arc 3. We later include constraints that ensure that only one of these arcs is assigned to a vehicle to ensure trip 3 is covered only once. The same counts for calculating the distances associated with each node arc.

4.1.2. Sets

In addition to the sets defined in Section 3.3.1, we define the following sets:

Set of nodes:

$$N=\{1,2,\dots ,n_N\},\mathrm{where}{n}_N=2·n_T+1$$

(4)

Set of depot nodes:

$$H=\{i\in N\mid i\mathrm{is}\mathrm{odd}\}$$

(5)

Set of trip nodes:

$$Z=\{i\in N\mid i\mathrm{is}\mathrm{even}\}$$

(6)

Set of feasible node arcs:

$$A=\left\{\right(i,j)\mid i,j\in N,i\le j,\mathrm{and}(i,j\left)\mathrm{is}\mathrm{feasible}\right\}$$

(7)

Energy consumption associated with each feasible node arc:

$$E=\{e_a\mid a\in A,e_a\in \mathbb{R}\}$$

(8)

Travel distance associated with each feasible node arc:

$$D=\{d_a\mid a\in A,d_a\in \mathbb{R}\}$$

The set of nodes (Equation (4)) is the set of trips, with depot nodes inserted between each trip and before and after the first and last trip. Accordingly, there are $2·n_T+1$ nodes. A node arc is a connection between any two nodes. The set of feasible node arcs (Equation ()) is the set of all node arcs (the set of 2-combinations of the set of nodes) with the infeasible node arcs removed. Because there are $2·n_T+1$ nodes, the number of possible node arcs can be expressed as $\left({\displaystyle \genfrac{}{}{0pt}{}{2·n_T+1}{2}}\right)$, representing the binomial coefficient $2·n_T+1$ choose 2. Node arcs are infeasible if the first node finishes after the second one starts.

4.1.3. Decision Variables

The predominant decision variable $x_{va}$ indicates which vehicles are assigned to which node arcs, as follows:

$$\begin{array}{ccc}\hfill x_{va}& =\left\{\begin{array}{cc}1,\hfill & \mathrm{if} \mathrm{vehicle} v \mathrm{is} \mathrm{assigned} \mathrm{to} \mathrm{node} \mathrm{arc} a\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\hfill & \hfill v\in V,a\in A.\end{array}$$

(9)

$w_{vn}$ indicates the remaining battery energy of vehicle v at node n:

$$\begin{array}{ccc}\hfill 1-1w_{vn}& \in [0,\beta ]\hfill & \hfill v\in V,n\in N.\end{array}$$

(10)

K represents the number of vehicles used in the solution:

$$\begin{array}{ccc}\hfill K& \in \mathbb{Z}\hfill & \hfill 1\le K\le n_V.\end{array}$$

(11)

4.1.4. Objective Function

If the objective is to minimise the number of vehicles required, we begin by specifying the maximum number; for example, it is equal to the number of trips to ensure feasibility. Then the MILP model will minimise the vehicles used with the objective function

$$\begin{array}{c}\hfill \min K.\end{array}$$

(12)

Alternatively, if the objective is to minimise the total distance travelled, the objective function becomes

$$\begin{array}{c}\hfill \min {\displaystyle \sum _{a\in A}}{d}_a·x_{va}.\end{array}$$

(13)

4.1.5. Constraints

w keeps track of a vehicle’s state-of-charge. We use less than or equal, rather than equal, to ensure that vehicles are not charged beyond their capacity. The term for node arcs to itself accounts for charging between two consecutive trips at the depot and is only subtracted when the self-arc is feasible.

$$\begin{array}{ccc}\hfill & w_{vj}\le \left\{\begin{array}{cc}{w}_{vi}-x_{v(i,j)}·e_{(i,j)}-x_{v(j,j)}·e_{(j,j)},\hfill & \mathrm{if}(j,j)\in A\hfill \\ w_{vi}-x_{v(i,j)}·e_{(i,j)},\hfill & \mathrm{if}(j,j)\notin A\hfill \end{array}\right.\hfill & \hfill \forall v\in V,\forall (i,j)\in A\end{array}$$

(14)

Each vehicle may travel to any node at most once, except if it is from itself.

$$\begin{array}{cc}{\displaystyle \sum _{i\in N\setminus \left\{j\right\}:(i,j)\in A}}{x}_{v(i,j)}\le 1\hfill & \hfill \forall v\in V,\forall j\in N\end{array}$$

(15)

Each vehicle may travel from any node at most once, except when it is to itself.

$$\begin{array}{cc}{\displaystyle \sum _{j\in N\setminus \left\{i\right\}:(i,j)\in A}}{x}_{v(i,j)}\le 1\hfill & \hfill \forall v\in V,\forall i\in N\end{array}$$

(16)

We use the following constraint to ensure proper vehicle flow. It guarantees that if any vehicle v travels to a specific node, it travels from the same node as well, and vice versa.

$$\begin{array}{cc}{\displaystyle \sum _{i\in N:(i,j)\in A}}{x}_{v(i,j)}={\displaystyle \sum _{k\in N:(j,k)\in A}}{x}_{v(j,k)}\hfill & \hfill \forall v\in V,\forall j\in N\setminus \{1,n_N\}\end{array}$$

(17)

We need an additional constraint to ensure no vehicle arrives and leaves a depot node with a charging arc. Note that $i,j,k$ are now elements of Q.

$$\begin{array}{cc}{\displaystyle \sum _{i\in Q:(i,j)\in A}}{x}_{v(i,j)}+{\displaystyle \sum _{k\in Q:(j,k)\in A}}{x}_{v(j,k)}\le 1\hfill & \hfill \forall v\in V,\forall j\in Q\end{array}$$

(18)

We employ two constraints to ensure Trip nodes are visited exactly once (depot nodes may be visited any number of times). The first constraint ensures that exactly one vehicle arrives at each trip node j.

$$\begin{array}{cc}{\displaystyle \sum _{i\in N:(i,j)\in A}}{x}_{v(i,j)}=1\hfill & \hfill \forall v\in V,\forall j\in H\end{array}$$

(19)

The following constraint ensures that exactly one vehicle departs from trip node j.

$$\begin{array}{cc}{\displaystyle \sum _{i\in N:(j,i)\in A}}{x}_{v(j,i)}=1\hfill & \hfill \forall v\in V,\forall j\in H\end{array}$$

(20)

We need an auxiliary variable, K, to represent the number of vehicles this solution uses. This variable is minimised as shown in Equation (12).

$$\begin{array}{ccc}\hfill & K\ge x_{va}·v\hfill & \hfill \forall v\in V,\forall a\in A\end{array}$$

(21)

This concludes the presentation of the MILP formulation. As shown later, it was implemented in the PuLP Python library [38] that calls the Coin-or branch-and-cut (CBC) open-source mixed integer linear programming solver [39].

Next, we discuss the second technique.

4.2. Metaheuristics Technique

We implemented a metaheuristic model of the E-VSP as described next.

4.2.1. Decision Variables

We specify the following decision variables:

$$\begin{array}{cc}{x}_t=v,\hfill & \hfill v\in V, t\in T\end{array}$$

(22)

$$\begin{array}{cc}{b}_t=\left\{\begin{array}{c}1, \mathrm{if} \mathrm{the} \mathrm{assigned} \mathrm{vehicle} \mathrm{returns} \mathrm{to} \mathrm{the} \mathrm{depot}\hfill \\ \mathrm{after} \mathrm{trip} t \mathrm{or} \mathrm{directly} \mathrm{continues} \mathrm{to} \mathrm{its} \mathrm{next} \mathrm{trip}\hfill \\ 0, \mathrm{otherwise}\hfill \end{array}\right.\hfill & \hfill t\in T\end{array}$$

(23)

4.2.2. Objective Function

We do not need to formulate the objective function as a linear function for the metaheuristic model. Instead, we can write any programmatic (Python in our case) function as long as it determines the objective value in a short time. The pseudocode in Algorithm 1 shows our implementation.

Algorithm 1 Multi-modal collaborative fusion

// Using parameters and decision variables declared in Section 3.3.2 and Section 4.2.1, respectively. 1: function ObjectiveFunction(x, b) 2:     $vehicles\leftarrow$ unique values in x 3:     $penalty\leftarrow 0$ 4:     $distance\leftarrow 0$ 5:     for $vehicle\in vehicles$ do                                                                              // Analyse feasibility of each vehicle 6:         $trips\leftarrow \{i\mid x[i]=vehicle\}$                                                               // Determine trips assigned to this vehicle 7:         $energy\leftarrow \beta$ 8:         $location\leftarrow p$ 9:         $time\leftarrow -9999$ 10:         for $t\in trips$ do                                                     // Analyse feasibility of each trip assigned to this vehicle 11:            $desiredStartTime\leftarrow s_t-T_{location,o_t}$                                                        // Start time of deadhead to this trip 12:            $penalty\leftarrow penalty+\max (0,time-desiredStartTime)$                                              // Add overlap penalty 13:            if $location==p$ then                                                                // If at depot, add possible charge energy 14:                $possibleCharge\leftarrow (desiredStartTime-time)·r$ 15:                $energy\leftarrow \min (60,energy+possibleCharge)$ 16:            end if 17:            $distance\leftarrow distance+D_{location,o_t}+D_{o_t,f_t}$                                                // Add distance of deadhead and trip 18:            $energy\leftarrow energy-D_{location,o_t}·\eta -D_{o_t,f_t}·\eta$                                    // Subtract energy of deadhead and trip 19:            if $t=trips\left[last\right]$or not $b\left[t\right]$ then                                                                             // If returning to depot 20:                $distance\leftarrow distance+D_{f_t,p}$                                                       // Add distance of deadhead back to depot 21:                $energy\leftarrow energy-D_{f_t,p}·\eta$                                                  // Subtract energy of deadhead back to depot 22:                $location\leftarrow p$ 23:                $time\leftarrow s_t+T_{o_t,f_t}+T_{f_t,p}$ 24:            else                                                                                          // If vehicle continues directly to next trip 25:                $location\leftarrow f_t$ 26:                $time\leftarrow s_t+T_{o_t,f_t}$ 27:            end if 28:            $penalty\leftarrow penalty+\max (0,-energy)$                                               // Penalty added if energy is negative 29:         end for 30:     end for 31:     if objective is distance then 32:         return $distance+penalty·10,000$       // Function returns total distance, plus penalty multiplied by a large number to ensure a feasible result 33:     else 34:         return $\left|vehicles\right|+penalty·maxVehicles$                // Function returns number of used vehicles, plus penalty multiplied by maximum number of vehicles to ensure additional vehicles are used to obtain a feasible result 35:     end if 36: end function

4.3. Heuristics Technique

We implement the heuristic algorithm we developed in [31]. The trips demanded are assigned chronologically to the vehicles according to the starting times of the trips. The predominant heuristic specifies choosing the feasible vehicle that is closest to the starting point of the next trip. If two or more vehicles are equally close, the one with the highest state of charge is chosen. Furthermore, the algorithm utilises a backtracking algorithm paradigm that resets the solution to an earlier time whenever a vehicle sits idle at a non-depot location for longer than 30 min. This ensures vehicles are used efficiently in cases where another trip starts close to where another recently ended.

A novel time–edges algorithm is employed to schedule charging. Before each trip is assigned in the main while loop of the algorithm, unoccupied chargers are assigned for the period between the previous trip’s starting time and the current trip’s starting time. If a vehicle is scheduled for charging, it occupies the charger until it is full, but its charging state can be interrupted if the vehicle is needed for a trip. In either case, the charger is immediately assigned to another vehicle (should the demand exist) after a vehicle stops charging.

Algorithm 2 contains the simplified pseudocode from [31], used for the heuristic algorithm.

Algorithm 2 Heuristic algorithm from [31].

1: Initialise variables from input (demand data, time and distance matrices etc.) 2: Sort demand data chronologically according to trip starting times 3: $currentTrip\leftarrow 0$ 4: $tripsNum\leftarrow$ get number of trips in input demand data 5: while currentTrip < tripsNum do 6:     Schedule all charging up to this trip’s starting time and store in $events$ dictionary 7:     Assign current trip to most appropriate vehicle (feasible and the closest) 8:     If no feasible vehicle could be found for $currentTrip$, increase its delay 9:     Backtrack to previous trip’s state if any vehicle has an idle time above certain threshold at a non-depot location                                                                                                                                                  // Prepare for next trip 10:     Store current state of $events$ dictionary for $currentTrip$. 11:     $currentTrip\leftarrow currentTrip+1$ 12: end while

5. Experimental Setup

First, we run each metaheuristic optimisation technique on three datasets. From that, we select the best metaheuristic algorithm and compare it to the heuristic and exact techniques.

5.1. Datasets

We used three datasets, shown in

Table 1. Dataset characteristics.

Reference	Number of Trips	Average Trip Distance (km)	Stop Locations
Random	30	20.8	15
Marabastad	65	54.1	4
Dobsonville	420	12.9	21

, to evaluate the three optimisation techniques. We use randomly generated data for the first and smallest dataset. The second and third datasets originate from passenger demand datasets from Marabastad (Pretoria) and Dobsonville (Johannesburg), respectively, in South Africa’s Gauteng province. These datasets emerged from a World Bank paratransit scheduling project where transportation specialists developed optimised diesel vehicle schedules based on demand studies and operational observations [40]. For our analysis, we excluded the deadheads. We only extracted the service trips from these schedules as the deadheads must be recalculated with every new fleet setup as part of the E-VSP.

5.2. Metaheuristics

We chose the algorithms shown in

Table 2. Candidate metaheuristic algorithms.

Label	Name	Control Parameters	Reference
SA_M	Simulated Annealing	Initial temperature: 100 Step size: 0.1	Mealpy [45]
SA_G	Simulated Annealing	Initial temperature: 10 Final temperature: 0.1	PyGMO [46]
PSO_M	Particle Swarm Optimisation	Local coefficient: 2.05 Global coefficient: 2.05 Inertia weight = 0.4	Mealpy [47]
PSO_G	Particle Swarm Optimisation	Social component: 2.05 Cognitive component: 2.05 Inertia weight: 0.7298	PyGMO
GA_M	Genetic Algorithm	Mutation probability: 0.025 Crossover probability: 0.95	Mealpy [48]
GA_G	Genetic Algorithm	Crossover probability: 0.02 Mutation probability: 0.90	PyGMO [49]
DE_M	Differential Evolution	Weighting factor: 0.1 Crossover probability: 0.9	Mealpy [50]
DE_G	Differential Evolution	Weighting factor: 0.80 Crossover probability: 0.90	PyGMO
EGA_M	Elite Multi-points Mutation Genetic Algorithm	Mutation probability: 0.025 Crossover probability: 0.95	Mealpy [48]
SEA_G	Simple Evolutionary Algorithm	Approach: (N+1)-ES	PyGMO
CRO_M	Coral Reefs Optimisation	Genetic change rate: 0.1 Initial occupation rate: 0.4	Mealpy [51]
ACOR_M	Ant Colony Optimisation	Sample count: 25 Intent factor: 0.5 Deviation-distance ratio: 1.0	Mealpy [52]

. Many algorithms are available, but we chose these specific algorithms for their popularity and relative ease of implementation. We focused on evolutionary algorithms after observing experimentally that they tend to perform better. Furthermore, a review by Rajwar et al. [41] of 540 metaheuristics concluded that most new generation algorithms have little originality and resemble existing algorithms, mainly particle swarm optimisation and genetic algorithms. We also included a trajectory-based metaheuristic to avoid limiting the study to population-based algorithms. We selected simulated annealing due to its wide historical use and simplicity of implementation [42]. We test the metaheuristic algorithms implemented with two popular Python (version 3.10) libraries (Mealpy 3.0.1 [43] and PyGMO 2.18.0 [44]). We include the most important control parameters of each algorithm in a separate column as reference. In most cases, however, we use the library’s defaults as we have experimentally found them to produce the best results, or make little difference. The library and original work’s citation are provided in the Reference column. For generation-based metaheuristics, we use 500 iterations and a population size of 100 for the Random and Marabastad datasets, and 2000 iterations and population size of 200 for the Dobsonville dataset.

5.3. Comparison of Optimisation Techniques

The processing time of the optimisation techniques is compared by running each technique on increasing problem sizes and plotting the results in Section 6.2.1. Reduced problem sizes are constructed using a random, but constant subset of trips from the original dataset. To compare minimisation of vehicle usage (Section 6.2.2) and total schedule distance (Section 6.2.3), we use each optimisation technique on each dataset and tabulate the results.

6. Results

Before we compare the three optimisation techniques, we first find an appropriate metaheuristic algorithm.

6.1. Metaheuristic Algorithms

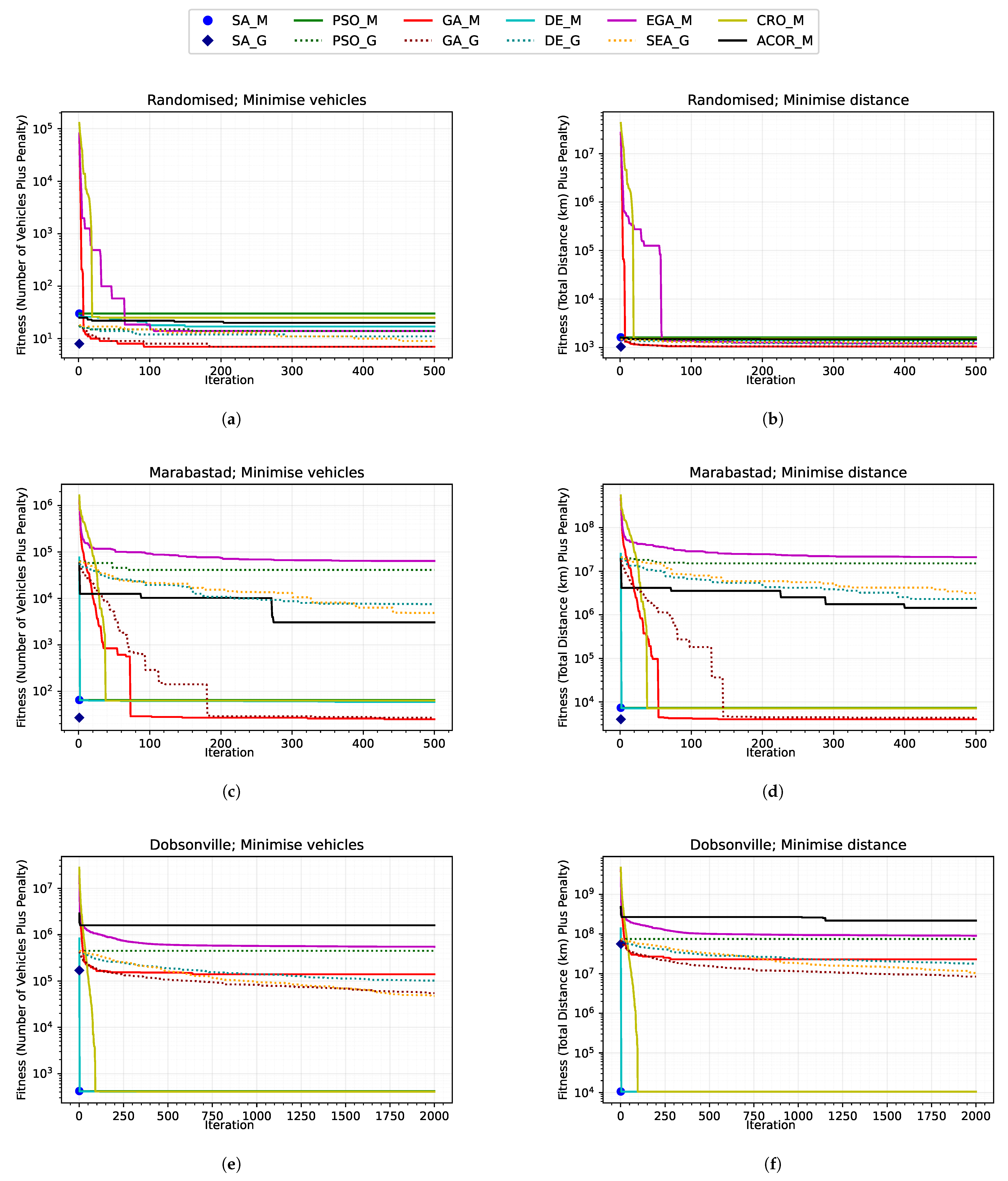
The results of comparing the various metaheuristic algorithms are shown in Figure 5. It contains six graphs presenting the fitness (objective) value as a function of the iteration number. The graphs on the left show the results of optimising to minimise the number of vehicles, while those on the right show the results of optimising to minimise the total schedule distance. The three rows correspond to the three datasets, as explained in Section 5.1.

First, we analyse the results in the left part of Figure 5, where the objective is to minimise the number of vehicles. The plots show the progress of the objective function value (fitness) against the number of iterations. For the Random and Marabastad datasets, we set $n_V$, the number of available vehicles, to 30, while Dobsonville had 100. This means any candidate solution with a fitness value above these values incurred penalties. Therefore, the candidate solution is infeasible. For the Random and Marabastad datasets, the only algorithms that found feasible solutions were genetic algorithms and PyGMO’s implementation of simulated annealing.

The results on the right demonstrate similar convergence properties, even with a different objective: minimising the total distance driven. Once again, only the genetic algorithms and simulated annealing showed promise.

Since Mealpy’s genetic algorithm (GA_M) performed more consistently and found feasible solutions quickest, we chose it for further comparison with other optimisation techniques.

6.2. Comparison of Optimisation Methods

Next, we compare the results of the different optimisation techniques in terms of several metrics.

6.2.1. Processing Time

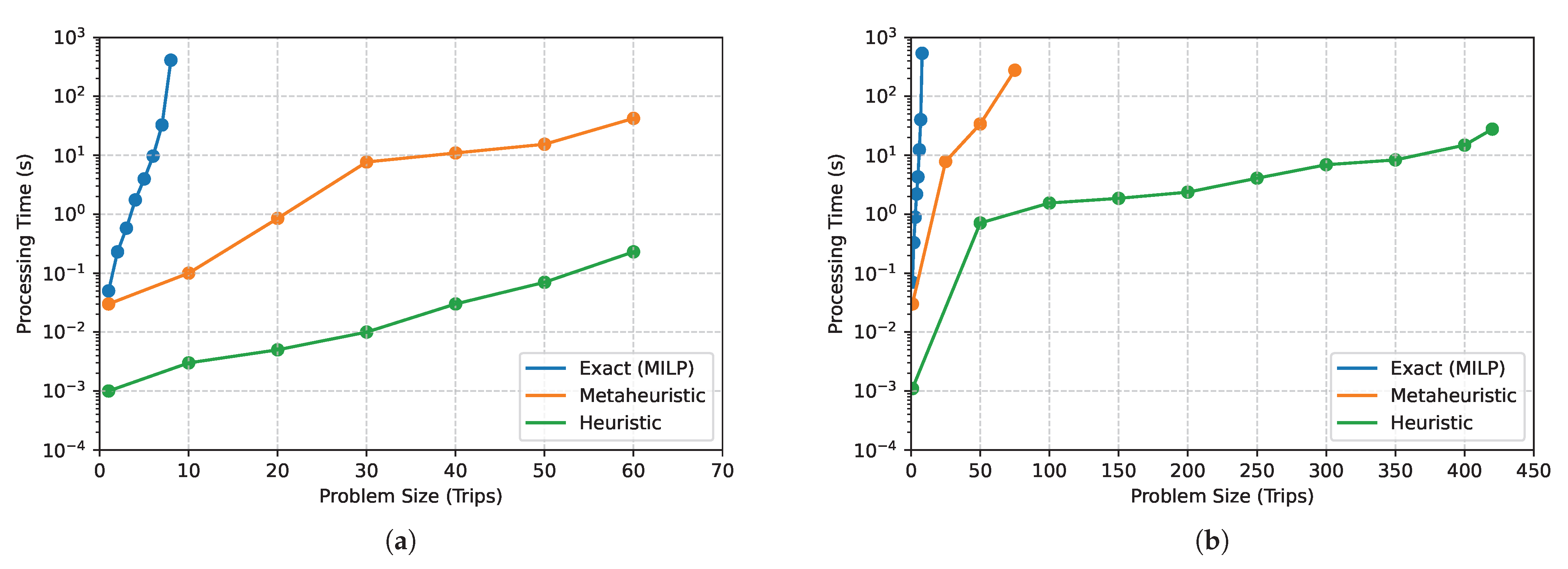
After running the various algorithms on different problem sizes, the difference in computational efficiency becomes clear, as indicated in Figure 6.

The worst performer is the exact model, which shows exponential growth in processing time, compared with the problem size. It cannot calculate an optimal solution for 10 trips in under 1000 s.

Although the metaheuristic and heuristic algorithms seem to have the same rate of time increase as the problem size increases, it is not the case. The processing time of the metaheuristic algorithm grows at a steady rate and seems to reach a ceiling where it stops finding feasible solutions when the problem size becomes large. However, the heuristic algorithm usually finishes processing a solution in under one second, so its recorded times are less representative. This is illustrated in Figure 6b with the right-most datapoint, where the heuristic algorithm finds its solution for the 420-trip Dobsonville problem in 28 s. The heuristic algorithm’s speed depends on the problem characteristics. For instance, if the trip start times are close to each other, it will take considerably longer, due to the backtracking paradigm of the heuristic algorithm. This allows it to solve exceptionally large instances (over 1000 trips), as long as they are sufficiently spaced out.

6.2.2. Minimisation of Vehicle Usage

In

Table 3. Number of vehicles of optimised solutions.

	Dataset	Randomised	Marabastad	Dobsonville
Algorithm
MILP with CBC		no solution	no solution	no solution
Metaheuristic		7	25	no solution
Heuristic		5	23	45
Alt. Heuristic 1		6	23	49

¹ Alternative setting for heuristic algorithm, allowing vehicles to stay at non-depot locations for longer.

, we compare the best solutions with minimised vehicle usage between the remaining optimisation techniques on different datasets. The entries labelled ‘no solution’ indicate that the algorithm could not find a solution for the given cases.

The heuristic algorithm consistently finds solutions using fewer electric vehicles to cover the same demand. Since the capital investment costs of even one EV are rather sizeable, it is critical to find the solution with minimum vehicle usage. The exact algorithm found no feasible solutions in a reasonable time (less than an hour) for any of the datasets, and the metaheuristic algorithm found no solution for the Dobsonville dataset.

6.2.3. Minimisation of Total Distance

When optimising for the minimum distance schedule, we find the results tabulated in

Table 4. Total distances (km) of optimised solutions.

	Dataset	Randomised	Marabastad	Dobsonville
Algorithm
MILP with CBC		no solution	no solution	no solution
Metaheuristic		1045	4022	no solution
Heuristic		1443	6034	7345
Alt. Heuristic 1		1132	4470	6846

¹ Alternative setting for heuristic algorithm, allowing vehicles to stay at non-depot locations for longer.

.

When optimising the total distance, the metaheuristic algorithm performs between 38% and 50% better than the heuristic algorithm and between 8% and 11% better than the alternative heuristic algorithm. However, this should be put in context. A key point for the heuristic is that vehicles may not stay at non-depot locations for longer than 30 min. This is why the distances (especially when the threshold is not relaxed) are worse. The vehicles return to the depot between the morning and afternoon peaks, accumulating more distance. However, it would be highly unusual to leave fleet vehicles at non-depot locations for such a long time, and therefore, the solutions by the heuristic (although longer) account for real-life factors better. Additionally, the heuristic optimises simultaneously to minimise the number of vehicles and the total schedule distance. In this case, then, the solution provided by the heuristic algorithm in Table 3 and Table 4 is the same underlying solution, unlike the distinct solutions of the metaheuristic algorithm, which are only optimised for one objective function. This can be overcome by performing multi-objective optimisation as explained at the end of Section 2.1. Once again, the metaheuristic finds no feasible solution for the large Dobsonville dataset, and the exact algorithm found no feasible solutions for any of the datasets.

6.2.4. Additional Features

Generally, a real-life E-VSP is more complex than the simplified version we defined in Section 3. There exist cases where most of our assumptions are debatable. For example, vehicles often operate from multiple depots, vehicles may have varying specifications or even consist of ICE vehicles and EVs, and different chargers usually have different charging rates.

The heuristic algorithm used in this article already provides for many of these variations, with virtually no impact on the processing time. Although it remains to be proven how good the solutions are using these additional features. Adding these features to the metaheuristic algorithm will be possible, but will impact the already relatively long processing time, especially if additional decision variables need to be added. As for the MILP model, it would be difficult to formulate the problem linearly with additional complexities such as those discussed, and this would worsen the computational efficiency further.

6.2.5. Formulation and Implementation Complexity

Since we have worked on each optimisation technique, we can provide a subjective overview of the complexity involved with their formulation and implementation. This is given in the summary of results in

Table 5. Summary of results.

	MILP with CBC	Metaheuristic	Heuristic
Maximum problem size (trips)	<10	<100	>1000
Minimising vehicles	Ideal	Good	Best
Minimising total distance	Ideal	Best	Good
Feature set	Bad	Moderate	Rich
Formulation complexity	Complex	Easy	Moderate
Implementation complexity	Moderate	Easy	Complex

.

6.2.6. Summary

The summary in Table 5 presents a condensed version of all the results presented so far.

7. Conclusions

This study compared exact, metaheuristic, and heuristic optimisation techniques for the E-VSP. Our analysis reveals trade-offs between solution quality, computational efficiency, and practical applicability across these approaches.

The exact MILP approach, while theoretically capable of providing optimal solutions, demonstrated computational limitations. For small problem instances of 10 trips, processing times of the CBC solver exceeded 1000 s, making this approach impractical for real-world transit operations where schedules typically contain hundreds of trips. This confirms the NP-hard nature of the VSP and illustrates why exact methods, despite their mathematical guarantees, have limited practical utility in operational settings.

Among metaheuristic approaches, genetic algorithms and simulated annealing outperformed other techniques. While metaheuristics achieved better distance minimisation than heuristics on smaller datasets, they struggled with feasibility on larger problem instances exceeding 100 trips. This scalability limitation represents a barrier to their adoption in transit systems.

The heuristic approach emerged as a viable solution method, processing the 420-trip Dobsonville dataset in 37 s. It found solutions requiring fewer vehicles than metaheuristic approaches across all datasets and demonstrated good scalability. While its distance minimisation performance appeared inferior, this reflected realistic operational constraints regarding vehicle positioning.

Our findings suggest that the choice of optimisation technique for the E-VSP should be guided by problem size and specific operational priorities. For small fleets, metaheuristic approaches may offer distance savings worth their computational cost. However, for typical urban transit operations, the heuristic approach offers a suitable combination of solution quality, computational efficiency, and adaptability to real-world constraints.

Future research should focus on improving metaheuristic scalability through problem decomposition and developing hybrid approaches that combine the strengths of multiple optimisation paradigms. The heuristic algorithm, while currently fast, performs a highly focused, narrow search and could be enhanced to explore a larger portion of the solution space. Machine learning represents a promising middle ground between heuristic and metaheuristic optimisation techniques and warrants further investigation.