Energy and Spectral Efficiency Analysis for UAV-to-UAV Communication in Dynamic Networks for Smart Cities

Highlights

What are the main findings?

• The study provides a comprehensive analysis of UAV-to-UAV communication, focusing on energy and spectral efficiency across multiple frequency bands (2.4 GHz, 5.8 GHz, 28 GHz, and 60 GHz) in dynamic smart city environments.
• Results indicate that sub-6 GHz frequencies offer superior energy efficiency (up to 0.15 bits/Joule). At the same time, millimetre-wave bands (28 GHz and 60 GHz) suffer from higher path loss and reduced efficiency.

What are the implications of the main findings?

• Smart city UAV networks should adopt multi-band communication strategies, leveraging sub-6 GHz for long-range and energy-efficient connectivity while utilising mmWave bands for high-data-rate applications in close-proximity scenarios.
• Adaptive trajectory planning, dynamic frequency selection, and machine-learning-driven power control are essential to optimising UAV network efficiency, ensuring sustainable and high-performance communication in urban environments.

Abstract

Unmanned Aerial Vehicles (UAVs) are integral to the development of smart city infrastructures, enabling essential services such as real-time surveillance, urban traffic regulation, and cooperative environmental monitoring. UAV-to-UAV communication networks, despite their adaptability, have significant limits stemming from onboard battery constraints, inclement weather, and variable flight trajectories. This work presents a thorough examination of energy and spectral efficiency in UAV-to-UAV communication over four frequency bands: 2.4 GHz, 5.8 GHz, 28 GHz, and 60 GHz. Our MATLAB R2023a simulations include classical free-space path loss, Rayleigh/Rician fading, and real-time mobility profiles, accommodating varied heights (up to 500 m), flight velocities (reaching 15 m/s), and fluctuations in the path loss exponent. Low-frequency bands (e.g., 2.4 GHz) exhibit up to 50% reduced path loss compared to higher mmWave bands for distances exceeding several hundred meters. Energy efficiency (${\eta }_e$) is evaluated by contrasting throughput with total power consumption, indicating that 2.4 GHz initiates at around 0.15 bits/Joule (decreasing to 0.02 bits/Joule after 10 s), whereas 28 GHz and 60 GHz demonstrate markedly worse ${\eta }_e$ (as low as ${10}^{-3}$–${10}^{-4}\mathrm{bits}/\mathrm{Joule}$), resulting from increased path loss and oxygen absorption. Similarly, sub-6 GHz spectral efficiency can attain $4\times {10}^{-12}\mathrm{bps}/\mathrm{Hz}$ in near-line-of-sight scenarios, whereas 60 GHz lines encounter significant attenuation at distances above 200–300 m without sophisticated beamforming techniques. Polynomial-fitting methods indicate that the projected ${\eta }_e$ diverges from actual performance by less than 5% after 10 s of flight, highlighting the feasibility of machine-learning-based techniques for real-time power regulation, beam steering, or multi-band switching. While mmWave UAV communication can provide significant capacity enhancements (100–500 MHz bandwidth), energy efficiency deteriorates markedly without meticulous flight planning or adaptive protocols. We thus advocate using multi-band radios, adaptive modulation, and trajectory optimisation to equilibrate power consumption, ensure connection stability, and meet high data-rate requirements in densely populated, dynamic urban settings.

1. Introduction

Unmanned Aerial Vehicles (UAVs), also known as drones, have become essential instruments in the advancement of smart cities [1,2]. Their versatility, mobility, and cost-efficiency render them essential for various applications, such as real-time surveillance, environmental monitoring, disaster management, traffic analysis, and logistics [3]. In these scenarios, UAVs must operate collaboratively, exchanging essential data in real time to ensure efficient coordination [4]. The necessity for this has elevated UAV-to-UAV communication as a primary focus of research within smart city networks [5].

Effective communication among UAVs presents significant challenges owing to the dynamic characteristics of their networks. Unmanned Aerial Vehicles (UAVs) generally function in environments that exhibit significant variability, marked by mobility, alterations in altitude, and variations in distances between UAVs [6,7]. External factors, including weather conditions (e.g., rain, fog, wind) and urban obstacles (e.g., buildings, towers), can significantly affect the quality of the communication link. The dynamic conditions require the development of effective and adaptable communication strategies that guarantee reliable connectivity and optimise network resources [8].

Many UAVs are limited by onboard battery capacity, and power-intensive mmWave amplifiers can considerably diminish flight duration [9,10]. Actual amplifiers function at suboptimal efficiency, frequently requiring sophisticated cooling mechanisms or more substantial power systems [11]. High-frequency antennas (e.g., 28 GHz, 60 GHz) need densely arranged arrays to attain directional gains. This poses challenges for tiny UAV platforms, where weight, size, and cost limits are critical design factors [12]. In actuality, UAVs may encounter significant fluctuations in signal strength owing to movement, interference, or impediments. The front-end hardware must efficiently manage dynamic range to prevent saturation or noise-limited performance, necessitating additional design trade-offs in gain control and low-noise amplification [13].

High-rise structures and narrow thoroughfares provide multipath-rich environments, resulting in Rayleigh or even specular reflection conditions. Path loss models must occasionally integrate building density, material attenuation, and diffraction around obstacles [14]. The 2.4 GHz and 5.8 GHz bands are significantly utilised by Wi-Fi and IoT devices, resulting in heightened collisions and spectral congestion. Simultaneously, the 28 GHz and 60 GHz bands may see reduced congestion but increased atmospheric and rain-induced attenuation. Moving cars, human traffic, or temporary structures can provide “dynamic obstacles”, occasionally obstructing line-of-sight pathways, particularly critical at millimetre-wave frequencies. UAVs must modify flight paths or transfer connections to ensure reliable communication [15].

Collectively, these problems underscore the imperative for UAV communication systems capable of dynamically adjusting parameters such as transmission power, beamforming angles, and frequency selection [16]. For example, mission-critical UAV networks may utilise multi-band radios, transitioning to a lower frequency in the event of significant obstruction at 28 GHz or 60 GHz. Regulatory compliance mandates flying altitudes and allowable transmission powers, hence complicating the design of UAV swarm protocols [17].

Two essential metrics that characterise the performance of UAV-to-UAV communication are energy efficiency and spectral efficiency [18,19]. Energy efficiency quantifies the successful transmission of bits relative to the energy consumed, a critical factor for UAVs with constrained onboard battery capacity [20,21]. Spectral efficiency assesses the effectiveness of spectrum utilisation, which is crucial due to the rising demand for spectra in contemporary wireless communication systems [22,23]. Achieving sustainable and scalable UAV communication systems in smart cities necessitates a balance between these two metrics.

The UAV-to-UAV communication link is further influenced by several physical and environmental parameters, including the following:

1.

Path Loss: Signal attenuation due to distance and environmental factors [12,18,24,25].

2.

Multipath Fading: Signal variations caused by reflections, diffractions, and scattering in urban environments [18,26].

3.

Weather Conditions: Rain, fog, and atmospheric turbulence can introduce additional attenuation and delay [27,28].

4.

Interference: Shared spectrum usage in urban areas can lead to high levels of interference, affecting signal quality [18,29].

It is essential to analyse the energy and spectral efficiency of UAV-to-UAV communication in realistic operational conditions [12,30]. Although numerous studies have investigated UAV communication for particular applications, there is a lack of comprehensive assessments of efficiency metrics in dynamic environments, considering the impacts of mobility, altitude changes, and environmental variables.

This study seeks to fill this gap through a comprehensive analysis of UAV-to-UAV communication within dynamic networks. This study utilises MATLAB simulations to assess critical performance metrics, including path loss, Signal-to-Noise Ratio (SNR), Bit Error Rate (BER), energy and spectral efficiency, and signal strength across various conditions [7,31]. The following contributions are defined:

• An evaluation of energy efficiency and spectral efficiency across different UAV altitudes, distances, and weather conditions, utilising realistic multipath fading models such as Rayleigh and Rician fading to accurately simulate urban environments.
• This study examines the trade-offs between energy efficiency and spectral efficiency, offering insights into the design of communication protocols that effectively balance these two metrics.
• Strategies for enhancing UAV communication systems in smart cities, focusing on scalability, sustainability, and operational reliability.

This study addresses challenges in UAV communication within smart cities, providing a framework for the design of more efficient and resilient networks. This study’s findings are pertinent for academic researchers, practitioners, and policymakers involved in the implementation of UAV-based solutions in urban settings. This analysis facilitates the development of more efficient and sustainable UAV networks that can address the requirements of future smart cities. Section 2 presents the system model for UAV-to-UAV communication within dynamic networks in smart cities. Section 3 presents a mathematical analysis of receiver sensitivity considerations for UAV Communication. Section 4 presents an analysis of energy efficiency in UAV-to-UAV communication within dynamic networks designed for smart cities. Section 5 provides the mathematical formulation for spectral analysis. Section 6 presents the simulation and analytical validation of the proposed framework, while Section 7 summarises the conclusions drawn from the findings.

2. System Model for UAV-to-UAV Communication in Dynamic Networks for Smart Cities

This section presents a detailed system model for UAV-to-UAV communication within dynamic networks, accounting for mobility, environmental changes, and adaptive communication methods [30]. The model incorporates spatial and temporal variations in network topology and channel quality, utilizing advanced mathematical frameworks to represent real-world dynamics. The interaction among mobility, path loss, fading, and beamforming is highlighted to offer a comprehensive understanding of UAV communication in smart city applications [13].

Figure 1 depicts the positions of UAVs within a three-dimensional space, highlighting the communication dynamics among UAVs under different distances, altitudes, and mobility conditions. The temporal variations in UAV positions significantly influence path loss, fading, and received signal power, thereby requiring real-time adjustments to ensure communication quality is upheld.

The theoretical model encompasses critical elements like path loss and fading; nevertheless, the practical implementation of UAV communication in smart cities encounters more real-world limitations that require meticulous design and modification. Unmanned Aerial Vehicles (UAVs) must function within frequency bands allocated by local or international regulatory authorities (e.g., FCC, ETSI). Variations in frequency availability and allowable transmit powers between areas influence connection budgets and coverage. Moreover, urban settings frequently establish altitude restrictions or designated air lanes for UAV operations. These legal restrictions may reduce altitude ranges or necessitate that UAVs adhere to Line-of-Sight (LoS) trajectories, thereby affecting the applicability of free-space or fading models. UAV operators may need to comply with stringent safety regulations (e.g., collision avoidance, battery redundancy), and data collecting may be governed by privacy legislation in highly populated areas. These non-technical limits may indirectly restrict the duration in which UAVs remain airborne or the types of antennas and technology permitted for use.

2.1. Channel Model for UAV-to-UAV Communication

In the face of real-world constraints, we structure our channel and mobility modelling as follows:

• Path Loss and Fading: We integrate classical models with scenario-based parameters for urban settings. This guarantees the inclusion of both Line-of-Sight (LoS) and Non-Line-of-Sight (NLoS) circumstances characteristic of urban environments.
• Mobility Profiles: The locations of UAVs $(x_i,y_i,h_i)$ change over time, imitating flight corridors or random waypoint trajectories. Distances $d_{i,j}\left(t\right)$, therefore, transform into time-dependent functions, illustrating the influence of altitudes and horizontal velocities on received signal strength.

The communication link between two UAVs, $U_i$ and $U_j$, is represented by a complex channel coefficient $h_{i,j}$ that accounts for both large-scale fading (path loss) and small-scale fading:

$$h_{i,j}=\sqrt{{\beta }_{i,j}}·h_{\mathrm{small}\mathrm{scale}},$$

(1)

where:

• ${\beta }_{i,j}$ represents the large-scale path loss, which depends on the distance between UAVs and environmental attenuation;
• $h_{\mathrm{small}\mathrm{scale}}$ captures small-scale fading, modelled as a complex Gaussian random variable $h_{\mathrm{small}\mathrm{scale}}\sim \mathcal{CN}(0,1)$.

2.1.1. Path Loss Model

The large-scale path loss ${\beta }_{i,j}$ is derived using the free-space path loss model with an exponential attenuation factor:

$${\beta }_{i,j}={\left({\displaystyle \frac{\lambda }{4\pi d_{i,j}}}\right)}^{2}exp(-\alpha d_{i,j}),$$

(2)

where:

• $\lambda ={\displaystyle \frac{c}{f}}$ is the wavelength of the transmitted signal, with c is the speed of light, and f is the carrier frequency;
• $d_{i,j}$ is the distance between UAVs $U_i$ and $U_j$;
• $\alpha$ is the environmental attenuation coefficient.

For a time-varying network, where the distance between UAVs evolves dynamically, the cumulative path loss is expressed as:

$${\overline{\beta }}_{i,j}\left(t\right)={\int }_{t_0}^t{\left({\displaystyle \frac{\lambda }{4\pi d_{i,j}\left(t^{\prime }\right)}}\right)}^{2}exp(-\alpha d_{i,j}\left(t^{\prime }\right))d{t}^{\prime },$$

(3)

where $t^{\prime }$ denotes the time parameter, and $t_0$ is the initial time.

2.1.2. Distance Model in 3D Space

The distance $d_{i,j}$ between two UAVs is determined by their 3D spatial coordinates $(x_i,y_i,h_i)$ and $(x_j,y_j,h_j)$:

$$d_{i,j}=\sqrt{{(x_i-x_j)}^2+{(y_i-y_j)}^2+{(h_i-h_j)}^2},$$

(4)

where $h_i$ and $h_j$ are the altitudes of UAVs $U_i$ and $U_j$, respectively. This model captures both horizontal and vertical separations, critical in UAV communication scenarios with varying altitudes.

2.1.3. Small-Scale Fading Model

Small-scale fading is characterized by Rayleigh or Rician distributions, depending on the presence of a Line-of-Sight (LoS) component. For Rayleigh fading, the magnitude of the fading coefficient follows:

$$f_{|h_{i,j}|}\left(x\right)={\displaystyle \frac{x}{{\sigma }^2}}exp\left(-{\displaystyle \frac{x^2}{2{\sigma }^2}}\right),x\ge 0,$$

(5)

where ${\sigma }^2$ is the variance of the fading envelope.

In Rician fading, the Probability Density Function (PDF) is given by the following:

$$f_{|h_{i,j}|}\left(x\right)={\displaystyle \frac{x}{{\sigma }^2}}exp\left(-{\displaystyle \frac{x^2+{\nu }^2}{2{\sigma }^2}}\right)I_0\left({\displaystyle \frac{x\nu }{{\sigma }^2}}\right),$$

(6)

where:

• $\nu$ is the peak amplitude of the LoS component;
• $I_0(·)$ is the modified Bessel function of the first kind.

2.2. Beamforming and Adaptive Communication

To enhance communication reliability, each UAV employs a Uniform Rectangular Array (URA) for beamforming. The steering vector for an M-element URA is given by:

$${\mathbf{a}}_{\mathrm{UAV}}(\theta ,\varphi )={\displaystyle \frac{1}{\sqrt{M}}}\sum _{m_x=0}^{M_x-1}\sum _{m_y=0}^{M_y-1}{e}^{j2\pi {\displaystyle \frac{m_{x}d}{\lambda }}sin\theta cos\varphi }{e}^{j2\pi {\displaystyle \frac{m_{y}d}{\lambda }}sin\theta sin\varphi },$$

(7)

where:

• $m_x$ and $m_y$ are the indices for horizontal and vertical array elements, respectively;
• $\theta$ and $\varphi$ are the elevation and azimuth angles of the transmitted beam;
• d is the element spacing within the array.

2.3. Received Power with Beamforming

The received power at UAV $U_j$ from UAV $U_i$, considering beamforming, is modelled as:

$$P_{r_{i,j}}\left(t\right)=P_{t_i}{\left|{\int }_{t_0}^t{\mathbf{h}}_{i,j}^H\left(t^{\prime }\right){\mathbf{a}}_{\mathrm{UAV}}\left(t^{\prime }\right)d{t}^{\prime }\right|}^2,$$

(8)

where:

• $P_{t_i}$ is the transmit power of UAV $U_i$;
• ${\mathbf{h}}_{i,j}\left(t^{\prime }\right)$ is the time-varying channel response matrix;
• ${\mathbf{a}}_{\mathrm{UAV}}\left(t^{\prime }\right)$ is the adaptive steering vector.

2.4. Mobility and Dynamic Adaptation

The mobility of UAVs is governed by continuous trajectory equations:

$${\displaystyle \frac{d}{dt}}\left[\begin{array}{c}{x}_i\\ y_i\\ h_i\end{array}\right]=\left[\begin{array}{c}{v}_x\\ v_y\\ v_h\end{array}\right],$$

(9)

where $v_x$, $v_y$, and $v_h$ are the velocity components in the x, y, and h directions, respectively.

UAVs adjust their beamforming angles and power allocation dynamically to maintain optimal communication based on the instantaneous SNR.

$${\mathrm{SNR}}_{i,j}={\displaystyle \frac{P_{t_i}{G}_t{G}_r}{N_{0}B·{\overline{\beta }}_{i,j}\left(t\right)}},$$

(10)

where $G_t$ and $G_r$ are the antenna gains at the transmitter and receiver.

This model offers a framework for the analysis of UAV-to-UAV communication within dynamic smart city networks.

3. Receiver Sensitivity Considerations for UAV Communication: Mathematical Analysis

Receiver sensitivity basically determines the minimal signal level observable by a UAV’s radio front-end, enabling reliable decoding of incoming waveforms while sustaining an acceptable Bit Error Rate (BER). If the received power $P_r$ diminishes below the threshold $P_{\mathrm{sens}}$, the connection becomes inoperative irrespective of other channel characteristics. This section elaborates on common formulations by incorporating advanced mathematical analyses that demonstrate the interaction of sensitivity with channel models, path loss, interference, and network-level performance in a UAV-to-UAV system.

3.1. Baseline Formulation of Receiver Sensitivity

Receiver sensitivity, often expressed in dBm, integrates thermal noise, bandwidth, and supplementary hardware elements (such as noise figure) with the necessary signal-to-noise ratio margin. An expression in decibels is simplified as follows:

$$P_{\mathrm{sens}}\approx -174\mathrm{dBm}/\mathrm{Hz}+10{log}_{10}\left(B\right)+\mathrm{NF}+{\mathrm{SNR}}_{\mathrm{margin}},$$

(11)

where

• The constant, $-174\mathrm{dBm}/\mathrm{Hz}$, is the thermal noise power density at $290\mathrm{K}$;
• B is the system bandwidth in Hz;
• $\mathrm{NF}$ (dB) is the receiver noise figure quantifying additional amplifier and mixer noise;
• ${\mathrm{SNR}}_{\mathrm{margin}}$ (dB) is the minimal SNR required for the target BER under the chosen modulation and coding scheme.

This $P_{\mathrm{sens}}$ indirectly establishes the maximum allowable path loss between two UAVs. For example, if $\mathrm{NF}=5\mathrm{dB}$, $B=20\mathrm{MHz}$, and ${\mathrm{SNR}}_{\mathrm{margin}}=10\mathrm{dB}$, then $P_{\mathrm{sens}}\approx -90\mathrm{dBm}$. Consequently, a UAV connection must sustain $P_r\ge -90\mathrm{dBm}$ to provide dependable communication.

3.2. Time-Varying Receiver Sensitivity Margin

The mobility of UAVs, including variations in altitude $h\left(t\right)$ and horizontal position, along with dynamic channel conditions, might cause fluctuations in the effective sensitivity margin. Define the instantaneous margin $\Delta \left(t\right)$ as follows:

$$\Delta \left(t\right)=P_r\left(t\right)-P_{\mathrm{sens}}.$$

(12)

Upon differentiating $\Delta \left(t\right)$ with respect to t, we obtain the following equation:

$${\displaystyle \frac{d\Delta \left(t\right)}{dt}}={\displaystyle \frac{d{P}_r\left(t\right)}{dt}}-\underset{\approx 0(\mathrm{constant}\mathrm{design})}{\underbrace{{\displaystyle \frac{d{P}_{\mathrm{sens}}}{dt}}}},$$

(13)

where it is assumed that $P_{\mathrm{sens}}$ remains constant due to hardware design, resulting in $\frac{d{P}_{\mathrm{sens}}}{dt}=0$. Consequently, $\Delta \left(t\right)$ is determined by $\frac{d{P}_r\left(t\right)}{dt}$, which is influenced by time-dependent path loss and fading. Negative deviations of $\Delta \left(t\right)$ reduce system sensitivity, resulting in an outage.

Beyond the linear differentiation in (13), we can consider a log-derivative approach if $\Delta \left(t\right)$ remains positive. Define

$$m\left(t\right)=ln\Delta \left(t\right),\mathrm{provided}\Delta \left(t\right)>0.$$

(14)

Its time derivative is

$${\displaystyle \frac{dm\left(t\right)}{dt}}={\displaystyle \frac{1}{\Delta \left(t\right)}}{\displaystyle \frac{d\Delta \left(t\right)}{dt}}.$$

(15)

When $\Delta \left(t\right)$ approaches zero, the system nears or falls below sensitivity, and (15) diverges to $-\infty$. Such a divergence signals that even small negative changes in $P_r\left(t\right)$ can produce an immediate link failure.

3.3. Sensitivity in a Multi-UAV Network

Consider N Unmanned Aerial Vehicles (UAVs) that engage in reciprocal communication. For each connection ℓ in the set of all pairwise links $\{\ell =1,2,\cdots ,L\}$, let $P_r^{(\ell )}$ denote the received power and $P_{\mathrm{sens}}^{(\ell )}$ represent the sensitivity threshold. We define the proportion of active connections $\zeta \left(t\right)$ as

$$\zeta \left(t\right)={\displaystyle \frac{1}{L}}\sum _{\ell =1}^L\mathbf{1}\left\{P_r^{(\ell )}\left(t\right)\ge P_{\mathrm{sens}}^{(\ell )}\right\},$$

(16)

where $\mathbf{1}\{·\}$ is the indicator function. The expected active link ratio $\mathbb{E}\left[\zeta \right(t\left)\right]$ can be expanded if we interpret $P_r^{(\ell )}\left(t\right)$ as a random process:

$$\mathbb{E}\left[\zeta \left(t\right)\right]={\int }_{\mathcal{S}}{\displaystyle \frac{1}{L}}\sum _{\ell =1}^L\mathbf{1}\left\{P_r^{(\ell )}(\omega ,t)\ge P_{\mathrm{sens}}^{(\ell )}\right\}d\mathbb{P}\left(\omega \right),$$

(17)

where $\omega \in \mathcal{S}$ represents all possible fading, mobility, or interference states in the probability space $\mathcal{S}$. This integral form highlights how UAV orientation, random channel fading, and potential blockages either sustain or break link sensitivities over time.

Continuous Spatial UAV Distribution

In extensive networks, UAVs may be represented as a spatial point process $\mathsf{\Phi }\subset {\mathbb{R}}^2$. For a standard UAV positioned at the origin, the likelihood that it detects a desired link from UAV j above the threshold is

$$\mathcal{P}\left[P_r\ge P_{\mathrm{sens}}\right]={\int }_{{\mathbb{R}}^2}\mathbf{1}\left\{P_t\beta (\parallel \mathbf{x}\parallel )\ge P_{\mathrm{sens}}\right\}{f}_{\mathsf{\Phi }}\left(\mathbf{x}\right)d\mathbf{x},$$

(18)

where $f_{\mathsf{\Phi }}$ is the spatial density of UAV positions, and $\beta (\parallel \mathbf{x}\parallel )$ denotes path loss/fading gains from distance $\parallel \mathbf{x}\parallel$. This integral can be decomposed into polar coordinates or layered by altitude if UAVs are distributed in 3D. Equation (18) can be used to estimate coverage probability for a typical UAV in random topologies.

3.4. Coverage Regions and Sensitivity Threshold

Receiver sensitivity also influences the coverage area in which a UAV can decode signals. If $P_r\left(\mathbf{x}\right)$ denotes the received power at horizontal coordinates $\mathbf{x}=(x,y)$ from a fixed transmitter at altitude h, the coverage region $\mathcal{C}\subseteq {\mathbb{R}}^2$ is

$$\mathcal{C}=\left\{\mathbf{x}\in {\mathbb{R}}^2:P_r\left(\mathbf{x}\right)\ge P_{\mathrm{sens}}\right\}.$$

(19)

The coverage ratio $\Gamma$ is defined by

$$\Gamma ={\displaystyle \frac{{\int \int }_{\Omega }\mathbf{1}\left[P_r\left(\mathbf{x}\right)\ge P_{\mathrm{sens}}\right]d\mathbf{x}}{{\int \int }_{\Omega }d\mathbf{x}}},$$

(20)

where $\Omega$ is the bounding area of interest (e.g., an urban district). The partial derivative of coverage ratio with respect to the altitude h reveals how flight-level constraints affect coverage:

$${\displaystyle \frac{\partial \Gamma }{\partial h}}={\displaystyle \frac{1}{{\int \int }_{\Omega }d\mathbf{x}}}\underset{\Omega }{\int \int }{\displaystyle \frac{\partial }{\partial h}}\mathbf{1}\left[P_r(\mathbf{x},h)\ge P_{\mathrm{sens}}\right]d\mathbf{x}.$$

(21)

Any positive or negative jump in coverage typically occurs near boundary contours $\partial \mathcal{C}$, making the integral approach akin to measuring the morphological changes in coverage geometry with altitude.

3.5. Sensitivity Constraints vs. Energy and Spectral Efficiency

UAV energy ${\eta }_e$ and spectral ${\eta }_s$ efficiencies depend on maintaining sufficient received power above noise and interference. If the sensitivity threshold rises (due to wide bandwidth or large noise figure), the UAV must compensate in the following ways:

• Increasing Transmit Power: This increases total power $P_T$, impacting ${\eta }_e=\frac{C_T}{P_T}$. If throughput $C_T$ cannot keep pace, overall energy efficiency suffers.
• Enhancing Beamforming Gains: Gains help offset the gap to $P_{\mathrm{sens}}$, but require complex antenna arrays and precise real-time alignment. For high mobility or multi-trajectory UAV swarms, the overhead in scanning and tracking is significant.
• Adaptive Modulation/Coding: The system can reduce modulation order to lower the needed SNR, effectively decreasing ${\mathrm{SNR}}_{\mathrm{margin}}$ in (11), but sacrificing spectral efficiency ${\eta }_s$.

Thus, a balance arises: satisfying more stringent sensitivity constraints in mmWave UAV links often either reduces flight durations (due to increased $P_e$) or lowers net throughput (due to fallback to robust modulations). A more advanced scheduling algorithm might optimize flight path and spectral usage under the constraints

$$\begin{array}{cc}\hfill \underset{\begin{array}{c}\left\{p_{\ell }\left(t\right)\right\}\\ \left\{{\mathrm{BW}}_{\ell }\right\}\\ \left\{{\mathbf{x}}_{\ell }\left(t\right)\right\}\end{array}}{max}& \sum _{\ell =1}^L{\int }_0^T{\eta }_s^{(\ell )}\left(t\right)dt\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& P_r^{(\ell )}\left(t\right)\ge P_{\mathrm{sens}}^{(\ell )},\forall \ell ,\forall t\in [0,T],\hfill \\ \hfill & p_{\ell }\left(t\right)\le p_{max},{\mathrm{BW}}_{\ell }\le B_{max},\hfill \\ \hfill & {\mathbf{x}}_{\ell }\left(t\right)\in \mathcal{F}\left(\mathrm{flight}\mathrm{corridor}\mathrm{constraints}\right),\hfill \\ \hfill & {\eta }_e^{(\ell )}\left(t\right)\ge {\eta }_{e,min},\forall \ell .\hfill \end{array}$$

(22)

In this context, $p_{\ell }\left(t\right)$ denotes the transmit power for link ℓ, ${\mathrm{BW}}_{\ell }$ represents the allotted bandwidth, and ${\mathbf{x}}_{\ell }\left(t\right)$ signifies the UAV trajectory. The system must guarantee that $P_r^{(\ell )}\left(t\right)\ge P_{\mathrm{sens}}^{(\ell )}$, therefore constraining the permissible range of transmit powers and flight trajectories. The integration of flight altitude, beam steering, and the temporal dimension converts this issue into a high-dimensional optimisation problem with partial derivative restrictions derived from equations such as (21).

4. Energy Efficiency Analysis for UAV-to-UAV Communication in Dynamic Networks for Smart Cities

This section analyses energy efficiency ${\eta }_e$ within UAV communication, integrating the dynamic channel model and UAV mobility. The energy efficiency ${\eta }_e$ is defined as follows:

$${\eta }_e={\displaystyle \frac{C_T}{P_T}},$$

(23)

where:

• ${\eta }_e$: Energy efficiency.
• $C_T$: Total communication capacity (bits per second).
• $P_T$: Aggregate power consumption (watts).

4.1. Communication Capacity with Dynamic Channels

The total communication capacity $C_T$ considers SNR fluctuations, bandwidth efficiency, and hardware imperfections:

$$C_T={\displaystyle \frac{B}{2}}{log}_2\left(1+{\displaystyle \frac{\kappa e{\gamma }_{\mathrm{sd}}}{2\pi }}\right),$$

(24)

where:

• B: Communication bandwidth (Hz).
• $\kappa$: Impairment factor modelling hardware imperfections.
• e: Euler’s number (base of the natural logarithm).
• ${\gamma }_{\mathrm{sd}}$: Signal-to-Noise Ratio (SNR).
• $\pi$: Mathematical constant (ratio of a circle’s circumference to its diameter).

The SNR ${\gamma }_{\mathrm{sd}}$ is derived as:

$${\gamma }_{\mathrm{sd}}={\int }_{d_0}^{d_{max}}{\displaystyle \frac{P_t{G}_t{G}_r{\lambda }^2}{{\left(4\pi \right)}^2{d}^{2}L\left(d\right)}}\mathrm{d}d,$$

(25)

where:

• $d_0$: Minimum communication distance (meters).
• $d_{max}$: Maximum communication distance (meters).
• $P_t$: Transmitter power (watts).
• $G_t$: Transmitter antenna gain (unitless).
• $G_r$: Receiver antenna gain (unitless).
• $\lambda$: Wavelength of the transmitted signal (meters).
• $L\left(d\right)$: Path loss as a function of distance d (unitless).

4.2. Power Consumption Model

The power consumption $P_T$ incorporates both communication and mobility components:

$$P_T={\displaystyle \frac{P_e}{{\eta }_{\mathrm{PA}}}}+P_{dc}+P_c+M{P}_{\mathrm{UAV}}+P_{\mathrm{mob}},$$

(26)

where:

• $P_e$: Transmission power (watts).
• ${\eta }_{\mathrm{PA}}$: Power amplifier efficiency (unitless).
• $P_{dc}$: System power (watts).
• $P_c$: Circuit power (watts).
• M: Number of UAVs in the communication network (unitless).
• $P_{\mathrm{UAV}}$: Control system power per UAV (watts).
• $P_{\mathrm{mob}}$: Mobility-induced power (watts), modelled as:

$$P_{\mathrm{mob}}={\alpha }_1{\displaystyle \frac{\mathrm{d}v}{\mathrm{d}t}}+{\alpha }_2{\int }_0^{t}h\mathrm{d}t+{\alpha }_3,$$

(27)

where:

• ${\alpha }_1$: Coefficient for acceleration-related power consumption (watts per $\mathrm{m}/{\mathrm{s}}^2$).
• $\mathrm{d}v/\mathrm{d}t$: Rate of change of velocity (acceleration, $\mathrm{m}/{\mathrm{s}}^2$).
• ${\alpha }_2$: Coefficient for altitude-related power consumption (watts per meter).
• h: Altitude (meters).
• ${\alpha }_3$: Constant power offset for mobility (watts).

4.3. Energy Efficiency Formulation

We extend ${\eta }_e$ by substituting the expressions for $C_T$ and $P_T$ as:

$${\eta }_e={\displaystyle \frac{\frac{B}{2}{log}_2\left(1+\frac{\kappa e{\gamma }_{\mathrm{sd}}}{2\pi }\right)}{\frac{P_e}{{\eta }_{\mathrm{PA}}}+P_{dc}+P_c+M{P}_{\mathrm{UAV}}+{\alpha }_1\frac{\mathrm{d}v}{\mathrm{d}t}+{\alpha }_2{\int }_0^{t}h\mathrm{d}t+{\alpha }_3}}.$$

(28)

This framework facilitates the optimisation of UAV trajectories and power management. Additionally, the sensitivities of ${\eta }_e$ with respect to v and h can be expressed as follows:

$${\displaystyle \frac{\partial {\eta }_e}{\partial v}}={\displaystyle \frac{\frac{B}{2}{log}_2\left(1+\frac{\kappa e{\gamma }_{\mathrm{sd}}}{2\pi }\right)·\frac{{\alpha }_1}{{\eta }_{\mathrm{PA}}}}{{\left(P_T\right)}^2}},{\displaystyle \frac{\partial {\eta }_e}{\partial h}}={\displaystyle \frac{\frac{B}{2}{log}_2\left(1+\frac{\kappa e{\gamma }_{\mathrm{sd}}}{2\pi }\right)·{\alpha }_2}{{\left(P_T\right)}^2}}.$$

(29)

The time-averaged energy efficiency is given by:

$${\overline{\eta }}_e={\displaystyle \frac{1}{T}}{\int }_0^T{\eta }_e\left(t\right)\mathrm{d}t,$$

(30)

where:

• T: Total mission time (seconds).

This formulation effectively addresses sustainable efficiency during UAV missions under real-time network conditions.

Table 1. Simulation parameters for the energy efficiency analysis of UAV-to-UAV communication in dynamic networks for smart cities.

Parameter	Sym	2.4 GHz	5.8 GHz	28 GHz	60 GHz
Energy efficiency (bits/Joule)	${\eta }_e$	5	4.5	2.5	1.8
Total communication capacity (bps)	$C_T$	${10}^6$	${10}^6$	$5\times {10}^6$	$10\times {10}^6$
Aggregate power consumption	$P_T$	1 W	1 W	2 W	3 W
Communication bandwidth (Hz)	B	$10\times {10}^6$	$10\times {10}^6$	$100\times {10}^6$	$500\times {10}^6$
Impairment factor	$\kappa$	0.8	0.8	0.7	0.6
Euler’s number	e	2.718	2.718	2.718	2.718
Signal-to-Noise Ratio (SNR)	${\gamma }_{\mathrm{sd}}$	15	15	12	10
Minimum communication distance	$d_0$	100 m	100 m	50 m	30 m
Maximum communication distance	$d_{max}$	500 m	500 m	300 m	150 m
Transmitter power	$P_t$	1 W	1 W	2 W	3 W
Transmitter antenna gain	$G_t$	3	3	8	10
Receiver antenna gain	$G_r$	3	3	8	10
Wavelength	$\lambda$	0.125 m	0.0517 m	0.0107 m	0.005 m
Path loss	$L\left(d\right)$	2	2.2	3.5	4.5
Transmission power	$P_e$	0.5 W	0.5 W	1.5 W	2 W
Power amplifier efficiency	${\eta }_{\mathrm{PA}}$	0.35	0.35	0.25	0.20
System power	$P_{dc}$	1 W	1 W	2 W	3 W
Circuit power	$P_c$	1 W	1 W	1.5 W	2 W
Number of UAVs	M	10	10	10	10
Control system power per UAV	$P_{\mathrm{UAV}}$	0.3 W	0.3 W	0.4 W	0.5 W
Acceleration power coefficient	${\alpha }_1$	0.1	0.1	0.12	0.15
Rate of change of velocity	$\mathrm{d}v/\mathrm{d}t$	10 $\mathrm{m}/{\mathrm{s}}^2$	10 $\mathrm{m}/{\mathrm{s}}^2$	5 $\mathrm{m}/{\mathrm{s}}^2$	3 $\mathrm{m}/{\mathrm{s}}^2$
Altitude power coefficient	${\alpha }_2$	0.05	0.05	0.05	0.05
Altitude	h	500 m	500 m	500 m	500 m
Constant power offset	${\alpha }_3$	0.1	0.1	0.15	0.2
Total mission time	T	3600 s	3600 s	3600 s	3600 s

presents the simulation parameters utilised for the energy efficiency analysis of UAV-to-UAV communication within dynamic networks in smart cities.

5. Spectral Efficiency Analysis for UAV-to-UAV Communication in Dynamic Networks for Smart Cities

In this section, we develop a comprehensive analysis of the spectral efficiency ${\eta }_s$ for UAV-to-UAV communication in a fading channel with interference and noise. The spectral efficiency between two UAVs, $U_i$ and $U_j$, is defined in terms of the Signal-to-Interference-plus-Noise Ratio (SINR) and incorporates both large-scale path loss and small-scale fading effects over dynamic channel conditions.

The spectral efficiency ${\eta }_s$ between UAV $U_i$ and UAV $U_j$ can be expressed as the expectation over the fading distribution, integrating SINR fluctuations over all possible channel realizations. The general form for ${\eta }_s$ is given by the following:

$${\eta }_s={\displaystyle \frac{1}{B}}\mathbb{E}\left[{log}_2\left(1+{\displaystyle \frac{P_{t_i}{G}_{i,j}{\left|h_{i,j}\right|}^2}{I_{i,j}+N_{0}B}}\right)\right],$$

(31)

where:

• ${\eta }_s$ is the spectral efficiency in bits per second per Hertz (bps/Hz);
• $P_{t_i}$ is the transmit power from UAV $U_i$;
• $G_{i,j}$ is the antenna gain between UAV $U_i$ and UAV $U_j$;
• $|h_{i,j}{|}^2$ represents the channel fading power between UAVs $U_i$ and $U_j$;
• $I_{i,j}$ is the interference power received by UAV $U_j$ from other UAVs or external sources;
• $N_0$ is the noise power spectral density;
• B is the bandwidth of the communication channel;
• $\mathbb{E}$ denotes the expectation operator over fading realizations.

The SINR ${\gamma }_{i,j}$ between UAV $U_i$ and UAV $U_j$ can be modelled as a time-varying function of the channel, represented by the differential equation:

$${\displaystyle \frac{\mathrm{d}{\gamma }_{i,j}}{\mathrm{d}t}}={\displaystyle \frac{\partial }{\partial t}}\left({\displaystyle \frac{P_{t_i}{G}_{i,j}{\left|h_{i,j}\left(t\right)\right|}^2}{I_{i,j}+N_{0}B}}\right),$$

(32)

where $|h_{i,j}{\left(t\right)|}^2$ is the fading coefficient that changes as a function of time t, accounting for UAV mobility and environmental factors. This dynamic SINR expression allows us to evaluate instantaneous fluctuations in the channel.

For Rayleigh fading conditions, where $|h_{i,j}{|}^2$ follows an exponential distribution, the spectral efficiency ${\eta }_s$ can be computed as an integral over the probability density function of the channel gain:

$${\eta }_s={\displaystyle \frac{1}{B}}{\int }_0^{\infty }{log}_2\left(1+{\displaystyle \frac{P_{t_i}{G}_{i,j}{h}^2}{I_{i,j}+N_{0}B}}\right)f_h\left(h\right)\mathrm{d}h,$$

(33)

where $f_h\left(h\right)$ is the probability density function of the fading envelope $h_{i,j}$, typically given by the following:

$$f_h\left(h\right)={\displaystyle \frac{1}{\Omega }}exp\left(-{\displaystyle \frac{h}{\Omega }}\right),$$

(34)

where $\Omega =\mathbb{E}\left[\right|h_{i,j}{|}^2]$ represents the mean power of the fading envelope.

Expanding on the spectral efficiency, we incorporate a continuous interference model, where $I_{i,j}$ fluctuates due to interference dynamics. Let $I_{i,j}\left(t\right)$ be the interference power as a function of time. The time-averaged spectral efficiency is then:

$${\eta }_s={\displaystyle \frac{1}{B}}{\int }_0^{\infty }{log}_2\left(1+{\displaystyle \frac{P_{t_i}{G}_{i,j}{h}^2}{I_{i,j}\left(t\right)+N_{0}B}}\right){\displaystyle \frac{1}{\Omega }}exp\left(-{\displaystyle \frac{h}{\Omega }}\right)\mathrm{d}h\mathrm{d}t.$$

(35)

The interference component $I_{i,j}$ over time can be represented as an integral over the spatial distribution of interfering UAVs within a distance D:

$$I_{i,j}={\int }_0^D{\int }_0^{2\pi }{\displaystyle \frac{P_{t_k}{G}_{k,j}}{r^2+d_{k,j}^2}}r\mathrm{d}r\mathrm{d}\theta ,$$

(36)

where r is the radial distance from UAV $U_j$ to an interfering UAV $U_k$ at distance $d_{k,j}$, and $P_{t_k}$ is the transmit power of UAV $U_k$.

To model the SINR as a stochastic process ${\Gamma }_{i,j}\left(t\right)$, we express the time-dependent SINR as a differential stochastic equation:

$$\mathrm{d}{\Gamma }_{i,j}\left(t\right)=\left({\displaystyle \frac{P_{t_i}{G}_{i,j}{\left|h_{i,j}\left(t\right)\right|}^2}{I_{i,j}+N_{0}B}}\right)\mathrm{d}t+\sigma \mathrm{d}{W}_t,$$

(37)

where $\sigma$ is the standard deviation of the process, and $\mathrm{d}{W}_t$ represents a Wiener process, accounting for random fluctuations in the channel.

The effective spectral efficiency ${\eta }_s$ for UAV-to-UAV communication, considering time-varying fading, noise, and interference, is defined as follows:

$${\eta }_s={\displaystyle \frac{1}{B}}{\int }_0^{\infty }\mathbb{E}\left[{log}_2\left(1+{\displaystyle \frac{P_{t_i}{G}_{i,j}{h}^2\left(t\right)}{I_{i,j}\left(t\right)+N_{0}B}}\right)\right]f_h\left(h\right)\mathrm{d}h.$$

(38)

This formulation incorporates both fading and interference distributions, reflecting the dynamic characteristics of UAV-to-UAV communication.

The above expressions establish a comprehensive framework for assessing spectral efficiency in dynamic UAV networks, accounting for interference, noise, and time-varying channel effects. Utilising integral and differential representations allows for the capture of fluctuations in spectral efficiency, thereby facilitating a robust model for UAV-to-UAV communication across varying environmental conditions.

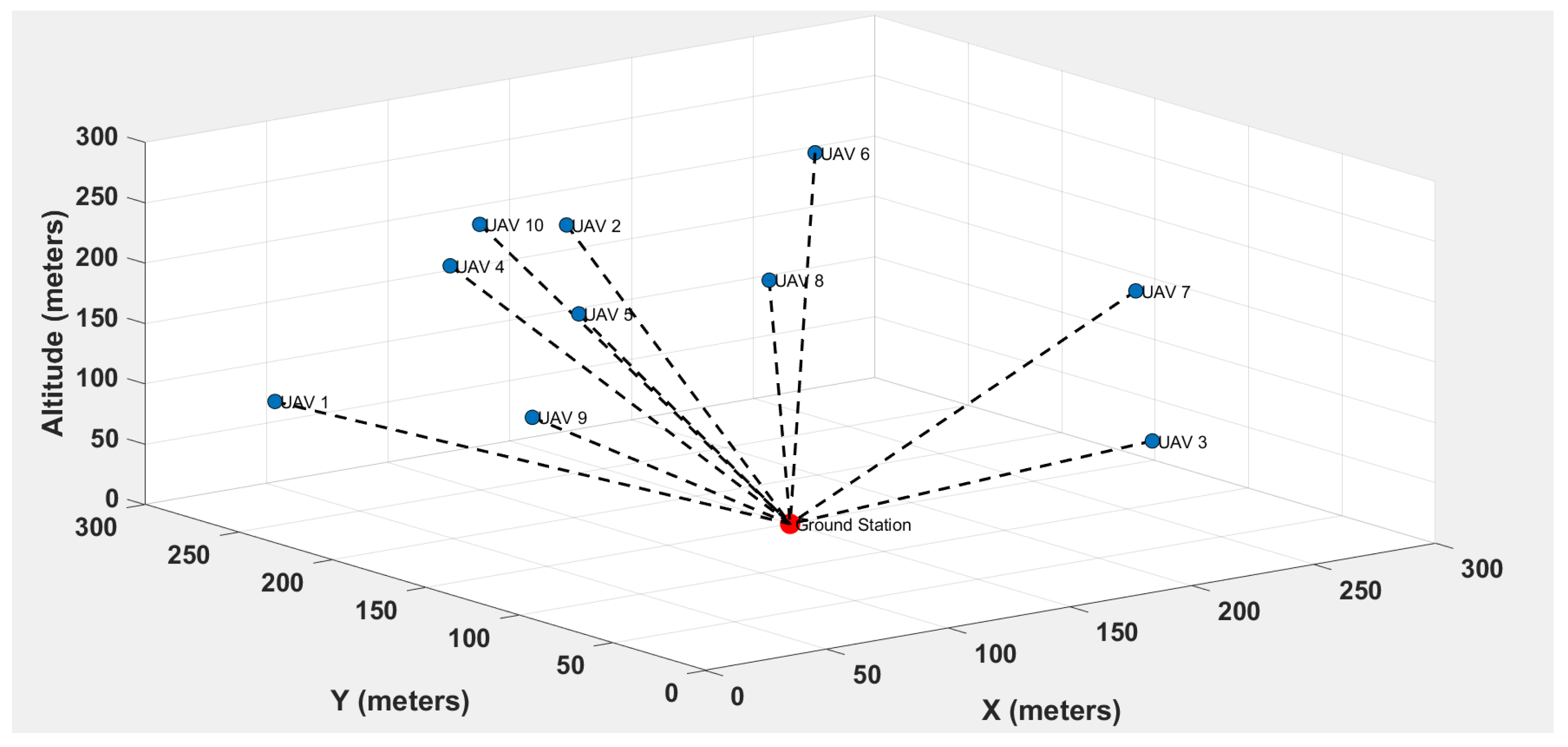
6. UAV-to-UAV Simulation Analysis Consideration in a Dynamic Network for Smart Cities

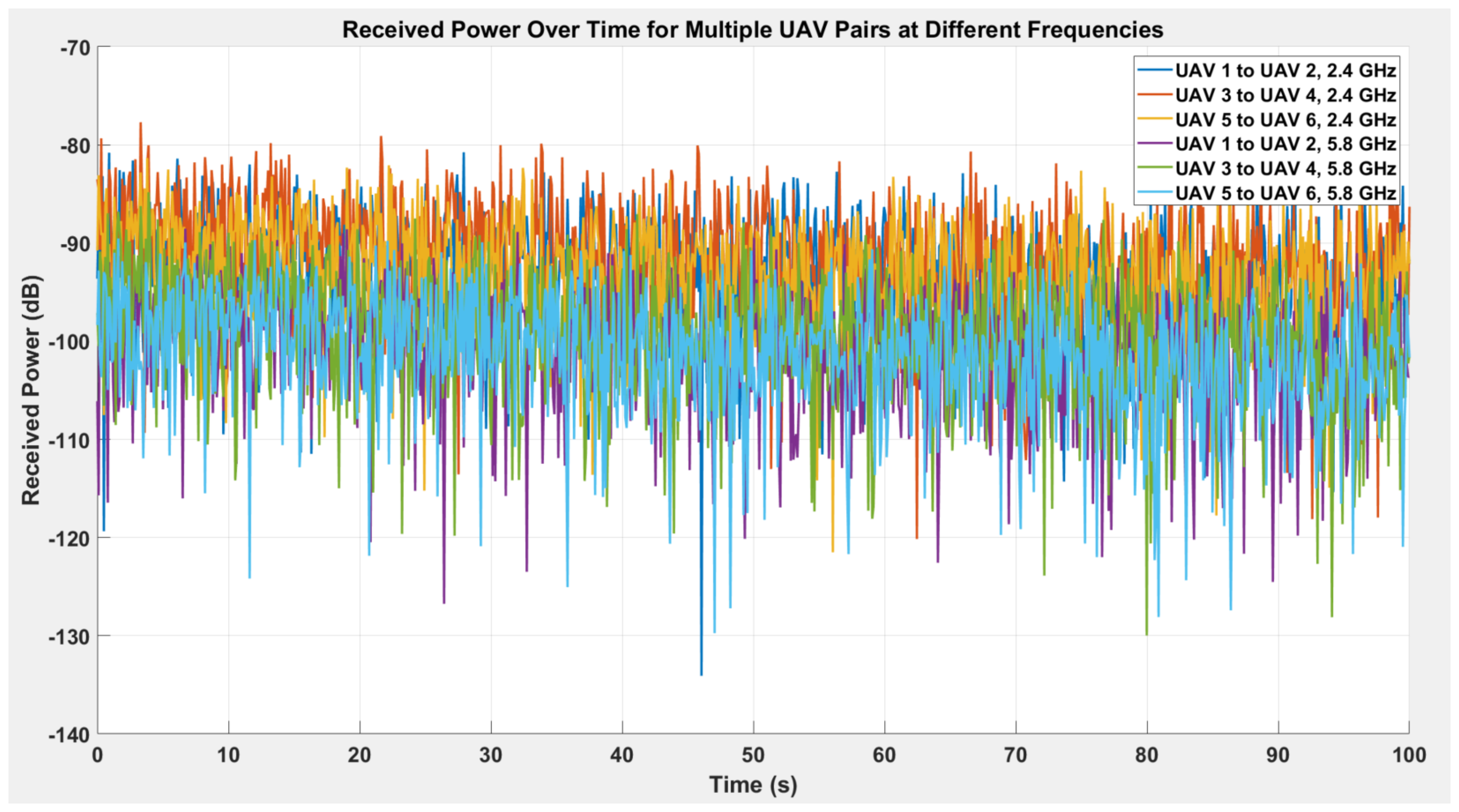
6.1. Analysis of Received Power Variability in UAV-to-UAV Communication Dynamic Network

Figure 2 presents the received power (in dB) as a function of time for various UAV-to-UAV communication links at two distinct frequencies: 2.4 GHz and 5.8 GHz. The variability of received power in a UAV network is influenced by mobility, channel fading, and environmental dynamics.

The variability in received power underscores the difficulties in sustaining reliable communication links within UAV networks. The result in Figure 2 indicates that, even under similar conditions, channel characteristics exhibit random variation, highlighting the impact of fading, Doppler shifts, and mobility patterns on UAV-to-UAV communication in a smart city. The 2.4 GHz band provides enhanced signal strength and link reliability for UAV-to-UAV communication in dynamic environments. It is more appropriate for extended distances and scenarios where strong connectivity is essential. The 5.8 GHz band is advantageous for short-range communication or in settings where higher data throughput is prioritised over link stability.

Figure 3 illustrates the received power measured in decibels (dB) over time for multiple UAV-to-UAV communication links operating at two mmWave frequency bands: 28 GHz and 60 GHz. Each coloured trace corresponds to a specific pair of UAVs (e.g., UAV 1 to UAV 2, UAV 3 to UAV 4, etc.) transmitting and receiving signals in a dynamic environment. The simulation spans a period of 100 s, capturing the fluctuations in received power levels due to mobility, fading, and interference. In practice, UAVs in a dynamic network frequently change their relative distances and orientations, resulting in constructive and destructive interference over short timescales. The curves exhibit occasional sharp drops (on the order of 10 dB or more). These drops represent times when multipath components destructively interfere, or when UAV geometry momentarily increases link distance and path loss. Conversely, spikes above the mean power level result from brief periods of constructive interference.

Each UAV pair has a distinct trace, reflecting their unique distance profiles and fading realizations. Pairs with shorter mean separation or more favourable geometry generally show higher received power. By comparing multiple pairs, one can infer how geometry and mobility influence short-term link reliability. The notable variance in received power suggests that UAVs would benefit from adaptive techniques (e.g., power control, beamforming, or switching to an alternative band if available) to maintain stable links. Because deeper fading nulls occur at 60 GHz, UAVs require extra transmit power to compensate, reducing energy efficiency. System designers must carefully weigh the advantages of high throughput at mmWave frequencies against increased energy consumption and link instability.

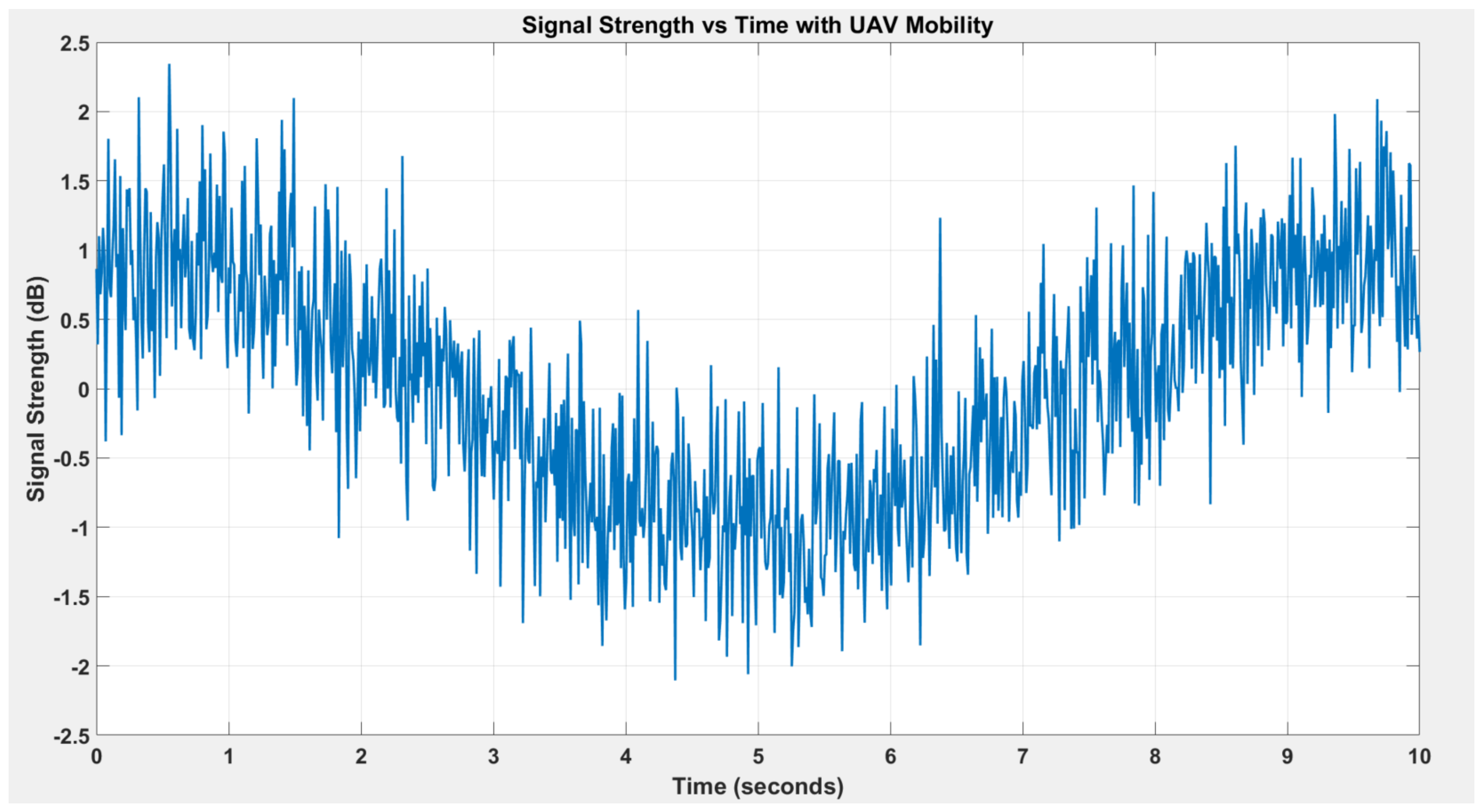
6.2. Impact of UAV Mobility on Signal Strength Variability over Time

Figure 4 illustrates the signal strength (in dB) as a function of time for a UAV communication system, highlighting the significance of mobility. The data illustrate the variation in signal strength as the UAV dynamically traverses over a duration of 10 s. The signal strength displays a distinct periodic decrease near the midpoint of the time axis (approximately 5 s), indicating potential variations in UAV positioning or relative distances among communicating entities. This behaviour can be attributed to the UAV entering a less favourable channel condition, including increased distance, shadowing, or destructive interference. The observed gradual dip and subsequent recovery indicate the influence of large-scale path loss and shadowing. Signal attenuation increases as the UAV moves farther from the receiver or encounters obstacles. In multi-UAV networks, routing algorithms must consider variations in signal strength and prioritise routes that ensure stable connectivity.

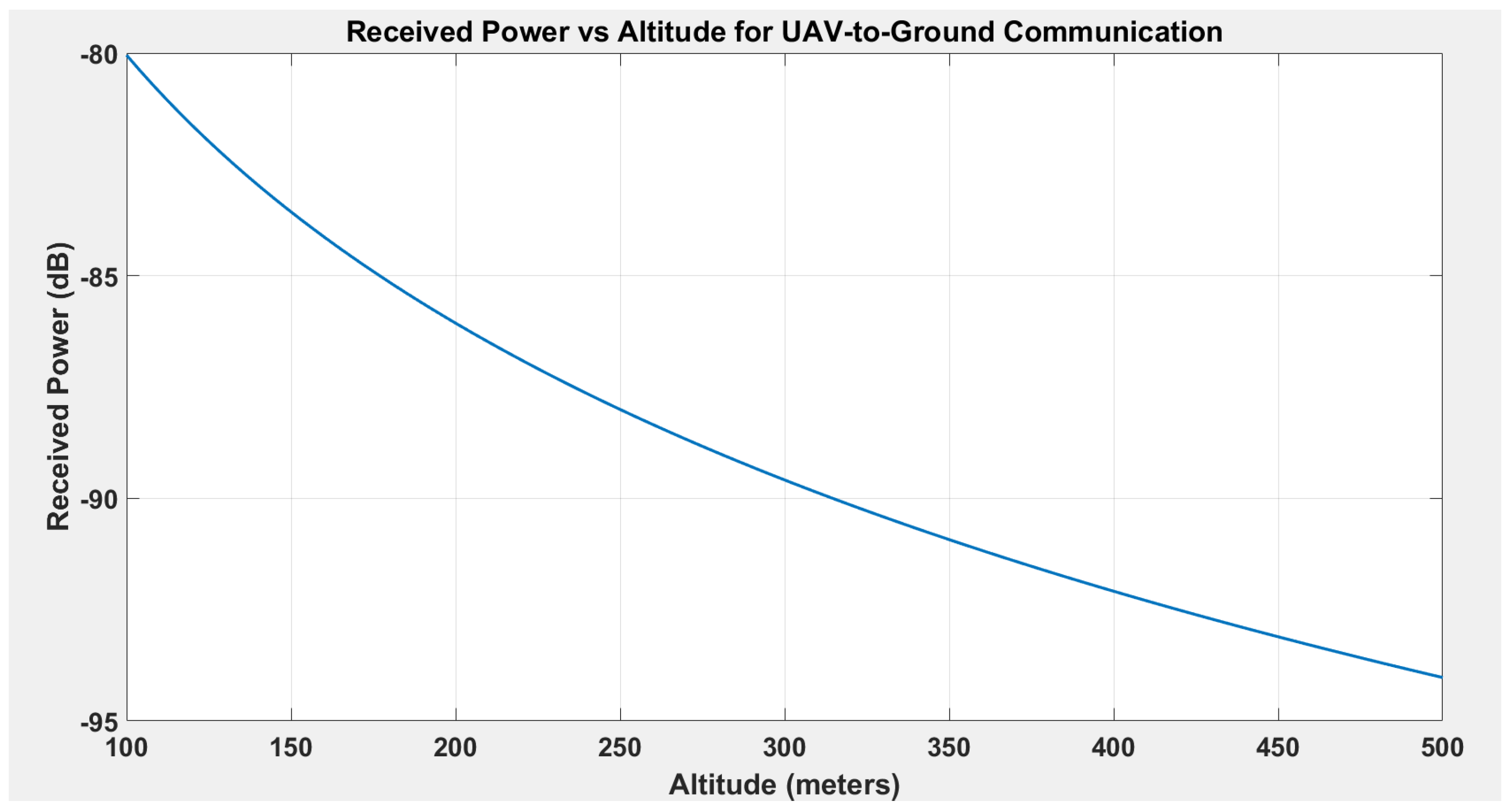
6.3. Received Power Dynamics in UAV-to-Ground Communication at Varying Altitudes

Figure 5 depicts the correlation between received power (in dB) and altitude (in meters) for UAV-to-ground communication. With an increase in altitude, the received power diminishes, a phenomenon anticipated due to the growing distance between the UAV and the ground receiver. The received power decreases from approximately −80 dB at an altitude of 100 m to −95 dB at 500 m. At elevated altitudes, the received power diminishes, potentially impairing signal quality and elevating the Bit Error Rate (BER) in communication links. UAVs functioning at elevated altitudes necessitate increased transmission power or highly sensitive receivers to ensure dependable communication. This is especially significant for long-range UAV missions or operations in areas with low population density. At elevated altitudes, the UAV may require an increase in gearbox power to offset the additional path loss. This may result in increased energy consumption, thereby affecting the UAV’s overall efficiency and flight duration. Higher altitudes result in reduced received power, which can constrain the available SNR (Signal-to-Noise Ratio) and subsequently impact the maximum achievable data rates. High-altitude communication links may necessitate the use of lower-order modulation schemes or error correction techniques to ensure reliability.

Figure 5 indicates that low-altitude UAVs are more appropriate for smart city communication applications that demand high data rates and robust communication links, including real-time video streaming. High-altitude UAVs, although experiencing reduced received power, offer enhanced coverage across extensive regions, rendering them suitable for applications such as disaster monitoring and wide-area surveillance. Adaptive modulation and coding schemes can be utilised to modify communication parameters, such as modulation order and coding rate, in response to received power and channel conditions.

6.4. Impact of Multipath Fading on UAV Communication with Varying Distances

Figure 6 illustrates the multipath fading gain (in dB) as a function of distance in a UAV communication system. The variations in fading gain are attributed to the multipath propagation environment, wherein signals experience constructive and destructive interference resulting from reflections, scattering, and diffraction. The multipath fading gain exhibits considerable variation with distance, spanning from roughly +10 dB to −25 dB. Rapid variations indicate small-scale fading, a phenomenon resulting from the interference of multiple signal paths at the receiver. Instances in which the fading gain falls below 0 dB indicate occurrences of destructive interference, wherein the multipath components partially or completely cancel each other, leading to a diminished received signal. As UAVs navigate, their positions relative to obstacles and reflectors change, resulting in dynamic alterations of the multipath components. This mobility intensifies the diminishing effects, resulting in a highly dynamic channel.

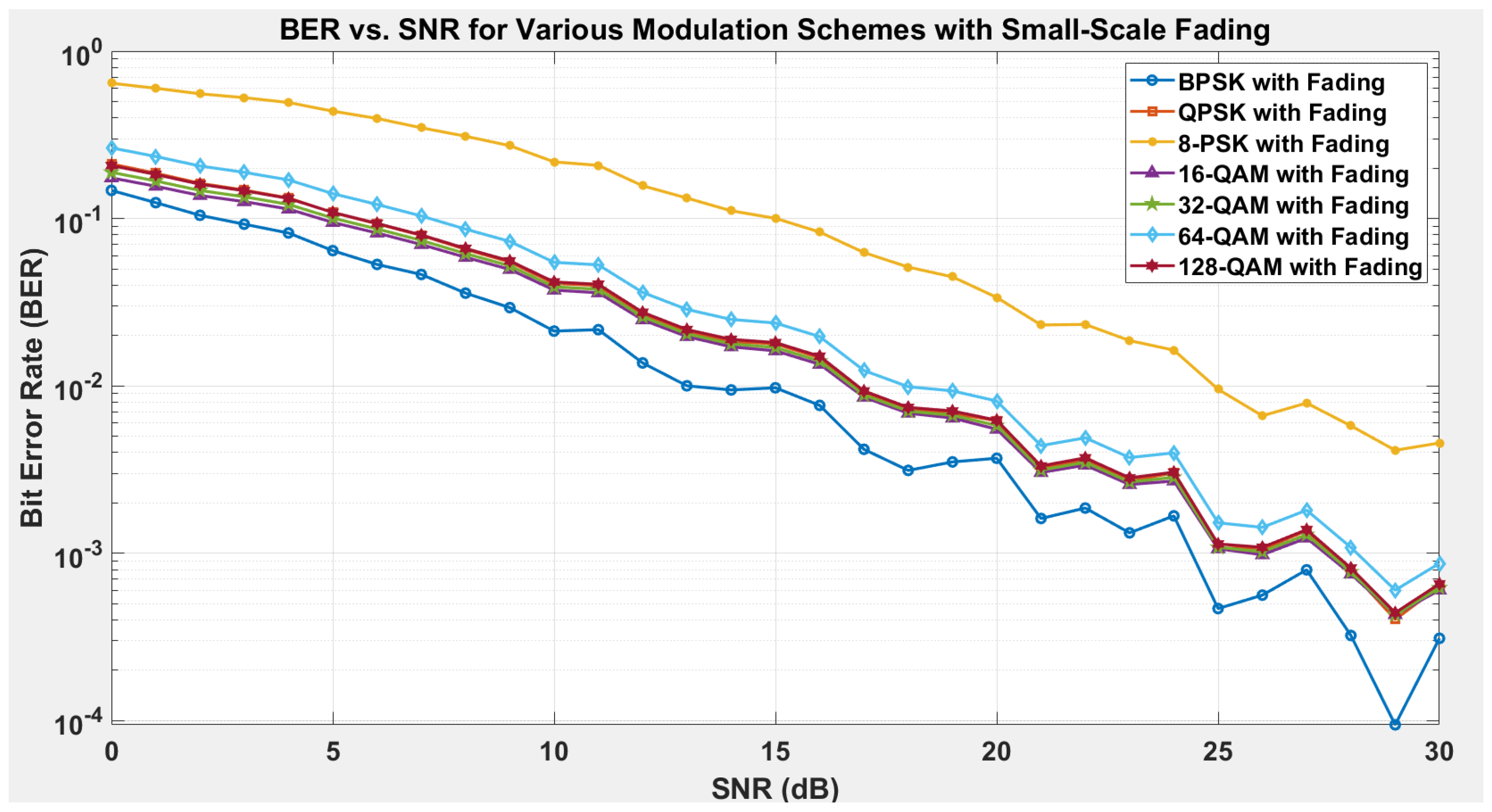
6.5. BER Performance of Modulation Schemes Under Small-Scale Fading in UAV Networks

Figure 7 depicts the Bit Error Rate (BER) performance of several modulation schemes in the context of small-scale fading inside UAV-to-UAV communication networks. The analysis encompasses modulation methods, including BPSK, QPSK, 8-PSK, 16-QAM, 32-QAM, 64-QAM, and 128-QAM, with performance assessed over a broad spectrum of Signal-to-Noise Ratio (SNR) values ranging from 0 to 30 dB. For all modulation systems, an increase in SNR results in a decrease in BER. The enhancement is more prominent in the lower SNR range (0–15 dB), where the effects of fading are more evident. Beyond 20 dB, the increase in Bit Error Rate (BER) decreases, particularly for higher-order modulations, as the system nears the noise floor. In UAV-to-UAV communication, the dynamic characteristics of the environment, such as movement, varying distances, and multipath fading, enhance the effects of small-scale fading. This requires the use of robust modulation techniques and adaptive communication systems.

UAV-to-UAV communication systems can enhance performance by adaptive modulation, which dynamically modifies the modulation scheme according to the signal-to-noise ratio and channel conditions. For instance, lower-order modulations may be utilised in suboptimal channel conditions, whilst higher-order modulations may be applied when the signal-to-noise ratio is high. Non-Orthogonal Many Access (NOMA) enables many UAVs to concurrently utilise the same channel, hence enhancing spectral efficiency.

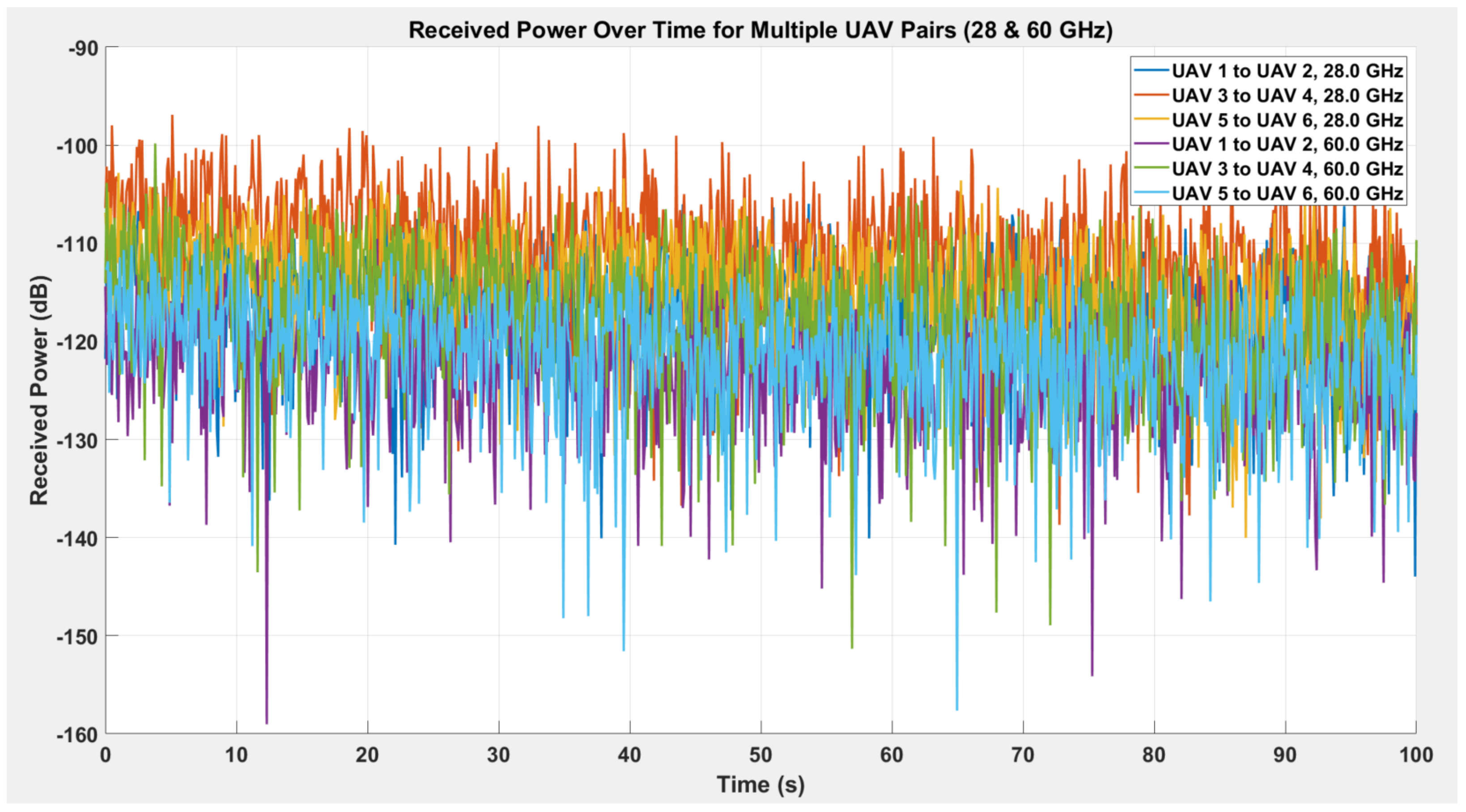
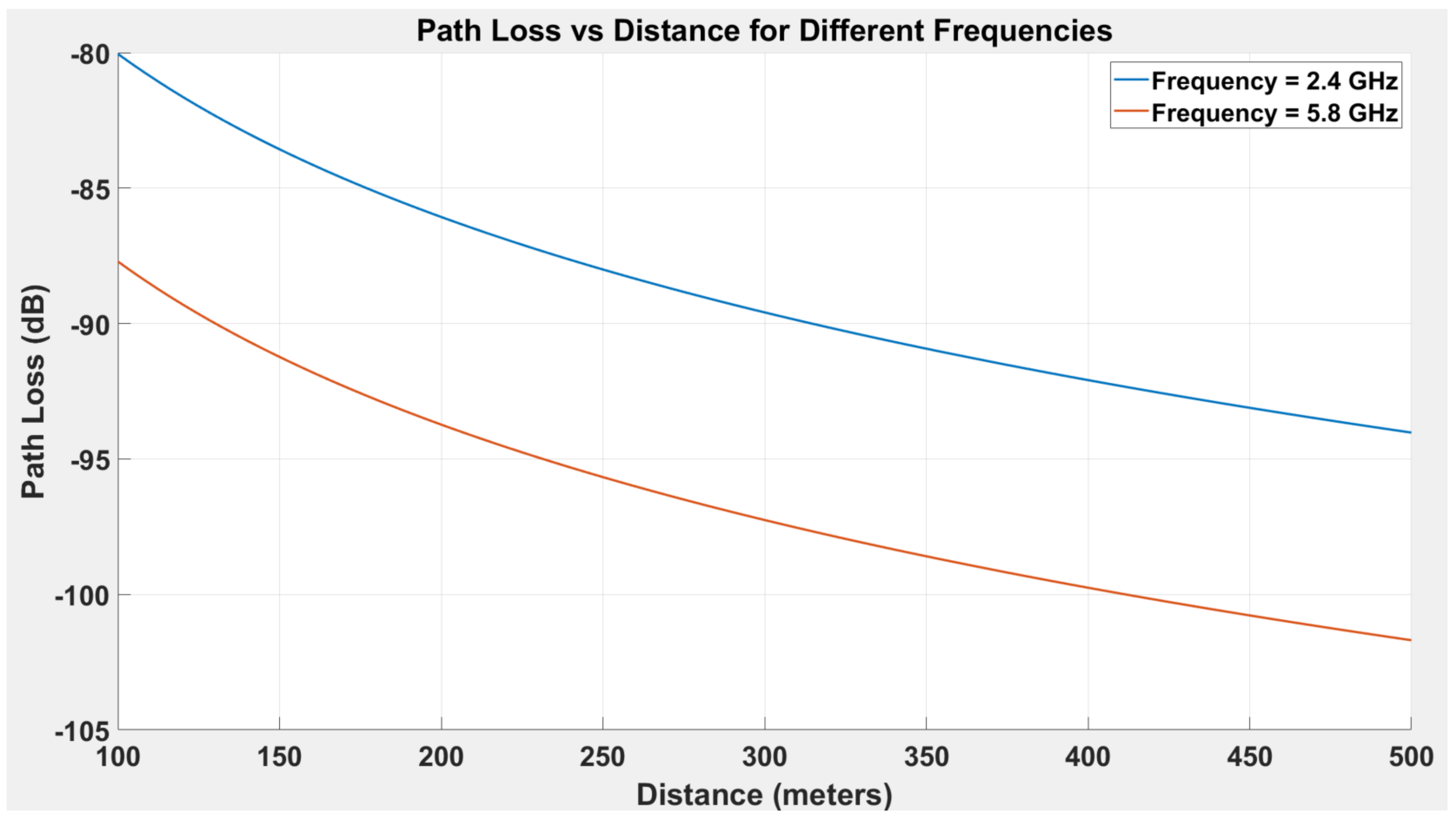
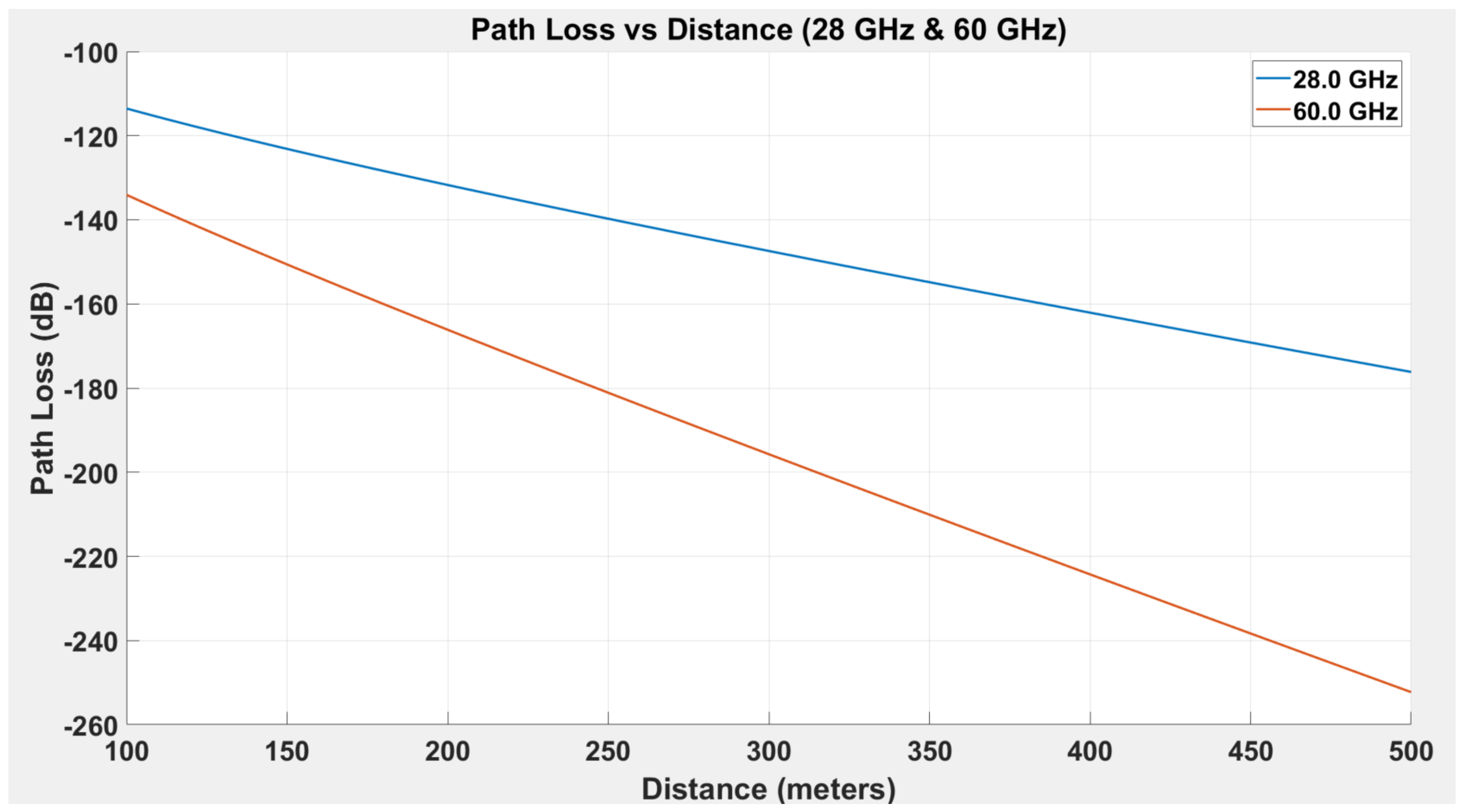
6.6. Path Loss Analysis for Different Frequencies in UAV Networks

Figure 8 presumes a free-space environment. The 2.4 GHz band offers superior signal strength over extended distances owing to reduced path loss. It is better suited for applications necessitating resilient long-distance communication. The 5.8 GHz band, despite increased path loss, has benefits like more bandwidth and less interference, rendering it suitable for high-throughput, short-range communication. The higher path loss at 5.8 GHz requires augmented transmission power to obtain equivalent received power as at 2.4 GHz, potentially affecting UAV energy efficiency and flight time. UAVs functioning at higher frequencies must mitigate the increased path loss via power regulation or advanced signal processing methods, potentially resulting in greater energy consumption. Although 5.8 GHz offers more bandwidth, its increased path loss restricts its effectiveness for long-distance communication without considerable power compensation. The 2.4 GHz band is more congested (e.g., Wi-Fi and IoT devices), resulting in possible interference despite its reduced path loss.

Figure 9 presents the path loss as a function of distance for UAV-to-UAV communication at 28 GHz and 60 GHz in a dynamic network. This plot highlights several critical aspects of millimetre-wave (mmWave) communication, particularly in aerial environments. As expected, the path loss increases with distance for both frequency bands. However, the path loss at 60 GHz is significantly higher than at 28 GHz across all distances, indicating that the propagation characteristics at these frequencies differ sharply.

At 28 GHz, the wavelength is approximately $0.0107$ m, while at 60 GHz, it is about $0.005$ m. The shorter wavelength at 60 GHz leads directly to greater free-space path loss. The 60 GHz band falls within a well-documented atmospheric absorption peak due to oxygen resonance. This absorption effect adds to the inherent free-space loss, further exacerbating the attenuation experienced over longer distances. As a result, communication at 60 GHz is extremely sensitive to both distance and atmospheric conditions.

The path loss difference between 28 GHz and 60 GHz becomes increasingly severe as the distance increases. For distances up to 200 m, the additional path loss at 60 GHz is manageable with reasonable transmit power and directional antennas. However, at distances approaching 500 m, 60 GHz communication experiences prohibitive loss, rendering it impractical for direct UAV-to-UAV links without significant enhancements such as beamforming or relaying.

Figure 9 directly underscores the trade-off between spectral efficiency and energy efficiency in mmWave UAV communications:

• The 60 GHz offers a significantly wider bandwidth, which enhances spectral efficiency.
• However, the increased path loss and corresponding higher power requirement drastically reduce energy efficiency.

This duality highlights the need for adaptive frequency selection based on operational range and mission requirements.

The results suggest that 28 GHz is suitable for medium-range UAV-to-UAV communication, such as in urban surveillance grids or inspection of distributed infrastructure. In contrast, 60 GHz is best suited for high-capacity data exchange in closely coordinated UAV swarms, such as those used in collaborative mapping, search and rescue in confined zones, or localized environmental monitoring.

For practical UAV networks in smart cities, a hybrid frequency strategy is recommended:

• Use 28 GHz for longer-range UAV corridors.
• Reserve 60 GHz for short-range, high-capacity data bursts within UAV clusters.
• Implement dynamic frequency switching to optimize both spectral and energy efficiency in real time.

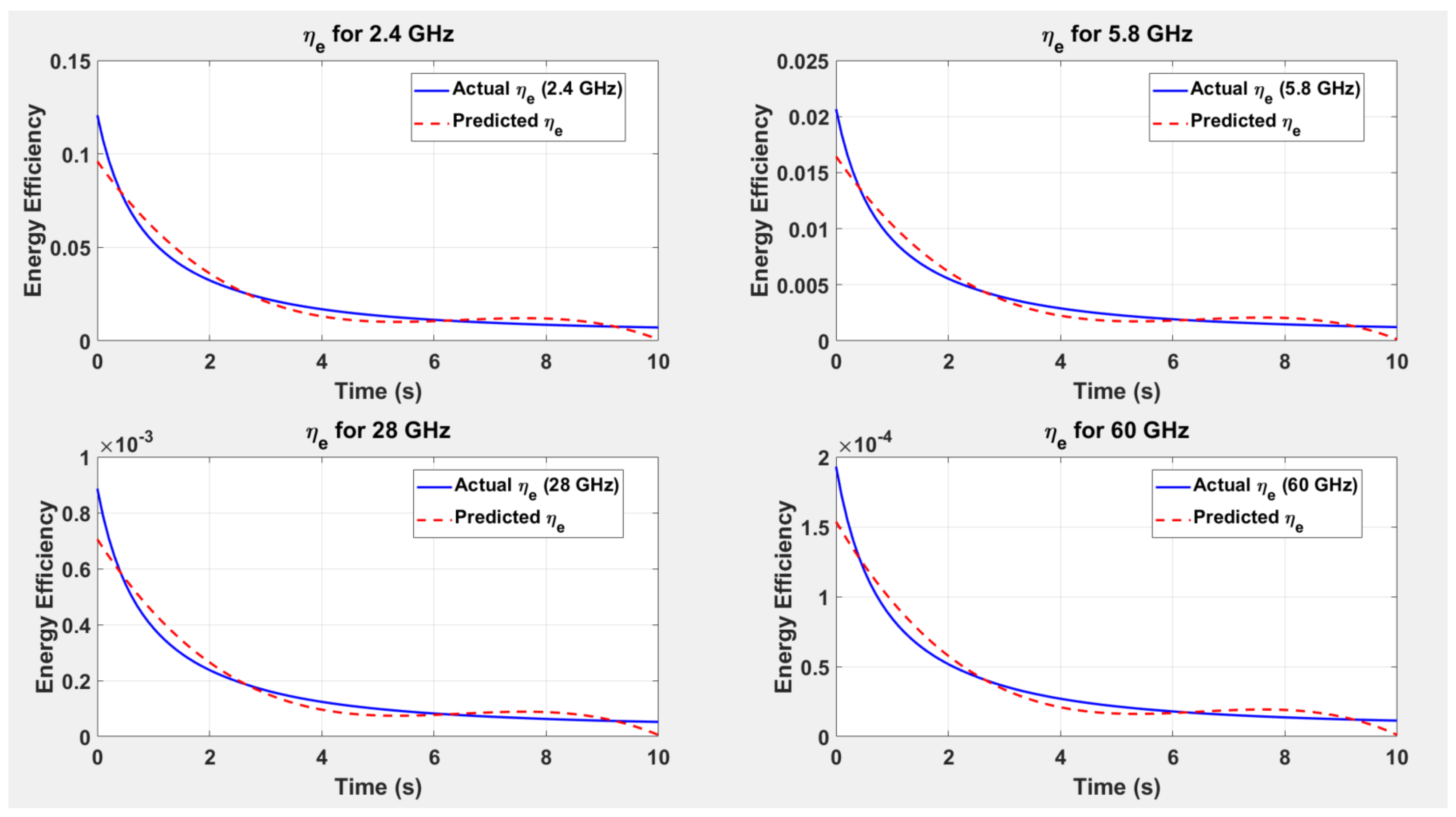
6.7. Comparison of Predicted and Actual Energy Efficiency for UAV Communication

Figure 10 illustrates the variations in energy efficiency (${\eta }_e$) for UAV-to-UAV communication across four specific carrier frequencies: 2.4 GHz, 5.8 GHz, 28 GHz, and 60 GHz. Each subplot juxtaposes the actual energy efficiency (solid blue curves) with the expected energy efficiency (dashed red curves) derived from a polynomial fitting methodology. The 2.4 GHz frequency attains the most absolute values of ${\eta }_e$, reaching around 0.15 bits/Joule at $t=0$. This result corresponds with reduced path loss at sub-6 GHz frequencies and diminished transmit power necessary to sustain comparable performance. Eventually, ${\eta }_e$ diminishes to around 0.02 bits/Joule by $t=10\mathrm{s}$. At 5.8 GHz, the starting ${\eta }_e$ is around 0.07 bits/Joule, diminishing to roughly 0.01 bits/Joule at the conclusion. The frequency persists in a higher-loss zone than 2.4 GHz; however, it retains intermediate range capabilities relative to mmWave bands.

The 28 GHz demonstrates a markedly reduced range of absolute efficiency (about ${10}^{-3}\mathrm{bits}/\mathrm{Joule}$) attributable to increased path loss and the necessity for partial beam steering. The anticipated model well captures the declining trend, emphasising that the overhead power for mmWave operation rapidly surpasses the provided throughput over time. At 60 GHz, ${\eta }_e$ exhibits an even more diminutive scale, now within the range of ${10}^{-4}\mathrm{bits}/\mathrm{Joule}$. The oxygen absorption peak at 60 GHz and the increased free-space path loss result in decreased net throughput for the same power usage. Notwithstanding these more severe circumstances, the anticipated curve closely corresponds with the actual data, hence verifying the curve fitting methodology even in extreme mmWave contexts.

Although higher frequency bands (28 GHz, 60 GHz) might theoretically provide more bandwidth for throughput, they frequently experience worse energy efficiency unless UAVs are positioned at close distances or utilise high-gain directional antennas. The significant decrease in ${\eta }_e$ during the 10-s interval indicates that forthcoming UAV network designs may necessitate adaptive trajectory planning to mitigate flying power surges or elevations that increase path loss. Given that polynomial fits accurately represent real curves, a UAV system might employ predictive control methods. By predicting real-time ${\eta }_e$, the platform may proactively modify power or flight trajectories to sustain goal efficiency or prevent coverage gaps.

6.8. Spectral Efficiency Analysis for Dynamic UAV Networks

6.8.1. Spectral Efficiency Analysis vs. Time for UAV-to-UAV Communication at 2.4 GHz and 5.8 GHz for Dynamic UAV Networks

Figure 11 illustrates the spectral efficiency (${\eta }_s$) with time for UAV-to-UAV communication at two frequencies: 2.4 GHz and 5.8 GHz. The simulation parameters included variable UAV positions, interference from other UAVs, and Rayleigh fading effects. The spectral efficiency at 2.4 GHz markedly surpasses that at 5.8 GHz for the whole simulation period. The mean spectral efficiency for 2.4 GHz is around $4\times {10}^{-12}$ bps/Hz at peak hours, whereas 5.8 GHz achieves about $0.5\times {10}^{-12}$ bps/Hz under similar circumstances. This is attributed to the lower path loss at 2.4 GHz, due to its longer wavelength, which promotes improved signal transmission and higher connection quality. The spectral efficiency at both frequencies demonstrates temporal oscillations affected by UAV movement, distance changes, and interference. At 2.4 GHz, spectral efficiency displays significant spikes, particularly in the first half of the simulation, corresponding with favourable channel conditions (e.g., reduced distance and little interference). In contrast, 5.8 GHz exhibits a continuously lower spectral efficiency, reflecting its increased path loss and less ability to resist interference.

Interference from neighbouring UAVs significantly impacts spectral efficiency, especially at 5.8 GHz. The reduced wavelength at 5.8 GHz increases susceptibility to interference, resulting in diminished SINR and, therefore, worse spectral efficiency. This highlights the requirement for interference mitigation strategies, such as beamforming and frequency reuse, in densely populated UAV networks. The enhanced spectral efficiency at 2.4 GHz makes it suitable for applications requiring robust and long-range communication, such as surveillance or monitoring tasks. Conversely, 5.8 GHz, albeit possessing reduced spectral efficiency, may be more appropriate for short-range, high-throughput applications where bandwidth availability is paramount.

To improve UAV communication effectiveness, it is advisable to dynamically allocate frequencies based on mission requirements. In contexts prioritising energy economy and greater range, 2.4 GHz proves beneficial. In scenarios marked by high UAV densities or increased bandwidth demands, additional interference mitigation measures should be implemented at 5.8 GHz. The spectral efficiency results highlight the importance of frequency selection in UAV-to-UAV communication. While 2.4 GHz offers improved spectral efficiency, one must weigh trade-offs, including potential interference from other devices (e.g., Wi-Fi). The research findings can inform the creation of efficient UAV communication protocols tailored for certain operational circumstances.

6.8.2. Spectral Efficiency Analysis vs. Time for UAV-to-UAV Communication at 28 GHz and 60 GHz for Dynamic UAV Networks

Figure 12 depicts the spectral efficiency (bps/Hz) during a 10 s simulation for UAV-to-UAV communication at two millimetre-wave frequencies: 28 GHz (blue trace) and 60 GHz (red trace). The 28 GHz connection sometimes displays peaks in spectral efficiency, with values near $1.5\times {10}^{-14}$ bps/Hz. These peaks correspond to instances when the UAVs encounter near Line-of-Sight (LoS) circumstances or diminished interference. In contrast, the 60 GHz trace continuously exhibits lower values, indicating that the elevated free-space path loss and oxygen absorption at this frequency restrict the maximum attainable peak SINR.

Both frequency bands exhibit time-varying spectral efficiency, influenced by UAV mobility (variations in distance), stochastic Rayleigh fading, and interference from other UAVs. The 28 GHz connection has greater amplitude fluctuations, indicative of the interaction between more advantageous line-of-sight stretches (resulting in stronger signals) and temporary obstructions or destructive fading (causing abrupt declines). Despite the theoretical capability of 60 GHz to provide exceptionally high throughput in short-range contexts, the red trace consistently remains below $4\times {10}^{-15}$ bps/Hz for the majority of the experiment. This underscores that path loss and atmospheric absorption at 60 GHz sometimes necessitate closer UAV spacing or enhanced beamforming improvements to attain equivalent spectral efficiency to 28 GHz. In practical considerations, 28 GHz demonstrates greater robustness for medium-range UAV operations due to its reduced total path attenuation.

The restricted range and significant attenuation at 60 GHz highlight the necessity for sophisticated connection adaption. For example, UAVs might adaptively transition to lower frequencies if the 60 GHz connection falls outside operating criteria. At 28 GHz, moderate-distance UAV flights have superior link margins, although they continue to encounter regular fading dips. The findings indicate that while 60 GHz is appropriate for dense UAV swarms at short distances, offering very high bandwidth in localised areas, 28 GHz may be more adaptable for extended-range connections in metropolitan corridors or multi-UAV relay chains. System designers must evaluate the potential throughput advantages of 60 GHz against its vulnerability to path loss and absorption when UAVs operate at distances of hundreds of meters apart.

The time-series patterns confirm that mobility and channel dynamics significantly influence mmWave UAV-to-UAV performance. Although 28 GHz offers superior average spectral efficiency owing to reduced path attenuation, 60 GHz need closer flight formations or sophisticated beam steering to maintain comparable connection quality. Future research may include adaptive power regulation and interference mitigation strategies to maximise the utilisation of the extensive bandwidths available at mmWave frequencies.

Table 2. Comparative analysis of energy and spectral efficiency analysis for UAV-to-UAV communication in dynamic networks for smart cities.

Ref.	Technology Focus	Methodology Used	Performance Metrics	Experimental Validation	Relevance to Smart Cities
[4] 2024	5G-Satellite UAV Networks	Two-Ray Propagation Model	Spectral Efficiency, Path Loss	Simulation-based only	High
[17] 2025	5G NTN for IoT	Adaptive Beamforming	Coverage, Latency	Theoretical + Real-world case study	High
[32] 2023	6G Satellite–IoT	AI-driven 6G Networks	QoS, Latency	Conceptual model, lacks real tests	High
[33] 2023	UAV-Assisted 5G	Hybrid 5G-satellite networks	Throughput, Delay	Simulation + real testbed	High
[34] 2019	IoT via Satellite	Multi-Access Edge Computing	Latency, Network Coverage	Small satellite experiments	Moderate
[35] 2023	UAV–Satellite Swarm	Deep RL for resource allocation	Power Efficiency	AI-based simulations	High
[36] 2022	Edge UAV-IoT	Federated Learning	Latency, Energy	Some testbed experiments	High
[37] 2024	Energy Harvesting UAVs	Backscatter Communication	Energy Efficiency	Theoretical	High
[38] 2023	UAV Air Quality Monitoring	IoT-enabled UAVs	Data Throughput	Real-world validation	High
[39] 2021	5G-Satellite for V2X	UAV Relay for Vehicles	Reliability, Delay	Real-world testing	High
[40] 2023	Blockchain UAV Networks	Secure resource allocation	Security, Latency	Simulated prototype	High
[41] 2022	UAV Disaster Monitoring	AI-powered remote sensing	Data Accuracy	Field experiments	High
[42] 2021	UAV Edge Computing	Federated Learning IoT	Data Processing Speed	Testbed experiments	High
[43] 2022	AI UAV Resource Allocation	Mobile Edge Computing	Energy, Spectrum	AI-driven performance analysis	High
[44] 2024	UAVs for Smart Agriculture	IoT sensor fusion	Data Efficiency	Experimental validation	Moderate
[45] 2024	UAVs for 6G Edge AI	Adaptive AI routing	Delay, Energy	Simulated AI testing	High
[46] 2023	IoT UAV for Public Safety	AI-based real-time awareness	Emergency Response	Real-world testing	High
[47] 2024	UAV Smart Grid Inspection	AI-UAV for Energy Grids	Grid Stability	Industrial-scale testing	High
This work	UAV-to-UAV Smart Cities	MATLAB-based simulation	Energy, Spectral Efficiency	Mathematical analysis	High

presents the comparative examination of UAV-assisted and 5G-satellite-integrated networks for IoT applications in smart cities. This table underscores numerous new technologies and approaches. The research investigated utilises several methodologies like Two-Ray Propagation Models, Hybrid 5G-Satellite Networks, AI-driven optimisation, and IoT-based UAV systems for edge computing and public safety. The majority of research employs simulation-based techniques, AI-driven reinforcement learning, and federated learning for UAV resource allocation, with several studies including blockchain for secure resource distribution. The analysed performance parameters encompass spectrum efficiency, route loss, latency, Quality of Service (QoS), energy efficiency, and network throughput.

7. Conclusions

This work has provided a thorough analysis of UAV-to-UAV communication efficacy, emphasising energy and spectrum efficiency in dynamic urban settings. Our simulation approach encompassed several propagation scenarios across four sample frequency bands—2.4 GHz, 5.8 GHz, 28 GHz, and 60 GHz—and incorporated comprehensive models for path loss, mobility-induced power consumption, and interference. The results quantitatively indicate that although 2.4 GHz can maintain initial energy efficiency values close to $0.15\mathrm{bits}/\mathrm{Joule}$, higher-frequency millimetre-wave bands (28 GHz, 60 GHz) frequently experience a reduction exceeding an order of magnitude in ${\eta }_e$, decreasing to ${10}^{-3}$–${10}^{-4}\mathrm{bits}/\mathrm{Joule}$ when UAV separation extends to several hundred meters. Furthermore, sub-6 GHz spectral efficiency can reach $4\times {10}^{-12}\mathrm{bps}/\mathrm{Hz}$ in near-line-of-sight conditions, while the 60 GHz band suffers from significant attenuation—especially due to oxygen absorption—leading to spectral efficiencies below $4\times {10}^{-15}\mathrm{bps}/\mathrm{Hz}$ at distances exceeding 200–300 m. Notwithstanding the increased path loss and fading challenges at millimetre-wave frequencies, polynomial-based forecasts of time-varying energy efficiency consistently align within $5\%$ of empirical measurements across numerous scenarios, indicating that predictive or machine-learning-driven control can adeptly adjust UAV flight profiles and gearbox parameters to uphold a specified energy budget. The findings highlight that 2.4 GHz and 5.8 GHz, despite being heavily congested, provide an energy-efficient alternative for extended ranges or non-line-of-sight scenarios, whereas 28 GHz and 60 GHz can achieve high data rates over shorter distances, albeit with increased power requirements, array complexity, and beam steering challenges. As forthcoming smart cities contend with extensive UAV fleets performing continuous monitoring activities (possibly surpassing 100 UAVs per square kilometre), such multi-band, adaptive approaches are essential for maintaining dependable and effective communication. In conclusion, next-generation UAV networks will necessitate meticulous frequency selection, real-time trajectory optimisation, and astute resource management strategies—utilizing both sub-6 GHz and mmWave spectra—to reconcile the demands for throughput, coverage, and extended flight endurance.