Highlights
The integration of advanced computational techniques into energy optimization is crucial to building sustainable and efficient urban energy systems. VPPs play a key role in smart cities by enabling the seamless management of renewable energy resources, energy storage, and electric vehicles. This study demonstrates how HPC and parallelized SA can optimize energy distribution, improve grid stability, and maximize social welfare. By addressing challenges like battery lifespan and real-time energy trading, this work supports the development of smarter, more sustainable cities with resilient and equitable energy systems.
What are the main findings?
- A novel parallelized SA algorithm was developed and implemented by using OpenMP on HPC infrastructure, delivering a substantial reduction in computational time for VPP scheduling.
- The approach showcases significant scalability, efficiently optimizing large-scale VPP networks with up to 512 prosumers, ensuring that the system remains robust as network complexity and size increase.
- By achieving near-linear speedup ratios across up to 32 cores, the algorithm leverages parallel computing to accelerate decision-making processes in real-time energy markets.
- The study integrates critical operational constraints, such as battery lifespan limitations and dynamic energy pricing, enabling sustainable and adaptive energy management while maintaining high-quality optimization outcomes.
- Extensive simulations demonstrate the effectiveness of the proposed framework in balancing energy acquisition, storage, and dispatch decisions across diverse DERs, contributing to smarter energy distribution systems.
What is the implication of the main findings?
- The enhanced computational efficiency and scalability of the parallelized SA approach make it a practical and advanced solution for real-time VPP scheduling, ensuring reliable and adaptive energy management in dynamic market environments.
- This framework supports the development of future smart city energy systems—as evidenced by its strategic deployment in Portugal in the national project New Generation Storage (NGS)—by enabling the seamless integration of renewable energy sources, electric vehicles, and energy storage systems, ultimately contributing to a resilient, low-carbon energy ecosystem.
- By optimizing energy distribution with a focus on maximizing social welfare, the framework aligns with the principles of economic sustainability, grid stability, and environmental responsibility in smart cities.
- The findings highlight the transformative role of HPC and parallel computing in addressing the growing complexity of energy systems, providing a scalable and efficient blueprint for enhancing energy optimization and distribution in urban settings.
Abstract
This work focuses on optimizing the scheduling of virtual power plants (VPPs)—as implemented in the Portuguese national project New Generation Storage (NGS)—to maximize social welfare and enhance energy trading efficiency within modern energy grids. By integrating distributed energy resources (DERs), including renewable energy sources and energy storage systems, VPPs represent a pivotal element of sustainable urban energy systems. The scheduling problem is formulated as a Mixed-Integer Linear Programming (MILP) task and addressed by using a parallelized simulated annealing (SA) algorithm implemented on high-performance computing (HPC) infrastructure. This parallelization accelerates solution space exploration, enabling the system to efficiently manage the complexity of larger DER networks and more sophisticated scheduling scenarios. The approach demonstrates its capability to align with the objectives of smart cities by ensuring adaptive and efficient energy distribution, integrating dynamic pricing mechanisms, and extending the operational lifespan of critical energy assets such as batteries. Rigorous simulations highlight the method’s ability to reduce optimization time, maintain solution quality, and scale efficiently, facilitating real-time decision making in energy markets. Moreover, the optimized coordination of DERs supports grid stability, enhances market responsiveness, and contributes to developing resilient, low-carbon urban environments. This study underscores the transformative role of computational infrastructure in addressing the challenges of modern energy systems, showcasing how advanced algorithms and HPC can enable scalable, adaptive, and sustainable energy optimization in smart cities. The findings demonstrate a pathway to achieving socially and environmentally responsible energy systems that align with the priorities of urban resilience and sustainable development.
1. Introduction
The increasing penetration of DERs, including renewable energy sources (RESs) like wind and sunlight, presents both opportunities and complexities in managing modern power systems. VPPs have emerged as a powerful framework to integrate and coordinate DERs for enhanced grid stability, economic efficiency, and active participation in energy markets [1,2].
VPPs act as single aggregated entities, facilitating seamless interaction with the grid. They coordinate diverse energy sources, such as RESs, electric vehicles (EVs), and energy storage systems (ESSs) [3,4]. In the context of smart cities, VPPs serve as dynamic facilitators of decentralized energy management by aggregating DERs to balance supply and demand, reduce carbon emissions, and enhance energy efficiency [5]. By integrating advanced technologies like Vehicle-to-Grid (V2G), VPPs can provide ancillary services, improve grid resilience, and enable smart energy systems tailored to urban environments [6]. These systems also allow urban planners to optimize energy flows by leveraging real-time data from interconnected devices, including smart streetlights and EV charging stations, thus promoting sustainable urban development [7].
However, optimizing the scheduling and operation of VPPs poses substantial challenges due to the uncertainties associated with RES generation, load demand, and market prices. These challenges necessitate sophisticated optimization strategies that can balance the supply–demand dynamics while maximizing economic and social benefits for VPP participants [8,9]. As a central component of smart city initiatives, VPPs must navigate the complexities of integrating diverse energy resources while maintaining operational flexibility and economic viability. The integration of EVs as mobile DERs adds further complexity, as their charging and discharging schedules impact not only grid stability but also the broader urban energy ecosystem [4,10]. Recent studies have addressed these challenges by exploring multi-agent systems and adaptive risk management to enhance the resilience and cybersecurity of distributed energy systems [11]; leveraging MILP-based algorithms for optimizing energy trading, load scheduling, and resource allocation [12]; and benchmarking open-source optimization tools to improve energy storage strategies and operational scalability in VPPs [13].
Traditional optimization techniques, such as MILP, often struggle to address the scalability and complexity requirements of large-scale VPP scheduling problems, especially under real-time constraints [14,15]. As the scale of VPPs grows, both in terms of the number of DERs and the sophistication of market mechanisms, there is a compelling need for robust optimization techniques capable of handling these demands efficiently [16]. Consequently, heuristic and metaheuristic methods, notably SA, have gained attention for their flexibility and effectiveness in navigating complex solution spaces typical in VPP scheduling [17,18].
SA, a stochastic optimization method inspired by the annealing process in metallurgy, has been widely applied to solve non-linear, multidimensional, and constraint-heavy optimization problems [16,19]. In VPP contexts, SA proves valuable in managing energy dispatch, balancing energy acquisition and storage usage, and optimizing market participation [16,20]. Recent research demonstrates that SA is effective in achieving competitive results in VPP scheduling, particularly when integrated with demand response (DR) programs and various DERs, including RESs and storage units [9,18]. Nevertheless, standalone SA approaches can face scalability issues in large VPP configurations involving numerous DERs and complex market constraints [15,21].
To address these scalability constraints, researchers have turned to HPC to facilitate parallelized versions of SA. Parallel computing, with advancements in both hardware and software platforms, has shown significant potential for accelerating optimization processes and handling the extensive data required for real-time VPP scheduling [15,22]. HPC-enabled parallel SA implementations allow for the decomposition of large-scale optimization problems into manageable subproblems, enhancing computational efficiency while maintaining solution quality [23]. By leveraging multi-threading, parallel SA algorithms reduce convergence times and enable the management of large VPP networks, making it feasible to optimize energy acquisition and dispatch at a high temporal resolution [24]. The role of HPC in enabling real-time VPP optimization extends beyond simple computational speedups. Parallelized SA studies show that HPC systems efficiently manage complex scheduling by processing detailed, time-sensitive data in real time [21,25]. This capability is particularly valuable for VPP operators, who must respond dynamically to fluctuations in renewable generation, load demand, and market conditions [26]. Moreover, parallel SA-based approaches enable the simultaneous evaluation of bidding strategies for VPPs, streamlining decision-making processes within local energy markets [23].
This paper introduces a novel parallelized SA algorithm for VPP scheduling, implemented on HPC infrastructure by using OpenMP. The model focuses on maximizing social welfare while respecting operational constraints, such as battery degradation and DER variability. This approach aims to achieve near-optimal scheduling solutions by leveraging parallelization to improve computational speed and solution quality. Through rigorous simulations, we demonstrate the effectiveness of our method in reducing optimization time while maintaining high-quality solutions across various VPP configurations [16,18].
The structure of this paper is designed to offer a comprehensive and sequential examination of our proposed approach. In Section 2, we begin by reviewing the recent literature on VPP optimization, applications of SA in energy resource management, and the critical role of HPC in enhancing optimization strategies. This foundation sets the stage for Section 3, where we outline the problem description and mathematical formulation of the VPP scheduling challenge. Within this section, a tailored search space representation is derived to address the specific requirements of parallelized algorithm design, and we introduce a customized parallel SA algorithm that efficiently navigates this search space by leveraging HPC capabilities.
Subsequently, Section 4 details the parameter tuning and parallelization techniques used to maximize the algorithm’s performance, including an in-depth overview of the HPC environment configurations and essential parameters employed for the design of the experiments.
We analyze the computational and scheduling outcomes in Section 5, emphasizing the scalability and solution quality achieved with the parallelized SA approach. This analysis provides insights into the performance gains enabled by the HPC-enhanced framework. Finally, in Section 6, we summarize our findings, highlighting the implications of this approach for advanced VPP scheduling and potential directions for future research in optimization and HPC applications in energy systems.
2. Related Works
The development of VPPs has become essential to modern power systems due to their ability to integrate DERs such as RESs, EVs, and ESSs. Effective VPP optimization frameworks are critical to ensuring that these resources contribute positively to grid stability, operational efficiency, and market participation. This section examines recent methodologies and advancements in VPP optimization, focusing on approaches aimed at achieving effective scheduling, energy management, and market alignment for VPPs.
2.1. Optimization Strategies for Virtual Power Plants
A wide range of optimization strategies has been developed for VPPs, to integrate DERs while ensuring operational efficiency and profitability. Optimization techniques for VPPs include heuristic and metaheuristic methods, game-theoretic approaches, and multi-objective optimization models.The work by Podder et al. [1] presents a categorization of 65 VPP optimization strategies, highlighting methods that integrate RESs and energy storage. The study shows that combining wind power with demand response effectively mitigates intermittency challenges, making VPP scheduling more resilient. Additionally, VPPs have been identified as a critical strategy for integrating distributed energy resources into smart city power systems. Comprehensive reviews [5] emphasize the use of hierarchical control techniques and secure communication networks to manage DERs and energy storage systems effectively. These approaches enable demand-side frequency control ancillary services (D-FCASs), enhancing grid stability and supporting the development of sustainable energy systems [7]. Similarly, surveys on microgrid, smart grid, and VPP technologies [27] highlight the role of advanced control mechanisms and technical solutions in achieving energy sustainability. The integration of these technologies is vital to balancing operational efficiency with environmental goals in smart cities [28]. By leveraging advanced market mechanisms, VPPs facilitate participation in energy markets while balancing electricity supply and demand in dynamic smart grid environments [10].
The role of game theory in VPP optimization is particularly notable for its ability to handle the interactions among multiple prosumers in a VPP, allowing for dynamic energy scheduling that aligns generation and consumption with real-time pricing. For example, Zhang et al. [8] demonstrates in their study a game-theoretic model that successfully enhances VPP operations with prosumer participation, resulting in optimal payoff distribution across both residential and commercial VPP users. Such approaches underscore the flexibility required in VPPs to adapt to market fluctuations and DER uncertainties.
Multi-level and multi-objective optimization frameworks are also prominent in VPP scheduling, enabling VPPs to balance competing objectives like cost minimization, emission reduction, and customer satisfaction. Ali et al. [4] proposes a multi-level, multi-objective optimization model that leverages advanced algorithms to achieve effective load scheduling, energy cost reduction, and greenhouse gas minimization within VPPs. The approach, which applies algorithms like AMO-GWO, demonstrates the capability of advanced optimization frameworks to incorporate various real-time constraints while enhancing VPP performance.
Researchers have developed hierarchical and adaptive optimization models to address the need for real-time adaptability in VPPs. Krishna et al. [29] explores an energy management approach using a teaching-and-learning-based optimization (TLBO) algorithm, showing that it can effectively minimize VPP operating costs. The TLBO-based model is particularly effective for optimizing over a 24 h horizon, which is useful for applications that require short-term energy management and quick decision making. Similarly, Muttaqi et al. [30] introduces an adaptive, predictive energy management strategy that combines model predictive control (MPC) with feedback correction to optimize real-time VPP operations, improving both economic outcomes and grid stability by effectively handling uncertainties.
Robust optimization frameworks are also widely applied in VPP scheduling to handle the uncertainties associated with RESs and fluctuating market conditions. For instance, Naughton et al. [31] discusses a robust scheduling model for VPPs that uses a receding horizon dispatch approach, maximizing revenue while managing system and market uncertainties in a three-stage optimization framework. The methodology was validated in a real-world case study, demonstrating its effectiveness in maximizing VPP flexibility and revenue in uncertain operating environments.
Furthermore, multi-scale and multi-time-scale approaches enable VPPs to coordinate their operations over varying timeframes. The study carried out by Yi et al. [32] proposes a multi-time-scale scheduling strategy that aggregates and disaggregates deferrable loads in a VPP, enabling more effective participation in both energy and reserve markets. This strategy addresses the scheduling complexity of handling deferrable loads, achieving economic efficiency while maintaining operational reliability in VPP systems.
Finally, innovative bidding strategies are being developed to improve VPP profitability in competitive energy markets. For example, the study conducted by Tang et al. [33] proposes a coordinated bidding and operation model for VPPs, focusing on optimizing energy storage and demand response integration. By incorporating robust optimization techniques, the model adapts to uncertain energy prices and RES variability, demonstrating improved profit margins in both day-ahead and real-time markets.
Collectively, these studies highlight the diverse strategies available for VPP optimization, each offering unique contributions to the challenges of managing DERs and maximizing VPP efficiency. With advances in computational techniques and algorithmic frameworks, the VPP paradigm continues to evolve, providing effective solutions for integrating renewable resources and managing demand in modern energy systems.
SA is a metaheuristic optimization technique extensively applied in energy resource management for VPPs due to its ability to handle complex, multidimensional problems effectively. SA, inspired by the physical annealing process, operates by probabilistically accepting suboptimal solutions in the early stages of the optimization process, thus allowing the algorithm to escape local optima and explore the global solution space more comprehensively [9]. This characteristic makes SA well suited to the non-linear, constraint-heavy nature of VPP scheduling, especially where DERs and market fluctuations contribute to significant uncertainty.
While SA offers significant advantages for optimizing VPP scheduling, it is essential to explore the broader array of metaheuristic algorithms being employed to enhance performance in this domain. The optimization of VPPs has emerged as a critical area of research, particularly given the rising reliance on renewable energy sources and the necessity for efficient management of decentralized energy resources. Recent studies have identified the application of diverse metaheuristic techniques, including Ant Colony Optimization (ACO) [34], Genetic Algorithms (GAs) [35], and the Whale Optimization Algorithm (WOA) [36], to formulate optimal bidding strategies aimed at maximizing profits within local energy markets (LEMs). These methodologies effectively navigate the complexities inherent to competitive electricity markets, underscoring the significance of strategic learning and agent interaction in enhancing market outcomes [23]. Angulo et al. [23] demonstrated the effectiveness of these metaheuristics in managing diverse energy resources within small microgrids. Additionally, Rädle et al. [37] proposed a flexible control methodology for optimizing hierarchical VPPs utilizing various computational intelligence (CI) metaheuristics, including SA and ACO, to minimize operating reserves and emissions and enhance power plant flexibility. This combination of hierarchical structures with CI techniques reflects an ongoing trend toward improving computational methods for robust and efficient VPP operations, addressing the unique challenges posed by the varying characteristics and constraints of different VPP configurations.
In recent years, researchers have leveraged SA in VPP contexts to address various challenges in energy dispatch, demand response integration, and grid stability. For instance, one study demonstrated that integrating SA with a custom heuristic improved the handling of electric vehicles (EVs) as distributed energy resources, optimizing charging and discharging schedules to enhance grid stability and maximize economic benefits for VPP operators [16]. Another application of SA in VPPs involved energy management systems that incorporate demand response strategies, showcasing SA’s capacity to adjust for demand fluctuations and reduce energy costs effectively. In simulations, the SA-based approach outperformed particle swarm optimization and other deterministic methods, indicating its robustness and adaptability under varying network conditions [17].
Furthermore, researchers have applied SA to optimize bidding strategies in electricity markets, with studies illustrating how SA-based algorithms can enhance the profitability of VPPs by strategically timing energy transactions [18]. By dynamically adjusting the bidding behavior based on real-time market data, SA-driven optimization has demonstrated improvements in computational efficiency and revenue maximization, solidifying SA’s relevance in competitive energy markets.
In addition to market participation, SA has proven effective in addressing the dynamic economic dispatch problem within VPPs, particularly when integrating renewable resources such as wind energy. By accommodating the intermittent nature of renewable energy sources, SA-based algorithms can minimize generation costs and maximize social welfare, showcasing their potential for sustainable energy management [19]. Studies implementing SA in economic dispatch frameworks have achieved lower generation costs and increased utilization of renewable resources, demonstrating SA’s capacity to adapt to the evolving energy landscape and support sustainable energy goals.
The adoption of SA in energy resource management for VPPs thus highlights its versatility and efficacy across various operational scenarios. Its adaptability to real-time conditions and robustness in handling uncertainty positions SA as a crucial tool in the pursuit of optimized, resilient, and profitable VPP operations.
2.2. Parallel Computing for VPP Optimization
The computational complexity of VPP optimization has driven interest in HPC and parallel computing methods as viable solutions to scale optimization processes effectively. Traditional optimization methods often fall short under the real-time constraints imposed by the dynamic and large-scale nature of VPPs, particularly as they expand in terms of DERs, market participation, and operational requirements [21]. Parallel computing, supported by HPC infrastructure, has demonstrated significant potential for accelerating optimization processes and enhancing solution quality, especially in VPP applications that require frequent adjustments based on real-time data.
A variety of studies have investigated parallel computing as a tool for addressing the high-dimensional optimization problem in VPPs. For instance, Alvarez et al. [24] explored the application of parallel processing in security-constrained optimal power flow analysis (SCOPF), demonstrating that parallelized models could reduce computational time without sacrificing solution quality. These methods are relevant in VPP contexts where security and contingency planning are essential to reliable grid integration.
Research has also highlighted the role of parallel computing in supporting stochastic and scenario-based optimization frameworks that manage uncertainty within VPP operations. A scalable framework for the stochastic optimization of complex energy systems, as presented in [15], leveraged parallel interior-point methods to solve large-scale dispatch problems involving wind power, achieving significant scalability and efficiency improvements. This framework underscores the value of HPC-enabled optimization in VPP scheduling, where DER variability and market fluctuations pose challenges to deterministic methods.
Another promising application of parallel computing for VPPs is in demand response and market participation. By utilizing exhaustive search through parallel computing, Angulo et al. [23] investigated bidding strategies for local energy markets, finding that metaheuristic approaches achieved near-optimal results within acceptable computational timeframes. These findings suggest that parallel processing can enhance the effectiveness of VPPs as market participants, providing competitive pricing and efficient resource allocation.
High-performance computing platforms such as the PIPS-IPM solver, as documented in [22], have enabled the real-time stochastic optimization of power grids with large-scale variables, further validating the role of parallel architectures in solving computationally intensive VPP scheduling tasks. The application of HPC here not only supports rapid decision making but also enhances grid stability by enabling VPPs to respond dynamically to load changes, renewable generation variability, and price signals.
Parallel computing approaches, when combined with adaptive optimization algorithms like SA, provide additional avenues for scaling VPP optimization. Hybrid methods incorporating SA with parallel processing have shown efficacy in handling the multidimensional, constraint-heavy optimization requirements inherent to VPPs, as demonstrated by [9]. This integration allows for distributed problem solving, whereby each node in the HPC cluster optimizes a subset of the VPP’s DERs, leading to faster convergence and higher-quality solutions in comparison to serial approaches.
Parallel computing represents a transformative approach to VPP optimization, especially as DER penetration increases and real-time market responsiveness becomes critical. Through multi-threading, distributed computation, and advanced parallel algorithms, VPP operators can efficiently schedule and manage a large network of DERs, ultimately contributing to a more flexible and responsive power grid.
2.3. Role of High-Performance Computing (HPC) in Advanced VPP Scheduling
The integration of HPC into virtual power plant (VPP) scheduling represents a significant step forward in managing the complexities associated with large-scale energy systems. With the growing penetration of DERs and the increasing demand for responsive, dynamic power systems, HPC provides the computational power needed to enable the real-time scheduling and management of VPPs. Researchers have demonstrated that HPC infrastructure can drastically enhance the scalability of optimization algorithms in energy systems, allowing for the decomposition of large-scale VPP scheduling tasks into manageable subproblems [21,22]. This scalability is crucial to maintaining solution quality, as VPPs incorporate diverse and variable energy sources, such as wind, sunlight, and electric vehicles (EVs), while adhering to market constraints.
Parallel computing frameworks, particularly those leveraging HPC clusters, have been applied to VPP scheduling to expedite solution times and handle increased complexity. Studies show that parallelized scheduling algorithms reduce computational times significantly, enabling VPP operators to make near-real-time adjustments based on load demand, renewable generation forecasts, and grid stability requirements [24]. These parallel architectures allow for the simultaneous optimization of multiple objectives, such as cost reduction, system reliability, and carbon emission minimization, which are essential to modern VPP operations [15].
Advanced HPC-enabled stochastic optimization techniques, like those developed for real-time power grid optimization, have also been adapted for VPP contexts. For instance, the PIPS-IPM solver, originally designed for complex power grid systems, has shown efficacy in addressing stochastic dispatch problems by supporting large datasets and processing power-intensive calculations in real time [22]. This advancement underscores HPC’s role in improving the precision of VPP scheduling, as high-performance solvers facilitate the integration of uncertainty in demand and generation forecasts, ultimately enhancing the robustness of VPP management strategies [23].
Moreover, the use of HPC allows for enhanced simulation and optimization techniques, supporting sophisticated bidding strategies in energy markets. By implementing exhaustive search algorithms and metaheuristic optimization on HPC frameworks, VPPs can simulate a range of market scenarios and derive optimal bidding strategies that maximize profitability under market uncertainty [9]. These HPC-based methods ensure that VPPs remain competitive and adaptive, effectively responding to dynamic market conditions and integrating higher levels of renewable generation [15].
HPC has emerged as an indispensable enabler for addressing the growing complexity and scalability challenges of VPP optimization. While the existing literature has extensively explored heuristic and metaheuristic methods, such as GA, PSO, and SA, for energy scheduling, their scalability and real-time applicability in large-scale networks often remain constrained. This study distinguishes itself by leveraging HPC to develop a parallelized version of the SA algorithm specifically tailored for the VPP scheduling problem. By capitalizing on OpenMP-enabled parallelism, the proposed approach overcomes computational bottlenecks typically associated with SA in high-dimensional, constraint-heavy optimization tasks.
The novelty of this work lies in the seamless integration of operational constraints, such as battery lifespan considerations and acquisition–dispatch exclusivity, into the optimization framework, ensuring both practical relevance and adaptability. Additionally, this study addresses a significant gap in the literature by demonstrating the scalability of a parallelized SA algorithm in optimizing VPP networks with hundreds of prosumers, achieving near-linear speedup ratios across multiple cores. This level of scalability is critical to modern VPPs, where the complexity of scheduling grows exponentially with the number of DERs and market dynamics.
Furthermore, this work advances the state of the art by emphasizing the real-time applicability of parallelized metaheuristics for VPP optimization. Unlike previous studies that focus primarily on static or small-scale problem instances, this approach is designed to adapt dynamically to evolving market conditions, providing responsive and reliable solutions for real-time energy trading and resource allocation. The HPC-enabled framework facilitates high-frequency decision making, allowing VPP operators to optimize scheduling efficiency and market participation in highly volatile energy environments.
In comparison to prior studies, which often evaluate optimization methods in idealized or simplified scenarios, this work bridges the gap between computational advancements and practical implementation. By coupling parallelized metaheuristic optimization with HPC capabilities, this study offers a scalable, high-performance solution to the increasingly sophisticated requirements of modern VPPs, positioning itself as a significant contribution to the ongoing evolution of sustainable energy systems.
3. Methodology
3.1. Problem Description
The VPP market optimization service is a critical framework designed to achieve efficient, real-time energy management by orchestrating the interactions between grid demands and prosumer activities. This service comprises two key components: forecasting and optimization. The forecasting component analyzes both real-time and historical data to predict future energy demand, supply trends, and market dynamics, providing the optimization module with essential insights. These forecasts enable the optimization service to determine prosumer schedules that maximize social welfare by balancing energy demand and supply across the VPP network.
At the heart of this optimization framework is the objective of maximizing social welfare through the strategic scheduling of energy transactions for each VPP entity. Each VPP functions as a prosumer, capable of buying or selling electricity to the grid within each period. The optimization service processes both forecasted and real-time data to compute the optimal quantities each prosumer can buy or sell. Importantly, the optimization does not involve price offers from prosumers; rather, it aligns prosumer transactions based on the predetermined price signals issued by the grid, which remain fixed per period.
The system architecture is supported by an Internet of Things (IoT) data streaming platform that facilitates continuous data flow between the prosumer devices and the optimization service. This platform manages the acquisition and storage of data from prosumer devices, including their energy generation, consumption, and battery states. Furthermore, it distributes the optimized scheduling decisions back to prosumer devices in real time, enabling them to execute the prescribed buy or sell quantities. This IoT-enabled data infrastructure thus supports the real-time decision-making capabilities essential to responsive VPP market operations.
The optimization service operates within a structured ecosystem that includes three primary entities: the grid, the prosumers (VPPs), and the internal VPP market. The grid sets the electricity price per period, while prosumers, restricted to submitting quantity offers, adjust their buy or sell behaviors in response to this fixed pricing. Within the VPP market, the optimization service coordinates these transactions to maximize overall market welfare while satisfying operational constraints. The optimization ensures that the market functions effectively by aligning prosumer activities with grid-imposed conditions to maintain market stability and operational resilience.
The design requirements for this optimization framework are as follows:
- Rolling-based Social Welfare Optimization: The primary goal is to maximize social welfare by scheduling energy transactions in a way that meets the collective needs of the grid and prosumers. This optimization is conducted on a rolling basis, allowing the model to respond dynamically to real-time changes in demand and supply, ensuring alignment with current market dynamics. By reformulating the problem as a minimization objective, the framework incorporates broader considerations, such as battery utilization and operational costs, ensuring that social welfare is achieved while maintaining efficiency and cost-effectiveness across the system.
- Scalability to Accommodate Expanding Market Demand: The framework must scale efficiently with an increasing number of prosumers, preserving computational efficiency and execution timeliness as the participant count grows. This scalability is essential to upholding the system’s performance standards within an expanding VPP market.
- Battery Health Constraints: To ensure the long-term operational viability of prosumer batteries, the optimization incorporates constraints that regulate battery charge and discharge cycles. These constraints maintain battery states within defined limits, promoting sustainable energy practices and prolonging battery life.
- Grid-Determined Pricing and Quantity-Based Scheduling: In this scenario, electricity prices are determined by the grid, with no price offers from prosumers. The optimization aligns each prosumer’s transactions with these predefined price signals, allowing prosumers to submit only the quantities they can generate or consume. This ensures a streamlined, price-sensitive scheduling approach within the VPP market.
The VPP market optimization model addresses a complex, dynamic problem that demands the seamless integration of forecasting, data streaming, and adaptive scheduling capabilities. To support the requirements of modern energy systems, this architecture must deliver scalability, real-time responsiveness, and robust data management. By harnessing predictive data and coordinating prosumer activities with established economic and operational constraints, the VPP optimization service strives to enhance market welfare, foster sustainable energy practices, and facilitate agile, market-aligned decision making in real-world energy management scenarios.
Figure 1 provides an overview of the VPP management framework in a grid-regulated pricing environment. The framework highlights the interactions among prosumers, the VPP market, and the grid. In this system, the VPP serves as an intermediary, coordinating energy trading activities among prosumers and ensuring alignment with centrally regulated electricity prices set by the grid.
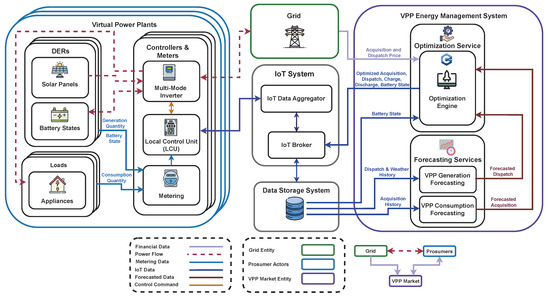
Figure 1.
A schematic of the VPP management framework, illustrating the core components and data flow among prosumers, the VPP market, and the grid. The VPP acts as an intermediary, facilitating energy trading under grid-regulated prices, with a central scheduler optimizing resource allocation.
Prosumers continuously transmit real-time data, including energy generation, consumption, and battery states, to the VPP market via an IoT-enabled data streaming platform. This platform forms the backbone of the system, enabling seamless communication and data exchange.
The VPP’s energy management system, which operates as a central scheduler, comprises two key modules. The first is a forecasting module that leverages real-time and historical data to predict energy generation and consumption patterns for each prosumer. These forecasts provide critical inputs for the optimization module, which dynamically schedules DERs. This module determines the optimal quantities of energy that each prosumer should buy, sell, or store within a given time period while adhering to grid constraints. By coordinating these activities, the VPP framework enhances overall efficiency, balances energy supply and demand, and contributes to the reliability of the energy system.
3.2. Problem Formulation
The VPP scheduling problem is modeled as an MILP problem to maximize social welfare, subject to energy acquisition, dispatch, and battery dynamics constraints [38].
3.3. Parameters and Variables
The parameters and decision variables essential to the VPP market optimization model are defined in Table 1. These include key parameters like energy prices, battery limits, and time intervals, alongside decision variables governing acquisition, dispatch, and battery charge/discharge activities. The table categorizes each element by type and provides a clear notation for vectors and scalars, supporting an organized approach to modeling the system’s dynamic energy management requirements.

Table 1.
Parameters and decision variables for VPP market optimization.
3.3.1. Objective Function
The primary objective of the optimization model is to minimize the total operational costs associated with the VPP. These costs include energy acquisition and dispatch expenses, battery-related costs (such as charging and discharging), and fixed operational overhead. This minimization is equivalent to solving the social welfare maximization problem, as it represents a negated version of the social welfare formulation. By minimizing costs, the model indirectly maximizes the net benefits to the system, ensuring economic efficiency for all stakeholders. This formulation captures the essence of the social welfare problem, where the trade-offs among energy supply, demand, and resource utilization are optimized to achieve an overall system benefit. Operational constraints, including battery capacity, charging and discharging limits, and energy balance requirements, are embedded within the model to ensure the feasibility and practicality of the solution.
The objective function, structured to reflect this cost minimization, forms the backbone of the optimization process. It enables the VPP to manage distributed energy resources efficiently while navigating dynamic market conditions, variable energy demands, and technical constraints. The mathematical expression of the objective function is defined as
3.3.2. Energy Balance Constraints
The energy balance ensures that at any given time, the total energy input (acquisition, generation, and discharge) equals the total output (dispatch, consumption, and charge). This is mathematically expressed as
3.3.3. Acquisition and Dispatch Decision Constraints
Binary decision variables control whether prosumers acquire or dispatch energy. The following constraints ensure proper acquisition and dispatch decisions:
Additionally, the following constraint ensures that acquisition and dispatch actions are not performed simultaneously:
3.3.4. Dispatch Breakdown
The energy dispatch is composed of two parts:
where the following apply:
- : paid energy dispatch at time t.
- : non-paid energy dispatch at time t.
The non-paid dispatch is subject to the following constraint:
The variable is defined as being equal to ∞.
3.3.5. Battery Dynamics
The battery state at is initialized as
For subsequent time periods, the battery state is updated as
3.3.6. Charge and Discharge Constraints
Charge and discharge constraints ensure non-simultaneous operations. Binary decision variables and control charging and discharging:
3.3.7. Battery Capacity Constraints
The battery state must remain within its capacity limits:
3.4. Problem Exploration and Parallel Computation
In the VPP optimization framework, each player i at any time step t must ensure an energy balance among the grid, battery, and their local generation and consumption. Decisions related to energy acquisition (buying) and dispatch (selling) from the grid, as well as battery charging and discharging, are mutually exclusive and subject to upper-bound constraints. This section provides a formal derivation of the energy balance equation, integrating these exclusivity and constraint conditions. It also illustrates how the valid search space, confined to a line rather than a plane, can be efficiently solved in parallel for each player.
3.4.1. Energy Balance with Mutual Exclusivity and Constraints
At any time step t, the energy balance equation for player i can be formulated as
Here, is the energy acquired from the grid, is the energy dispatched to the grid, is the energy charged to the battery, is the energy discharged from the battery, is the energy generated (e.g., from solar PVs), and is the energy consumed by the player’s loads.
3.4.2. Mutually Exclusive Flip-Flop Mechanism for Grid and Battery Operations
The energy interactions with the grid and battery in the VPP model are controlled through a mutually exclusive mechanism, ensuring that at any time t, each player i can either acquire energy from or dispatch energy to the grid and can either charge or discharge the battery—but never simultaneously. This mutual exclusivity not only maintains coherent energy flows but also prevents contradictory actions.
The conditions governing this mutual exclusivity are as follows:
To facilitate this exclusive control, the mechanism operates like a flip-flop. By using binary decision variables, the algorithm effectively “toggles” between states for each operation—either on or off—depending on the player’s action requirements. Flip-flop control ensures that once an energy acquisition action is set (e.g., charging), the opposite action (e.g., discharging) is automatically restricted.
The binary decision variables governing this flip-flop behavior are expressed as
where the following apply:
- enables energy acquisition while setting .
- enables energy dispatch while setting .
- initiates charging while setting .
- initiates discharging while setting .
This dual-layered design—mutual exclusivity and flip-flop functionality—ensures that all grid and battery operations remain coherent, maintaining stability within the VPP optimization model.
3.4.3. Upper-Bound Constraints on Energy Flows
In addition to mutual exclusivity, the decision variables for energy acquisition, dispatch, charging, and discharging are constrained by upper bounds representing the maximum allowable energy flow in each case:
These constraints ensure that the player’s decisions remain within physically feasible limits.
3.4.4. Linearized Energy Balance Equation
To simplify the balance equation, we define two quantities that capture the net energy exchanged with the grid and battery,
respectively.
Additionally, the net energy difference between the player’s generation and load is defined as
Thus, the energy balance equation can be rewritten in a linear form:
Here, the following apply:
- -
- represents the player’s net battery activity (charging/discharging).
- -
- represents the net grid interaction (acquisition/dispatch).
- -
- represents the net energy generated or consumed.
This equation captures the player’s energy balance at each time step, ensuring that the battery activity equals the available net energy from the grid and the player’s own generation and consumption.
3.4.5. Complete Energy Balance with Constraints
The complete energy balance equation for each player must satisfy both the mutual exclusivity and upper-bound constraints. This yields the following system:
The binary decision variables ensure that the player’s actions at each time step are mutually exclusive, preventing invalid combinations like acquiring and dispatching simultaneously.
Figure 2 illustrates the process of search space reduction in the context of Equation (14). Initially, each prosumer’s decision space is represented as a planar 2D space with multiple degrees of freedom, encompassing various possible energy interactions. Through the optimization process, this multidimensional space is reduced to a linear path confined by the upper and lower bounds derived from Equation (14). This reduction not only ensures that all decisions remain feasible within the constraints imposed by mutual exclusivity and upper bounds but also significantly enhances computational efficiency. By simplifying the decision space, the framework effectively supports real-time optimization and enables the management of larger networks of prosumers with improved scalability.
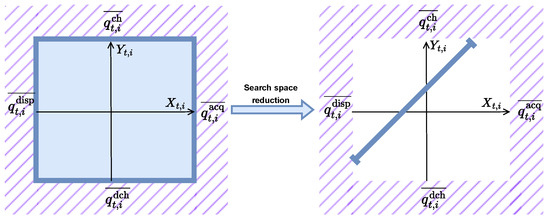
Figure 2.
Diagram illustrating the process of search space reduction for each prosumer. Initially, the decision space is represented as a planar 2D space. Optimization simplifies this to a linear path confined by upper and lower bounds, enhancing computational efficiency and enabling the system to manage larger networks of prosumers effectively.
3.5. Solver Design and Algorithm Development
In order to address the VPP scheduling problem with computational precision and efficiency, we implemented two distinct solver approaches: an exact solver based on Mixed-Integer Linear Programming (MILP) using Gurobi and a parallelized SA algorithm.
SA was selected as the optimization algorithm due to its proven strengths in solving complex, non-linear, and non-convex optimization problems. It effectively navigates multidimensional solution spaces through its stochastic nature, which allows for the probabilistic acceptance of worse solutions in early iterations to escape local minima and avoid premature convergence. Its simplicity and adaptability to problem-specific constraints make it suitable for a wide range of applications [39]. Compared with more computationally intensive metaheuristics, such as genetic algorithms or particle swarm optimization, it provides a balanced trade-off between computational efficiency and solution quality [39]. Additionally, its trajectory-based mechanism for exploring the solution space results in relatively lower computational intensity, making it an ideal choice for parallelization in computationally demanding contexts, like VPP optimization. Furthermore, given the nature of the VPP problem, the implementation of the parallel SA algorithm using OpenMP significantly enhances its scalability and suitability for high-performance optimization tasks [40,41,42,43]. This combination of scalability, efficiency, and solution quality makes SA a robust and practical choice to complement the exact MILP solver, particularly in addressing the computational demands of large-scale VPP scheduling problems.
3.5.1. Exact Solver
In this work, we employed the Gurobi optimizer to solve the VPP scheduling problem formulated as an MILP model. Gurobi’s solver engine follows the conventional branch-and-bound method for MILP, incorporating advanced presolve techniques, heuristics, and cuts to expedite the search for an optimal solution within feasible timeframes. This approach ensures that the scheduling model achieves a precise, globally optimal solution.
While the primary focus of this study is our parallel SA approach for large-scale scenarios, we utilize Gurobi solutions as a baseline reference to assess the convergence and performance of SA. Comparisons between the exact MILP outcomes and the results from the SA method enable a thorough evaluation of SA’s accuracy, thereby confirming its suitability for handling larger and more complex scheduling problems.
3.5.2. Parallel Simulated Annealing Solver
While Gurobi, our chosen exact solver, offers robust scalability and efficiency, it is a licensed, paid software application. To enhance computational flexibility and support scenarios where an alternative may be advantageous, we implemented a parallelized SA solver. This solver is designed to provide near-optimal solutions swiftly for large-scale VPP scheduling, leveraging adaptive, heuristic-driven search techniques to address the dynamic and complex nature of VPP optimization. SA is a probabilistic heuristic that mimics the physical annealing process, wherein a material is gradually cooled to reach a state of minimal energy. This technique is particularly effective for complex optimization problems with vast solution spaces, as it allows the search to explore beyond local minima, enhancing the likelihood of finding a globally optimal or near-optimal solution.
Our SA approach operates by iteratively adjusting the scheduling decisions for each player over all periods, minimizing the overall operational cost. To achieve scalability, we employed OpenMP to parallelize the optimization process across multiple threads, with each thread handling the scheduling optimization for an individual player. The structure of this parallel SA approach is outlined in Algorithm 1.
| Algorithm 1: Simulated annealing with parallel optimization using OpenMP | |
| 1: Input: Initial state , Initial temperature , Cooling rate , Perturbation scale , Number of iterations , Number of players , Number of periods , Battery dynamics, and cost parameters from the input. | |
| 2: Output: Best global state , Best global cost | |
| 3: Initialize: Shared memory for global best state and global best cost to store optimization results. | |
| 4: Initialize temperature , objective function for cost calculation. | |
| 5: #pragma omp parallel for shared() private() reduction(+: ) | // Parallelized loop for each player i |
| 6: for to do | // Each player is solved independently in parallel |
| 7: Initialize local state , local cost | |
| 8: Set , , | |
| 9: Initialize period states for player i across all periods. | |
| 10: Calculate initial battery state based on input parameters and previous period states. | |
| 11: for to do | // Iterative optimization process |
| 12: for to do | // Optimize for each period t for player i |
| 13: Perturb player state for period t using | |
| 14: Compute new balance for the player, update charge/discharge states | |
| 15: Calculate new battery state for period t | |
| 16: end for | |
| 17: Compute new cost | // Moved outside of inner loop |
| 18: Calculate acceptance probability | |
| 19: if then | // Random value |
| 20: Update | |
| 21: if then | |
| 22: Update | |
| 23: end if | |
| 24: end if | |
| 25: Apply cooling schedule: | |
| 26: end for | |
| 27: Update global cost using OpenMP reduction. | |
| 28: end for | |
| 29: Return: Best global state , Best global cost | |
The SA process starts with an initial state and a high temperature . This allows the algorithm to explore the solution space effectively by accepting suboptimal solutions, with the acceptance probability guided by the Boltzmann distribution. The acceptance probability decreases as the temperature is lowered, controlled by the cooling rate , leading to a gradual reduction in exploration in favor of exploitation. This process is effective in escaping local minima, thus increasing the chances of identifying a near-optimal solution for the VPP scheduling problem.
The use of OpenMP for parallelization allows each player’s problem to be optimized independently, where each thread adjusts player states across all periods based on the balance equation and battery constraints. This parallelized structure greatly reduces computation time and enhances scalability, making the SA highly suitable for large-scale, real-time VPP scheduling scenarios. By leveraging parallel SA, the solver achieves an efficient balance between computational performance and solution quality, supporting adaptive and cost-effective VPP operations in complex energy markets.
As illustrated in Figure 3, the HPC cluster architecture supports this parallelization by assigning each VPP to a separate physical node, where each node independently manages the VPP scheduling optimization process. By using parallel SA with OpenMP, each node efficiently computes the scheduling optimization, maximizing scalability and computational efficiency to meet the demands of real-time, responsive energy management.
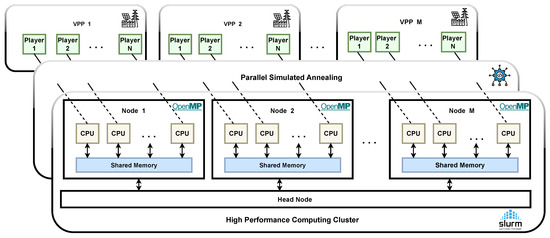
Figure 3.
A schematic of the high-performance computing cluster architecture: This diagram illustrates the HPC cluster infrastructure, where each physical node manages the optimization process of an independent VPP. Within each node, a soft computing layer executes parallel SA by using OpenMP, enabling efficient parallelization across VPP operations and ensuring optimized scheduling. This configuration enhances scalability and computation speed, supporting real-time VPP management and maximizing energy system responsiveness.
3.6. Experimental Design for High-Performance Computing
The experimental setup is structured to evaluate the computational performance of the parallel SA solver on an HPC infrastructure. The primary aim of these experiments is to assess the scalability and efficiency of the parallel SA algorithm under varying conditions, including the number of computational cores and the scale of the VPP market, represented by the number of players (prosumers).
The independent variables in this experimental framework are defined as follows:
- Number of cores: Experiments were conducted with the number of CPU cores varying from 1 to 32. This range allows us to evaluate the performance gains from parallelization at different levels of computational resources.
- Number of players (prosumers): To simulate the scalability of the algorithm in larger VPP markets, we varied the number of players from 32 to 512. This variable directly influences the complexity of the optimization problem, as each player requires independent state updates and balancing within the SA framework.
The dependent variables, measured as indicators of performance, include the following:
- Averaged execution time (in seconds): This metric records the average time required to execute the SA algorithm across different core and player configurations. By observing how execution time scales with the number of cores and players, we assess the algorithm’s computational efficiency and identify any diminishing returns in speedup with the increase in cores.
- Speedup ratio: The speedup ratio is calculated as the ratio of execution time on a single core to that on multiple cores, providing a normalized measure of performance gain from parallelization. This metric is crucial to understanding the algorithm’s scalability in high-performance environments, particularly for identifying bottlenecks and parallel efficiency under increased core utilization.
3.6.1. Experimental Procedure
Each experiment initialized the SA solver with fixed parameters such as initial temperature, cooling rate, and perturbation scale, selected to balance exploration and precision, ensuring consistency across runs. The HPC environment was configured to allocate exclusive resources per experiment to eliminate variability from resource sharing. We executed the algorithm multiple times for each core–player configuration and recorded the averaged results to account for any fluctuations due to inherent stochasticity in the SA process.
The experiments were designed to simulate real-world VPP scheduling scenarios, where varying numbers of players engage in an energy market. The experimental design provides insights into the absolute and relative performance improvements achievable through parallel computing by systematically increasing the number of players and computational cores. In particular, the speedup ratio highlights the efficiency of OpenMP-based parallelization as the number of players increases, reflecting the scalability potential of the SA solver in handling larger VPP markets.
3.6.2. Analysis and Interpretation
This experimental framework enables a comprehensive analysis of the SA algorithm’s performance, focusing on both execution time and speedup ratio across configurations. By observing the impact of core and player variations, we can quantify the effectiveness of parallelization in reducing execution time and identify optimal core allocations relative to problem size. This approach provides actionable insights for high-performance VPP scheduling, highlighting the computational gains achievable in complex, large-scale scenarios.
4. Implementation
4.1. HPC Environment Specifications
The VPP scheduling simulations were executed on the Oblivion HPC cluster, consisting of 88 nodes with dual Intel Xeon Gold 6154 processors (Intel Corp., 36 cores per node) and 192 GB RAM per node, yielding a total of 3168 cores. This configuration provides the computational density and memory bandwidth necessary to support extensive parallelism in our optimization framework.
The Oblivion HPC cluster provides the low-latency communication and high throughput essential to parallelizing VPP optimization. Its multi-core architecture supports the decomposition of the scheduling problem, allowing each prosumer to be solved independently, thus significantly reducing execution time.
To ensure compatibility and optimal performance, GCC 11.3.0 was used in conjunction with Intel-specific optimization and OpenMP support, tuned to fully exploit the Xeon architecture’s capabilities. This environment setup enabled high-resolution, efficient parallel processing, crucial to the scale and complexity of virtual power plant scheduling.
4.2. Model Parameters and Outputs
This section outlines the essential parameters and outputs for the VPP scheduling optimization model. The parameters define the model’s initial conditions and constraints, capturing the technical, operational, and economic aspects critical to effective energy management. The outputs represent the results of the optimization process, providing actionable insights for energy allocation and battery management.
4.2.1. Model Input Parameters
The parameters in Table 2 encompass time-based, operational, and economic factors that influence VPP decision making. These inputs define the scope and constraints under which the optimization algorithm operates, ensuring that the model is responsive to varying energy demands, generation forecasts, and market conditions.

Table 2.
Model input parameters for VPP scheduling.
These parameters enable the VPP scheduling model to adapt to various operating scenarios, addressing both the technical limits and economic aspects of battery storage, energy acquisition, and dispatch. By defining clear boundaries, the model can optimize energy management decisions with precision, ensuring efficient use of resources in alignment with market constraints.
4.2.2. Optimization Outputs
The results produced by the optimization algorithm are detailed in Table 3. These outputs represent the optimized energy management actions for the VPP, covering energy acquisition, dispatch, storage, and cost-effective strategies.

Table 3.
Optimization outputs in vector notation.
These outputs include critical variables that influence operational decisions, from energy acquisition and dispatch volumes to battery charge and discharge levels. By providing optimized energy transactions and battery state trajectories, the outputs support cost-effective, balanced energy management strategies. The precision of these outputs allows for actionable insights, enabling the VPP to meet demand requirements while minimizing costs and enhancing operational efficiency.
4.3. Hyperparameter Optimization
Optimizing the SA approach for VPP scheduling requires the careful tuning of key hyperparameters. In this study, we optimized four primary hyperparameters—initial temperature, cooling rate, maximum iterations, and perturbation scale—to balance solution quality with computational efficiency. A preliminary grid search was conducted to explore broad parameter ranges and understand initial trends, followed by targeted optimization using advanced methods, including Gaussian Process Minimization (GP), Random Forest Minimization (RF), and Gradient-Boosted Regression Tree Minimization (GBRT).
The use of these algorithms was motivated by their ability to efficiently explore and exploit complex parameter spaces. GP [44,45,46] was selected for its effectiveness in modeling smooth, continuous parameter surfaces, allowing for the identification of optimal configurations with minimal evaluations. RF [47] was incorporated due to its capability to handle large-scale, high-dimensional problems effectively, as well as its strength in capturing non-linear interactions between parameters. This makes it particularly suitable for exploring complex parameter spaces in the SA optimization framework. Finally, GBRT [48,49] was employed for its adaptability in refining parameter values through iterative learning and its robustness in addressing parameter spaces with varying dimensionality. These algorithms provided complementary strengths, ensuring that the hyperparameter tuning process was both comprehensive and efficient, resulting in a well-calibrated SA algorithm for the VPP scheduling problem.
4.3.1. Parameter Ranges and Search Strategy
The parameter ranges were established based on theoretical insights into SA behavior and initial grid search observations:
- Initial temperature: Varied from to , it controls the acceptance of worse solutions in the early iterations. Higher initial temperatures, closer to , allow for broader exploration by increasing the probability of accepting suboptimal solutions, helping the algorithm escape local minima. As the temperature decreases, this probability decreases, shifting the focus toward refining promising solutions.
- Cooling rate: Varied from to , it determines the rate of temperature reduction throughout the optimization process. A slower cooling rate, near , maintains higher temperatures for longer, promoting diverse solution exploration. Faster rates, closer to , accelerate convergence by focusing on local refinement.
- Perturbation scale: Examined between and , it manages the magnitude of adjustments to the solution in each iteration. Larger perturbations, near , facilitate broad exploration in the early stages, while smaller perturbations, closer to , ensure fine-tuned precision as the algorithm approaches convergence.
The initial grid search provided a foundational understanding of hyperparameter effects, indicating that higher initial temperatures and lower cooling rates tend to improve exploration in early phases of the search. Following these findings, three advanced optimization algorithms were employed to refine the configurations: GP, RF, and GBRT. Each of these algorithms has unique properties that contribute to hyperparameter tuning, with RF and GBRT showing particular strength in capturing non-linear interactions.
Table 4 summarizes the optimized hyperparameter configurations for the Stochastic Algorithm employed in VPP scheduling. Each method demonstrates distinct parameter settings and corresponding performance scores, with the Random Forest Minimization method achieving the highest score of 85.83, indicating its superior effectiveness in this context.

Table 4.
Optimized hyperparameter configurations for SA in VPP scheduling. Each method’s performance score reflects solution quality under the respective parameter settings.
4.3.2. Analysis of Results
The optimization process revealed valuable insights into how each hyperparameter influences SA’s performance in the VPP scheduling problem. High initial temperature values (close to 400.0) were generally advantageous, allowing for extensive initial exploration and helping the algorithm avoid local minima in the early iterations. Conversely, a lower cooling rate (close to 0.85) was found to foster gradual convergence, maintaining solution diversity over extended iterations and reducing the risk of premature convergence.
The perturbation scale emerged as a pivotal parameter, with values around 0.065–0.077 providing a suitable balance between localized search precision and broader search space exploration. While the maximum iteration count showed limited impact due to its narrow predefined range, it provided a sufficient search depth to achieve stable convergence across all configurations.
Each optimization method demonstrated distinct strengths. Random forest minimization achieved the highest score, likely due to its effective handling of complex, non-linear interactions between parameters, which can be critical to SA’s adaptive search dynamics. Gradient-Boosted Regression Tree also performed well, offering a competitive configuration with a slightly higher cooling rate, favoring faster convergence in later stages of the optimization.
4.4. Convergence Phases in Simulated Annealing
Following hyperparameter tuning in the VPP optimization framework, the convergence path of the SA algorithm is segmented into distinct phases: initialization, exploration, and exploitation. Each phase reflects the algorithm’s systematic approach, with initialization establishing a foundational search, broadly exploring the solution space, and exploitation honing in on optimal solutions within set parameter bounds. This structured convergence highlights the algorithm’s balance between global search diversity and local refinement, effectively achieving robust optimization outcomes in VPP scheduling.
Figure 4 illustrates the convergence behavior of the SA algorithm applied to the VPP scheduling problem. It demonstrates the algorithm’s progression through its convergence phases, showcasing its ability to efficiently navigate the solution space and achieve reliable optimization results within the defined computational constraints.
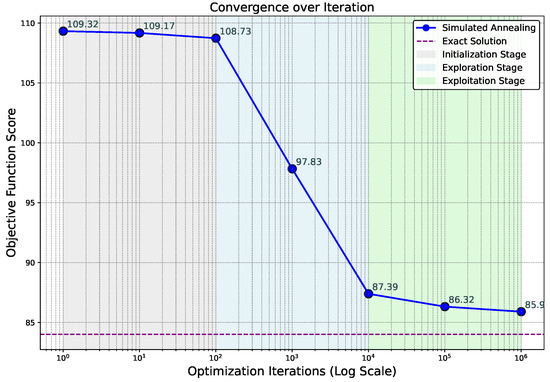
Figure 4.
Convergence behavior of the SA algorithm for the VPP scheduling problem, highlighting its progression through initialization, exploration, and exploitation phases to efficiently achieve optimal solutions.
4.5. Parallelization and Load Balancing Techniques
The design of the parallelized SA solver for virtual power plant (VPP) optimization leverages OpenMP to achieve high computational efficiency and balance workload distribution effectively across multiple cores. The parallelization strategy centers on decomposing the optimization process into discrete, independent tasks, where each task corresponds to optimizing the scheduling decisions of an individual player within the VPP. This structure not only reduces computational overhead but also maximizes the scalability of the algorithm by allowing each player to be processed concurrently on separate threads.
4.5.1. Thread-Based Parallelization with OpenMP
In this implementation, OpenMP directives manage parallel threads to ensure the optimal utilization of processing units. The parallel loop distributes each player’s optimization across multiple cores by using the #pragma omp parallel for directive, which assigns players to threads at compile time by using static scheduling. This approach leverages the uniformity in task complexity, as each player undergoes an identical optimization process over a consistent number of periods. Consequently, the computational demand is evenly distributed across threads, minimizing load imbalance and maximizing processing efficiency.
Static scheduling was selected due to the predictability of workload distribution, reducing runtime overhead associated with dynamic task assignment. By parallelizing the outer loop across players, the solver achieves high concurrency, while the inner loop within each player’s optimization cycle handles iterative temperature reduction, state perturbation, and cost evaluation. This structure allows each player’s state to be optimized independently, eliminating inter-thread dependencies and enabling a high degree of parallelism, which is crucial to scaling the approach to larger problem instances.
4.5.2. Unexplored Load Balancing Strategies
While this implementation uses OpenMP with static scheduling to handle the parallelization of player optimization, certain load balancing strategies were not implemented. Specifically, dynamic scheduling and guided scheduling were not applied. These approaches, which assign tasks to threads at runtime, could dynamically redistribute workload among threads if computational variance existed. However, this added flexibility was deemed unnecessary for the current problem, where task complexity is uniform across players. Static scheduling’s pre-assignment of tasks proved sufficient and avoided the runtime overhead introduced by dynamic strategies.
Additionally, more advanced load balancing techniques, such as hierarchical or task-based parallelism, were not explored. These could be beneficial in cases involving highly irregular workloads, inter-thread dependencies, or a need for finer-grained parallelism. However, such complexity is not required for the homogeneous structure of this problem, where each player operates independently with consistent computational requirements.
4.5.3. Scalability and Computational Efficiency
The SA solver’s parallel design was tested across varying configurations of core counts, from a single core up to 32 cores. Each experiment measured the execution time and speedup ratio to evaluate scalability and the effectiveness of the load balancing technique. The results indicated that the solver maintained near-linear speedup up to 32 cores, with minimal deviation from the ideal speedup curve. This performance confirms that the parallelization strategy is highly scalable, capable of handling an increase in problem size (i.e., number of players) with consistent computational gains.
As the number of players scales up, the parallelization strategy effectively distributes the workload across cores, ensuring that additional computational resources lead to proportional reductions in execution time. This behavior is essential to VPP scheduling contexts where the system must adapt to real-time market fluctuations and evolving demand patterns. The observed results show that as the problem size grows, the parallelized SA solver not only maintains efficiency but also aligns closely with the ideal speedup, making it robust for deployment in high-demand, real-time optimization environments.
5. Results and Discussion
The performance evaluation of the parallelized SA solver for the virtual power plant (VPP) optimization problem was conducted in an HPC environment, with experiments designed to assess both computational efficiency and scalability. The experiments specifically explored the relationship between the number of computational cores and the number of players (prosumers) in the VPP market. This section presents the results in terms of execution time, speedup ratio, and scalability, with insights into how the parallelized SA solver performs under varying core and player configurations.
5.1. Execution Time and Speedup Analysis
The primary metrics for evaluating the parallel SA solver’s performance were averaged execution time and speedup ratio. Figure 5 illustrates the execution time as a function of the number of cores for different player counts, ranging from 32 to 512. The results show a consistent reduction in execution time with an increase in core count, demonstrating the efficacy of the OpenMP parallelization strategy. For each configuration, execution times were averaged across multiple runs to ensure robust results.
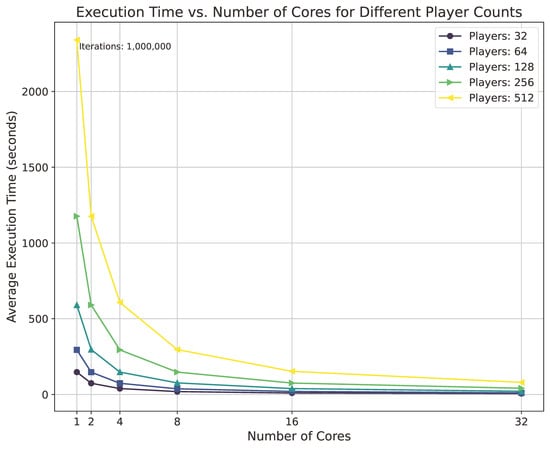
Figure 5.
Execution time vs. number of cores for different player counts, benchmarked using 1 × 106 iterations of simulated annealing.
The speedup ratio, defined as the ratio of execution time on a single core to that on multiple cores, quantifies the computational gains from parallelization. As shown in Figure 6, it approaches the ideal linear curve, especially for larger player configurations (e.g., 256 and 512 players) due to more efficient task distribution across cores. The use of OpenMP’s default static scheduling ensures that iterations are pre-assigned to threads, reducing runtime overhead and maximizing throughput. This highlights the scalability of the parallelized SA approach in handling complex VPP markets with increasing computational demands.
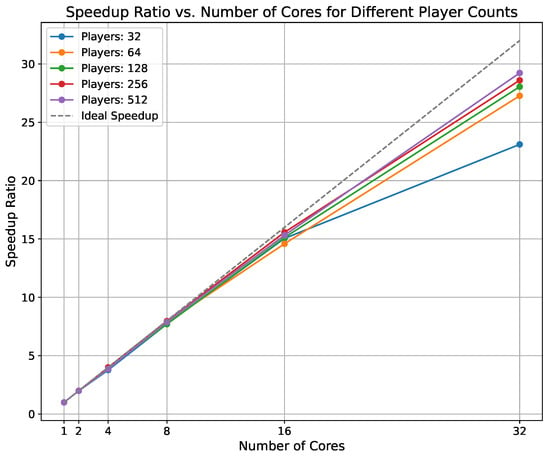
Figure 6.
Speedup ratio vs. number of cores for different player counts with ideal speedup line.
These results underline the practical implications of the solver’s performance in the context of large-scale VPP scheduling. The consistent reduction in execution time with the increase in core count highlights the algorithm’s ability to meet the real-time computational requirements of energy systems, where rapid decision making is critical to market participation and resource optimization. The near-linear speedup observed for configurations with 256 and 512 players further demonstrates the algorithm’s robustness in scaling with problem complexity, making it well suited for dynamic and high-demand energy markets.
The results also emphasize the efficiency gains achieved through the parallelization strategy. By leveraging OpenMP’s static scheduling, which pre-assigns iterations to threads, the solver minimizes the overhead associated with task distribution. This ensures optimal resource utilization and reduces bottlenecks, particularly in configurations with higher player counts. Such efficiency is crucial to maintaining consistent performance across diverse VPP scenarios, even as the system scales.
The observed behavior of the speedup ratio approaching the ideal linear curve indicates the balanced workload distribution achieved by the parallel SA algorithm. This suggests that the algorithm effectively utilizes available computational resources, even in high-dimensional optimization scenarios. The ability to maintain this efficiency across multiple runs ensures the reliability and predictability of the solver under varying conditions.
5.2. Scalability Assessment
Scalability is a critical aspect of the parallelized SA solver, particularly for large-scale VPP scenarios. A near-linear increase in speedup characterizes ideal scalability as the number of cores increases. The results demonstrate that the parallel SA solver achieves high scalability up to 32 cores, maintaining near-ideal speedup behavior across all player configurations. As the number of players increases, the algorithm’s scalability improves, with speedup curves for higher player counts closely following the ideal speedup line. This trend suggests that the parallelized SA is well suited for large VPP problems where substantial computational resources are required to maintain efficiency.
The results indicate that the efficiency gains of the parallel SA approach are maintained even as the problem size scales, reflecting the robustness of the OpenMP-based parallelization in managing larger VPP markets. For configurations with 512 players, the speedup performance remained stable and efficient, demonstrating the algorithm’s capability to handle extensive player interactions without a significant drop in parallel efficiency.
5.3. Efficiency and Resource Utilization
Efficiency in resource utilization is also crucial to high-performance computing applications. By monitoring CPU and memory usage during the experiments, we observed optimal resource distribution across the allocated cores. CPU utilization remained high throughout the experiments, with minimal idle times, indicating that the parallelization strategy effectively distributed the computational workload. Memory usage remained within the expected limits, ensuring stability and preventing resource contention issues.
The efficient use of computational resources underscores the effectiveness of the parallel SA solver in optimizing VPP operations in real time. The scalability of the solver across different core and player configurations illustrates its adaptability in HPC environments, making it an effective tool for large-scale VPP scheduling.
5.4. Quality of Optimization Outcomes
A critical consideration in parallelization is the potential impact on solution quality. To ensure that parallel execution did not compromise the quality of the optimization results, we compared the solutions generated by the parallelized SA with those from sequential SA implementation. Analysis confirmed that the parallel SA solver consistently reached comparable solution quality, maintaining optimal or near-optimal results across all core and player configurations. This validates the parallelization approach, as it enhances computational efficiency without sacrificing the algorithm’s ability to explore the solution space effectively.
5.5. Summary of Findings
The experimental results demonstrate that the parallelized SA solver for VPP scheduling achieves significant computational gains while maintaining solution quality. Key findings include the following:
- Near-ideal speedup ratio:The speedup ratio approached the ideal linear speedup curve, particularly at higher player counts, indicating strong scalability.
- High efficiency and optimal resource utilization: CPU and memory utilization were maintained at efficient levels, supporting stable execution across varied configurations.
- Consistent solution quality: Parallelization did not compromise optimization outcomes, as the parallel SA solver consistently delivered results comparable to the sequential version.
These findings underscore the effectiveness of the parallel SA solver in handling the complex, large-scale scheduling demands of VPP optimization, providing a reliable and efficient solution for high-performance computing applications.
5.6. Application Cases
The proposed parallelized SA solver demonstrates significant applicability within the context of VPP operations. Its scalability and computational efficiency make it particularly well suited for managing the challenges posed by large-scale VPP systems, where a vast number of prosumers and distributed energy resources must be optimized in real-time. By solving high-dimensional optimization problems with tight time constraints, the solver enables VPP operators to minimize operational costs, balance energy supply and demand, and enhance participation in dynamic energy markets. Furthermore, the solver’s ability to adapt to market fluctuations allows it to optimize resource allocation strategies, including energy pricing and demand response programs, ensuring stable and cost-effective operations. Additionally, the solver can handle multi-energy integration challenges within VPPs, such as coordinating electricity, storage systems, and ancillary services, to improve overall efficiency and sustainability. These capabilities position the parallelized SA solver as a robust and reliable tool for addressing the computational demands of modern VPP systems, providing practical solutions to the complexities of real-time energy management.
5.7. Practical Implications for the VPP Market
This study offers meaningful implications for grid operators, VPP operators, and policymakers, emphasizing the broader impact of deploying the proposed parallelized SA solver in modern energy markets. Unlike the specific focus on technical application scenarios in the previous section, this discussion explores strategic, operational, and policy-level considerations for real-world adoption.
For grid operators, the demonstrated scalability and computational efficiency of the solver provide a powerful framework for managing large-scale energy systems with diverse prosumers. By enabling real-time optimization, the solver allows operators to respond to dynamic market conditions, integrate renewable energy sources effectively, and ensure grid stability under varying demand and generation patterns. This capability is crucial to meeting the operational challenges associated with the increasing penetration of decentralized energy resources (DERs), such as sunlight, wind, and energy storage systems.
For VPP operators, the solver’s ability to handle high-dimensional optimization problems ensures streamlined resource allocation, enabling operators to enhance participation in energy markets. This includes supporting advanced pricing strategies, optimizing energy dispatch schedules, and facilitating demand response programs. The parallelized SA solver also empowers operators to maximize profitability in competitive energy markets while maintaining operational resilience. Its adaptability to multi-energy systems further supports the efficient coordination of electricity, storage, and ancillary services, fostering integrated and sustainable energy management practices.
From a policymaker’s perspective, the findings underscore the critical role of advanced optimization tools and HPC infrastructure in achieving broader energy transition goals. Policymakers can leverage this study to advocate for investment in scalable computational frameworks that enable efficient market participation for VPPs while addressing challenges like grid decarbonization and resilience. By supporting such innovations, policymakers can foster an ecosystem that promotes equitable access to energy markets, encourages the integration of renewable resources, and aligns with global sustainability and carbon neutrality targets.
Additionally, the solver’s capacity to scale seamlessly with increasing numbers of prosumers suggests a pathway for modernizing energy markets to handle growing complexity and demand. This aligns with long-term energy transition objectives, including increased flexibility in grid operations, reduced dependency on fossil fuels, and improved responsiveness to market volatility. As energy markets evolve, the insights from this study can guide policymakers in formulating strategies to regulate and incentivize the adoption of robust computational frameworks that prioritize both economic and environmental sustainability.
6. Conclusions and Future Work
This study has successfully demonstrated the effectiveness of parallelized SA, facilitated by OpenMP, in optimizing VPP scheduling for improved computational efficiency and responsiveness. By integrating OpenMP to parallelize SA operations, significant reductions in computation times were achieved, enabling the solver to handle large-scale VPP configurations with high efficiency. The experimental results showed that with careful parameter selection and parallelization strategies, the SA solver achieved fast convergence towards near-optimal solutions, yielding substantial improvements in execution time and speedup ratio across varying player and core configurations.
The performance evaluation indicated that the parallelized SA algorithm maintained high scalability, with speedup ratios closely aligning with the ideal linear curve, particularly as the number of players increased. This behavior underscores the potential of parallel computing to enhance the scalability, adaptability, and computational feasibility of VPP operations, presenting a significant advancement in the field of energy system optimization. The results also validated that the parallelization of the SA did not compromise solution quality, as the optimization outcomes consistently reached levels comparable to sequential SA. This balance between computational efficiency and solution integrity is essential to the real-world applicability of SA in dynamic and large-scale VPP scheduling scenarios.
Furthermore, the findings illustrate how the proposed optimization approach contributes to the broader objectives of sustainable urban energy management. By addressing challenges such as real-time decision making, battery lifespan constraints, and dynamic energy pricing, the study advances the role of VPPs as integral components of smart city infrastructure. These advancements enable decentralized energy management, improve grid resilience, and support the seamless integration of renewable energy sources and electric vehicles, all of which are pivotal to achieving the energy efficiency and sustainability targets of smart cities.
Future work will focus on refining the parallelization approach to further reduce computational overhead and enhance scalability. This may include exploring advanced OpenMP features and dynamic scheduling mechanisms and potentially integrating alternative parallel computing frameworks to boost performance in even larger VPP networks. Additionally, extending the application of the parallelized SA solver to more complex and dynamic VPP models—incorporating real-time market changes, demand fluctuations, and multi-energy interactions—will be a crucial area of future research. Efforts will also be directed towards creating robust simulation environments that replicate evolving smart city scenarios, ensuring that the proposed solutions remain adaptable and effective in meeting the demands of modern urban energy landscapes. Additionally, the study will include stress testing with a significantly large number of players to evaluate the scalability and robustness of the proposed methods under high-demand scenarios. Furthermore, an extensive benchmarking study will be conducted to evaluate the performance of the VPP optimization problem when solved using various metaheuristic algorithms, such as parallel implementations of GA and PSO. These studies will leverage both CPU and GPU acceleration to explore the potential of advanced parallel and distributed computing frameworks. By comparing the proposed parallelized metaheuristic solvers with commercial exact solvers, such as Gurobi, CPLEX, and MOSEK, this analysis aims to provide a comprehensive evaluation of scalability, computational efficiency, and solution quality. It will also offer deeper insights into the relative strengths, weaknesses, and computational trade-offs of the various methodologies. Furthermore, the evaluation will assess the scalability and practical applicability of these techniques for solving large-scale, real-world energy system problems.
Author Contributions
Conceptualization, A.A. and R.A.R.; software, A.A. and R.A.R.; investigation, F.A.; writing—original draft preparation, A.A. and R.A.R.; writing—review and editing, F.A. and J.L.S.; visualization, F.A. and R.A.R.; supervision, J.L.S. and R.R.; funding acquisition, R.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Union through the Recovery and Resilience Plan (PRR) as part of the Innovation Pact “NGS—New Generation Storage” (reference 58). This initiative is co-financed by NextGenerationEU under the Incentive System “Agendas para a Inovação Empresarial” (“Agendas for Business Innovation”).
Data Availability Statement
The data and code used in this study are proprietary and cannot be shared due to confidentiality agreements with the private company involved. As a result, they are not publicly available.
Acknowledgments
The authors gratefully acknowledge the support of the high-performance computing infrastructure provided through the project “High-Performance Computing for Enhanced Virtual Power Plant Efficiency” (reference 2024.00036.CPCA.A1). This infrastructure has been instrumental in facilitating the computational tasks required for this research. The project has been assigned the DOI https://doi.org/10.54499/2024.00036.CPCA.A1, accessed on 27 February 2025.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Podder, A.K.; Islam, S.; Kumar, N.M.; Chand, A.A.; Rao, P.N.; Prasad, K.A.; Logeswaran, T.; Mamun, K.A. Systematic Categorization of Optimization Strategies for Virtual Power Plants. Energies 2020, 13, 6251. [Google Scholar] [CrossRef]
- Nafkha-Tayari, W.; Ben Elghali, S.; Heydarian-Forushani, E.; Benbouzid, M. Virtual Power Plants Optimization Issue: A Comprehensive Review on Methods, Solutions, and Prospects. Energies 2022, 15, 3607. [Google Scholar] [CrossRef]
- Venegas-Zarama, J.F.; Muñoz-Hernandez, J.I.; Baringo, L.; Diaz-Cachinero, P.; De Domingo-Mondejar, I. A Review of the Evolution and Main Roles of Virtual Power Plants as Key Stakeholders in Power Systems. IEEE Access 2022, 10, 47937–47964. [Google Scholar] [CrossRef]
- Ali, J.U.A.B.W.; Kazmi, S.A.A.; Altamimi, A.; Khan, Z.A.; Alrumayh, O.; Malik, M.M. Smart Energy Management in Virtual Power Plant Paradigm with a New Improved Multilevel Optimization Based Approach. IEEE Access 2022, 10, 50062–50077. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, Y.; Lee, W.-J.; Lin, Z.; Shamash, Y.A. Virtual Power Plants for Grid Resilience: A Concise Overview of Research and Applications. IEEE/CAA J. Autom. Sin. 2024, 11, 329–343. [Google Scholar] [CrossRef]
- Roy, S.; Das, D.C.; Sinha, N. Optimizing Smart City Virtual Power Plants with V2G Integration for Improved Grid Resilience. In Proceedings of the 2024 IEEE International Conference on Interdisciplinary Approaches in Technology and Management for Social Innovation (IATMSI), Gwalior, India, 14–16 March 2024. [Google Scholar] [CrossRef]
- Ou, M.; Huang, G.; Chen, S. Design of a Smart Light Device in Virtual Power Plants for New Energy Regulation. In Proceedings of the 2023 4th International Conference on Advanced Electrical and Energy Systems (AEES), Shanghai, China, 1–3 December 2023. [Google Scholar] [CrossRef]
- Zhang, J.; Seet, B.-C.; Lie, T.T. Dynamic Energy Scheduling for Virtual Power Plant with Prosumer Resources Using Game Theory. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Sousa, T.; Pinto, T.; Morais, H.; Vale, Z. Intelligent Electric Vehicle Heuristic for Energy Resource Management Using Simulated Annealing. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Venegas-Zarama, J.F.; Muñoz-Hernandez, J.I. A General Description of Virtual Power Plants as Smart Manager in Power Systems. In Proceedings of the 2022 IEEE European Technology and Engineering Management Summit (E-TEMS), Bilbao, Spain, 9–11 March 2022; pp. 83–87. [Google Scholar] [CrossRef]
- Pereira, A.; Rodrigues, N.; Barbosa, J.; Leitão, P. Trust and Risk Management Towards Resilient Large-Scale Cyber-Physical Systems. In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics (ISIE), Taipei, Taiwan, 28–31 May 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Alves, F.; Ribeiro, R.; Petiz, M.; Abbasi, A.; Carvalho, P.; Faia, R.; Faria, P.; Vale, Z.; Rodrigues, R. Virtual Power Plant Optimization Service–Benchmark of Solvers. In Proceedings of the 19th Conference on Computer Science and Intelligence Systems (FedCSIS), Belgrade, Serbia, 8–11 September 2024; pp. 279–287. [Google Scholar] [CrossRef]
- Alves, F.; Petiz, M.; Ribeiro, R.; Abbasi, A.; Carvalho, P.N.; Rodrigues, R. An N-Queens Benchmark Using MILP Solvers: Comparison Between Open-Source Optimization Tools. In Optimization, Learning Algorithms and Applications; OL2A 2024. Communications in Computer and Information Science; Springer: Cham, Switzerland, 2024; Volume 2281. [Google Scholar] [CrossRef]
- Aoun, A.; Adda, M.; Ilinca, A.; Ghandour, M.; Ibrahim, H. Optimizing Virtual Power Plant Management: A Novel MILP Algorithm to Minimize Levelized Cost of Energy, Technical Losses, and Greenhouse Gas Emissions. Energies 2024, 17, 4075. [Google Scholar] [CrossRef]
- Lubin, M.; Petra, C.G.; Anitescu, M.; Zavala, V. Scalable Stochastic Optimization of Complex Energy Systems. In Proceedings of the 2011 International Conference for High Performance Computing, Networking, Storage and Analysis (SC), Seattle, WA, USA, 12–18 November 2011; pp. 1–64. [Google Scholar] [CrossRef]
- Sousa, T.; Morais, H.; Vale, Z.; Faria, P.; Soares, J. Intelligent Energy Resource Management Considering Vehicle-to-Grid: A Simulated Annealing Approach. IEEE Trans. Smart Grid 2012, 3, 535–542. [Google Scholar] [CrossRef]
- Sousa, T.; Vale, Z.; Morais, H. Simulated Annealing Approach Applied to the Energy Resource Management Considering Demand Response for Electric Vehicles. In Proceedings of the 17th International Conference on Intelligent System Applications to Power Systems (ISAP), Tokyo, Japan, 1–4 July 2013; pp. 1–6. [Google Scholar]
- Faia, R.; Pinto, T.; Vale, Z. Optimization of Electricity Markets Participation with Simulated Annealing. In Proceedings of the International Conference on Practical Applications of Agents and Multi-Agent Systems (PAAMS), Sevilla, Spain, 1–3 June 2016; Springer: Cham, Switzerland; pp. 27–39. [Google Scholar] [CrossRef]
- Bouddou, R.; Benhamida, F.; Haba, M.; Belgacem, M.; Meziane, M.A. Simulated Annealing Algorithm for Dynamic Economic Dispatch Problem in the Electricity Market Incorporating Wind Energy. Ing. Syst. d’Inf. 2020, 25, 719–727. [Google Scholar] [CrossRef]
- Hannan, M.A.; Abdolrasol, M.G.M.; Faisal, M.; Ker, P.J.; Begum, R.A.; Hussain, A. Binary Particle Swarm Optimization for Scheduling MG Integrated Virtual Power Plant Toward Energy Saving. IEEE Access 2019, 7, 107937–107951. [Google Scholar] [CrossRef]
- Al-Shafei, A.; Zareipour, H.; Cao, Y. A Review of High-Performance Computing and Parallel Techniques Applied to Power Systems Optimization. arXiv 2022, arXiv:2207.02388. [Google Scholar]
- Petra, C.G.; Schenk, O.; Anitescu, M. Real-Time Stochastic Optimization of Complex Energy Systems on High-Performance Computers. Comput. Sci. Eng. 2014, 16, 32–42. [Google Scholar] [CrossRef]
- Angulo, A.; Rodríguez, D.; Garzón, W.; Gómez, D.F.; Al Sumaiti, A.; Rivera, S. Algorithms for Bidding Strategies in Local Energy Markets: Exhaustive Search through Parallel Computing and Metaheuristic Optimization. Algorithms 2021, 14, 269. [Google Scholar] [CrossRef]
- Alvarez, D.; Rodriguez, D.; Rivera, S. Parallel Computing for Reducing Time in Security Constrained Optimal Power Flow Analysis. Rev. Int. Metod. Numer. Calc. Diseño Ing. 2023, 39, 1–5. [Google Scholar] [CrossRef]
- Epperly, T.; Edmunds, T.; Lamont, A.; Meyers, C.; Smith, S.; Yao, Y.; Drayton, G. High-Performance Computing for Electric Grid Planning and Operations. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar] [CrossRef]
- Caramanis, M.; Ntakou, E.; Hogan, W.W.; Chakrabortty, A.; Schoene, J. Co-Optimization of Power and Reserves in Dynamic T&D Power Markets with Nondispatchable Renewable Generation and Distributed Energy Resources. Proc. IEEE 2016, 104, 807–836. [Google Scholar] [CrossRef]
- Khan, R.; Islam, N.; Das, S.K.; Muyeen, S.M.; Moyeen, S.I.; Ali, M.F.; Tasneem, Z.; Islam, M.R.; Saha, D.K.; Badal, M.F.; et al. Energy Sustainability—Survey on Technology and Control of Microgrid, Smart Grid, and Virtual Power Plant. IEEE Access 2021, 9, 104663–104694. [Google Scholar] [CrossRef]
- Sarmiento-Vintimilla, J.C.; Torres, E.; Larruskain, D.M.; Pérez-Molina, M.J. Applications, Operational Architectures and Development of Virtual Power Plants as a Strategy to Facilitate the Integration of Distributed Energy Resources. Energies 2022, 15, 775. [Google Scholar] [CrossRef]
- Krishna, R.; Hemamalini, S. Optimal Energy Management of Virtual Power Plants with Storage Devices Using Teaching-and-Learning-Based Optimization Algorithm. Int. Trans. Electr. Energy Syst. 2022, 2022, 1727524. [Google Scholar] [CrossRef]
- Muttaqi, K.M.; Sutanto, D. Adaptive and Predictive Energy Management Strategy for Real-Time Optimal Power Dispatch from VPPs Integrated with Renewable Energy and Energy Storage. IEEE Trans. Ind. Appl. 2021, 57, 1958–1972. [Google Scholar] [CrossRef]
- Naughton, J.; Wang, H.; Cantoni, M.; Mancarella, P. Co-Optimizing Virtual Power Plant Services under Uncertainty: A Robust Scheduling and Receding Horizon Dispatch Approach. IEEE Trans. Power Syst. 2021, 36, 3960–3972. [Google Scholar] [CrossRef]
- Yi, Z.; Xu, Y.; Gu, W.; Wu, W. A Multi-Time-Scale Economic Scheduling Strategy for Virtual Power Plant Based on Deferrable Loads Aggregation and Disaggregation. IEEE Trans. Sustain. Energy 2019, 11, 1332–1346. [Google Scholar] [CrossRef]
- Tang, W.; Yang, H.-T. Optimal Operation and Bidding Strategy of a Virtual Power Plant Integrated with Energy Storage Systems and Elasticity Demand Response. IEEE Access 2019, 7, 79798–79809. [Google Scholar] [CrossRef]
- Lezama, F.; Faia, R.; Soares, J.; Faria, P.; Vale, Z. Learning Bidding Strategies in Local Electricity Markets Using Ant Colony Optimization. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Mousavi, S.H.; Nazemi, A.; Hafezalkotob, A. Using and Comparing Metaheuristic Algorithms for Optimizing Bidding Strategy Viewpoint of Profit Maximization of Generators. J. Ind. Eng. Int. 2015, 11, 59–72. [Google Scholar] [CrossRef][Green Version]
- Jain, P.; Saxena, A. Profit Maximization Bidding Strategy for a GENCO Using Whale Optimization Algorithm. In Proceedings of the 2019 Women Institute of Technology Conference on Electrical and Computer Engineering (WITCON ECE), Dehradun, India, 22–23 November 2019; pp. 100–103. [Google Scholar] [CrossRef]
- Rädle, S.; Mast, J.; Gerlach, J.; Bringmann, O. Computational Intelligence Based Optimization of Hierarchical Virtual Power Plants. Energy Syst. 2021, 12, 517–544. [Google Scholar] [CrossRef]
- Peik-Herfeh, M.; Seifi, H.; Sheikh-El-Eslami, M.K. Decision Making of a Virtual Power Plant under Uncertainties for Bidding in a Day-Ahead Market Using Point Estimate Method. Int. J. Electr. Power Energy Syst. 2013, 44, 88–98. [Google Scholar] [CrossRef]
- Henderson, D.; Jacobson, S.H.; Johnson, A.W. The Theory and Practice of Simulated Annealing. In Handbook of Metaheuristics; Glover, F., Kochenberger, G.A., Eds.; International Series in Operations Research & Management Science; Springer: Boston, MA, USA, 2003; Volume 57, pp. 287–319. [Google Scholar] [CrossRef]
- Janaki Ram, D.; Sreenivas, T.H.; Ganapathy Subramaniam, K. Parallel Simulated Annealing Algorithms. J. Parallel Distrib. Comput. 1996, 37, 207–212. [Google Scholar] [CrossRef]
- Ferreiro, A.M.; García, J.A.; López-Salas, J.G.; Vázquez, C. An Efficient Implementation of Parallel Simulated Annealing Algorithm in GPUs. J. Glob. Optim. 2013, 57, 863–890. [Google Scholar] [CrossRef]
- Chen, D.-J.; Lee, C.-Y.; Park, C.-H.; Mendes, P. Parallelizing Simulated Annealing Algorithms Based on High-Performance Computer. J. Glob. Optim. 2007, 39, 261–289. [Google Scholar] [CrossRef]
- Greening, D.R. Parallel Simulated Annealing Techniques. Comput. Oper. Res. 1990, 18, 41–49. [Google Scholar] [CrossRef]
- Osborne, M.A.; Garnett, R.; Roberts, S.J. Gaussian Processes for Global Optimization; Technical Report; University of Oxford: Oxford, UK, 2009. [Google Scholar]
- Lamparth, M.; Bestehorn, M.; Märkisch, B. Gaussian Processes and Bayesian Optimization for High Precision Experiments. arXiv 2022, arXiv:2205.07625. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, H.; Phillips, J.M.; Zhe, S. Standard Gaussian Process Can Be Excellent for High-Dimensional Bayesian Optimization. arXiv 2024, arXiv:2402.02746. [Google Scholar] [CrossRef]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential Model-Based Optimization for General Algorithm Configuration. In Learning and Intelligent Optimization: 5th International Conference, LION 5, Rome, Italy, 17–21 January 2011. Selected Papers 5; Springer: Berlin/Heidelberg, Germany, 2011; pp. 507–523. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A Comparative Analysis of Gradient Boosting Algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Jiang, J.; Cui, B.; Zhang, C.; Fu, F. DimBoost: Boosting Gradient Boosting Decision Tree to Higher Dimensions. In Proceedings of the 2018 International Conference on Management of Data (SIGMOD ’18), Houston, TX, USA, 10–15 June 2018; pp. 1363–1376. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
