Optimizing Smart City Street Design with Interval-Fuzzy Multi-Criteria Decision Making and Game Theory for Autonomous Vehicles and Cyclists
Abstract
Highlights
- Safety is the most critical factor in designing urban streets that integrate cyclists and autonomous vehicles (AVs);
- Green infrastructure and smart technology adoption are the optimal integration strategies.
- These strategies foster a balanced coexistence of cyclists and AVs, leading to a more efficient transport system and a more sustainable urban environment in the driverless era.
- This research provides valuable guidance for urban planners and decision makers on the implementation of AVs on our streets, while advocating for sustainable and active mobility.
Abstract
1. Introduction
2. Literature Review
2.1. Street Design for Cyclists and AVs
2.2. Methods Used to Assess and Estimate Urban Design and Planning Challenges and Policies
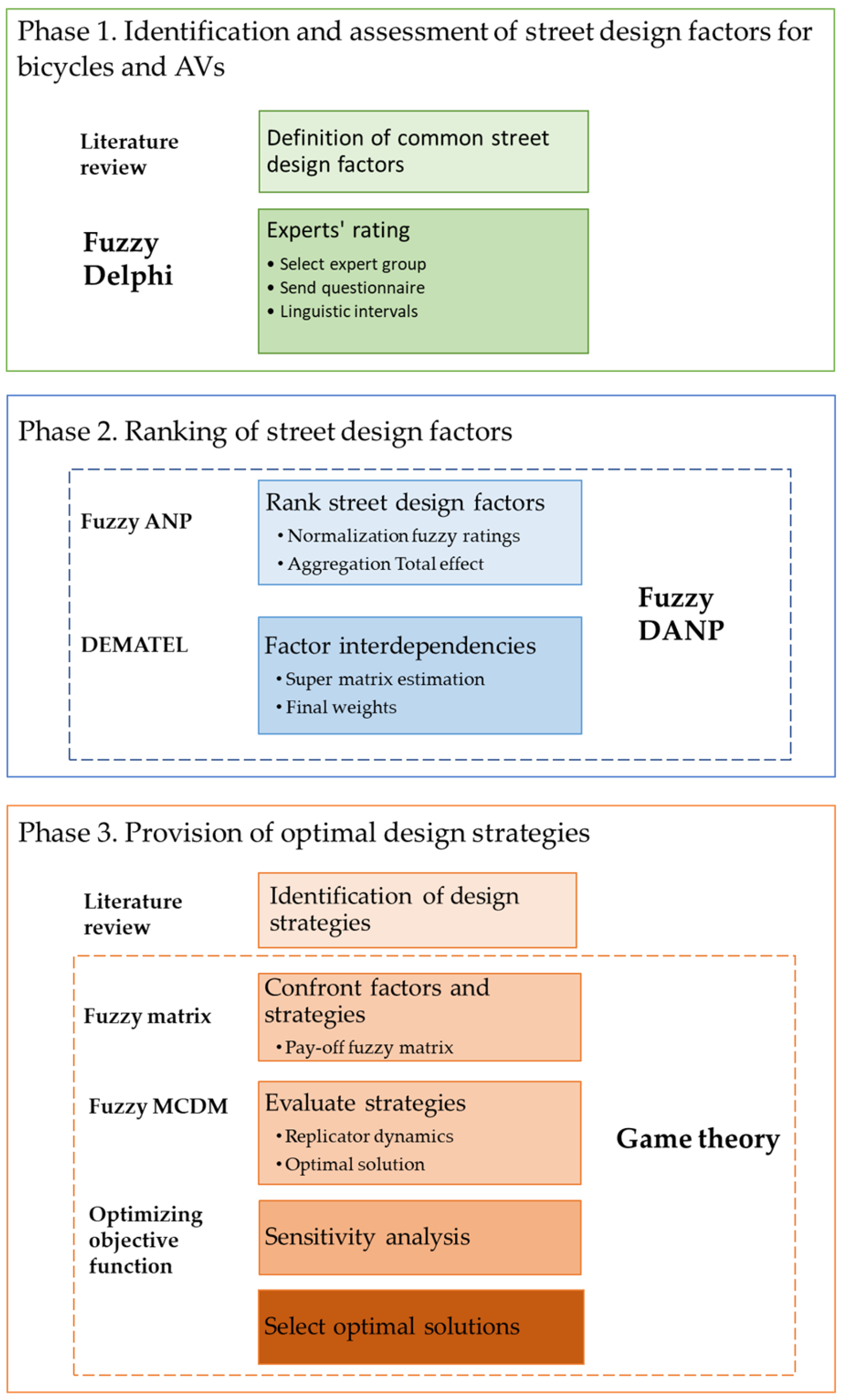
3. Research Methodology
- Decision makers are rational and aim to optimize the model’s defined objectives;
- The methods applied (fuzzy Delphi, fuzzy DANP, and Game theory) effectively manage uncertainties and complex interdependencies among the factors;
- Interactions between factors and strategies are modeled linearly using normalized weights derived from the fuzzy ANP;
- The data collected from expert surveys are reliable and accurately represent real-world priorities.
3.1. Identifying Factors for Bicycles and AVs Street Design with Interval Fuzzy Delphi Technique
3.2. Ranking and Importance of Street Design Factors with Interval-Fuzzy DANP
3.2.1. Fuzzy ANP
- Initial Computation: Experts’ assessment on the mutual influence of the n factors selected is derived from IVFE according to Equation (1).where such that .
- 2.
- Standardization and Aggregation: The direct impact matrix D is standardized and then used to obtain the comprehensive impact matrix using Equation (2), which provides an absorbing state of a Markov chain process as the limit of matrices D1, D2, … Dm [82]:where denotes the comprehensive impact matrix and the I is the identity matrix, corresponding to Equations (3) and (4).Also:
- 3.
- Computation Using Coefficient of Variation: In order to compute the normalized effect matrix, we used the Variable Homogeneity Factor of the Coefficient of Variation (VHFCV), a measure of the relative variability. To achieve this objective, we first apply the VHFCV operator to the direct effect matrix in Equations (5) and (6).
- 4.
- Normalization: The direct impact matrix is then normalized by using the following Equations (7) and (8):
- 5.
- Total Effect Determination: The last step is to determine the total influential matrix by using the relation in Equation (9):
- 6.
- Calculation of r and c: Values r and c are typically the row and column sums of the relation matrix, used to determine the prominence and relation of each factor in the decision-making process. These values are calculated based on Equation (10):
- Normalization: Normalize each interval weight by the sum of all interval weights. For an interval [ai, bj], the normalized interval is given as follows:
- Summing the Intervals: Compute the sum of the lower bounds and the upper bounds of all interval weights.
- Normalization Calculation: Normalize each interval weight by dividing each lower and upper bound by the corresponding sums computed in the previous step.
3.2.2. DEMATEL
3.3. Identifying Strategies with Fuzzy Game Theory
3.3.1. Identification of Strategies
3.3.2. Game Theory with Fuzzy Matrix
4. Results
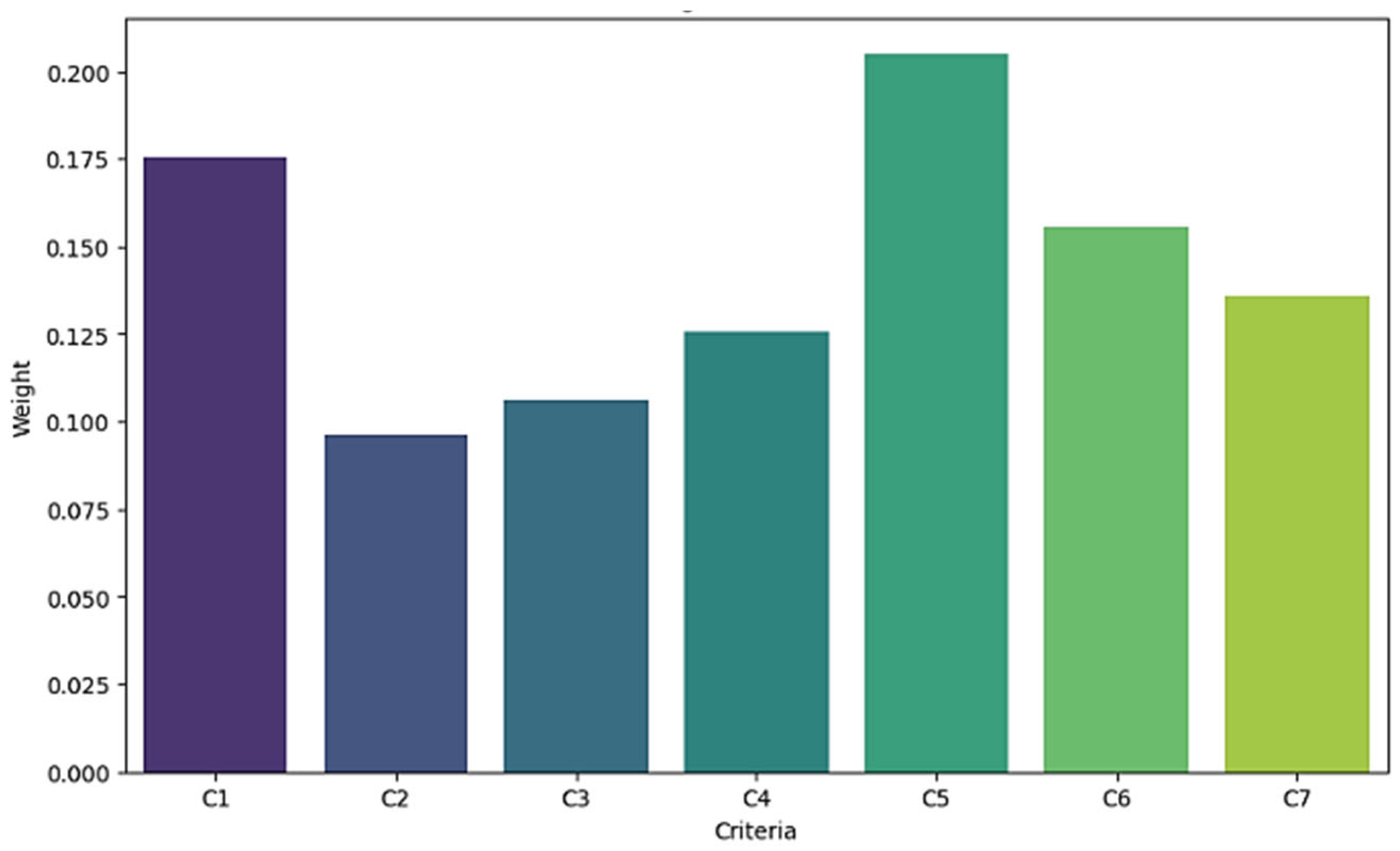
4.1. Identification and Ranking of Final Factors
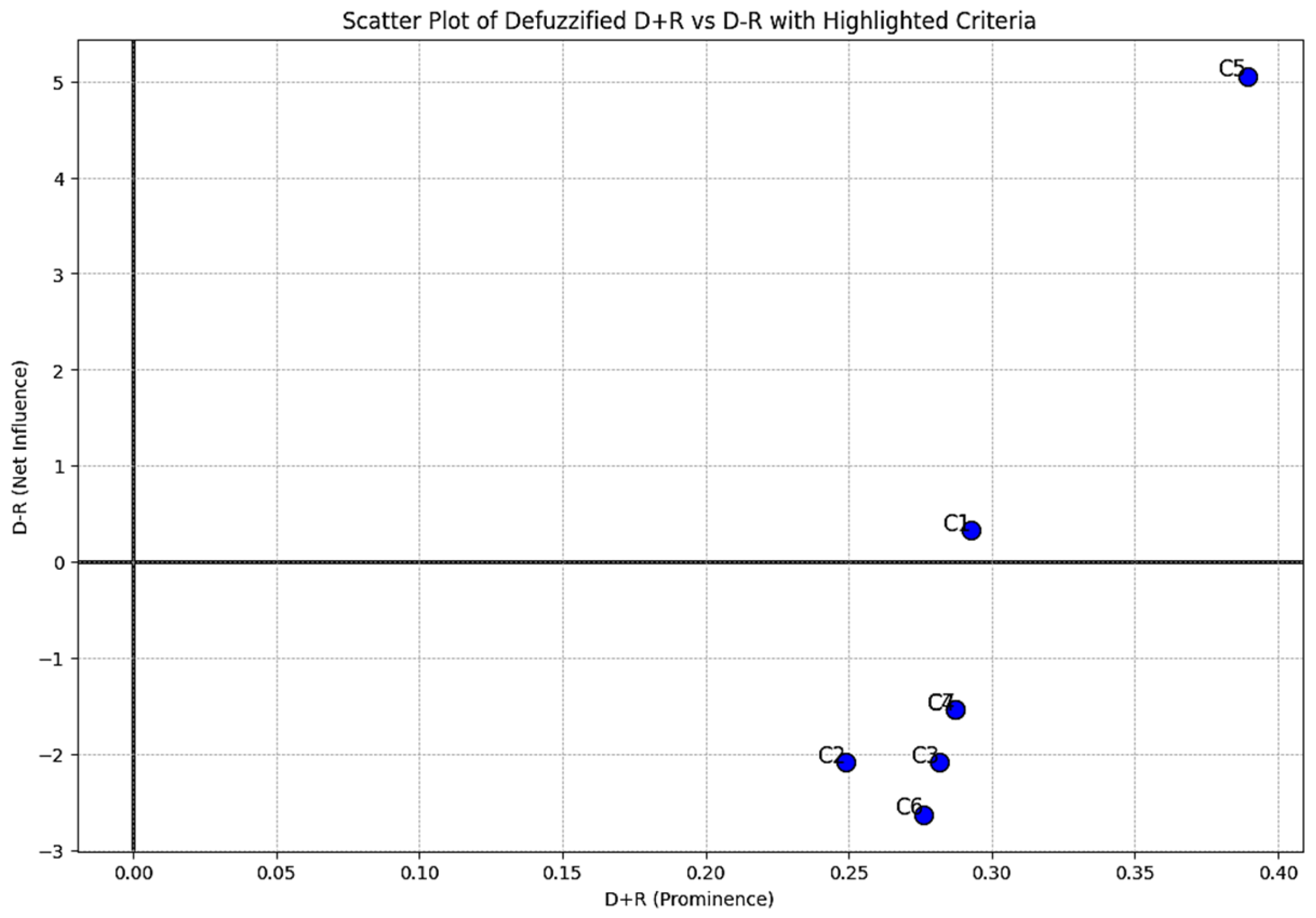
4.2. Relevance of Street Design Factors
4.3. Strategies
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AVs | Autonomous vehicles |
| AHP | Analytical Hierarchical Process |
| ANP | Analytic Network Process |
| CAVs | Connected and autonomous vehicles |
| DANP | Decision-Making Trial and Evaluation Laboratory ANP |
| DEMATEL | Decision-Making Trial and Evaluation Laboratory |
| FDM | Fuzzy Delphi method |
| HVs | Human-driven vehicles |
| IVFE | Interval-Fuzzy Element |
| MCDM | Multi-Criteria Decision Making |
References
- Larsen, J. The Making of a Pro-Cycling City: Social Practices and Bicycle Mobilities. Environ. Plan. A Econ. Space 2017, 49, 876–892. [Google Scholar] [CrossRef]
- Liu, S.; Shen, Z.-J.M.; Ji, X. Urban Bike Lane Planning with Bike Trajectories: Models, Algorithms, and a Real-World Case Study. Manuf. Serv. Oper. Manag. 2022, 24, 2500–2515. [Google Scholar] [CrossRef]
- Ferretto, L.; Bruzzone, F.; Nocera, S. Pathways to Active Mobility Planning. Res. Transp. Econ. 2021, 86, 101027. [Google Scholar] [CrossRef]
- Khreis, H.; May, A.D.; Nieuwenhuijsen, M.J. Health Impacts of Urban Transport Policy Measures: A Guidance Note for Practice. J. Transp. Health 2017, 6, 209–227. [Google Scholar] [CrossRef]
- Rojas-Rueda, D.; Nieuwenhuijsen, M.J.; Khreis, H.; Frumkin, H. Autonomous Vehicles and Public Health. Annu. Rev. Public Health 2020, 41, 329–345. [Google Scholar] [CrossRef]
- Freudendal-Pedersen, M. Cyclists as Part of the City’s Organism: Structural Stories on Cycling in Copenhagen. City Soc. 2015, 27, 30–50. [Google Scholar] [CrossRef]
- Freemark, Y.; Hudson, A.; Zhao, J. Are Cities Prepared for Autonomous Vehicles? J. Am. Plan. Assoc. 2019, 85, 133–151. [Google Scholar] [CrossRef]
- Khayyam, H.; Javadi, B.; Jalili, M.; Jazar, R.N. Artificial Intelligence and Internet of Things for Autonomous Vehicles. In Nonlinear Approaches in Engineering Applications; Springer International Publishing: Cham, Switzerland, 2020; pp. 39–68. [Google Scholar] [CrossRef]
- Yoganandhan, A.; Subhash, S.D.; Hebinson Jothi, J.; Mohanavel, V. Fundamentals and Development of Self-Driving Cars. Mater. Today Proc. 2020, 33, 3303–3310. [Google Scholar] [CrossRef]
- Rahman, M.M.; Thill, J.-C. Impacts of Connected and Autonomous Vehicles on Urban Transportation and Environment: A Comprehensive Review. Sustain. Cities Soc. 2023, 96, 104649. [Google Scholar] [CrossRef]
- Shafiei, S.; Gu, Z.; Grzybowska, H.; Cai, C. Impact of Self-Parking Autonomous Vehicles on Urban Traffic Congestion. Transportation 2023, 50, 183–203. [Google Scholar] [CrossRef]
- Deng, Q.; Sun, H.; Chen, F.; Shu, Y.; Wang, H.; Ha, Y. An Optimized FPGA-Based Real-Time NDT for 3D-LiDAR Localization in Smart Vehicles. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3167–3171. [Google Scholar] [CrossRef]
- Terzi, S.; Savvaidis, C.; Votis, K.; Tzovaras, D.; Stamelos, I. Securing Emission Data of Smart Vehicles with Blockchain and Self-Sovereign Identities. In Proceedings of the 2020 IEEE International Conference on Blockchain (Blockchain), Virtual, 2–6 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 462–469. [Google Scholar] [CrossRef]
- Chougule, A.; Chamola, V.; Sam, A.; Yu, F.R.; Sikdar, B. A Comprehensive Review on Limitations of Autonomous Driving and Its Impact on Accidents and Collisions. IEEE Open J. Veh. Technol. 2024, 5, 142–161. [Google Scholar] [CrossRef]
- Nascimento, A.M.; Vismari, L.F.; Molina, C.B.S.T.; Cugnasca, P.S.; Camargo, J.B.; de Almeida, J.R.; Inam, R.; Fersman, E.; Marquezini, M.V.; Hata, A.Y. A Systematic Literature Review About the Impact of Artificial Intelligence on Autonomous Vehicle Safety. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4928–4946. [Google Scholar] [CrossRef]
- Pyrialakou, V.D.; Gkartzonikas, C.; Gatlin, J.D.; Gkritza, K. Perceptions of Safety on a Shared Road: Driving, Cycling, or Walking near an Autonomous Vehicle. J. Saf. Res. 2020, 72, 249–258. [Google Scholar] [CrossRef]
- Duarte, F.; Ratti, C. The Impact of Autonomous Vehicles on Cities: A Review. J. Urban Technol. 2018, 25, 3–18. [Google Scholar] [CrossRef]
- Barnett, J.; Gizinski, N.; Mondragon-Parra, E.; Siegel, J.; Morris, D.; Gates, T.; Kassens-Noor, E.; Savolainen, P. Automated Vehicles Sharing the Road: Surveying Detection and Localization of Pedalcyclists. IEEE Trans. Intell. Veh. 2021, 6, 649–664. [Google Scholar] [CrossRef]
- Wang, Y.; Chau, C.K.; Ng, W.Y.; Leung, T.M. A Review on the Effects of Physical Built Environment Attributes on Enhancing Walking and Cycling Activity Levels within Residential Neighborhoods. Cities 2016, 50, 1–15. [Google Scholar] [CrossRef]
- Hull, A.; O’Holleran, C. Bicycle Infrastructure: Can Good Design Encourage Cycling? Urban Plan. Transp. Res. 2014, 2, 369–406. [Google Scholar] [CrossRef]
- Lee, C.; Moudon, A.V. Neighbourhood Design and Physical Activity. Build. Res. Inf. 2008, 36, 395–411. [Google Scholar] [CrossRef]
- Fishman, E.; Washington, S.; Haworth, N. Barriers and Facilitators to Public Bicycle Scheme Use: A Qualitative Approach. Transp. Res. Part F Traffic Psychol. Behav. 2012, 15, 686–698. [Google Scholar] [CrossRef]
- Lee, C.; Moudon, A.V. Physical Activity and Environment Research in the Health Field: Implications for Urban and Transportation Planning Practice and Research. J. Plan. Lit. 2004, 19, 147–181. [Google Scholar] [CrossRef]
- Fraser, S.D.S.; Lock, K. Cycling for Transport and Public Health: A Systematic Review of the Effect of the Environment on Cycling. Eur. J. Public Health 2011, 21, 738–743. [Google Scholar] [CrossRef]
- Winters, M.; Davidson, G.; Kao, D.; Teschke, K. Motivators and Deterrents of Bicycling: Comparing Influences on Decisions to Ride. Transportation 2011, 38, 153–168. [Google Scholar] [CrossRef]
- Garrard, J.H.S.D.J. Women and Cycling. In City Cycling; Pucher, J., Buehler, R., Eds.; The MIT Press: Cambridge, MA, USA, 2012; pp. 211–233. [Google Scholar]
- Parkin, J.; Wardman, M.; Page, M. Models of Perceived Cycling Risk and Route Acceptability. Accid. Anal. Prev. 2007, 39, 364–371. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wang, W.; Liu, P.; Ragland, D.R. Physical Environments Influencing Bicyclists’ Perception of Comfort on Separated and on-Street Bicycle Facilities. Transp. Res. D Transp. Environ. 2012, 17, 256–261. [Google Scholar] [CrossRef]
- Clayton, W.; Parkin, J.; Billington, C. Cycling and Disability: A Call for Further Research. J. Transp. Health 2017, 6, 452–462. [Google Scholar] [CrossRef]
- Clayton, W.; Musselwhite, C. Exploring Changes to Cycle Infrastructure to Improve the Experience of Cycling for Families. J. Transp. Geogr. 2013, 33, 54–61. [Google Scholar] [CrossRef]
- Krizek, K.J.; Roland, R.W. What Is at the End of the Road? Understanding Discontinuities of on-Street Bicycle Lanes in Urban Settings. Transp. Res. D Transp. Environ. 2005, 10, 55–68. [Google Scholar] [CrossRef]
- Daniels, S.; Brijs, T.; Nuyts, E.; Wets, G. Injury Crashes with Bicyclists at Roundabouts: Influence of Some Location Characteristics and the Design of Cycle Facilities. J. Saf. Res. 2009, 40, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Akar, G. Street Intersection Characteristics and Their Impacts on Perceived Bicycling Safety. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 41–54. [Google Scholar] [CrossRef]
- Parkin, J.; Clark, B.; Clayton, W.; Ricci, M.; Parkhurst, G. Understanding Interactions Between Autonomous Vehicles and Other Road Users: A Literature Review; UWE Bristol Research Repository: Bristol, UK, 2016. [Google Scholar]
- Wood, J.M. Nighttime Driving: Visual, Lighting and Visibility Challenges. Ophthalmic Physiol. Opt. 2020, 40, 187–201. [Google Scholar] [CrossRef] [PubMed]
- Wood, J.M.; Lacherez, P.F.; Marszalek, R.P.; King, M.J. Drivers’ and Cyclists’ Experiences of Sharing the Road: Incidents, Attitudes and Perceptions of Visibility. Accid. Anal. Prev. 2009, 41, 772–776. [Google Scholar] [CrossRef] [PubMed]
- Gagliardi, G.; Lupia, M.; Cario, G.; Tedesco, F.; Cicchello Gaccio, F.; Lo Scudo, F.; Casavola, A. Advanced Adaptive Street Lighting Systems for Smart Cities. Smart Cities 2020, 3, 1495–1512. [Google Scholar] [CrossRef]
- Li, H.; Harvey, J.T.; Holland, T.J.; Kayhanian, M. The Use of Reflective and Permeable Pavements as a Potential Practice for Heat Island Mitigation and Stormwater Management. Environ. Res. Lett. 2013, 8, 015023. [Google Scholar] [CrossRef]
- Titze, S.; Stronegger, W.J.; Janschitz, S.; Oja, P. Association of Built-Environment, Social-Environment and Personal Factors with Bicycling as a Mode of Transportation among Austrian City Dwellers. Prev. Med. 2008, 47, 252–259. [Google Scholar] [CrossRef]
- Rodríguez, D.A.; Joo, J. The Relationship between Non-Motorized Mode Choice and the Local Physical Environment. Transp. Res. D Transp. Environ. 2004, 9, 151–173. [Google Scholar] [CrossRef]
- Helbich, M.; Böcker, L.; Dijst, M. Geographic Heterogeneity in Cycling under Various Weather Conditions: Evidence from Greater Rotterdam. J. Transp. Geogr. 2014, 38, 38–47. [Google Scholar] [CrossRef]
- Blau, M.; Akar, G.; Nasar, J. Driverless Vehicles’ Potential Influence on Bicyclist Facility Preferences. Int. J. Sustain. Transp. 2018, 12, 665–674. [Google Scholar] [CrossRef]
- Eichholz, L.; Mellinger, N.; Manz, W. Urban Cycling and Automated Vehicles (Rad-Auto-Nom Project). In Proceedings of the 28th Annual European Real Estate Society Conference, Milan, Italy, 22–25 June 2022; European Real Estate Society: Amsterdam, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Berge, S.H.; Hagenzieker, M.; Farah, H.; de Winter, J. Do Cyclists Need HMIs in Future Automated Traffic? An Interview Study. Transp. Res. Part F Traffic Psychol. Behav. 2022, 84, 33–52. [Google Scholar] [CrossRef]
- Elliott, D.; Keen, W.; Miao, L. Recent Advances in Connected and Automated Vehicles. J. Traffic Transp. Eng. (Engl. Ed.) 2019, 6, 109–131. [Google Scholar] [CrossRef]
- Hagenzieker, M.P.; van der Kint, S.; Vissers, L.; van Schagen, I.N.L.G.; de Bruin, J.; van Gent, P.; Commandeur, J.J.F. Interactions between Cyclists and Automated Vehicles: Results of a Photo Experiment *. J. Transp. Saf. Secur. 2020, 12, 94–115. [Google Scholar] [CrossRef]
- Vlakveld, W.; van der Kint, S.; Hagenzieker, M.P. Cyclists’ Intentions to Yield for Automated Cars at Intersections When They Have Right of Way: Results of an Experiment Using High-Quality Video Animations. Transp. Res. Part F Traffic Psychol. Behav. 2020, 71, 288–307. [Google Scholar] [CrossRef]
- Hou, M.; Mahadevan, K.; Somanath, S.; Sharlin, E.; Oehlberg, L. Autonomous Vehicle-Cyclist Interaction: Peril and Promise. In Proceedings of the 2020 CHI Conference on Human Factors in Computing Systems, Honolulu, HI, USA, 25–30 April 2020; ACM: New York, NY, USA, 2020; pp. 1–12. [Google Scholar] [CrossRef]
- Gwak, J.; Jung, J.; Oh, R.; Park, M.; Rakhimov, M.A.K.; Ahn, J. A Review of Intelligent Self-Driving Vehicle Software Research. KSII Trans. Internet Inf. Syst. 2019, 13, 5299–5320. [Google Scholar] [CrossRef]
- Carrese, S.; Nigro, M.; Patella, S.M.; Toniolo, E. A Preliminary Study of the Potential Impact of Autonomous Vehicles on Residential Location in Rome. Res. Transp. Econ. 2019, 75, 55–61. [Google Scholar] [CrossRef]
- Ngwu, O.L.; Rimu, A.; Deb, S. How to Design Traffic Infrastructure to Support Cyclists’ Interaction with Autonomous Vehicles: Teenage Cyclists’ Perceptions. Hum. Factors Syst. Interact. 2022, 52. [Google Scholar] [CrossRef]
- Botello, B.; Buehler, R.; Hankey, S.; Mondschein, A.; Jiang, Z. Planning for Walking and Cycling in an Autonomous-Vehicle Future. Transp. Res. Interdiscip. Perspect. 2019, 1, 100012. [Google Scholar] [CrossRef]
- Soteropoulos, A.; Berger, M.; Mitteregger, M. Compatibility of Automated Vehicles in Street Spaces: Considerations for a Sustainable Implementation. Sustainability 2021, 13, 2732. [Google Scholar] [CrossRef]
- Alves, G.V.; Schwammberger, M. Towards a Digital Highway Code Using Formal Modelling and Verification of Timed Automata. Electron. Proc. Theor. Comput. Sci. 2022, 371, 77–85. [Google Scholar] [CrossRef]
- Seilabi, S.E.; Pourgholamali, M.; Homem de Almeida Correia, G.; Labi, S. Robust Design of CAV-Dedicated Lanes Considering CAV Demand Uncertainty and Lane Reallocation Policy. Transp. Res. D Transp. Environ. 2023, 121, 103827. [Google Scholar] [CrossRef]
- Park, C.; Sohn, S.Y. An Optimization Approach for the Placement of Bicycle-Sharing Stations to Reduce Short Car Trips: An Application to the City of Seoul. Transp. Res. Part A Policy Pract. 2017, 105, 154–166. [Google Scholar] [CrossRef]
- Shunmuga Perumal, P.; Wang, Y.; Sujasree, M.; Tulshain, S.; Bhutani, S.; Suriyah, M.K.; Kumar Raju, V.U. LaneScanNET: A Deep-Learning Approach for Simultaneous Detection of Obstacle-Lane States for Autonomous Driving Systems. Expert. Syst. Appl. 2023, 233, 120970. [Google Scholar] [CrossRef]
- Roy, K.; Hoang, N.H.; Vu, H.L. Modeling Autonomous Vehicles Deployment in a Multilane AV Zone With Mixed Traffic. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23708–23720. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Wang, Y.; Zhao, W.; Liu, T. Evidence of Automated Vehicle Safety’s Influence on People’s Acceptance of the Automated Driving Technology. Accid. Anal. Prev. 2024, 195, 107381. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, S.K.; Goswami, S.S. A Comprehensive Review of Multiple Criteria Decision-Making (MCDM) Methods: Advancements, Applications, and Future Directions. Decis. Mak. Adv. 2023, 1, 25–48. [Google Scholar] [CrossRef]
- Rejeb, A.; Rejeb, K.; Keogh, J.G.; Zailani, S. Barriers to Blockchain Adoption in the Circular Economy: A Fuzzy Delphi and Best-Worst Approach. Sustainability 2022, 14, 3611. [Google Scholar] [CrossRef]
- Liu, M.; Wan, Y.; Lewis, F.L.; Nageshrao, S.; Filev, D. A Three-Level Game-Theoretic Decision-Making Framework for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 20298–20308. [Google Scholar] [CrossRef]
- Liu, H.; Yang, M.; Guan, C.; Chen, Y.S.; Keith, M.; You, M.; Menendez, M. Urban Infrastructure Design Principles for Connected and Autonomous Vehicles: A Case Study of Oxford, UK. Comput. Urban Sci. 2023, 3, 34. [Google Scholar] [CrossRef]
- Kiciński, M.; Solecka, K. Application of MCDA/MCDM Methods for an Integrated Urban Public Transportation System—Case Study, City of Cracow. Arch. Transp. 2018, 46, 71–84. [Google Scholar] [CrossRef]
- Ashofteh, P.-S.; Far, S.M.; Golfam, P. Application of Multi-Criteria Decision-Making of CODAS and SWARA in Reservoir Optimal Operation Using Marine Predator Algorithm Based on Game Theory. Water Resour. Manag. 2023, 37, 4385–4412. [Google Scholar] [CrossRef]
- Collins, B.C.; Kumral, M. Examining Impact and Benefit Agreements in Mineral Extraction Using Game Theory and Multiple-Criteria Decision Making. Extr. Ind. Soc. 2022, 10, 101094. [Google Scholar] [CrossRef]
- Punetha, N.; Jain, G. Game Theory and MCDM-Based Unsupervised Sentiment Analysis of Restaurant Reviews. Appl. Intell. 2023, 53, 20152–20173. [Google Scholar] [CrossRef] [PubMed]
- Kaviari, F.; Mesgari, M.S.; Seidi, E.; Motieyan, H. Simulation of Urban Growth Using Agent-Based Modeling and Game Theory with Different Temporal Resolutions. Cities 2019, 95, 102387. [Google Scholar] [CrossRef]
- Ibrahim, M.A.R.; Jaini, N.I.; Khalif, K.M.N.K. A Comprehensive Review of Hybrid Game Theory Techniques and Multi-Criteria Decision-Making Methods. J. Phys. Conf. Ser. 2021, 1988, 012056. [Google Scholar] [CrossRef]
- Cortés-Berrueco, L.E.; Gershenson, C.; Stephens, C.R. Traffic Games: Modeling Freeway Traffic with Game Theory. PLoS ONE 2016, 11, e0165381. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, D.; Cheng, Z.; Yu, X.; Zheng, B. A Model to Manage the Lane-Changing Conflict for Automated Vehicles Based on Game Theory. Sustainability 2023, 15, 3063. [Google Scholar] [CrossRef]
- Chellappa, V.; Ginda, G. Application of Multiple-Criteria Decision Making Methods for Construction Safety Research. Proc. Inst. Civ. Eng.-Manag. Procure. Law 2024, 177, 127–136. [Google Scholar] [CrossRef]
- Alimohammadlou, M.; Alinejad, S. Challenges of Blockchain Implementation in SMEs’ Supply Chains: An Integrated IT2F-BWM and IT2F-DEMATEL Method. Electron. Commer. Res. 2023. [Google Scholar] [CrossRef]
- Mubarik, M.S.; Kazmi, S.H.A.; Zaman, S.I. Application of Gray DEMATEL-ANP in Green-Strategic Sourcing. Technol. Soc. 2021, 64, 101524. [Google Scholar] [CrossRef]
- Wu, H.; Zhong, W.; Zhong, B.; Li, H.; Guo, J.; Mehmood, I. Barrier Identification, Analysis and Solutions of Blockchain Adoption in Construction: A Fuzzy DEMATEL and TOE Integrated Method. Eng. Constr. Archit. Manag. 2023. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, G.; Wu, P.; Qiu, J. An Integrated Gray DEMATEL and ANP Method for Evaluating the Green Mining Performance of Underground Gold Mines. Sustainability 2022, 14, 6812. [Google Scholar] [CrossRef]
- Liu, T.; Deng, Y.; Chan, F. Evidential Supplier Selection Based on DEMATEL and Game Theory. Int. J. Fuzzy Syst. 2018, 20, 1321–1333. [Google Scholar] [CrossRef]
- Nematkhah, F.; Raissi, S.; Ghezavati, V. An Integrated Fuzzy DEMATEL-Fuzzy ANP Approach to Nominate Diagnostic Method and Measuring Total Predictive Performance Score. Saf. Reliab. 2017, 37, 48–72. [Google Scholar] [CrossRef]
- Chatterjee, K.; Kar, S. Multi-Criteria Analysis of Supply Chain Risk Management Using Interval Valued Fuzzy TOPSIS. OPSEARCH 2016, 53, 474–499. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Sabzalian, M.H.; Zhang, C.; Castillo, O.; Sakthivel, R.; El-Sousy, F.F.M. Training Interval Type-2 Fuzzy Systems Based on Error Backpropagation. In Modern Adaptive Fuzzy Control Systems; Springer: Cham, Switerland, 2023; pp. 49–93. [Google Scholar] [CrossRef]
- Chaqooshi, A.F.; Rajabani, N.; Khalili Esbuei, S.; Hakimi, N. Identifying and Ranking Appropriate Resilience Supply Chain Strategies, Hybrid Approach of Game Theory and Fuzzy MCDM. J. Ind. Manag. Perspect. 2019, 9, 9–31. [Google Scholar] [CrossRef]
- Zhou, X.; Hu, Y.; Deng, Y.; Chan, F.T.S.; Ishizaka, A. A DEMATEL-Based Completion Method for Incomplete Pairwise Comparison Matrix in AHP. Ann. Oper. Res. 2018, 271, 1045–1066. [Google Scholar] [CrossRef]
- Debnath, A.; Bandyopadhyay, A.; Roy, J.; Kar, S. Game Theory Based Multi Criteria Decision Making Problem under Uncertainty: A Case Study on Indian Tea Industry. J. Bus. Econ. Manag. 2018, 19, 154–175. [Google Scholar] [CrossRef]
- Almutairi, K.; Hosseini Dehshiri, S.J.; Hosseini Dehshiri, S.S.; Mostafaeipour, A.; Hoa, A.X.; Techato, K. Determination of optimal renewable energy growth strategies using SWOT analysis, hybrid MCDM methods, and game theory: A case study. Int. J. Energy Res. 2022, 46, 6766–6789. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Y. Integrated Optimization of Planning and Operations for Shared Autonomous Electric Vehicle Systems. Transp. Sci. 2023, 57, 106–134. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, C.; Yang, Y. Design and Optimization of Solar-Powered Shared Electric Autonomous Vehicle System for Smart Cities. IEEE Trans. Mob. Comput. 2023, 22, 2053–2068. [Google Scholar] [CrossRef]
- Othman, K. Impact of Autonomous Vehicles on the Physical Infrastructure: Changes and Challenges. Designs 2021, 5, 40. [Google Scholar] [CrossRef]
- Rana, M.M.; Hossain, K. Connected and Autonomous Vehicles and Infrastructures: A Literature Review. Int. J. Pavement Res. Technol. 2023, 16, 264–284. [Google Scholar] [CrossRef]
- Vo, H.V.; Chae, B.; Olson, D.L. Dynamic MCDM: The Case of Urban Infrastructure Decision Making. Int. J. Inf. Technol. Decis. Mak. 2002, 1, 269–292. [Google Scholar] [CrossRef]
- Elassy, M.; Al-Hattab, M.; Takruri, M.; Badawi, S. Intelligent Transportation Systems for Sustainable Smart Cities. Transp. Eng. 2024, 16, 100252. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, H.; Ogata, Y. Game Based Multi-Agent Equilibrium in Intelligent City Transportation System Design. DEStech Trans. Comput. Sci. Eng. 2018, 1–5. [Google Scholar] [CrossRef][Green Version]
- Dabiri, A.; Hegyi, A.; Hoogendoorn, S. Optimized Speed Trajectories for Cyclists, Based on Personal Preferences and Traffic Light Information-A Stochastic Dynamic Programming Approach. IEEE Trans. Intell. Transp. Syst. 2022, 23, 777–793. [Google Scholar] [CrossRef]
- Guo, Z.; Sun, D.; Zhou, L. Game Algorithm of Intelligent Driving Vehicle Based on Left-Turn Scene of Crossroad Traffic Flow. Comput. Intell. Neurosci. 2022, 2022, 9318475. [Google Scholar] [CrossRef]
- Schlossberg, M.; Riggs, W.; Adam Millard-Ball, L.A.; Shay, E. Rethinking the Street in an Era of Driverless Cars. 2018. Available online: www.urbanismnext.com (accessed on 30 September 2024).
- Radakovic, D.; Singh, A.; Varde, A.S.; Lal, P. Enriching Smart Cities by Optimizing Electric Vehicle Ride-Sharing through Game Theory. In Proceedings of the 2022 IEEE 34th International Conference on Tools with Artificial Intelligence (ICTAI), Macao, China, 30 October–2 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 755–759. [Google Scholar] [CrossRef]


| Linguistic Variables | Very Low | Low | Medium Low | Medium | Medium High | High | Very High |
|---|---|---|---|---|---|---|---|
| Equivalent interval numbers | [0.0–0.15] | [0.15–0.3] | [0.3–0.45] | [0.45–0.6] | [0.6–0.75] | [0.75–0.9] | [0.9–1.0] |
| Player 2 | ||||
|---|---|---|---|---|
| Strategy 1 | Strategy 2 | Strategy n | ||
| Player 1 | Challenge 1 | (a11, b11) | (a12, b12) | (a1n, b1n) |
| Challenge 2 | (a21, b21) | (a22, b22) | (a31, b31) | |
| Challenge n | (an1, bn1) | (an2, bn2) | (ann, bnn) | |
| Linguistic Variables * | Likert Scale | Fuzzy Scale |
|---|---|---|
| EH | 9 | (7, 9, 9) |
| VH | 7 | (5, 7, 9) |
| M | 5 | (3, 5, 7) |
| VL | 3 | (1, 3, 5) |
| EL | 1 | (1, 1, 3) |
| Factors in Smart City Street Design for Autonomous Vehicles and Cyclists | Code | Interval Average | Score | Result |
|---|---|---|---|---|
| Structure | C1 | [2.3, 2.9] | 0.685 | Acceptable |
| Sustainability | C2 | [2.2, 2.8] | 0.634 | Acceptable |
| Atmospheric environmental conditions | C3 | [1.8, 2.6] | 0.500 | Acceptable |
| Visual aspect | C4 | [2.5, 3.3] | 0.857 | Acceptable |
| Safety | C5 | [2.8, 3.4] | 0.970 | Acceptable |
| Slope | C6 | [2.3, 2.9] | 0.685 | Acceptable |
| Accessibility | C7 | [2.5, 3.3] | 0.857 | Acceptable |
| R | D | D − R | D + R | |
|---|---|---|---|---|
| C1 | [0.109 0.182] | [0.109 0.184] | [−1.387 2.044] | [0.219 0.366] |
| C2 | [0.100 0.169] | [0.081 0.147] | [−1.907 −2.249] | [0.181 0.316] |
| C3 | [0.114 0.188] | [0.095 0.165] | [−1.907 −2.249] | [0.209 0.353] |
| C4 | [0.114 0.188] | [0.100 0.171] | [−1.430 −1.635] | [0.214 0.359] |
| C5 | [0.109 0.182] | [0.200 0.286] | [9.062 1.042] | [0.310 0.468] |
| C6 | [0.114 0.188] | [0.090 0.159] | [−2.384 −2.862] | [0.205 0.347] |
| C7 | [0.114 0.188] | [0.100 0.171] | [−1.430 −1.635] | [0.214 0.359] |
| D − R (Cause) | D + R (Effect) | |
|---|---|---|
| C1 | 0.328 | 0.292 |
| C2 | −2.078 | 0.249 |
| C3 | −2.078 | 0.281 |
| C4 | −1.533 | 0.287 |
| C5 | 5.052 | 0.389 |
| C6 | −2.623 | 0.276 |
| C7 | −1.533 | 0.287 |
| Second Player | ||||||
|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | MAX | ||
| First Player | C1 | 6 | 8 | 7 | 9 | 9 |
| C2 | 6 | 8 | 8 | 7 | 8 | |
| C3 | 5 | 2 | 2 | 3 | 5 | |
| C4 | 5 | 3 | 5 | 6 | 6 | |
| C5 | 8 | 8 | 5 | 8 | 8 | |
| C6 | 5 | 8 | 3 | 8 | 8 | |
| C7 | 1 | 2 | 2 | 6 | 6 | |
| MIN | 1 | 2 | 2 | 3 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fayyaz, M.; Fusco, G.; Colombaroni, C.; González-González, E.; Nogués, S. Optimizing Smart City Street Design with Interval-Fuzzy Multi-Criteria Decision Making and Game Theory for Autonomous Vehicles and Cyclists. Smart Cities 2024, 7, 3936-3961. https://doi.org/10.3390/smartcities7060152
Fayyaz M, Fusco G, Colombaroni C, González-González E, Nogués S. Optimizing Smart City Street Design with Interval-Fuzzy Multi-Criteria Decision Making and Game Theory for Autonomous Vehicles and Cyclists. Smart Cities. 2024; 7(6):3936-3961. https://doi.org/10.3390/smartcities7060152
Chicago/Turabian StyleFayyaz, Maryam, Gaetano Fusco, Chiara Colombaroni, Esther González-González, and Soledad Nogués. 2024. "Optimizing Smart City Street Design with Interval-Fuzzy Multi-Criteria Decision Making and Game Theory for Autonomous Vehicles and Cyclists" Smart Cities 7, no. 6: 3936-3961. https://doi.org/10.3390/smartcities7060152
APA StyleFayyaz, M., Fusco, G., Colombaroni, C., González-González, E., & Nogués, S. (2024). Optimizing Smart City Street Design with Interval-Fuzzy Multi-Criteria Decision Making and Game Theory for Autonomous Vehicles and Cyclists. Smart Cities, 7(6), 3936-3961. https://doi.org/10.3390/smartcities7060152






