Optimising Urban Freight Logistics Using Discrete-Event Simulation and Cluster Analysis: A Stochastic Two-Tier Hub-and-Spoke Architecture Approach

Abstract

The transport of freight involves numerous intermediate steps, such as freight consolidation, truck allocation, and routing, all of which exhibit high day-to-day variability. On the delivery side, drivers usually cover specific geographic regions, also known as clusters, to optimise operational efficiency. A crucial aspect of this process is the effective allocation of resources to match business requirements. The discrete-event simulation (DES) technique excels in replicating intricate real-world operations and can integrate a multitude of stochastic variables, thereby enhancing its utility for decision making. The objective of this study is to formulate a routing architecture that integrates with a DES model to capture the variability in freight operations. This integration is intended to provide robust support for informed decision-making processes. A two-tier hub-and-spoke (H&S) architecture was proposed to simulate stochastic routing for the truck fleet, which provided insights into travel distance and time for cluster-based delivery. Real industry data were employed in geographic information systems (GISs) to apply the density-based spatial clustering of applications with noise (DBSCAN) clustering method to identify customer clusters and establish a truck plan based on freight demand and truck capacity. This clustering analysis and simulation approach can serve as a planning tool for freight logistics companies and distributors to optimise their resource utilisation and operational efficiency, and the findings may be applied to develop plans for new regions with customer locations and freight demands. The original contribution of this study is the integration of variable last-mile routing and an operations model for freight decision making.

1. Introduction

The field of freight logistics encompasses various sources of stochasticity, including freight consolidations, handling, and transport activities [1]. Notably, freight consignments exhibit substantial variability in terms of customer addresses and consignment attributes. Truck drivers are typically assigned to serve specific geographic regions, such as a set of suburbs or business areas within a given territory [2]. Therefore, truck routes exhibit diversity in activities on a day-to-day basis, which produces a need to achieve better cost optimisation and operational efficiencies [3].

While well-established territories often rely on historically developed and subjectively optimised delivery runs, the allocation of runs becomes a specific challenge when entering new territories. In such cases, a freight company might possess a list of potential customers and some indications of their freight demands, which are likely to be irregular. Consequently, decision making for freight companies to improve efficiency and reduce costs is important, such as devising an optimal truck allocation plan.

There are several tools that could support the decision making of freight companies. Geographic information systems (GISs) provide a powerful tool for capturing and analysing spatial data, including customer locations, road networks, and other relevant geographical features. By incorporating GISs into the logistics simulation process, researchers and practitioners can gain a comprehensive understanding of the spatial dynamics and optimise the allocation of resources accordingly.

In this context, discrete-event simulation (DES) proves to be a valuable technique for modelling the intricate and dynamic nature of logistics operations with stochasticity. By simulating the discrete events, such as truck allocation, vehicle movements, and delivery processes, DES allows for evaluating different scenarios and assessing their impact on key performance indicators (KPIs) such as delivery time, resource utilisation, and overall cost efficiency.

In the face of evolving market dynamics and growing customer expectations, contemporary freight companies find themselves under significant pressure to optimise their operational efficiency. In response to this challenge, the utilisation of advanced methodologies becomes crucial. Hence, the DES technique can offer a robust framework for dissecting and analysing complex operational processes. Although DES can mimic several aspects of real operations to facilitate decision making, it is difficult to simulate stochastic routing using this method. This paper proposes a two-tier H&S architecture to address the stochastic nature of freight truck routing to be integrated with a DES model for last-mile operational decision making. Compared to existing last-mile methods, the proposed method simulates real operational processes with more stochastic values and routes. Furthermore, this method provides potentially valuable pragmatic insights into the realm of business operations.

2. Literature Review

The development of urban cities calls for the optimisation of urban logistics systems to enhance efficiency and accommodate the needs of the growing population. Hence, digitalising last-mile delivery and implementing smart city logistics have emerged as prominent and highly discussed subjects. Smart city logistics require interdisciplinary knowledge, necessitating innovative advancements in logistics business practices and the integration of new technologies [4,5]. Moreover, to effectively assess and manage logistics systems, the development and application of more comprehensive metrics are imperative.

Last-mile modelling comprises a comprehensive range of elements, spanning from operations modelling and routing to clustering and structural analysis. Within the context of this study, the literature review segment embarked on an exploration of various facets. It firstly reviewed freight last-mile modelling techniques, followed by clustering and the H&S architecture.

2.1. Modelling Freight Last Mile

Various freight last-mile models have been created, including mathematical models, computer simulation models, and GIS-based models.

2.1.1. Vehicle Routing Problem

Existing mathematical techniques were applied to solve freight routing, called vehicle routing problems (VRPs). The variants of VPRs include the node routing problem (NRP) [6,7], travelling salesman problem (TSP) [8,9,10], arc routing problem (ARP) [11,12,13], rural postman problem (RPP) [14,15], and Chinese postman problem (CPP) [16,17,18]. Locations and routes are simplified as vertices, arcs (directed routes), and edges (undirected routes). These mathematical models have a prescribed objective function and constraints [19]. They are used to optimise the route in terms of travel time, travel distance, and transportation costs.

The benefit of using mathematical models is the model is easy to formulate. However, in order to reduce the complexity of calculation, mathematical models used to solve the problem need to make simplifications [20,21]. Furthermore, stochastic parameters and various systems and operations are difficult to incorporate into these models [22], so it can be challenging to represent real logistics cases.

2.1.2. Computer Simulation Techniques

Computer simulation techniques are applied to solve logistics problems. Typical techniques are discrete-event simulation (DES) and agent-based simulation (ABS). The main difference between them is that ABS takes into account individual behaviour, whereas DES structures the entire system [23]. These techniques can deal with stochastic randomness by using probability distributions and the Monte Carlo method and capture the detailed operational behaviour of systems. Therefore, the result can be more realistic and can reflect the variability of the system [24]. Hence, these simulation models tend to be more versatile than conventional mathematical models to describe complex systems [19].

DES has been applied to various areas of logistics. A DES model of a rail network in SIMUL 8 was designed by Marinov and Vigeas [25]. The rail network was decomposed into flat-shunted rail yards, rail freight terminals, railway double lines, and rail passenger stations. Automatic guided vehicles (AGVs) were evaluated in a production logistics system by DES [26]. The number, speed, and load capacity of AGVs and logistics buffers were optimised regarding resource allocation. Service network design was conducted by DES to include stochastic transportation times [27]. The vehicle routing problem was involved in estimating intermodal and unimodal transport in terms of costs and delays.

One approach used to simulate last-mile delivery across multiple clusters is to develop a DES model based on intersections [28]. Nevertheless, due to the effort involved in the development of the model, it is not well-suited for representing the intricate activities that occur within urban regions. A two-tier architecture was proposed to simulate freight operations for a large cluster incorporating cluster analysis [29]. The study outlines the methodology for modelling freight operations and how the cluster approach can be utilised to construct a DES model.

While computer simulation techniques are powerful, they have the limitation of being unable to conduct any geographical analysis. They need the delivery network to be predefined before building the simulation model; hence, they are unable to optimise geographic parameters.

2.1.3. Geographic Information System

GIS is a tool that can be used to manage and analyse a large set of spatial data. It has aided in solving various logistics problems, including hub location problems [30], emergency logistics distribution [31], urban logistics system design [2], CO₂ emissions reduction of distribution [32], and logistics process monitoring [33]. Clustering analyses were also conducted by taking advantage of GISs to display larger spatial data [34,35,36]. Specifically, it has been used to develop a last-mile delivery model by solving the TSP algorithm [28].

However, there are some limitations of GIS-based last-mile delivery models, particularly their requirement for deterministic input data. They cannot accommodate variability or stochasticity. Although the method can show routes, the variability of freight operations is difficult to include, such as random customer locations and freight demands, as this potentially results in different routes each day. While this is somewhat true of the adaptability of real driver behaviour, it is unhelpful when considering routes over a longer period of time, such as a year’s operation. In addition, other important freight operations, including freight consolidation and pickup-and-delivery (PUD) activities, are unable to be incorporated into the model.

2.2. Clustering Methods

Clustering analysis is important to freight transport modelling since the models involve the distribution of customer locations. To analyse a group of homogeneous locations and simplify the network, clustering methods are used to partition and differentiate locations. The clustering method has been used in different disciplines to group data points such as biology [37], medicine [38], chemistry [39], and computer science [40].

Clustering methods have been applied to logistics problems in group locations. The most common methods are density-based clustering and K-means clustering. The density-based clustering method works by sensing areas of points that are more concentrated or sparse [41]. The outlier points excluded from the part of a cluster are labelled as noise. Additionally, the time of the points can also be used to find potential groups of points that cluster in a given space and time. This approach relies on unsupervised machine learning clustering algorithms, which autonomously discern patterns by considering the spatial proximity and distance between neighboring points. There are several algorithms of this method, including density-based spatial clustering of applications with noise (DBSCAN) [42], hierarchical density-based spatial clustering of applications with noise (HDBSCAN) [43], and ordering points to identify the clustering structure (OPTICS) [44]. Density-based clustering has been applied to select providers for healthcare manufacturers [45] and cluster areas for crowdsourcing [46].

The Euclidean clustering method is similar to the density-based clustering method, as both methods consider Euclidean distances in their processes. However, there are notable distinctions between the two approaches. While the density-based clustering method delineates distances based on circular regions, the Euclidean clustering method calculates distances between individual data points [47]. Consequently, the density-based clustering method yields clusters of varying sizes, while the Euclidean clustering method produces clusters of more uniform sizes with reduced noise. Nevertheless, the presence of noise impacts the formation of clusters.

Consequently, the density-based clustering method is particularly valuable in scenarios characterised by fluctuating cluster densities, irregular geometries, and the need for robust noise point identification. In contrast, Euclidean methods find applicability in situations where clusters are anticipated to exhibit consistent sizes and spherical shapes, especially when the number of clusters is either predetermined or can be reliably estimated. In freight logistics, the considerable diversity in customer locations results in varying cluster densities, shapes, and sizes. In such cases, the employment of the density-based clustering method proves to be more advantageous and appropriate.

The K-means clustering method is a centroid-based clustering method. Centroids are initially deployed and data points are assigned based on the sum of distances [48]. The goal of K-means is to group similar data points and assign them to clusters, where each cluster is represented by its centroid. Applications of the K-means algorithm include clustering restaurants around distribution centres [49], hub location optimisation [50], urban freight loading bay management [51], and locating urban facilities [52]. One significant disadvantage of the K-means clustering method is that similarity is not considered in the development of clusters [53].

In comparison with the density-based clustering method, the K-means clustering technique strives to minimise inter-data distances and finds its relevance in situations where clusters are expected to display consistent sizes and shapes. Therefore, within the context of freight logistics, the density-based clustering method emerges as a more appropriate choice for accommodating data variations.

2.3. Hub and Spoke Architecture

The H&S architecture has been used to describe urban freight transport. It is occasionally combined with clustering analysis. The benefits of applying a clustering algorithm to freight delivery models are that customer locations can be represented as clusters in an H&S architecture, with corresponding truck allocation plans. In an H&S architecture, hubs refer to warehouse points and are connected by travel routes, which are simplified as spokes. The H&S architecture has been applied to structure logistics systems; for example, freight line-haul transport [54,55], intra-city metro logistics [56], retail distribution systems [57], and parcel mail delivery [58,59]. A genetic-based fuzzy C-means clustering method was applied to develop an H&S model for an underground logistics system [60]. These models are mathematic models that were used to optimise systems in terms of lead times, truck utilisation rates, and transportation costs. Last-mile routes formulated by these models are deterministic. However, in practical freight operations, routes are stochastic in last-mile delivery.

However, there is little to no use of this structure in simulating the last-mile route. This is probably because many last-mile delivery problems have an approximately homogenous distribution of addresses, so it is difficult to distinguish any structure. Also, last-mile delivery is notoriously for the day-to-day variability of addresses and consignment attributes of weight and volume. Hence, there is a need to formulate a last-mile delivery model with stochastic parameters.

2.4. Gaps in Modelling Last-Mile Delivery

Modelling urban last-mile delivery operations has historically been challenging. The existing H&S-based mathematical models and GIS-based models have been designed to address specific delivery scenarios with a large number of deterministic values, and are easy to construct and useful in specific cases. However, real-world freight operations are far more complex, and these simplified models prove inadequate for informed decision making by freight companies [61]. The complexity arises from the massive and unpredictable nature of customer locations, with high day-to-day variability of both addresses and the weight (or volume) of consignments.

Although computer simulation techniques such as DES have been employed to simulate freight logistics for decision making, the geographic question—namely the variability in routing—is problematic in these techniques. Consequently, there arises a need to develop a method that can support computer simulation techniques for running last-mile simulations while incorporating stochastic routing variables to facilitate more effective decision making about truck allocation.

The proposed method integrates the two-tier H&S architecture with a DES model. This integration—which has otherwise not been shown in the literature—enables the incorporation of extensive stochastic operational and route values, facilitating a more comprehensive and realistic representation of complex operational scenarios. Consequently, the proposed integration establishes a framework for logistics that aligns with the intricate demands of modern large-scale logistics operations.

3. Method

3.1. Research Objective

The objective of this study was to develop a routing architecture integrating a DES last-mile delivery model for a city scale to capture the variability in operations and support decision making. The method is intended to either optimise current freight operations or evaluate operations for new territories.

3.2. Context

Christchurch city is the business area under consideration, and is the largest city on the South Island of New Zealand. There are various residential and industrial areas in this city. The city encompasses a diverse range of residential and industrial zones, contributing to its dynamic nature. Consequently, freight consignments in this area exhibit substantial daily fluctuations in demand. The business mode was investigated, known as less-than-container-load (LCL), wherein consignments from various customers are consolidated onto a single truckload. This consolidation is then efficiently carried out using milk runs within the urban area pickup or delivery. Typically, the number of consignments handled ranges between 10 and 15 per truckload. The transportation process involves morning freight deliveries to expedite dock clearance, followed by afternoon freight pickups. Consequently, it is expected that the duration of the delivery run should ideally remain within a 2-h timeframe. In practice, the research team had access to one quarter’s actual delivery data for the whole city, including the allocated runs. The data for each quarter exhibit similar patterns of customers, thereby providing adequate insights for analysis.

3.3. Two-Tier H&S architecture

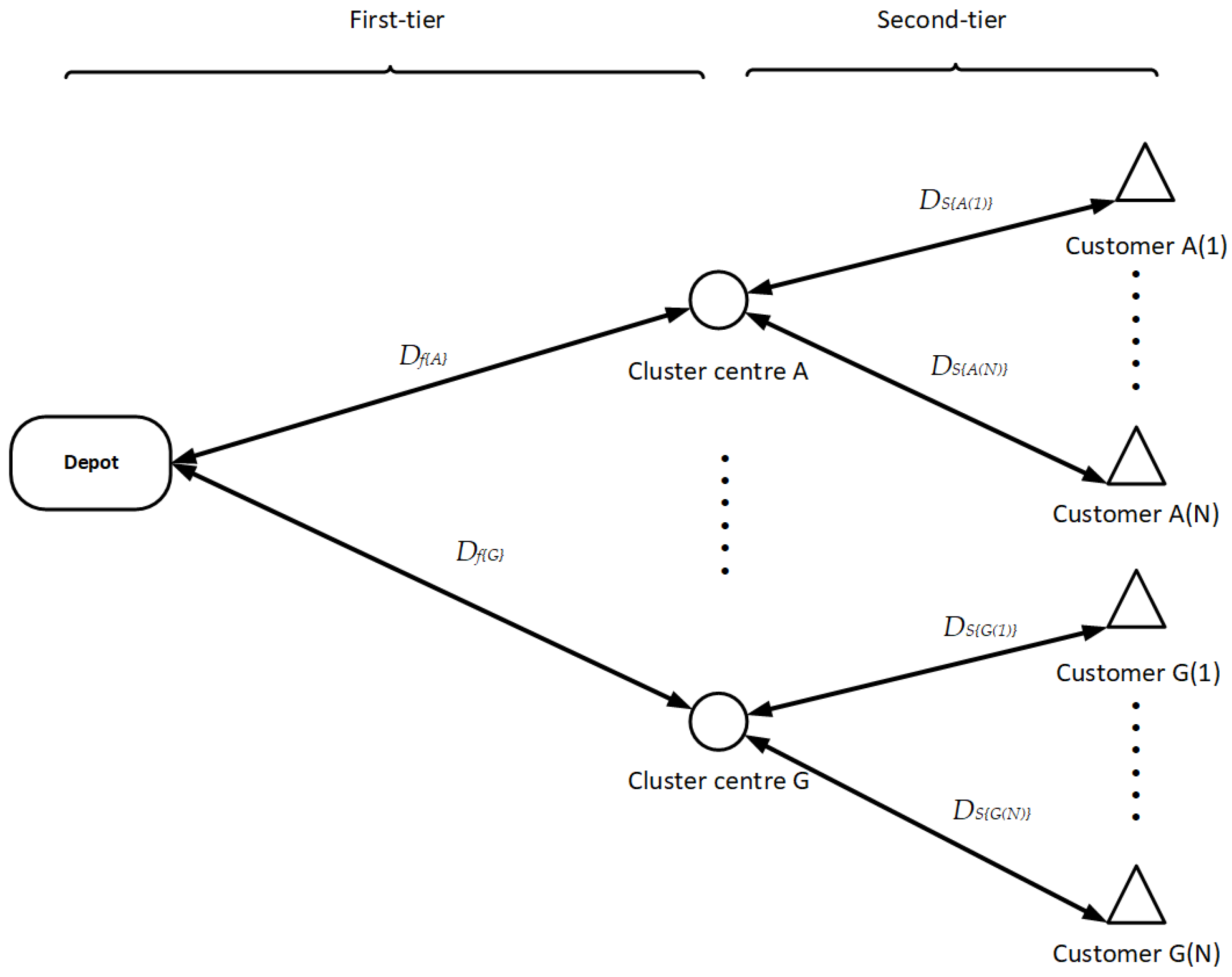
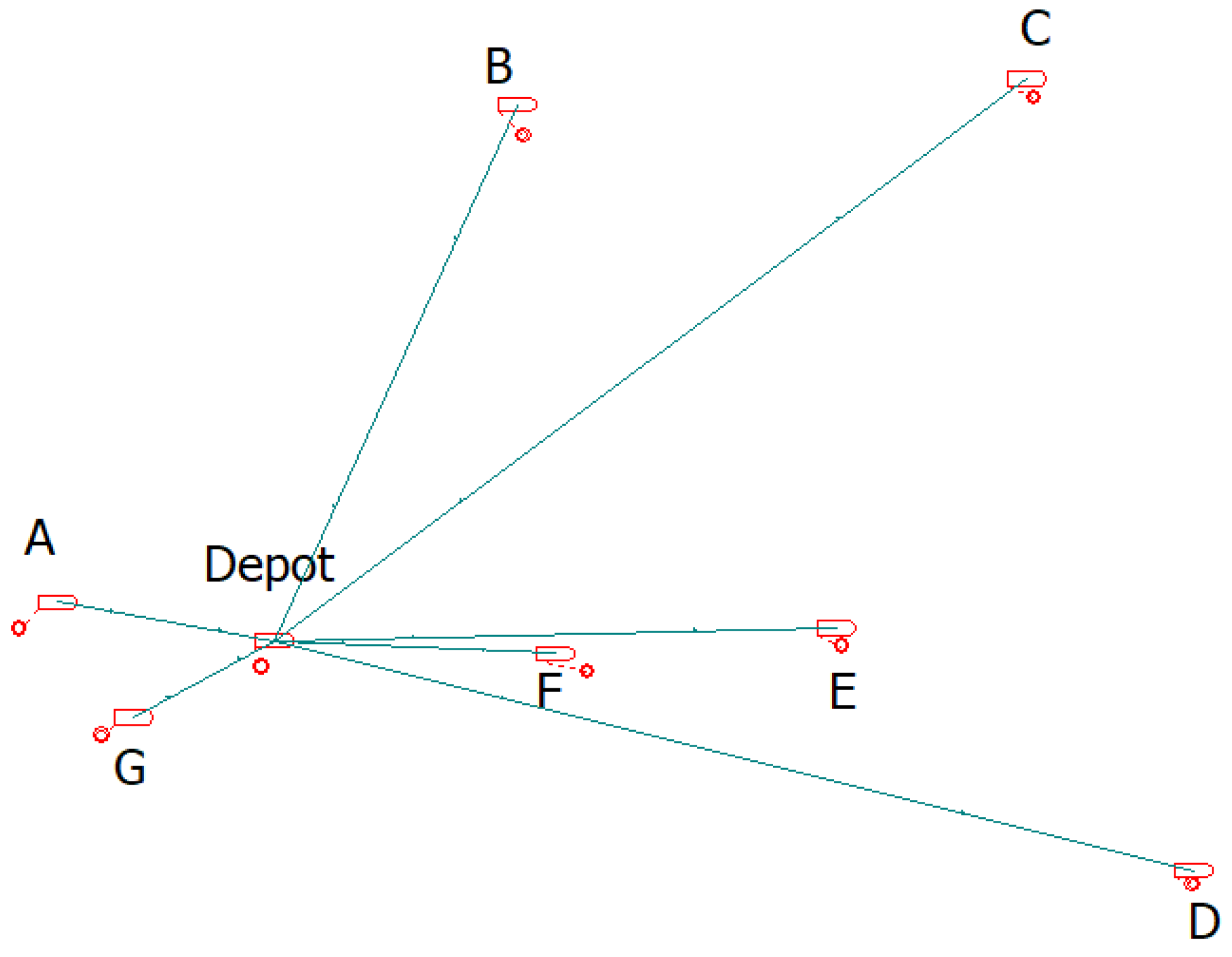
In order to capture variability in truck routing for various clusters and accommodate the inherent structure of DES, the routes need to be represented by a simplified architecture. A two-tier H&S architecture was developed to simulate the variable truck routes for each cluster by fluctuating route distances. The delivery route was partitioned into two tiers for the entire H&S architecture, as illustrated in Figure 1. The first-tier spans from the depot to each cluster centre, while the second tier extends from the cluster centre to each customer. Specifically, the hubs in this architecture refer to cluster centres rather than physical logistics hubs.

To compute the first-tier distance ${(D}_f)$, the cluster mean centre should be determined first [29]. Subsequently, the second-tier distance ($D_s$) for each customer location exhibits a stochastic nature, which can be computed by multiplying the Euclidean distance ($D_e$) between the cluster centre and the customer locations by a factor R. Hence, the total travel distance ($D_{total}$) for the journey can be computed as:

$$D_{total}=2\times D_f+\sum D_s\left(i\right)\hspace{1em}\forall i\in N$$

(1)

$$D_s\left(i\right)=R\times D_e\left(i\right)\hspace{1em}\forall i\in N$$

(2)

The R-value is introduced to adjust the total second-tier distance and approximate the actual delivery distance. To determine the R-value, a TSP simulation technique can be optimised to simulate delivery routes and calculate the total route distance ($D_t$). By using Equation (3), the hypothetical second-tier distance ($D_m$) can be computed, and Equation (4) can then be employed to determine a suitable R-value based on a single TSP simulation.

$$D_m=D_t-2\times D_f$$

(3)

$$R=\frac{D_m}{\sum D_s}$$

(4)

3.4. Approach

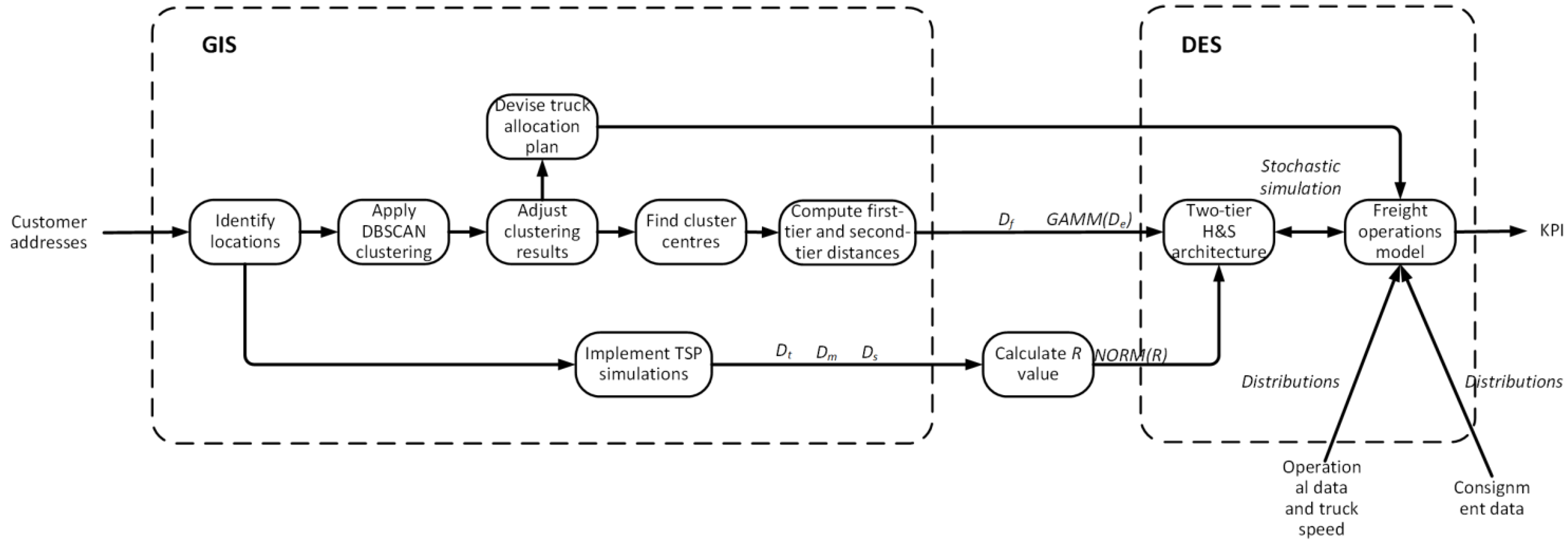
The first stage was to use GIS methods to determine delivery clusters at a city level. This was then followed by the development of a two-tier H&S architecture, which was then implemented in DES. The modelling process includes multiple stages as Figure 2 shows.

Stage 1: Customer locations based on the consignment data were identified by using ArcGIS^® Pro (version 3.0.1) software. DBSCAN clustering technique was applied to determine distinct clusters. Through several iterations, adjustments were made to refine the clustering results. The DBSCAN results were evaluated based on two criteria: ensuring that cluster size is not excessively large and that cluster shapes align with the requirements of the H&S model. Hence, the initial clustering results were adapted considering freight attributes such as weight, volume, and geographic considerations.

Stage 2: The cluster centres were identified to calculate the first-tier and second-tier distances. The second-tier distances were fitted into gamma distributions.

Stage 3: A truck allocation plan was defined based on clustering results. The principle was to match the appropriate trucks to the expected freight volume and weight for efficient delivery based on the freight demand for each cluster and the capacities of the available trucks.

Stage 4: TSP simulations were conducted for each cluster based on customer locations. The results were used to calculate the R-values for adjusting the two-tier H&S architecture. The R-values were fitted into normal distributions.

Stage 5: A two-tier H&S architecture was developed and integrated with a DES model, which represents the freight operations, to conduct stochastic simulation. Operational data, consignment data, and truck speeds were input into the DES model.

3.5. Determining Clustering Methods in ArcGIS

There are multiple density-based clustering methods, including DBSCAN, HDBSCAN, and OPTICS; see

Table 1. Comparison of density-based clustering methods.

Clustering Methods	Attributes	Parameters
DBSCAN	Clusters have the same density	Minimum number of data points and search distance
HDBSCAN	Density is varied for clusters	Minimum number of data points
OPTICS	The reachability plot is defined to vary density for clusters	Minimum number of data points, search distance, and cluster sensitivity

. All three methods were attempted, and DBSCAN was selected based on the following criteria. Firstly, geographical consistency and cluster shape are crucial, as clusters should exhibit clear partitioning and concentration. In addition, it is important that consignment fulfilment requirements are met, i.e., clusters must cover specific suburbs rather than having overlapping runs. Furthermore, operational simplicity is another key factor, as the clustering method should be able to handle a large number of location points and adjust according to real freight operations.

The ‘number of data points’ corresponds to the data points on the map, whereas the concept of the ‘minimum number of data points’ pertains to clusters that contain fewer data points than this designated threshold. Clusters falling below this minimum data point count are designated as noise due to their inability to form a substantial grouping worthy of classification as a cluster. Alternatively, these smaller clusters may be merged with neighboring clusters, facilitating adherence to the stipulated minimum data point count criterion.

The ‘search distance’ parameter serves the purpose of seeking out the ‘number of data points’ within a specified range. This entails identifying data points that fall within a certain proximity of a given reference point, contributing to the determination of the data point count within the specified distance.

4. Results

4.1. Clustering for Christchurch City

One-quarter of consignment locations were input and identified by ArcGIS^® Pro (version 3.0.1). The clustering analysis was executed for the whole city using DBSCAN, with iterations being conducted to decide the cluster results. A changing set of values for input parameters (minimum number of data points and search distance) was used. The ‘minimum number of data points’ refers to customer locations (addresses).

Table 2. Parameters for iterations.

Iteration Number	Input Parameter: Minimum Number of Data Points per Cluster ${\mathit{N}}_{\mathit{m}\mathit{i}\mathit{n}}$	Input Parameter: Search Distance ${\mathit{R}}_{\mathit{s}\mathit{e}\mathit{a}\mathit{r}\mathit{c}\mathit{h}}$	Resulting Number of Clusters ${\mathit{N}}_{\mathit{c}\mathit{l}\mathit{u}\mathit{s}\mathit{t}\mathit{e}\mathit{r}\mathit{s}}$
1	20	2000	4
2	250	1250	5
3	50	280	28
4	150	280	19

indicates the parameters used for cluster determination. The initial iteration ($N_{min}=20$, $R_{search}=2000)$ yielded four clusters. One of these clusters was dislocated from all the others, and hence retained as an independent cluster. The remaining three clusters were then reanalysed in Iteration 2 ($N_{min}=250$, $R_{search}=1250)$, where these parameters were determined by a trial-and-error process. The objective was to produce clusters that were geographically distinct. Repetition of this process resulted in the progressive identification of clusters; see Figure 3.

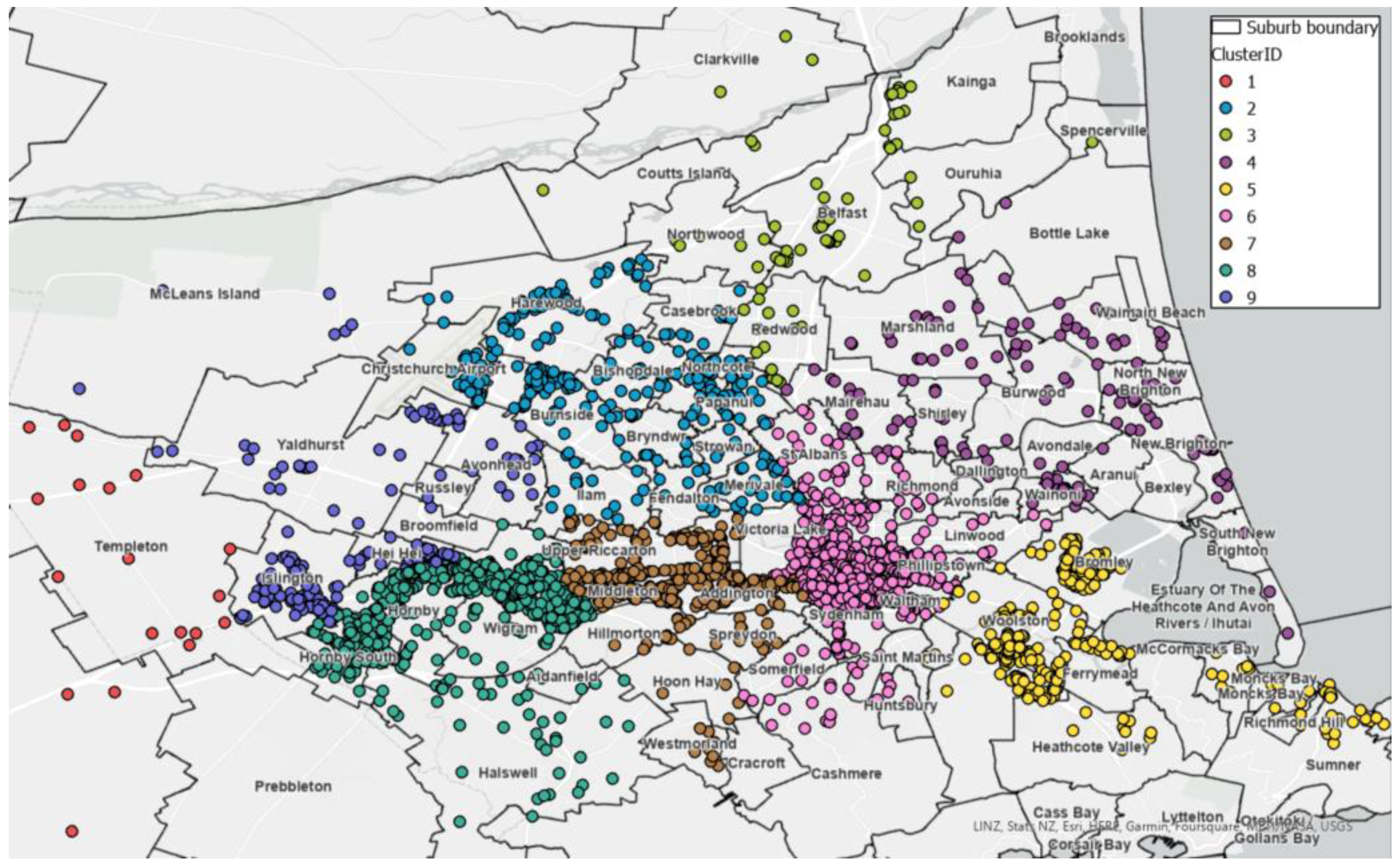
After the four iterations of clustering, the residual noise points—addresses that had not been assigned to a cluster—were manually assigned to the nearest clusters. Clustering results for the whole of Christchurch city at the end of this process are shown in Figure 4.

The nine independent clusters represent a number of suburb areas grouped together considering the proximity of noise points to the initially designated clusters. The consignment demands for clusters are shown in

Table 3. Consignment demands for initial clustering results.

Cluster ID	Total Consignment Number	Average Consignment Number per Day	Average Total Weight per Day (t)	Max Total Weight per Day (t)	Average Total Volume per Day (m3)	Max Total Volume per Day (m3)
1	69	2	0.4	2.4	2.5	22.4
2	1802	20	7.6	23.5	25.2	80.0
3	519	8	3.4	17.8	8.1	39.7
4	706	9	3.0	16.1	10.1	29.4
5	1634	21	13.0	49.0	34.7	103.6
6	3709	46	13.8	29.9	49.1	100.2
7	3197	40	16.5	53.4	49.8	104.9
8	6365	81	45.2	120.0	123.6	283.1
9	1676	21	14.4	51.8	36.0	137.3

.

The suburbs are allocated based on the results from DBSCAN and the noise points around the cluster. The cluster sizes vary depending on the business volumes (weight, volume, and shipments) for individual suburb areas. From the study, Cluster 6, 7, and 8 have relatively high numbers of shipments per day. Also, the average weight and volume are higher for these clusters. Cluster 2, 5, and 9 have moderate levels of shipments per day. The average weight and volume are also moderate for these clusters. For Cluster 1, 3, and 4, the number of shipments per day is only 2, 8, and 9, respectively, which is not a sustainable solution. The average weight and volume are the lowest for these clusters.

Although the DBSCAN method was used for city clustering, it provided only a basic level of cluster formation. Limitations were small clusters, mixed clusters, and a lack of incorporation of route realities. Thus, further manual judgment was required to arrive at practical results, as shown next.

4.2. Modified Clustering Results

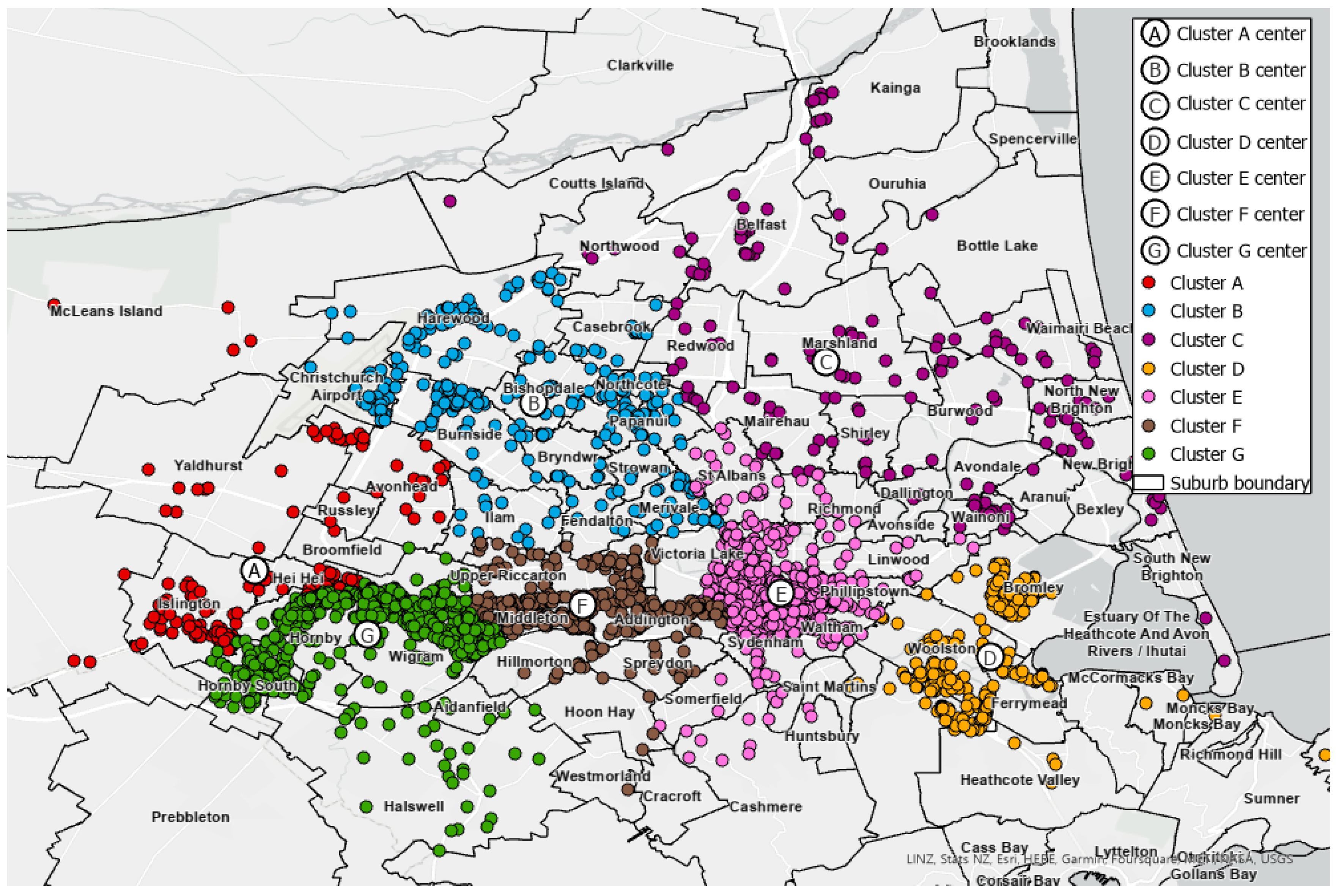
Considering freight demand and geographical distribution, modifications of the initial clustering results were conducted. Clusters were further regrouped considering the density of consignments in a particular area. Clusters 1 and 9 were grouped into Cluster A, and Cluster 3 and 4 were merged into Cluster C. As shown in Figure 5, seven clusters were formed with cluster mean centres, namely A, B, C, D, E, and G. This was executed to manage clusters and achieve better control of route efficiencies and workload balancing.

Figure 6 presents the adjusted clustering results, which have been integrated into the two-tier H&S architecture within the Arena® (version 16.2) DES software for simulation purposes. The corresponding consignment demands are shown in

Table 4. Consignment results for modified clustering results.

Cluster ID	Total Consignment Number	Average Consignment Number per Day	Average Total Weight per Day (t)	Max Total Weight per Day (t)	Average Total Volume per Day (m3)	Max Total Volume per Day (m3)
A	1745	23	14.8	54.2	38.5	159.7
B	1802	20	7.6	23.5	25.2	80.0
C	1225	17	6.4	33.9	18.2	69.1
D	1634	21	13.0	49.0	34.7	103.6
E	3709	46	13.8	29.9	49.1	100.2
F	3197	40	16.5	53.4	49.8	104.9
G	6365	81	45.2	120.0	123.6	283.1

.

4.3. Truck Allocation

Several functional factors were considered for the allocation of resources, including freight average and maximum demands, truck capacities, filling rate, workload balancing for business requirements, and real-world operational constraints. Based on the practical truck fleet, two types of LCL trucks were considered. The first one is the regular truck, with a capacity of 27 t and 48 m³. The second is the truck with a trailer with a capacity of 54 t and 96.1 m³. One float truck was allocated to serve all clusters to level off the daily variations in the freight business. The detailed explanation of the truck allocation for each cluster is as follows.

The average daily total weight and volume for clusters A and B are sufficient for being accommodated by one regular truck each. However, the maximum weight or volume is sometimes beyond the capacity. The truck with a trailer was allocated to deal with variations. In addition, there are several open roads in these two areas, which are appropriate for the truck with a trailer.

For clusters C and D, the average daily demand is lower than the capacity of the regular truck. Therefore, one regular truck was allocated to each cluster. The excess volume would be carried by the floater. As these two clusters are mainly residential areas, the truck with a trailer is inappropriate for the road conditions.

For clusters E and F, two regular trucks were allocated to each cluster, respectively, to handle the demand. The truck with a trailer was not chosen because these two clusters are business areas. Long trucks have constraints in these areas.

For cluster G, four regular trucks were selected to cope with the large demand. In addition, this cluster is located in the industrial area and near the depot so the regular trucks can provide a rapid response rather than big trucks.

Table 5. Truck allocation based on clustering results.

Cluster ID	Regular Truck	Truck with Trailer
A	-	1
B	-	1
C	1	-
D	1	-
E	2	-
F	2	-
G	4	-

presents the truck allocation for clusters.

Based on the allocation result, a total of 12 regular trucks of varying capacities and 1 float truck for the potential excess shipments were allocated for an average of 248 shipments per day.

4.4. Developing a Two-Tier H&S Architecture

The parameters for the H&S network were obtained using ArcGIS^® Pro (version 3.0.1) software, which employed the ‘near’ function to calculate the linear distances between the mean centre and each customer address, as well as the distance between the depot and the mean centre. The result of this process produced ten groups of R values (see Equation (2)), which represented the variability in R as a probability distribution. For this study, the normal distribution was chosen due to its compatibility with positive R values and its lower bound per [29]. The spoke distances were established by using gamma distributions.

The daily average shipments for each cluster were used to determine the number of consignments considered, as it was deemed the most reliable instance for each cluster on a day-to-day basis. However, distribution fitting methods could be utilised for larger samples to determine the optimal distribution. A delivery run was simulated using the daily average number of shipments for each cluster. Ten sets of random consignment addresses were generated for each cluster, with each set corresponding to the average consignment number.

Using the ‘Near’ function in ArcGIS^® Pro (version 3.0.1), the linear distance between the mean centre and each customer address for each of the seven clusters was calculated. Finally, optimised routes for each set were generated using the ‘Find Routes’ function, which determines the shortest path used to visit each address and provides driving directions, information about the visited address, route paths, travel time, and distance. The value of R is defined as the ratio of the last-mile distance obtained from the ‘Find Routes’ function (TSP) and the second-tier linear distances obtained from the ‘Near’ function. To determine the extent of variability of actual and second-tier distances across different clusters, a statistical analysis of R values was conducted using the normal distribution method for all clusters.

Table 6. Parameters for H&S model.

Cluster ID	Average Total Distance by TSP (km)	Distance from Depot to Cluster Centre (km)	Total Distance by H&S Model (km)	Mean R-Value	R-Value Std Dev	Gamma Distribution for Spoke Distances
A	33.5	3.2	59.6	0.508	0.091	GAMMA (481.265, 4.931)
B	39.7	6.1	55.9	0.630	0.061	GAMMA (326.818, 6.847)
C	59.9	10.8	78.5	0.676	0.044	GAMMA (923.190, 3.731)
D	40.7	11.4	55.8	0.545	0.072	GAMMA (239.600, 6.503)
E	42.3	7.3	42.3	0.726	0.087	GAMMA (383.468, 3.051)
F	20.5	3.4	20.5	0.606	0.140	GAMMA (345.955, 3.472)
G	22.3	1.0	36.4	0.591	0.077	GAMMA (211.819, 8.171)

indicates the parameters for the H&S model.

4.5. Discrete-Event Simulation

4.5.1. Architecture of DES Model

The freight delivery model for Christchurch city was built from the clusters developed from ArcGIS^® Pro (version 3.0.1) and then implemented in a simulation model using Arena^® (version 16.2) software. The total distance travelled by each truck was divided into a three-segment path for simplification: from the depot to the mean centre of each cluster, from the mean centre of the cluster to each customer address, and finally from the mean centre to the warehouse depot. Arena^® uses graphic block diagram models to represent the logical flow of job entities. A high-level view of the hub–spoke model is shown in Figure 5.

4.5.2. Input Data

Poisson distributions for consignment numbers were obtained by fitting, and normal distributions of R values and gamma distributions of last-mile distance for clusters were as above. Trucks were defined based on the allocation plan. The truck speed was considered the same for all trucks, which is 30.6 km/h according to the real GPS data. Simulation input parameters are shown in

Table 7. Simulation input parameters.

Cluster ID	Daily Consignment Number	Truck Consignment Capacity
A	POISSON (26.212)	23
B	POISSON (26.576)	20
C	POISSON (18.569)	17
D	POISSON (24.545)	21
E	POISSON (55.773)	46
F	POISSON (48.091)	40
G	POISSON (96.152)	81

.

4.5.3. Implementation

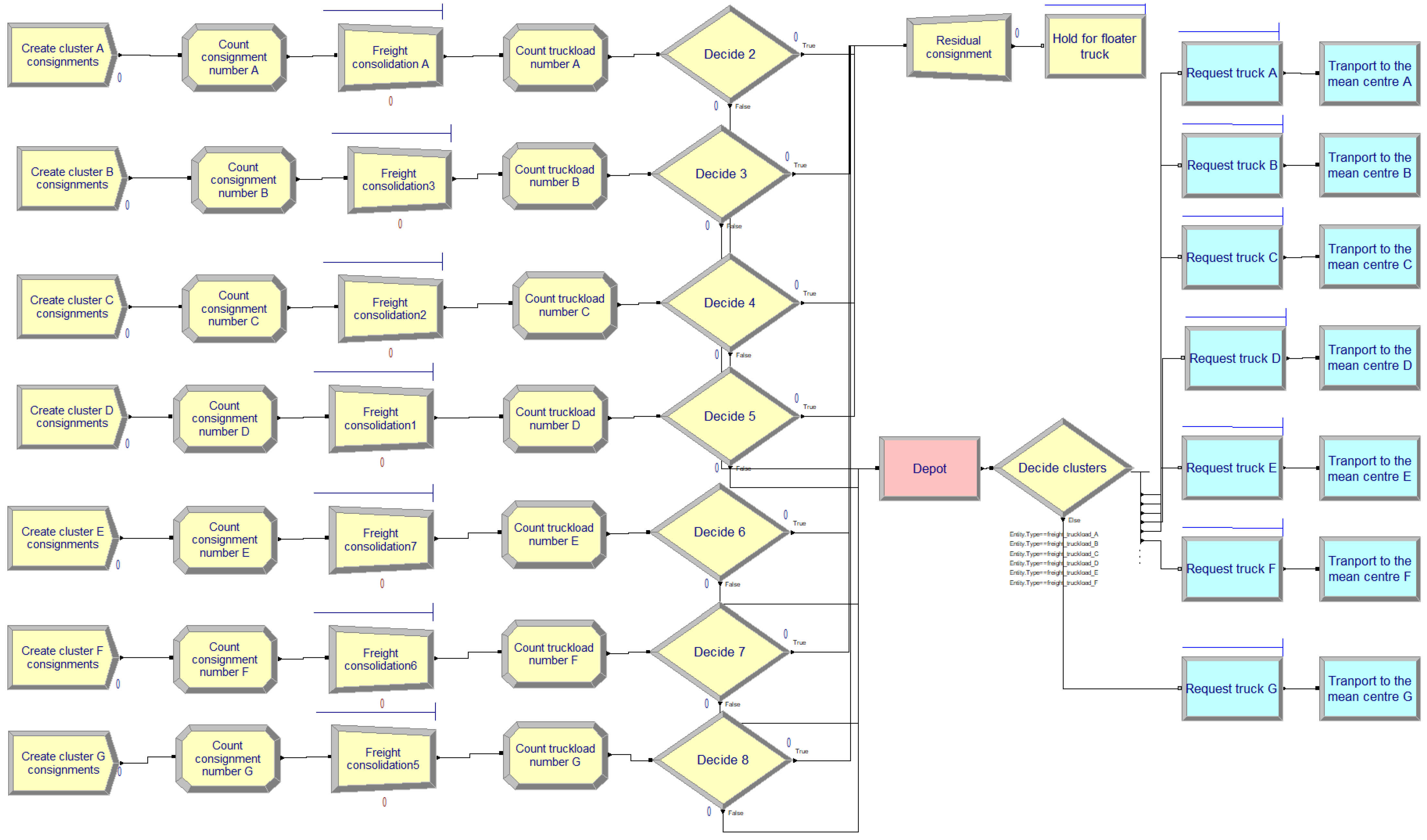
The DES model was divided into two modules, truck allocation and first-tier delivery, and the second-tier delivery. The architecture of the truck allocation and first-tier delivery is shown in Figure 7.

The module of the second tier for each cluster is similar. Figure 8 illustrates the second-tier delivery for cluster A.

4.5.4. Simulation Results

The simulation was performed for 100 replications, each representing a day’s worth of consignments. For each replication, a random number of consignments and a random last-mile distance were generated. The KPI results of the simulation are presented in

Table 8. Simulation results for KPIs.

Clusters	Average Travel Distance per Truck (km)	Average Travel Time per Truck (h)
Cluster A	32.9	1.1
Cluster B	40.4	1.3
Cluster C	58.0	1.9
Cluster D	39.9	1.3
Cluster E	30.9	1.0
Cluster F	21.2	0.7
Cluster G	25.4	0.8

.

The travel distance per truck encompasses both the forward and return distances originating from the depot. The travel time for Cluster C is large due to its considerable distance from the depot and the largest cluster size. The travel times for the rest of the clusters are around 1 h. Based on the simulation results, the average residual shipment number for the city (over all the clusters) is 17, which means that these consignments cannot be delivered by the regular trucks and would require the use of floater trucks. One floater truck should be sufficient for handling these remaining shipments.

The results also show that the trucks serving Cluster C have the longest travel distance and time, as this cluster is the furthest from the depot. On the other hand, trucks serving Clusters F and G have shorter travel distances and time because they are closer to the depot. Based on this information, it may be possible to reduce the number of trucks used for these two clusters and have another delivery round, which could potentially save transportation costs.

5. Discussion

5.1. Comparison with Current Truck Allocation

The predicted number of trucks is smaller than the current number. In the actual delivery operations for the Christchurch city area, there are 18 trucks serving the city. The comparison of daily consignment weight and volume between the current truck allocation and the proposed truck allocation is shown in

Table 9. Comparison of current truck allocation and proposed truck allocation.

Truck ID	Current Daily Average Total Consignment Weight (t)	Proposed Daily Average Total Consignment Weight (t)	Current Daily Average Total Consignment Volume (m3)	Proposed Daily Average Total Consignment Volume (m3)
1	5.9	14.8	23.0	38.5
2	5.3	7.6	19.4	25.2
3	12.3	6.4	29.3	18.2
4	5.6	13.0	17.5	34.7
5	5.4	6.9	18.2	24.6
6	0.8	6.9	4.1	24.6
7	6.2	8.25	19.2	24.9
8	1.4	8.25	7.4	24.9
9	8.3	11.3	28.3	30.9
10	11.2	11.3	31.1	30.9
11	5.4	11.3	19.4	30.9
12	9.6	11.3	13.4	30.9
13	5.9	-	16.2	-
14	7.8	-	20.9	-
15	7.3	-	18.1	-
16	1.1	-	6.0	-
17	3.5	-	13.1	-
18	14.3	-	34.6	-
Average	6.5	9.8	18.8	28.3
Std dev	3.6	2.6	8.2	5.3

.

The proposed truck allocation plan reduced the overall number of regular trucks and floater trucks while increasing the utilisation of freight weight and volume for each individual truck. The standard deviation indicates a more balanced distribution of freight among the trucks, suggesting a greater similarity in the assignment of freight loads to each truck. The reduction in the overall number of trucks has the potential to significantly mitigate the company’s operating expenses, leading to substantial cost savings.

The delivery approach adopted by the freight company was variable in nature and the distribution map appears to be flexible with multiple overlaps and is not limited to serving specific areas. Further analysis of this situation revealed that a clustering method in such a context is hardly plausible due to the high variability in the current distribution strategy. Nominally, each driver is allocated to one suburb, and some suburbs (such as the central city) may have two drivers allocated. However, the actual allocations show extensive overlap. In particular, many suburbs are serviced by multiple drivers, up to six in some cases. Some of these deliveries are outliers, which implies that the driver was filling in capacity.

Even so, the operational model of the freight company is much more one of overlapping provision than strict geographic territorialism [62]. Presumably, this strategy gives the organisation redundancy against driver non-availability, and surges in workload [63].

5.2. Implications

Logistics practitioners can leverage the DBSCAN clustering method in various ways within an academic context. One potential application involves utilising the method to develop an optimised network for a new business area. By providing a list of potential customers within a previously unexplored region, the cluster method can estimate the necessary fleet size and associated resource requirements. Additionally, it can generate valuable insights regarding delivery performance indicators, such as the time taken to complete each delivery round. These metrics play a critical role as it is typically imperative to clear the dock of all consignments within a single day, minimising the need to carry excessive workloads forward to subsequent days.

Freight logistics companies and distributors could consider clustering analysis and the DES approach presented in this work as a basis for resource planning and cost-controlling measures for large freight business models. Business owners and drivers could consider developing delivery groups, route planning, and improving operational efficiencies by adopting the findings from this work. Logistic managers could use the results from the work to effectively manage a dynamic operation setup and lower costs to improve resource utilisation. This research work attempts to solve real-life freight logistics problems for Christchurch city by using density-based clustering analysis and the DES approach.

To adequately address the clustering problem, in effect, a combination of the DBSCAN method and additional manual processing and judgements was required to reach feasible and improved results. The DBSCAN method produced good clusters when considering distance as the prime variable. However, it was ineffective from the perspective of driver workload (number of consignments). For example, some clusters had only 2 consignments per day, whereas others had up to 81 consignments per day. This is impractical for real operations of truck allocation, and is also an inefficient use of trucks. Consequently, it was necessary to manually regroup by merging small clusters into nearest other clusters. It may also be necessary to split excessively large clusters, though another solution is to allocate more than one truck, as here. The DBSCAN algorithm implicitly assumes that a truck is an infinitely flexible resource—it does not take into account that trucks are of fixed capacity and that the filling rate (utilisation) needs to be high for economic reasons. Such intervention in the DBSCAN results would be necessary each time the consignment profile changed radically. Nonetheless, human intervention is relatively easy to perform—the total time including the GIS processing would be several hours of human effort. Hence, the method may be less suitable where there is high variability in the consignment profile. It is inevitable that human judgements will have a subjective element.

5.3. Limitations

One limitation of the study is that the trucks were assumed to travel at the same speed. This is a reasonable simplifying assumption for an urban region where the roads are all of the same speed limits and congestion is homogenous. In practice, variations across a city are expected, e.g., certain trucks may have better capabilities to optimise trunk routes, which could result in different speeds. In principle, a cluster model could be developed to accommodate different speeds on the routes. A GIS model can be leveraged to establish these parameters, as demonstrated in a previous study [28].

The DBSCAN algorithm needs human inventions to achieve practical results due to the nature of the mechanism. Hence, the clustering results could be improved by incorporating more constraints in the future.

5.4. Future Work

There are some areas that could be explored in future work. The study revealed that further optimisation could be performed based on more practical constraints for each cluster, such as road and traffic conditions, parking issues, and driver availability. Due to the development of urban cities, these constraints hold considerable relevance in shaping efficient freight operations. Another area is to explore the use of alternative transportation modes, such as drones or autonomous vehicles, for enhancing last-mile delivery efficiency. This avenue could be further explored by subjecting the simulation model to various scenarios. This could involve assessing the feasibility and cost-effectiveness of integrating these modes into the existing truck-based delivery system. Additionally, the model could be extended to include environmental considerations, such as carbon emissions and air quality, to support sustainable transportation planning. The application of emerging modes could facilitate smart city logistics, thereby fostering comprehensive urban development.

6. Conclusions

This study introduces a two-tier H&S architecture to address route variability and integrate with a DES model for operational decision making. The operations simulation component of the approach has proven to be particularly useful, providing insights into the travel distance and time associated with the delivery operations. This information can serve as a foundation for future efforts aimed at enhancing the efficiency of delivery operations. The DBSCAN clustering method was employed to derive customer clusters and facilitate the truck allocation plan. By employing the proposed architecture, clusters of customers can be efficiently assigned to drivers and simulated with an operations model, thereby improving resource allocation and operational efficiency.

The integration of spatial analysis, stochastic modelling, and simulation techniques offers practical benefits for logistics practitioners seeking to establish optimised delivery networks and truck allocation in new territories. This research contributes to the field by providing a methodological framework that can be readily applied in real-world logistics scenarios, leading to improved resource allocation, reduced costs, and enhanced operational performance.