Macroscopic Lane Change Model—A Flexible Event-Tree-Based Approach for the Prediction of Lane Change on Freeway Traffic

Abstract

Binary logistic regression has been used to estimate the probability of lane change ($LC$) in the Cell Transmission Model (CTM). These models remain rigid, as the flexibility to predict $LC$ for different cell size configurations has not been accounted for. This paper introduces a relaxation method to refine the conventional binary logistic $LC$ model using an event-tree approach. The $LC$ probability for increasing cell size and cell length was estimated by expanding the $LC$ probability of a pre-defined model generated from different configurations of speed and density differences. The reliability of the proposed models has been validated with NGSIM trajectory data. The results showed that the models could accurately estimate the probability of $LC$ with a slight difference between the actual $LC$ and predicted $LC$ (95% Confidence Interval). Furthermore, a comparison of prediction performance between the proposed model and the actual observations has verified the model’s prediction ability with an accuracy of 0.69 and Area Under Curve ($AUC$) value above 0.6. The proposed method was able to accommodate the presence of multiple LCs when cell size changes. This is worthwhile to explore the importance of such consequences in affecting the performance of $LC$ prediction in the CTM model.

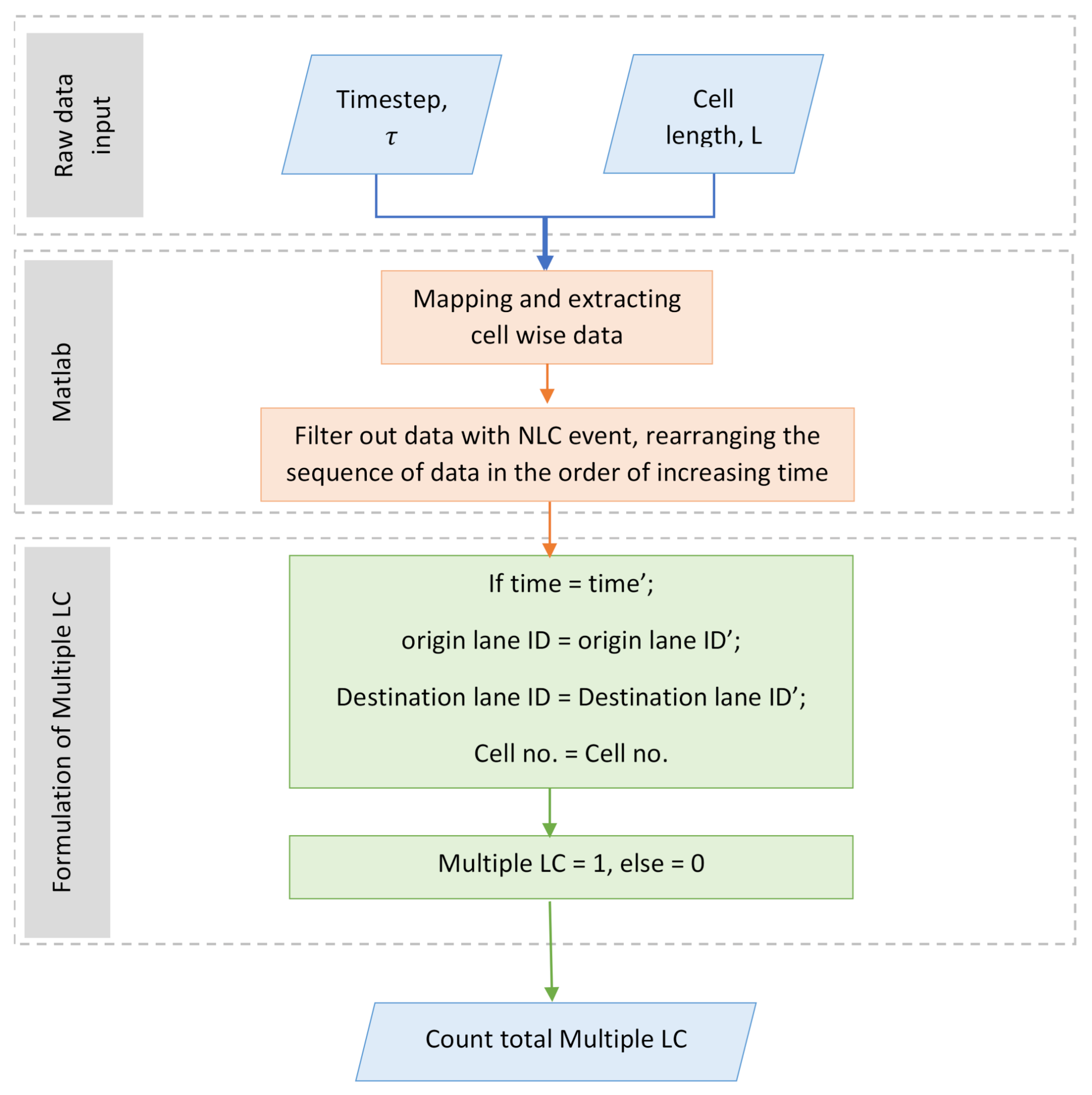
1. Introduction

Modeling lane changing is a challenging task that involves interactions of a vehicle and its immediate following and leading vehicle [1,2]. The existing lane change ($LC$) algorithms (e.g., trajectory planning, maneuver planning algorithm) focus on maximizing the benefits to individual vehicles [3,4,5,6,7,8]. These algorithms require detailed microscopic traffic variables (i.e., relative speed and positions) of the surrounding subject vehicles, gaps between host and following and leading vehicles, which often depend not only on the behavior and movement of the surrounding vehicles, but also on macroscopic traffic dynamics [2]. Hence, a simplified, yet reliable, macroscopic $LC$ prediction model that forecasts the probability of $LC$ occurrence in a relaxed cell (changes in time and space) is required [1], moreso when the decision-making of lane changing is a critical link to drive the mission of connected autonomous vehicles in complex urban environments. Current research projects have focused on developing autonomous vehicle technologies to improve vehicle safety, particularly when performing its fundamental tasks, including car following, lane-keeping, and lane changing [3,4,5,6,7,8].

Studies related to macroscopic lane change ($LC$) prediction have gained increasing attention in the macroscopic aspect of traffic simulation [9,10]. Efforts have been devoted to understanding various characteristics of $LC$ traffic based on the theoretical work of kinematic wave (KW), which ha viewed vehicular traffic as a continuous fluid flow and described the traffic dynamics by the changes in time and space [11,12,13]. Among these macroscopic models, the cell transmission model (CTM)—a discretized version of the kinematic wave (LWR-KW)—model has been recognized as the simplest means to model the evolution of traffic dynamics and features [14]. While fewer parameters are needed [15], some limitation still exists, in which all the events related to $LC$ could not be explained fully in the current macroscopic traffic simulation models, partly due to lack of available data in a macroscopic form. Previous studies have considered the components of a lane change in developing the CTM model. Ref. [16], e.g., assigned a fixed percentage of left-turn flow (i.e., 30%) when formulating the diverge movement to simulate oversaturated arterials. Their improved form of the CTM model, which introduced a novel conditional cell at the intersection, has enhanced the reliability of the CTM. However, some limitations still exist, where the assigned percentage of $LC$ at a fixed probability were not comprehensively taken into consideration and remain a question to be answered. Even though the percentage of $LC$ may be identified empirically from field observation or a defined lane changing rate, this does not mean it can be applied for any size of cells. These cells are influenced either by the surrounding traffic environment (i.e., speed and density between lanes) [17,18,19,20] or some unknown factors (i.e., driving attitude), which might affect the variance in the percentage of turning, or in a proper term, the probability of lane change. With the lack of comprehensive lane change in the rigid CTM model, the simulated traffic flow condition may not be accurately estimated with the actual traffic. Ref. [21] have considered lane change in CTM, where they introduced $w_i^{\tau }$ (i.e., the number of vehicles that wish to change lane at cell $i$, time step $\tau$) as a variable to determine the cell occupancies in the following time step. However, this variable has not been validated with actual data.

Due to its complex process, a macroscopic $LC$ algorithm that predicts the occurrence of $LC$ in a controlled zone, defined by space over time, was introduced [17]. In a controlled space of a cell defined by space over time, the occurrence of lane change can be predicted in a logic binary form of either 0 ($NLC$ or non-lane change) or 1 ($LC$ or lane change). In other words, each cell can capture the snapshot of the presence of $LC$ activities and the condition of the surrounding vehicles in the cell at any given stretch of road. Such discrete behavior of lane change has been evaluated in the previous studies using a statistical approach. One of the well-known statistical approaches is the binary logistic regression (BLR) technique. Few studies, however, have adopted the BLR to model the prediction of a lane change. Ref. [17] have used the logistic regression to develop a lane change model-based, whereby macroscopic traffic variables (i.e., speed, density difference) are extracted and aggregated in a cell-based form. Their model predicted the probability of a lane change and showed statistically significant and non-linear relationships with macroscopic traffic variables. In their model, the occurrence of lane change was predicted at a 10-s time and 150 m length window. Ref. [22] refined and further simplified the binary logistic lane change model suggested by [17] by introducing the direction of the $LC$ and using lesser input variables. Ref. [22] validated the proposed model with actual data and evaluated its performance using the area under the curve ($AUC$).

However, these studies had not considered the presence of multiple-lane change vehicles that is likely to occur simultaneously in this cell window [17,22]. Moreover, the expected probability of $LC$ will no longer be the same when the size of the cell windows changes with time step, $\tau$ and cell length, $L$, which are affected by the surrounding traffic speed, $v$. It is known that the cell length, $L$ is a product of speed, $v$, and time step $\tau$. The fact that the actual traffic speed varies over time gives us the reason why it is crucial to replace the conventional logistic $LC$ model with the dynamic properties considering the changes of cell sizes, thus making the model less rigid in predicting $LC$.

Aims of the Study

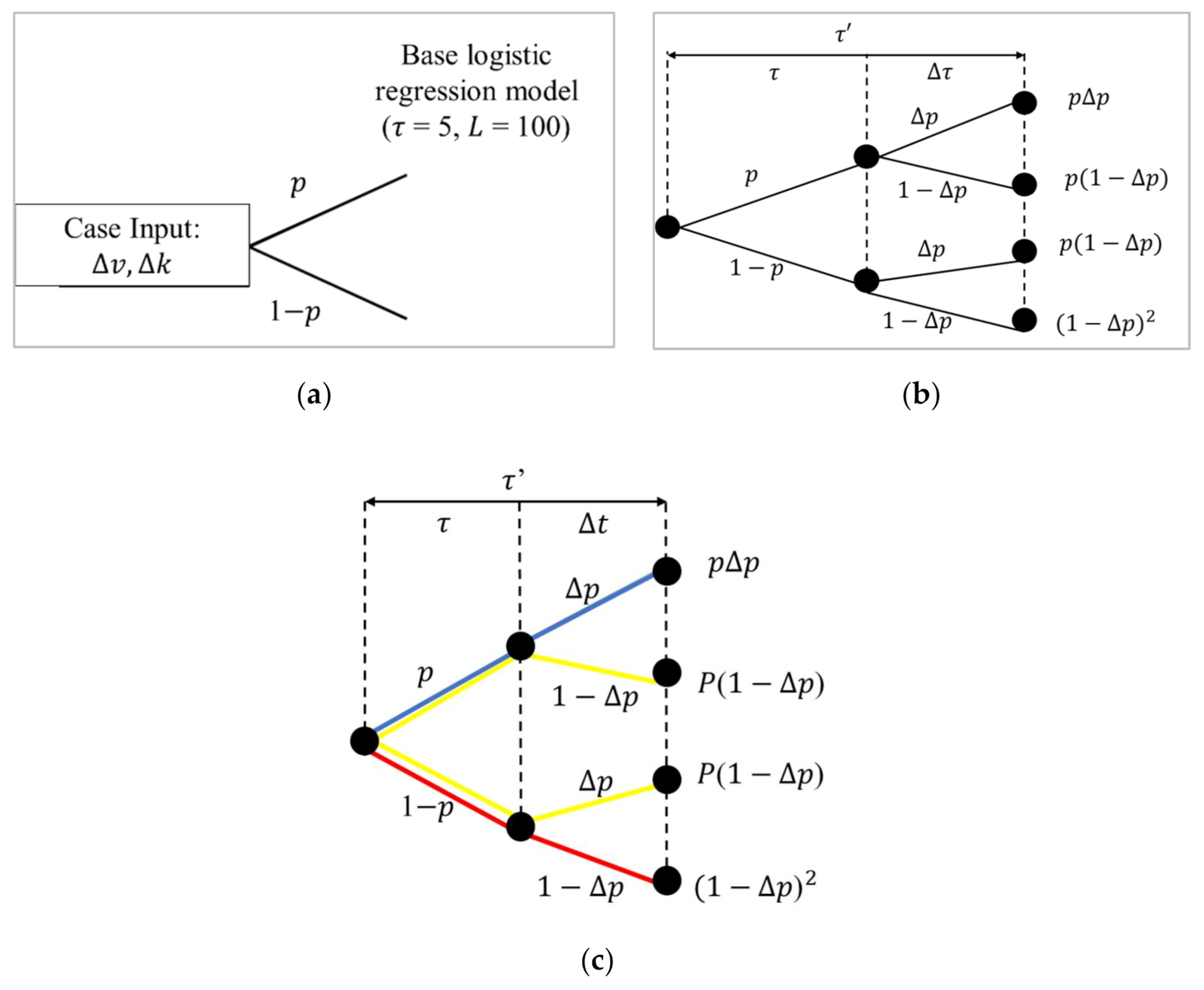
Indeed, abundant works focused on modeling $LC$ behavior prediction and its improvement have been done in past research. However, some issues still need to be solved in emulating the complex behavior of lane change. A crucial drawback of current logistic regression lane change models is that they do not address the flexibility of the model in predicting lane change when the cell sizes, defined by space over time, change. Since the current logistic regression model only limits predicting the probability of $LC$ from the binary response, the observations of two or more consecutive $LC$ events are not possible using this regression approach.

Intending to overcome the aforementioned deficiencies, this study developed an improved version of the logistic model by proposed an event tree to expand the probability estimation of the conventional logistic regression for both single and multiple events of the lane change. Expanding the probability of $LC$ with an event tree in the form of nodes and branches has the potential in dealing with the decision-making process for the issues as identified earlier. An event tree produces the probability outcome that is generated based on predetermined cell size. By tracing the event tree, one can observe the different outcomes on the probability of lane change based on any inputs of macroscopic traffic variables and the ability to predict lane change of any cell sizes while observing the events of single and multiple lane changes. Considering the limitations of the conventional logistic regression, none have yet attempted to expand this model using this method, which is worth exploring. Therefore, this study proposes a macroscopic $LC$ prediction model to calculate the probability of $LC$ occurrence based on an event tree approach.

The main work of this paper includes the following four parts: (1) developing a pre-defined $LC$ event-based logistic regression model based on field data; (2) introducing the framework of the event tree, which expands upon a pre-defined logistic regression model; and (3) predicting the $LC$ occurrence as zone sizes changes; and (4) evaluating the performance of the proposed model.

The remainder of the paper is organized as follows. Section 2 introduces the basic terminology of the logistic regression model and the variables used in the study. The framework for the extended model based on the event tree approach is provided in Section 3. The main work includes the following three parts: (1) developing a pre-defined $LC$ event-based logistic regression model; (2) introducing the framework of the event tree, which is expanded upon a base logistic regression model; and (3) predicting the $LC$ occurrence as zone sizes changes; and (4) evaluating the performance of the proposed model by presenting the empirical results. Section 4 gives a brief description of the training data used for the regression model. Section 5 describes the methods of evaluating the performance of the regression models. In Section 6, results and discussion are provided, and the effectiveness of the extended model is validated and compared with the actual status of $LC$ at different conditions. Lastly, the conclusion of the paper is provided in Section 7.

2. Logistic Regression Model

Basic Terminology

The binary logistic regression is a popular non-linear statistical model where a flexible logistic function is introduced to constitute the basic mathematical form of the logistic model [23]. The logistic regression model has been widely used in many fields [24,25,26,27,28,29,30,31,32]. Some studies have suggested that the logistic regression model is more accurate and efficient than the other multivariate statistical methods such as frequency ratio, bivariate statistics, artificial neural networks, support vector machines, and classification trees in some circumstances [33,34,35,36,37,38].

Logistic regression is a part of a larger class of algorithms, known as the Generalised Linear Model proposed by [39], as a means for problems that were not directly suited for applying linear regression. The logistic function may ensure that whatever estimate of the prediction, the result will always be some number between 0 and 1, which is why the logistic model is often the first choice when a probability is to be estimated. The model based on logistic regression has the ability to describe the relationship between the probability of a binary response variable and a set of corresponding explanatory variables. Moreover, it has no restrictions on the explanatory variables, which might be either continuous or discrete, or a mixture of both types, and the variables need not be normally distributed [29].

The basic logistic regression model is formed as in Equations (1) or (2).

$$Logit\left(P\right)=\ln \left(\frac{p}{1-p}\right)={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_m{x}_m$$

(1)

$$P=\frac{\exp \left({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_m{x}_m\right)}{1+\exp \left({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_m{x}_m\right)},$$

(2)

where $P$ is the probability of an event occurring; $x_1$, $x_2$, …, and $x_m$ refer to the explanatory variables; ${\beta }_0$, ${\beta }_1$, ${\beta }_2$, …, ${\beta }_m$ are the model’s parameters or coefficients which could be established by the so-called maximum likelihood estimation method [23]; $m$ is the number of selected variables; $Logit\left(P\right)$ means a logit transformation of $P$ by the natural log of the odds (being defined as the ratio of occurrence probability to non-occurrence probability). The beta values (i.e., the model’s parameters) for fitting the logistic regression model can be calculated using the so-called maximum likelihood estimation method.

For this study, the value of $P$ is defined as the estimated probability of lane change identified from the actual $LC$ status (1 (‘$LC$’)) or 0 (‘$NLC$’)) with their corresponding independent variables observed from field data. $P$ can take any value between 0 and 1, and exceeding this range is not possible due to the logarithmic characteristic found in the property of logistic regression. In order to define a relationship that is bounded between 0 and 1, the logistic regression gives the assumption that the relationship between independent and dependent variables resembles a curve of an S-shaped (see Figure 1) [40]. In this case, the independent variables, $x_1$, $x_2$, …, and $x_m$, used are the density difference ($∆k$) and speed difference ($∆v$), which were the main contributing factors of traffic characteristics at the macroscopic level. Details on how these variables were taken will be discussed in the next section.

3. Extending Prediction Model Using Event Tree

An event tree is a decision-making framework that estimates the probability of a set of pre-defined events using a tree-like decision-making process. Each branch or node of the tree represents a set of possible outcomes for a particular event, increasing specificity with each step. Progression to the next branch is accomplished when the probability estimate for the preceding node exceeds a pre-defined threshold. In this study, the event tree is rooted from a base model—a model (with a given coefficient of the parameters) determined at a state with minimal events of multiple $LC$ observed for a specific cell length and time step. The following section (Section 3.1) will highlight some of the steps in identifying this base model.

3.1. Identifying Base Model

In order to identify the base model, the vehicle trajectory dataset was post-processed with a trial of different cell sizes until a minimal observation of multiple $LC$ was achieved. This can be achieved by starting from a smaller cell size. When the cell size is small, the perimeter of the observations can be narrow up to a point where only the size of single vehicles can be observed. However, it is still preferable to use a bigger cell size that can group multiple vehicles as a cell size that is too small may contradict our objectives of studying the macroscopic behavior of traffic flow. Figure 2 presents a flowchart showing the steps for selecting the base model. When the total number of multiple $LC$ events is counted, cell size with the lowest count of multiple $LC$ will be used as the base model. Though there may still be a small number of multiple $LC$ events observed (i.e., <10), it can be considered negligible with such a large dataset.

3.2. Observing the Number of Observations Based on Changes in Cell Sizes

A different number of observations will be produced when the cell size changes, but the total number of $LC$ events remains the same for all cases. For instance, when the cell size is smaller, more cells are needed to occupy the same amount of space. Despite how large or small is the cell size, the total number of observations for $LC$ events will maintain the same since they can only be observed in an instant shot. However, when more cells are used, the number of observations for the $NLC$ event will increase due to the increase of multiple shots that will form within the same zone. Equations (3) and (4) thus give the formulation based on this concept.

The division between the total duration gives the total number of observations, $N$, $T$, and the simulation time step, $\tau$:

$$N=T/\tau$$

(3)

where $N$ consisted of both lane change $LC$ and $NLC$ events:

$$N=N_{LC}+N_{NLC}$$

(4)

3.3. The Model Formulation for Expanding the Branches

Upon having a base model, this section provides the steps to derive the event tree based on the logistic regression. Given the configuration of cell size, $(Y_L^{\tau }{)}_{∆v, ∆k}$ that one wishes to use, the next step is to identify the number of branches needed, starting with the root of the base model (as shown in Figure 3a). In this configuration, $L$ denotes cell length (in meters), and $\tau$ is the simulation time steps (in seconds) under a specific input of $∆v$ (speed difference) and $∆k$ (density difference). The density difference $\Delta k$ between the origin and the target cell was computed using Equation (5).

$$∆k=k_{i,origin}-k_{i,target}.$$

(5)

The speed differences of the vehicles from origin to target cell were also obtained at the instant when lane change occurred (see Equation (6)).

$$∆v=v_{i,origin}-v_{i,target}.$$

(6)

The branches for the event tree are categorized into two types: (i) fully-developed branches and (ii) partially-developed branches. Given a model with cells configured at $Y_{L=100}^{\tau =5}$ as the base model, for instance, a fully-developed branch is used when a predetermined $Y_L^{\tau }$ is able to expand fully from the base model. In contrast, the remaining that were not able to expand to a full base model, a partially-developed branch is used. As an example, for a predetermined cell configuration at $Y_{L=100}^{\tau =10}$, two fully-developed branches of $Y_{L=100}^{\tau =5}$ are needed, given $Y_{L=100}^{\tau =5}$ as the base model. Whereas for a predetermined cell configuration at $Y_{L=100}^{\tau =8}$, two branches are needed—the first branch is fully-developed $Y_{L=100}^{\tau =5}$, and subsequently, the remaining $\tau =3$ s will be placed in the second branch that is partially-developed $Y_{L=100}^{\tau =3}$. A similar concept to this also applies to the changes in cell length, $L$. At the end of the branches, each node gives the probability $P_{LC}\left(\tau ,L\right)$ for a specific event estimated from the binary logistic regression (obtained from Equation (2)).

$$P_{LC}\left(\tau \right)=\frac{N_{LC}\left(\tau \right)}{N\left(\tau \right)}$$

(7)

$$P_{NLC}\left(\tau \right)=1-P_{LC}\left(\tau \right).$$

(8)

When observing the changes for increasing time step $\tau$, the probability of $LC$, $P_{LC}\left({\tau }^{\prime }\right)$ for a fully-developed branch is updated as follows:

$${N^{\prime }}_{LC}\left({\tau }^{\prime }\right)=N^{\prime }\left({\tau }^{\prime }\right)-N_{NLC}^{\prime } \left({\tau }^{\prime }\right)$$

(9)

$$\left.N^{\prime }\left({\tau }^{\prime }\right)=\frac{T}{{\tau }^{\prime }} \right| N^{\prime }<N$$

(10)

where

$$\left.{\tau }^{\prime }=\tau +∆\tau \right| ∆\tau <\tau$$

(11)

$$P_{LC}\left({\tau }^{\prime }\right)=\frac{{N^{\prime }}_{LC}\left({\tau }^{\prime }\right)}{N^{\prime }\left({\tau }^{\prime }\right)}.$$

(12)

For a partially-developed branch, the probability of lane change is updated based on the proportion of the increment in the remaining time step. The increment of this probability denoted as $∆P_{LC}\left({\tau }^{\prime }\right)$, is defined as:

$$∆P_{LC}\left({\tau }^{\prime }\right)=P_{LC}\left(\tau \right)·\frac{∆\tau }{\tau }.$$

(13)

Probability for a partially-developed branch is then updated as follows:

$$P_{LC}\left({\tau }^{\prime }\right)=P_{LC}\left(\tau \right)·∆P_{LC}\left({\tau }^{\prime }\right)$$

(14)

$$P_{NLC}\left({\tau }^{\prime }\right)=1-P_{LC}\left({\tau }^{\prime }\right).$$

(15)

With the above formulation, the observation for the changes in cell length, $L$, can also be defined in the same way as the time step, $\tau$, discussed above. A simplified structure of the tree diagram showing the changes to the time step is represented in Figure 3b. However, it should be noted that a tree like this is only applicable for a specific case of the input variables, $∆v$, and $∆k$. Different input variables will generate trees with different probability outcomes. Even though the event tree is useful for presenting in detail the many possible outcomes when the cell size changes, a large amount of space is required to occupy these trees. Hence, the tree diagram is modeled in an Excel spreadsheet to enable easy generation for the outcomes of all possible scenarios.

The formulation of the event tree becomes complicated when observing changes for increasing both the time steps and the cell length at the same time. To do so, a step-forward method that connects the $\tau$-tree with the $L$-tree diagram is used. The overall probabilities for $LC$ and $NLC$ from the $\tau$-tree are transferred to the first node of the $L$-tree diagram and continue to expand until the required cell length is reached.

3.4. Deriving the Observation of Multiple $LC$ Events

One can identify the number of lane change events in a given cell size in the tree diagram. Understanding how this concept is formed can be seen in a typical probability tree diagram that observes the number of successes and failures in an event. For instance, in Figure 4b, the blue path consisting of two success events, $P$ in the given cell size; the yellow paths consisting of one successful event; and the red path do not have any successful event. The number of this successful event for each path can be represented by the number of lane changes observed in the given cell size. Thus, it can be inferred that, for a tree that expanded up to two branches, one can observe up to two vehicles that simultaneously change lanes. In other words, a higher number of multiple $LC$ events can be observed when the branches of the tree diagram increase. This can also be explained in the real-life scenario, where a snapshot with a broader view of the road can capture up to a few $LC$ events.

As the probability of $NLC$, $P\left(NLC\right)$ seen in the actual data is always higher than the probability of $LC$ events, $P\left(LC\right)$, the estimated probability of multiple $LC$ events will always be much lesser than the $P\left(NLC\right)$. Logically, this estimation is reasonable when on the road, the $NLC$ events are usually seen in higher proportions than the $LC$ events.

The equations below derive the probability for each of the path using simple multiplicative and summative rules:

$$\sum P\left(LC=2\right)=P\Delta P$$

(16)

$$\sum P\left(LC=1\right)=2P\left(1-\Delta P\right)$$

(17)

$$\sum P\left(LC=0\right)={\left(1-\Delta P\right)}^2.$$

(18)

4. Vehicle Trajectory Training Data

In this study, a dataset containing a series of individual microscopic trajectories from the well-known NGSIM (Next Generation Simulation) database [41] was used to extract the information needed to develop the lane change model. The NGSIM project is an open-source data collection, funded by Federal Highway Administration (FHWA), in an effort for the public to develop and/or validate potential traffic models. This study uses the vehicle trajectory data collected at a segment of US Highway 101 (Hollywood Freeway) in Los Angeles, California. The lane numbering of the study area can be observed in Figure 4a.

Assumptions:

• This study does not differentiate between discretionary and mandatory $LC$. Only discretionary lane change events will be considered.
• Since the study considered discretionary lane change, the subject vehicles originally traveled in lanes 1 to 5 were used. Vehicles from lanes 6 to 8 were not considered to eliminate the possibility of drivers perform mandatory lane changes when vehicles are entering from the upstream on-ramp or when vehicles are exiting at the downstream off-ramp.

5. Performance Measures

From a theoretical aspect, extended the logistic regression lane change model using the branching of event trees has demonstrated (in the previous section) the possibility of the model to predict the probability of both single $LC$ and multiple $LC$ in any cell size. However, the improved model still needs validation with the actual data in order to be reliable at predicting the probability of $LC$.

With that in mind, the performance of the extended model is assessed by examining the discriminating power of classifying the agreement between the predictions and the actual outcomes. These classifications can be determined using a confusion matrix table that can further give specific performance measures, such as the true-positive rate, false-negative rate, true-negative rate, and the false-positive rate. Furthermore, predictive accuracy has also been widely used to assess the predictive capability of the logistic regression models. In this case, accuracy is the proportion of $LC$ and $NLC$ that our models correctly classified. Thus, accuracy together with $AUC$ was used to evaluate the performance of the tree-based logistic lane change models.

$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}$$

(19)

where $TP$ (true positive) and $TN$ (true negative) are the numbers of $LC$ events that are correctly classified, and $FP$ (false positive) and $FN$ (false negative) are the numbers of $LC$ events incorrectly classified.

The relationship between the true and false positives can also be depicted by a receiver operating characteristics ($ROC$) curve for visualization, organization, and selection of the classification model on the basis of their performance. To compare classification models, the performance measure of $ROC$ can be reduced to a single number which is represented as the area under the $ROC$ curve, abbreviated as $AUC$ [42]. In general, the bigger its $AUC$, the better the discriminative ability of a classification model, or in other words, the better is the overall performance of a model. Hence, $AUC$ > 0.9 are considered outstanding, $AUC$ between 0.8 and 0.9 are considered excellent, $AUC$ between 0.7 and 0.8 are considered acceptable, and $AUC$ between 0.6 and 0.7 are considered poor, non-discriminative if the $AUC$ equals 0.5 [43].

6. Results and Discussion

Following the need for a base model to be used as the root of the event tree, this section will first explore the NGSIM dataset by processing the data for different cell sizes in the search for the least multiple $LC$ events. After having a base model selected, the results will then compare the prediction of lane change between the event tree, its logistic regression, and the actual observations seen in the dataset. To see the reliability of the improved logistic regression model in predicting the lane change, the results will then present the model’s performance based on what has been discussed in Section 5.

6.1. Selection of Base Model—Based on the Number of Observations

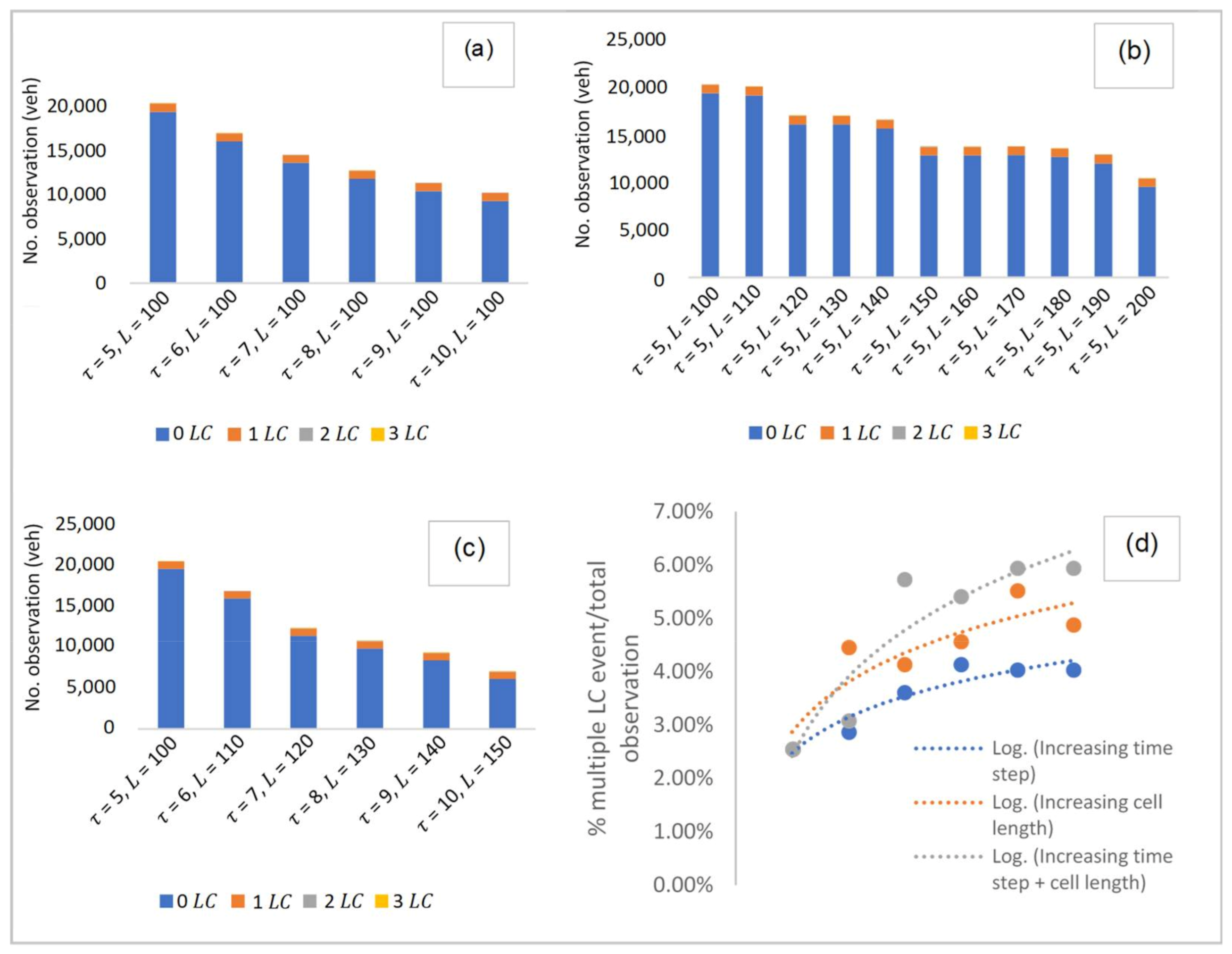
Several cases were explored in selecting the base model. As shown in Figure 5, these cases were divided into: (i) observing at increasing time step in the same cell length, (ii) observing at increasing cell length for the same time step and, (iii) observing at increasing time step and cell length. Raw datasets from NGSIM were macroscopically processed based on each of the cases provided. In case (i), datasets were observed from $\tau$ = 5 s, increasing at an interval of 1 s, up to $\tau$ = 10 s in a fixed cell length of 100 m. Case (ii) observed datasets from cell length, $L=$ 100 m, increasing up to $L=$ 200 m at an interval of 10 m. Lastly, case (iii) observed the datasets whereby the time step and cell length are simultaneously increased at an interval of 1 s and 10 m, respectively, from $\tau$ = 5 s, $L=$ 100 m to $\tau$ = 10 s, $L=$ 150 m.

Here, a total number of observations for $LC$ and $NLC$ events were found for each of these cases. In this figure (i.e., Figure 5), it can be observed that the number of $NLC$ events is significantly much higher than the number of $LC$ events. Overall, a total of 943 $LC$ events can be seen in the 45-minute collected within the discretionary lanes considered in the study area. Of these $LC$ events, some multiple events of $LC$ occurred simultaneously. However, when compared to the total number of $LC$ events, the events with multiple $LC$ constitute a relatively smaller percentage, i.e., approximately 2–4% for 2 $LC$ events and <1% for 3 $LC$ events. These are considered negligible when compared with the number of 1 $LC$ events, which in turn, expect a low probability of $LC$. Having known that a base model is required to be used as the root of the event tree for further prediction of multiple $LC$ events, the base model will thus be chosen, if possible, with the one with no multiple $LC$ events. In Figure 5d, the number of multiple $LC$ events was compared for each case. It is observed that cell sizes with the smallest time step and cell length have the least multiple $LC$ events. In this case, the cell size of $\tau$ = 5 s, $L=$ 150 m were chosen as the ideal fit for the base model as it gives the lowest percentage of multiple $LC$ events at approximately 2%, which is considered negligible.

6.2. Prediction of $LC$—Comparing Different Approaches

In this section, a comparison is made to observe the probability of lane change predicted for different cell sizes. Specifically, the cell size considered were based on increasing time step and cell length ($\tau =$ 5, $L=$ 100; $\tau =$ 8, $L=$ 130; $\tau =$ 10, $L=$ 150), which are then used to validate the predictions based on the following approaches:

• Event tree for a specific cell size
• Logistic regression processed for the respective cell size considered in (i). Note that different coefficients of the parameters are expected for different cell sizes.
• Probability estimated from the actual $LC$ status for the cell size considered in (i) and (ii), ($P\left(LC\right)$ = number of $LC$ observations/Total number of observations).

In all these, four separate quadrants observed among different input variables (i.e., speed and density difference) were also studied.

6.3. Observing Prediction of Single $LC$ Events

Table 1. Summary statistics for the prediction of single LC events based on the test of Analysis of Variance (ANOVA).

Groups	Count	Sum	Average	Variance
Regression	852	62.2927	0.0731	0.0011
Derivation ($P(LC=1)$)	852	64.5671	0.0758	0.0013
Source of Variation	SS	df	MS	$F$	$p$-value	$F$ crit
Between Groups	0.0030	1	0.0030	2.5799	0.1084	3.8469
Within Groups	2.0026	1702	0.0012
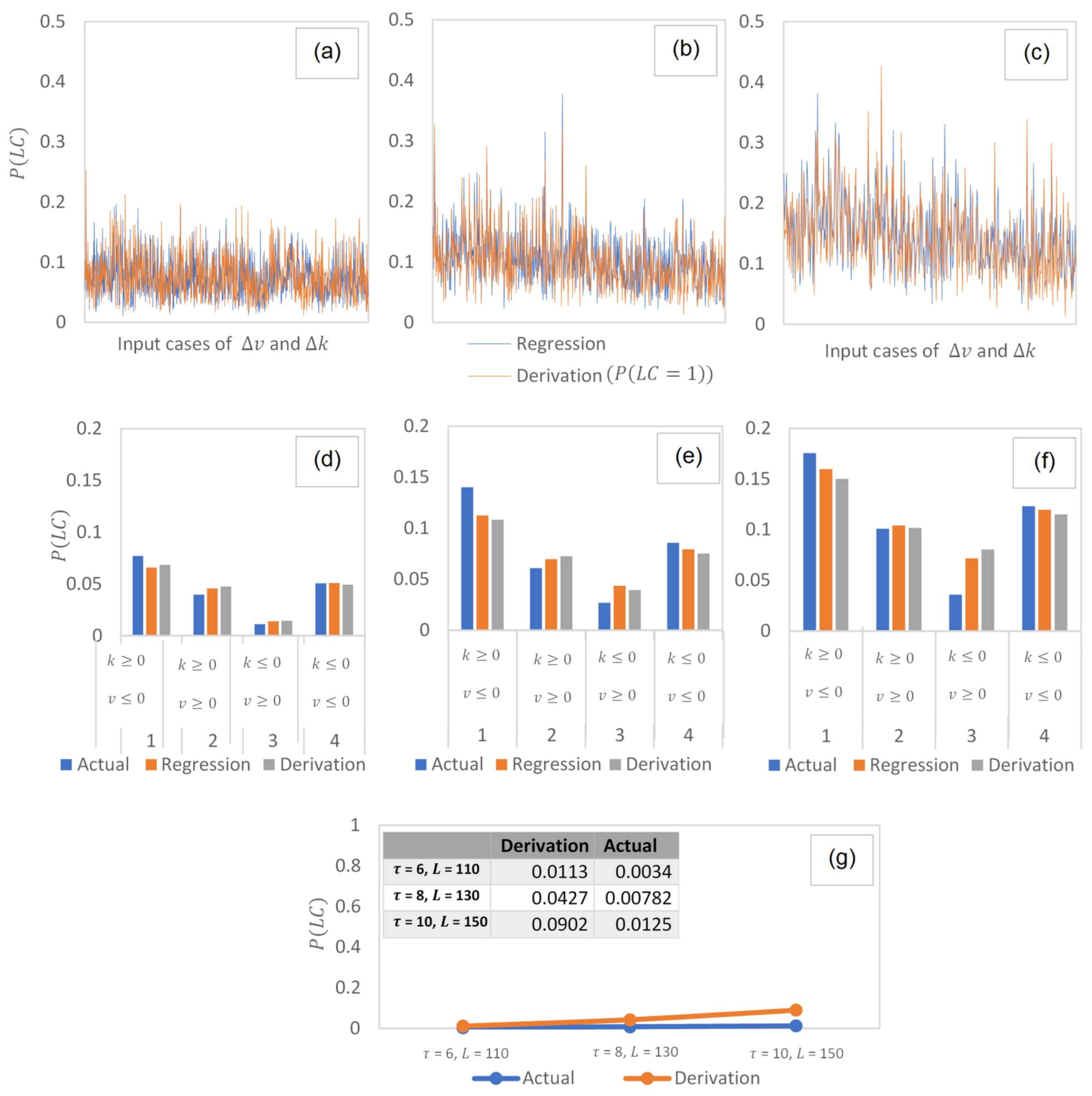
Total	2.0056	1703

shows part of the results for the predicted probabilities in a cell size of $\tau =$ 6, $L=$ 110. Here, we wish to see whether there is a difference in the probability estimated between the event tree and the logistic regression for the respective cell size. To compare these approaches, an analysis of variance (ANOVA) was conducted on the probabilities estimated for the different input values obtained from data. The ANOVA tests whether the mean probability values are the same:

$$\begin{gathered} H_o:{\mu }_{ET}={\mu }_{LR} \\ {H}_a:\mathrm{not}\mathrm{all}{\mu }_i\mathrm{are}\mathrm{equal}, \end{gathered}$$

(20)

where ${\mu }_i$ are the mean probability values at any approach $i$. Suppose a Type I error is controlled at $\alpha$ = 0.05, then $F$ (0.95, 1, 1703) = 3.85 with 1 and 1703 as the degrees of freedom associated with the factor level and the error term of the given data. The decision rule is thus:

$$\begin{gathered} \mathrm{if}F*\le 3.85,\mathrm{conclude}{H}_o \\ \mathrm{if}F*>3.85,\mathrm{conclude}{H}_a. \end{gathered}$$

(21)

In this table, the $p$-value = 0.11 > 0.05 and the $F$_crit = 3.85 > $F$ = 2.58. This shows that the null hypothesis, which states that all means are equal, cannot be rejected. In this case, the sample data (90% of the $LC$ data used) is thus consistent with the hypothesis that population means are equal between groups. In other words, the predicted probability for the event tree does not differ much from the probabilities estimated from the logistic regression.

For $\tau =$ 6, $L=$ 110, approximately 65% of the $LC$ data have attained similar consistency between the two approaches ($p$-value = 0.11, $F$ = 2.46), whereas 47% of the $LC$ data were found consistent at $\tau =$ 10, $L=$ 150 ($p$-value = 0.06, $F$ = 3.67). Thus, as the cell size increases, lower accuracy is expected in predicting single lane change events. This can be explained by the presence of multiple-lane change events, which is much higher when the cell size increased (6% Multiple $LC$ events at $\tau =$ 10, $L=$ 150), see Figure 6d.

Figure 6a–c provides the relative comparison of the probabilities estimated between the event tree and the logistic regression for (a) $\tau =$ 6, $L=$ 110, (b) $\tau =$ 8, $L=$ 130 and (c) $\tau =$ 10, $L=$ 150. For the x-axis, the figure is plotted based on the outcomes of all the inputs (speed and density difference) found in the sample data. In these figures, it can also be clearly seen that the overall trends between the event tree and the logistic regression do not deviate much when predicting single observations of $LC$.

6.4. Observing Prediction of Single $LC$ Events at Different Input Variables

Figure 6d–f observes the ability of the extended model to predict the probabilities at different input variables. The dataset is further divided into four separate quadrants based on the positive and negative values of speed and density differences. In a plot of speed difference ($∆v$) against density difference ($∆k$), the four quadrants are defined as follow: (i) Quadrant 1 ($∆v\le 0$, $∆k\ge 0$), (ii) Quadrant 2 ($∆v\ge 0$, $∆k\ge 0$), (iii) Quadrant 3 ($∆v\ge 0$, $∆k\le 0$), and (iv) Quadrant 4 ($∆v\le 0$, $∆k\le 0$). A positive density difference means the origin lane has a higher density over the target lane, while a positive speed difference means that the origin lane has a higher speed over the target lane.

The comparison for each of the quadrants is made between (i) event tree, (ii) the logistic regression, and (iii) the actual $LC$ in the dataset. For (iii), the probability is taken by dividing the number of $LC$ observations by the total number of observations in the considered quadrants. Here, it is observed that all the three approaches (i), (ii), and (iii) have estimated probabilities that are close within the range of ±0.05 in each of the quadrants. The probabilities estimated were observed highest in Quadrant 1, where the origin lane is denser and at a speed lesser than the destination lane. This quadrant can also be categorized under the intention of discretionary lane change for the purpose of speed gain and travel time reduction.

6.5. Observing Prediction of Multiple $LC$ Events

Figure 6g compares the prediction of multiple $LC$ events for different cell sizes. In this figure, the overall mean probability is taken for all the input cases found in the datasets of different cell sizes. It is observed that in a large sample size, the estimated average probability obtained for multiple $LC$ is <0.1. This is considerably smaller when observed in the field.

Comparing the average between the event tree with the actual observations, it is seen that the prediction of $P \left(LC=2\right)$ for the size at $\tau =$ 6, $L=$ 110, and $\tau =$ 8, $L=$ 130 are relatively close to each other. Further, a pairwise $t$-test was conducted to compare the difference between the event tree with the actual observations. Results have confirmed no significant difference between the two samples (given $t$-stat = 1.976 < $t$ critical two-tail = 4.303). Thus, the prediction for single and multiple observations of $LC$ can successfully and accurately follow the pattern of actual data, which indicates the strong predicting ability of the event tree model.

6.6. Performance Measures of the Event Tree

In modeling the predictions of lane change, it is necessary to evaluate and assess the quality of the models for different cases. In this study, the models’ predictive accuracy, $ROC$ curves, and $AUC$ values were analyzed. Three evaluation statistics, namely, standard error, confidence interval at 95%, and significance level $p$, are included (see

Table 2. Summary statistics for comparing the performance between the regression and the event tree.

	Logistic Regression	Event Tree
Mean	0.7619	0.7119
Variance	0.0010	0.0005
Observations	3	3
Pearson Correlation	0.2267
Hypothesized Mean Difference	0
df	2
$t$ Stat	2.5565
$P\left(T\le t\right)$ one-tail	0.0625
$t$ Critical one-tail	2.9200
$P\left(T\le t\right)$ two-tail	0.1250
$t$ Critical two-tail	4.3027

and

Table 3. Summary statistics for the logistic regression of different cell sizes.

		Estimate	Std. Error	Z Value	Odds Ratio	Confidence Interval
$\mathit{\tau }=$$\mathbf{6},\mathit{L}=$110	Intercept	$-$3.0196	0.0390	$-$77.36 ***	0.0488	[0.0452, 0.0527]
	∆k	0.0244	0.0023	10.23 ***	1.0247	[1.0199, 1.0295]
	$∆v$	$-$0.0502	0.0050	$-$10.09 ***	0.9510	[0.9418, 0.9603]
$\mathit{\tau }=$$\mathbf{8},\mathit{L}=$130	Intercept	$-$2.5473	0.0398	$-$63.87 ***	0.0783	[0.0724, 0.0847]
	$∆k$	0.0368	0.0027	9.93 ***	1.0271	[1.0217, 1.0326]
	∆v	$-$0.0575	0.0054	$-$10.74 ***	0.9441	[0.9343, 0.9541]
$\mathit{\tau }=$$\mathbf{10},\mathit{L}=$150	Intercept	$-$2.0737	0.0410	$-$50.62 ***	0.1257	[0.1160, 0.1362]
	$∆k$	0.0259	0.0029	9.05 ***	1.0262	[1.0205, 1.0320]
	$∆v$	$-$0.0678	0.0058	$-$11.66 ***	0.9345	[0.9239, 0.9452]

*** Significance < 0.001.

). The standard errors for each variable are reasonably small, confidence intervals are relatively narrow, and $p$-values are also small for all cases. All these results indicate a reasonable goodness-of-fit for the binary logistic regression with the dataset.

The prediction capabilities of the event tree were evaluated using validation, and results are shown in Figure 7A–C. It can be seen that the logistic regression has a better prediction capability than the event tree with the highest accuracy value of 0.69 at the optimum cut-off point, an $AUC$ value of 0.79. The other evaluation statistics for other cell sizes also indicate that the logistic regression exhibit reasonably good prediction capabilities. However, the capability of the event tree is not far off compared with the logistic regression, as they also have a numerically close prediction.

Finally, to compare the statistically significant difference between the logistic regression with the event tree, a pairwise comparison of these models was conducted on the performance figures. The null hypothesis is that there is no difference between the logistic regression and the event tree at the 95% significance level. An independent sample $t$-test and $p$-values are used to evaluate significant differences between them. When $t$-values exceed the critical values of $t$ (4.30) and $p$-values are smaller than the significance level (0.05), the null hypothesis will be rejected. Therefore, the performances of the logistic regression with the event tree are notably different. The results of the Wilcoxon signed-rank test are shown in Table 2. It can be seen that the performance of both the logistic regression and the event tree is not significantly different for all cases of increasing cell sizes ($p$-value = 0.12, $t$-value = 2.92).

The probability estimated for both single and multiple $LC$ of the proposed event tree method was compared against the logistic regression for approximately 10,000 data points with the variable of varying speed and density differences from NGSIM. An overview of the result significantly shows an improvement in the accuracy up to 5.5% when comparing to the single $LC$. The probabilities estimated considering multiple $LC$, in general, generate smaller differences with the logistic regression model. It can also be observed that the accuracy improves as the cell configuration increases in its sizes from (1) to (5) at the cell size from $\tau =6, L=100$ to $\tau =10, L=150$, as shown in Figure 8. It should be noted that the negative % in the figure is an indication that shows multiple $LC$ being closer to regression than the single $LC$. Considering multiple $LC$, therefore, helps to improve the model accuracy for larger cell sizes.

The probability estimated for both single and multiple $LC$ of the proposed event tree method was compared against the logistic regression for approximately 10,000 data points with the variable of varying speed and density differences from NGSIM. An overview of the result significantly shows an improvement in the accuracy up to 5.5% when comparing to the single $LC$. The probabilities estimated considering multiple $LC$, in general, generate smaller differences with the logistic regression model. It can also be observed that the accuracy improves as the cell configuration increases in its sizes from (1) to (5) at the cell size from $\tau =6, L=100$ to $\tau =10, L=150$, as shown in Figure 8. It should be noted that the negative % in the figure is just an indication that shows multiple $LC$ being closer to regression than the single $LC$. Considering multiple $LC$, therefore, helps to improve the model accuracy for larger cell sizes.

7. Conclusions

In this paper, we have investigated the behavior of macroscopic prediction of lane change and proposed a relaxation method to improve the conventional logistic lane change model. Here, we have used an event tree method to expand the logistic regression from a base model that contains minimal observations of multiple lane changes. With speed and density as the input variable, the event tree is then extended according to a predetermined cell size defined by various time steps and cell length.

The reliability of the improved model is tested for the prediction of single and multiple $LC$ events at different cell sizes and input variables. The findings from this study suggest that the use of the event tree can potentially replace the conventional logistic regression model in predicting lane change. Particularly, the prediction of the lane change based on the event tree approach has accurately followed the patterns of actual observation and the regression, which indicates the strong predicting ability of the event tree model.

However, results have shown that the conventional logistic regression still performs slightly better than the event tree in classifying the lane change and non-lane change events correctly. Regarding the the lower prediction capability of the event tree, they had managed to produce reasonable estimations when the conventional logistic regression models were not able to predict uncertainty due to changes in cell sizes and the presence of multiple-lane change events. The event tree is still acceptable for modeling the prediction of a lane change. It is generalized, simple, and easy to construct, thus lessen the amount of time to do regression numerously when the cell size changes.

In previous studies, researchers generally consider the model based on a restricted cell size that has yet to predict the presence of multiple-lane change events [17]. In the same direction of modeling the lane change probabilities, [44] also limit their interest to the scenario where each time interval is short as such, the lane change of each vehicle can only take place once. Hence, incorporating the event tree to extend the conventional logistic lane change model fills the gap of this study. The proposed method allows the relaxation to a different configuration of cell size, thus making the lane changing logic much simpler compared to the existing microscopic lane change models.

Finally, the model presented here can be extended to multiple vehicle classes by specifying class-specific lane changing probabilities. It is fully recognized that the reported results are based only on limited observation in a single location, which may not be sufficient to represent the general lane changing characteristics. Further studies to collect more data in different roadway layouts and identify some critical factors will be needed in the future. The improved lane change model will be integrated into the macroscopic Cell Transmission Model for traffic simulation with the consideration of multiple lane changes in future research. Analysis to be conducted comparing the outcomes of different Cell Transmission Models.