Sparse Measurement-Based Coordination of Electric Vehicle Charging Stations to Manage Congestions in Low Voltage Grids
Abstract
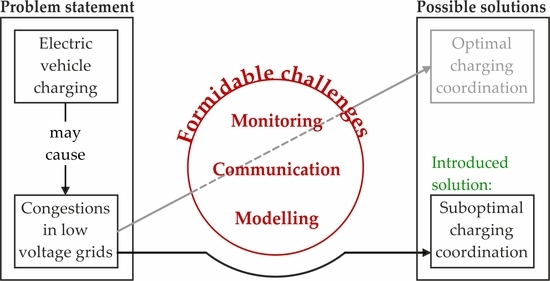
1. Introduction
2. Materials and Methods
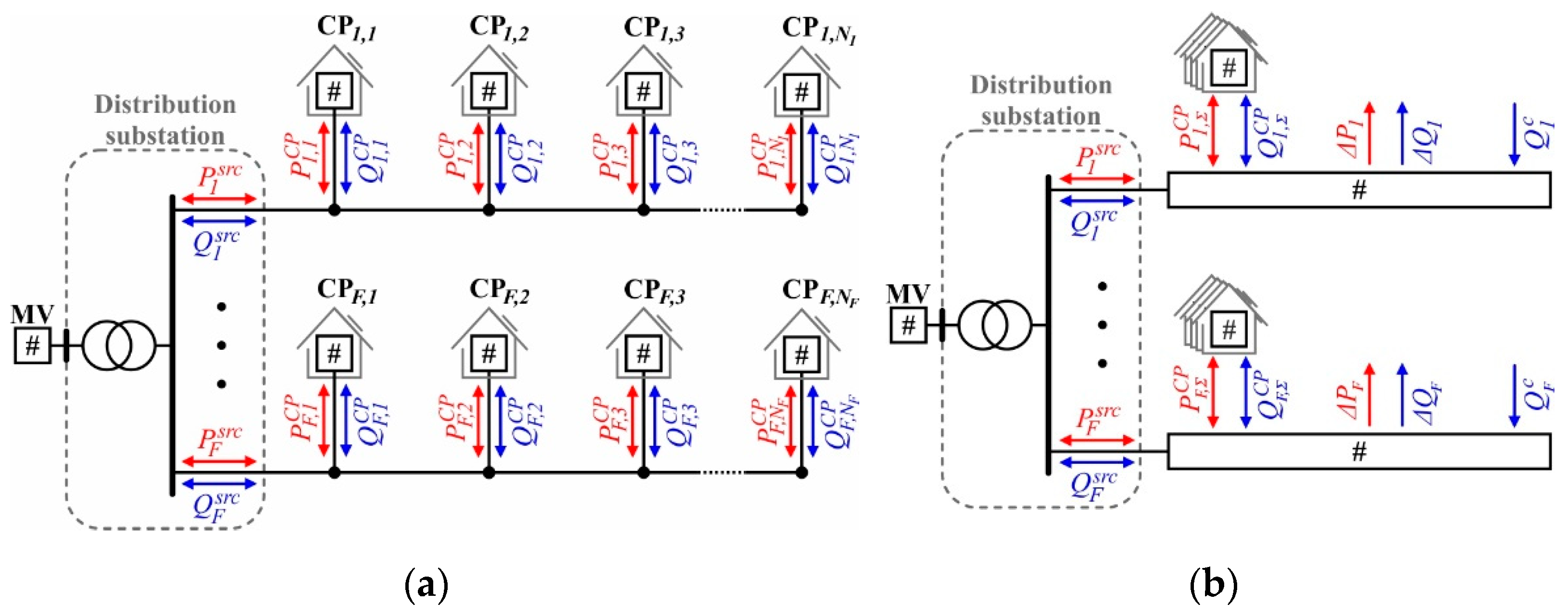
2.1. Sparse Measurement-Based Detection of Feeder Congestions
2.1.1. Mathematical Formulation
- The aggregate active () and reactive power injection (), defined in Equations (2a) and (2b), flows through the same line segment of the feeder.
- This line segment is subject to the lowest feeder voltage ().
- This line segment has the lowest thermal limit current () of all line segments.where , , and are determined by Equations (3a)–(3d).
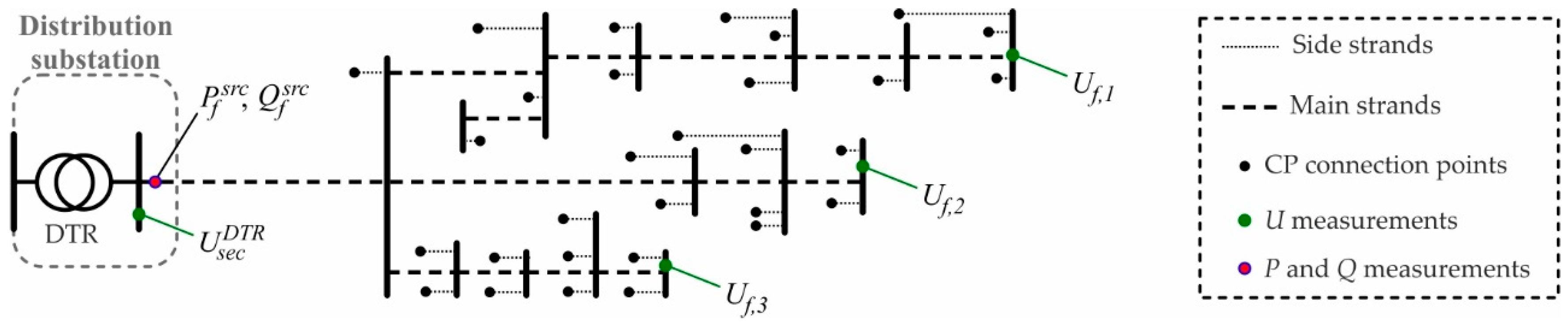
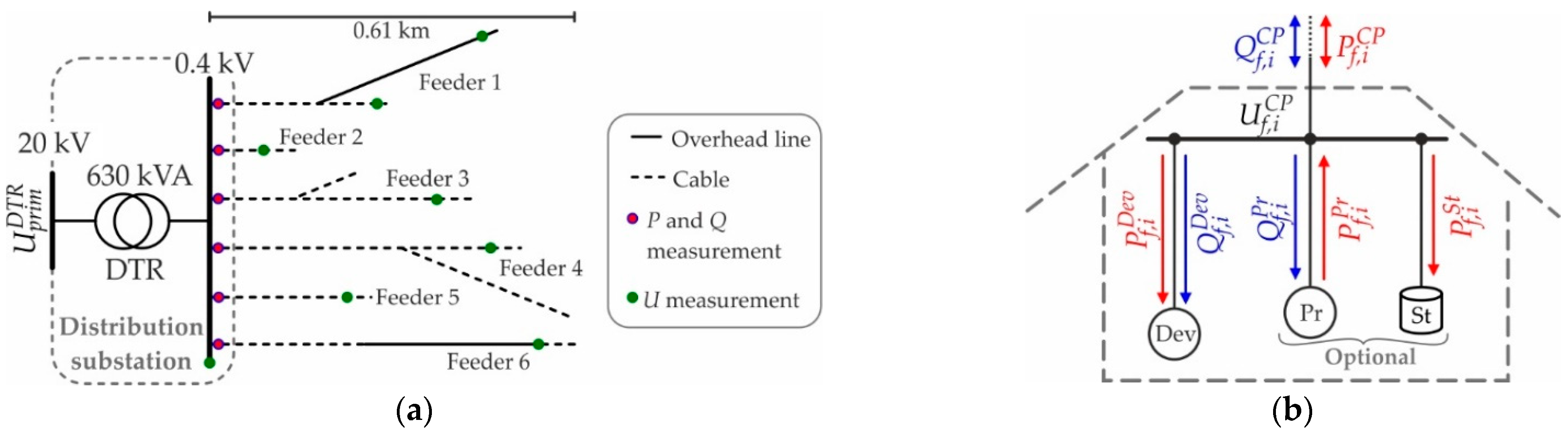
2.1.2. Application to Real LV Grid
| Derived from grid data | |
| Derived from measurements | |
| Estimated |
- Grid Data
- Measurements
- Estimations
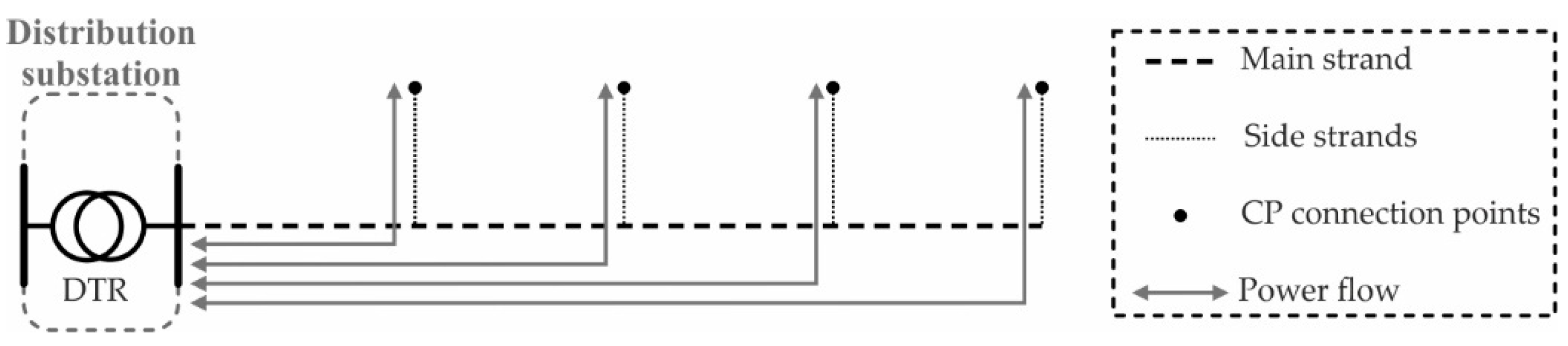
2.2. Detection of DTR Congestions
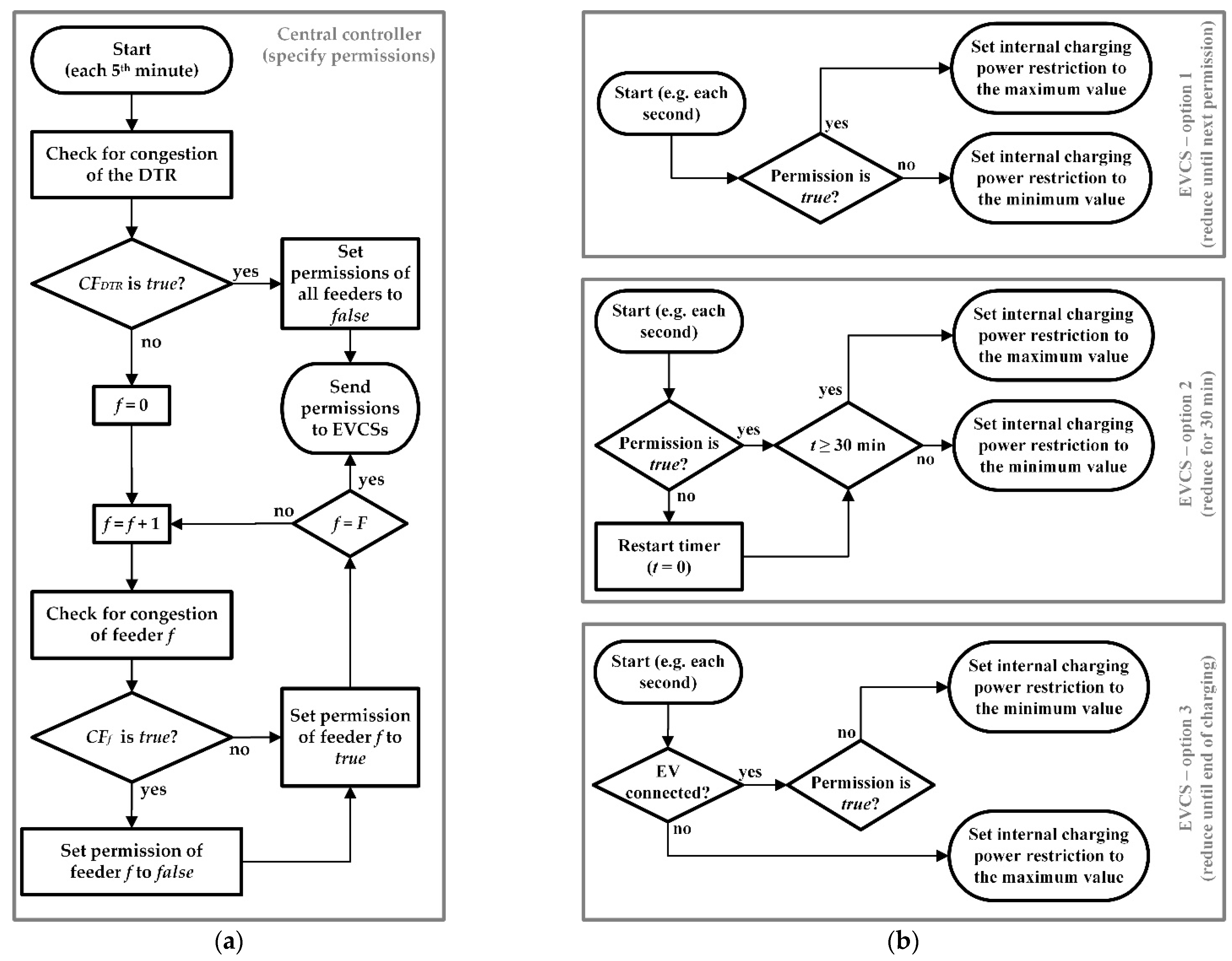
2.3. Coordination Algorithms
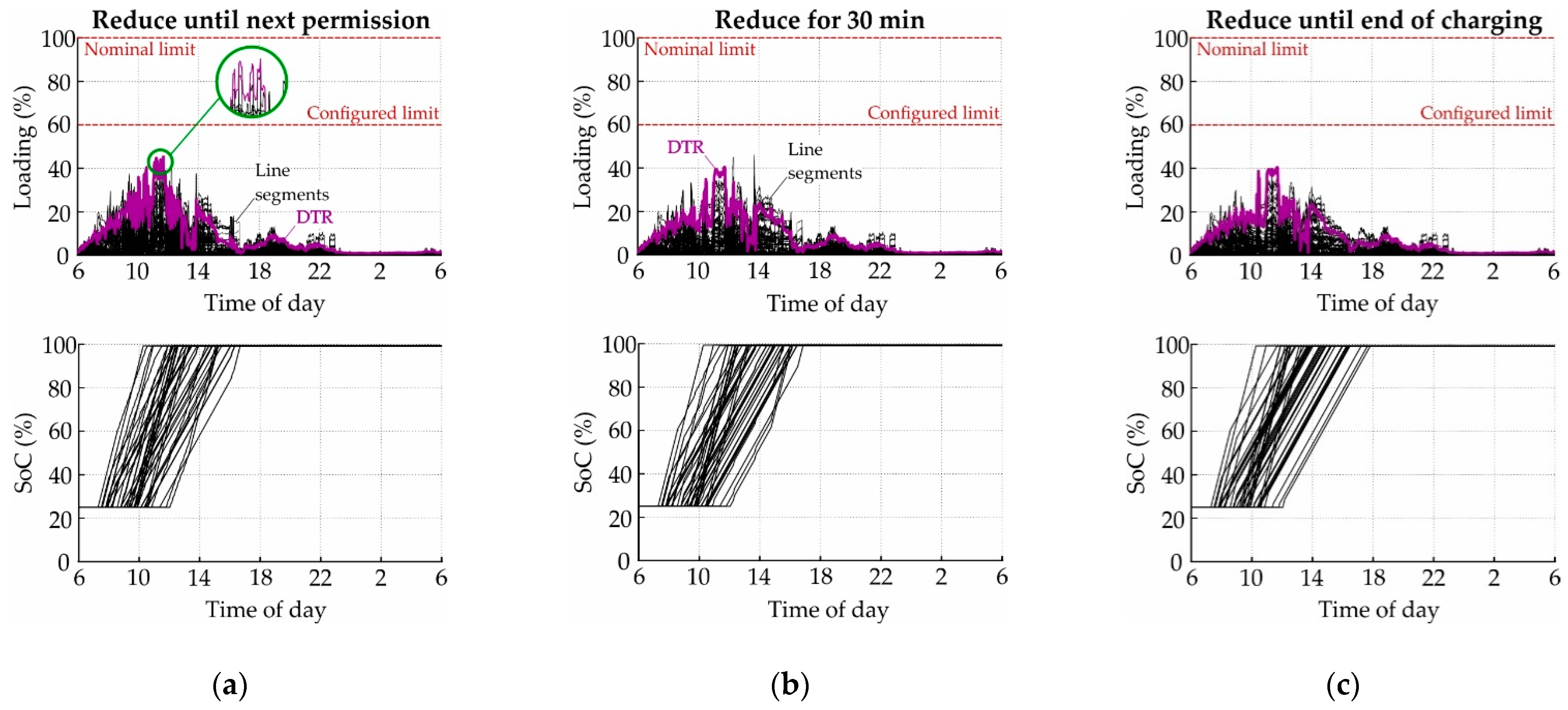
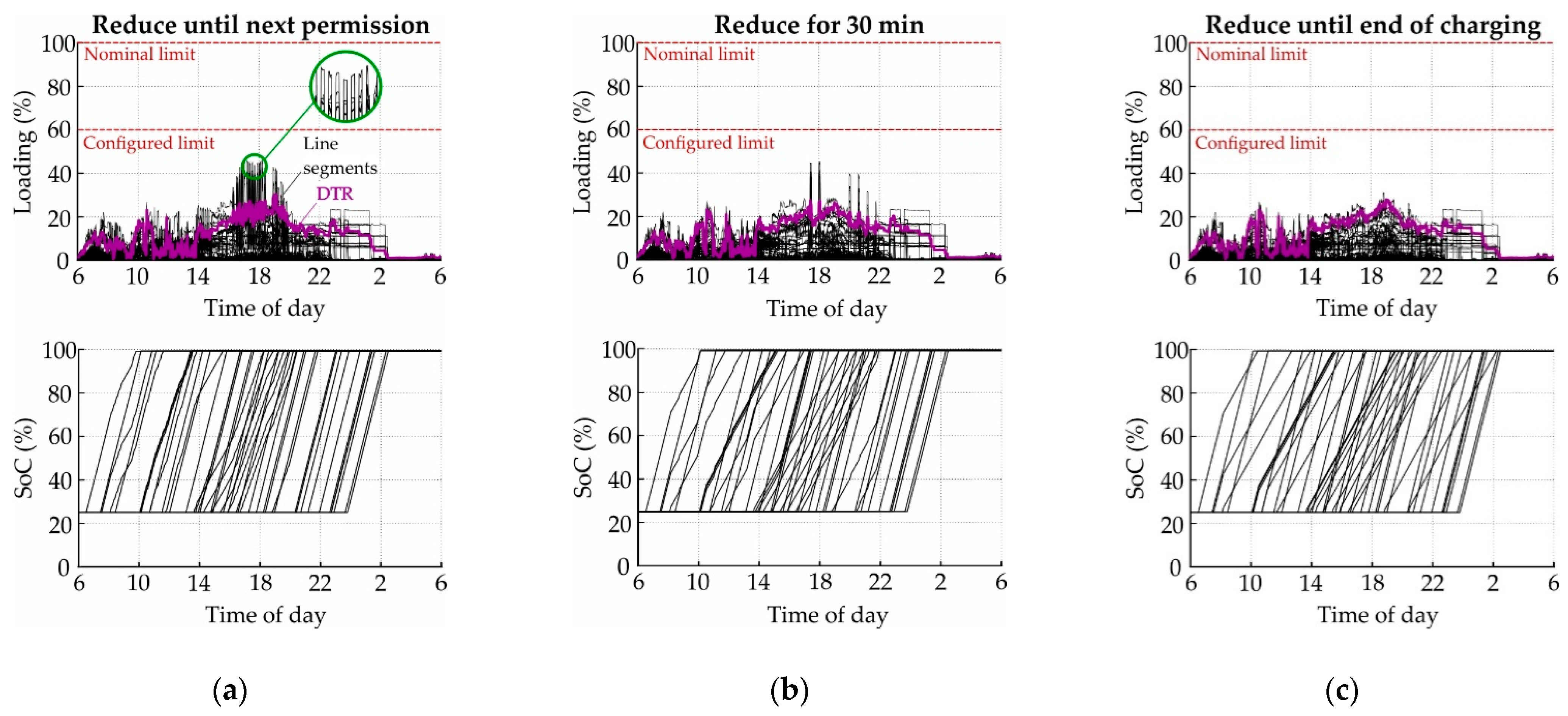
- Reduce until next permission
- Reduce for 30 min
- Reduce until end of charging
2.4. Test Setup
2.4.1. Simulation Software
2.4.2. Power System Model
- Low voltage grid
- Customer plants
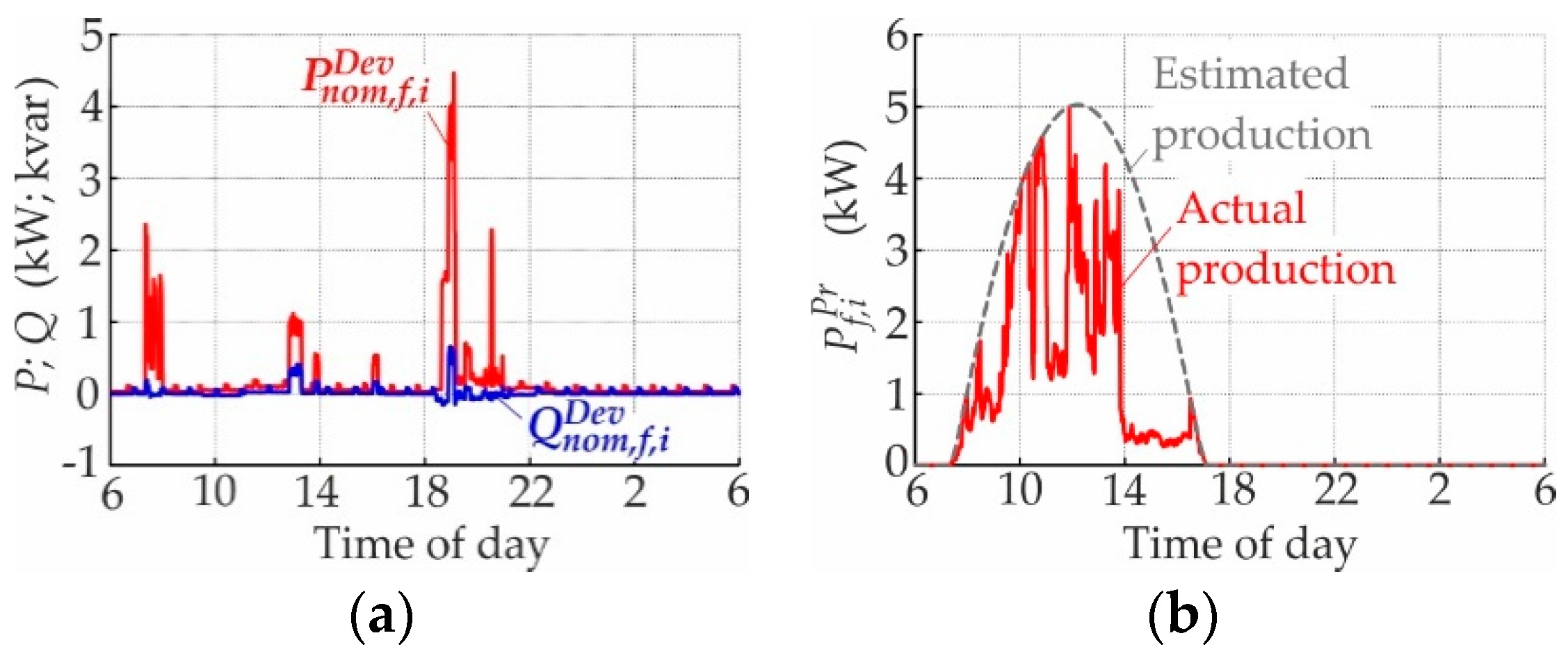
- Scenario definition
3. Results
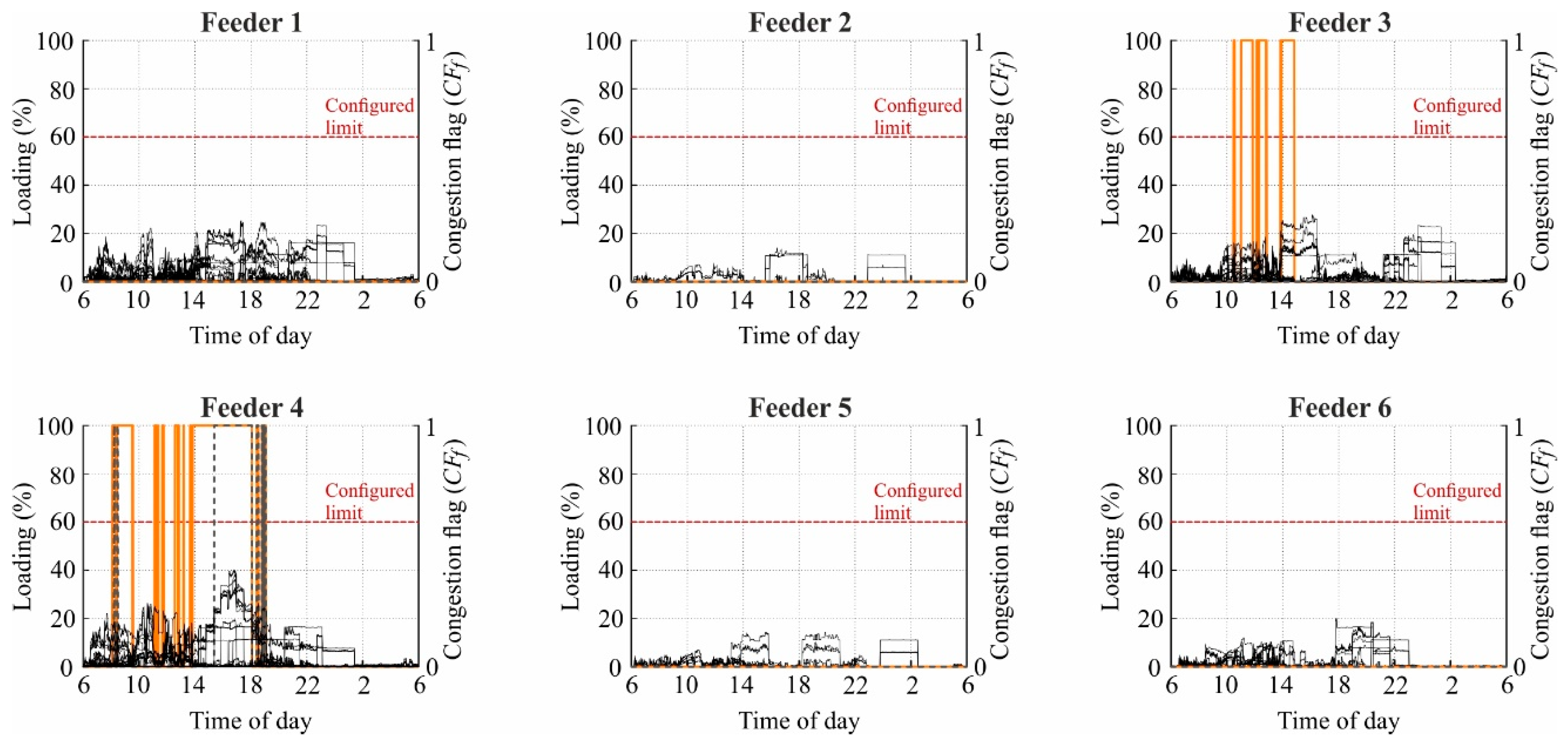
3.1. Sparse Measurement-Based Detection of Feeder Congestions
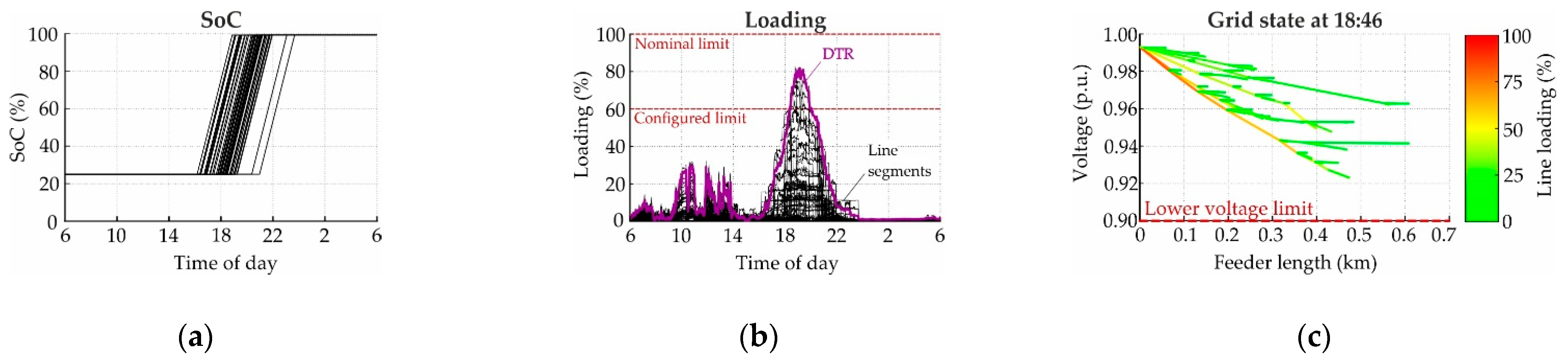
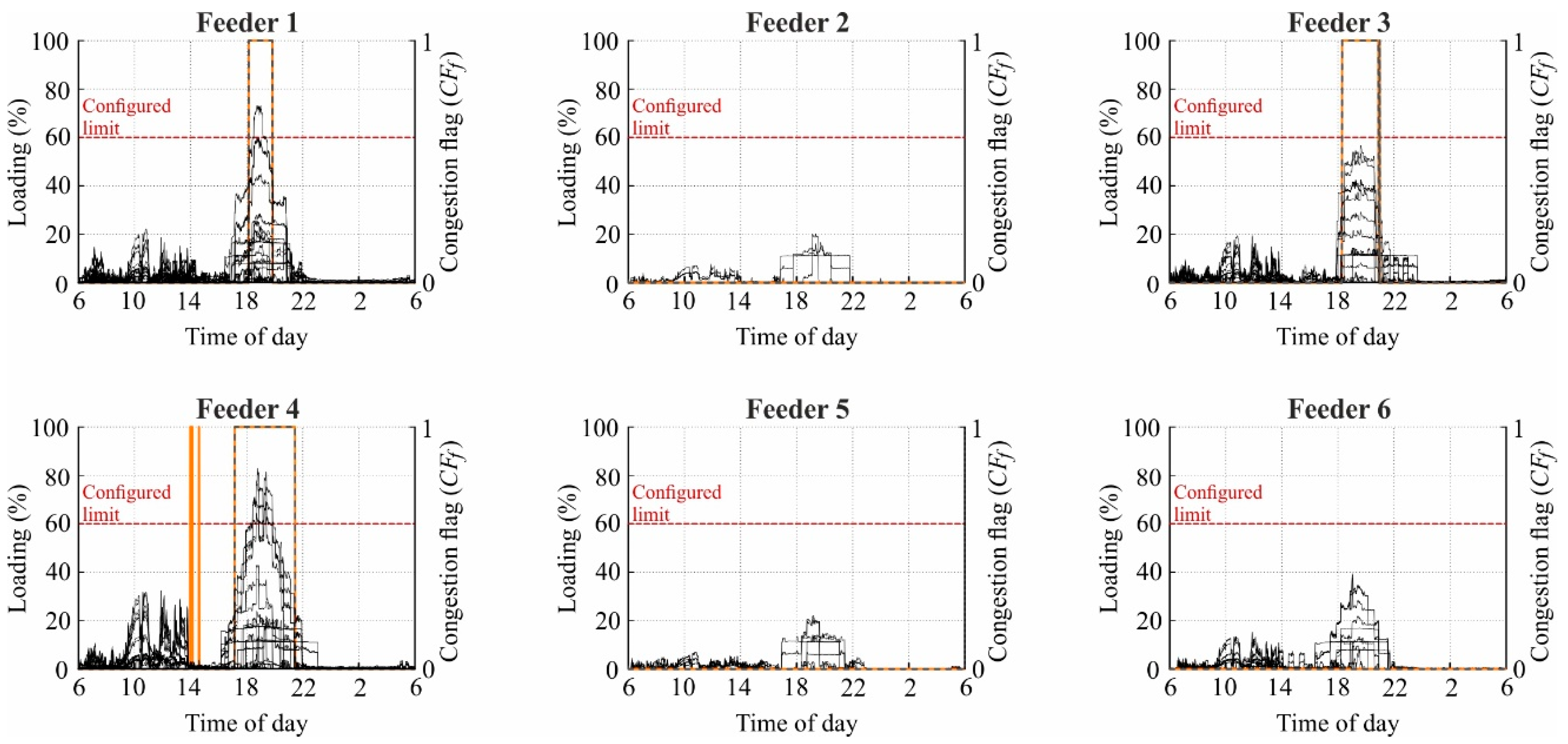
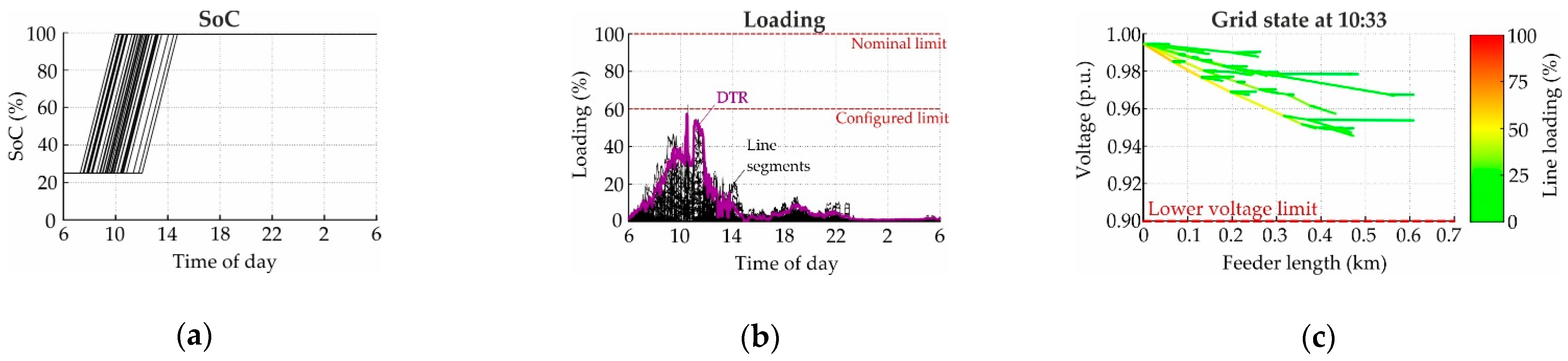
3.1.1. Simultaneous Charging in the Evening
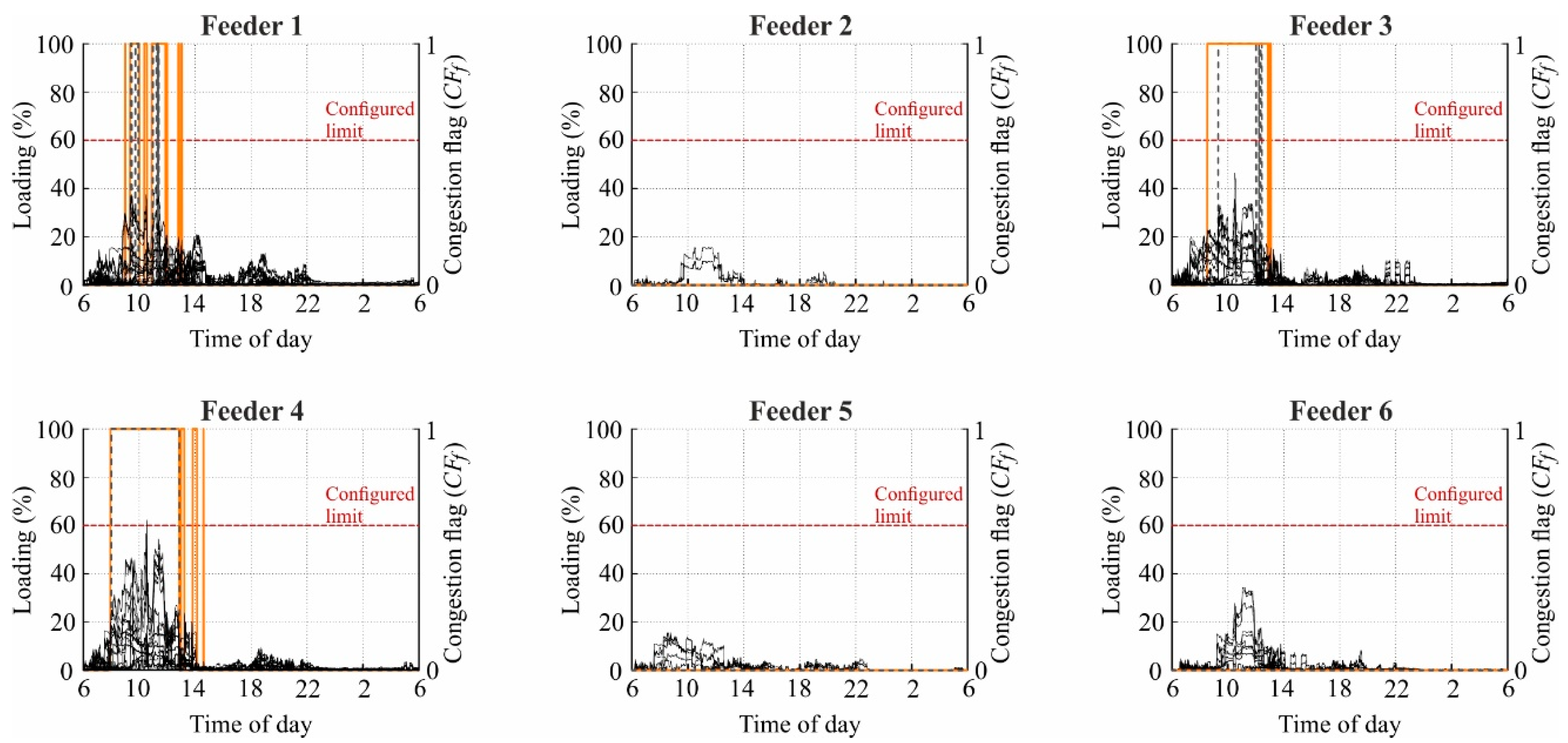
3.1.2. Simultaneous Charging in the Morning
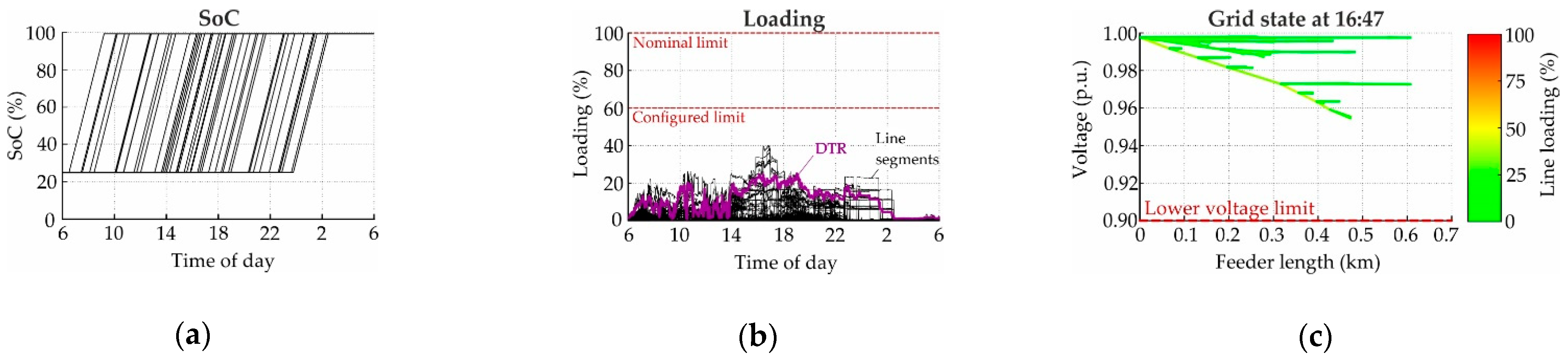
3.1.3. Charging throughout the Day
3.2. Coordination Algorithms
3.2.1. Simultaneous Charging in the Evening
3.2.2. Simultaneous Charging in the Morning
3.2.3. Charging throughout the Day
4. Discussion
4.1. Sparse Measurement-Based Detection of Feeder Congestions
4.2. CoordinationAalgorithms
4.3. Applicability of the Concept
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| CP | Customer Plant | EVCS | Electric Vehicle Charging Station |
| DER | Distributed energy resource | LF | Load flow |
| Dev | Device | LV | Low voltage |
| DSO | Distribution system operator | OLTC | On-load tap changer |
| DSSE | Distribution system state estimation | Pr | Producer |
| DTR | Distribution transformer | PV | Photovoltaic |
| EV | Electric vehicle | St | Storage |
| Active and reactive power flows at the beginning of feeder f. | |
| Active and reactive power contributions of CP i connected to feeder f. | |
| Active and reactive power losses in the series impedances of all line segments of feeder f. | |
| Reactive power production of the shunt capacitances of all line segments of feeder f. | |
| Aggregate active and reactive power injections into feeder f. | |
| Minimal voltage of feeder f. | |
| Minimal thermal limit current of all line segments of feeder f. | |
| Voltage at the primary bus bar of the DTR. | |
| Voltage at the secondary bus bar of the DTR. | |
| Active and reactive power injections at the beginning of feeder f. | |
| Active and reactive power injections of CP i connected to feeder f. | |
| Number of customer plants connected to feeder f. | |
| Number of feeders. | |
| Estimated value of the maximum line segment loading of feeder f. | |
| Congestion flag related to feeder f. | |
| Apparent power injection at the beginning of feeder f. | |
| Limit of the line segment loading of feeder f. | |
| Thermal limit current of line segment , which is part of the main strands of feeder . | |
| Voltage measurement at feeder . | |
| Aggregate active and reactive power contributions of all consuming devices included in CP i connected to feeder f. | |
| Aggregate active and reactive power contributions of all producers included in CP i connected to feeder f. | |
| Aggregate active and reactive power contributions of all storages included in CP i connected to feeder f. | |
| Maximal active and reactive power injections of the producer included in CP i connected to feeder f. | |
| Rated apparent power of the distribution transformer. | |
| Loading of the distribution transformer. | |
| Congestion flag related to the distribution transformer. | |
| Limit of the distribution transformer loading. | |
| Active and reactive power contributions of the device model included in CP i connected to feeder f for nominal supply voltage. | |
| Normalized supply voltage of CP i connected to feeder f. | |
| Supply voltage of CP i connected to feeder f. | |
| State-of-charge of the electric vehicle battery included in CP i connected to feeder f. | |
| Active power contribution of the storage model included in CP i connected to feeder f for nominal supply voltage. | |
| Resolution of the load profiles. | |
| Storage capacity of the electric vehicle battery included in CP i connected to feeder f. | |
| Instant of time. | |
| Instant of time in which the charging process of the electric vehicle battery included in CP i connected to feeder f is started. | |
| Energy loss of the complete low voltage grid. | |
| Average charging time per electric vehicle battery. | |
| Active power loss of the distribution transformer. | |
| Active power loss of the line segment l. | |
| Charging time of electric vehicle charging station e. | |
| Number of electric vehicle charging stations. | |
| Number of instants of time in which the congestion flag related to feeder f is correctly set. | |
| Number of simulated instants of time. | |
| Detection accuracy related to feeder f. |
References
- Ilo, A.; Gawlik, W. The Way from Traditional to Smart Power Systems. In Proceedings of the IEWT 2015, Vienna, Austria, 11–13 February 2015. [Google Scholar]
- Sun, H.; Guo, Q.; Qi, J.; Ajjarapu, V.; Bravo, R.; Chow, J.H.; Li, Z.; Moghe, R.; Nasr, E.; Tamrakar, U.; et al. Review of Challenges and Research Opportunities for Voltage Control in Smart Grids. IEEE Trans. Power Syst. 2019, 34, 2790–2801. [Google Scholar] [CrossRef]
- Katiraei, F.; Aguero, J.R. Solar PV Integration Challenges. IEEE Power Energy Mag. 2011, 9, 62–71. [Google Scholar] [CrossRef]
- Nappu, M.B.; Arief, A.; Bansal, R.C. Transmission management for congested power system: A review of concepts, technical challenges and development of a new methodology. Renew. Sustain. Energy Rev. 2014, 38, 572–580. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of the Impact of Vehicle-to-Grid Technologies on Distribution Systems and Utility Interfaces. IEEE Trans. Power Electron. 2013, 28, 5673–5689. [Google Scholar] [CrossRef]
- Kundur, P. Reactive power and voltage control. In Power System Stability and Control, 1st ed.; Balu, N.J., Lauby, M.G., Eds.; McGraw-Hill Inc.: New York, NY, USA, 1994; pp. 627–687. [Google Scholar]
- Pillay, A.; Karthikeyan, S.P.; Kothari, D. Congestion management in power systems—A review. Int. J. Electr. Power Energy Syst. 2015, 70, 83–90. [Google Scholar] [CrossRef]
- Sarimuthu, C.R.; Ramachandaramurthy, V.K.; Agileswari, K.; Mokhlis, H. A review on voltage control methods using on-load tap changer transformers for networks with renewable energy sources. Renew. Sustain. Energy Rev. 2016, 62, 1154–1161. [Google Scholar] [CrossRef]
- Marggraf, O.; Laudahn, S.; Engel, B.; Lindner, M.; Aigner, C.; Witzmann, R.; Schoeneberger, M.; Patzack, S.; Vennegeerts, H.; Cremer, M.; et al. U-Control—Analysis of Distributed and Automated Voltage Control in current and future Distribution Grids. In Proceedings of the International ETG Congress 2017, Bonn, Germany, 28–29 November 2017. [Google Scholar]
- Ilo, A.; Schultis, D.-L.; Schirmer, C. Effectiveness of Distributed vs. Concentrated Volt/Var Local Control Strategies in Low-Voltage Grids. Appl. Sci. 2018, 8, 1382. [Google Scholar] [CrossRef]
- Rossi, M.; Viganò, G.; Moneta, D.; Clerici, D.; Carlini, C. Analysis of active power curtailment strategies for renewable distributed generation. In Proceedings of the 2016 AEIT International Annual Conference (AEIT), Capri, Italy, 5–7 October 2016; pp. 1–6. [Google Scholar]
- Li, B.; Chen, M.; Cheng, T.; Li, Y.; Hassan, M.A.S.; Xu, R.; Chen, T. Distributed Control of Energy-Storage Systems for Voltage Regulation in Distribution Network with High PV Penetration. In Proceedings of the 2018 UKACC 12th International Conference on Control (CONTROL), Sheffield, UK, 5–7 September 2018; pp. 169–173. [Google Scholar]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The Impact of Charging Plug-In Hybrid Electric Vehicles on a Residential Distribution Grid. IEEE Trans. Power Syst. 2009, 25, 371–380. [Google Scholar] [CrossRef]
- Deilami, S.; Masoum, A.S.; Moses, P.S.; Masoum, M.A.S. Real-Time Coordination of Plug-In Electric Vehicle Charging in Smart Grids to Minimize Power Losses and Improve Voltage Profile. IEEE Trans. Smart Grid 2011, 2, 456–467. [Google Scholar] [CrossRef]
- Ilo, A.; Prata, R.; Strbac, G.; Giannelos, S.; Bissell, G.R.; Kulmala, A.; Constantinescu, N.; Samovich, N.; Iliceto, A. Holistic Architectures for Future Power Systems. ETIP SNET White Paper. 2019. Available online: https://www.etip-snet.eu/etip_publ/white-paper-holistic-architectures-future-power-systems/ (accessed on 22 December 2020).
- Ilo, A. Use cases in Sector Coupling as part of the LINK-based holistic architecture to increase the grid flexibility. In Proceedings of the CIRED 2020 Berlin Workshop, Berlin, Germany, 22–23 September 2020. [Google Scholar]
- Ilo, A. “Link”—The smart grid paradigm for a secure decentralized operation architecture. Electr. Power Syst. Res. 2016, 131, 116–125. [Google Scholar] [CrossRef]
- Veetil, V.P. Coordination in Centralized and Decentralized Systems. Int. J. Microsimulation 2017, 10, 86–102. [Google Scholar] [CrossRef]
- Schweppe, F.C.; Wildes, J. Power System Static-State Estimation, Part I: Exact Model. IEEE Trans. Power Appar. Syst. 1970, 1, 120–125. [Google Scholar] [CrossRef]
- Primadianto, A.; Lu, C.-N. A Review on Distribution System State Estimation. IEEE Trans. Power Syst. 2016, 32, 3875–3883. [Google Scholar] [CrossRef]
- Ahmad, F.; Rasool, A.; Ozsoy, E.; Sekar, R.; Sabanovic, A.; Elitaş, M. Distribution system state estimation-A step towards smart grid. Renew. Sustain. Energy Rev. 2018, 81, 2659–2671. [Google Scholar] [CrossRef]
- Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Hu, J.; You, S.; Lind, M.; Ostergaard, J. Coordinated Charging of Electric Vehicles for Congestion Prevention in the Distribution Grid. IEEE Trans. Smart Grid 2014, 5, 703–711. [Google Scholar] [CrossRef]
- Bhattarai, B.P.; Bak-Jensen, B.; Pillai, J.R.; Mahat, P. Two-stage electric vehicle charging coordination in low voltage distribution grids. In Proceedings of the 2014 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Hong Kong, China, 7–10 December 2014; pp. 1–5. [Google Scholar]
- Sundstrom, O.; Binding, C. Flexible Charging Optimization for Electric Vehicles Considering Distribution Grid Constraints. IEEE Trans. Smart Grid 2011, 3, 26–37. [Google Scholar] [CrossRef]
- Dixon, J.; Bukhsh, W.; Edmunds, C.; Bell, K. Scheduling electric vehicle charging to minimise carbon emissions and wind curtailment. Renew. Energy 2020, 161, 1072–1091. [Google Scholar] [CrossRef]
- Schultis, D.-L. Coordinated electric vehicle charging—Performance analysis of developed algorithms. In Proceedings of the CIRED 2021 Conference, Geneva, Switzerland, 21–24 June 2021. [Google Scholar]
- Einfalt, A.; Brunner, H.; Pruggler, W.; Schultis, D.-L.; Herbst, D.; Beidinger, T.; Hauer, D.; Lugmaier, A. Efficient utilisation of existing grid infrastructure empowering smart communities. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar]
- Strunz, K. Benchmark Systems for Network Integration of Renewable and Distributed Energy Resources. Cigre Task Force C 2014, 6, 78. [Google Scholar]
- Schultis, D.-L.; Ilo, A. Adaption of the Current Load Model to Consider Residential Customers Having Turned to LED Lighting. In Proceedings of the 2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Macao, China, 1–4 December 2019. [Google Scholar]
- IEEE. IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces; IEEE: New York, NY, USA, 2018; pp. 1–138. [Google Scholar]
- Leemput, N.; Geth, F.; Van Roy, J.; Büscher, J.; Driesen, J. Reactive power support in residential LV distribution grids through electric vehicle charging. Sustain. Energy, Grids Netw. 2015, 3, 24–35. [Google Scholar] [CrossRef]
- Wang, J.; Bharati, G.R.; Paudyal, S.; Ceylan, O.; Bhattarai, B.P.; Myers, K.S. Coordinated Electric Vehicle Charging With Reactive Power Support to Distribution Grids. IEEE Trans. Ind. Inform. 2019, 15, 54–63. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-De-Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Schultis, D.-L.; Ilo, A.; Schirmer, C. Overall performance evaluation of reactive power control strategies in low voltage grids with high prosumer share. Electr. Power Syst. Res. 2019, 168, 336–349. [Google Scholar] [CrossRef]
- Schultis, D.-L. Comparison of Local Volt/var Control Strategies for PV Hosting Capacity Enhancement of Low Voltage Feeders. Energies 2019, 12, 1560. [Google Scholar] [CrossRef]
- Bokhari, A.; Alkan, A.; Dogan, R.; Diaz-Aguilo, M.; De Leon, F.; Czarkowski, D.; Zabar, Z.; Birenbaum, L.; Noel, A.; Uosef, R.E. Experimental Determination of the ZIP Coefficients for Modern Residential, Commercial, and Industrial Loads. IEEE Trans. Power Deliv. 2014, 29, 1372–1381. [Google Scholar] [CrossRef]
- Shukla, A.; Verma, K.; Kumar, R. Multi-stage voltage dependent load modelling of fast charging electric vehicle. In Proceedings of the 2017 6th International Conference on Computer Applications In Electrical Engineering-Recent Advances (CERA), Roorkee, India, 5–7 October 2017; pp. 86–91. [Google Scholar]
- Load Profile Generator. Available online: https://www.loadprofilegenerator.de/ (accessed on 20 November 2020).
- McKenna, E.; Thomson, M.; Barton, J. CREST Demand Model; Data Set; Loughborough University: Loughborough, UK, 2015. [Google Scholar] [CrossRef]

| Feeder | Cable Share in % | Maximal Feeder Length in km | Total Line Length in km | Number of Connected CPs | |
|---|---|---|---|---|---|
| In Total | With EVCS and PV System | ||||
| 1 | 51.92 | 0.49 | 1.040 | 26 | 10 |
| 2 | 100 | 0.15 | 0.205 | 4 | 3 |
| 3 | 100 | 0.43 | 0.810 | 18 | 9 |
| 4 | 93.55 | 0.61 | 1.550 | 23 | 15 |
| 5 | 100 | 0.27 | 0.490 | 7 | 3 |
| 6 | 61.36 | 0.61 | 0.880 | 13 | 6 |
| Scenario | Coordination Algorithm | |
|---|---|---|
| Central Controller | Distributed EVCSs | |
| Simultaneous charging in the evening | None | None |
| Specify permissions | Reduce until next permission | |
| Reduce for 30 min | ||
| Reduce until end of charging | ||
| Simultaneous charging in the morning | None | None |
| Specify permissions | Reduce until next permission | |
| Reduce for 30 min | ||
| Reduce until end of charging | ||
| Charging throughout the day | None | None |
| Specify permissions | Reduce until next permission | |
| Reduce for 30 min | ||
| Reduce until end of charging | ||
| PV Production | Scenario | Detection Accuracy by the Feeder in % | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Estimated | Simultaneous charging in the evening | 92.92 | 100 | 89.11 | 81.26 | 100 | 100 |
| Simultaneous charging in the morning | 91.46 | 100 | 81.54 | 77.17 | 100 | 100 | |
| Charging throughout the day | 100 | 100 | 89.45 | 73.07 | 100 | 100 | |
| Exact | Simultaneous charging in the evening | 92.92 | 100 | 89.11 | 82.03 | 100 | 100 |
| Simultaneous charging in the morning | 97.57 | 100 | 88.27 | 79.67 | 100 | 100 | |
| Charging throughout the day | 100 | 100 | 100 | 87.30 | 100 | 100 | |
| Scenario | Coordination Algorithm | Energy Loss in kWh | Average Charging Time in min | |
|---|---|---|---|---|
| Central Controller | Distributed EVCSs | |||
| Simultaneous charging in the evening | None | None | 56.65 | 161.00 |
| Specify permissions | Reduce until next permission | 44.54 | 233.43 | |
| Reduce for 30 min | 39.38 | 273.89 | ||
| Reduce until end of charging | 37.80 | 285.50 | ||
| Simultaneous charging in the morning | None | None | 22.28 | 161.00 |
| Specify permissions | Reduce until next permission | 16.15 | 248.11 | |
| Reduce for 30 min | 15.19 | 279.74 | ||
| Reduce until end of charging | 14.76 | 287.04 | ||
| Charging throughout the day | None | None | 21.31 | 161.00 |
| Specify permissions | Reduce until next permission | 21.00 | 183.41 | |
| Reduce for 30 min | 20.31 | 213.24 | ||
| Reduce until end of charging | 19.63 | 233.59 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schultis, D.-L. Sparse Measurement-Based Coordination of Electric Vehicle Charging Stations to Manage Congestions in Low Voltage Grids. Smart Cities 2021, 4, 17-40. https://doi.org/10.3390/smartcities4010002
Schultis D-L. Sparse Measurement-Based Coordination of Electric Vehicle Charging Stations to Manage Congestions in Low Voltage Grids. Smart Cities. 2021; 4(1):17-40. https://doi.org/10.3390/smartcities4010002
Chicago/Turabian StyleSchultis, Daniel-Leon. 2021. "Sparse Measurement-Based Coordination of Electric Vehicle Charging Stations to Manage Congestions in Low Voltage Grids" Smart Cities 4, no. 1: 17-40. https://doi.org/10.3390/smartcities4010002
APA StyleSchultis, D.-L. (2021). Sparse Measurement-Based Coordination of Electric Vehicle Charging Stations to Manage Congestions in Low Voltage Grids. Smart Cities, 4(1), 17-40. https://doi.org/10.3390/smartcities4010002