Method and System for Heart Rate Estimation Using Linear Prediction Filtering †
Abstract
1. Introduction
2. Materials and Methods
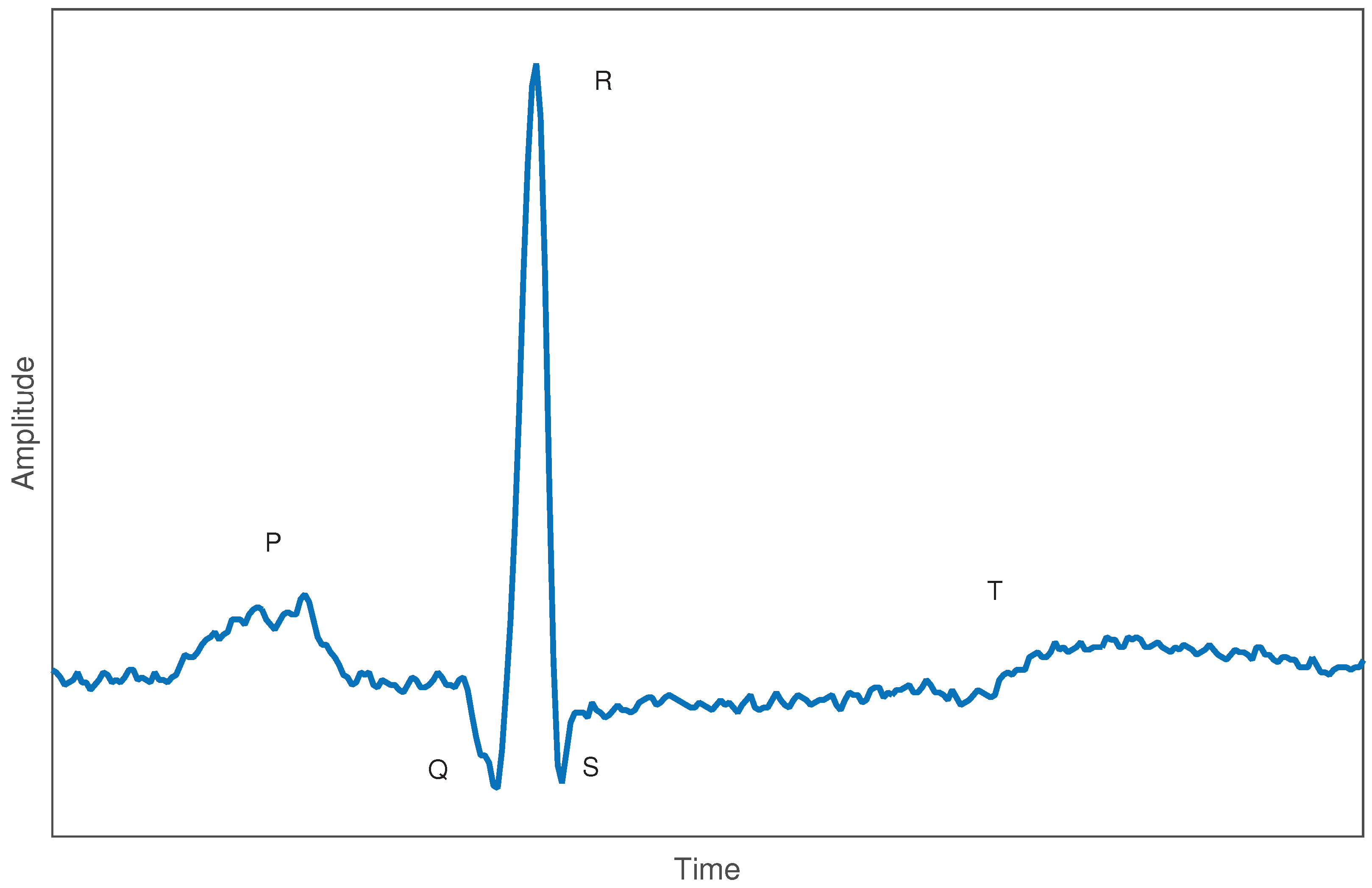
2.1. Electrocardiogram Signals
2.2. LPC—Linear Prediction Coefficients
2.3. LPC: Heart Rhythm Estimation
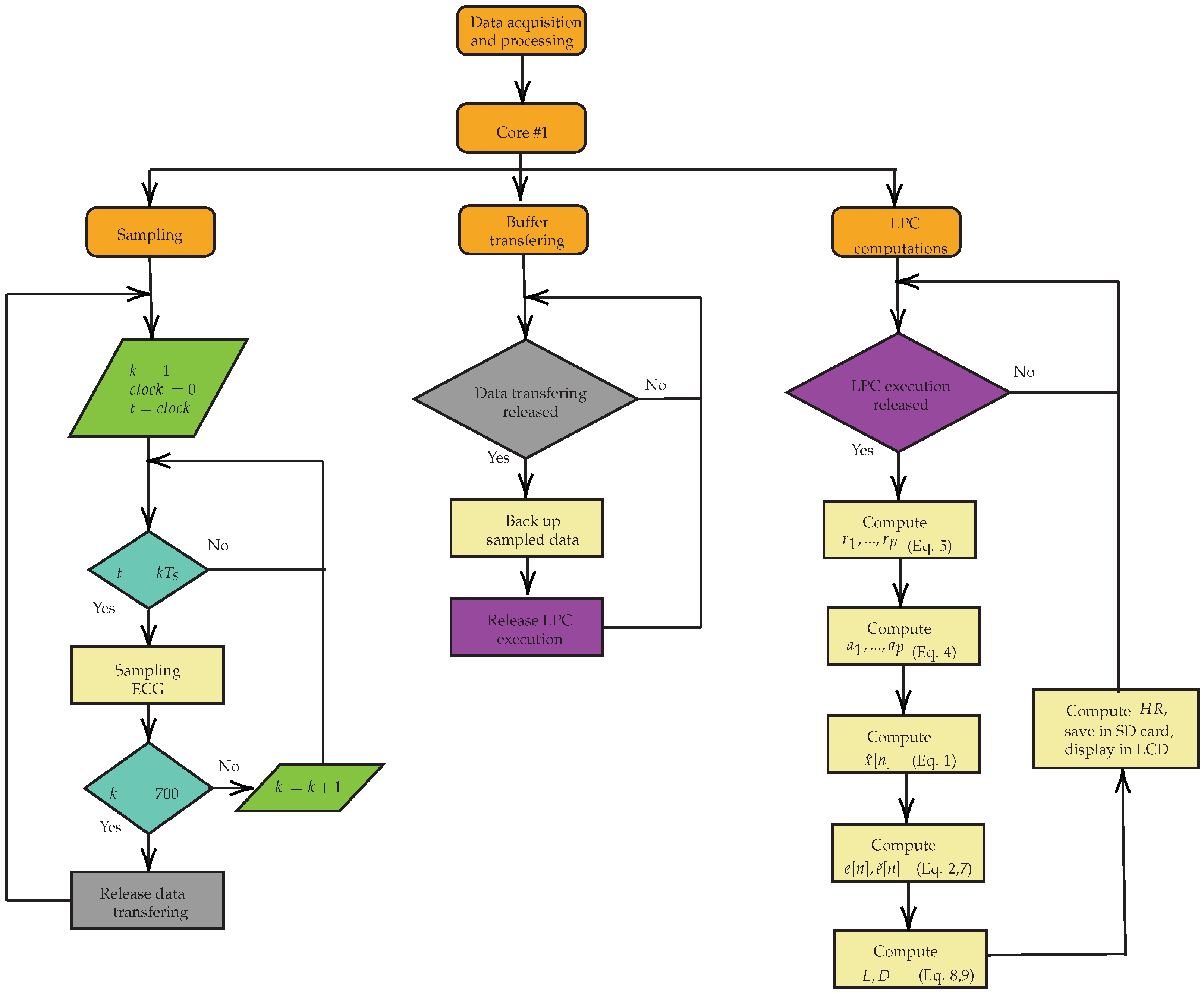
2.4. Experimental Setup
- Sampling rate 250 samples/s and 12-bit resolution;
- Use of instrumentation amplifier;
- 0.5 to 40 Hz bandpass filter or a high-pass filter together with a low-pass filter;
- Notch filter at 60 Hz;
- Use of processor compatible with the implementation;
- Use of 1 GB microSD card electronics;
- Use of LCD, TFT or OLED screen;
- Use of charge control electronics for lithium-ion batteries.
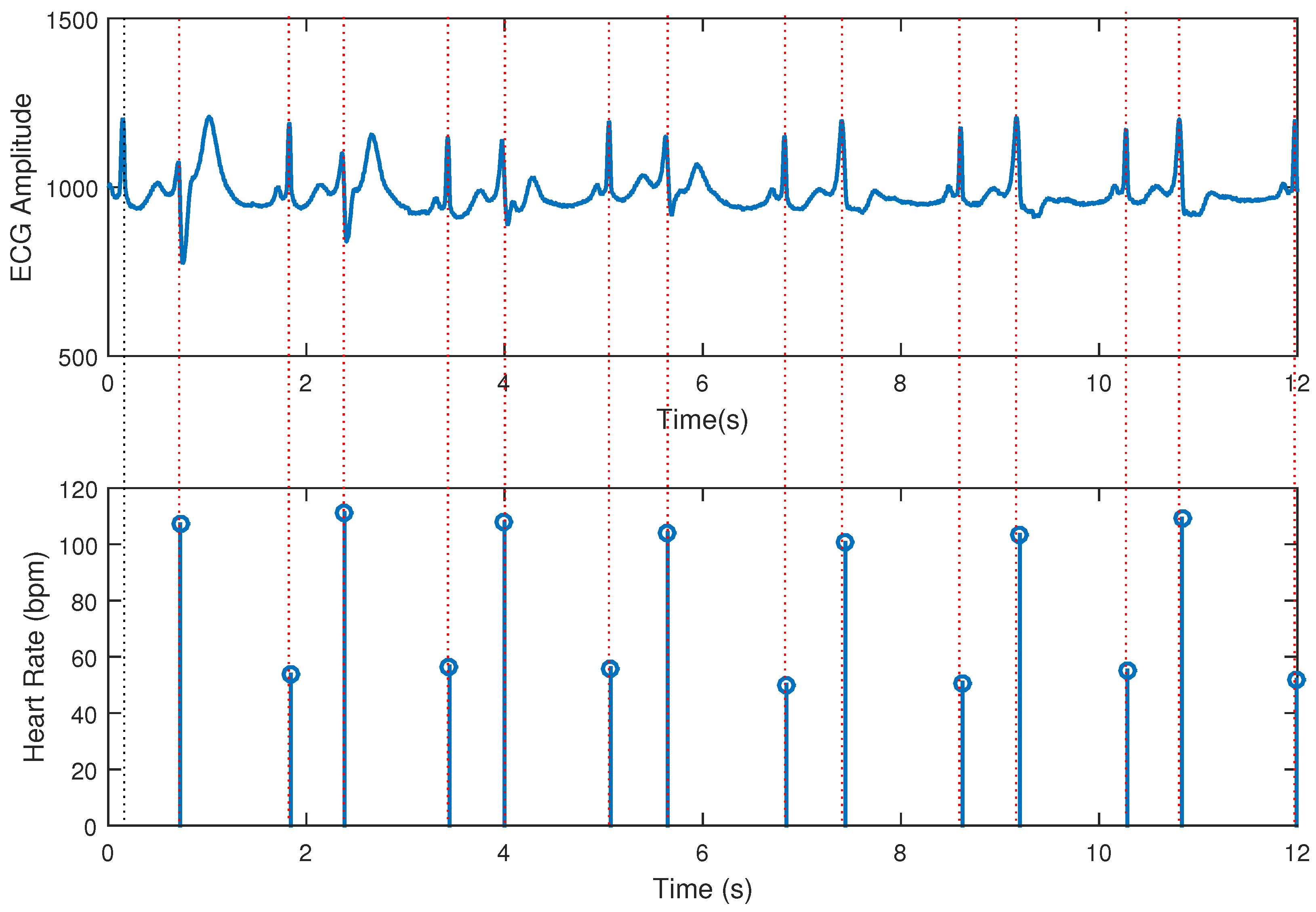
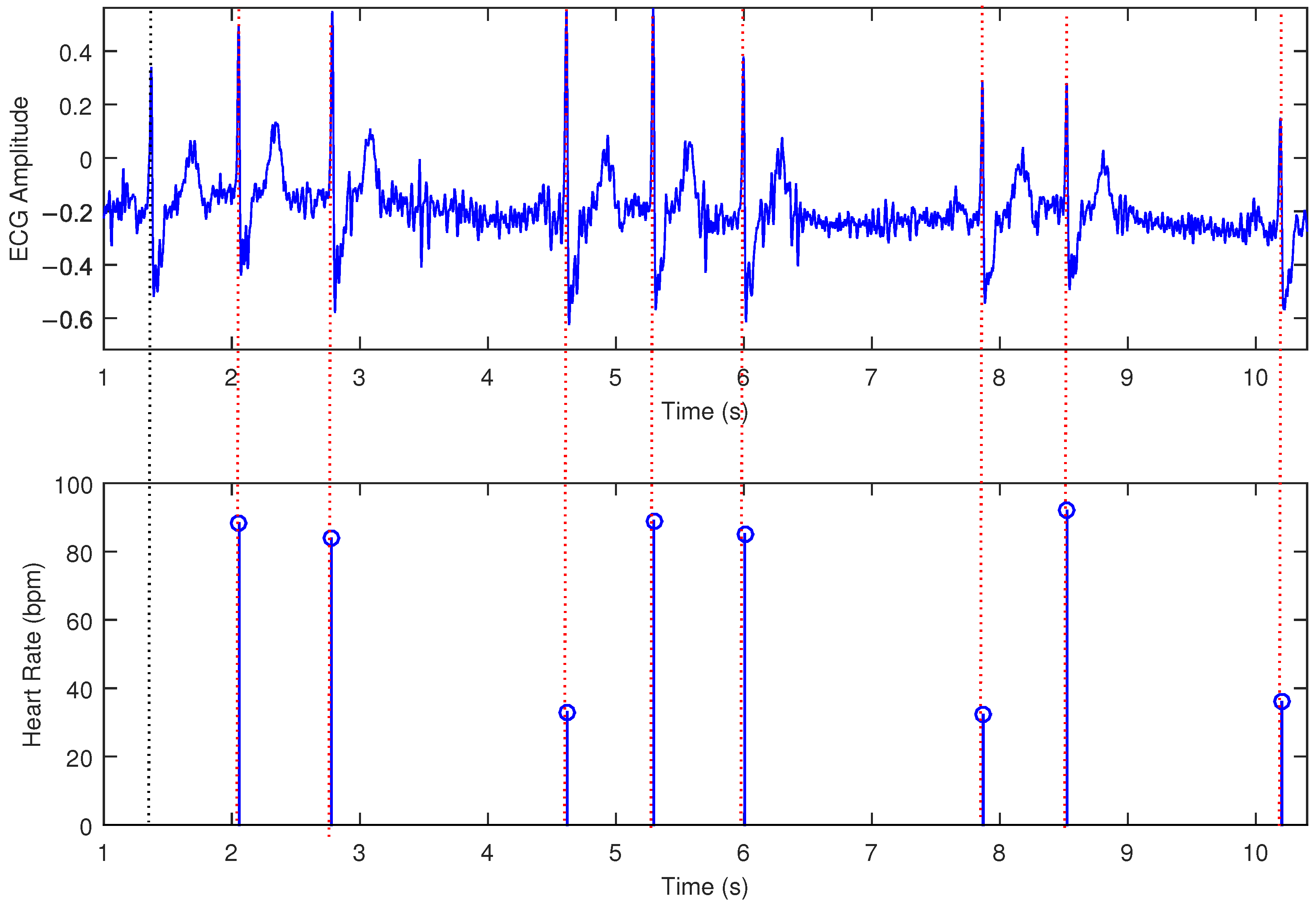
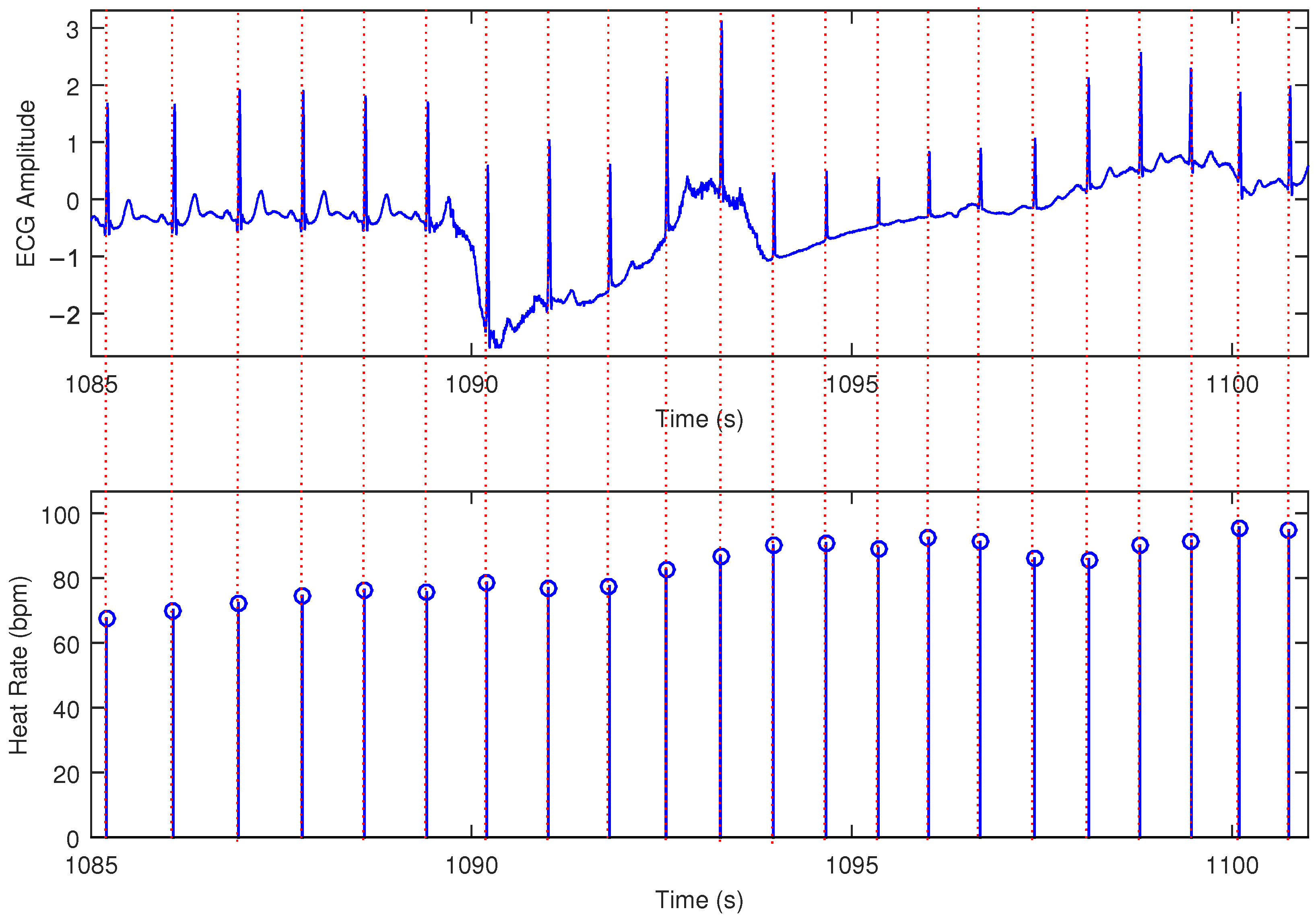
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chaitanya, M.K.; Sharma, L.D.; Roy, A.; Rahul, J. A review on artificial intelligence for electrocardiogram signal analysis. In Big Data Analytics and Artificial Intelligence in the Healthcare Industry; IGI Global: Hershey, PA, USA, 2022; pp. 38–72. [Google Scholar]
- Précoma, D.B.; Oliveira, G.M.M.d.; Simão, A.F.; Dutra, O.P.; Coelho, O.R.; Izar, M.C.d.O.; Póvoa, R.M.d.S.; Giuliano, I.d.C.B.; Alencar, A.C.d.; Machado, C.A.; et al. Atualização da diretriz de prevenção cardiovascular da Sociedade Brasileira de Cardiologia. Arq. Bras. Cardiol. 2019, 113, 787–891. [Google Scholar] [PubMed]
- Stevens, B.; Pezzullo, L.; Verdian, L.; Tomlinson, J.; George, A.; Bacal, F. Os custos das doenças cardíacas no Brasil. Arq. Bras. Cardiol. 2018, 111, 29–36. [Google Scholar]
- Oliveira, G.M.M.d.; Brant, L.C.C.; Polanczyk, C.A.; Malta, D.C.; Biolo, A.; Nascimento, B.R.; Souza, M.d.F.M.d.; Lorenzo, A.R.D.; Fagundes Júnior, A.A.d.P.; Schaan, B.D.; et al. Estatística Cardiovascular–Brasil 2021. Arq. Bras. Cardiol. 2022, 118, 115–373. [Google Scholar] [CrossRef] [PubMed]
- Kruse, C.S.; Soma, M.; Pulluri, D.; Nemali, N.T.; Brooks, M. The effectiveness of telemedicine in the management of chronic heart disease—A systematic review. JRSM Open 2017, 8, 2054270416681747. [Google Scholar] [CrossRef]
- Zhu, Y.; Gu, X.; Xu, C. Effectiveness of telemedicine systems for adults with heart failure: A meta-analysis of randomized controlled trials. Heart Fail. Rev. 2020, 25, 231–243. [Google Scholar] [CrossRef]
- Amaral, F.; Fernandes, E.; Drabowski, N.; Alves, M.; Nunes, A.; da Silva, E.; Bastos, M.; Romera, J.; de Castro Figueroa, R. Estudo de caso de Tarumã: O uso de telemedicina e Inteligência Artificial para redução da mortalidade por doenças cardíacas e otimização dos recursos em saúde. Scielo 2022, Preprints. [Google Scholar] [CrossRef]
- Salgueiro, A.T.F. Detecção de Problemas Cardíacos Usando Sinais de Electrocardiograma (ECG). Master’s Thesis, Universidade de Coimbra, Coimbra, Portugal, 2020. [Google Scholar]
- Andrade, M.V.; Maia, A.C.; Cardoso, C.S.; Alkmim, M.B.; Ribeiro, A.L.P. Custo-benefício do serviço de telecardiologia no Estado de Minas Gerais: Projeto Minas Telecardio. Arq. Bras. Cardiol. 2011, 97, 307–316. [Google Scholar] [CrossRef]
- Ktata, F.; Ben Kalboussi, K. Real Time Mobile E-Health Platform for Vital Signals Monitoring and ECG Classification Using 1D CNN; Research Gate Preprint. 2021. Available online: https://www.researchgate.net/publication/358921899_Real_time_mobile_E-Health_platform_for_vital_signals_monitoring_and_ECG_classification_using_1D_CNN (accessed on 18 March 2025).
- Shaker, A.M.; Tantawi, M.; Shedeed, H.A.; Tolba, M.F. Heartbeat Classification Using 1D Convolutional Neural Networks; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 502–511. [Google Scholar]
- Falhi, H.M.; Hussain, K.K. Design an Intelligent Real Time ECG Monitoring System Using Convolution Neural Network. Revue d’Intell. Artif. 2023, 37, 323. [Google Scholar] [CrossRef]
- Ardhapurkar, S.; Manthalkar, R.; Gajre, S. Electrocardiogram compression by linear prediction and wavelet sub-band coding techniques. In Proceedings of the 2011 Computing in Cardiology, Hangzhou, China, 18–21 September 2011; pp. 141–144. [Google Scholar]
- Bazzi, A.; Slock, D.T.M.; Meilhac, L. A Newton-type Forward Backward Greedy method for multi-snapshot compressed sensing. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1178–1182. [Google Scholar] [CrossRef]
- Hassan, A.M.A.; Mohsen, S. Compression of electrocardiogram signals using compressive sensing technique based on curvelet transform toward medical applications. Multimed. Tools Appl. 2024. [Google Scholar] [CrossRef]
- Schirato, S.R.; El-Dash, I.; El-Dash, V.; Natali, J.E.; Starzynski, P.N.; Chaui-Berlinck, J.G. Heart rate variability changes as an indicator of decompression-related physiological stress. Undersea Hyperb. Med. 2018, 45, 173–182. [Google Scholar] [CrossRef]
- Natali, J.E.S.; Starzynski, P.N.; Chaui-Berlinck, J.G. Oscillatory patterns in heart rate variability and complexity: A meta-analysis. Biomed. Signal Process. Control 2017, 33, 66–71. [Google Scholar] [CrossRef]
- Santos, M.; Fonseca, J.; Barros, A. New method to heart instantaneous frequency estimation. In Proceedings of the 2004 14th IEEE Signal Processing Society Workshop Machine Learning for Signal Processing, Sao Luis, Brazil, 29 September–1 October 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 473–480. [Google Scholar] [CrossRef]
- Silva, A.F.; Carmo, J.P.; Mendes, P.M.; Correia, J.H. Simultaneous cardiac and respiratory frequency measurement based on a single fiber Bragg grating sensor. Meas. Sci. Technol. 2011, 22, 075801. [Google Scholar] [CrossRef]
- Damla, O.; Altug, C.; Pinar, K.K.; Alper, K.; Dilek, I.G.; Kadriye, A. Heart rate variability analysis in patients with multiple sclerosis. Mult. Scler. Relat. Disord. 2018, 24, 64–68. [Google Scholar] [CrossRef] [PubMed]
- Badr, A.; Badawi, A.; Rashwan, A.; Elgazzar, K. XBeats: A Real-Time Electrocardiogram Monitoring and Analysis System. Signals 2022, 3, 189–208. [Google Scholar] [CrossRef]
- Yen, H.T.; Kurosawa, M.; Kirimoto, T.; Hakozaki, Y.; Matsui, T.; Sun, G. Non-Contact Estimation of Cardiac Inter-Beat Interval and Heart Rate Variability Using Time-Frequency Domain Analysis for CW Radar. IEEE J. Electromagn. Microwaves Med. Biol. 2023, 7, 457–467. [Google Scholar] [CrossRef]
- Mason, H.T.; Martinez-Cedillo, A.P.; Vuong, Q.C.; Garcia-de Soria, M.C.; Smith, S.; Geangu, E.; Knight, M.I. A Complete Pipeline for Heart Rate Extraction from Infant ECGs. Signals 2024, 5, 118–146. [Google Scholar] [CrossRef]
- Thakur, S.; Chao, P.C.P.; Tsai, C.H. Precision Heart Rate Estimation Using a PPG Sensor Patch Equipped with New Algorithms of Pre-Quality Checking and Hankel Decomposition. Sensors 2023, 23, 6180. [Google Scholar] [CrossRef]
- Zakynthinaki, M.S.; Kapetanakis, T.N.; Lampou, A.; Ioannidou, M.P.; Vardiambasis, I.O. A Neural Network Model for Estimating the Heart Rate Response to Constant Intensity Exercises. Signals 2021, 2, 852–862. [Google Scholar] [CrossRef]
- Lima, J.S.; Silva, F.G.S.; Araujo, J.M. An LPC-Based Approach to Heart Rhythm Estimation. In XXVII Brazilian Congress on Biomedical Engineering; Bastos-Filho, T.F., de Oliveira Caldeira, E.M., Frizera-Neto, A., Eds.; Springer: Cham, Switzerland, 2022; pp. 1795–1799. [Google Scholar] [CrossRef]
- Becker, D.E. Fundamentals of Electrocardiography Interpretation. Anesth. Prog. 2006, 53, 53–64. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, X.; Tang, Z.; Ahn, A.C. Sparse representation-based ECG signal enhancement and QRS detection. Physiol. Meas. 2016, 37, 2093–2110. [Google Scholar] [CrossRef]
- Marvi, H.; Esmaileyan, Z.; Harimi, A. Estimation of LPC Coefficients using Evolutionary Algorithms. J. AI Data Min. 2013, 1, 111–118. [Google Scholar]
- Beraldo, O.A. Processamento Digital do Sinal de Eletrocardiograma para Aplicação em Experimentos de Fisiologia Cardíaca. Ph.D. Thesis, Universidade de São Paulo, São Carlos, Brazil, 1997. [Google Scholar]
- Araujo, J.M.; Embirucu, M.; Fontes, C.H.O.; de Andrade Lima, L.; Kalid, R. Melhoria da performance em reconciliação de dados pela eliminação de outliers com pré-filtro por predição linear. In Proceedings of the 8th International Seminar on Electrical Metrology, João Pessoa, Brazil, 17–19 June 2009; pp. 1–5. [Google Scholar]
- Serhani, M.A.; T. El Kassabi, H.; Ismail, H.; Nujum Navaz, A. ECG monitoring systems: Review, architecture, processes, and key challenges. Sensors 2020, 20, 1796. [Google Scholar] [CrossRef]
- Bansal, A.; Joshi, R. Portable out-of-hospital electrocardiography: A review of current technologies. J. Arrhythmia 2018, 34, 129–138. [Google Scholar]
- Ardeti, V.A.; Kolluru, V.R.; Varghese, G.T.; Patjoshi, R.K. An Overview on State-of-the-Art Electrocardiogram Signal Processing Methods: Traditional to AI-Based Approaches. Expert Syst. Appl. 2023, 217, 119561. [Google Scholar]
- Anbukarasu, P.; Nanisetty, S.; Tata, G.; Ray, N. Tiny-HR: Towards an interpretable machine learning pipeline for heart rate estimation on edge devices. arXiv 2022, arXiv:2208.07981. [Google Scholar]
- Asutkar, S.; Chalke, C.; Shivgan, K.; Tallur, S. TinyML-enabled edge implementation of transfer learning framework for domain generalization in machine fault diagnosis. Expert Syst. Appl. 2023, 213, 119016. [Google Scholar]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar]
- Plawiak, P. ECG Signals (1000 Fragments); Version 3; Mendeley Data; Mendeley: London, UK, 2017. [Google Scholar] [CrossRef]
- Aniyan, A. ECG Beat Calculation; MATLAB Central File Exchange. 2025. Available online: https://www.mathworks.com/matlabcentral/fileexchange/24628-ecg-beat-calculation (accessed on 18 March 2025).
- Krupa, A.J.D.; Dhanalakshmi, S.; Sanjana, N.; Manivannan, N.; Kumar, R.; Tripathy, S. Fetal heart rate estimation using fractional Fourier transform and wavelet analysis. Biocybern. Biomed. Eng. 2021, 41, 1533–1547. [Google Scholar]
- Lo, C.I.; Chang, S.S.; Tsai, J.P.; Kuo, J.Y.; Chen, Y.J.; Huang, M.Y.; Lee, C.H.; Sung, K.T.; Hung, C.L.; Hou, C.J.-Y.; et al. Evaluation of the accuracy of ECG captured by CardioChip through comparison of lead I recording to a standard 12-lead ECG recording device. Acta Cardiol. Sin. 2018, 34, 144–151. [Google Scholar]
- Parak, J.; Salonen, M.; Myllymäki, T.; Korhonen, I. Comparison of heart rate monitoring accuracy between chest strap and vest during physical training and implications on training decisions. Sensors 2021, 21, 8411. [Google Scholar] [CrossRef]













| Heart Rate (bpm) | Performance in One Hundred Estimations | Mean (bpm) | Std. Deviation (bpm) | Accuracy |
|---|---|---|---|---|
| 30 | 30 bpm (66 samples) 29 bpm (34 samples) | 29.66 | 0.48 | |
| 60 | 60 bpm (87 samples) 59 bpm (13 samples) | 59.87 | 0.34 | |
| 120 | 120 bpm (94 samples) 119 bpm (6 samples) | 119.94 | 0.24 | |
| 180 | 180 bpm (87 samples) 178 bpm (13 samples) | 179.27 | 0.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souza, V.O.T.; Silva, F.G.S.; Araújo, J.M.; Lima, J.S. Method and System for Heart Rate Estimation Using Linear Prediction Filtering. Signals 2025, 6, 15. https://doi.org/10.3390/signals6020015
Souza VOT, Silva FGS, Araújo JM, Lima JS. Method and System for Heart Rate Estimation Using Linear Prediction Filtering. Signals. 2025; 6(2):15. https://doi.org/10.3390/signals6020015
Chicago/Turabian StyleSouza, Vitor O. T., Fabrício G. S. Silva, José M. Araújo, and Jaimilton S. Lima. 2025. "Method and System for Heart Rate Estimation Using Linear Prediction Filtering" Signals 6, no. 2: 15. https://doi.org/10.3390/signals6020015
APA StyleSouza, V. O. T., Silva, F. G. S., Araújo, J. M., & Lima, J. S. (2025). Method and System for Heart Rate Estimation Using Linear Prediction Filtering. Signals, 6(2), 15. https://doi.org/10.3390/signals6020015






