Acoustic Rocket Signatures Collected by Smartphones
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Data Alignment
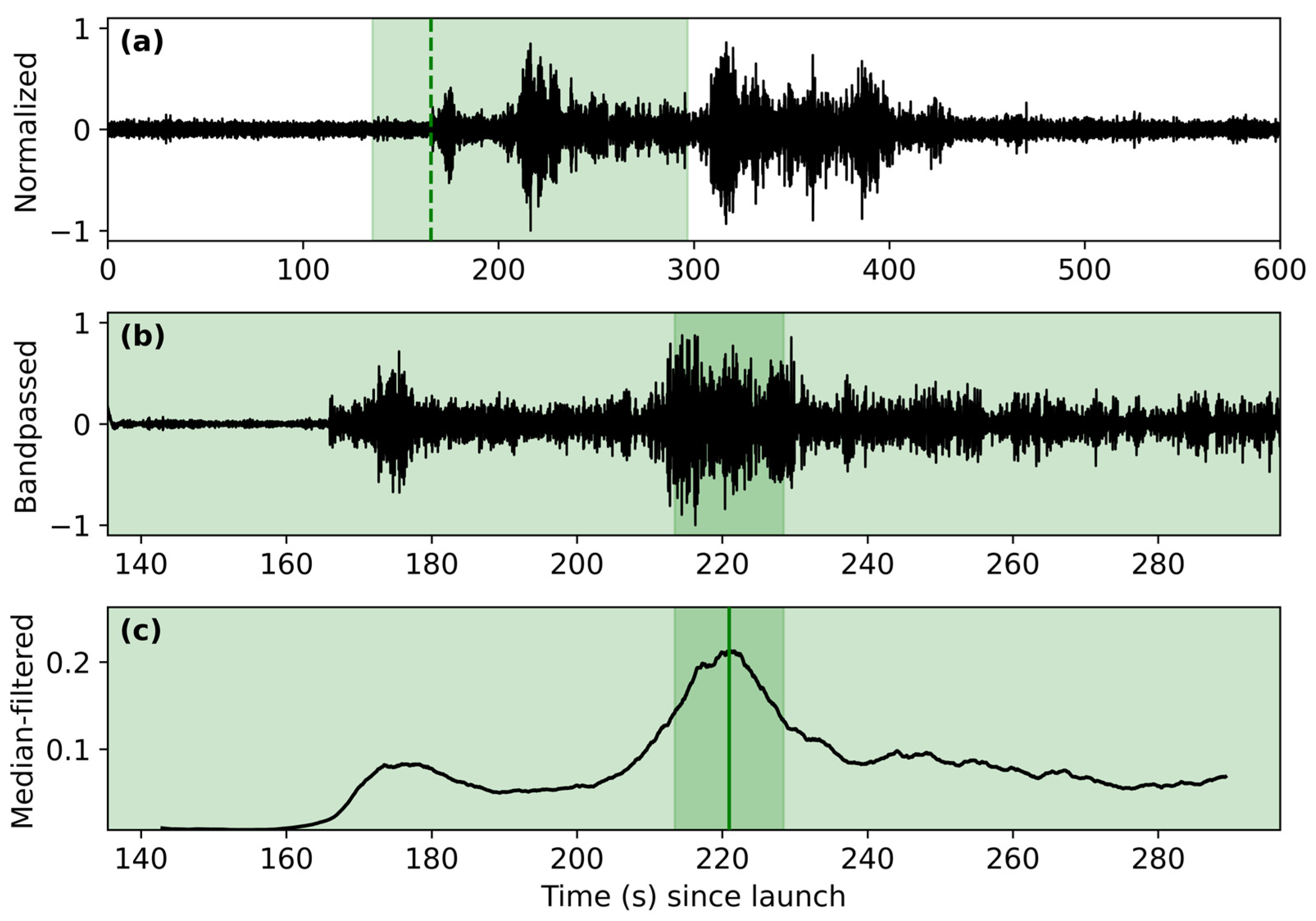
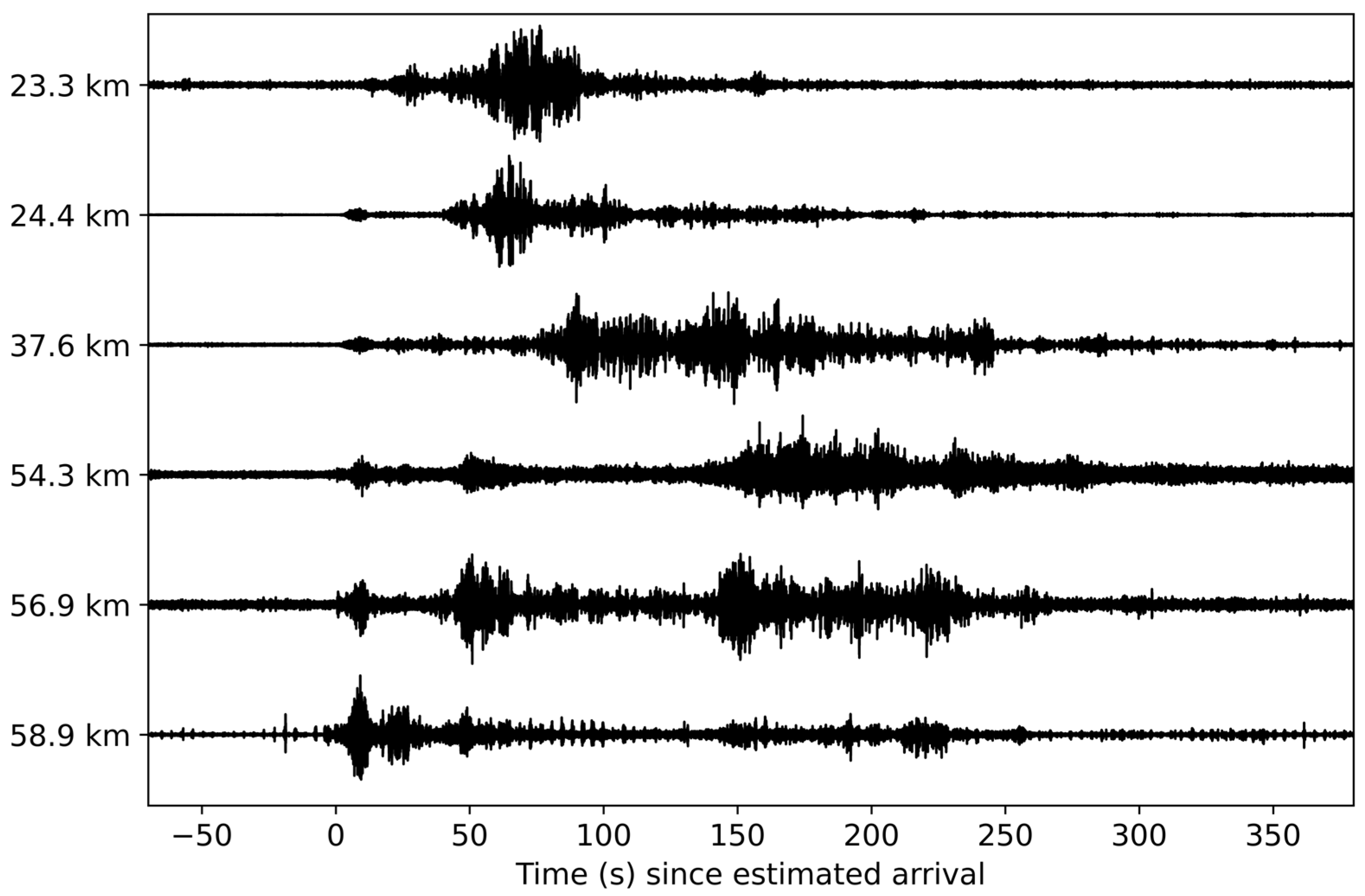
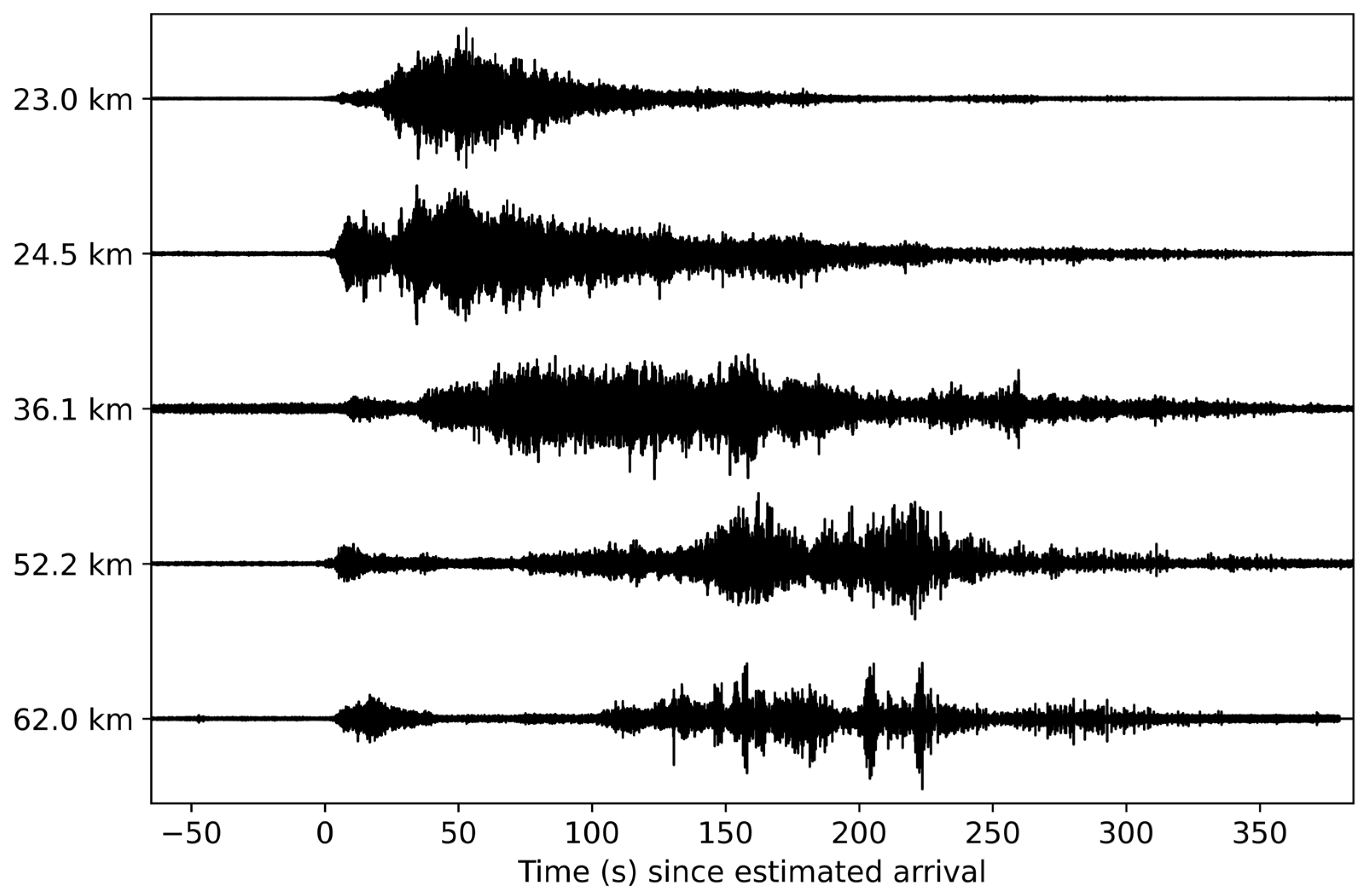
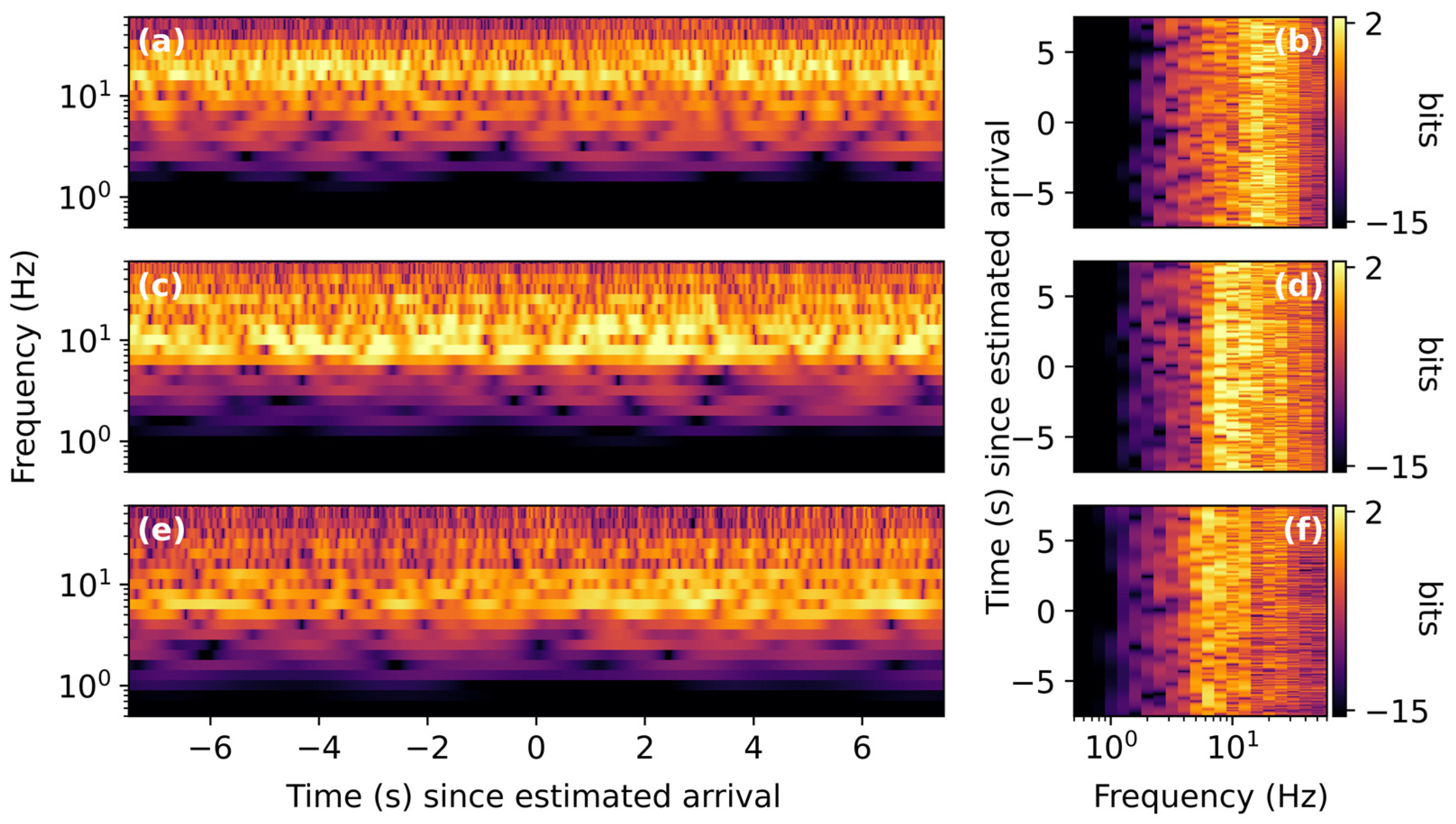
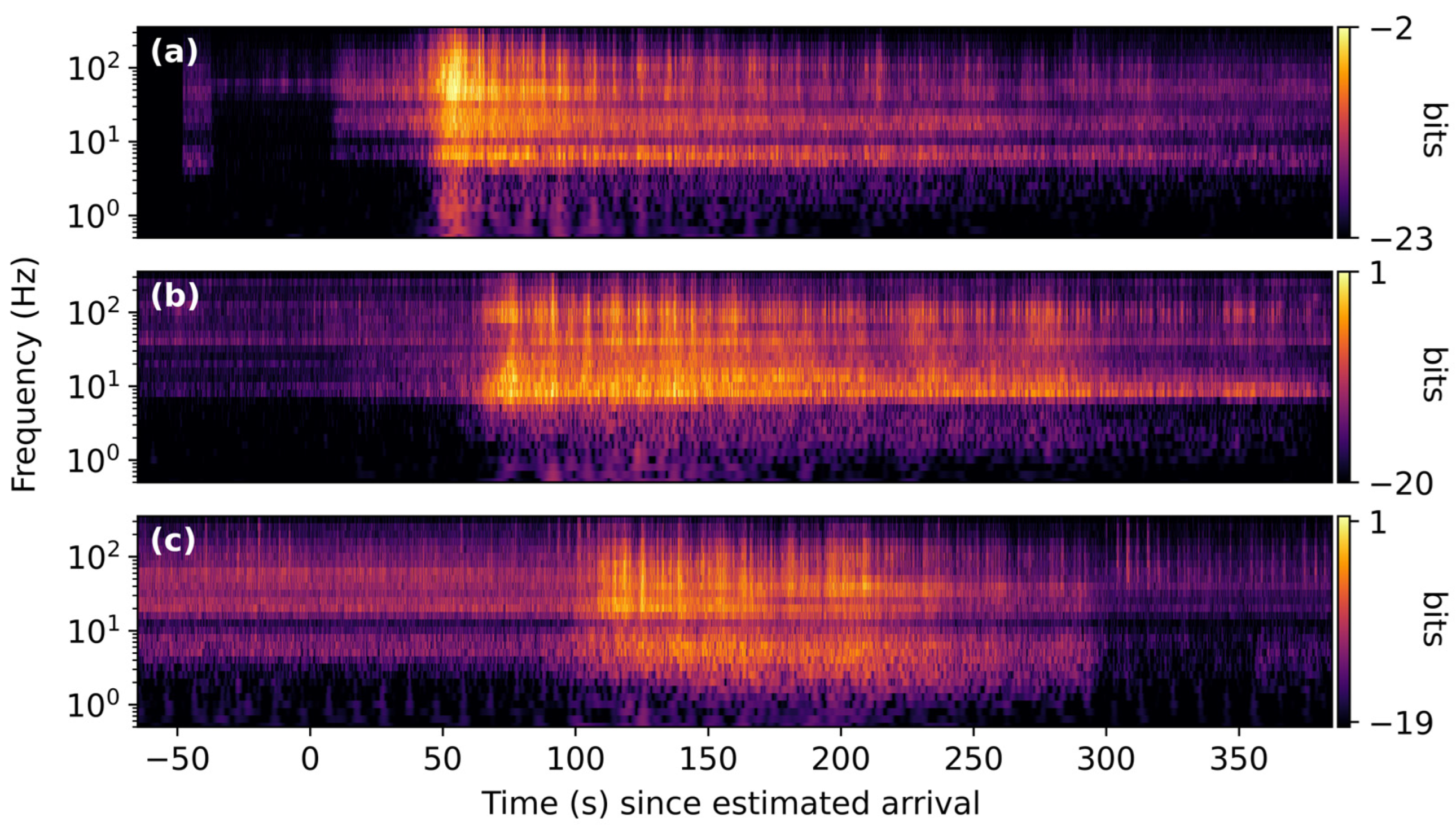
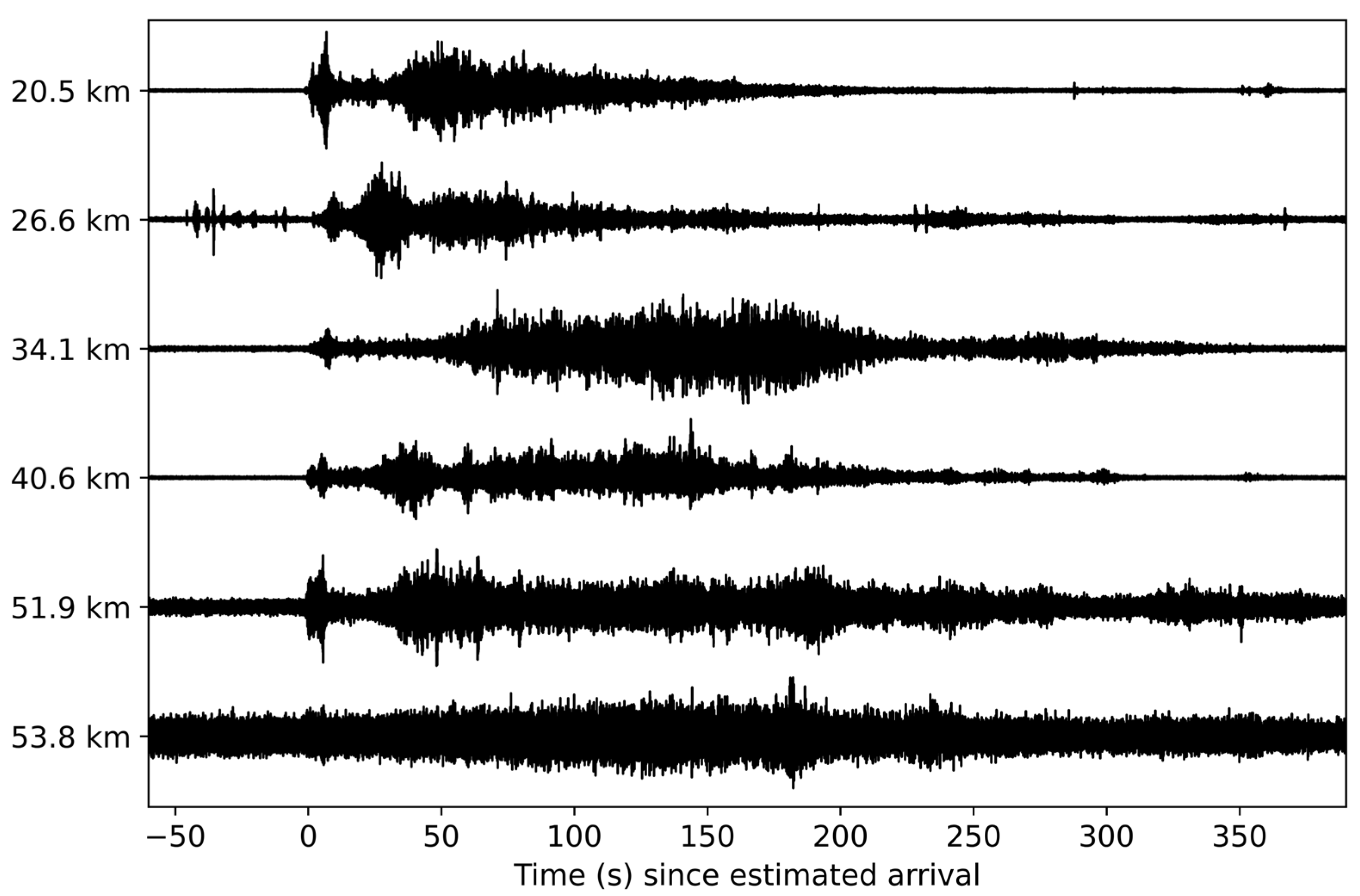
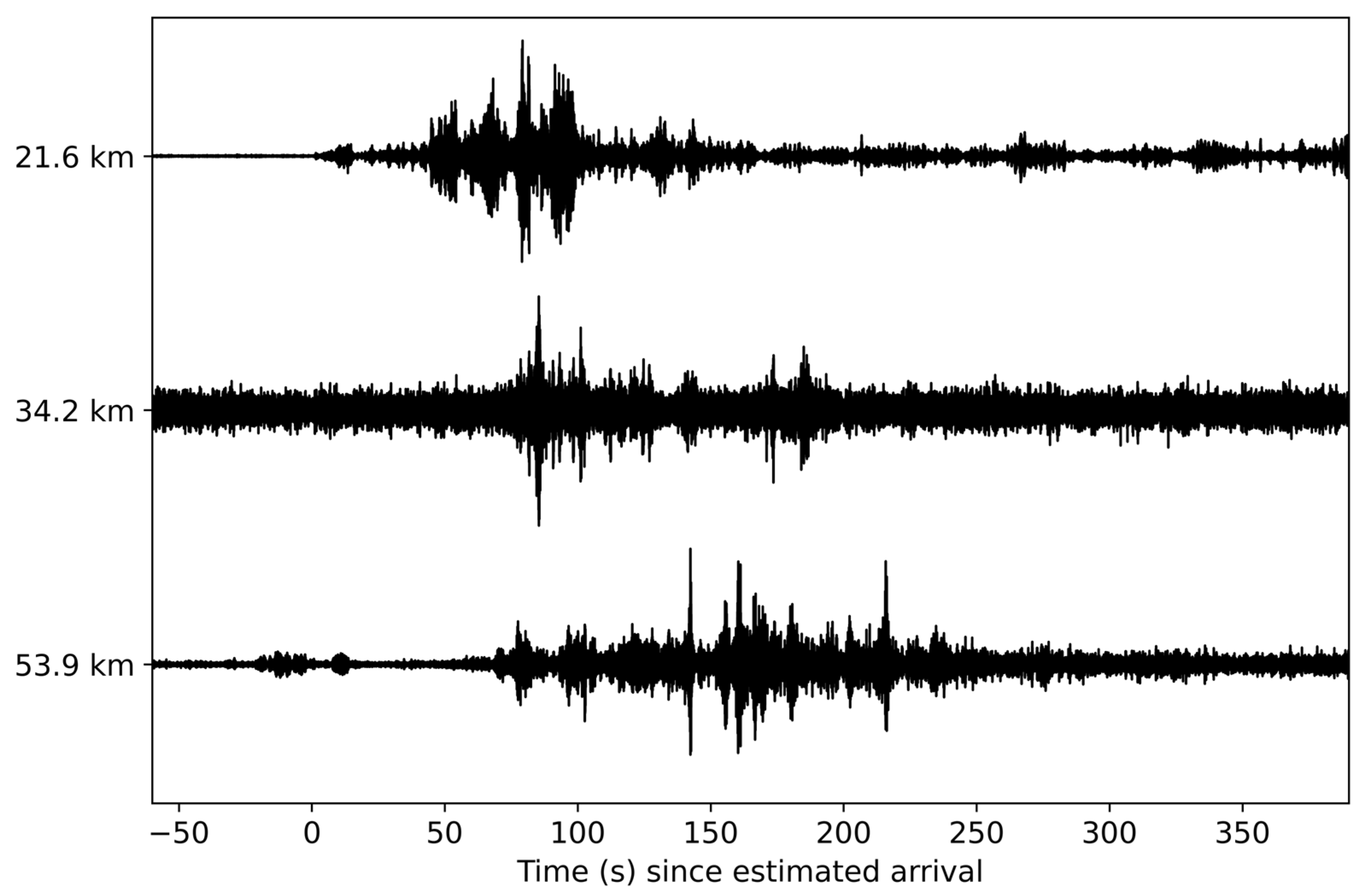
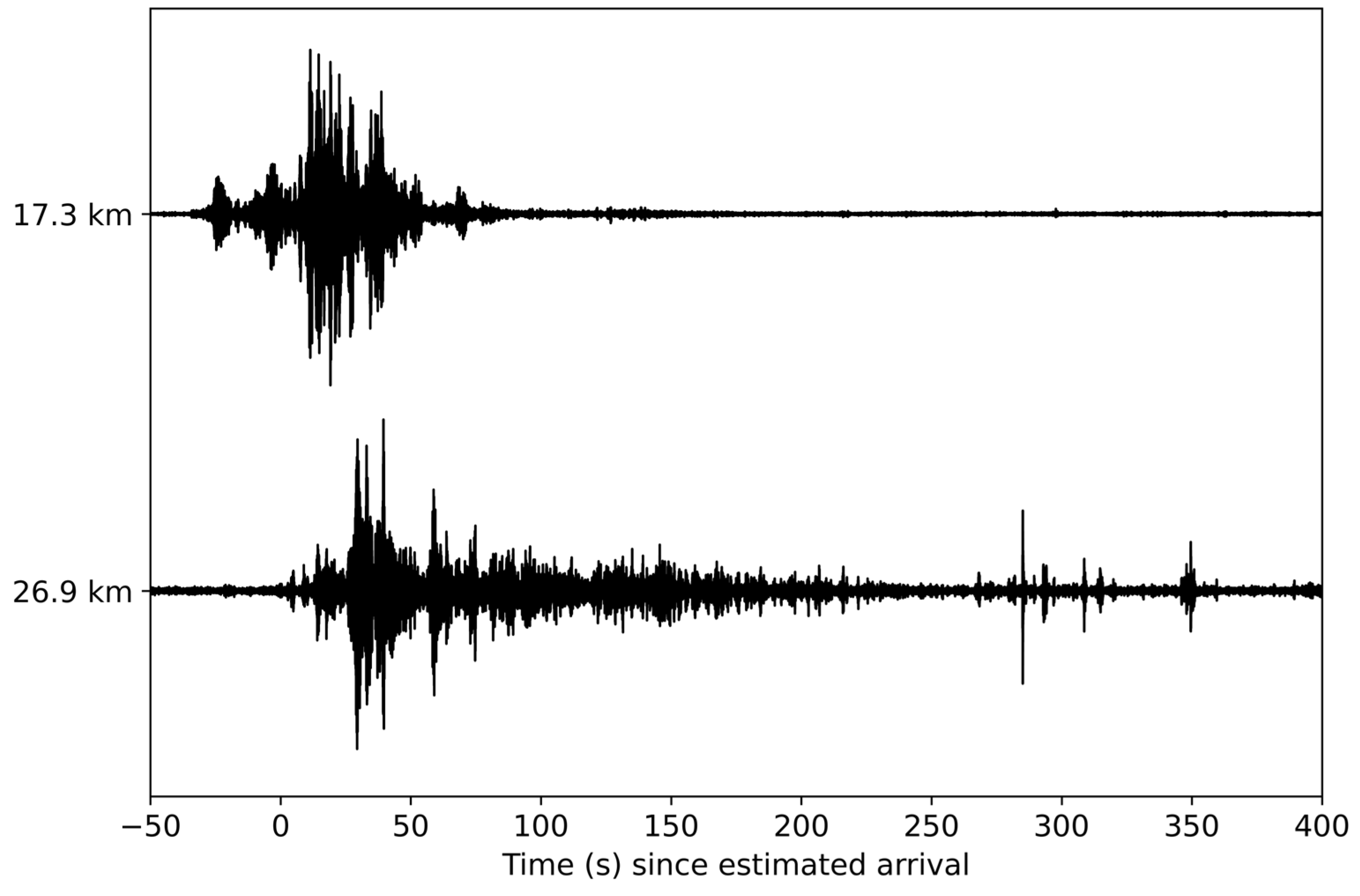
3. Results
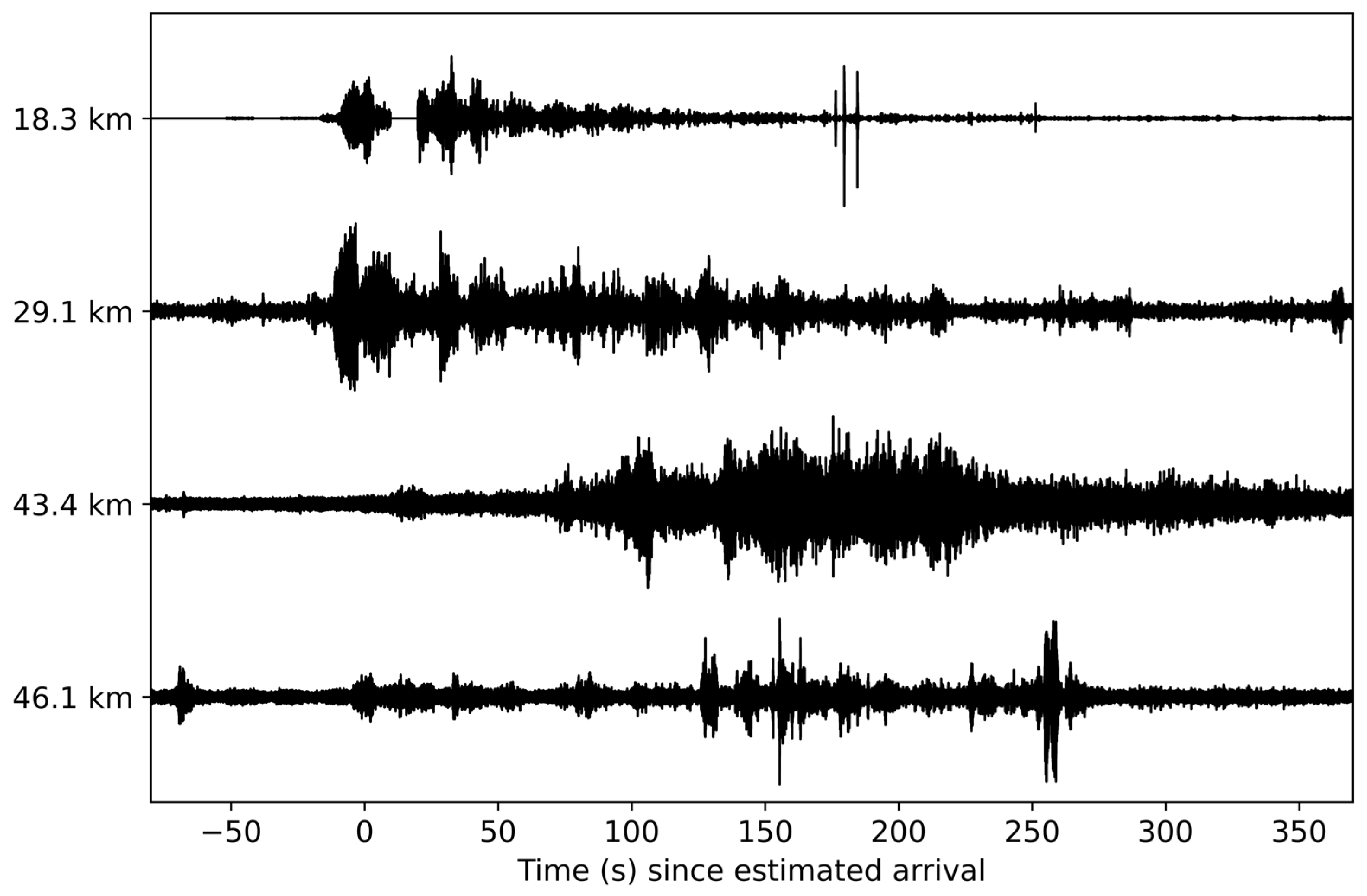
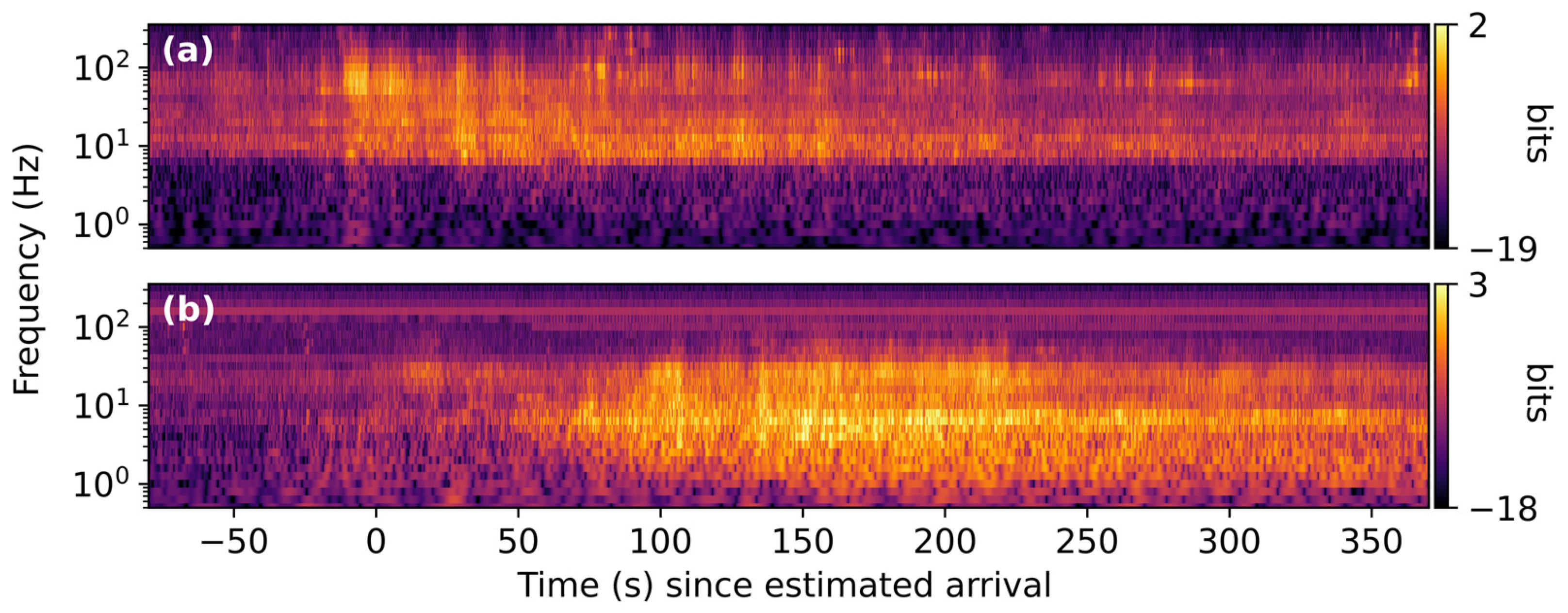
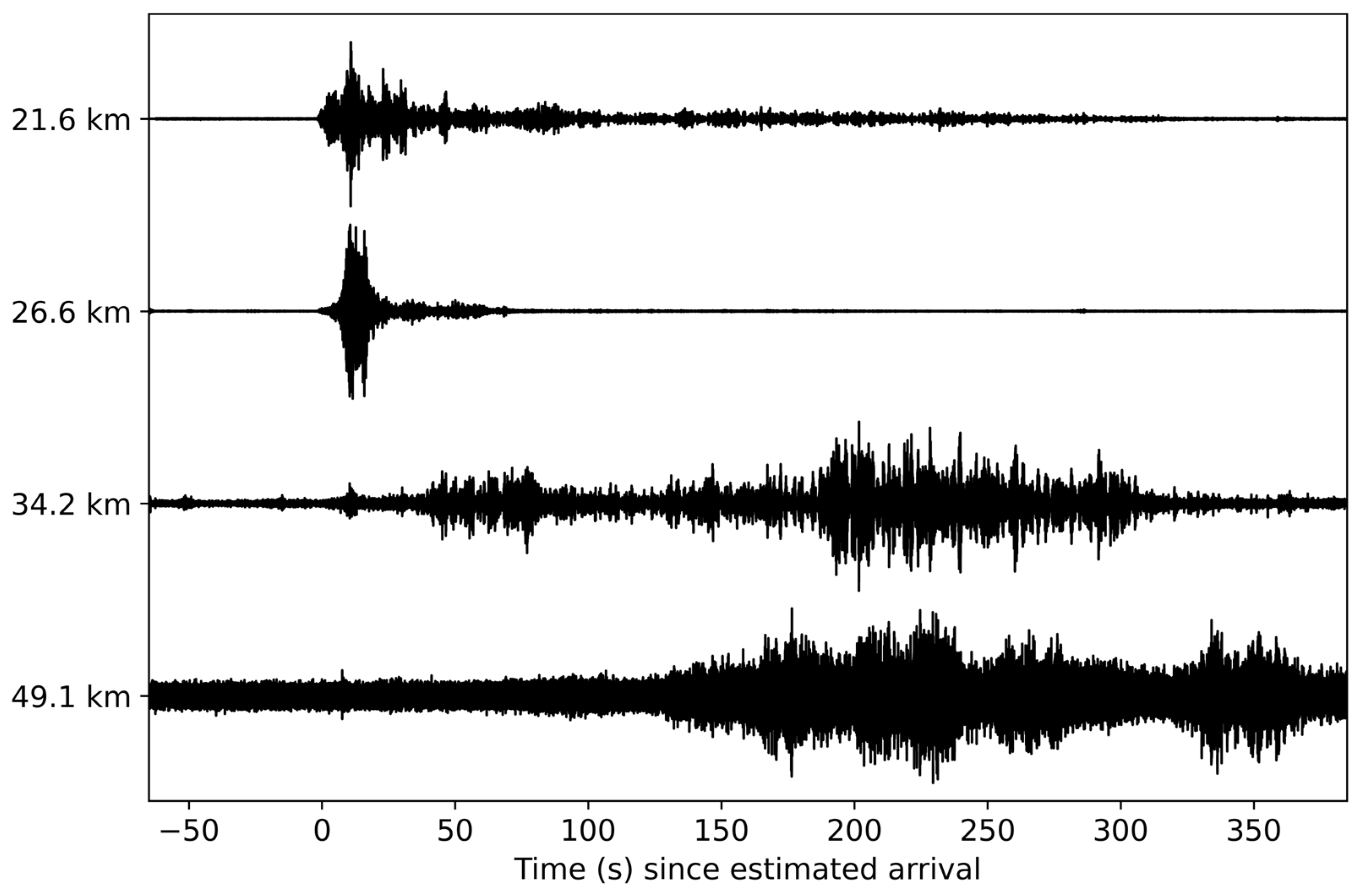
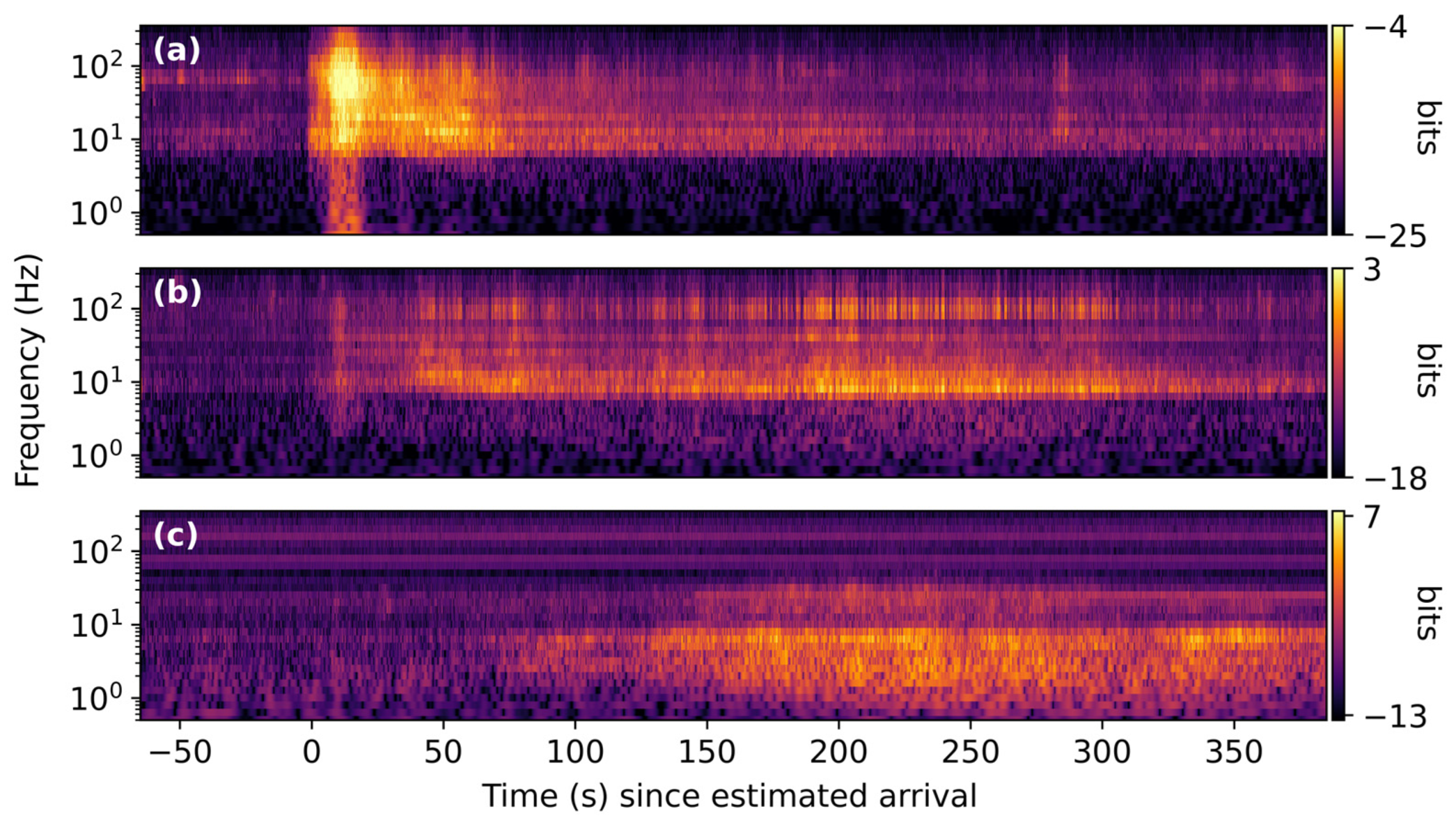
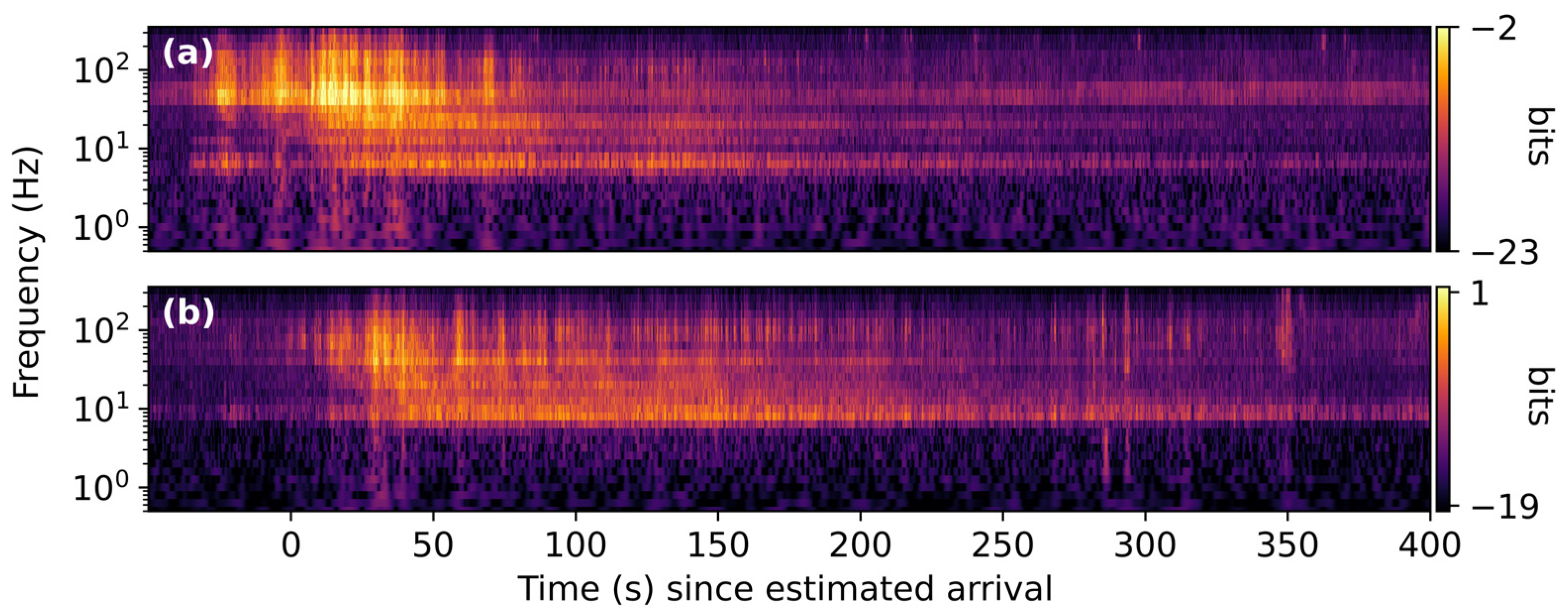
3.1. Space Launch System B1
3.2. Falcon Heavy
3.3. Delta IV Heavy
3.4. Vulcan Centaur
3.5. Falcon 9
3.6. Atlas V
3.7. Small-Lift Launch Vehicles
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schwardt, M.; Pilger, C.; Gaebler, P.; Hupe, P.; Ceranna, L. Natural and Anthropogenic Sources of Seismic, Hydroacoustic, and Infrasonic Waves: Waveforms and Spectral Characteristics (and Their Applicability for Sensor Calibration). Surv. Geophys. 2022, 43, 1265–1361. [Google Scholar] [CrossRef]
- Lamb, O.D.; Lees, J.M.; Bowman, D.C. Detecting Lightning Infrasound Using a High-Altitude Balloon. Geophys. Res. Lett. 2018, 45, 7176–7183. [Google Scholar] [CrossRef]
- Pilger, C.; Gaebler, P.; Hupe, P.; Kalia, A.C.; Schneider, F.M.; Steinberg, A.; Sudhaus, H.; Ceranna, L. Yield Estimation of the 2020 Beirut Explosion Using Open Access Waveform and Remote Sensing Data. Sci. Rep. 2021, 11, 14144. [Google Scholar] [CrossRef] [PubMed]
- Pilger, C.; Hupe, P.; Gaebler, P.; Ceranna, L. 1001 Rocket Launches for Space Missions and Their Infrasonic Signature. Geophys. Res. Lett. 2021, 48, e2020GL092262. [Google Scholar] [CrossRef]
- Hupe, P.; Ceranna, L.; Le Pichon, A.; Matoza, R.S.; Mialle, P. International Monitoring System Infrasound Data Products for Atmospheric Studies and Civilian Applications. Earth Syst. Sci. Data 2022, 14, 4201–4230. [Google Scholar] [CrossRef]
- Donn, W.L.; Posmentier, E.; Fehr, U.; Balachandran, N.K. Infrasound at Long Range from Saturn V, 1967. Science 1968, 162, 1116–1120. [Google Scholar] [CrossRef] [PubMed]
- Kaschak, G.; Donn, W.L.; Fehr, U. Long-Range Infrasound from Rockets. J. Acoust. Soc. Am. 1970, 48, 12–20. [Google Scholar] [CrossRef]
- Evers, L.G.; Assink, J.D.; Smets, P.S.M. Infrasound from the 2009 and 2017 DPRK Rocket Launches. Geophys. J. Int. 2018, 213, 1785–1791. [Google Scholar] [CrossRef]
- Pilger, C.; Hupe, P. The Infrasonic Signature of Three Exceptional Rocket Launches. Proc. Meet. Acoust. 2024, 52, 040006. [Google Scholar] [CrossRef]
- Cotten, D.; Donn, W.L. Sound from Apollo Rockets in Space. Science 1971, 12, 565–567. [Google Scholar] [CrossRef] [PubMed]
- Cotten, D.E.; Donn, W.L.; Oppenheim, A. On the Generation and Propagation of Shock Waves from Apollo Rockets at Orbital Altitudes. Geophys. J. R. Astron. Soc. 1971, 26, 149–159. [Google Scholar] [CrossRef]
- Blom, P.; Marcillo, O.; Arrowsmith, S. Analysis and Modeling of Infrasound from a Four-Stage Rocket Launch. J. Acoust. Soc. Am. 2016, 139, 3134–3138. [Google Scholar] [CrossRef]
- Tenney, S.M.; Noble, J.M.; Whitaker, R.W.; ReVelle, D.O. Acoustic/Infrasonic Rocket Engine Signatures. In Unattended Ground Sensor Technologies and Applications V, Proceedings of the AeroSense 2003, Orlando, Florida, USA, 18 September 2003; Carapezza, E.M., Ed.; SPIE: Bellingham, WA, USA, 2003; Volume 5090, pp. 30–41. [Google Scholar]
- Balachandran, N.K.; Donn, W.L. Characteristics of Infrasonic Signals from Rockets. Geophys. J. R. Astron. Soc. 1971, 26, 135–148. [Google Scholar] [CrossRef]
- Mclaughlin, K.L.; Brown, D.J.; Australia, G. Infrasound Detection of Rocket Launches. In Proceedings of the 22nd Annual DoD/DOE Seismic Research Symposium, New Orleans, LA, USA, 15 September 2000. [Google Scholar]
- Olson, J. Infrasound Rocket Signatures. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 11–14 September 2012; pp. 638–645. [Google Scholar]
- Smith, K.; Solomon, M.; Bryan, K.J.; Smith, A.O.; Peter, A.M. Near-Field Infrasound Classification of Rocket Launch Signatures. In Chemical, Biological, Radiological, Nuclear, and Explosives (CBRNE) Sensing XIX, Proceedings of the SPIE Defense + Security, Orlando, FL, USA, 23 May 2018; Guicheteau, J.A., Fountain, A.W., Howle, C.R., Eds.; SPIE: Bellingham, WA, USA, 2018; Volume 10629, p. 106291F. [Google Scholar]
- Popenhagen, S.K. Aggregated Smartphone Timeseries of Rocket-Generated Acoustics (ASTRA). Available online: https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/ZKIS2K (accessed on 21 November 2024).
- Takazawa, S.K.; Popenhagen, S.K.; Ocampo Giraldo, L.A.; Hix, J.D.; Thompson, S.J.; Chichester, D.L.; Zeiler, C.P.; Garcés, M.A. Explosion Detection Using Smartphones: Ensemble Learning with the Smartphone High-Explosive Audio Recordings Dataset and the ESC-50 Dataset. Sensors 2024, 24, 6688. [Google Scholar] [CrossRef] [PubMed]
- Kong, Q.; Martin-Short, R.; Allen, R.M. Toward Global Earthquake Early Warning with the Myshake Smartphone Seismic Network, Part 1: Simulation Platform and Detection Algorithm. Seismol. Res. Lett. 2020, 91, 2206–2217. [Google Scholar] [CrossRef]
- Slad, G.; Merchant, B.J. Evaluation of Low Cost Infrasound Sensor Packages; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA; Livermore, CA, USA, 2021.
- Asmar, K.; Garces, M.; Williams, B. A Method for Estimating the Amplitude Response of Smartphone Built-in Microphone Sensors below 4 KHz. J. Acoust. Soc. Am. 2019, 146, 172–178. [Google Scholar] [CrossRef] [PubMed]
- Takazawa, S.K.; Popenhagen, S.K.; Ocampo Giraldo, L.A.; Cardenas, E.S.; Hix, J.D.; Thompson, S.J.; Chichester, D.L.; Garcés, M.A. A Comparison of Smartphone and Infrasound Microphone Data from a Fuel Air Explosive and a High Explosive. J. Acoust. Soc. Am. 2024, 156, 1509–1523. [Google Scholar] [CrossRef]
- Brown, R.; Evans, L. Acoustics and the Smartphone. In Proceedings of the Acoustics, Gold Coast, Australia, 2 November 2011; Volume 106. [Google Scholar]
- Popenhagen, S.K.; Bowman, D.C.; Zeiler, C.; Garcés, M.A. Acoustic Waves From a Distant Explosion Recorded on a Continuously Ascending Balloon in the Middle Stratosphere. Geophys. Res. Lett. 2023, 50, e2023GL104031. [Google Scholar] [CrossRef]
- RedVox SDK. Available online: https://pypi.org/project/redvox/ (accessed on 21 November 2024).
- Garcés, M.A.; Bowman, D.; Zeiler, C.; Christe, A.; Yoshiyama, T.; Williams, B.; Colet, M.; Takazawa, S.; Popenhagen, S. Skyfall: Signal Fusion from a Smartphone Falling from the Stratosphere. Signals 2022, 3, 209–234. [Google Scholar] [CrossRef]
- Python. Available online: https://docs.python.org/release/3.9.1/ (accessed on 21 November 2024).
- RedVox-Pandas Framework. Available online: https://pypi.org/project/redvox-pandas/ (accessed on 21 November 2024).
- Quantized Information Entropy, Nth Octave. Available online: https://pypi.org/project/quantum-inferno/ (accessed on 21 November 2024).
- The Pandas Development Team Pandas-Dev/Pandas: Pandas. Available online: https://zenodo.org/records/13819579 (accessed on 21 November 2024).
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; van der Walt, S., Millman, J., Eds.; SciPy: Austin, TX, USA, 2010; pp. 56–61. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service (2023): ERA5 Hourly Data on Single Levels from 1940 to Present. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels (accessed on 26 November 2024).









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popenhagen, S.K.; Garcés, M.A. Acoustic Rocket Signatures Collected by Smartphones. Signals 2025, 6, 5. https://doi.org/10.3390/signals6010005
Popenhagen SK, Garcés MA. Acoustic Rocket Signatures Collected by Smartphones. Signals. 2025; 6(1):5. https://doi.org/10.3390/signals6010005
Chicago/Turabian StylePopenhagen, Sarah K., and Milton A. Garcés. 2025. "Acoustic Rocket Signatures Collected by Smartphones" Signals 6, no. 1: 5. https://doi.org/10.3390/signals6010005
APA StylePopenhagen, S. K., & Garcés, M. A. (2025). Acoustic Rocket Signatures Collected by Smartphones. Signals, 6(1), 5. https://doi.org/10.3390/signals6010005





