1. Introduction
A linear time-invariant (LTI) system is sufficiently described by the unit impulse response function (IRF). Given an LTI system with an unknown IRF, we can use any input function to obtain the IRF. A conceptually simple way to determine a system’s IRF is to use a unit impulse and unit step function as input. However, as a unit impulse has an infinitely short duration and a unit step function has an infinitely long duration, they are not always practical to produce in reality. A more practical and convenient input test function is the rectangular function. For a discrete system, this corresponds to a sequence of uniform pulses. For example, let us have the input to a discrete LTI system as
and the corresponding output is
. It can be seen that the IRF is
= [1, 0,
1, −1, …], which is an infinite sequence with the repeating pattern underlined. For an LTI system, the standard method to find the system’s IRF is to inverse Fourier transform the frequency transfer function
, where
and
are the discrete Fourier transform (DFT) of the input and output sequences, respectively. In this example, however, inverse discrete Fourier Transform (IDFT) cannot be applied since a singularity (pole) exists. In this article, we are largely concerned only with the singular frequency transfer function (SFTF) of marginally stable systems. In general, deconvolution via IDFT is not doable for SFTF and part of the information is considered lost [
1].
To be more general, let the input sequence
have
consecutive unit impulses, i.e.,
. The corresponding output of an LTI system is a sequence of real values,
. The last non-zero value in
occurs at index
, i.e.,
and
for
. In this study, we are confined to finite
and
. To find the IRF,
, we can carry out a time-domain deconvolution via polynomial division or a recursive sum (e.g., [
2,
3]). Alternatively, the IRF for the above defined
can be found through the convolution sum
as
Since
for
,
].
becomes periodic with a period of
starting at
or sooner, where
max is the maximum operator. The number of independent points in
is
.
can alternatively be expressed as
where
, and
is the unit step function. In general, such an LTI system has an infinite IRF.
Fundamental to LTI systems is that they are sufficiently described by either
or its Fourier transform, the frequency transfer function
(e.g., [
3,
4]). If
and
are indeed equivalent in characterizing an LTI system, a logical conclusion is that we can
always obtain one from the other. The fact that we cannot find
from a singular
via IDFT may not be because
has incomplete information but because we have not found the right way to carry it out. Otherwise, we have to admit
and
are not always equivalent. The problem appears to be simple and yet fundamental to LTI systems. Although LTI theory is very mature, obtaining IRF from an SFTF has not received much attention. Despite extensive searches in the Web of Science database and the open internet, the author cannot find any references on the direct conversion from SFTF to IRF. There are possibly two reasons for this: (1) we cannot apply DFT or IDFT when there are singularities; (2) alternative ways, such as polynomial division, can be used to obtain
. General discussions on the zeros of the discrete-time system can be found in [
5,
6]. The stability of fractional oscillators is analyzed by Li et al. [
7]. Schluter and Darup [
8] showed that linear dynamic controllers with integer coefficients are usually unstable. Park et al. [
9] discussed uniformly marginally stable zeros of linear sampled data systems and its application to stable inversion-based control. In the following, we demonstrate that we can recover
from
when
, the DFT of the input function, is a
sinc function.
To describe the problem more precisely, let us consider the details of
. To perform the discrete Fourier transform (DFT), we zero-pad
and
to
elements. Let
and
be the DFT of the zero-padded sequence of
and
, respectively. The
-point DFT of
is defined as
In this article, we restrict our input to
. For
, we have
where
and
.
has zeros at
, where
. We denote the set of the zeros of
as
. Denoting
as the
-point DFT of
, i.e.,
,
, the frequency transfer function is thus
The poles, which characterize the stability of a system, are at
ko, which are all on the unit cycle in the corresponding
-transform and
. Such a system is considered to be marginally stable [
10]. IDFT cannot be directly performed on
to obtain
when there are singularities.
If we limit our objective to obtain
from
, we may attempt to avoid poles in
. As we are concerned with discrete operations, we can sample
in such a way that there are no poles. In fact, when
is not divisible by
,
does not necessarily have a singularity. In this first approach, the inverse transform, however, does not yield
, as shown in
Figure 1. In this example,
and
Alternatively, when
is divisible by
, we can assign a large value at
to attempt for an approximation of
. We show an example of this second approach in
Figure 2, where
,
and
. The approach does not work in two aspects. The
computed from the IDFT method yields values proportional
we artificially set and it is not even proportionally correct at the beginning indices. This invalidates the notion that a large enough real value is a reasonable numerical approximation when there is a zero in the denominator.
In the following, we show that when the input function
is a rectangular function and the output
is a finite length sequence,
can indeed be recovered from
and
when
is divisible by
. Before we delve into the proofs, we outline our method of obtaining
from
in
Section 2. The proof of our method is facilitated by three interesting discrete Fourier transform pairs, which are discussed in
Section 3. Each of the three DFT pairs is presented as a lemma.
Section 4 contains the proof of our method and we point out some potential questions to be explored further in
Section 5.
5. Conclusions
The frequency transfer function, of a linear time-invariant system is generally considered to be equivalent to the unit impulse response function . The normal process of obtaining the impulse function from the frequency transfer function via the DFT, however, breaks down when the latter has singularities for discrete systems. This happens when the input time-domain function is a uniform train of pulses and the transfer function contains zeros on the unit cycle. We show that the frequency transfer function contains complete information to determine the IRF in such a case. A broader fundamental question to be answered is whether the IRF can always be determined from a frequency transfer function containing singularities. If the answer is positive, the ensuring question is how to find from with any kind of pole in general.
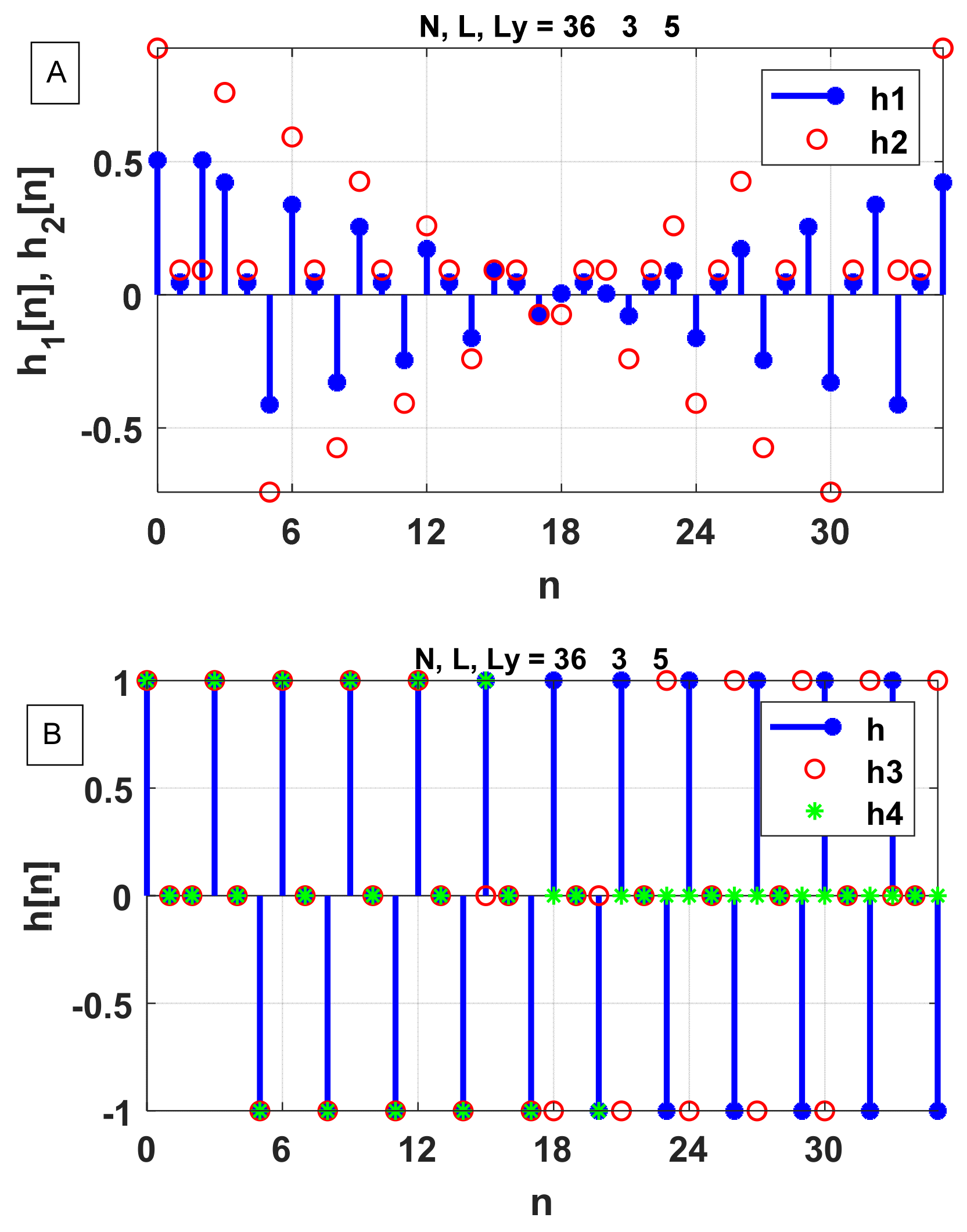
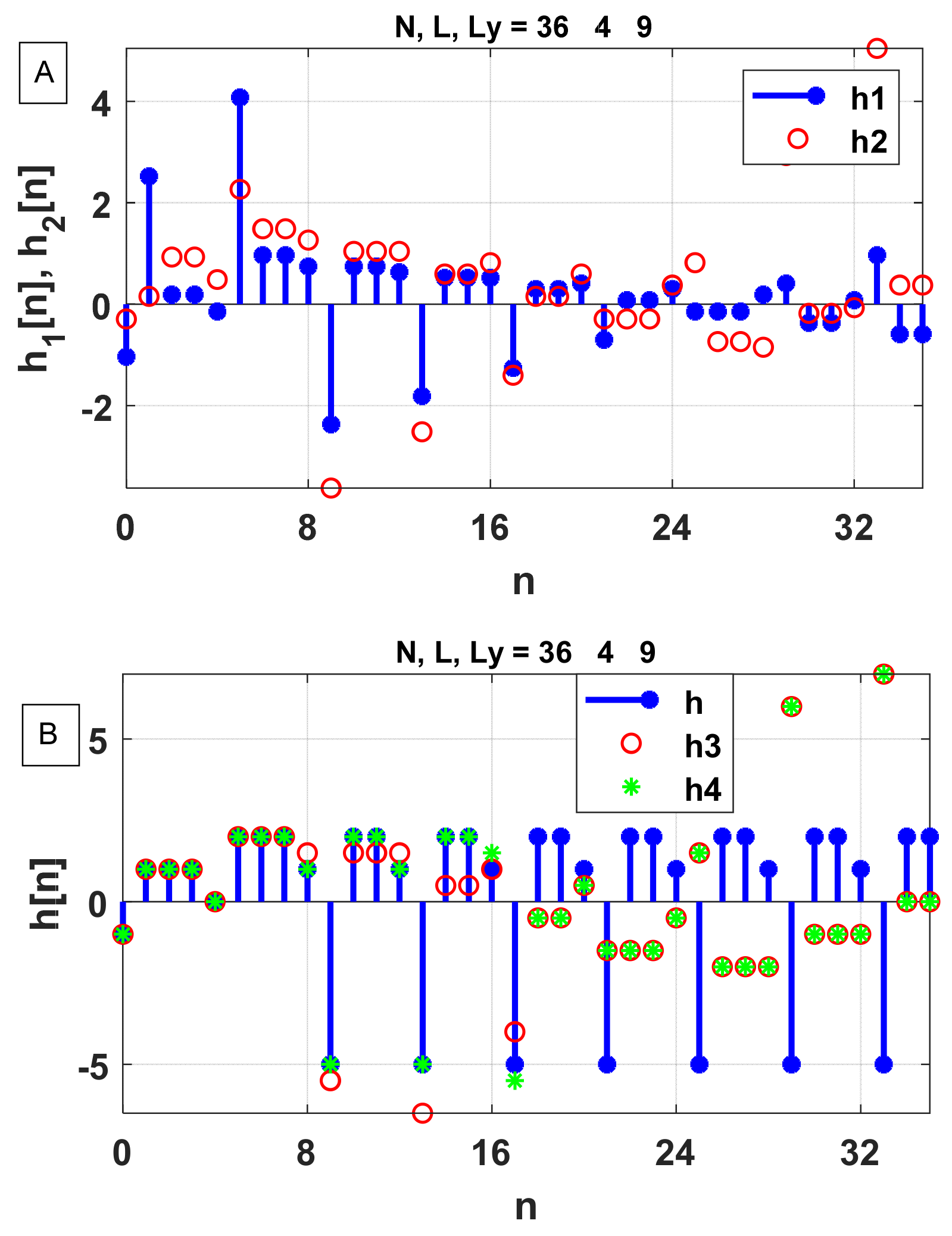
Our method to obtain from involves performing the inverse Fourier transform of the transfer function by excluding the poles to obtain a time-domain function, . We show that a linear combination of and its shifts can yield . It is important to note that the poles in the transfer function discussed here are all on the unit circle in the z-domain. Such systems are marginally stable and is periodic after points. The number of independent points in , , is the larger of or . Our method requires the length of the discrete transfer function, , to be at least to correctly capture the first points in . It is of interest to explore whether it is possible to obtain the first points of using .
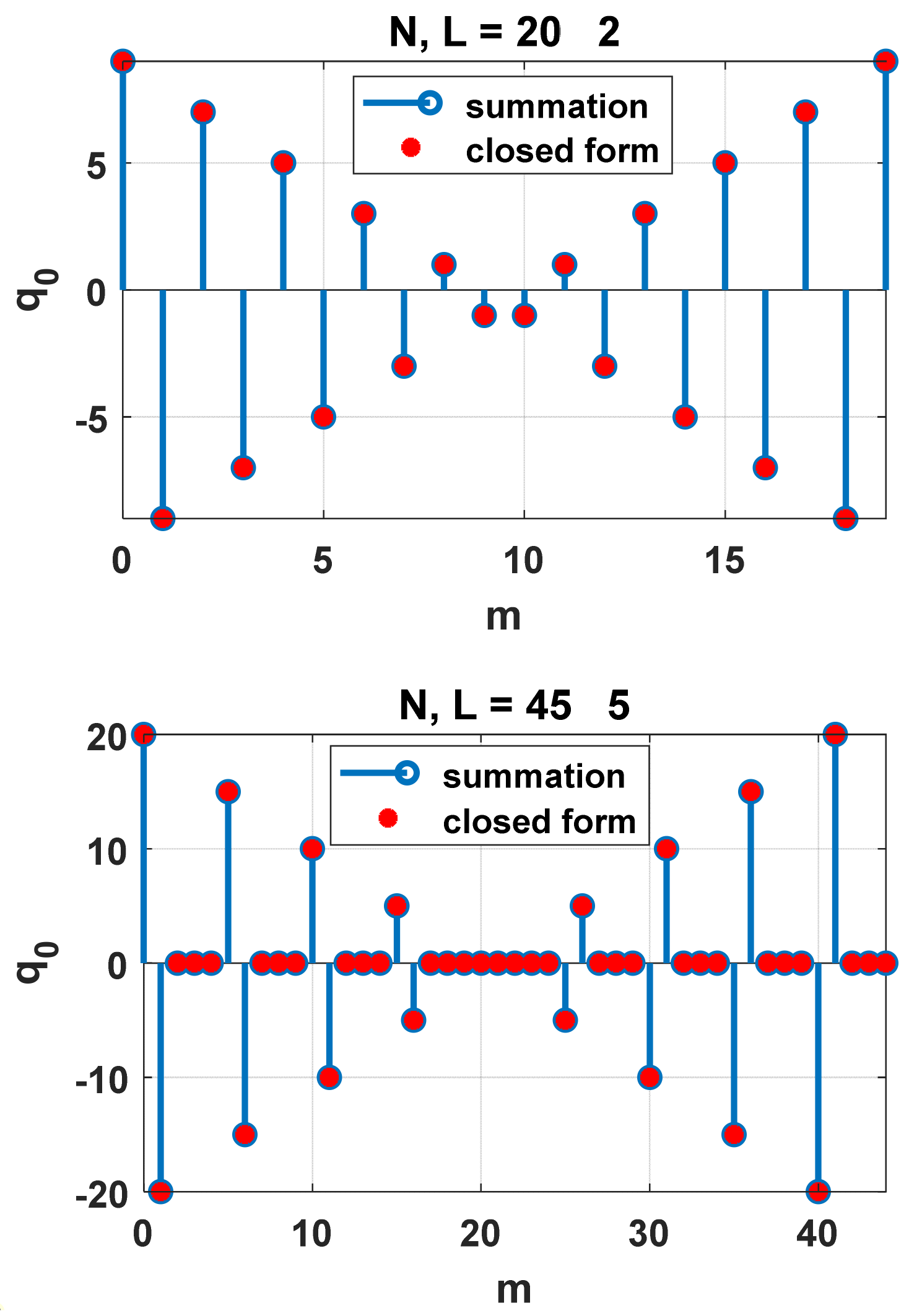
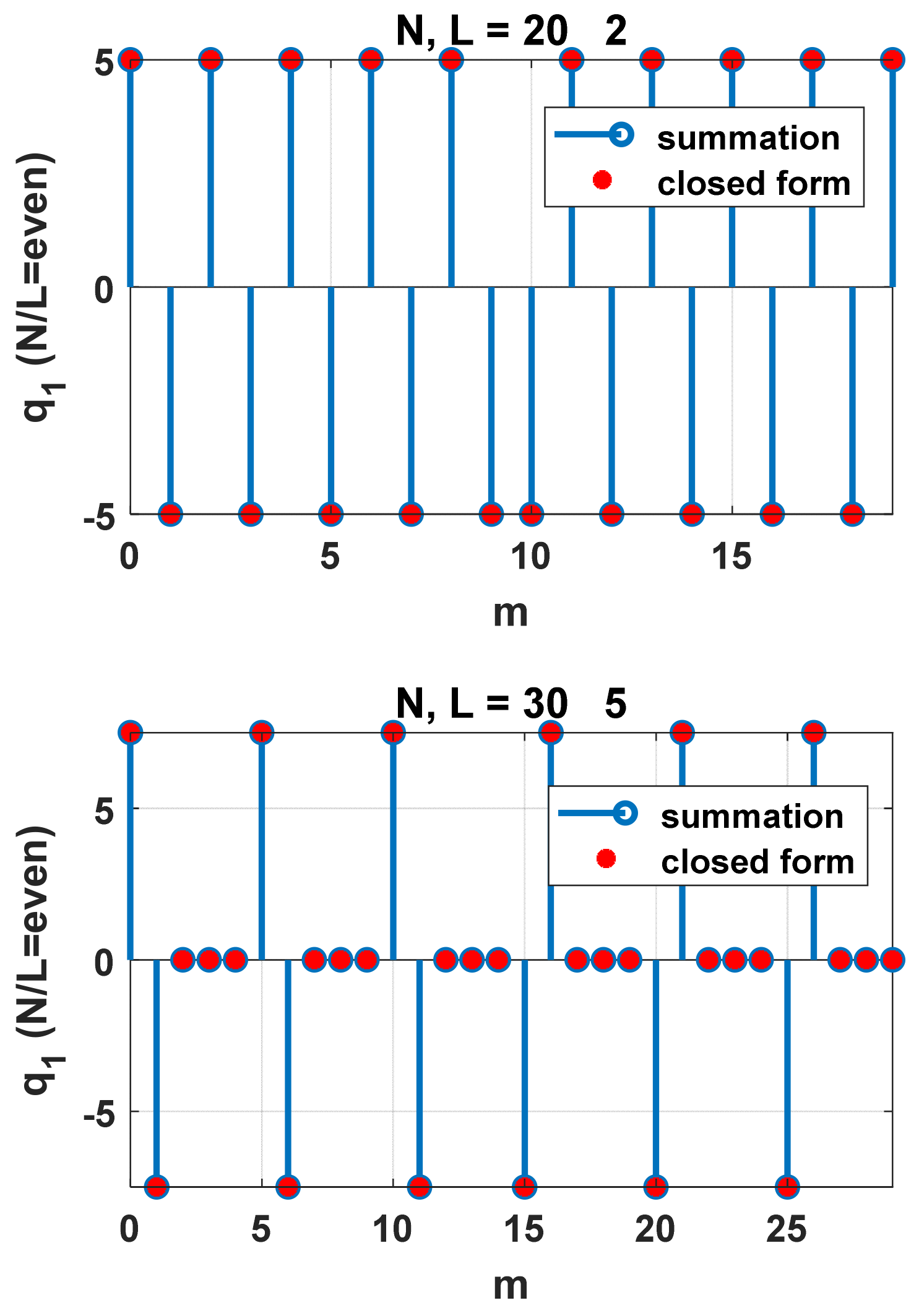
In demonstrating that can be obtained using the DFT method, we have explored three interesting Fourier transform pairs. These DFT pairs are used not only for obtaining from but can be used to yield various trigonometric sums involving , where N is a multiple of integer L and k is the summing integer variable.