Approaching Electroencephalographic Pathological Spikes in Terms of Solitons
Abstract
1. Introduction
2. Nonlinear Media and Solitons
Nervous Nonlinear Medium
3. Equations for Solitons
Solitons in the Electrical Domain and in EEG Spikes
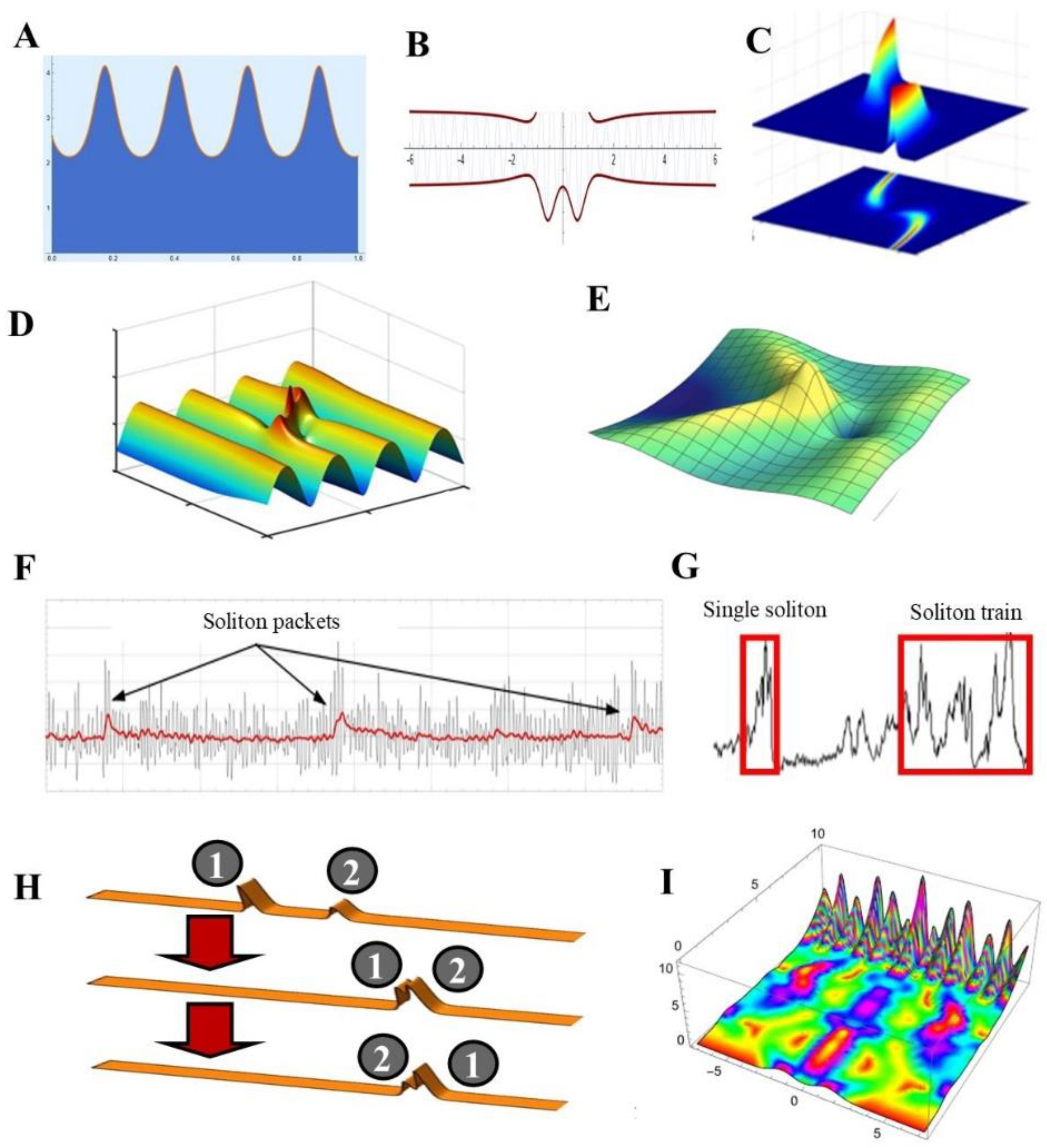
4. The Remarkable Physical Features of Solitons
4.1. Different Shapes for Different Solitary Waves
4.2. Solitons in Healthy EEG Traces
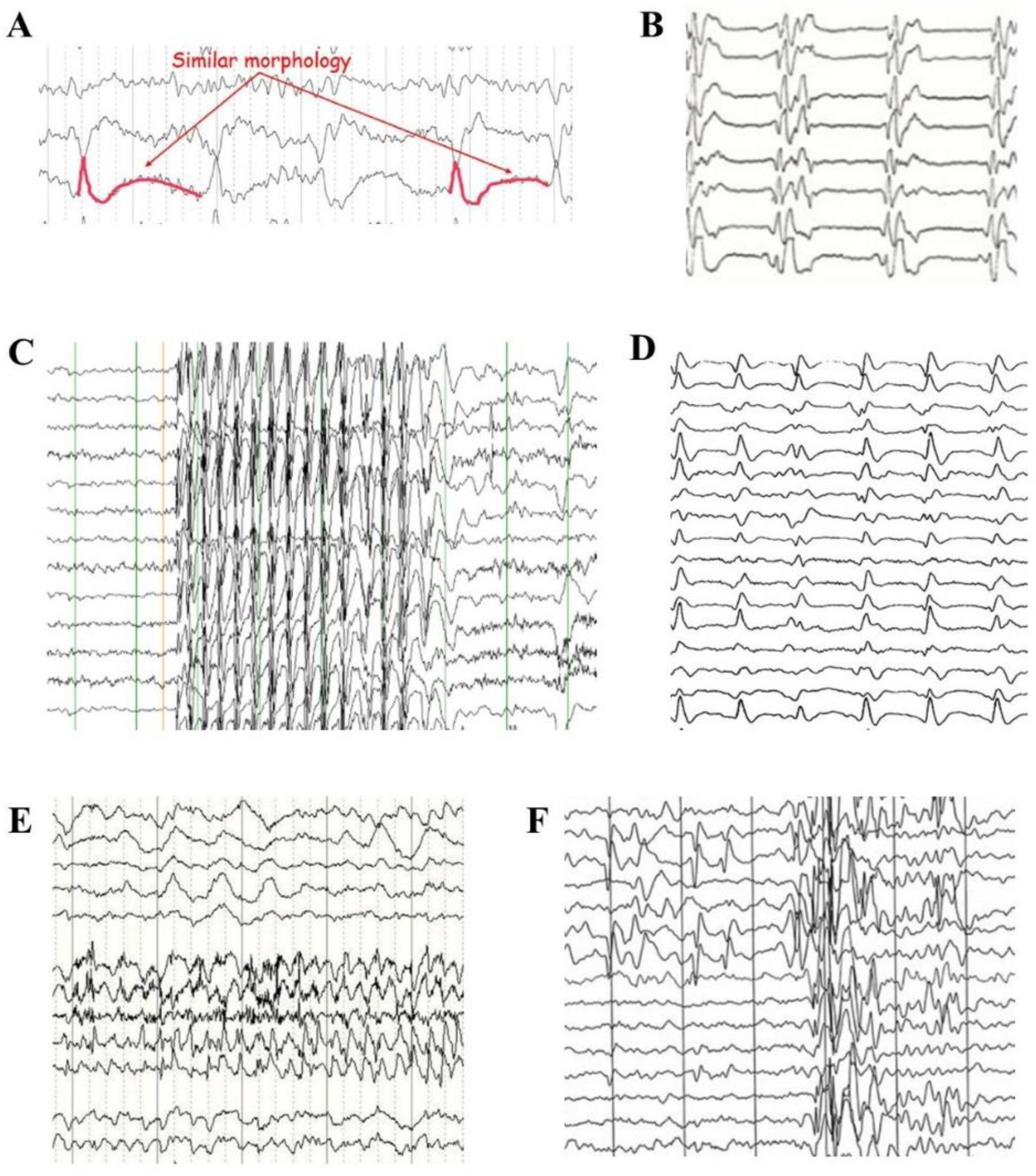
4.3. Solitons in Pathological EEG Traces
- Figure 2C illustrates an example of a 3 to 4 Hz generalized spike-wave in a child affected by juvenile absence epilepsy; modified from https://www.epilepsy.com/what-is-epilepsy/syndromes/juvenile-absence-epilepsy (accessed on 23 March 2024).
- Figure 2D illustrates a typical EEF in a case of sporadic Creutzfeldt–Jacob disease. Note the disease-typical periodic sharp wave complexes that occur in the middle and late stages; modified from https://www.eurocjd.ed.ac.uk/images/typical-eeg-sporadic-cjd (accessed on 23 March 2024).
5. Dynamics of Solitary Waves
5.1. Interactions between Solitons
5.2. Dynamics of Solitary Waves
- (a)
- Figure 2E illustrates the coexistence of generalized normal and focal pathological discharges that are spatially separated.
- (b)
- Figure 2F illustrates the coexistence of generalized and focal epileptiform discharges that are spatially mixed.
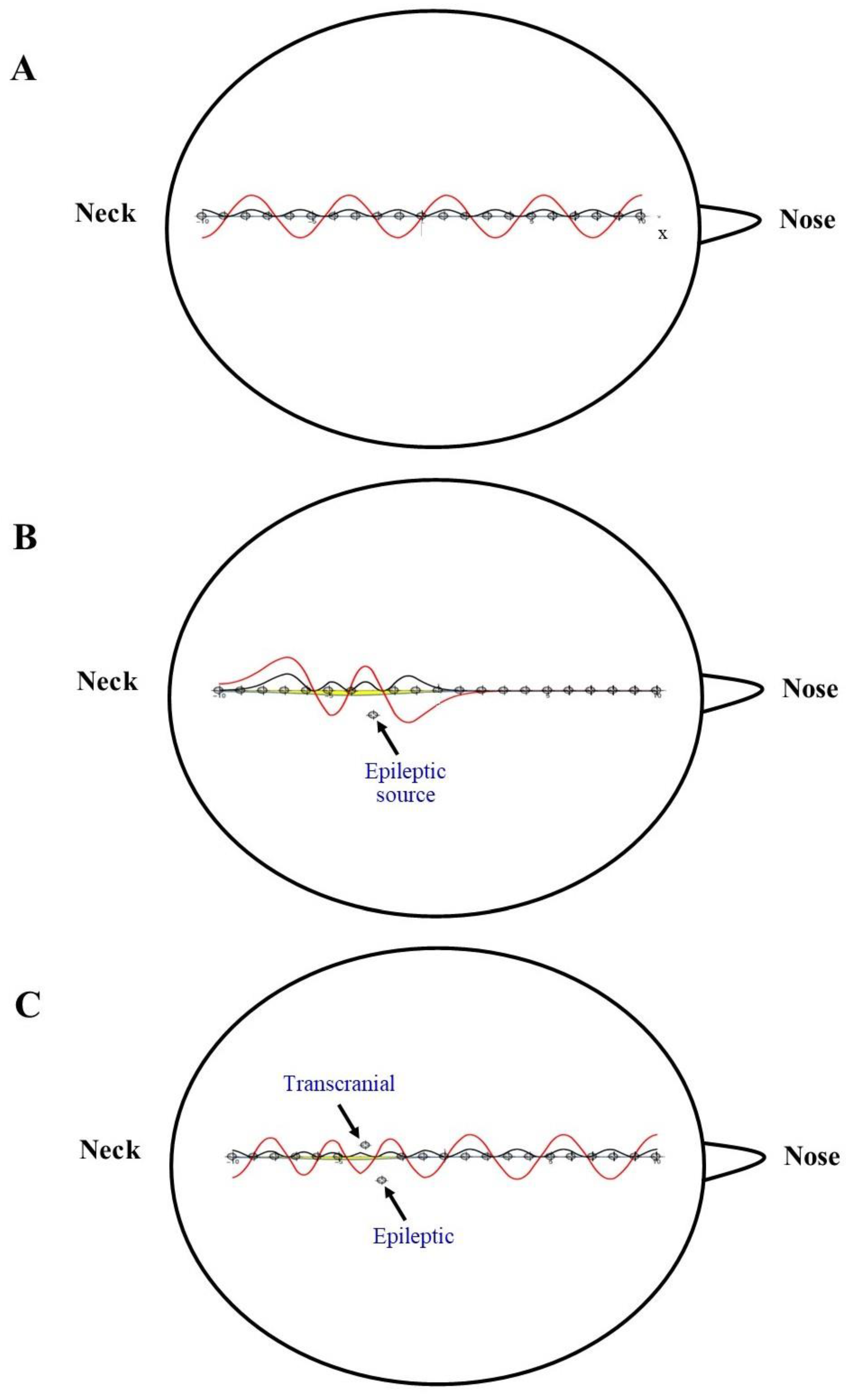
6. Solitons’ Generation
Generation of Neuronal Solitons
- (a)
- The nervous solitons detectable on the scalp are electric waves produced by the underlying neuronal tissue. In this case, solitons are produced INSIDE the electric fields.
- (b)
- The nervous solitons detectable on the scalp are pressure waves that only later become electric currents. In this case, solitons are produced OUTSIDE the electric fields. This can be accomplished in several ways, including the piezoelectric effect, e.g., a simple electromechanical interaction between the mechanical stress and the electrical fields.
- (c)
- The nervous solitons can be naturally produced in the healthy brain.
- (d)
- The nervous solitons can be produced in the pathological brain, e.g., by the spared tissue adjacent to injured areas.
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chabchoub, A.; Slunyaev, A.; Hoffmann, N.; Dias, F.; Kibler, B.; Genty, G.; Dudley, J.; Akhmediev, N. The Peregrine Breather on the Zero-Background Limit as the Two-Soliton Degenerate Solution: An Experimental Study. Front. Phys. 2021, 9, 633549. [Google Scholar] [CrossRef]
- Poznanski, R.R.; Cacha, L.A.; Al-Wesabi, Y.M.; Ali, J.; Bahadoran, M.; Yupapin, P.P.; Yunus, J. Solitonic conduction of electrotonic signals in neuronal branchlets with polarized microstructure. Sci. Rep. 2017, 7, 2746. [Google Scholar] [CrossRef]
- Sharma, A.; Malik, H.K.; Kumar, H.; Goyal, S. Effect of magnetic field on electromagnetic soliton evolution by different pulses. J. Theor. Appl. Phys. 2019, 13, 31–37. [Google Scholar] [CrossRef]
- Ye, Y.; Bu, L.; Wang, W.; Chen, S.; Baronio, F.; Mihalache, D. Peregrine Solitons on a Periodic Background in the Vector Cubic-Quintic Nonlinear Schrödinger Equation. Front. Phys. 2020, 8, 596950. [Google Scholar] [CrossRef]
- Minardi, S.; Eilenberger, F.; Kartashov, Y.V.; Szameit, A.; Röpke, U.; Kobelke, J.; Schuster, K.; Bartelt, H.; Nolte, S.; Torner, L.; et al. Three-dimensional light bullets in arrays of waveguides. Phys. Rev. Lett. 2010, 105, 263901. [Google Scholar] [CrossRef]
- Redor, I.; Barthélemy, E.; Michallet, H.; Onorato, M.; Mordant, N. Experimental Evidence of a Hydrodynamic Soliton Gas. Phys. Rev. Lett. 2019, 122, 214502. [Google Scholar] [CrossRef]
- Krylov, S.F.; Yankov, V.V. The role of solitons in strong turbulence. Zhurnal Eksperimental Teor. Fiz. 1980, 79, 8246. [Google Scholar]
- Diebel, F.; Timotijević, D.V.; Jović Savić, D.M.; Denz, C. Soliton formation by interacting Airy beams. In Complex Light and Optical Forces X; Proceedings Volume 9764; SPIE: Basel, Switzerland, 2016; p. 97640S. [Google Scholar] [CrossRef]
- Kayum, A.; Ara, A.; Barman, H.K.; Ali Akbar, M. Soliton solutions to voltage analysis in nonlinear electrical transmission lines and electric signals in telegraph lines. Results Phys. 2020, 18, 103269. [Google Scholar] [CrossRef]
- Bouchet, T.; Marsal, N.; Sciamanna, M.; Wolfersberger, D. Two dimensional Airy beam soliton. Sci. Rep. 2022, 12, 9064. [Google Scholar] [CrossRef] [PubMed]
- Manley, M.E.; Sievers, A.J.; Lynn, J.W.; Kiselev, S.A.; Agladze, N.I.; Chen, Y.; Alatas, A. Intrinsic localized modes observed in the high-temperature vibrational spectrum of NaI. Phys. Rev. B 2009, 79, 134304. [Google Scholar] [CrossRef]
- Kachulin, D.; Dyachenko, A.; Zakharov, V. Soliton Turbulence in Approximate and Exact Models for Deep Water Waves. Fluids 2020, 5, 67. [Google Scholar] [CrossRef]
- Strecker, K.E.; Partridge, G.B.; Truscott, A.G.; Hulet, R.G. Formation and propagation of matter-wave soliton trains. Nature 2002, 417, 150–153. [Google Scholar] [CrossRef] [PubMed]
- Li, B.-X.; Borshch, V.; Xiao, R.-L.; Paladugu, S.; Turiv, T.; Lavrentovich, O.D. Electrically driven three-dimensional solitary waves as director bullets in nematic liquid crystals. Nat. Commun. 2018, 9, 2912. [Google Scholar] [CrossRef] [PubMed]
- Ciblis, P.; Cosic, I. The Possibility of Soliton/Exciton Transfer in Proteins. J. Theor. Biol. 1997, 184, 331–338. [Google Scholar] [CrossRef]
- Sinkala, Z. Soliton/exciton transport in proteins. J. Theor. Biol. 2006, 241, 919–927. [Google Scholar] [CrossRef]
- Heimburg, T. The thermodynamic soliton theory of the nervous impulse and possible medical implications. Prog. Biophys. Mol. Biol. 2022, 173, 24–35. [Google Scholar] [CrossRef]
- Heimburg, T.; Jackson, A.D. On soliton propagation in biomembranes and nerves. Proc. Natl. Acad. Sci. USA 2005, 102, 9790–9795. [Google Scholar] [CrossRef]
- Andersen Søren, S.L.; Jackson, A.D.; Heimburg, T. Towards a thermodynamic theory of nerve pulse propagation. Prog. Neurobiol. 2009, 88, 104–113. [Google Scholar] [CrossRef]
- Heimburg, T.; Jackson, A.D. On the action potential as a propagating density pulse and the role of anesthetics. arXiv 2006, arXiv:physics/0610117. [Google Scholar] [CrossRef]
- Johnson, A.S.; Winlow, W. The Soliton and the Action Potential—Primary Elements Underlying Sentience. Front. Physiol. 2018, 9, 357787. [Google Scholar] [CrossRef]
- Rowley, M.; Hanzard, P.H.; Cutrona, A.; Bao, H.; Chu, S.T.; Little, B.E.; Morandotti, R.; Moss, D.J.; Oppo, G.L.; Totero Gongora, J.S.; et al. Self-emergence of robust solitons in a microcavity. Nature 2022, 608, 303–309. [Google Scholar] [CrossRef]
- Hernandez, C.I.; Kargarnovin, S.; Hejazi, S.; Karwowski, W. Examining electroencephalogram signatures of people with multiple sclerosis using a nonlinear dynamics approach: A systematic review and bibliographic analysis. Front. Comput. Neurosci. 2023, 17, 1207067. [Google Scholar] [CrossRef]
- Poikonen, H.; Zaluska, T.; Wang, X.; Magno, M.; Kapur, M. Nonlinear and machine learning analyses on high-density EEG data of math experts and novices. Sci. Rep. 2023, 13, 8012. [Google Scholar] [CrossRef]
- Luo, C.; Li, F.; Li, P.; Yi, C.; Li, C.; Tao, Q.; Zhang, Y.; Yao, D.; Yin, G.; Song, P.; et al. A survey of brain network analysis by electroencephalographic signals. Cogn. Neurodyn. 2022, 16, 17–41. [Google Scholar] [CrossRef]
- Meisel, C.; Olbrich, E.; Shriki, O.; Achermann, P. Fading Signatures of Critical Brain Dynamics during Sustained Wakefulness in Humans. J. Neurosci. 2013, 33, 17363–17372. [Google Scholar]
- Mahgoub, A.; Qaraqe, M. Automatic detection of ictal activity in EEG using synchronization and chaos-based attributes. Med. Biol. Eng. Comput. 2023, 61, 3387–3396. [Google Scholar] [CrossRef]
- Alquran, M.; Jaradat, I.; Yusuf, A.; Sulaiman, T.A. Heart-cusp and bell-shaped-cusp optical solitons for an extended two-mode version of the complex Hirota model: Application in optics. Opt. Quant. Electron. 2021, 53, 26. [Google Scholar] [CrossRef]
- Costa, A.; Osborne, A.R.; Resio, D.T.; Alessio, S.; Chrivì, E.; Saggese, E.; Bellomo, K.; Long, C.E. Soliton Turbulence in Shallow Water Ocean Surface Waves. Phys. Rev. Lett. 2014, 113, 108501. [Google Scholar] [CrossRef]
- Karjanto, N. The nonlinear Schrödinger equation: A mathematical model with its wide-ranging applications. arXiv 2019, arXiv:1912.10683. [Google Scholar]
- Fotopoulos, G.; Frantzeskakis, D.J.; Karachalios, N.I.; Kevrekidis, P.G.; Koukouloyannis, V.; Vetas, K. Extreme wave events for a nonlinear Schrödinger equation with linear damping and Gaussian driving. Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 105058. [Google Scholar] [CrossRef]
- Xia, W.; Ma, Y.; Dong, G.; Zhang, J.; Ma, X. Emergence of Solitons from Irregular Waves in Deep Water. J. Mar. Sci. Eng. 2021, 9, 1369. [Google Scholar] [CrossRef]
- Rubino, E.; McLenaghan, J.; Kehr, S.C.; Belgiorno, F.; Townsend, D.; Rohr, S.; Kuklewicz, C.E.; Leonhardt, U.; König, F.; Faccio, D. Negative-Frequency Resonant Radiation. Phys. Rev. Lett. 2012, 108, 253901. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.-F.; Lü, X.; Wang, J.-P. Dynamical behavior and modulation instability of optical solitons with spatio-temporal dispersion. Phys. Lett. A 2024, 496, 129317. [Google Scholar] [CrossRef]
- Bilman, D.; Buckingham, R. Large-Order Asymptotics for Multiple-Pole Solitons of the Focusing Nonlinear Schrödinger Equation. J. Nonlinear Sci. 2019, 29, 2185–2229. [Google Scholar] [CrossRef]
- Shah, A.; Rehman, S.-U.; Haque, Q.-U.L.; Mahmood, S. Solitons and Turbulence in Solar Wind at 1 au: Multi-satellite Data and FDTD Simulations. Astrophys. J. 2020, 890, 1. [Google Scholar] [CrossRef]
- Bradley, P.J.; De Angelis, C. Soliton dynamics and surface waves at the interface between saturable nonlinear dielectrics. Opt. Commun. 1996, 130, 205–218. [Google Scholar] [CrossRef]
- Chai, X.; Lao, D.; Fujimoto, K.; Ramas, C. Magnetic soliton: From two to three components with SO(3) symmetry. Phys. Rev. Res. 2020, 3, L012003. [Google Scholar] [CrossRef]
- Shen, Y.; Dierking, I. Dynamics of electrically driven solitons in nematic and cholesteric liquid crystals. Commun. Phys. 2020, 3, 14. [Google Scholar] [CrossRef]
- Yamgoué, S.B.; Deffo, G.R.; Tala-Tebue, E.; Pelap, F.B. Exact solitary wave solutions of a nonlinear Schrödinger equation model with saturable-like nonlinearities governing modulated waves in a discrete electrical lattice. Chin. Phys. B 2018, 27, 126303. [Google Scholar] [CrossRef]
- Körpınara, T.; Demirkola, R.C.; Körpınara, Z. Soliton propagation of electromagnetic field vectors of polarized light ray traveling along with coiled optical fiber on the unit 2-sphereS2. Rev. Mex. Fis. 2020, 65, 626. [Google Scholar] [CrossRef]
- Lima, F.M.S. What Exactly is the Electric Field at the Surface of a Charged Conducting Sphere? Reason 2018, 23, 1215–1223. [Google Scholar] [CrossRef]
- Wabnig, J.; Resch, J.; Theuerkauf, D.; Anmasser, F.; Faber, M. Numerical Evaluation of a Soliton Pair with Long Range Interaction. arXiv 2022, arXiv:2210.13374. [Google Scholar]
- Chabchoub, A.; Kimmoun, O.; Branger, H.; Hoffmann, N.; Proment, D.; Onorato, M.; Akhmediev, N. Experimental Observation of Dark Solitons on the Surface of Water. Phys. Rev. Lett. 2013, 110, 124101. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Wang, P.; Zhang, J.; Guo, T.; Gao, R.; Ren, S. Controllable soliton propagation of Airy-Gaussian beams under the fractional effect. Optik 2021, 243, 167431. [Google Scholar] [CrossRef]
- Didenkulova, E. Soliton turbulence in weakly nonlinear and weakly dispersive media. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021; p. EGU21-552. [Google Scholar] [CrossRef]
- Peregrine, D.H. Water waves, nonlinear Schrödinger equations and their solutions. J. Austral. Math. Soc. B 1983, 25, 16–43. [Google Scholar] [CrossRef]
- Sen, S. A global method of generating action potentials and EEG oscillations in a topological surface network. BiorXiv 2022. biorXiv:2022-06. [Google Scholar] [CrossRef]
- Zhang, H.; Watrous, A.J.; Patel, A.; Jacobs, J. Theta and Alpha Oscillations Are Traveling Waves in the Human Neocortex. Neuron 2018, 98, P1269–P1281.e4. [Google Scholar] [CrossRef]
- Cole, S.R.; Voytek, B. Brain Oscillations and the Importance of Waveform Shape. Trends Cogn. Sci. 2017, 21, 137–149. [Google Scholar] [CrossRef]
- Handa, P.; Mathur, M.; Goel, N. Open and free EEG datasets for epilepsy diagnosis. arXiv 2021, arXiv:2108.01030. [Google Scholar]
- Gélisse, P.; Tatum, W.O.; Crespel, A.; Jallon, P.; Kaplan, P.W. Determining ICU EEG periodic patterns and why it matters. J. Neurol. 2023, 270, 4744–4752. [Google Scholar] [CrossRef]
- Gadoth, N. Subacute Sclerosing Pan-Encephalitis (SSPE)—Past and Present. In Pathogenesis of Encephalitis; Hayasaka, D., Ed.; IntechOpen: London, UK, 2011. [Google Scholar] [CrossRef]
- Chari, G.; Yadav, K.; Nishijima, D.; Omurtag, A.; Zehtabchi, S. Improving the ability of ED physicians to identify subclinical/electrographic seizures on EEG after a brief training module. Int. J. Emerg. Med. 2019, 12, 11. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Torre, J.L. First Chapter: Interictal EEG. In Atlas of Epilepsies; Panayioutopoulos, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kartashov, Y.V.; Vysloukh, V.A.; Torner, L. Soliton trains in photonic lattices. Opt. Express 2004, 12, 2831–2837. [Google Scholar] [CrossRef] [PubMed]
- Genevet, P.; Barland, S.; Giudici, M.; Tredicce, J.R. Cavity Soliton Laser Based on Mutually Coupled Semiconductor Microresonators. Phys. Rev. Lett. 2008, 101, 123905. [Google Scholar] [CrossRef]
- Fritsch, A.R.; Guo, S.; Koh, S.M. Dark solitons in Bose–Einstein condensates: A dataset for many-body physics research. Mach. Learn.: Sci. Technol. 2022, 3, 047001. [Google Scholar] [CrossRef]
- Halperin, E.J.; Bohn, J.L. Quench-produced solitons in a box-trapped Bose-Einstein condensate. Phys. Rev. Res. 2020, 2, 043256. [Google Scholar] [CrossRef]
- Gaur, D.S.; Purohit, A.; Mishra, A.K. Trapping and guiding soliton through Airy pulse. Opt. Commun. 2024, 556, 130300. [Google Scholar] [CrossRef]
- Shaukat, M.I.; Castro, E.V.; Terças, H. Quantum dark solitons as qubits in Bose-Einstein condensates. Phys. Rev. A 2017, 95, 053618. [Google Scholar] [CrossRef]
- Chung, S.W.; Sullivan, C.; Rogasch, N.C.; Hoy, K.E.; Bailey, N.W. The effects of individualized intermittent theta burst stimulation in the prefrontal cortex: A TMS-EEG study. Hum Brain Mapp 2019, 40, 608–627. [Google Scholar] [CrossRef]
- Kohli, S.; Casson, A. Machine learning validation of EEG tACS artefact removal. J. Neural. Eng. 2019, 17, 016034. [Google Scholar] [CrossRef]
- Hirota, R. Exact Solution of the Korteweg–de Vries Equation for Multiple Collisions of Solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tozzi, A. Approaching Electroencephalographic Pathological Spikes in Terms of Solitons. Signals 2024, 5, 281-295. https://doi.org/10.3390/signals5020015
Tozzi A. Approaching Electroencephalographic Pathological Spikes in Terms of Solitons. Signals. 2024; 5(2):281-295. https://doi.org/10.3390/signals5020015
Chicago/Turabian StyleTozzi, Arturo. 2024. "Approaching Electroencephalographic Pathological Spikes in Terms of Solitons" Signals 5, no. 2: 281-295. https://doi.org/10.3390/signals5020015
APA StyleTozzi, A. (2024). Approaching Electroencephalographic Pathological Spikes in Terms of Solitons. Signals, 5(2), 281-295. https://doi.org/10.3390/signals5020015






