Nearly Linear-Phase 2-D Recursive Digital Filters Design Using Balanced Realization Model Reduction

Abstract

This paper presents a new method for the design of separable-denominator 2-D IIR filters with nearly linear phase in the passband. The design method is based on a balanced realization model reduction technique. The nearly linear-phase 2-D IIR filter is designed using 2-D model reduction from a linear-phase 2-D FIR filter, which serves as the initial filter. The structured controllability and observability Gramians $P^s$ and $Q^s$ serve as the foundation for this technique. onal positive-definite matrices that satisfy 2-D Lyapunov equations. An efficient method is used to compute these Gramians by minimizing the traces of $P^s$ and $Q^s$ under linear matrix inequality (LMI) constraints. The use of these Gramians ensures that the resulting 2-D IIR filter preserves stability and can be implemented using a separable-denominator 2-D filter with fewer coefficients than the original 2-D FIR filter. Numerical examples show that the proposed method compares favorably with existing techniques.

1. Introduction

Two-dimensional (2-D) infinite impulse response (IIR) digital filters have been used in many signal processing applications such as image processing, video signal filtering, satellite image processing, beam filters, X-ray, TV transmission, and biomedical imaging [1,2,3,4,5]. Many methods have been proposed for the design of 2-D IIR digital filters (see, e.g., [6,7,8,9,10]). Some methods used linear programming approaches and mirror-image polynomials for the design of 2-D IIR digital filters with separable and nonseparable denominators (see, e.g., [11,12,13,14]). Optimization is also used for the design of separable and non-separable-denominator 2-D IIR filters [15]. Stability criteria based on the system matrix are also used for the design of separable-denominator 2-D IIR filters [16]. Some methods used genetic algorithms [17,18]. Other methods are based on 2-D FIR filters or use model reduction for the design of 2-D IIR digital filters (see, e.g., [19,20,21,22,23]). 2-D finite impulse response (FIR) digital filters have several advantages. They are simple and involve only localized computations [9]. They are always stable and can have a constant group delay. In comparison to 2-D IIR filters, the fundamental downside is that a high 2-D FIR filter order is frequently needed to meet performance requirements with high selectivity [9]. On the other hand, one of the key challenges in dealing with the construction of nearly linear-phase 2-D IIR filters is stability issues [10]. Some methods confine the filters to having denominators in the form of cascaded low-order factors [10], for which sufficient and necessary stability conditions are available [11,12,24]. Other methods used a state-space approach to investigate the stability of 2-D discrete systems using the sufficiency of the 2-D Lyapunov equation to ensure 2-D stability. Although studying the stability problems in state space might lead to strong stability constraints, it has been shown in [25] that the existence of a positive-definite solution pair to the 2-D Lyapunov equation is a sufficient but not necessary condition for 2-D stability.

For 2-D IIR filters with a separable denominator $D(z_1,z_2)=D_1\left(z_1\right)D_2\left(z_2\right)$, the stability is much easier to guarantee than the stability of non-separable-denominator filters [9,26]. Two-dimensional (2-D) IIR filters with separable denominators have received more attention because, in addition to fewer stability constraints, the complexity of the implementation is reduced due to fewer coefficients with a separable denominator than with a nonseparable denominator of the same order [9,27,28]. The process of designing separable filters often results in filters that have high order. For various reasons, it is desirable to replace a high-order filter with a lower-order one to reduce the implementation cost and improve computational efficiency. Many academics have been studying balanced realization model reduction strategies for 2-D digital filters over the past few years as a solution to this challenge, and the findings have been shown to be helpful in the design of digital filters [8,29]. Since the controllability and observability Gramians of the system determine a balanced realization in the main, different types of Gramians can be appropriately described for a given 2-D system. As a result, for a given 2-D discrete system, there are many balanced realization types that result in various balanced approximations [30]. This paper is concerned with a balanced realization model reduction of 2-D digital filters based on the structured controllability Gramian $P^s$ and the structured observability Gramian $Q^s$, where $P^s$ and $Q^s\in {\mathbb{R}}^{n\times n}$. In other words, to use a balanced truncation, the controllability Gramian P and the observability Gramian Q are needed. Linear matrix inequality (LMI) methods in the MATLAB environment can be employed to compute these Gramians. The theory of LMI has captured the interest of various research communities, particularly those working in the field of control systems [31,32,33]. Given that linear programming problems are easily handled by computers, the idea of LMI and its applications is founded on this fact [34]. Some of the earlier design work using LMI includes the work of Li and Paganini [35], and Vandendorpe [36]. In [36], frequency-weighted balanced and closed-loop balanced truncation are used to solve the same problem. In addition, block-diagonal solutions of LMI are used in model reduction of uncertain systems, where the state partitions correspond to different frequency variables [37]. One of the most important steps in creating a coordinate system with balanced realization is to calculate the leading diagonal block matrices of the Gramians of the supplied 2-D system [38]. There have been many 2-D IIR filter design techniques that satisfy magnitude specifications using various methods [21,22]. The approach proposed in this paper differs in the sense that it ensures almost linear phase in the passband. Methods satisfying such specifications have been few [6,8,14,18,19,20,29,39,40]. The paper introduces a new method for designing nearly linear-phase 2-D IIR filters by leveraging a balanced realization model reduction technique, with a focus on controllability and observability Gramians to ensure stability and reduced coefficients, demonstrating favorable results in numerical examples. The contributions of this paper in the area of 2-D IIR filter design include the emphasis on achieving nearly linear phase in the passband, the use of balanced realization model reduction, the incorporation of 2-D FIR filters, the utilization of structured Gramians, efficient computation method for Gramians through LMIs, stability preservation of the obtained filter, and the reduction of the number of filter coefficients. Additionally, the paper’s comparison with existing techniques highlights its contribution to the field of 2-D IIR filter design.

The paper is organized as follows: In Section 2, the definition of structured controllability and observability Gramians of 2-D discrete systems is presented. Section 3 presents an LMI-based algorithm for computing the structured controllability $P^s$ and structured observability $Q^s$ Gramians. In Section 4, a design procedure for a balanced realization model reduction technique for separable-denominator 2-D IIR digital filters is proposed. To demonstrate the effectiveness of the suggested approach, several examples, including plane wave filtering using a 2-D fan filter, are provided in Section 5. Section 6 concludes the paper.

2. Gramians of 2-D Discrete Systems

For a given 2-D system, multiple types of Gramians can be specified correctly. Similarly, for a 2-D discrete system, there are various types of balanced realizations that result in various balanced approximations [25,30]. In this section, we are interested in the structured controllability and observability Gramians for 2-D discrete systems. The benefits of using this type of Gramians over the others are that the resulting positive-definite block-diagonal Gramians satisfy the 2-D Lyapunov equation and are, therefore, sufficient for 2-D stability [25]. Further, they can be used to obtain a block-diagonal similarity transformation which will lead, as it will be discussed in Section 4, to a guaranteed stable 2-D reduced-order system. We use an LMI-based algorithm to compute these Gramians where the problem is formulated as a minimization problem that can be solved numerically by minimizing the trace of the Gramians $P^s$ and $Q^s$ under LMI constraints. Using this algorithm, the Gramians $P^s\in {\mathbb{R}}^{n\times n}$, $Q^s\in {\mathbb{R}}^{n\times n}$ are constrained to be positive-definite $P^s>0$, $Q^s>0$, symmetric $P^s=P^{sT}$, $Q^s=Q^{sT}$, and block-diagonal $P^s=diag(p_1,p_2)$, $Q^s=diag(q_1,q_2)$.

Consider a 2-D discrete state-space system realization $\Sigma =(A,b,c,d)$ described by Roesser’s model [41]:

$$\begin{array}{ccc}\hfill \left[\begin{array}{c}{x}^h(i+1,j)\\ \\ x^v(i,j+1)\end{array}\right]& =& \left[\begin{array}{cc}{A}_{11}& A_{12}\\ \\ A_{21}& A_{22}\end{array}\right]\left[\begin{array}{c}{x}^h(i,j)\\ \\ x^v(i,j)\end{array}\right]+\left[\begin{array}{c}{b}_1\\ \\ b_2\end{array}\right]u(i,j)\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & \equiv \mathbf{Ax}(i,j)+\mathbf{bu}(i,j)\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill y(i,j)& =& \left[c_1{c}_2\right]x(i,j)+du(i,j)\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & \equiv \mathbf{cx}(i,j)+\mathbf{du}(i,j)\hfill \end{array}$$

(4)

where $x^h(i,j)\in {\mathbb{R}}^{m\times 1}$ is the horizontal state vector, $x^v(i,j)\in {\mathbb{R}}^{n\times 1}$ is the vertical state vector, $u(i,j)\in \mathbb{R}$ is the input, $y(i,j)\in \mathbb{R}$ is the output, and $A_{11},A_{12},A_{21},A_{22},b_1,b_2,c_1,c_2,$ and d are real matrices with appropriate dimensions.

The structured controllability and observability Gramians [30] are defined by the positive-definite solutions $P^s$ and $Q^s$ of the following Lyapunov inequalities:

$$\begin{array}{cc}\hfill A{P}^s{A}^T-P^s+b{b}^T& <0\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill A^T{Q}^{s}A-Q^s+c^{T}c& <0\hfill \end{array}$$

(6)

The matrices $P^s$ and $Q^s$ are block-diagonal matrices, $P^s=diag\left(p_1,p_2\right)$ and $Q^s=diag\left(q_1,q_2\right)$, representing the solutions to the above Lyapunov inequalities. In the following section, a method to obtain the structural controllability and observability Gramians using LMI will be presented.

3. Proposed Computation Method for Structured Gramians

LMIs’ versatility and computational efficiency for handling a wide range of system design challenges have made them an effective computational design tool in systems and control engineering [32,42,43,44,45].

In general, an LMI has the form:

$$\begin{array}{c}\hfill F\left(x\right)\triangleq F_0+\sum _{i=1}^m{x}_i{F}_i>0,\end{array}$$

(7)

where $x=(x_1,\dots ,x_m)$ is a vector of m real numbers called the decision variables, i.e., $x_i\in {\mathbb{R}}^m$, for $i=0,\dots ,m$ and $F_i\in {\mathbb{R}}^{n\times n}$ are given symmetric matrices. The problem is to determine if there is a vector x that exists and satisfies the matrix inequality.

In [46,47], it has been shown that for certain special cases, the rank minimization problem can be reduced to a semi-definite problem. Under these hypotheses, it is possible to say that the solution can be obtained by solving the associated LMI. One effective heuristic, applicable when the matrix variable is symmetric and positive semi-definite, is to minimize the trace instead of the rank [32,42]. This results in a semi-definite problem (SDP), which can be efficiently solved. This heuristic obviously does not apply to problems in which the matrix is non-square, since the trace is not even defined [32,42,48]. In the following, we use an LMI-based algorithm to compute the Gramian matrices $P^s$ and $Q^s$ of a 2-D discrete system represented by Roesser’s model.

Given a 2-D system in state-space form represented by Roesser’s model $\Sigma =(A,b,c,d)$, then the block-diagonal positive-definite solutions $P^s$ and $Q^s$ of the Lyapunov inequalities given by (5) and (6) are the structured controllability and structured observability Gramians. The existence of such $P^s$ and $Q^s$ ensures the stability of the system $\Sigma$, but the converse does not hold, as shown in [6,25]. Finding $P^s$ and $Q^s$ satisfying (5) and (6) can be solved by formulating an optimization problem using the traces of $P^s$ and $Q^s$.

Given a 2-D system realization $\Sigma =(A,b,c,d)$, one can find $P^s$ by minimizing

$$mintr\left(P^s\right)$$

(8)

subject to

$$\begin{array}{c}\hfill A{P}^s{A}^T-P^s+b{b}^T<0\end{array}$$

$$\begin{array}{c}\hfill P^s>0\end{array}$$

(9)

$$\begin{array}{c}\hfill P^s=P^{s^T}\\ \hfill P^s=diag(p_1,p_2)\end{array}$$

(10)

and

$$mintr\left(Q^s\right)$$

(11)

subject to

$$\begin{array}{c}\hfill A^T{Q}^{s}A-Q^s+c^{T}c<0\end{array}$$

$$\begin{array}{c}\hfill Q^s>0\end{array}$$

(12)

$$\begin{array}{c}\hfill Q^s=Q^{s^T}\\ \hfill Q^s=diag(q_1,q_2)\end{array}$$

(13)

This problem can be solved as a linear objective minimization problem under LMI constraints. The controllability and observability Gramian matrices $P^s$ and $Q^s$ obtained by using this method are block-diagonal positive-definite matrices.

We refer the reader to Appendix A, where several numerical examples, including separable and non-separable-denominator 2-D systems, are presented. These examples illustrate the use of the LMI to solve 2-D Lyapunov inequalities.

4. Balanced Realization/Truncation Technique for 2-D IIR Digital Filters

Balanced realizations are known to be useful realizations for model reduction. The internally balanced realization gives an indication of the dominance of the system states in the input/output behavior [49]. The idea of a balanced realization model reduction, in general, is to remove from the system matrices the blocks corresponding to the smaller Hankel singular values [19,20,50,51]. In the following section, we present the design procedures for nearly linear-phase 2-D IIR digital filters with separable denominators.

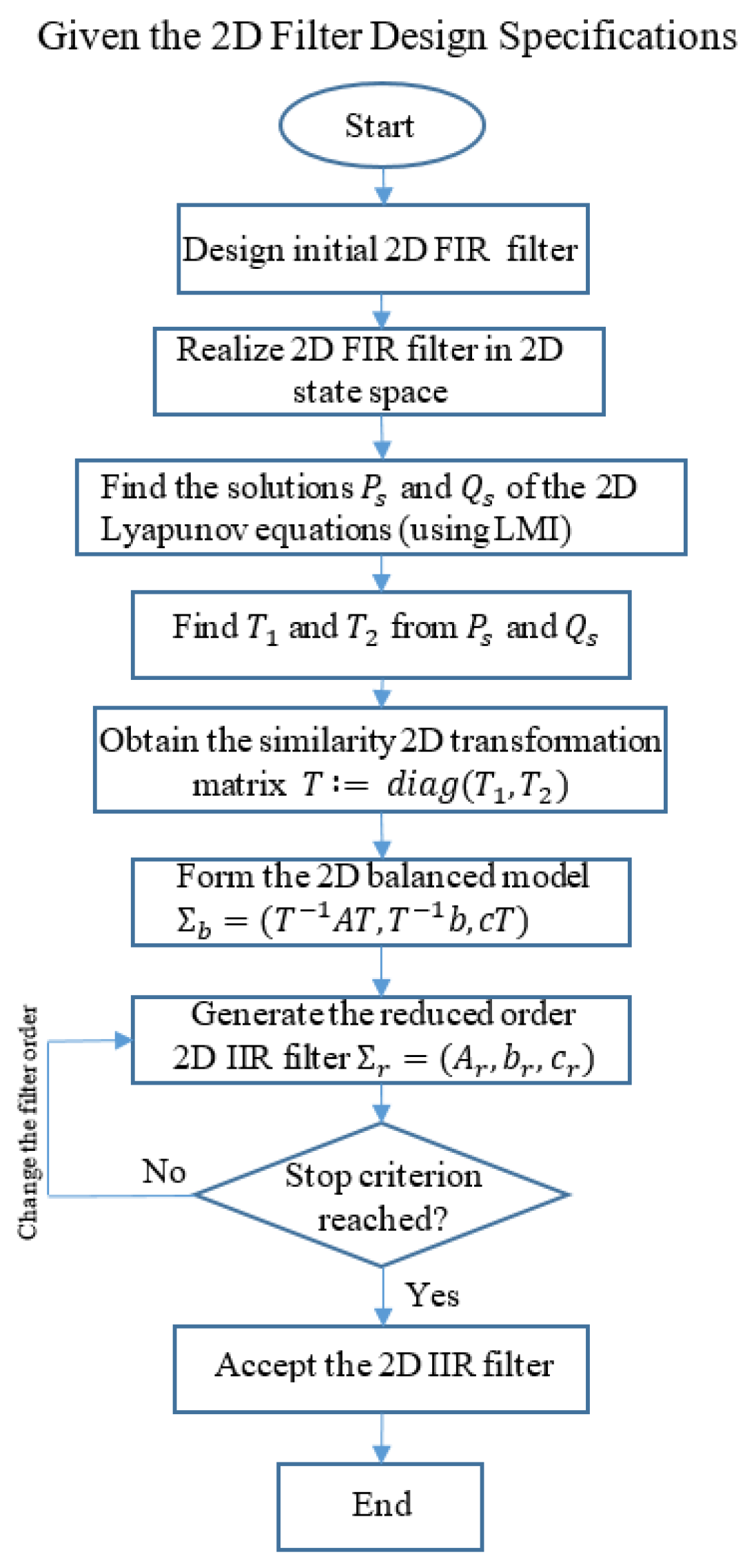
Design Procedures

For a 2-D IIR filter with a separable denominator, it is assumed that either $A_{12}=0$ or $A_{21}=0$. The design steps proposed for this type of 2-D filter are described as follows:

• Design a linear-phase 2-D FIR digital filter that approximates the required frequency response.
• Realize the designed 2-D FIR filter $H(z_1,z_2)$ in state space using Roesser’s model [6,41] as follows:

  $$\left[\begin{array}{c}{X}^h(i+1,j)\\ X^v(i,j+1)\end{array}\right]=\left[\begin{array}{c}{A}_{11}{A}_{12}\\ A_{21}{A}_{22}\end{array}\right]\left[\begin{array}{c}{x}^h(i,j)\\ x^v(i,j)\end{array}\right]+\left[\begin{array}{c}{b}_1\\ b_2\end{array}\right]u(i,j)$$

  (14)

  $$y(i,j)=\left[\begin{array}{c}{c}_1{c}_2\end{array}\right]\left[\begin{array}{c}{x}^h(i,j)\\ x^v(i,j)\end{array}\right]+du(i,j),$$

  (15)

  where $A_{11},A_{12},A_{21},A_{22},b_1,b_2,c_1,c_2,$ and d are real matrices.
• Compute the structured controllability Gramian $P^s$ and the structured observability Gramian $Q^s$ using the LMI-based algorithm proposed in Section 3. Note that since either $A_{12}$ or $A_{21}$ is zero, the equations are simplified and the computational cost of these Gramians is reduced. The obtained structured controllability and structured observability Gramians are block-diagonal matrices, i.e., $P^s=diag(p_1,p_2)$ and $Q^s=diag(q_1,q_2)$.
• Find the invertible matrices $T_1$ and $T_2$ such that

  $$\begin{array}{cc}\hfill T_i^{-1}{p}_i{\left(T_i^{-1}\right)}^T& ={\Sigma }_i=T_i^T{q}_i{T}_i\hfill \\ \hfill & =diag({\sigma }_{1i},{\sigma }_{2i},\dots {\sigma }_{n_{i}i}),i=1,2.\hfill \end{array}$$

  (16)
  • Compute the matrices $M_{1i}=p_i{q}_i,i=1,2$.
  • Decompose the matrices $M_{1i}$ as $[u_i,s_i,v_i]=svd\left(M_{1i}\right),i=1,2.$
    where the full singular value decomposition of an m-by-n matrix M involves:
    •  m-by-m matrix u.
    •  m-by-n matrix s.
    •  n-by-n matrix v.
  • Compute the matrices $T_i=u_i\sqrt{s_i},i=1,2$.
• Obtain the similarity transformation matrix
  $T:=diag(T_1,T_2)$.
• Form the balanced realization model ${\Sigma }_b=(T^{-1}AT,T^{-1}b,cT)$.
• Obtain the reduced-order $(r_1,r_2)$ filter by partitioning the balanced realization obtained in the above step ${\Sigma }_r=(A_r,b_r,c_r)$.

Figure 1 shows the flowchart of the proposed method.

The following section provides some design examples and a discussion of the implementation and evaluation details of this algorithm.

5. Illustrative Examples and Numerical Evaluation

In this section, we present several design examples to illustrate the effectiveness of the proposed method. In these examples, 2-D FIR lowpass, bandstop, and fan digital filters are first designed using window methods, and then the reduced-order 2-D IIR filters are obtained by using the proposed method. The implementation of the resulting filter designs is investigated and evaluated with respect to the maximum ripple in the passband region ${\Delta }_p$, the maximum ripple in the stopband region ${\Delta }_s$, the maximum ripple of the group delay in the passband region ${\Delta }_{\tau }$, and the number of arithmetic operations.

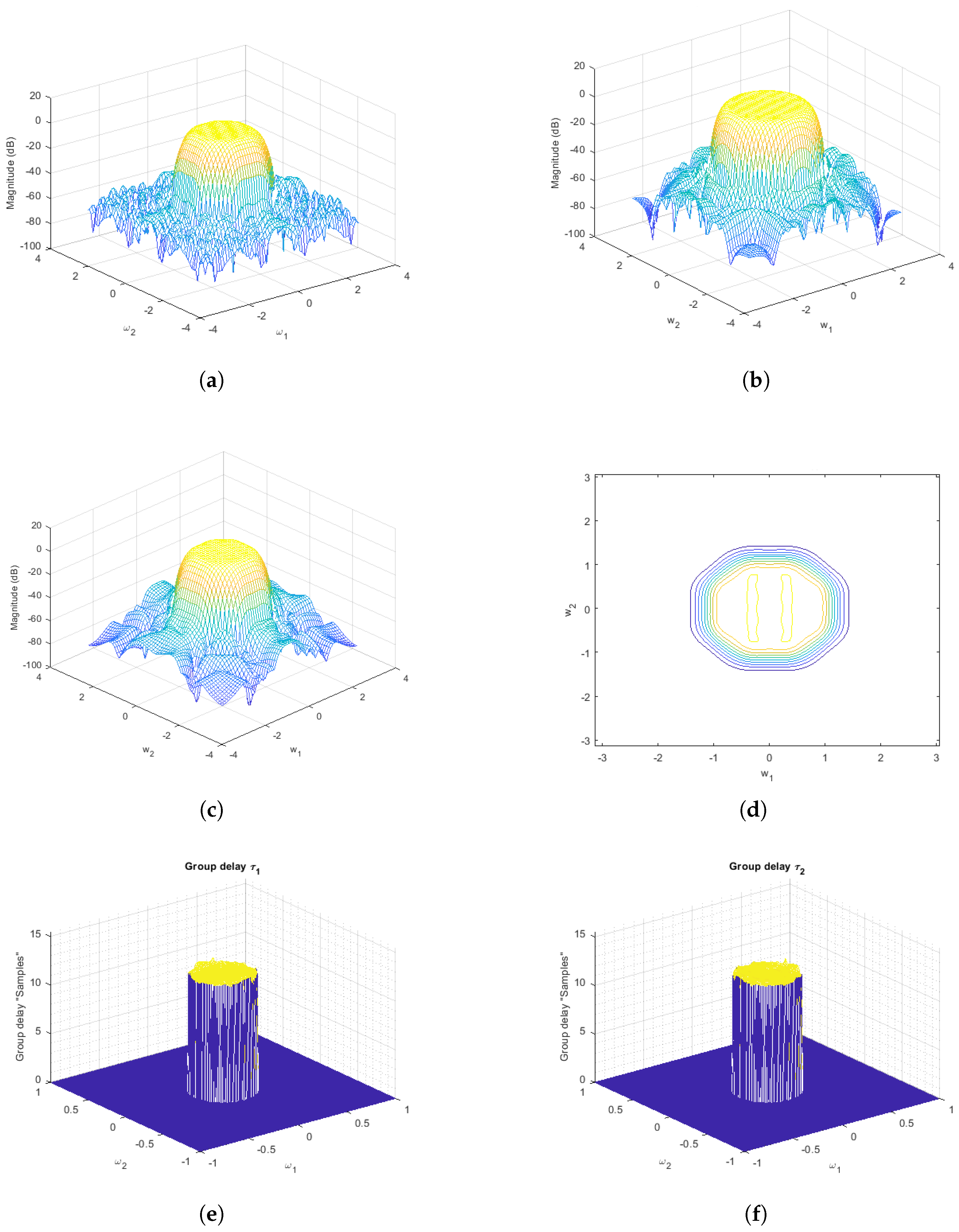
5.1. 2-D Lowpass Filters

For the sake of comparison, we carried out a study of an example of separable-denominator 2-D IIR lowpass filter with nearly linear phase in the passband. This example was presented by Xiao and Agathoklis in [6], where it is required to design a 2-D lowpass filter to satisfy the following specifications:

$$\begin{array}{c}\hfill \mid H({\omega }_1,{\omega }_2)\mid =\left\{\begin{array}{cc}1& {{\omega }_1}^2+{{\omega }_2}^2\le {\omega }_p^2\hfill \\ 0& {{\omega }_1}^2+{{\omega }_2}^2\ge {\omega }_s^2\hfill \end{array}\right.\end{array}$$

(17)

where the passband edge ${\omega }_p=0.4\pi$ and the stopband edge ${\omega }_s=0.6\pi$. First, the linear-phase 2-D FIR filter prototype of order (24,24) was designed using the window method. After that, the proposed algorithm is guaranteed to obtain a stable 2-D IIR filter with nearly linear phase in the passband. The solution was computable in a reasonable amount of time on a PC with an Intel (R) Core (TM) i5-2450M CPU @ 2.50 GHz and RAM of 6.00 GB. The computation time for the controllability Gramian $P^s$ and the observability Gramian $Q^s$ was 7.46 s. The magnitude response of the full-order, (24,24), 2-D FIR lowpass filter is shown in Figure 2a. Figure 2b shows the magnitude response of the reduced-order (13,13) 2-D IIR filter presented in [6]. Figure 2c shows the magnitude response of the reduced-order (13,13) 2-D IIR filter using the proposed method. The magnitude contour of the obtained filter is shown in Figure 2d. Figure 2e,f show the passband group delays, ${\tau }_1={\tau }_2\approx 12$ samples, of the reduced-order 2-D IIR filter.

Table 1. Comparison results of the 2-D IIR filters.

	Proposed Method	Method in [6]	Method in [52]
Orders	(13,13)	(13,13)	(18,18)
Group Delay	(12,12)	(12,12)	(12,12)
${\Delta }_p$	0.0102	0.0124	0.0128
${\Delta }_s$	0.0060	0.0111	0.0350
${\Delta }_{\tau }$	0.0425	0.0725	-
$C_{FIR}$	625	625	676
$C_{IIR}$	224	224	399

summarizes the results of the filter designed by the proposed method, the filter presented in [6], and the results of the filter reported in Table 1 of [52]. These results are presented in terms of the reduced order, the obtained group delays ${\tau }_1$ and ${\tau }_2$ and their ripple ${\Delta }_{\tau }$, the maximum ripple ${\Delta }_p$ in the passband region, and the maximum ripple in the stopband region ${\Delta }_s$. The proposed method gives a filter with comparable performance to that of the same order filter obtained in [6,52], with improvements in the maximum passband ripple ${\Delta }_p$, the stopband ${\Delta }_s$, and the group delay ripple ${\Delta }_{\tau }$, as shown in Table 1 below. The table also shows that a smaller number of coefficients is required by the obtained 2-D IIR filter than the original 2-D FIR.

We also analyze the complexity of the implementation based on the number of non-zero coefficients in the transfer function of the filter. When implementing a general $N_1\times N_2$ 2-D FIR filter, the number of filter coefficients C is $(N_1+1)(N_2+1)$, so the cost of implementation increases rapidly as $N_1$ or $N_2$ increases. In this example, for the 2-D FIR filter of order (24,24), C is 625, whereas for the reduced-order (13,13) 2-D IIR filter with a separable denominator, C is $14\times 14$ for the numerator plus $2\times 14$ for the denominator (i.e., $C=224$). We can see that implementing the 2-D IIR filter designed by the proposed method requires less than half of the number of coefficients required by the 2-D FIR filter.

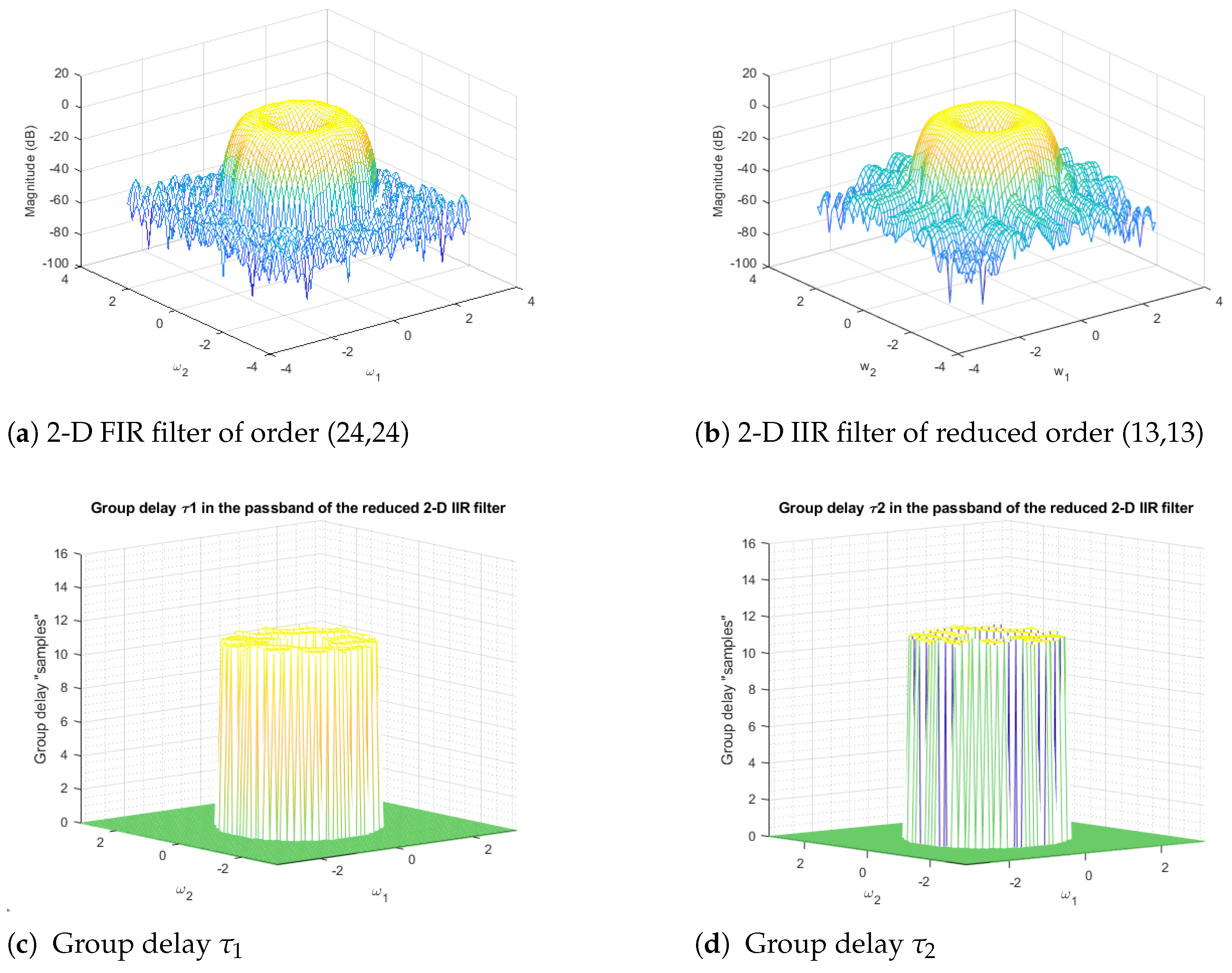
5.2. 2-D Bandpass Filter

In this example, we design a 2-D bandpass filter to satisfy the following specifications:

$$\begin{array}{c}\hfill \mid H({\omega }_1,{\omega }_2)\mid =\left\{\begin{array}{cc}1& {\omega }_{p1}^2\le {{\omega }_1}^2+{{\omega }_2}^2\le {\omega }_{p2}^2\hfill \\ 0& otherwise\hfill \end{array}\right.\end{array}$$

(18)

where ${\omega }_{p1}=0.2\pi$ and ${\omega }_{p2}=0.5\pi$. First, a linear-phase 2-D FIR filter of order (24,24) is designed using a window method to satisfy the design specifications. Then, a 2-D IIR bandpass filter of a reduced order (13,13) is obtained by using the proposed method. In this example, the computation time for controllability Gramian $P^s$ and observability Gramian $Q^s$ was 6.88 s. The number of coefficients for the FIR filter of order (24,24) is $(N_1+1)\times (N_2+1)=625$, while the obtained IIR filter of a reduced order of (13,13) has a reduced number of coefficients equal to 224. The magnitude response of the full-order (24,24) 2-D FIR bandpass filter is shown in Figure 3a. The reduced-order (13,13) filter is stable, and its magnitude response is shown in Figure 3b. The group delays ${\tau }_1$ and ${\tau }_2$ over the passband are illustrated in Figure 3c,d.

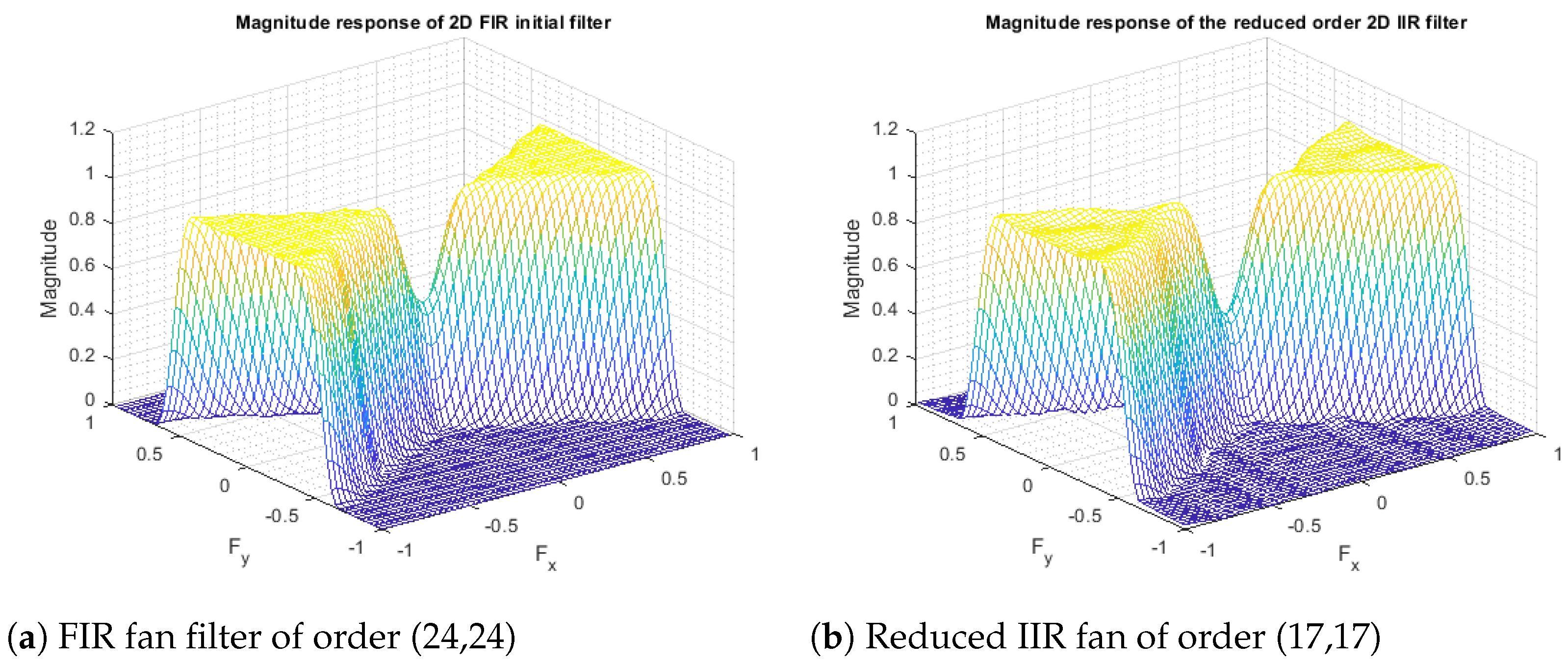
5.3. Two-Dimensional Fan Filter

Fan filters constitute an important class of 2-D filters that find applications, for example, in geological and seismological data processing and beamforming [53,54]. This type of 2-D filter has the capability of directional filtering, where the signal is passed or rejected according to its direction. In this example, the proposed method is employed in the design of a 2-D fan filter having the magnitude response described in [55], with ${\omega }_1$ and ${\omega }_2$ as the two frequency variables where $-\pi \le {\omega }_1,{\omega }_2\le \pi$.

$$\begin{array}{c}\hfill \mid H({\omega }_1,{\omega }_2)\mid =\left\{\begin{array}{cc}1& |{\omega }_2|\le |{\omega }_1|\hfill \\ 0& otherwise\hfill \end{array}\right.\end{array}$$

(19)

The first step is to construct a 2-D linear-phase FIR fan filter with order (49,49). Figure 4a shows the magnitude response of the initial 2-D FIR fan filter. Second, a reduced-order nearly linear-phase 2-D IIR fan filter of order (34,34) is obtained using the method proposed in Section 4. The magnitude response of the reduced-order 2-D IIR fan filter is illustrated in Figure 4b. The group delays ${\tau }_1$ and ${\tau }_2$ of the reduced-order 2-D IIR fan filter are shown in Figure 4c,d, respectively. Figure 4e shows the impulse response of the reduced-order 2-D IIR fan filter. The magnitude contour of the same reduced-order 2-D IIR fan filter is illustrated in Figure 4f. The number of multiplications and additions for the 2-D FIR initial filter of order (49,49) is $(N_1+1)\times (N_2+1)=2500$ and 2499, respectively. For implementation purposes, the obtained 2-D IIR fan filter with a reduced order of (34,34) has fewer computations: 1295 multiplications and 1294 additions. The computation time for controllability Gramian $P^s$ and observability Gramian $Q^s$ is 6.53 s. As can be seen, the designed 2-D IIR fan filter has a lower order compared with the 2-D FIR filter, which would lead to reducing the computational complexity in the implementation to achieve the same performance.

5.4. Fan Filtering of Plane Wave Image

We present a 2-D fan filter for ground roll attenuation in this section. A specific kind of Rayleigh wave with low frequency, low velocity, and high amplitude is called ground roll. It is the main type of coherent noise in land seismic surveys [56]. We generate an image via the sum of plane waves (PWs) with two angles, ${\theta }_1={80}^{\circ }$ and ${\theta }_2={100}^{\circ }$, measured counterclockwise from the horizontal. The wave has ${\omega }_1=100/512\times 2\pi$ rad/pixels and ${\omega }_2=53/512\times 2\pi$ rad/pixels over the size $N=512$ pixels of the output image. 2-D FIR and IIR fan filters are designed to be applied to this PW image, where it is required to design a reduced-order 2-D IIR fan filter to satisfy the following design specifications:

$$\begin{array}{c}\hfill \mid H({\omega }_1,{\omega }_2)\mid =\left\{\begin{array}{cc}1& |{{\omega }_1}^2|\le 0.57|{\omega }_2^2|\hfill \\ 0& |{{\omega }_1}^2|>0.57|{\omega }_2^2|\hfill \end{array}\right.\end{array}$$

(20)

Figure 5a shows the magnitude response of the initial 2-D FIR fan filter of order (24,24) designed using the window method. The reduced 2-D IIR fan filter of order (17,17) obtained by using the proposed method is shown in Figure 5b.

For comparison purposes, the 2-D FIR fan filter of order (24,24) shown in Figure 5a is applied to this PW image first, where Figure 6 shows the original and filtered images and their 2-D spectra. The reduced-order 2-D IIR fan filter of order (17,17) shown in Figure 5b is then applied to the same image, and the result is shown in Figure 7. In terms of the computation complexity, the 2-D FIR fan filter of order (24,24) has a number of coefficients C equal to 625, whereas for the reduced-order (17,17) 2-D IIR fan filter, we have $18\times 18$ for the numerator plus $2\times 18$ for the denominator (i.e., the number of coefficients is $C=360$), which is reduced to less than 58%. For implementation, we can see that the obtained 2-D IIR fan filter requires less than half the number of coefficients required by the 2-D FIR fan filter. The results show that the reduced-order 2-D IIR fan filter designed using the proposed method has good filtering performance on the PW image as well as the advantage of a low implementation cost in terms of adders and multipliers over the 2-D FIR fan filter.

6. Conclusions

A method to design nearly linear-phase 2-D filters has been presented. The method is based on the model reduction of 2-D filters using balanced realization. The design method starts with the design of a 2-D linear-phase FIR filter and its state-space representation as a 2-D system with a separable denominator. The balanced realization of this system can be obtained using the 2-D structural controllability and structural observability Gramians of the system. These block-diagonal Gramians satisfy a set of Lyapunov inequalities, which are solved using an optimization approach under linear matrix inequality constraints. The use of the structural Gramians ensures that the resulting reduced-order system satisfies a 2-D Lyapunov equation and is, therefore, 2-D stable. The proposed method is illustrated by numerical examples that have shown that the method is suitable for the design of reduced-order 2-D IIR filters with nearly linear phase in the passband. The performance of the obtained 2-D IIR filters compares favorably with existing techniques, while at the same time they can be implemented using a separable-denominator filter with less computational complexity than the original 2-D FIR filter. Although the phase of the reduced-order 2-D IIR filter is only nearly linear, we can see that the reduced-order 2-D IIR filter offers good selectivity, computation efficiency, and reduced system delay when compared to the corresponding 2-D FIR filter.