Abstract
In this paper, we propose robust image-smoothing methods based on gradient minimization with novel gradient constraints to effectively suppress pseudo-edges. Simultaneously minimizing the gradient, i.e., the number of nonzero gradients in an image, and the data fidelity results in a smooth image. However, this optimization often leads to undesirable artifacts, such as pseudo-edges, known as the “staircasing effect”, and halos, which become more visible in image enhancement tasks, like detail enhancement and tone mapping. To address these issues, we introduce two types of gradient constraints: box and ball. These constraints are applied using a reference image (e.g., the input image is used as a reference for image smoothing) to suppress pseudo-edges in homogeneous regions and the blurring effect around strong edges. We also present an gradient minimization problem based on the box-/ball-type gradient constraints using an alternating direction method of multipliers (ADMM). Experimental results on important applications of gradient minimization demonstrate the advantages of our proposed methods compared to existing gradient-based approaches.
1. Introduction
Image smoothing is a key technique in image processing and is used in applications such as deblurring [1,2,3,4], detail enhancement [5,6], tone mapping [7,8,9], and so on. Furthermore, it is used in various fields, such as in medical imaging [10,11,12], computer graphics [13,14,15], remote sensing [16,17,18], and character recognition [4,19,20].
Filtering-based smoothing methods, e.g., a bilateral filter [6,21], a guided filter [22,23,24,25], and a nonlocal mean filter [26,27], have been actively studied for a long time and are often used in practical situations, as they can easily obtain smooth images that roughly maintain the structural gradients of input images with a relatively low computational cost.
Optimization-based smoothing methods were recently proposed in [1,28,29,30,31,32,33,34,35,36,37,38,39,40,41], and they can flexibly incorporate a priori information into minimization problems. The most standard a priori knowledge of natural images is local smoothness. The popular total variation (TV) [1] is designed as the total magnitude of the vertical and horizontal discrete gradients of an image and promotes this smoothness property on optimization. This method can be employed in more advanced image restoration problems, e.g., reflection removal [42,43], rain streak removal [44,45,46], intrinsic image decomposition [36,47,48], image blending [49], and multispectral pansharpening [50,51,52,53], which are complex problems to solve using filtering-based techniques; this is because optimization-based methods can explicitly and quantitatively design observation models by modeling using some norms and specific functions approximately. For example, we can flexibly define not only the commonly used -norm but also the -norm [54,55] and Huber loss function [49,56,57], which are robust to outliers, and so on, as a data-fidelity term in minimization problems.
Among these optimization-based methods, the gradient minimization proposed in [31] is known to provide the best approximation of the properties of the local piece-wise flatness of natural images, which is among the most essential prior knowledge in image processing. In this method, the gradient, which is the number of nonzero gradients of an image, is minimized together with the data fidelity to an input image. Recently, the applications of this method were actively studied, such as algorithm acceleration [58], deblurring [3,4], multi-dimensional data smoothing [58], and layer separation [48,59]. Ono investigated the gradient projection in [37], which allows us to control the degree of smoothing of the output image intuitively. Several extensions of the gradient minimization were recently proposed to flexibly separate the structure and texture components in smoothing texture-rich images [39,40,41].
However, the gradient-based smoothing methods have inherent issues, resulting in undesirable artifacts, such as pseudo-edges and halos in the output images. When an input image contains regions with gradations, the output image often exhibits a piecewise constant appearance, commonly referred to as the staircasing effect. These gradation regions produce strong edges in the output, which are not present in the input image. These issues arise because characteristics related to the intensity and sign of gradients within the observed images are not explicitly considered constraints in optimization problems. Furthermore, these artifacts become more noticeable, particularly in detail enhancement and tone-mapping applications. For example, although these applications are frequently used for diagnosing X-ray images, the staircasing effect introduces a potential risk of misdiagnosis. Similarly, tone mapping is often applied in low-light scenes, such as autonomous driving applications. However, this effect may lead to a reduction in object recognition accuracy. Our primary objective is to mitigate those unexpected artifacts caused by the staircasing effect by incorporating appropriate constraints into the gradient domain within optimization problems.
In this paper, we propose effective smoothing methods based on minimizing the gradient with novel gradient constraints that suppress those pseudo-edge artifacts. In particular, we introduce two types of gradient constraints: a box-type gradient constraint and a ball-type constraint. We incorporate them in the gradient minimization problem. These constraints are imposed using an appropriate reference image (e.g., an input image is used as a reference for image smoothing) to suppress pseudo-edges in homogeneous regions and the blurring effect of strong edges. We find a solution to the proposed minimization problems via the alternating direction method of multipliers (ADMM) [37,60,61] for nonconvex optimization.
The contributions of this paper are as follows.
- Image smoothing while maintaining gradient characteristics of reference image: Existing smoothing methods based on the gradient and TV do not explicitly consider any constraints in the gradient domain. In the proposed method, the local smoothness properties of a reference image can be explicitly considered constraints in the gradient domain. Therefore, we can suppress artifacts, including the staircasing effect, through image smoothing.
- Strict or flexible gradient constraints on the sign of gradients: Since the box-type gradient constraint is strict with respect to the sign of gradients, gradient reversals are well suppressed. In contrast, the ball-type constraint is flexible with respect to the sign of gradients, allowing robust image smoothing, even when a reference image is degraded by noise and has different shading characteristics, including gradient reversals.
The remainder of this paper is organized as follows. In Section 2, we present several mathematical preliminaries and the ADMM algorithm. In Section 3, we introduce the novel box- and ball-type gradient constraints and the minimization problems for image smoothing. In Section 4, several examples are shown to confirm the validity of the proposed methods compared with the existing smoothing methods based on the gradient. Finally, Section 5 concludes the paper.
In the previous paper [62], we introduced only the box-type gradient constraint to extend the gradient minimization. Additionally, robustness to noise and performance when using some reference images with different luminance and colors with/without reversed edges were not sufficiently evaluated. In this paper, we show the limitation of the box-type gradient constraint and propose a novel ball-type gradient constraint that can be applied flexibly, even when using references with noise or edge reversals. We also extend the proposed gradient constraints to the gradient projection [37] and the details of the algorithm derivation. Furthermore, we examine an experiment on JPEG artifact removal.
2. Preliminaries
Throughout this paper, bold-faced lowercase and uppercase letters indicate vectors and matrices, respectively, and denotes N-dimensional vector space. We define the set of real-valued matrices as , and the block diagonal matrix of by . The transpose operation of a vector and matrix is denoted as .
2.1. Gradient
Let be an input vector. The pseudo-norm (note that this norm does not satisfy the properties of the norm; for simplicity in this paper, we refer to the pseudo-norm as the -norm) counts the number of nonzero elements, and it is denoted by
Let be a vectorized color image, and let N be the number of pixels. Further, let and be the vertical and horizontal first-order differential operators with a Neumann boundary, respectively; the differential operator is then defined by for a gray image and for a color image. In the gradient minimization, the group sparsity of the gradients is considered by concatenating the -norm [31,37,48], and it is defined as
A piece-wise smooth image is obtained by minimizing an optimization problem based on (2). In [31,48], a half quadratic optimization method is used to solve this optimization problem.
2.2. Alternating Direction Method of Multipliers
Alternating the direction method of multipliers (ADMM) [60] is a method of the proximal splitting algorithm that can treat convex optimization problems of the form
where F and G are usually assumed to be quadratic and proximable functions, respectively, and is a matrix with full-column rank. For any and , the ADMM algorithm is given by
2.3. Proximal Tools
The proximity operator [63] is a key tool of proximal splitting techniques. Let be an input vector. For any , the primary operator of f over is defined by
For a given nonempty closed convex set , the indicator function of is defined by
The proximity operator of is expressed as
The solution of should be in the set and minimize . Thus, for any index , this proximity operator is equivalent to the metric projection onto , i.e., .
Let and be the lower and upper bounds, respectively. The box constraint forces each element of into the dynamic range for , and its closed convex set is defined as
The computation of the metric projection onto for is given by
The ball constraint forces the Euclidean distance between the vector and the centered vector to be less than the radius , and its closed convex set is defined as
The computation of the metric projection onto is given by
3. Proposed Methods
To suppress the undesirable artifacts mentioned in Section 1, we introduce the following two types of gradient constraints.
3.1. Gradient Constraints
3.1.1. Box-Type Gradient Constraint
Let be a vectorized color image. We introduce the box-type gradient constraints in the positive and negative ranges:
where is a vectorized reference color image, is the differential operator for a color image introduced in (2), and , are gradient images. The notations and are the index sets of positive and negative elements in , respectively, where these sets satisfy and . The gradient intensity of an output image obtained by solving a minimization problem with (12) and (13) is limited to the range of the gradient values of the reference image . Thus, these constraints suppress pseudo-edges that do not exist in the reference image.
The major drawback of minimizing the total variation regularization based on the - or -norms is that it yields pseudo-edge artifacts, such as an undesirable staircasing effect on the homogeneous regions in many cases. These artifacts are more severe in the case of the -norm, as it has significant flattening effects. Figure 1 plots an example of the vertical first-order gradient signals of an input image and the smoothing results obtained by the two conventional methods—one is the gradient minimization [31], and the other is the gradient projection [37]—and the proposed methods with the box-type gradient constraint. The gradient signals of the gradient minimization and the gradient projection contain the gradients denoted by arrows that do not originally exist in the input image. Owing to the proposed gradient constraint, the gradient signal of the proposed methods is lower than that of the input image. When a reference image has local smoothness properties, artifacts such as halos and pseudo-edges can be suppressed by the proposed constraint. Similar results are obtained with the other channels and the horizontal direction.
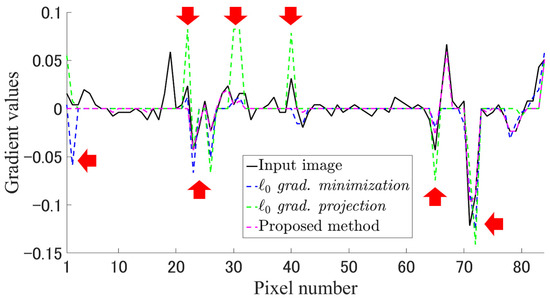
Figure 1.
Example of image smoothing: The black line, the dotted blue line, the dotted green line, and the dotted red line show the gradient signals of the input image, the smoothing results of the gradient minimization [31], the gradient projection [37], and ours with the box-type gradient constraints, respectively. Each gradient signal is the vertical first-order gradient of the G channel. The red arrows indicate pseudo-edges.
Figure 2a illustrates an example of the box-type gradient constraint in the case where the vertical gradient is positive, and the horizontal gradient is negative in the reference image. We see from the figure that the ideal gradient is not included in the box-type gradient constraint. This often occurs when there is noise in the input image. Because the sign of gradients is sensitive to noise, our method generates better results for noise-free images; however, the method may generate unexpected artifacts for noisy images. To overcome this limitation, we introduce a ball-type gradient constraint.
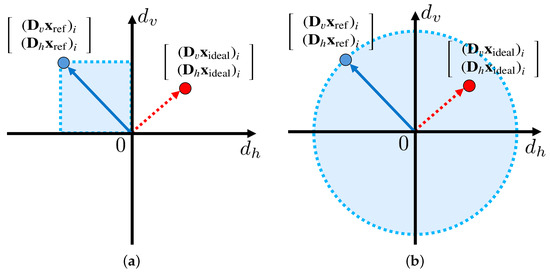
Figure 2.
Examples of the proposed gradient constraints: vertical and horizontal axes and represent gradient values of vertical and horizontal directions, respectively. The blue solid arrow and the dotted red arrow indicate the gradient vectors of reference and ideal images, respectively. The dotted blue box and circle represent areas that satisfy the gradient constraints, respectively. (a) Box-type gradient constraint. (b) Ball-type gradient constraint.
3.1.2. Ball-Type Gradient Constraint
Let the sets of indexes be for . We introduce the ball-type gradient constraint with respect to the n-th pixel as
where is the n-th sub-vector of with the entries specified by , such as
The ball-type gradient constraint limits the magnitude of the gradients of an output image to less than that of a reference image. Note that the signs of the gradients are not considered explicitly in these constraints.
Figure 2b illustrates an example of the ball-type gradient constraint with the same reference image as in Figure 2a. We see from this figure that the ball-type constraint is defined by a circle whose radius is the gradient magnitude of the reference image (see the dotted blue circle). Furthermore, the range of the ball-type constraint is more relaxed compared with the box-type one in Figure 2a, even with the same reference image. Therefore, even when we use a noisy image as a reference, in which the sign of the gradients varies locally, the ball-type constraint enables us to generate a smooth image that is locally smoother and more natural than the box-type one.
As described above, the ball-type constraint can obtain better results than the box-type one for a noisy image. However, when it is applied to a noise-free image, gradient reversals may occur, especially in the case of small-magnitude texture.
3.2. -Smoothing Based on Box-Type Gradient Constraint
3.2.1. Minimization Problem
Let and be a vectorized input color image and a vectorized reference image for the proposed box-type gradient constraint, respectively. The image-smoothing problem with the proposed gradient constraints (12) and (13) is defined by
where is a balancing weight of the two costs. The first term in (16) is defined by (2). The second term is a data-fidelity term calculating the squared error between the input and output images. Note that the objective function, excluding the gradient constraints from (16), is equivalent to that of the gradient minimization introduced in [31].
To find a solution of (16), we use ADMM described in Section 2.2. Since the first term of (16) is a nonconvex function, there is no guarantee that the solution obtained by ADMM is a global minimum solution of (16). However, as stated in [37,61], we experimentally confirmed that a reasonable solution satisfying the constraints can be obtained by carefully decreasing the step size of the algorithm in each iteration.
3.2.2. Optimization
Let , , where and are the matrices that extract the elements from corresponding to the indexes included in and , respectively. The convex sets and are defined as
where and denote the number of the indices in their sets, which satisfy , and is a vector filled with zeros. To apply ADMM, we first reformulate (16) into the following unconstrained problem:
where and are the indicator functions (let be an input vector; for a given non-empty closed convex set , the indicator function of is defined by , which returns 0 if , and otherwise) of and . These functions guarantee that the positive and negative gradient intensities of the optimal image fall in the ranges and . The role of the third and fourth terms of (17) correspond to the role of the first and second constraints of (16), respectively.
By introducing auxiliary variables , and , we rewrite the minimization problem (17) into the following equivalent expression:
The algorithm for solving Equation (18) with is summarized in Algorithm 1.
| Algorithm 1 Proposed algorithm for (18). |
|
The update of in Algorithm 1 is achieved by solving the following quadratic minimization problem (hereafter, the superscript () is omitted for simplicity):
Thus, by setting the first-order derivative to zero, the optimal solution is characterized by the system of linear equations:
where is a matrix of size , is a -dimensional vector, and is an identity matrix. The optimal solution is obtained by the inverse problem . If we set , the third term of the right side in the formula can be rewritten as . Since the boundary condition of is periodic and the matrix is a block circulant matrix with circulant blocks (BCCB), it is diagonalized by the 2D fast discrete Fourier transform (2DFFT). Thus, the inverse problem of (20) can be calculated as
where and are the 2D-FFT and its inverse matrices, respectively, and is the diagonal matrix with its entries being the Fourier-transformed Laplacian filter kernel. Therefore, its inversion is reduced to entry-wise division.
For the update of , we need to compute the pseudo-proximity operator of the -norm. By dividing to sub-vectors as , in which is introduced in Section 3.1.2 and can be regarded as the auxiliary variable for (see (15)), the pseudo-proximity operator equals to a group hard-thresholding operation for each sub-vector [48,61]. Thus, the optimal solution of the n-th sub-vector is obtained by
where is the m-th element of .
To update and , we need to compute the proximity operator of the indicator functions and . By (9), these are simply projections onto each set, respectively, i.e., for by
and for by
To stabilize ADMM for nonconvex optimization, a scalar is introduced to gradually decrease the value of as in the 11th–13th lines of Algorithm 1. The algorithm continues until the following stopping criterion is satisfied:
where we set a small value to (e.g., ). Although there is no theoretical guarantee of convergence for our algorithm, we show that the sequence generated by this algorithm experimentally converges to a reasonable solution with sufficiently small values for ; similar strategies have been employed in the existing minimization algorithms for the -norm [37,48,61].
3.3. -Smoothing Based on Ball-Type Gradient Constraint
The image-smoothing problem with the proposed ball-type gradient constraint (14), which is the modified version of (16), is defined by
Similar to the preceding section, we solve the minimization problem (26) by applying ADMM to it. Now, the convex set is defined for by
where . We reformulate (26) into the following unconstrained problem by introducing the indicator functions of , and then, we also introduce auxiliary variables and to non-differential functions
where is the n-th sub-vector of specified by .
The algorithm for solving (28) is obtained by slightly modifying Algorithm 1. In particular, the update of in line 4 of Algorithm 1 is obtained by
In the update of , we calculate the following metric projection onto the ball according to (11) instead of the 8th and 9th lines of Algorithm 1, i.e., for , by
3.4. Gradient Projection with Gradient Constraint
Our proposed box-/ball-type gradient constraints can be incorporated with not only the minimization problem of the gradient minimization [31] but also with that of the gradient projection [37]. An image-smoothing problem based on the gradient projection (for simplicity, we only discuss using the ball-type gradient constraint; note that the box-type gradient constraints can be also used as well) with the proposed gradient constraint is defined by
where is the parameter specified by a user that is the least upper bound of . It allows us to intuitively control the degree of smoothing of the output image .
Similar to the preceding section, a solution of (31) can be estimated based on Algorithm 1 after transforming it into an equation applicable to ADMM (the indicator function of the inequality constraint on is defined in (9) of [37], and its pseudo-metric projection is derived in (16) of [37]).
4. Experiments
To clarify the differences in the characteristics of the proposed methods with the box- and ball-type gradient constraints, we first conducted noise removal experiments using some reference images. We then applied the proposed methods to various applications, such as image smoothing, detail enhancement, tone mapping, and JPEG artifact removal, and the results were compared with those of two existing methods based on the gradient: gradient minimization [31], and gradient projection [37] (for the implementation of the existing methods, we used the source code distributed by the authors of each paper).
All experiments were performed using MATLAB R2021a on a computer with an AMD EPYC 7402P 2.80 GHz processor and 128 GB RAM. To accelerate the computation time of the proposed methods, we used an NVIDIA GeForce RTX 3090 GPU. For the parameters of our methods, we set , , and in all experiments. For the reference image , we set in the three experiments described in Section 4.2, Section 4.3 and Section 4.4, respectively. Note that the dynamic range of input images was normalized in .
4.1. Box-Type vs. Ball-Type Gradient Constraint
The performance of our methods depend on the variation of the luminance and color in a reference image. Accordingly, we studied the sensitivity of our methods with respect to a reference image by conducting an experiment on Gaussian noise removal.
We generated a noisy image, which is shown in Figure 3b, by adding zero-mean Gaussian noise with standard deviation to the ground truth image shown in Figure 3a. Then, four types of images, shown in Figure 4(a-1) ground truth image, a-2 horizontally flipped image of a-1, a-3 hue shift image of a-1, and a-4 horizontally flipped and hue shift image of a-1, were prepared, each of which was used as a reference image of our proposed gradient constraints. For the quality metric, we used the peak signal-to-noise ratio (PSNR). For the smoothing parameter setting, the balancing weight was set to maximize PSNR. Note that the purpose of this experiment is not to evaluate the pure performance of noise removal but to clarify the sensitivity of the method.

Figure 3.
Ground truth and input images on zero-mean Gaussian noise removal (). (a) Ground truth. (b) Input image.
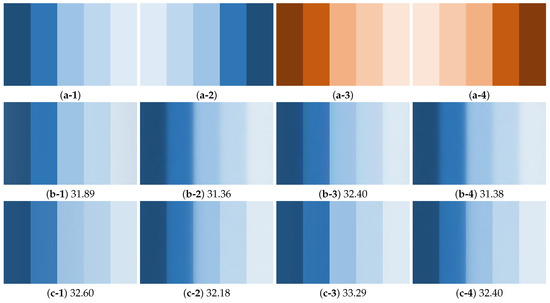
Figure 4.
Noise removal results and their PSNR values [dB]: (from left to right) (a1–4) reference images, (b1–4) our image with the box-type constraint, and (c1–4) our image with the ball-type one.
Figure 4 shows the noise removal results and their PSNR values. One can see from Figure 4b,c that our images with the ball-type constraint have higher PSNR and visually better results than the box-type image for all cases. The results of Figure 4(b-2,b-4) are over-smoothed because the reference images have luminance variations that are considerably different from those of the input image (there are flipped relationships between the luminance variations of the input and reference images in the horizontal direction). This is because the sign of the gradients of the reference images is often reversed from the ideal one around the edges. The box-type constraint does not prevent the smoothed image from having the gradients whose sign is reversed from that of the reference image, thus yielding blurred images. In Figure 4(b-1,b-3), this constraint generates a better smooth result with sharper edges similar to those of the ground truth image; however, pseudo-color artifacts often occur around edges as shown in Figure 4(b-3). Thus, this constraint is very sensitive to the sign of image gradients unless an input image is used as a reference. In contrast, the ball-type constraint robustly generates a better smooth result with sharper edges that is the same as that in the input image, even if the reference images have luminance and color variations considerably different from those in the input image.
4.2. Detail Enhancement
Based on the methods [5,6], we performed the detail enhancement as follows: (i) obtain a base layer by applying each method to an input image; (ii) calculate a detail layer by subtracting the base layer from the input image; (iii) amplify the detail layer by scaling factor ; and (iv) reconstruct a detail-enhanced image by summing the base layer and the enhanced detail layer.
Figure 5 and Figure 6 show the smoothing and detail enhancement results obtained by the existing methods and the proposed methods (we took input images from an extensive database of royalty-free images https://pixabay.com/en/ accessed on 8 January 2018). In Section 4.2 and Section 4.3, since there are visually no differences between the results of the proposed methods with the box- and ball-type gradient constraints, we only show the results of the proposed method with the box-type gradient constraint. For a fair comparison, we adjusted the smoothing parameters of each method so that the -norms are the same in the input and output images. The scaling factor s was set to . Figure 5 and Figure 6 indicate that the contrast in the entire image is maintained for all methods. However, the results of [31] have halo-like artifacts in the region with gradation indicated by the red square window in (b), and the color of the clouds is changed. Pseudo-edge artifacts, such as the staircasing effect, occur in the sky region of the results of [37] (indicated by the yellow and red square windows in (c)). In contrast, our methods do not have these undesirable artifacts because the gradient constraints suppress pseudo-edges in the homogeneous regions.

Figure 5.
Detail enhancement results 1: (upper) smoothing results and (lower) detail enhancement results. (a) Input. (b) gradient minimization [31]. (c) gradient projection [37]. (d) Ours. ©2018 IEEE. Reprinted, with permission, from [62].

Figure 6.
Detail enhancement results 2: (upper) smoothing results and (lower) detail enhancement results. (a) Input. (b) gradient minimization [31]. (c) gradient projection [37]. (d) Ours. ©2018 IEEE. Reprinted, with permission, from [62].
4.3. Tone Mapping
Next, we applied these methods for layer separation in the tone-mapping framework [7].
Figure 7 shows the tone-mapping results, where we also show the result of Reinhard et al.’s global tone-mapping operator [64] for reference. Figure 7b,c show that the halo and pseudo-edge artifacts occurred, especially at the boundary between the bright and dark regions. In contrast, the proposed methods sufficiently suppressed these artifacts.

Figure 7.
Tone-mapping results. (a) Global operator [64]. (b) gradient minimization [31]. (c) gradient projection [37]. (d) Ours. ©2018 IEEE. Reprinted, with permission, from [62].
To show the robustness of the degree of smoothing, we applied the gradient minimization [31] and the proposed methods to an input HDR image with different smoothing parameters. The smoothing parameters were adjusted so that the mean squared error (MSE) of the smoothing results was and , and these results are shown in Figure 8. One sees from Figure 8(b-1,c-1,d-1) that the staircasing effects and pseudo-color edges occur. In addition, these artifacts are more noticeable as the smoothing degree increases. In contrast, the results of the proposed methods have few artifacts. Even in Figure 8(d-2), which is the smoothest result, noticeable artifacts do not appear. In Section 4.2 and Section 4.3, we applied the proposed methods to dozens of images and obtained similar results.

Figure 8.
Tone-mapping results obtained by different smoothing parameters and their MSE values: (a) Reinhard et al.’s global operator [64], (b–d) are obtained by Durand and Dorsey’s tone-mapping framework [7] with (·-1) gradient minimization [31] and (·-2) our methods. ©2018 IEEE. Reprinted, with permission, from [62].
4.4. JPEG Artifact Removal in Clip-Art Images
Input images were generated from clip-art images (we took ten test images from the dataset provided in https://google.github.io/cartoonset/ accessed on 20 July 2019), which were compressed by standard JPEG with quality values in the range of . The resultant images were evaluated by using two quality metrics: PSNR and structural similarity (SSIM) [65]. In each method, we adjusted the degree of noise removal to obtain the visually best restoration results, i.e., maximizing the smoothness while preserving the edges of the images as much as possible (we only showed the results of the proposed methods obtained with the ball-type gradient constraint because it is more robust than the box-type constraint for noise removal).
Figure 9a,b plot the PSNR [dB] and SSIM values averaged over ten test images, respectively. It can be seen that the PSNR and SSIM of the proposed methods are higher than those of the existing methods in most cases.
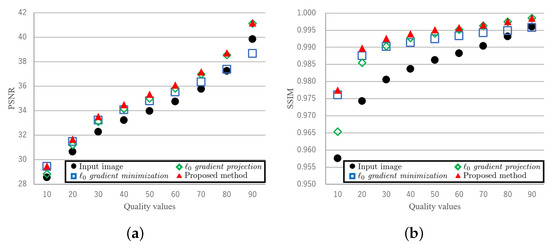
Figure 9.
Comparison PSNR and SSIM for clip-art JPEG artifact removal. (a) Peak signal-to-noise ratio (PSNR) [dB]. (b) Structural similarity (SSIM) [65].
Figure 10 shows the results and their PSNR values [dB] of two images in the cases of the quality value with 20. Block-wise artifacts in the JPEG images shown in Figure 10(b-1,b-2) are sufficiently removed by the proposed methods, while the existing methods retain them (see close-up images indicated by the red and blue boxes). Our methods have the highest PSNR in both images.
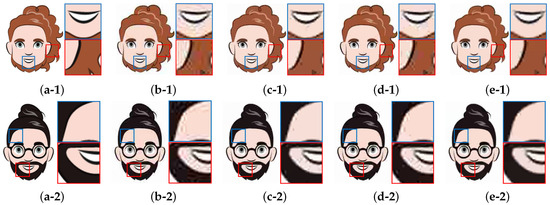
Figure 10.
Results of clip-art JPEG artifact removal and their PSNR [dB]. (a) Ground truth, (b) Input image, (c-1) [31], 31.51, (c-2) [31], 32.18, (d-1) [37], 31.19, (d-2) [37], 31.89, (e-1) Ours, 31.81, (e-2) Ours, 32.23.
5. Conclusions
We proposed effective smoothing methods based on minimizing the gradient using novel gradient constraints. To suppress the pseudo-edge artifacts such as the staircasing effect, box- and ball-type gradient constraints were introduced. These constraints limited the gradient intensity of an output image to the range of a reference image. By solving the gradient minimization problem based on the proposed gradient constraints via ADMM for nonconvex optimization, we effectively preserved the strong edges and removed weak edges without yielding pseudo-edges and halo artifacts. It was confirmed that the smoothed image obtained by the proposed method can generate better contrast-enhanced images and tone map images without pseudo-edges or halos. These results suggest the potential for delivering more dependable image diagnosis and recognition outcomes in medical imaging and autonomous driving applications, where image enhancement applications are essential. Throughout all our experiments, we consistently observed the effectiveness of the proposed methods in comparison to existing gradient-based methods.
In future work, we will apply our proposed gradient constraints for other optimization problems, e.g., intrinsic image decomposition, reflection removal, and flash/no-flash image blending.
Author Contributions
Methodology, R.M. and M.O.; software, R.M.; validation, R.M. and M.O.; formal analysis, R.M. and M.O.; investigation, R.M. and M.O.; data curation, R.M.; writing—original draft preparation, R.M. and M.O.; writing—review and editing, R.M. and M.O.; project administration, R.M. and M.O.; funding acquisition, R.M. and M.O. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by JSPS KAKENHI Grant Number 21K17767 and MEXT Promotion of Distinctive Joint Research Center Program Grant Number #JPMXP 0621467946. The experiments in this paper were performed using DeeplearningBOX/Alpha Workstation at The University of Kitakyushu.
Data Availability Statement
Data will be shared with interested third parties on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear Total Variation Based Noise Removal Algorithms. Physics D 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A. An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems. IEEE Trans. Image Process. 2011, 20, 681–695. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Zheng, S.; Jia, J. Unnatural L0 Sparse Representation for Natural Image Deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; pp. 1107–1114. [Google Scholar] [CrossRef]
- Pan, J.; Hu, Z.; Su, Z.; Yang, M. Deblurring Text Images via L0-Regularized Intensity and Gradient Prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 2901–2908. [Google Scholar] [CrossRef]
- Farbman, Z.; Fattal, R.; Lischinski, D.; Szeliski, R. Edge-preserving Decompositions for Multi-scale Tone and Detail Manipulation. ACM Trans. Graph. 2008, 27, 67. [Google Scholar] [CrossRef]
- Gastal, E.S.L.; Oliveira, M.M. Domain Transform for Edge-aware Image and Video Processing. ACM Trans. Graph. 2011, 30, 69. [Google Scholar] [CrossRef]
- Durand, F.; Dorsey, J. Fast Bilateral Filtering for the Display of High-dynamic-range Images. ACM Trans. Graph. 2002, 21, 257–266. [Google Scholar] [CrossRef]
- Fattal, R. Edge-avoiding Wavelets and Their Applications. ACM Trans. Graph. 2009, 28, 22. [Google Scholar] [CrossRef]
- Liang, Z.; Xu, J.; Zhang, D.; Cao, Z.; Zhang, L. A Hybrid L1-L0 Layer Decomposition Model for Tone Mapping. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 4758–4766. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Bioucas-Dias, J.M. Restoration of Poissonian Images Using Alternating Direction Optimization. IEEE Trans. Image Process. 2010, 19, 3133–3145. [Google Scholar] [CrossRef]
- Xu, Q.; Yu, H.; Mou, X.; Zhang, L.; Hsieh, J.; Wang, G. Low-Dose X-ray CT Reconstruction via Dictionary Learning. IEEE Trans. Med. Imaging 2012, 31, 1682–1697. [Google Scholar] [CrossRef]
- Ramani, S.; Fessler, J.A. A Splitting-Based Iterative Algorithm for Accelerated Statistical X-Ray CT Reconstruction. IEEE Trans. Med. Imaging 2012, 31, 677–688. [Google Scholar] [CrossRef]
- Graber, G.; Pock, T.; Bischof, H. Online 3D reconstruction using convex optimization. In Proceedings of the IEEE International Conference on Computer Vision Workshops (ICCV Workshops), Barcelona, Spain, 6–13 November 2011; pp. 708–711. [Google Scholar] [CrossRef]
- Ferstl, D.; Reinbacher, C.; Ranftl, R.; Ruether, M.; Bischof, H. Image Guided Depth Upsampling Using Anisotropic Total Generalized Variation. In Proceedings of the IEEE International Conference on Computer Vision Workshops (ICCV), Sydney, Australia, 1–8 December 2013; pp. 993–1000. [Google Scholar] [CrossRef]
- Wang, Q.; Tao, Y.; Lin, H. Edge-Aware Volume Smoothing Using L0 Gradient Minimization. Comput. Graph. Forum 2015, 34, 131–140. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Shen, H. Hyperspectral Image Denoising Employing a Spectral-Spatial Adaptive Total Variation Model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3660–3677. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Shen, H. Hyperspectral Image Denoising with a Spatial-Spectral View Fusion Strategy. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2314–2325. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral Image Denoising Employing a Spatial-Spectral Deep Residual Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1205–1218. [Google Scholar] [CrossRef]
- Likforman-Sulem, L.; Darbon, J.; Smith, E.H.B. Enhancement of historical printed document images by combining Total Variation regularization and Non-local Means filtering. Image Vis. Comput. 2011, 29, 351–363. [Google Scholar] [CrossRef]
- Ge, F.; He, L. A de-noising method based on L0 gradient minimization and guided filter for ancient Chinese calligraphy works on steles. EURASIP J. Image Vid. Process. 2019, 2019, 32. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the IEEE International Conference on Computer Vision Workshops (ICCV), Bombay, India, 7 January 1998; pp. 839–846. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Seo, H.J.; Milanfar, P. Robust flash denoising/deblurring by iterative guided filtering. EURASIP J. Adv. Signal Process. 2012, 2012, 3. [Google Scholar] [CrossRef][Green Version]
- Baba, T.; Matsuoka, R.; Shirai, K.; Okuda, M. Misaligned Image Integration With Local Linear Model. IEEE Trans. Image Process. 2016, 25, 2035–2044. [Google Scholar] [CrossRef]
- Matsuoka, R.; Shirai, K.; Okuda, M. Reference-based local color distribution transformation method and its application to image integration. Signal Process. Image Comm. 2019, 76, 231–242. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A Non-Local Algorithm for Image Denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–26 June 2005; pp. 60–65. [Google Scholar] [CrossRef]
- Zhan, Y.; Ding, M.; Xiao, F.; Zhang, X. An Improved Non-local Means Filter for Image Denoising. In Proceedings of the International Conference on Intelligent Computation and Bio-Medical Instrumentation (ICBMI), Wuhan, China, 14–17 December 2011; pp. 31–34. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A.T. A New TwIST: Two-Step Iterative Shrinkage/Thresholding Algorithms for Image Restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient Projection for Sparse Reconstruction: Application to Compressed Sensing and Other Inverse Problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Wright, S.J.; Nowak, R.D.; Figueiredo, M.A.T. Sparse Reconstruction by Separable Approximation. IEEE Trans. Signal Process. 2009, 57, 2479–2493. [Google Scholar] [CrossRef]
- Xu, L.; Lu, C.; Xu, Y.; Jia, J. Image Smoothing via L0 Gradient Minimization. ACM Trans. Graph. 2011, 30, 174. [Google Scholar] [CrossRef]
- Miyata, T.; Sakai, Y. Vectorized total variation defined by weighted L infinity norm for utilizing inter channel dependency. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Orlando, FL, USA, 30 September–3 October 2012; pp. 3057–3060. [Google Scholar] [CrossRef]
- Xu, L.; Yan, Q.; Xia, Y.; Jia, J. Structure Extraction from Texture via Relative Total Variation. ACM Trans. Graph. 2012, 31, 139. [Google Scholar] [CrossRef]
- Condat, L. A Generic Proximal Algorithm for Convex Optimization—Application to Total Variation Minimization. IEEE SPS Lett. 2014, 21, 985–989. [Google Scholar] [CrossRef]
- Ono, S.; Yamada, I. Decorrelated Vectorial Total Variation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 4090–4097. [Google Scholar] [CrossRef]
- Bi, S.; Han, X.; Yu, Y. An L1 Image Transform for Edge-preserving Smoothing and Scene-level Intrinsic Decomposition. ACM Trans. Graph. 2015, 34, 78. [Google Scholar] [CrossRef]
- Ono, S. L0 Gradient Projection. IEEE Trans. Image Process. 2017, 26, 1554–1564. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, I.; Matsuoka, R. A Study on JPEG Artifact Removal by Four-Directional Difference-based ℓ0,1 norm Regularization. In Proceedings of the IEEE Global Conference on Consumer Electronics (GCCE), Osaka, Japan, 18–21 October 2022; pp. 724–725. [Google Scholar] [CrossRef]
- Ma, X.; Li, X.; Zhou, Y.; Zhang, C. Image smoothing based on global sparsity decomposition and a variable parameter. Comput. Vis. Media 2021, 7, 483–497. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, P.; Lei, Y.; Huang, X.; Yang, J.; Ng, M. A Generalized Framework for Edge-Preserving and Structure-Preserving Image Smoothing. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 6631–6648. [Google Scholar] [CrossRef]
- Huang, J.; Wang, H.; Wang, X.; Ruzhansky, M. Semi-Sparsity for Smoothing Filters. IEEE Trans. Image Process. 2023, 32, 1627–1639. [Google Scholar] [CrossRef]
- Li, Y.; Brown, M.S. Single Image Layer Separation Using Relative Smoothness. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 2752–2759. [Google Scholar] [CrossRef]
- Shibata, T.; Akai, Y.; Matsuoka, R. Reflection Removal Using RGB-D Images. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 1862–1866. [Google Scholar] [CrossRef]
- Li, Y.; Tan, R.T.; Guo, X.; Lu, J.; Brown, M.S. Single Image Rain Streak Decomposition Using Layer Priors. IEEE Trans. Image Process. 2017, 26, 3874–3885. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Huang, T.; Zhao, X.; Deng, L.; Wang, Y. A Novel Tensor-Based Video Rain Streaks Removal Approach via Utilizing Discriminatively Intrinsic Priors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2818–2827. [Google Scholar] [CrossRef]
- Jiang, T.; Huang, T.; Zhao, X.; Deng, L.; Wang, Y. FastDeRain: A Novel Video Rain Streak Removal Method Using Directional Gradient Priors. IEEE Trans. Image Process. 2019, 28, 2089–2102. [Google Scholar] [CrossRef] [PubMed]
- Jeon, J.; Cho, S.; Tong, X.; Lee, S. Intrinsic Image Decomposition Using Structure-Texture Separation and Surface Normals. In European Conference Computer Vision (ECCV); Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer: Cham, Switzerland, 2014; pp. 218–233. [Google Scholar]
- Matsuoka, R.; Baba, T.; Rizkinia, M.; Okuda, M. White Balancing by Using Multiple Images via Intrinsic Image Decomposition. IEICE Trans. Inf. Syst. 2015, 98, 1562–1570. [Google Scholar] [CrossRef]
- Matsuoka, R.; Ono, S.; Okuda, M. Transformed-Domain Robust Multiple-Exposure Blending With Huber Loss. IEEE Access 2019, 7, 162282–162296. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. A New Pansharpening Algorithm Based on Total Variation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 318–322. [Google Scholar] [CrossRef]
- He, X.; Condat, L.; Bioucas-Dias, J.M.; Chanussot, J.; Xia, J. A New Pansharpening Method Based on Spatial and Spectral Sparsity Priors. IEEE Trans. Image Process. 2014, 23, 4160–4174. [Google Scholar] [CrossRef] [PubMed]
- Takeyama, S.; Ono, S.; Kumazawa, I. Robust and Effective Hyperspectral Pansharpening Using Spatio-Spectral Total Variation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 1603–1607. [Google Scholar] [CrossRef]
- Takeyama, S.; Ono, S.; Kumazawa, I. Hyperspectral Pansharpening Using Noisy Panchromatic Image. In Proceedings of the APSIPA Annual Summit and Conference (APSIPA ASC), Honolulu, HI, USA, 12–15 November 2018; pp. 880–885. [Google Scholar] [CrossRef]
- Zach, C.; Pock, T.; Bischof, H. A Globally Optimal Algorithm for Robust TV-L1 Range Image Integration. In Proceedings of the IEEE International Conference on Computer Vision Workshops (ICCV), Venice, Italy, 22–29 October 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Sénchez Pèrez, J.; Meinhardt-Llopis, E.; Facciolo, G. TV-L1 Optical Flow Estimation. Image Process. Line 2013, 3, 137–150. [Google Scholar] [CrossRef]
- Huber, P.J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Ono, S.; Yamada, I. Signal Recovery With Certain Involved Convex Data-Fidelity Constraints. IEEE Trans. Signal Process. 2015, 63, 6149–6163. [Google Scholar] [CrossRef]
- Nguyen, R.M.H.; Brown, M.S. Fast and Effective L0 Gradient Minimization by Region Fusion. In Proceedings of the IEEE International Conference on Computer Vision Workshops (ICCV), Santiago, Chile, 7–13 December 2015; pp. 208–216. [Google Scholar] [CrossRef]
- Arvanitopoulos, N.; Achanta, R.; Süsstrunk, S. Single Image Reflection Suppression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1752–1760. [Google Scholar] [CrossRef]
- Gabay, D.; Mercier, B. A dual algorithm for the solution of nonlinear variational problems via finite element approximation. Comput. Math. Appl. 1976, 2, 17–40. [Google Scholar] [CrossRef]
- Matsuoka, R.; Kyochi, S.; Ono, S.; Okuda, M. Joint Sparsity and Order Optimization Based on ADMM With Non-Uniform Group Hard Thresholding. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 1602–1613. [Google Scholar] [CrossRef]
- Akai, Y.; Shibata, T.; Matsuoka, R.; Okuda, M. L0 Smoothing Based on Gradient Constraints. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 3943–3947. [Google Scholar] [CrossRef]
- Moreau, J.J. Fonctions convexes duales et points proximaux dans un espace hilbertien. C. R. Acad. Sci. 1962, 255, 2897–2899. [Google Scholar]
- Reinhard, E.; Stark, M.; Shirley, P.; Ferwerda, J. Photographic Tone Reproduction for Digital Images. ACM Trans. Graph. 2002, 21, 267–276. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).