A Nonlinear Optimization Design Algorithm for Nearly Linear-Phase 2D IIR Digital Filters
Abstract
1. Introduction
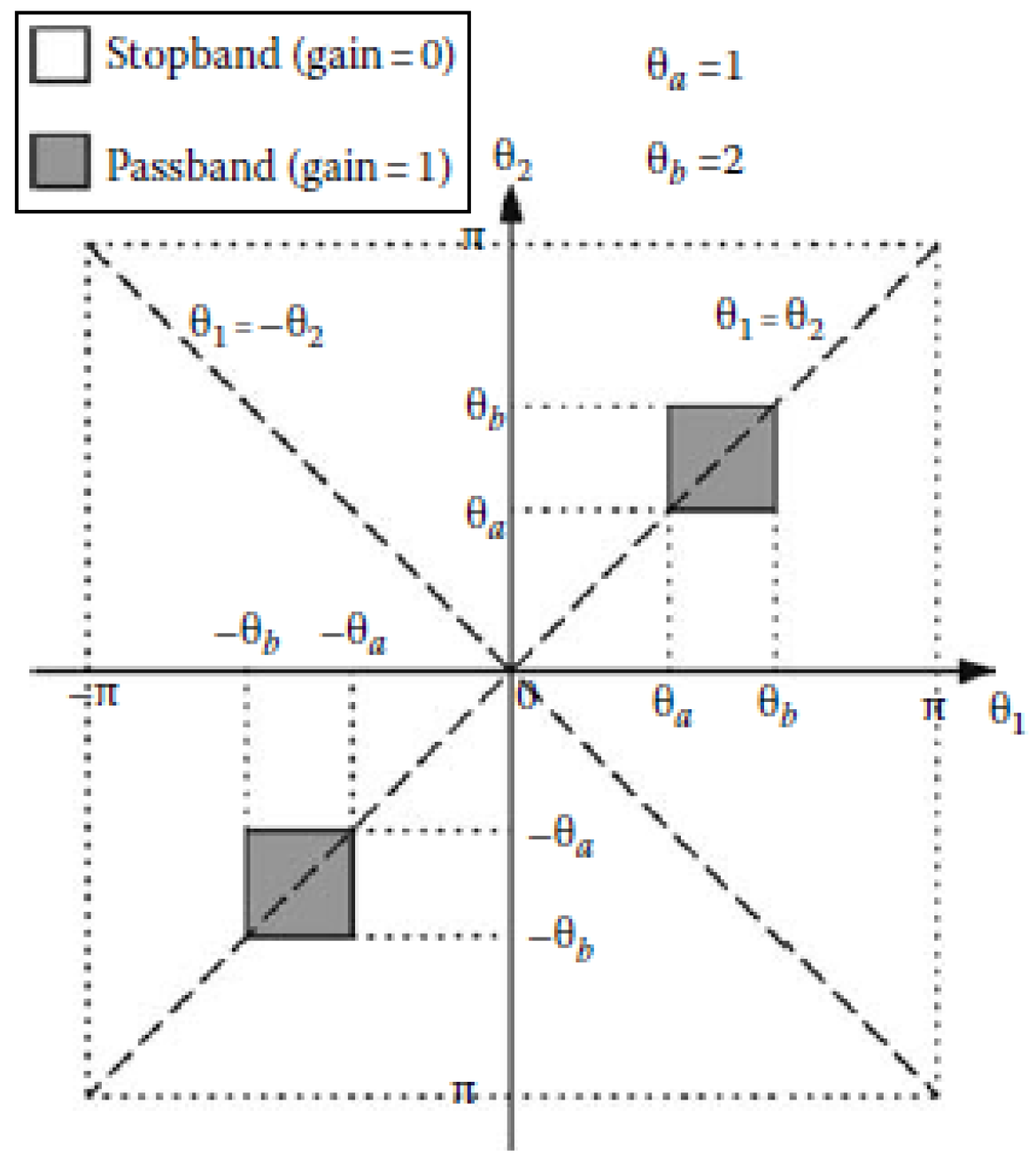
2. Formulation of the Design Problem
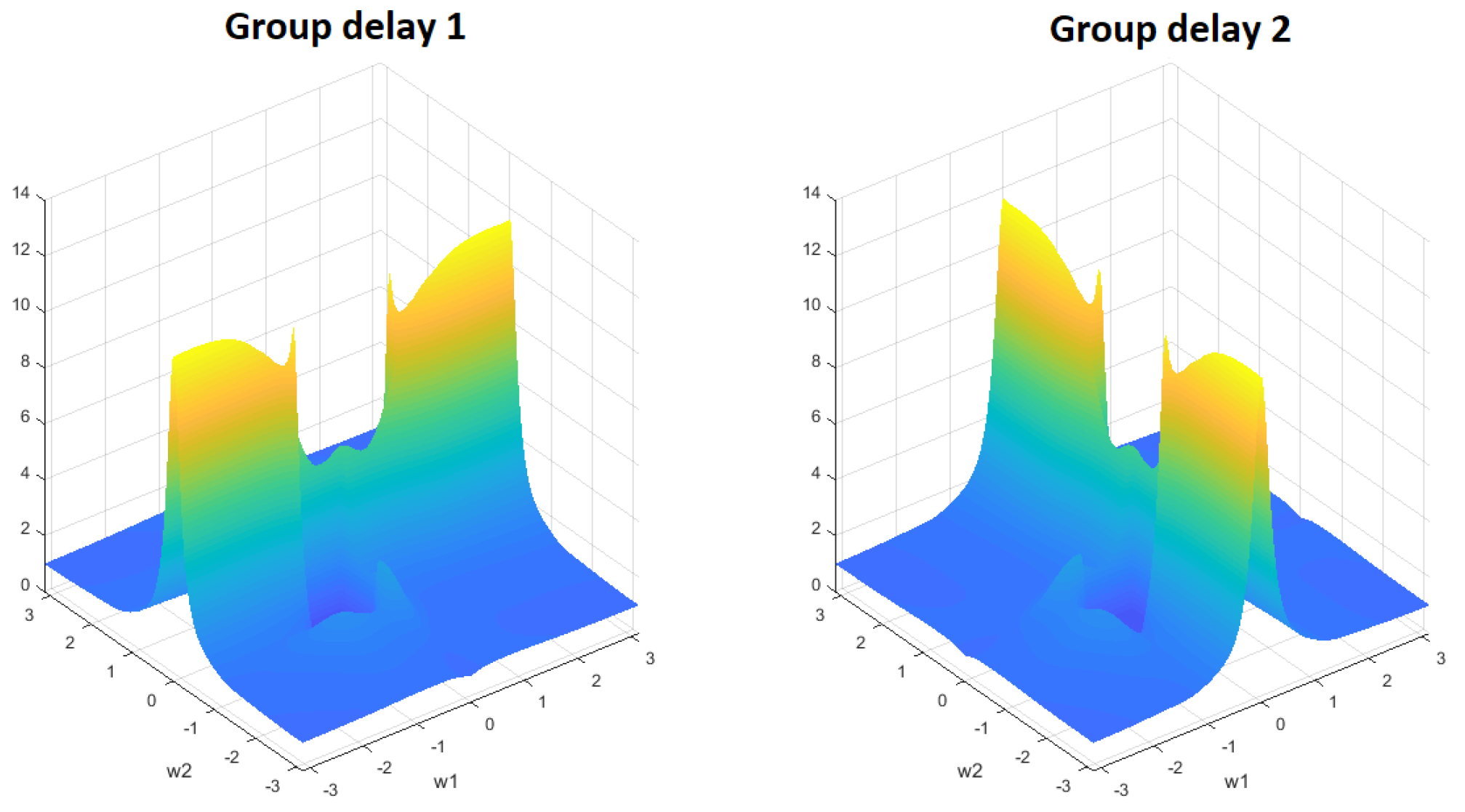
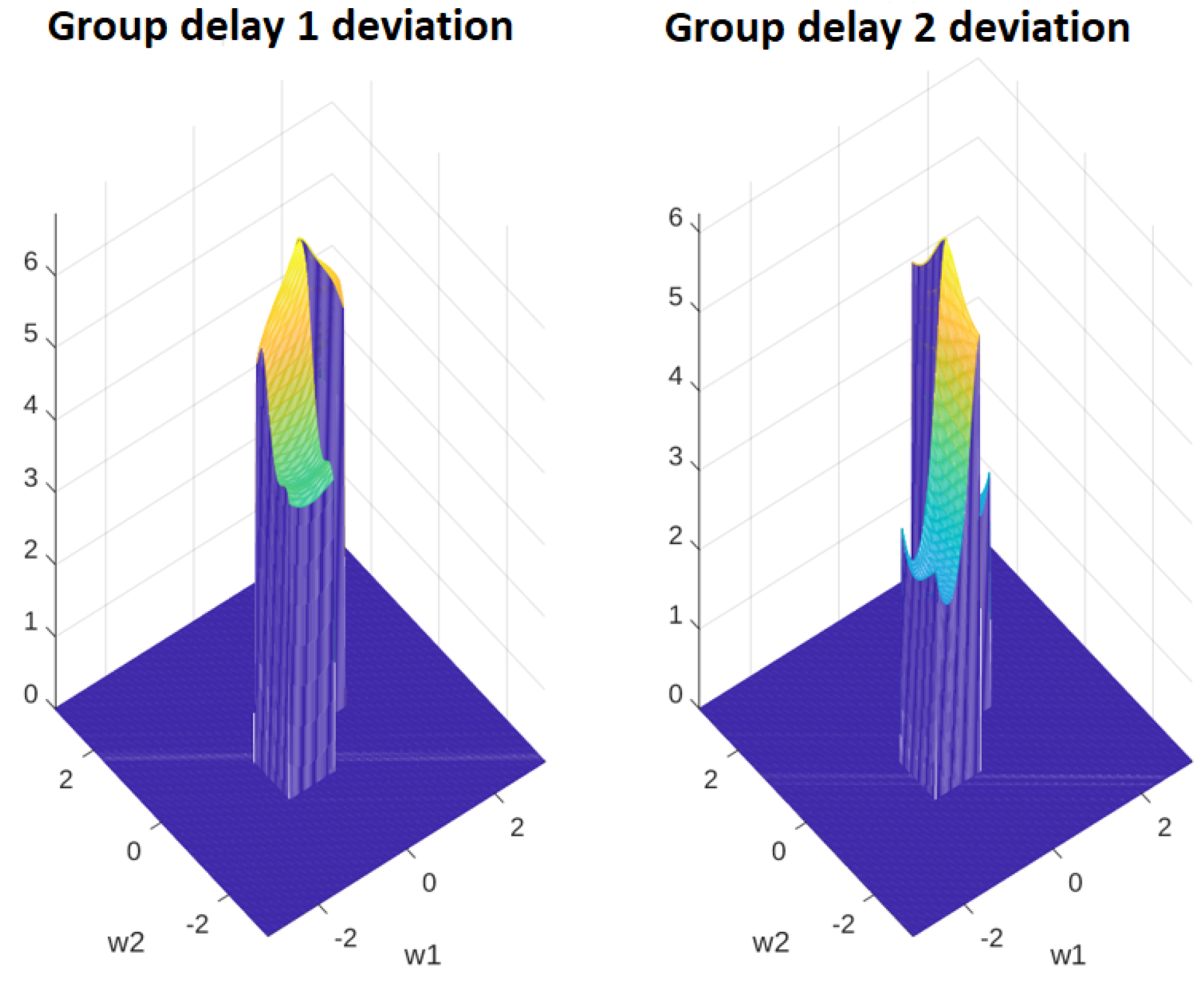
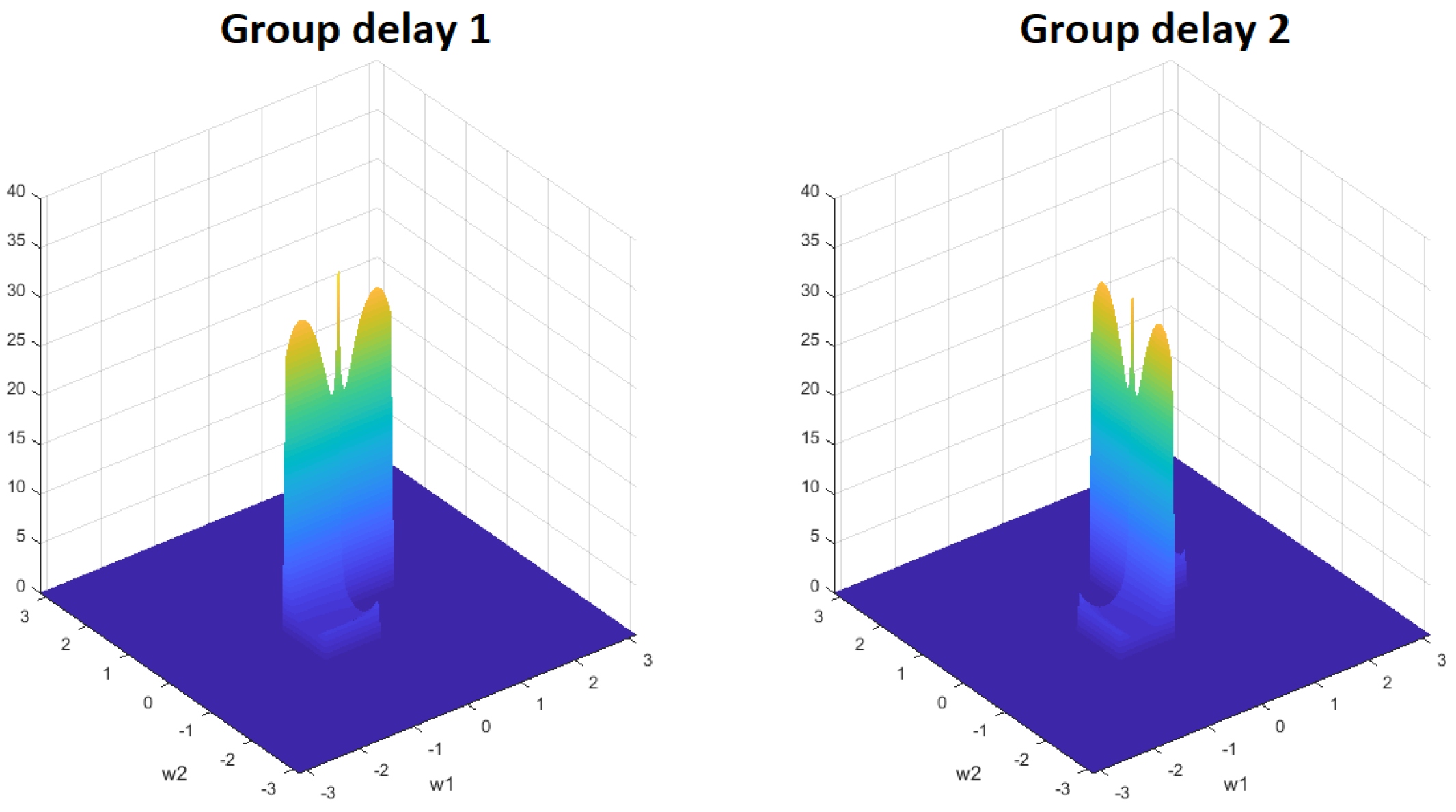
2.1. Passband Group Delay Deviations
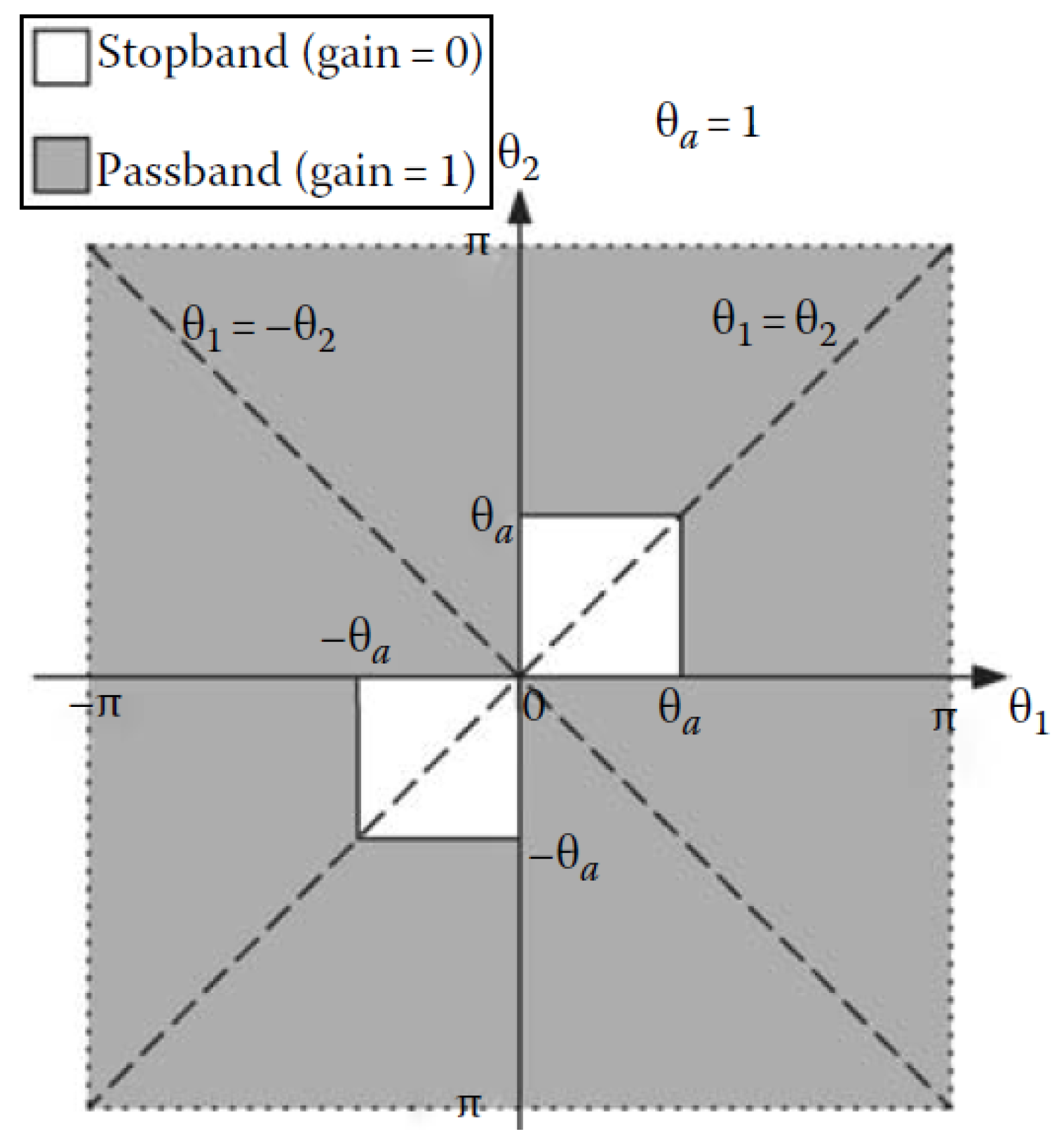
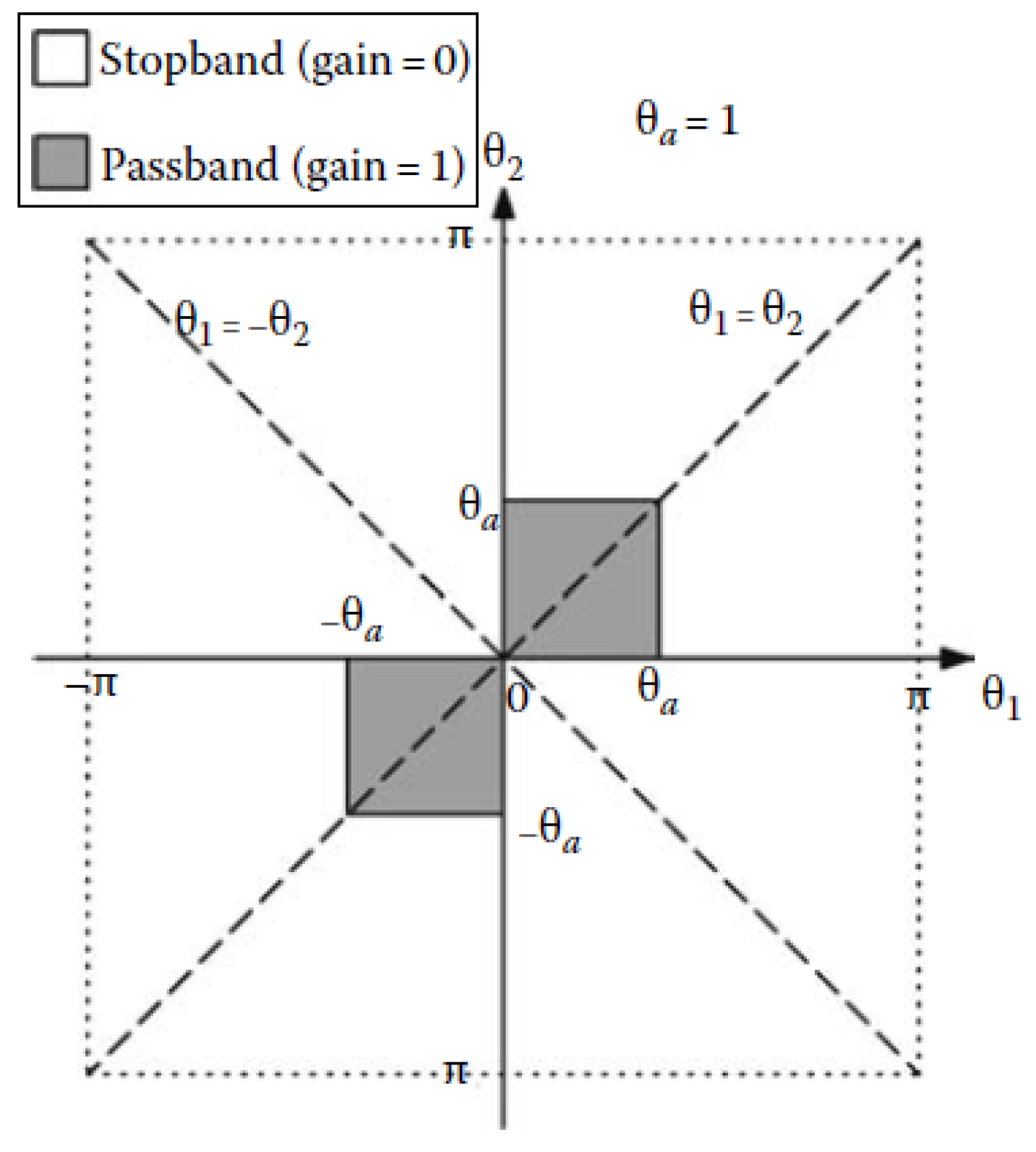
2.2. Passband Amplitude Error
3. Filter Stability
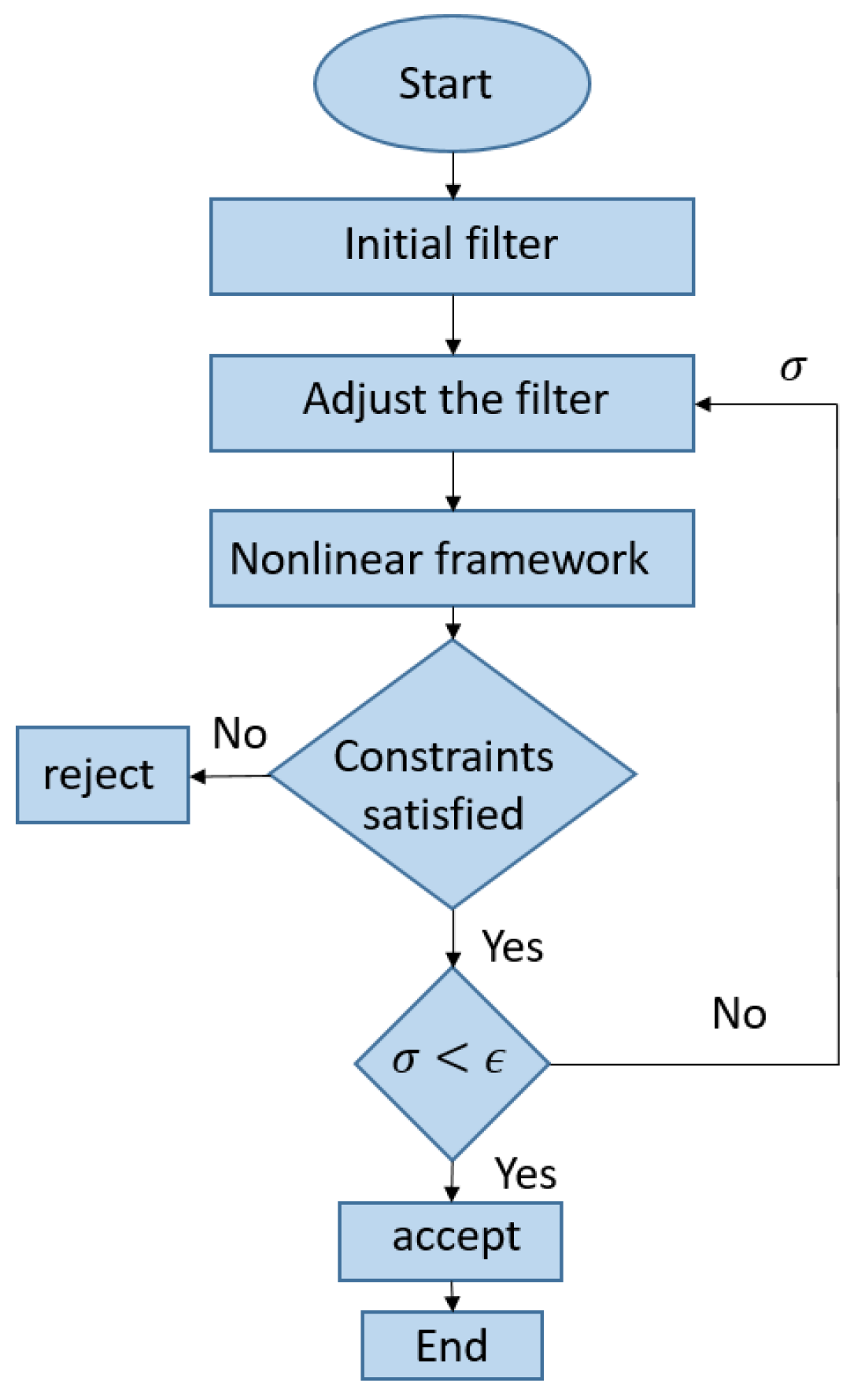
4. The Constrained Optimization Problem
5. Quality of the Design
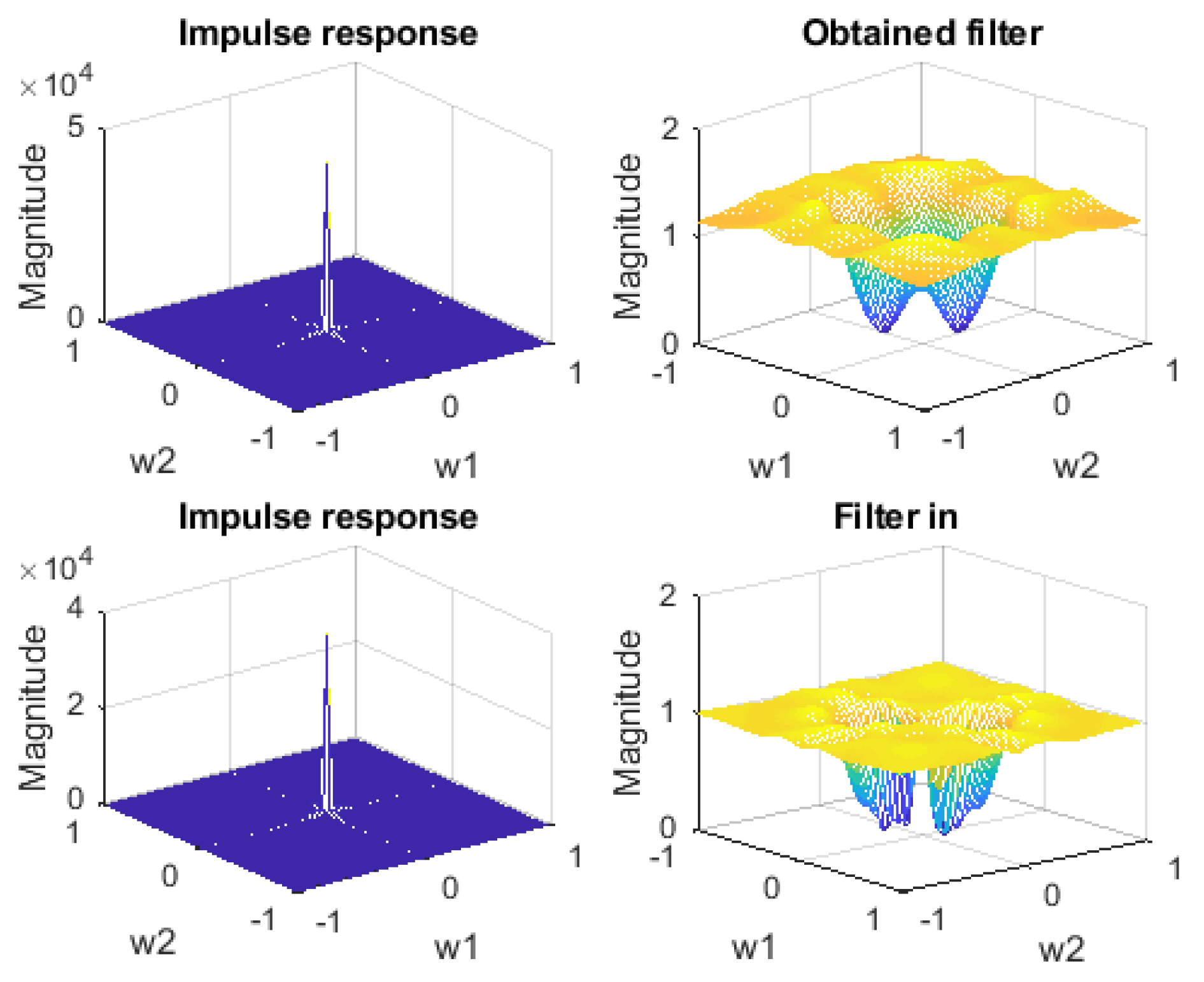
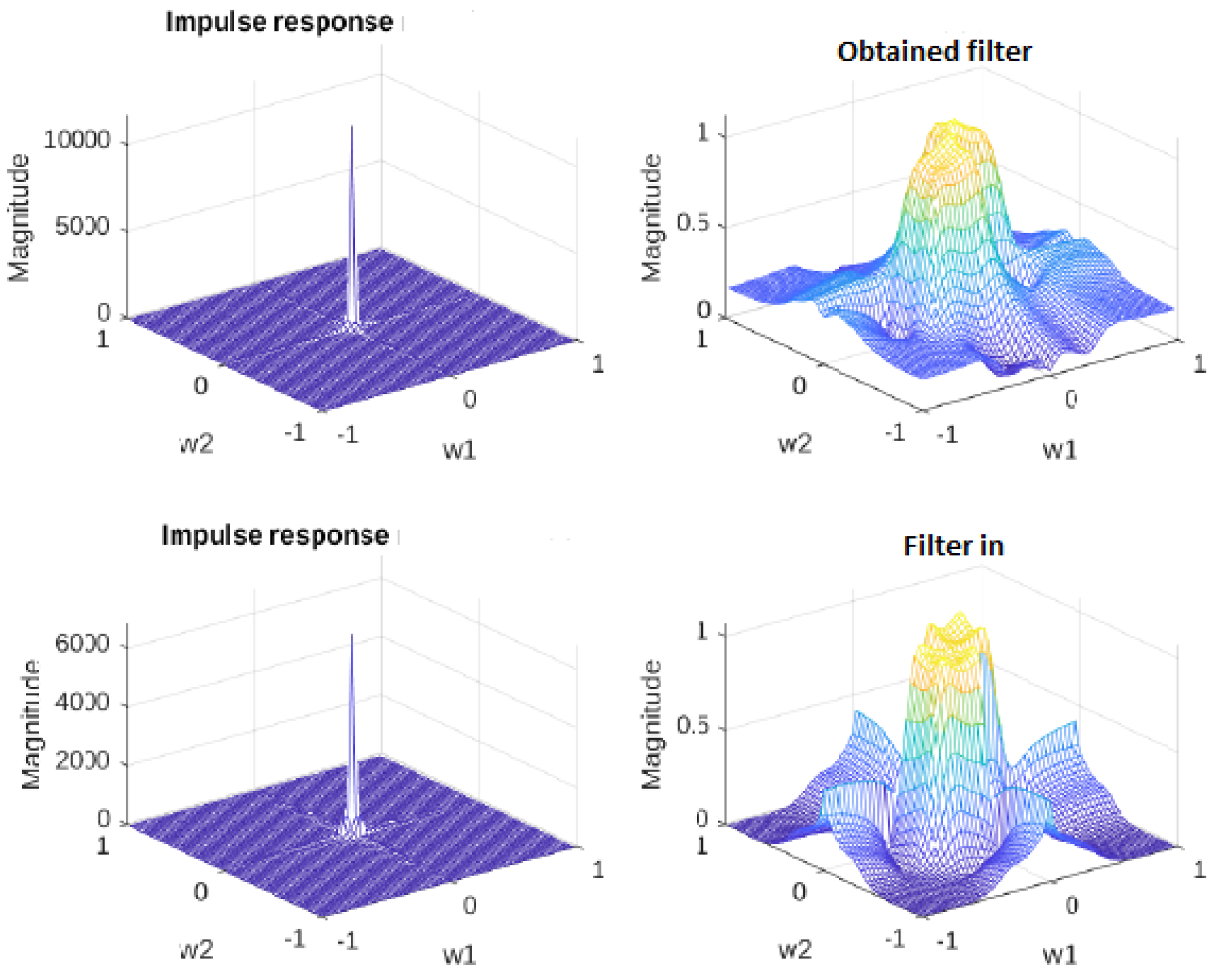
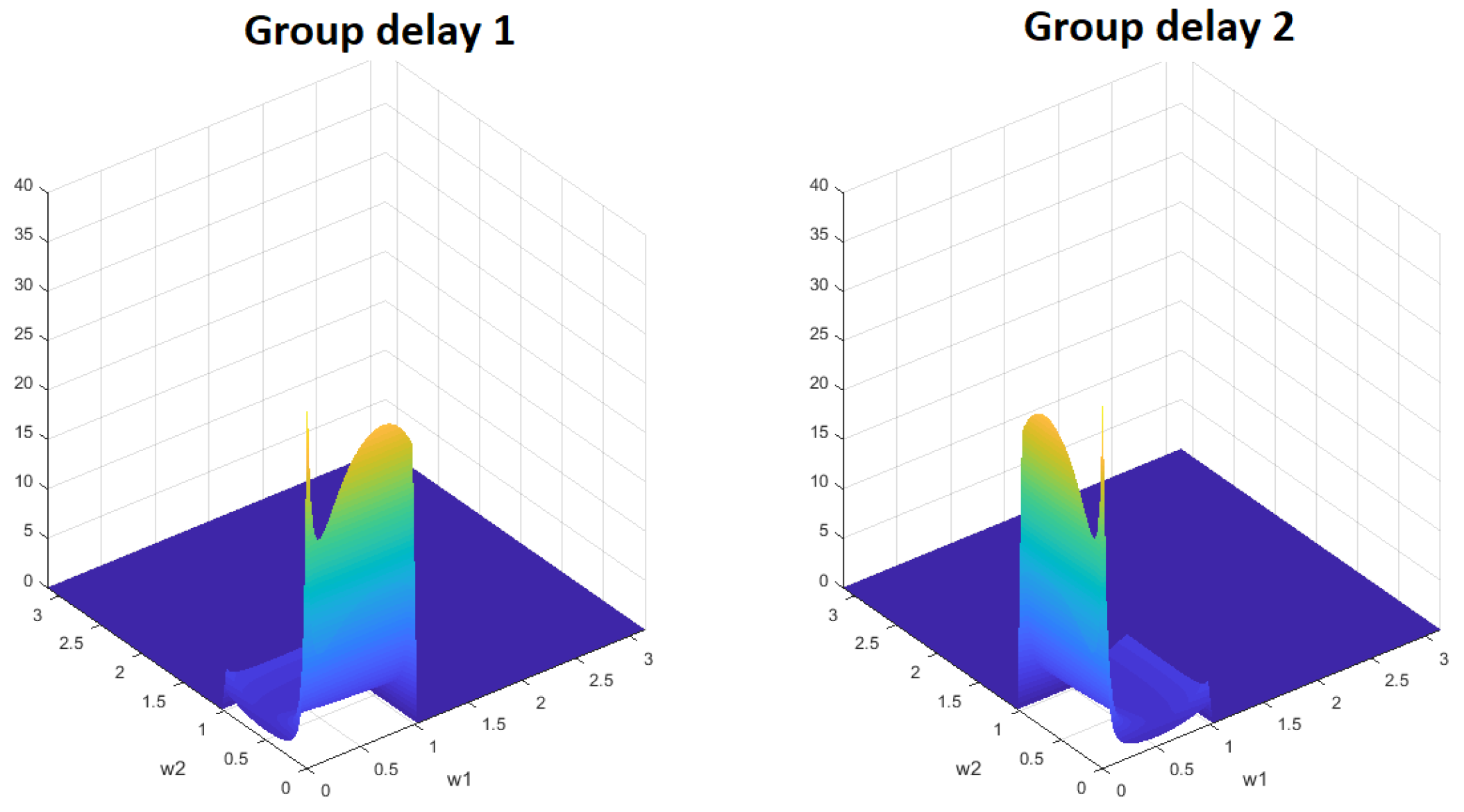
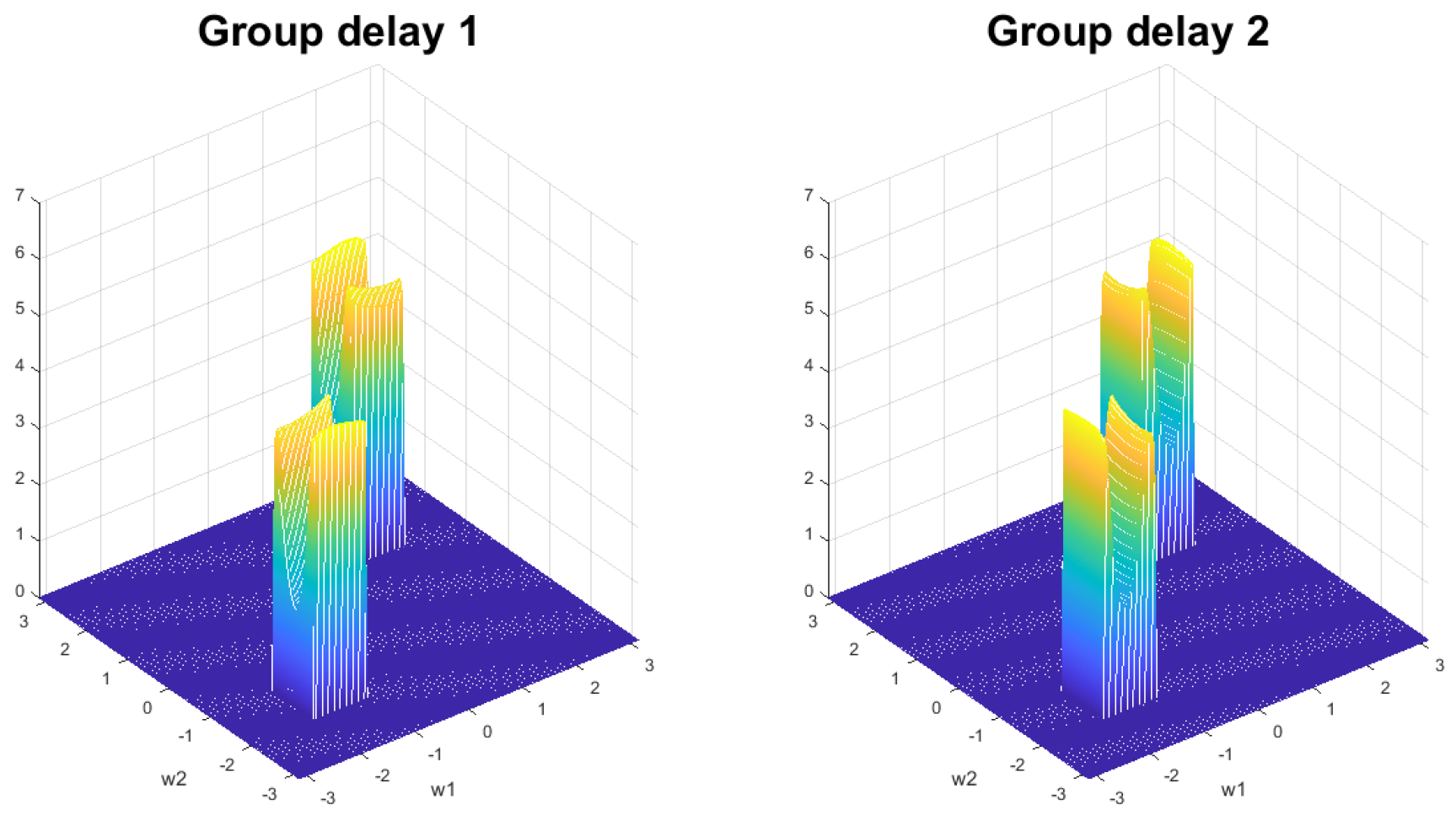
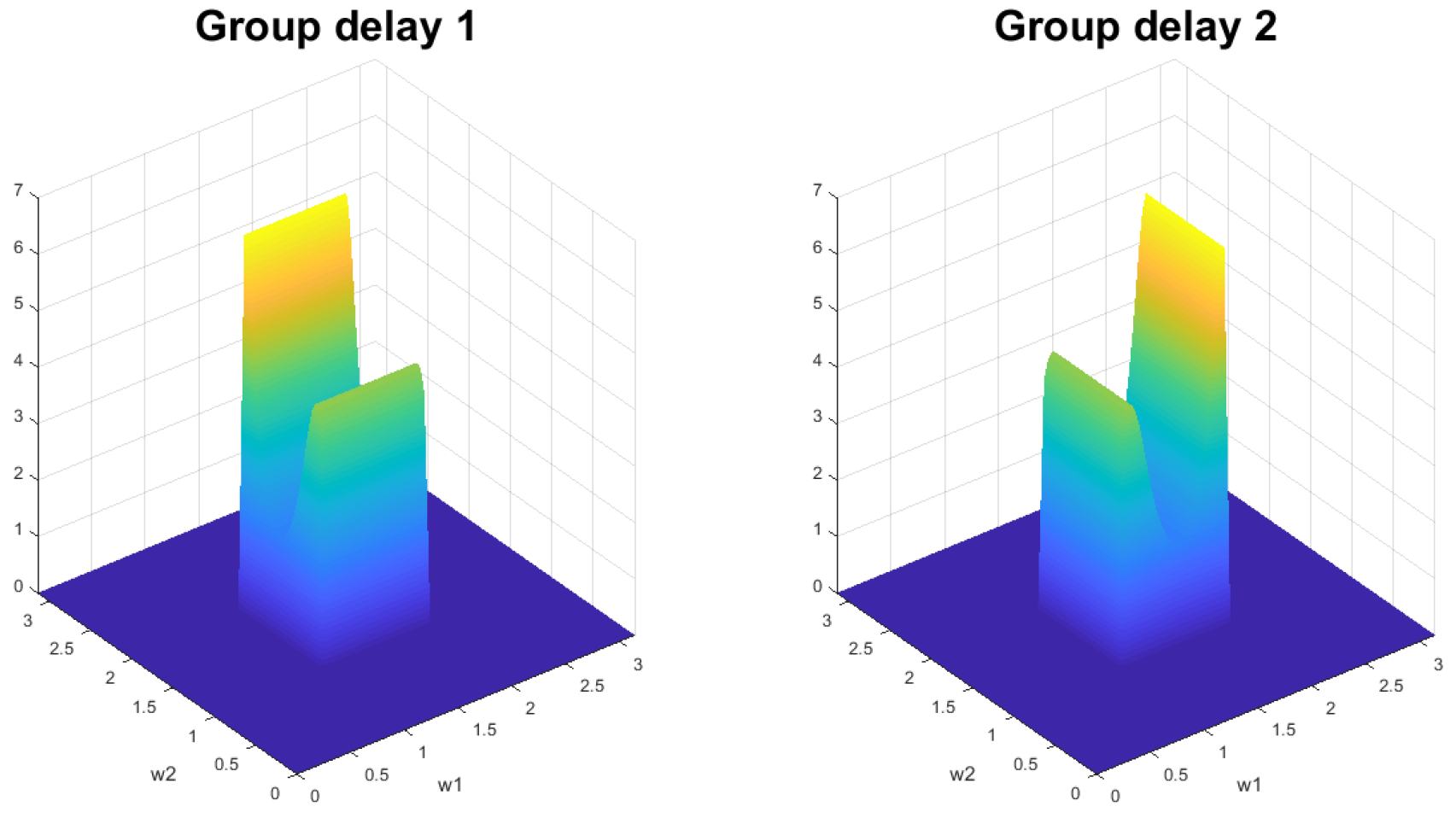
6. Experimental Results
6.1. 2D Highpass Filter
6.2. 2D Lowpass Filter
6.3. 2D Bandpass Filter
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2D | Two Dimensional |
| 1D | One Dimensional |
| IIR | Infinite Impulse Response |
| FIR | Finite Impulse Response |
| IP | Interior Point |
| SDP | Semi Definite Programming |
| GA | Genetic Algorithm |
| Min | Minimum |
| Max | Maximum |
| U | Unit Circle |
References
- Antoniou, A. Digital Signal Processing: Signals, Systems, and Filters; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Matei, R. Analytic design of directional and square-shaped 2D IIR filters based on digital prototypes. Multidimens. Syst. Signal Process. 2019, 30, 2021–2043. [Google Scholar] [CrossRef]
- Chan, T.S.; Kumar, A. Reliable ear identification using 2-D quadrature filters. Pattern Recognit. Lett. 2012, 33, 1870–1881. [Google Scholar] [CrossRef]
- Wu, C.W. Bit-level pipelined 2-D digital filters for real-time image processing. IEEE Trans. Circuits Syst. Video Technol. 1991, 1, 22–34. [Google Scholar] [CrossRef]
- Wijesekara, R.T.; Edussooriya, C.U.; Bruton, L.T.; Agathoklis, P. A low-complexity 2-D spatially-interpolated FIR trapezoidal filter for enhancing broadband plane waves. In Proceedings of the 2017 10th International Workshop on Multidimensional (nD) Systems (nDS), IEEE, Zielona Gora, Poland, 13–15 September 2017; pp. 1–6. [Google Scholar]
- Hua, J.; Kuang, W.; Gao, Z.; Meng, L.; Xu, Z. Image denoising using 2-D FIR filters designed with DEPSO. Multimed. Tools Appl. 2014, 69, 157–169. [Google Scholar] [CrossRef]
- Lu, W.S. Two-Dimensional Digital Filters; CRC Press: Boca Raton, FL, USA, 1992; Volume 80. [Google Scholar]
- Chen, W.K. The Circuits and Filters Handbook; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing; Pearson Education: Atlanta, GA, USA, 2014. [Google Scholar]
- Dudgeon, D.E.; Mersereau, R.M. Multidimensional Digital Signal Processing; Prentice-Hall Signal Processing Series; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Nongpiur, R.C.; Shpak, D.J.; Antoniou, A. Improved design method for nearly linear-phase IIR filters using constrained optimization. IEEE Trans. Signal Process. 2013, 61, 895–906. [Google Scholar] [CrossRef]
- Holford, S.; Agathoklis, P. The use of model reduction techniques for designing IIR filters with linear phase in the passband. IEEE Trans. Signal Process. 1996, 44, 2396–2404. [Google Scholar] [CrossRef]
- Lertniphonphun, W.; McClellan, J.H. Unified design algorithm for complex FIR and IIR filters. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Proceedings (Cat. No. 01CH37221), Salt Lake City, UT, USA, 7–11 May 2001; Volume 6, pp. 3801–3804. [Google Scholar]
- O’connor, B.; Huang, T. Stability of general two-dimensional recursive digital filters. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 550–560. [Google Scholar] [CrossRef]
- Katayama, T. Subspace Methods for System Identification; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994; Volume 15. [Google Scholar]
- Lim, J.S. Two-Dimensional Signal and Image Processing; Prentice Hall: Englewood Cliffs, NJ, USA, 1990; 710p. [Google Scholar]
- Lu, W.S.; Hinamoto, T. Optimal design of IIR digital filters with robust stability using conic-quadratic-programming updates. IEEE Trans. Signal Process. 2003, 51, 1581–1592. [Google Scholar]
- Lai, X.; Lin, Z. Minimax design of IIR digital filters using a sequential constrained least-squares method. IEEE Trans. Signal Process. 2010, 58, 3901–3906. [Google Scholar] [CrossRef]
- Kockanat, S.; Karaboga, N. The design approaches of two-dimensional digital filters based on metaheuristic optimization algorithms: A review of the literature. Artif. Intell. Rev. 2015, 44, 265–287. [Google Scholar] [CrossRef]
- Jiang, A.; Kwan, H.K. IIR digital filter design with new stability constraint based on argument principle. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 583–593. [Google Scholar] [CrossRef]
- Anderson, B.; Agathoklis, P.; Jury, E.; Mansour, M. Stability and the matrix Lyapunov equation for discrete 2-dimensional systems. IEEE Trans. Circuits Syst. 1986, 33, 261–267. [Google Scholar] [CrossRef]
- Lodge, J.; Fahmy, M. Stability and overflow oscillations in 2-D state-space digital filters. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1161–1171. [Google Scholar] [CrossRef]
- Lu, W.S.; Lee, E. Stability analysis for two-dimensional systems via a Lyapunov approach. IEEE Trans. Circuits Syst. 1985, 32, 61–68. [Google Scholar] [CrossRef]
- Reddy, H.; Rajan, P. A comprehensive study of two-variable Hurwitz polynomials. IEEE Trans. Educ. 1989, 32, 198–209. [Google Scholar] [CrossRef]
- Paraskevopoulos, P.; Panagopoulos, P.; Vaitsis, G.; Varoufakis, S.; Antoniou, G. Model reduction of 2-D systems via orthogonal series. Multidimens. Syst. Signal Process. 1991, 2, 69–83. [Google Scholar] [CrossRef]
- Guo, T.Y.; Hwang, C.; Shieh, L.S.; Chen, C.H. Reduced-order models of 2-D linear discrete separable-denominator system using bilinear Routh approximations. In IEE Proceedings G (Electronic Circuits and Systems); IET: London, UK, 1992; Volume 139, pp. 45–56. [Google Scholar]
- Knorn, S.; Middleton, R.H. Stability of two-dimensional linear systems with singularities on the stability boundary using LMIs. IEEE Trans. Autom. Control 2013, 58, 2579–2590. [Google Scholar] [CrossRef]
- Lai, X.; Meng, H.; Cao, J.; Lin, Z. A sequential partial optimization algorithm for minimax design of separable-denominator 2-D IIR filters. IEEE Trans. Signal Process. 2017, 65, 876–887. [Google Scholar] [CrossRef]
- Dumitrescu, B. Optimization of two-dimensional IIR filters with nonseparable and separable denominator. IEEE Trans. Signal Process. 2005, 53, 1768–1777. [Google Scholar] [CrossRef]
- Gorinevsky, D.; Boyd, S. Optimization-based design and implementation of multidimensional zero-phase IIR filters. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 372–383. [Google Scholar] [CrossRef][Green Version]
- Wysocka-Schillak, F. Design of separable 2-D IIR Filters with approximately linear phase in the passband using genetic algorithm. In Proceedings of the 2008 Conference on Human System Interactions, IEEE, Krakow, Poland, 25–27 May 2008; pp. 66–70. [Google Scholar]
- Lu, W.S. A unified approach for the design of 2-D digital filters via semidefinite programming. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2002, 49, 814–826. [Google Scholar] [CrossRef]
- Mladenov, V.M.; Mastorakis, N.E. Design of two-dimensional recursive filters by using neural networks. IEEE Trans. Neural Netw. 2001, 12, 585–590. [Google Scholar] [CrossRef] [PubMed]
- Mastorakis, N.E.; Gonos, I.F.; Swamy, M. Design of two-dimensional recursive filters using genetic algorithms. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2003, 50, 634–639. [Google Scholar] [CrossRef]
- Tsai, J.T.; Ho, W.H.; Chou, J.H. Design of two-dimensional IIR digital structure-specified filters by using an improved genetic algorithm. Expert Syst. Appl. 2009, 36, 6928–6934. [Google Scholar] [CrossRef]
- Liang, L.; Ahmadi, M.; Sid-Ahmed, M. Design of 2D IIR filters with canonical signed-digit coefficients using genetic algorithm. In Proceedings of the 2003 46th Midwest Symposium on Circuits and Systems, IEEE, Cairo, Egypt, 27–30 December 2003; Volume 2, pp. 633–635. [Google Scholar]
- Kawamata, M.; Imakubo, J.; Higuchi, T. Optimal design method of 2-D IIR digital filters based on a simple genetic algorithm. In Proceedings of the Proceedings of 1st International Conference on Image Processing, IEEE, Austin, TX, USA, 13–16 November 1994; Volume 1, pp. 780–784. [Google Scholar]
- Lv, C.; Yan, S.; Cheng, G.; Xu, L.; Tian, X. Design of two-dimensional IIR digital filters by using a novel hybrid optimization algorithm. Multidimens. Syst. Signal Process. 2017, 28, 1267–1281. [Google Scholar] [CrossRef]
- Shpak, D.J.; Antoniou, A. A generalized Remez method for the design of FIR digital filters. IEEE Trans. Circuits Syst. 1990, 37, 161–174. [Google Scholar] [CrossRef]
- Charalambous, C. Design of 2-dimensional circularly-symmetric digital filters. In IEE Proceedings G (Electronic Circuits and Systems); IET: London, UK, 1982; Volume 129, pp. 47–54. [Google Scholar]
- Lu, W.S.; Pei, S.C.; Tseng, C.C. A weighted least-squares method for the design of stable 1-D and 2-D IIR digital filters. IEEE Trans. Signal Process. 1998, 46, 1–10. [Google Scholar] [CrossRef]
- Miyata, T.; Aikawa, N.; Sugita, Y.; Yoshikawa, T. A design method for separable-denominator 2D IIR filters with a necessary and sufficient stability check. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2009, 92, 307–310. [Google Scholar] [CrossRef]
- Omar, A.; Shpak, D.; Agathoklis, P. Improved Design Method for Nearly Linear-Phase IIR Filters Using Constrained Optimization. J. Circuits Syst. Comput. 2021, 30, 2150207. [Google Scholar] [CrossRef]
- Omar, A.; Shpak, D.; Agathoklis, P. Nearly Linear-Phase 2-D Recursive Digital Filters Design Using Balanced Realization Model Reduction. J. Circuits Syst. Comput. 2022; submitted in October. [Google Scholar]
- Kim, K.; Kim, J.; Nam, S. Design of computationally efficient 2D FIR filters using sampling-kernel-based interpolation and frequency transformation. Electron. Lett. 2015, 51, 1326–1328. [Google Scholar] [CrossRef]
- Aly, S.; Fahmy, M. Design of two-dimensional recursive digital filters with specified magnitude and group delay characteristics. IEEE Trans. Circuits Syst. 1978, 25, 908–916. [Google Scholar] [CrossRef]
- Antoniou, A.; Lu, W.S. Design of two-dimensional digital filters by using the singular value decomposition. IEEE Trans. Circuits Syst. 1987, 34, 1191–1198. [Google Scholar] [CrossRef]
- Guindon, D.; Shpak, D.J.; Antoniou, A. Design methodology for nearly linear-phase recursive digital filters by constrained optimization. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 57, 1719–1731. [Google Scholar] [CrossRef]
- Andersen, E.D.; Gondzio, J.; Mészáros, C.; Xu, X. Implementation of Interior Point Methods for Large Scale Linear Programming; HEC/Université de Geneve: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Liu, L.; Fan, L. The complexity analysis of an efficient interior-point algorithm for linear optimization. In Proceedings of the 2010 Third International Joint Conference on Computational Science and Optimization, IEEE, Huangshan, China, 28–31 May 2010; Volume 2, pp. 21–24. [Google Scholar]
- Wirski, R. Synthesis and Realization of Two-Dimensional Separable Denominator Orthogonal Systems via Decomposition Into 1-D Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 4309–4322. [Google Scholar] [CrossRef]
- Reddy, H.C.; Khoo, I.H.; Rajan, P. 2-D symmetry: Theory and filter design applications. IEEE Circuits Syst. Mag. 2003, 3, 4–33. [Google Scholar] [CrossRef]





| Proposed Method | Method in [8] | |
|---|---|---|
| Orders | (4,4) | (4,4) |
| 0.437 | 0.262 | |
| 1.338 | 1.066 | |
| 50.76 | 60.54 | |
| 0.664 | 0.849 | |
| 0.389 | 0.426 | |
| 8.104 | ||
| 0.962 | 0.009 | |
| 4.397 | 11.614 | |
| 64.09 | 99.84 |
| Proposed Method | Method in [8] | |
|---|---|---|
| Orders | (4,4) | (4,4) |
| 0.843 | 0.642 | |
| 1.120 | 1.069 | |
| 14.25 | 25.26 | |
| 1.0079 | 1.020 | |
| 0.403 | 0.446 | |
| 0.916 | 2.275 | |
| 2.217 | 1.738 | |
| 6.864 | 54.091 | |
| 47.650 | 93.774 |
| Proposed Method | Method in [8] | |
|---|---|---|
| Orders | (4,4) | (4,4) |
| 0.809 | 0.633 | |
| 1.191 | 1.167 | |
| 19.100 | 29.667 | |
| 0.855 | 0.798 | |
| 0.324 | 0.268 | |
| 0.668 | 0.734 | |
| 1.822 | 1.828 | |
| 5.073 | 6.737 | |
| 47.150 | 57.315 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omar, A.; Shpak, D.; Agathoklis, P.; Moa, B. A Nonlinear Optimization Design Algorithm for Nearly Linear-Phase 2D IIR Digital Filters. Signals 2023, 4, 575-590. https://doi.org/10.3390/signals4030030
Omar A, Shpak D, Agathoklis P, Moa B. A Nonlinear Optimization Design Algorithm for Nearly Linear-Phase 2D IIR Digital Filters. Signals. 2023; 4(3):575-590. https://doi.org/10.3390/signals4030030
Chicago/Turabian StyleOmar, Abdussalam, Dale Shpak, Panajotis Agathoklis, and Belaid Moa. 2023. "A Nonlinear Optimization Design Algorithm for Nearly Linear-Phase 2D IIR Digital Filters" Signals 4, no. 3: 575-590. https://doi.org/10.3390/signals4030030
APA StyleOmar, A., Shpak, D., Agathoklis, P., & Moa, B. (2023). A Nonlinear Optimization Design Algorithm for Nearly Linear-Phase 2D IIR Digital Filters. Signals, 4(3), 575-590. https://doi.org/10.3390/signals4030030





