New Optimal Design of Multimode Shunt-Damping Circuits for Enhanced Vibration Control
Abstract
1. Introduction
2. Methodology
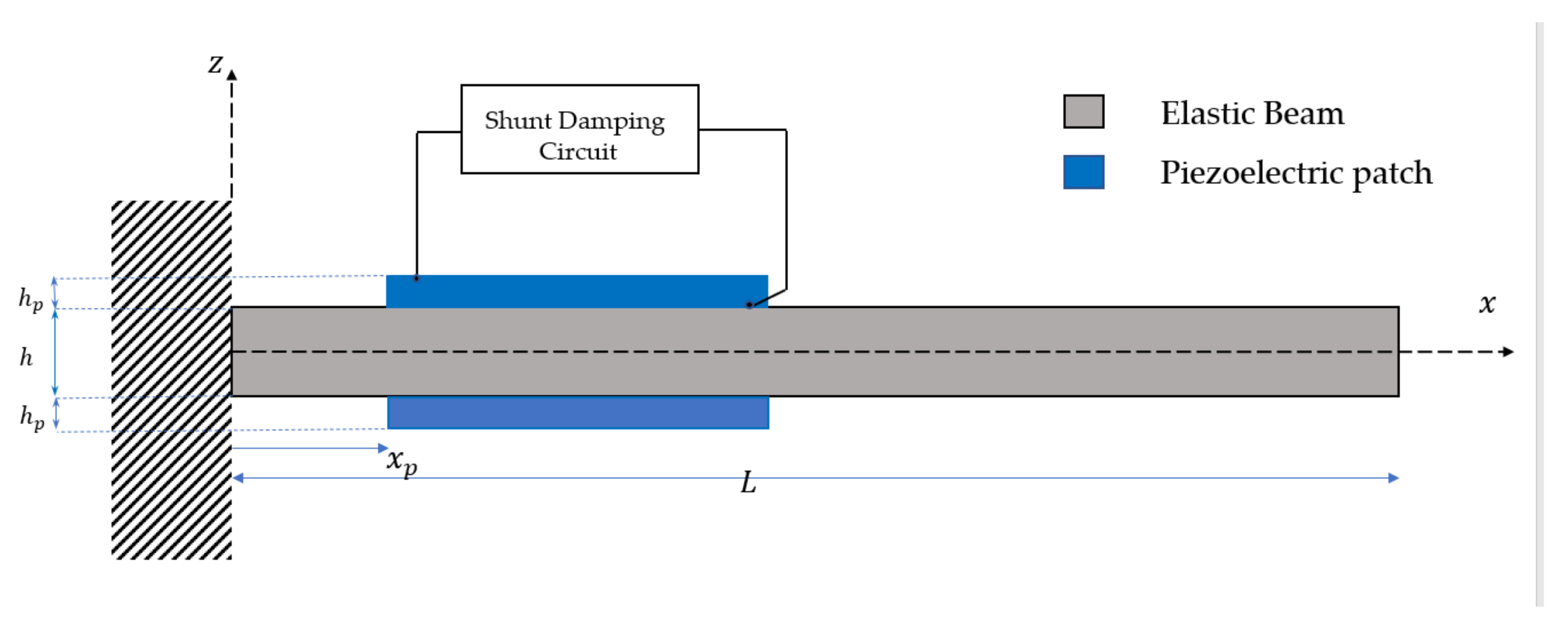
2.1. Finite-Element Model of the Laminated Composite Beam
2.1.1. Strains and Electrical Field
2.1.2. Constitutive Relations
2.1.3. Variational Formulation
2.1.4. Displacement and Electric Field Discretization
2.1.5. Coupled Electromechanical System
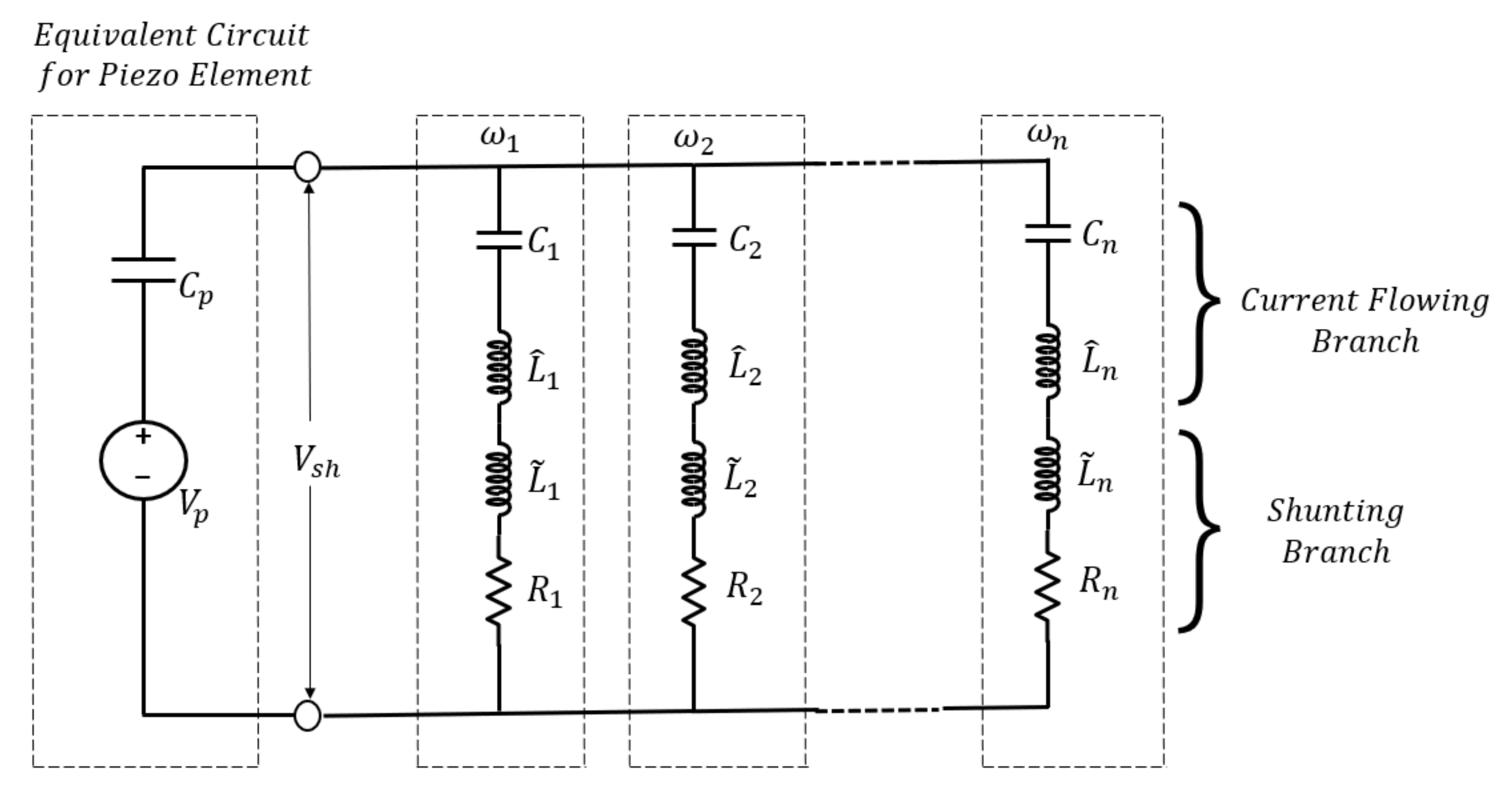
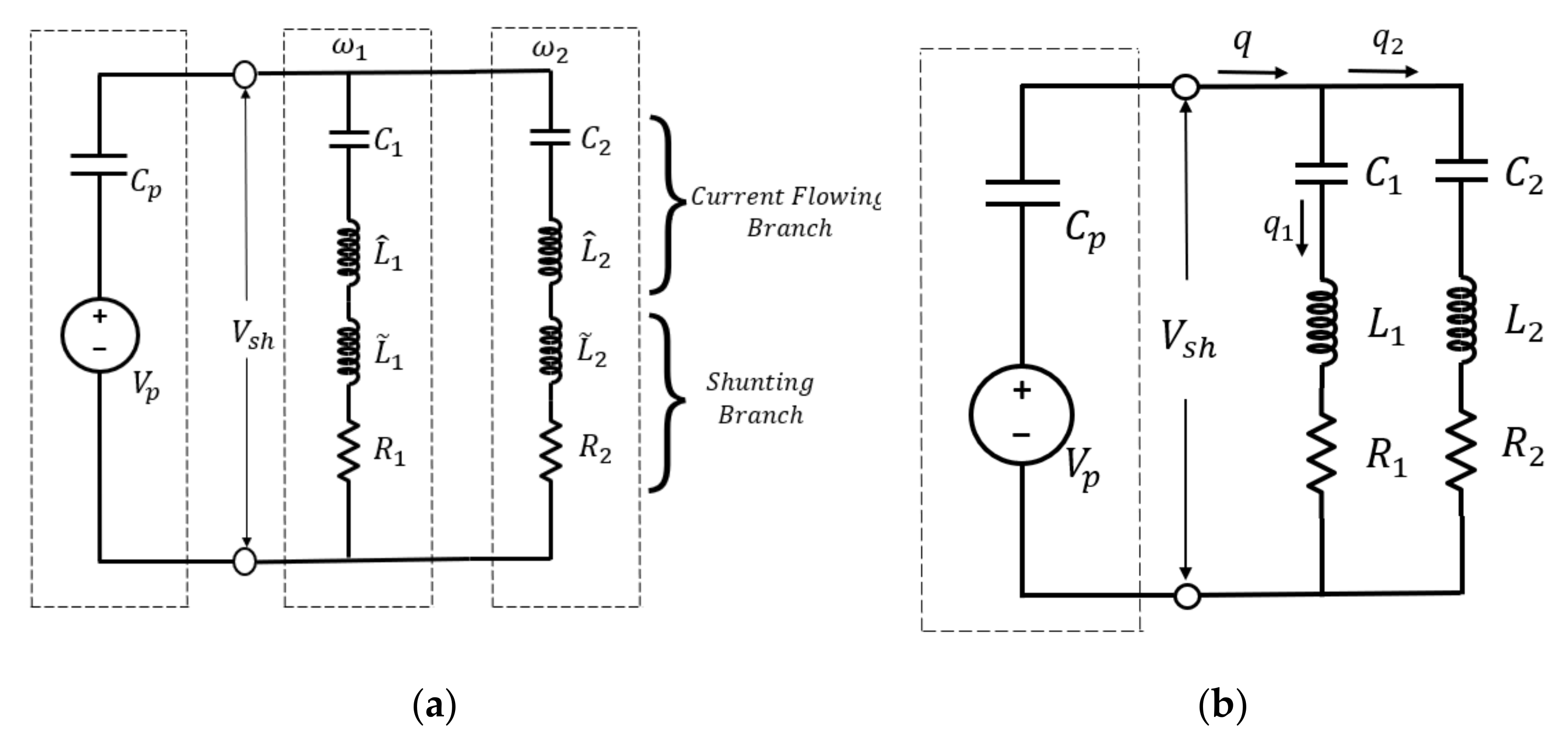
2.2. Multiple-Mode Shunt-Damping Circuit
2.3. State-Space Model of the Structure with Current-Flowing Circuit
2.4. Design Optimization
2.4.1. Design Variables
2.4.2. Objective Function
2.4.3. Optimization Problem
- Model 1 (Proposed Method):
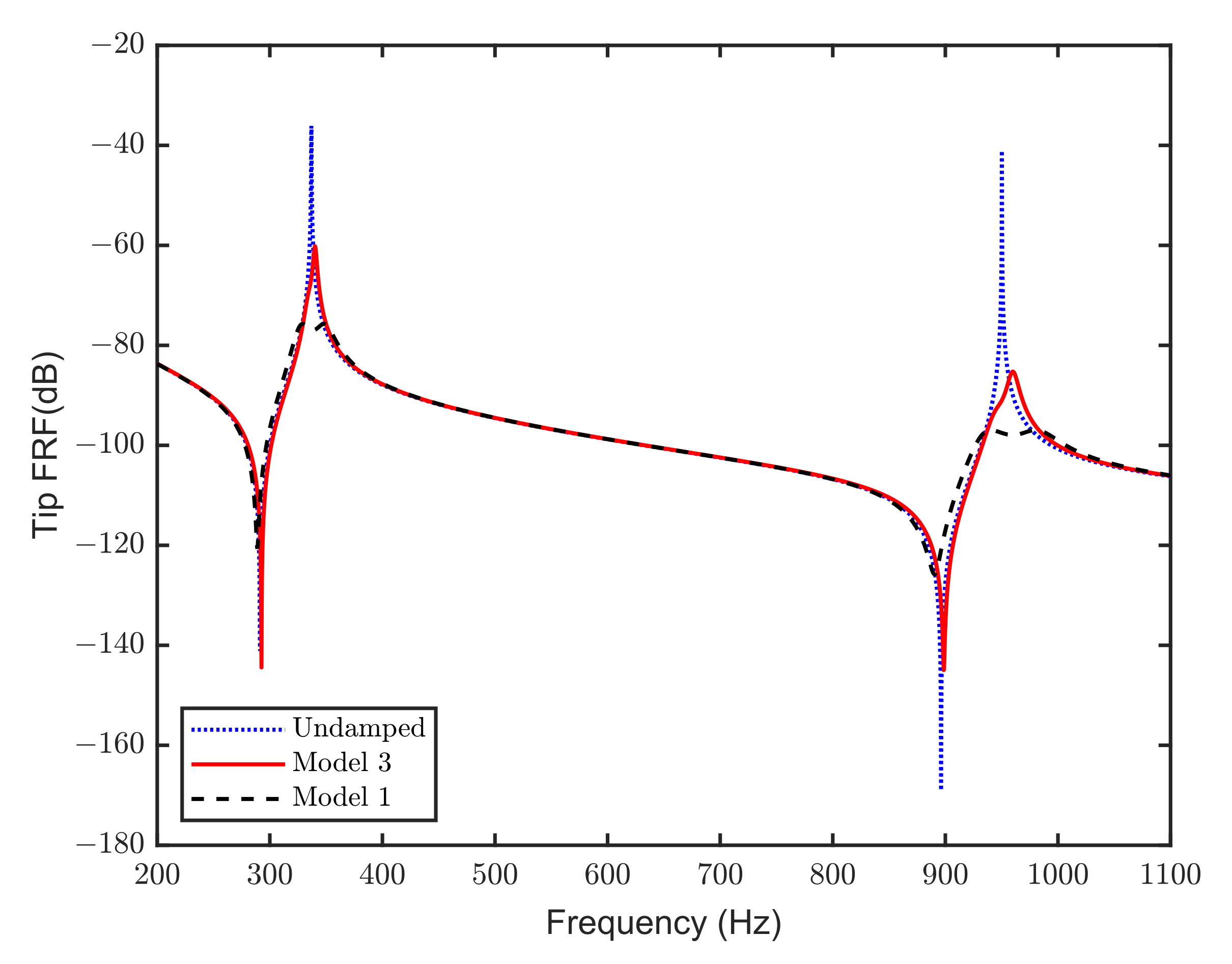
- Model 3 (Case Study):
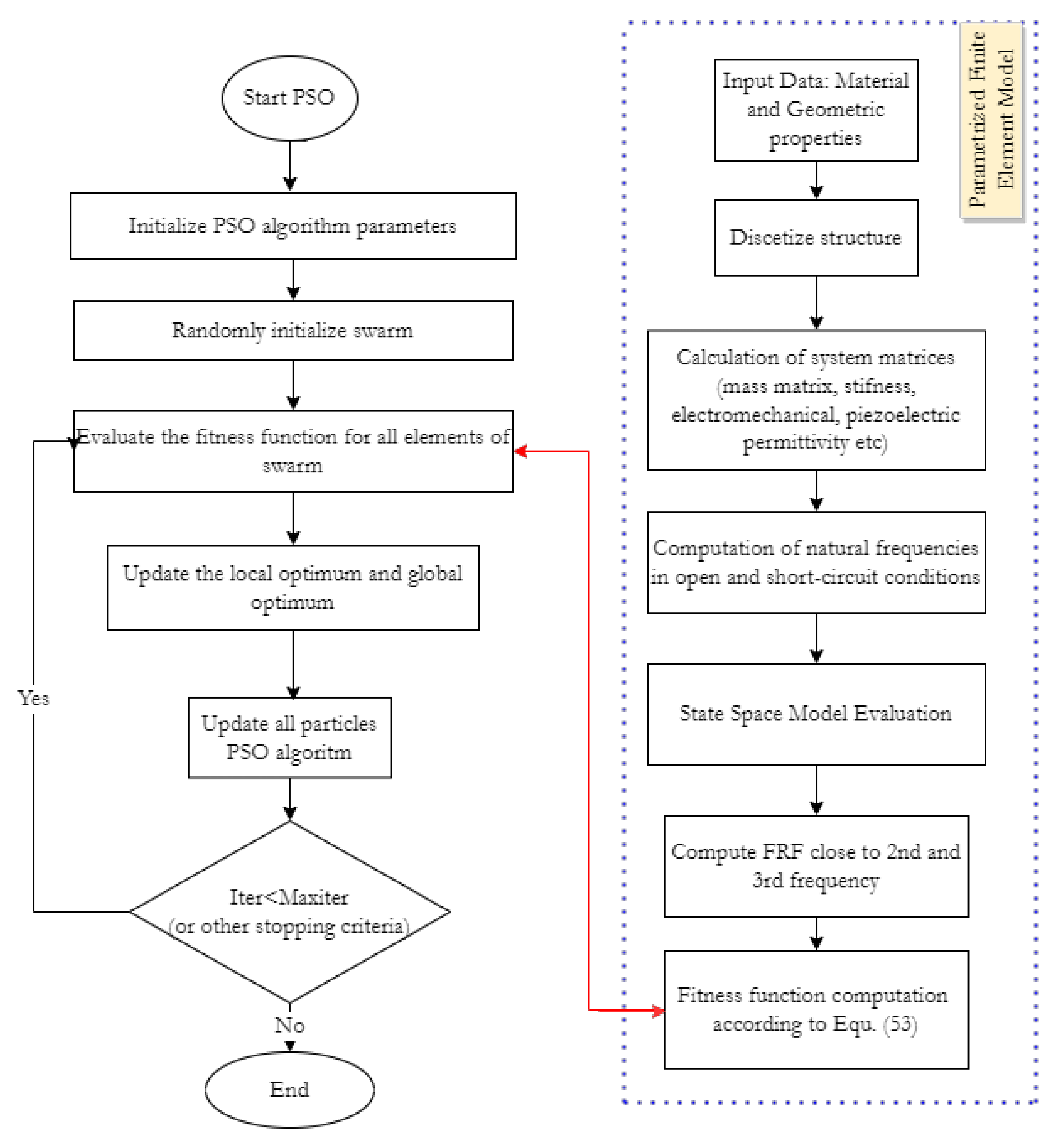
2.4.4. Particle Swarm Optimization (PSO)
- The PSO algorithm is simple to implement, making it applicable to both engineering and scientific research problems;
- It has fewer parameters to be adjusted;
- PSO is more efficient since only the most optimistic particle may pass information to the other particles over the evolution of generations, and, therefore, the optimization procedure moves quite quickly to better fitness values.
3. Results and Discussion
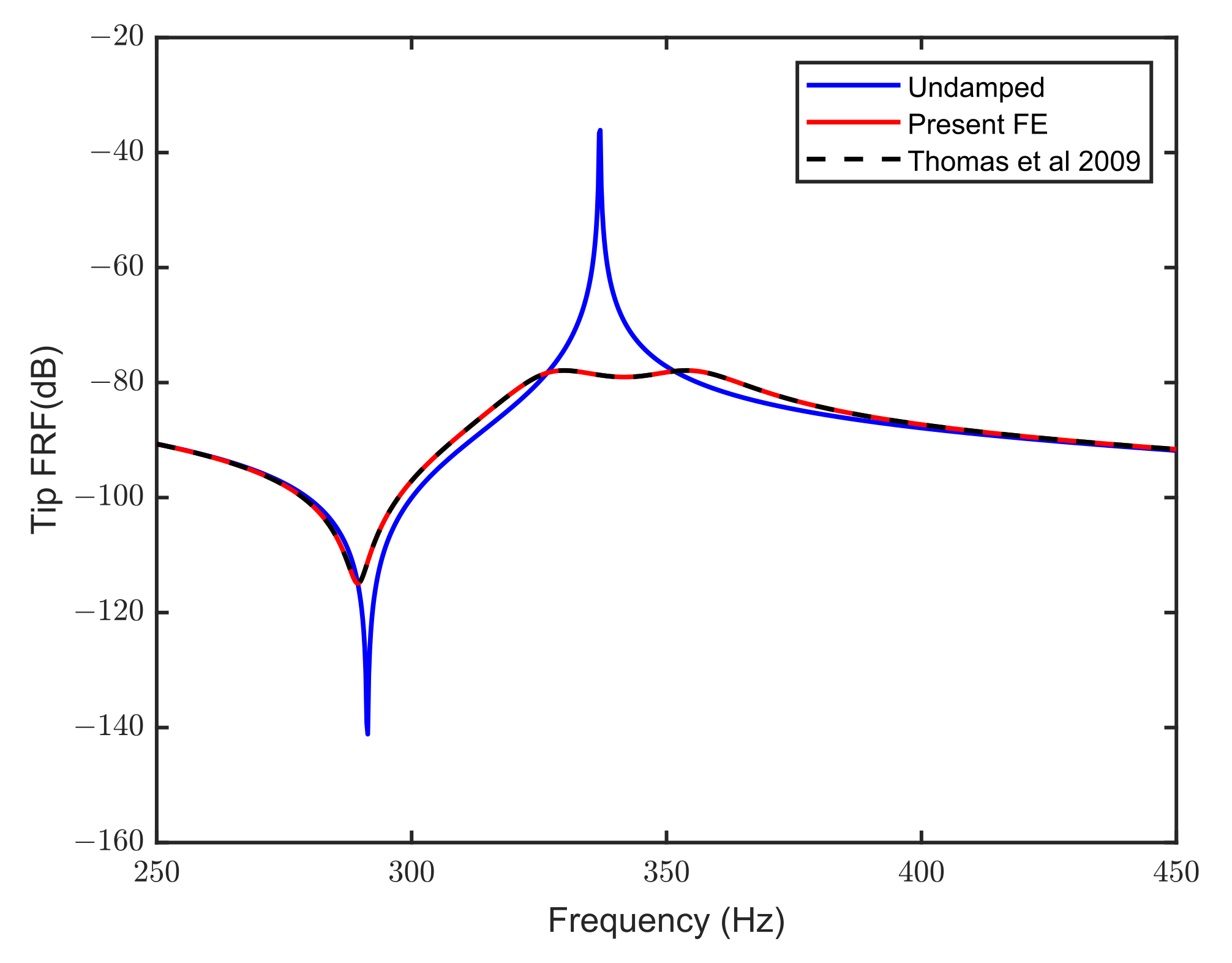
3.1. Validation versus Results from a Cantilever Beam Connected to a Shunt Circuit
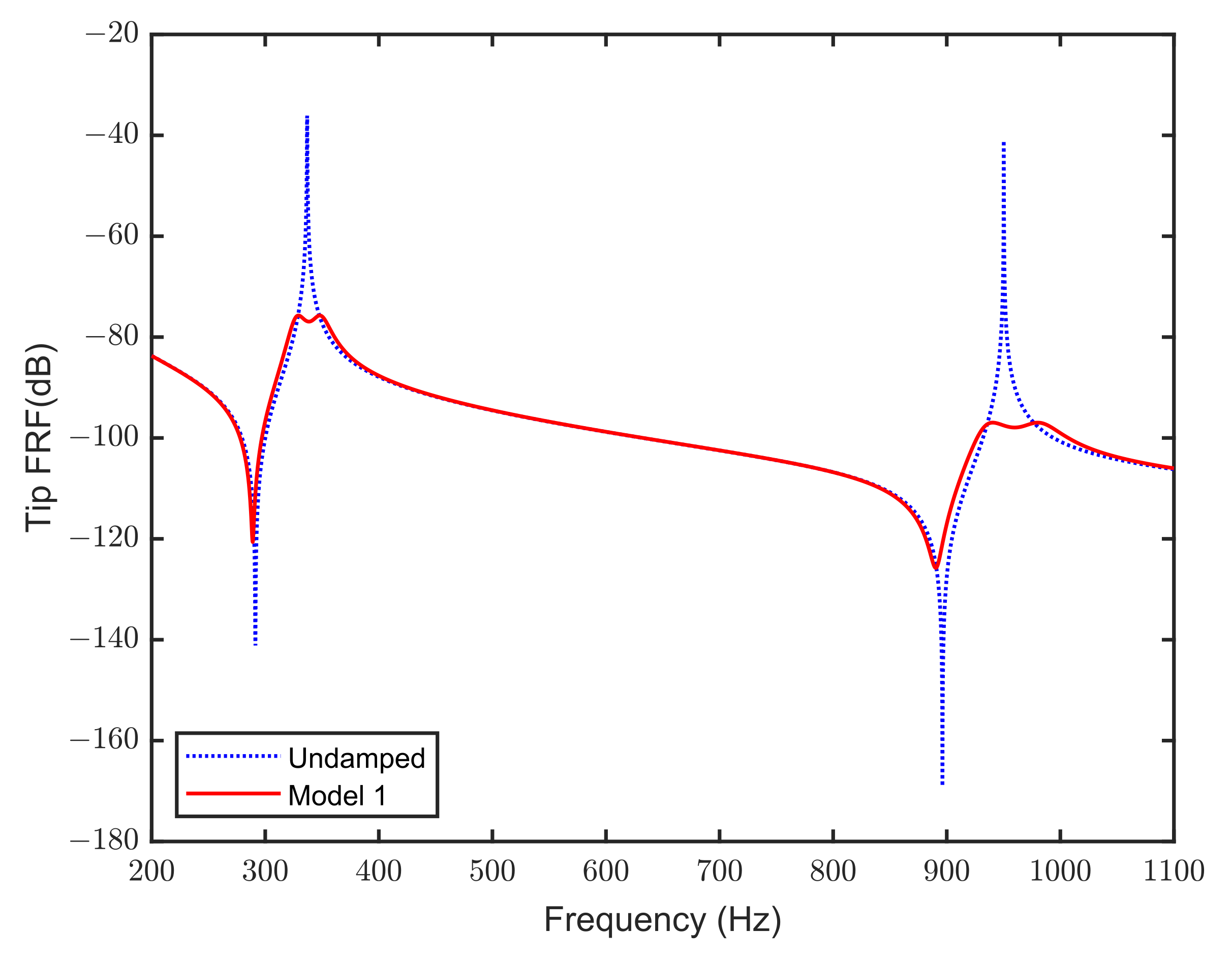
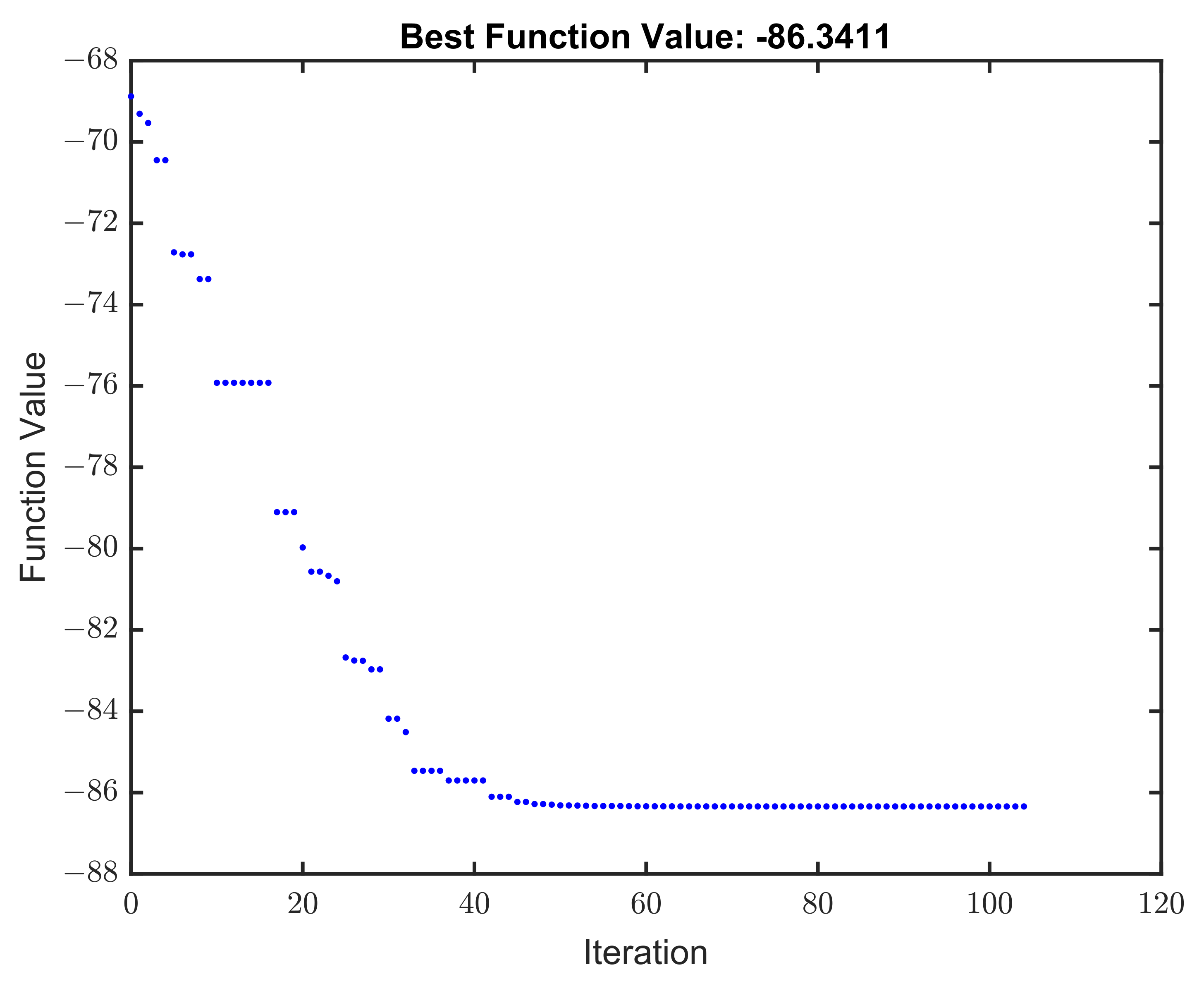
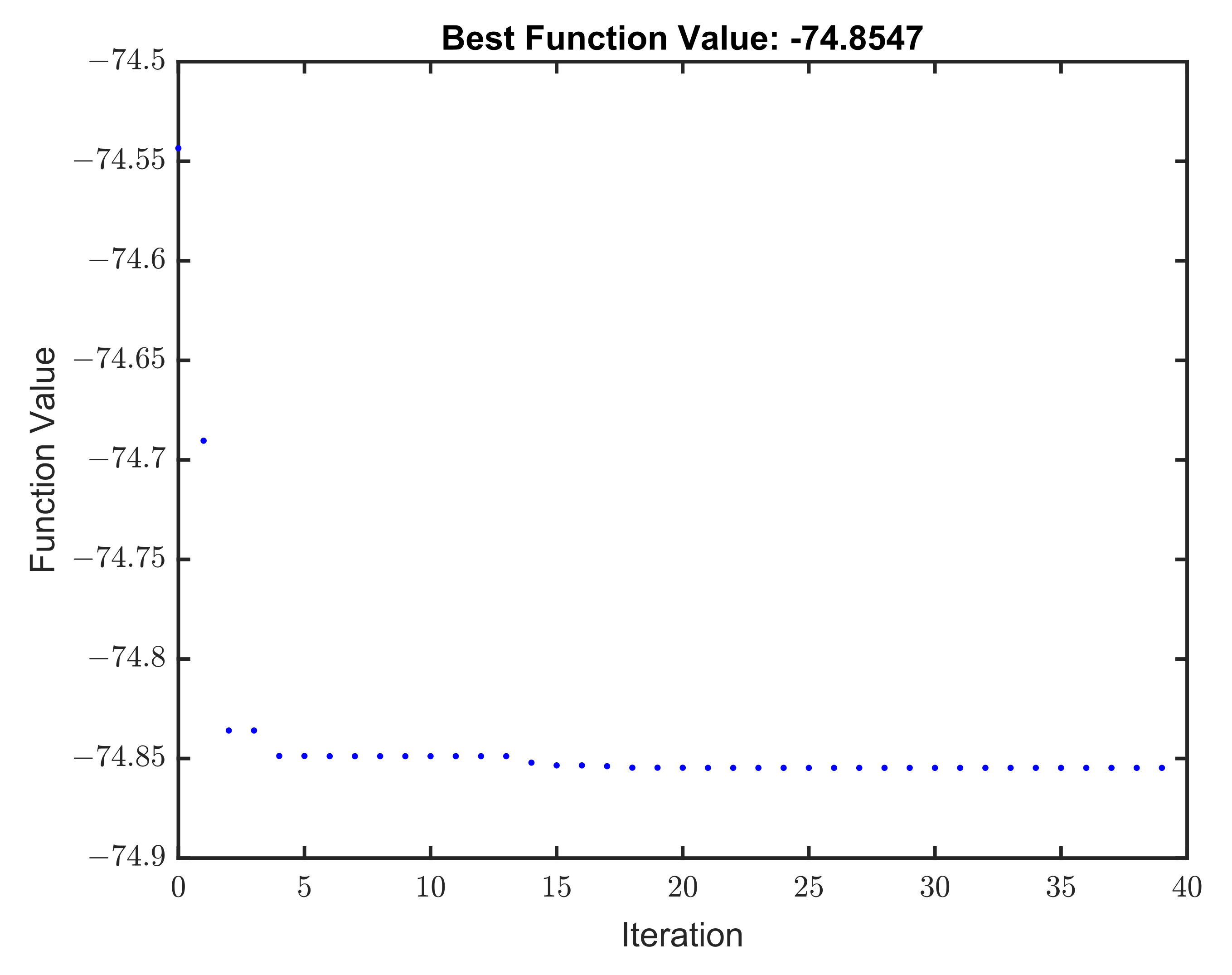
3.2. Solution of Optimization Problem: Model 1
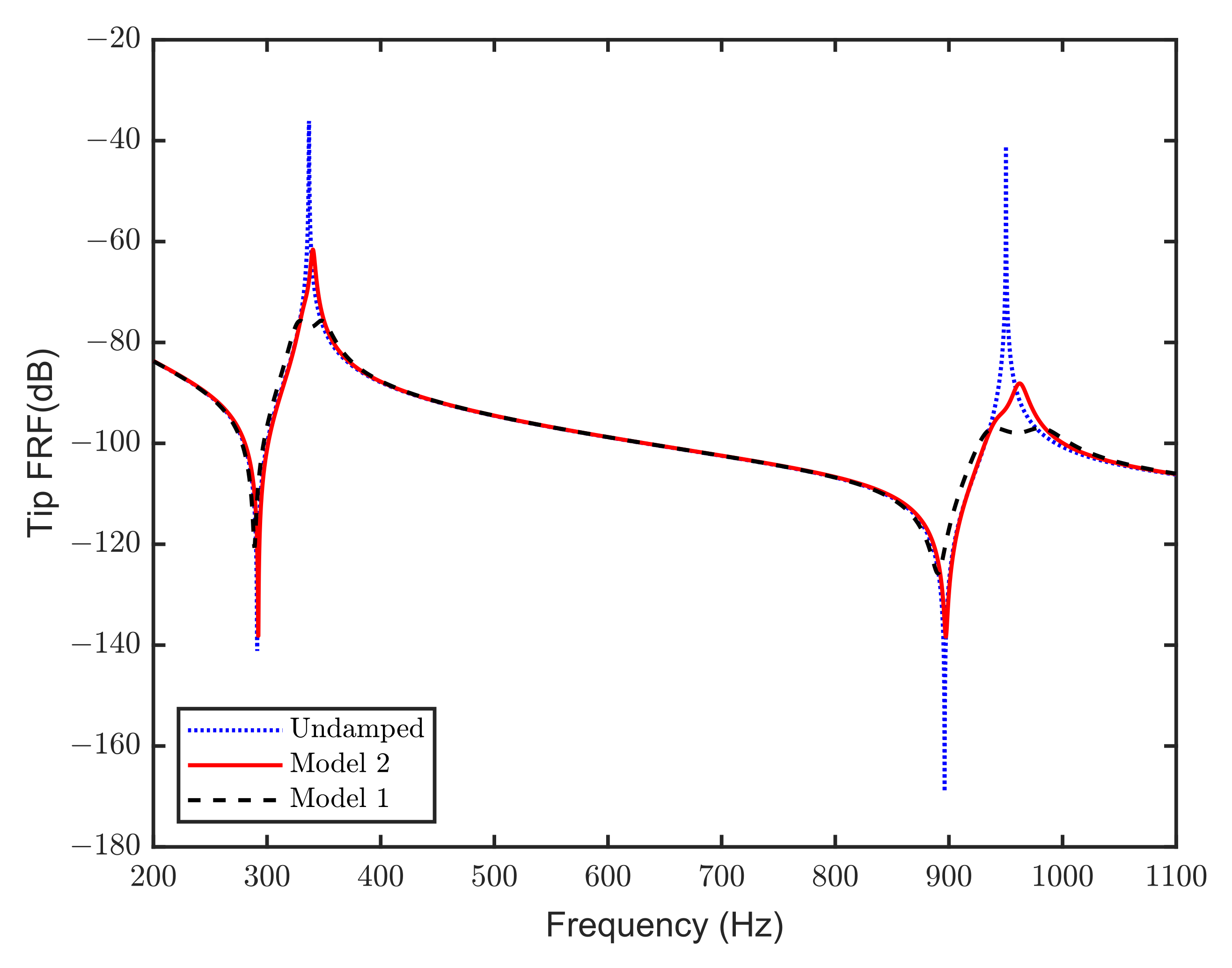
3.3. Solution of Optimization Problem: Model 2
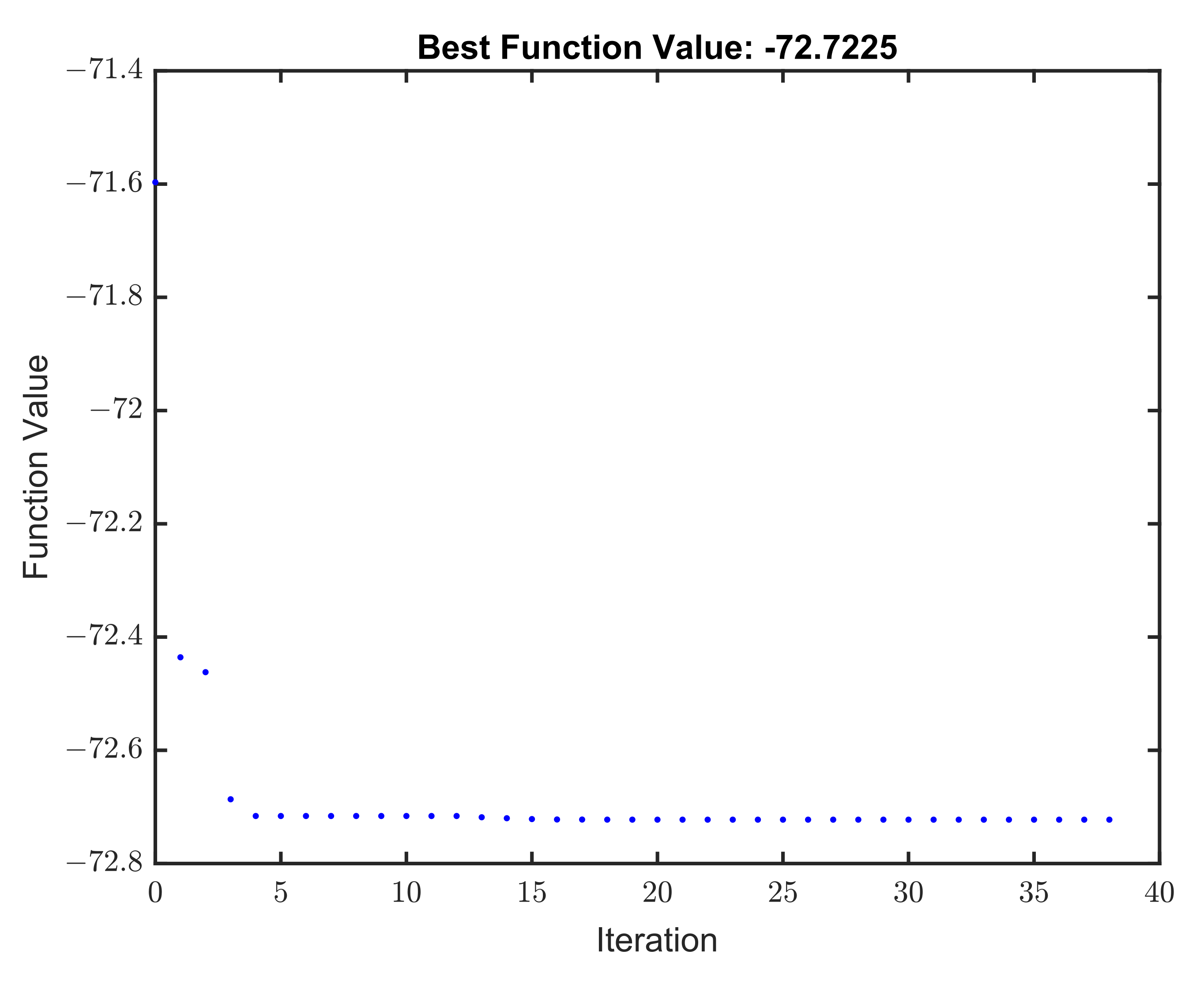
3.4. Solution of Optimization Problem: Model 3
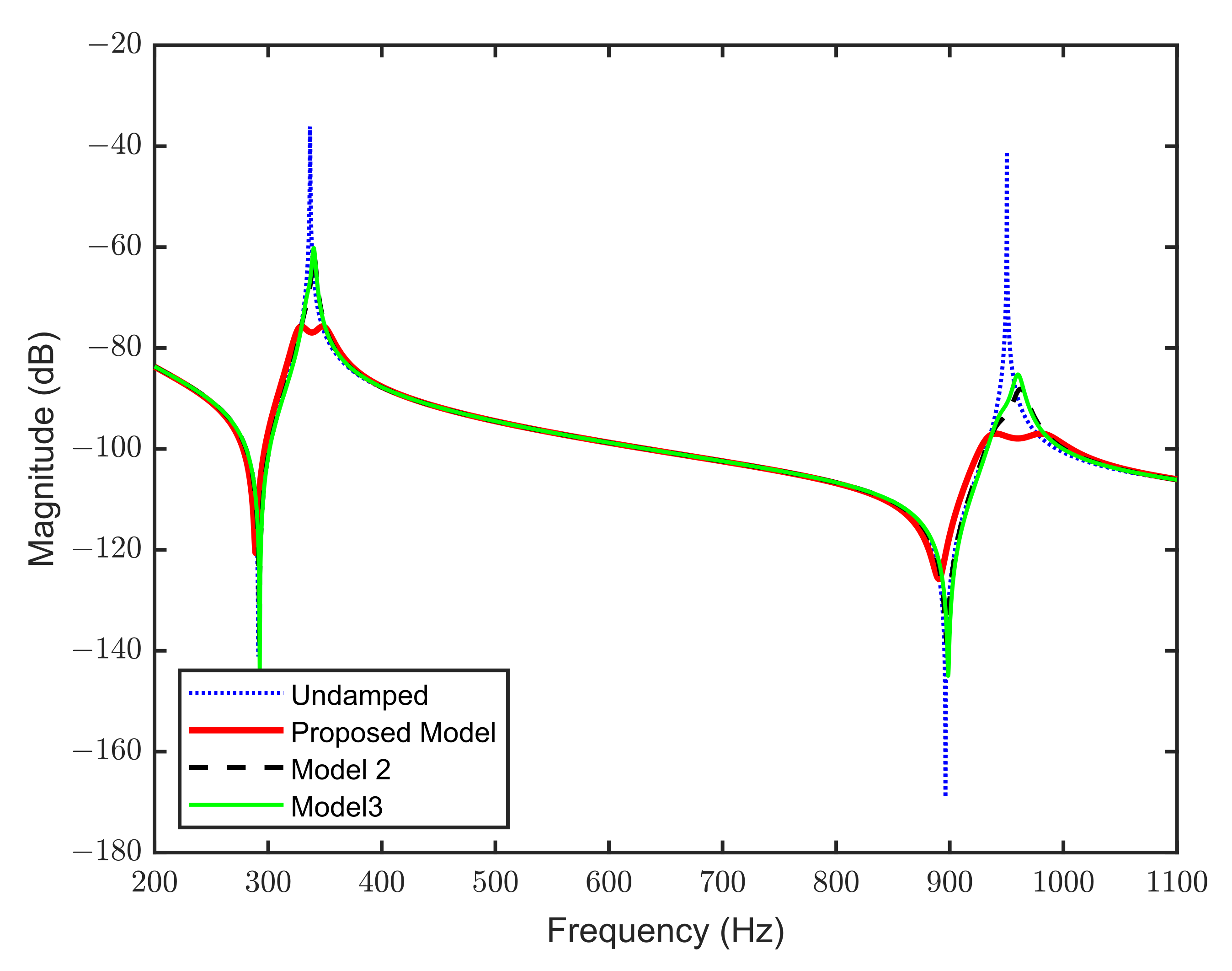
3.5. Comparison between the Three Models
3.6. A Comparison between PSO and GA Algorithms
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, B.; Wang, K.; Hu, Z.; Wu, C.; Zhang, X. Shunt Damping Vibration Control Technology: A Review. Appl. Sci. 2017, 7, 494. [Google Scholar] [CrossRef]
- Marakakis, K.; Tairidis, G.K.; Koutsianitis, P.; Stavroulakis, G.E. Shunt Piezoelectric Systems for Noise and Vibration Control: A Review. Front. Built Environ. 2019, 5, 64. [Google Scholar] [CrossRef]
- Forward, R.L. Electronic Damping of Vibrations in Optical Structures. Appl. Opt. 1979, 18, 690. [Google Scholar] [CrossRef] [PubMed]
- Hagood, N.W.; von Flotow, A. Damping of Structural Vibrations with Piezoelectric Materials and Passive Electrical Networks. J. Sound Vib. 1991, 146, 243–268. [Google Scholar] [CrossRef]
- Park, C.H. Dynamics Modelling of Beams with Shunted Piezoelectric Elements. J. Sound Vib. 2003, 268, 115–129. [Google Scholar] [CrossRef]
- Pietrzko, S.; Mao, Q. Control of Structural Sound Radiation and Vibration Using Shunt Piezoelectric Materials. JSDD 2011, 5, 752–764. [Google Scholar] [CrossRef][Green Version]
- Tairidis, G.K.; Marakakis, K.; Koutsianitis, P.; Foutsitzi, G.; Deü, J.F.; Stavroulakis, G.E.; Ohayon, R. Vibration Control of Smart Composite Plates Using Shunted Piezoelectric Elements. In Proceedings of the 9th ECCOMAS Thematic Conference on Smart Structures and Materials, SMART 2019, Paris, France, 8–12 July 2019. ⟨hal-03179056⟩. [Google Scholar]
- Raze, G.; Dietrich, J.; Lossouarn, B.; Kerschen, G. Modal-Based Synthesis of Passive Electrical Networks for Multimodal Piezoelectric Damping. Mech. Syst. Signal Process. 2022, 176, 109120. [Google Scholar] [CrossRef]
- Bo, L.D.; He, H.; Gardonio, P.; Li, Y.; Jiang, J.Z. Design Tool for Elementary Shunts Connected to Piezoelectric Patches Set to Control Multi-Resonant Flexural Vibrations. J. Sound Vib. 2022, 520, 116554. [Google Scholar] [CrossRef]
- Hollkamp, J.J. Multimodal Passive Vibration Suppression with Piezoelectric Materials and Resonant Shunts. J. Intell. Mater. Syst. Struct. 1994, 5, 49–57. [Google Scholar] [CrossRef]
- Wu, S.-Y. Method for Multiple Mode Piezoelectric Shunting with Single PZT Transducer for Vibration Control. J. Intell. Mater. Syst. Struct. 1998, 9, 991–998. [Google Scholar] [CrossRef]
- Behrens, S.; Reza Moheimani, S.O. Optimal Resistive Elements for Multiple Mode Shunt Damping of a Piezoelectric Laminate Beam. In Proceedings of the 39th IEEE Conference on Decision and Control (Cat. No.00CH37187), Sydney, Australia, 12–15 December 2000; IEEE: Sydney, NSW, Australia, 2000; Volume 4, pp. 4018–4023. [Google Scholar]
- Behrens, S.; Moheimani, S.O.R. Current Flowing Multiple-Mode Piezoelectric Shunt Dampener; Agnes, G.S., Ed.; SPIE: San Diego, CA, USA, 2002; pp. 217–226. [Google Scholar]
- Behrens, S.; Moheimani, S.O.R.; Fleming, A.J. Multiple Mode Passive Piezoelectric Shunt Dampener 1. IFAC Proc. Vol. 2002, 35, 161–166. [Google Scholar] [CrossRef]
- Behrens, S.; Moheimani, S.O.R.; Fleming, A.J. Multiple Mode Current Flowing Passive Piezoelectric Shunt Controller. J. Sound Vib. 2003, 266, 929–942. [Google Scholar] [CrossRef]
- Fleming, A.J.; Behrens, S.; Moheimani, S.O.R. Reducing the Inductance Requirements of Piezoelectric Shunt Damping Systems. Smart Mater. Struct. 2003, 12, 57–64. [Google Scholar] [CrossRef]
- Fleming, A.J.; Behrens, S.; Reza Moheimani, S.O. Optimization and Implementation of Multimode Piezoelectric Shunt Damping Systems. IEEE/ASME Trans. Mechatron. 2002, 7, 87–94. [Google Scholar] [CrossRef]
- Jeon, J.-Y. Passive Vibration Damping Enhancement of Piezoelectric Shunt Damping System Using Optimization Approach. J. Mech. Sci. Technol. 2009, 23, 1435–1445. [Google Scholar] [CrossRef]
- Raze, G.; Dietrich, J.; Kerschen, G. Tuning and Performance Comparison of Multiresonant Piezoelectric Shunts. J. Intell. Mater. Syst. Struct. 2022, 33, 2470–2491. [Google Scholar] [CrossRef]
- Raze, G.; Dietrich, J.; Kerschen, G. Passive Control of Multiple Structural Resonances with Piezoelectric Vibration Absorbers. J. Sound Vib. 2021, 515, 116490. [Google Scholar] [CrossRef]
- Toftekær, J.F.; Høgsberg, J. Multi-Mode Piezoelectric Shunt Damping with Residual Mode Correction by Evaluation of Modal Charge and Voltage. J. Intell. Mater. Syst. Struct. 2020, 31, 570–586. [Google Scholar] [CrossRef]
- Wu, S. Piezoelectric Shunts with a Parallel R-L Circuit for Structural Damping and Vibration Control. In Proceedings of the 1996 Symposium on Smart Structures and Materials, San Diego, CA, USA, 25–29 February 1996; SPIE: Bellingham, WA, USA, 1996; Volume 2720, pp. 259–269. [Google Scholar] [CrossRef]
- Thomas, O.; Deü, J.-F.; Ducarne, J. Vibrations of an Elastic Structure with Shunted Piezoelectric Patches: Efficient Finite Element Formulation and Electromechanical Coupling Coefficients. Int. J. Numer. Meth. Engng 2009, 80, 235–268. [Google Scholar] [CrossRef]
- Foutsitzi, G.; Gogos, C.; Antoniadis, N.; Magklaras, A. Multicriteria Approach for Design Optimization of Lightweight Piezoelectric Energy Harvesters Subjected to Stress Constraints. Information 2022, 13, 182. [Google Scholar] [CrossRef]
- Foutsitzi, G.; Gogos, C.; Hadjigeorgiou, E.; Stavroulakis, G. Actuator Location and Voltages Optimization for Shape Control of Smart Beams Using Genetic Algorithms. Actuators 2013, 2, 111–128. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004; ISBN 978-0-8493-1592-3. [Google Scholar]
- Foutsitzi, G.; Hadjigeorgiou, E.; Gogos, C.; Stavroulakis, G.E. Modal Shape Control of Smart Composite Beams Using Piezoelectric Actuators. In Proceedings of the 10th HSTAM International Congress on Mechanics, Chania, Greece, 25 December 2013. [Google Scholar]
- Gripp, J.A.B.; Rade, D.A. Vibration and Noise Control Using Shunted Piezoelectric Transducers: A Review. Mech. Syst. Signal Process. 2018, 112, 359–383. [Google Scholar] [CrossRef]
- Caruso, G. A Critical Analysis of Electric Shunt Circuits Employed in Piezoelectric Passive Vibration Damping. Smart Mater. Struct. 2001, 10, 1059–1068. [Google Scholar] [CrossRef]
- Beck, B.S.; Cunefare, K.A.; Collet, M. The Power Output and Efficiency of a Negative Capacitance Shunt for Vibration Control of a Flexural System. Smart Mater. Struct. 2013, 22, 065009. [Google Scholar] [CrossRef]
- De Marneffe, B.; Preumont, A. Vibration Damping with Negative Capacitance Shunts: Theory and Experiment. Smart Mater. Struct. 2008, 17, 035015. [Google Scholar] [CrossRef]
- Berardengo, M.; Manzoni, S.; Vanali, M.; Bonsignori, R. Enhancement of the Broadband Vibration Attenuation of a Resistive Piezoelectric Shunt. J. Intell. Mater. Syst. Struct. 2021, 32, 2174–2189. [Google Scholar] [CrossRef]

| References | Single-Mode Control | Multi- Mode Control | Single Piezo Patch | Multiple Piezo Patches | PSO | Other Optimization Approach | Current-Flowing Method | Other Shunt Method |
|---|---|---|---|---|---|---|---|---|
| Forward (1979) [3] | ✓ | ✓ | ||||||
| Hagood et al. (1991) [4] | ✓ | ✓ | ||||||
| Park (2003) [5] | ✓ | ✓ | ||||||
| Pietrzko et al. (2011) [6] | ✓ | ✓ | ||||||
| Tairidis et al. (2019) [7] | ✓ | ✓ | ✓ | |||||
| Raze et al. (2022) [8] | ✓ | ✓ | ✓ | ✓ | ||||
| Bo et al. (2022) [9] | ✓ | ✓ | ✓ | |||||
| Hollkamp (1994) [10] | ✓ | ✓ | ✓ | ✓ | ||||
| Wu (1998) [11] | ✓ | ✓ | ||||||
| Behrens et al. (2000) [12] | ✓ | ✓ | ✓ | |||||
| Behrens et al. (2002) [13,14,15] | ✓ | ✓ | ✓ | ✓ | ||||
| Fleming et al. (2003) [16,17] | ✓ | ✓ | ✓ | ✓ | ||||
| Jeon (2009) [18] | ✓ | ✓ | ✓ | ✓ | ||||
| Raze et al. (2022) [19] | ✓ | ✓ | ✓ | |||||
| Raze et al. (2020) [20] | ✓ | ✓ | ✓ | |||||
| Toftekær et al. (2020) [21] | ✓ | ✓ | ✓ | ✓ | ||||
| Wu (1996) [22] | ✓ | ✓ | ✓ | ✓ |
| Parameter | Beam | PZT |
|---|---|---|
| Length L (mm) | 170 | 25 |
| Width (mm) | 20 | 20 |
| Thickness (mm) | 2 | 0.5 |
| Young’s modulus (GPa) | 72 | 66.7 |
| Shear modulus (GPa) | 27.48 | 25.46 |
| Poisson’s ratio | 0.31 | 0.31 |
| Density ) | 2800 | 8500 |
| Piezoelectric constant () | - | −14 |
| Dielectric constant (nF/m) | - | 2068 |
| Variable | Minimal Value | Maximum Value |
|---|---|---|
| 0 | 30 | |
| 0 | 30 | |
| 10−8 | 1 | |
| 10−8 | 1 | |
| 1 | 20 | |
| 1 | 20 |
| Modes | Short-Circuit Frequencies (Hz) | Open-Circuit Frequencies (Hz) | ||||
| FE [24] | Exp. [24] | Present FE | FE [24] | Exp. [24] | Present FE | |
| 1 | 48.96 | 51.64 | 48.96 | 49.42 | 52.17 | 49.2 |
| 2 | 337.1 | 337.0 | 336.9 | 340.7 | 340.2 | 338.68 |
| 3 | 951.8 | 936.3 | 950.23 | 960.6 | 940.0 | 954.64 |
| Parameter | Value |
|---|---|
| 1.40 | |
| 2.36 | |
| 1 | |
| 0.0083 | |
| 7.43 | |
| 1.68 | |
| 7.68 | |
| 5.06 |
| Parameter | Value |
|---|---|
| 12.29 | |
| 4.02 | |
| 1.83 | |
| 1.83 | |
| 134.07 | |
| 16.85 |
| Parameter | Value |
|---|---|
| 16.34 | |
| 5.43 | |
| 0.001 | |
| 0.001 | |
| 235.36 | |
| 29.59 |
| Model 1 | Model 2 | Model 3 | |
|---|---|---|---|
| Mode 2 | 39.60 | 25.47 | 24.07 |
| Mode 3 | 55.92 | 47.08 | 44.22 |
| Number of Runs | Best Fitness | Time (s) | Total Iterations | Function Evaluations |
|---|---|---|---|---|
| 1 | −84.77 | 8326.053 | 250 | 23,855 |
| 2 | −70.5 | 6513.69 | 250 | 23,855 |
| 3 | −80.96 | 7823.02 | 250 | 23,855 |
| 4 | −69.33 | 3644.80 | 111 | 10,650 |
| 5 | −83.34 | 7231.36 | 250 | 23,855 |
| 6 | −70.72 | 7508.04 | 250 | 23,855 |
| 7 | −70.24 | 4252.65 | 189 | 18,060 |
| 8 | −69.6 | 2168.00 | 72 | 6945 |
| 9 | −80.7 | 7050.17 | 250 | 23,855 |
| 10 | −83.58 | 7220.28 | 250 | 23,855 |
| Avg Total | −76.374 | 6173.81 | 212.2 | 20,264 |
| Number of Runs | Best Fitness | Time (s) | Total Iterations | Function Evaluations |
|---|---|---|---|---|
| 1 | −70.19 | 4277.75 | 112 | 11,300 |
| 2 | −86.34 | 3897.51 | 105 | 10,600 |
| 3 | −86.23 | 6653.82 | 230 | 23,100 |
| 4 | −86.23 | 3428.34 | 132 | 13,300 |
| 5 | −70.19 | 2256.21 | 90 | 9100 |
| 6 | −86.18 | 8431.59 | 250 | 25,100 |
| 7 | −86.21 | 5426.75 | 173 | 17,400 |
| 8 | −86.23 | 8045.17 | 250 | 25,100 |
| 9 | −70.19 | 3946.70 | 142 | 14,300 |
| 10 | −86 | 7613.49 | 250 | 25,100 |
| Avg Total | −81.399 | 5397.73 | 173.4 | 17,440 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marakakis, K.; Tairidis, G.K.; Foutsitzi, G.A.; Antoniadis, N.A.; Stavroulakis, G.E. New Optimal Design of Multimode Shunt-Damping Circuits for Enhanced Vibration Control. Signals 2022, 3, 830-856. https://doi.org/10.3390/signals3040050
Marakakis K, Tairidis GK, Foutsitzi GA, Antoniadis NA, Stavroulakis GE. New Optimal Design of Multimode Shunt-Damping Circuits for Enhanced Vibration Control. Signals. 2022; 3(4):830-856. https://doi.org/10.3390/signals3040050
Chicago/Turabian StyleMarakakis, Konstantinos, Georgios K. Tairidis, Georgia A. Foutsitzi, Nikolaos A. Antoniadis, and Georgios E. Stavroulakis. 2022. "New Optimal Design of Multimode Shunt-Damping Circuits for Enhanced Vibration Control" Signals 3, no. 4: 830-856. https://doi.org/10.3390/signals3040050
APA StyleMarakakis, K., Tairidis, G. K., Foutsitzi, G. A., Antoniadis, N. A., & Stavroulakis, G. E. (2022). New Optimal Design of Multimode Shunt-Damping Circuits for Enhanced Vibration Control. Signals, 3(4), 830-856. https://doi.org/10.3390/signals3040050







