Abstract
Most environments change over time. Being able to adapt to such non-stationary environments is vital for real-world applications of many machine learning algorithms. In this work, we propose CORAL, a computationally efficient regression algorithm capable of adapting to a non-stationary target. CORAL is based on Bayesian linear regression with a sliding window and offline/online meta-learning. The sliding window makes our model focus on the recently received data and ignores older observations. The meta-learning approach allows us to learn the prior distribution of the model parameters. It speeds up the model adaptation, complements the sliding window’s drawback, and enhances the performance. We evaluate CORAL on two tasks: a toy problem and a more complex blood glucose level prediction task. Our approach improves the prediction accuracy for the non-stationary target significantly while also performing well for the stationary target. We show that the two components of our method work in a complementary fashion to achieve this.
1. Introduction
Adapting to a non-stationary environment is important for applying many machine learning algorithms to the real world [1]. Most environments exhibit some sort of variations over time, e.g., physical mechanisms may wear out and change their characteristics, a task related to personal assistance (email classification [2], sentiment classification [3], etc.) also changes over time due to variations in the person’s status, and any task in a competitive environment also varies over time as its competitors learn and improve their behaviours [4].
In this work, we consider a task performed on a stream of data in such a non-stationary environment. This requires the model to learn as it receives data to perform better for the new incoming data. We assume that there is some prior knowledge (or data) about the task. The knowledge or data do not need to be accurate and precise since our model exploits them as long as they give an indication about the task. The data may be synthetically generated with a simulator, which is unlikely to match the real target. Having prior knowledge (or data) is not a mandatory requirement for using our method—we can incorporate prior knowledge whenever it exists.
We tackle the task by learning the model from the data in a sliding window. As it turns out, this method does not perform well for complex target models, requiring much more data than the data available in the window. We resolve this issue by introducing Bayesian meta-learning [5,6], which can also be seen as hierarchical Bayes [7] or empirical Bayes [8]. The empirical Bayes approach learns the model parameter priors from all available data. Because it learns the prior distributions rather than a point estimate, Bayesian meta-learning is robust against overfitting and can introduce uncertainties over the priors, which helps optimally combine the priors and training data to compute the posterior distribution of the parameters in the prediction stage.
Our approach consists of three stages of learning. The first stage is offline meta-learning that learns the prior distribution with available data before the deployment. The second stage is online meta-learning that improves the prior to better fit the actual target. The third stage is Bayesian regression with the sliding window, which learns a model to compute a predictive posterior distribution with the time-windowed data. We propose a computationally efficient method for the online learning parts (the second and third stages), which is important for deploying the algorithm in practice.
The meta-learning approach is common in the few-shot learning domain [9,10], and previous work exists. However, they consider discrete switching between tasks, and often offline learning algorithms. In contrast, our target task is a single task within a gradually changing environment. Our approach provides offline and online meta-learning to learn the priors from the data available before the task and after the deployment. There are a few works in the few-shot learning domain with online meta-learning. We discuss them in Section 4.
Our contributions are summarised as follows:
- We propose a method to adapt to a non-stationary target (concept drift) consisting of two components: Offline/Online Bayesian meta-learning (empirical Bayes) and Bayesian regression with sliding window.
- We show that these components work complementarily and achieve good performance for both stationary and non-stationary tasks.
- We decompose the algorithm with a computationally efficient recursive form.
This paper is organised as follows. Section 2 introduces some background information for Bayesian linear regression and meta-learning. In Section 3, we introduce our method—concept-drift online recursive adaptive learning (CORAL). In Section 4, we discuss connections between our approach and the other related works. Section 5 presents our evaluation tasks and the results. Finally, Section 6 provides a conclusion of our work.
2. Preliminaries
We consider an online prediction task, which generates a prediction from input data . It observes actual in the next time step and updates the prediction model. We assume that the model producing , i.e., , is incrementally changed over time (concept drift [11,12]); hence, the prediction model needs to adapt to the drift over time. Due to the drift, it cannot use all the past data. Only recent n samples can be seen as the data generated by the model same as (or similar enough to) the current generative model.
Our approach utilises Bayesian multivariate linear regression in feature space to compute the predictive posterior and priors of the linear regression coefficients are learned by meta-learning with the empirical Bayes approach. The feature space is either manually designed or produced by a parameterised model, such as a deep neural network (DNN), and the model parameters are learned in the meta-learning stage. This top-level structure of our model is the same as in previous works [9,13]. In this section, we review the Bayesian linear regression algorithm and the meta-learning used by the previous work [13].
2.1. Bayesian Linear Regression
Bayesian multivariate linear regression allows a closed-form analytic computation of the predictive posterior, and it is both sample and computationally efficient. Here, we consider a regression task predicting from . It forms the linear regression over basis functions . It can be written as , where is a coefficient matrix, is zero mean Gaussian noise with the variance , i.e., . By defining and , the likelihood of Y given and is
where tr(.) denotes the trace operation. It is natural to choose a conjugate prior of K, which is the matrix normal distribution. , where is a precision matrix. Then, the posterior distribution of K becomes , and the predictive posterior distribution for can be derived by
where
Equation (3) can be rewritten in the following recursive form
where is initialised as , and is the prior’s precision matrix. Because and can be very large, Equation (4) is computationally expensive for obtaining the predictive posterior at every time step, as it involves computing the inverse of at every time step. Instead of inverting the precision matrix, we can recursively update directly by applying the Woodbury matrix inversion identity [14] to the first line of Equation (4), which gives
This still requires computing once at the very beginning; however, this computation can be conducted offline.
2.2. Offline Meta-Learning
In this subsection, we review the offline meta-learning algorithm proposed as a part of the Adaptive Learning for Probabilistic Connectionist Architecture (ALPaCA) algorithm [13]. ALPaCA also utilises Bayesian linear regression in a feature space combined with offline meta-learning. Its offline meta-learning algorithm learns the coefficients’ prior distributions and the feature space (the basis functions).
ALPaCA assumes the basis function is parameterised with w; typically, is a DNN, and w are its weights. It learns w as well as the prior distribution of K, such as and , offline. ALPaCA takes an empirical Bayes approach for offline meta-learning. To learn the parameters (w, , ), it relies on a stochastic gradient descent (SGD) algorithm to maximise the predictive posterior log probability Equation (2) with a given offline training dataset. Therefore, its loss function can be defined as the negative log posterior as follows:
In the following section, we introduce the CORAL algorithm as an extension of the algorithms described in this section.
3. The CORAL Algorithm
We consider a task on a stream of data generated by a non-stationary target, which requires our method to adapt to the variations. CORAL builds upon previous works such as the Bayesian linear regression on a feature space and offline meta-learning algorithms [9,13]. We have extended the algorithm in two ways. One is introducing the sliding window for adapting to the target variations, and the other is adding online meta-learning. The target adaptation reduces the amount of data available, which we mitigate by employing online meta-learning.
In this section, we first introduce the target adaptation approach in the Bayesian linear regression then describe the online meta-learning method.
3.1. Non-Stationary Target Adaptation
Standard Bayesian linear regression utilises all the training data equally to compute the predictive posterior, which is why it has superior sample efficiency. However, in the case of a non-stationary target, equal treatment of the data causes serious performance degradation. To adapt to a non-stationary target, it is required to compute the predictive posterior with the recent data and forget older data that can degrade the prediction. Here, we propose using a sliding window approach that computes the predictive posterior with a time windowed data .
There are other approaches to incorporate forgetting older data. We pick the sliding window because it works well with the online meta-learning algorithm, as we discuss in Section 4. We can implement the sliding window as shown in Equation (7). Compared with the conventional recursive update equations (Equation (4)), it has an extra term in the first and second equations to remove the older data. In this paper, we assume the time window size n is given and fixed. Adaptive window size algorithms are an interesting research topic, and we discuss some of them in Section 4.
Here, is initialised as , and is the prior’s precision matrix. Again, we can simplify the above computation by updating directly using the Woodbury matrix identity. Here, we need to apply it twice—once for adding a new sample and the second time for removing the older data. The update can be written as
where is an intermediate precision matrix obtained after adding the new data component and before subtracting the old data component . By replacing the first line of Equation (7) with Equation (8), we obtain a recursive method for the predictive posterior with the windowed data.
3.2. Online Meta-Learning
We now extend our approach to incorporate online meta-learning—incrementally learning the prior parameters while receiving a data stream. Online meta-learning is advantageous when no data from the actual target models is available before deployment. In such cases, offline meta-learning can only learn weak priors. In contrast, online meta-learning can improve the prior based on data obtained in the actual deployed environment. Having the better prior may not be so significant in the stationary target case because the predictive posterior can use all observed data to improve its accuracy. However, in our non-stationary scenario, it is essential to have a good prior as the predictor can only rely on a limited number of observation samples. We propose a computationally efficient online meta-learning method that works well with the sliding window target adaptation method described in the previous section. Computational efficiency becomes essential for online learning settings as it requires working in real-time and often working on a device with limited computational power.
The online meta-learning could use the same algorithm as the offline meta-learning described in Section 2.2. However, a straightforward implementation of offline meta-learning is computationally expensive. This is because the recursive methods (Equations (4) and (7)) assume that the prior parameters ( and ) are fixed. Observe that the prior parameters are used to initialise the matrix and , and they are updated with new data. If the prior parameters change, the recursive update of (Equation (5) or Equation (8)) requires a matrix inversion, which is computationally expensive.
Our method consists of two stages, as shown in Figure 1. The first stage is the preparation stage, which computes and from the updated prior. By exploiting the fact that they depend only on the prior and the past n time steps’ data (the data in the sliding window), they can be computed as follows. First, and are initialised with the updated prior parameters, and , respectively, then the following update for n time steps is recursively applied, which are similar to Equations (4) and (5).
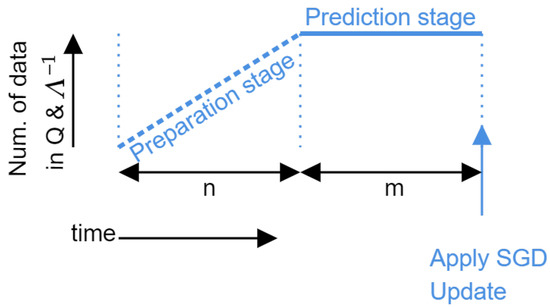
Figure 1.
This figure shows one cycle of our algorithm. It has two stages: The first n time steps (preparation stage) computes and with the updated prior parameters. The next m time steps (prediction stage) produces the predictive posterior and accumulates the prior updates. At the end of the second stage, the accumulated the prior updates are applied and change the prior parameters.
The second stage is the prediction stage, which updates and , produces the predictive posterior and accumulates the prior updates. The and are updated with the recursive update equations with the sliding window, as shown in Equations (7) and (8). The update equations are as follows:
The predictive posterior computation becomes:
Finally, we compute the prior updates (online meta-learning) by applying SGD with the loss function shown in the offline meta-learning Equation (6). It is repeated here for convenience.
Note that CORAL does not actually update the prior during the prediction stage, which lasts for a fixed period (m time steps). It only accumulates the prior parameter updates during the period, and they are applied at the end of the prediction stage. Then, the updated prior is applied in the following preparation stage. The longer prediction stage period m requires a smaller computational load; however, it slows down the online meta-learning speed. Typically, we set the prediction stage period m equal to the sliding window size n. Although it depends upon the target applications, we empirically find it is a reasonable choice, at least for our evaluations.
The other thing to note is that the preparation stage does not produce predictions. To avoid the gap in the prediction computation, we instantiate multiple tasks, each of them running these two stages in a staggered manner. To simplify the discussion, we assume that the prediction state period is equal to the sliding window width (). In this case, we require two tasks, staggered as shown in Figure 2. As the figure suggests, at each point in time, one task is in the preparation stage, while the other task is producing the predictions. In case the two stages have different lengths (), we require tasks to avoid any prediction gaps (here, is the smallest integer not smaller than x) and schedule them in a staggered manner. This approach allows CORAL to maintain the computational complexity , where a conventional meta-learning approach has complexity.
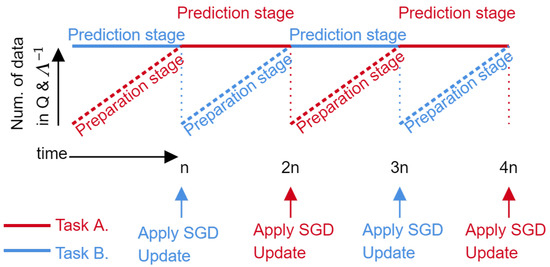
Figure 2.
This figure shows how the tasks are scheduled for case. When task A is in the preparation stage, task B is in the prediction stage to produce the predictive posteriors and accumulate the online meta-learning updates. When task B is in the preparation stage, task A is in the prediction stage to produce the predictive posteriors and accumulate the updates.
Pseudocode for CORAL is given in Algorithm 1. The first two lines are for re-indexing data for convenience. Then, the algorithm initialises the matrices with the latest prior parameters before updating them recursively in lines 3–4. At lines 6–7, and are updated recursively. After n time steps (), the prediction state starts, which computes the predictive posterior and accumulates the prior parameter updates. Finally, the prior parameters are updated with the accumulated values, and the posterior parameters are returned with re-indexing. One final note is that this algorithm still requires inverting the initial prior precision matrix . It is sensible to introduce some restrictions to make the matrix easily invertible. In our evaluation, we use a diagonal matrix for , which we found to work well in our experiments.
| Algorithm 1 One cycle of the CORAL algorithm. |
Require: and
|
4. Related Work
A widely used meta-learning algorithm is model-agnostic meta-learning (MAML) [15], which is applied to a range of different models and shows good performance in practice. MAML learns an initial set of parameters for the model—typically, a neural network. It achieves good performance with a few gradient steps. A recent work interprets MAML as a special case of hierarchical Bayes [7]. Hierarchical Bayes obtains distributions of the priors, whereas MAML learns point estimates of the priors with maximum a posteriori probability (MAP) algorithm. Other works extend MAML to learn distributions rather than point estimates—Bayesian MAML [6,16,17].
Another popular state of the art meta-learning approach is ALPaCA, which performs Bayesian linear regression in the feature space. Interestingly, it learns the feature space as well as prior distributions for the linear regression coefficients as offline meta-learning. It generates predictive posteriors analytically with a computationally efficient recursive method. Compared to the MAML algorithm, the ALPaCA algorithm is computationally and sample efficient, whereas Bayesian MAML can capture wider distribution families. CORAL is close to ALPaCA in terms of structure. However, ALPaCA does not support the non-stationary target scenario, and its meta-learning happens in an offline manner. In contrast, CORAL explicitly tackles non-stationary targets using online meta-learning with a computationally efficient algorithm. Online meta-learning is useful, especially when there are no prior training data available of the target or only very general data are available.
It is also worth mentioning the connection with the few-shot learning literature. Some of the approaches use Bayesian linear regression on a learned feature space [9,10]. They also use (offline) meta-learning to learn the feature space and the prior distributions of the linear regression coefficients. Although the structure is similar to CORAL, they target discrete (abrupt) task switching using offline meta-learning.
Regarding algorithms for non-stationary tasks with meta-learning, this has been addressed in the reinforcement learning literature [4]. There, the authors use MAML to learn a set of initial values of the policy parameters and train the policy parameters for every new task starting from the learned initial value. Although it deals with similar tasks to ours, it re-trains the model for every new task, whereas CORAL incrementally updates the model to adapt to the new task and hence is more computationally efficient.
In what follows, we focus on three concepts that are present across the literature, namely sliding windows, forgetting methods and filtering, and discuss their links to our approach.
4.1. Sliding Windows
The concept of sliding window is commonly used to deal with non-stationary targets [1,18]. The most recent and relevant work is meta-learning via online change point analysis (MOCA). It employs both the sliding window idea and meta-learning and also detects a task-switching point without explicit task switch timing from outside [19]. It uses Bayesian online change point detection (BOCPD) [20] to detect a task-switch timing and combines it with an online meta-learning algorithm to learn multiple tasks without task boundary information. BOCPD computes the probability distribution of the task length. It builds a graphical model and applies a message passing algorithm to compute the posterior of the current task length (they call it “run length”) , where is the run length at time t, and is observed data up to time t. MOCA extends it to support a supervised learning setting, computing an expectation of the predictive posterior over all possible task lengths with regard to the posterior of the task length. In other words, it takes a weighted average of the predictive posteriors for all possible task lengths with the posteriors of the task length as their weight. MOCA performs well for multi-task learning even without the task boundaries information. Because MOCA assumes and is evaluated only on a discrete (abrupt) task-switching case, it is not clear if it still works well on tasks with incremental changes over time. The optimal sliding window length for the non-stationary targets should be obtained by balancing two sources of errors—one due to a lack of data (by having short a sliding window) and the other one due to failing to track the target variation (by having a long sliding window). Although the basic idea of BOCPD should be applicable to the non-stationary target, it is worth investigating if a better method could be applied to the non-stationary target case. Another potential issue with MOCA would be its high computational complexity for calculating the predictive posterior for all possible task lengths. As a result, for the longest possible sliding window length , it has linear complexity with . Conversely, CORAL has linear complexity with the number of tasks . Typically, we use , so CORAL complexity stays low even for a large n. This is not a very fair comparison because MOCA adaptively adjusts its sliding window size, whereas CORAL does not. However, it is true that the MOCA algorithm could not reduce its complexity even if we fixed the sliding window size. The complexity of MOCA might be fine for a relatively short task length case, but we need a computationally efficient method for a long task length case.
4.2. Forgetting Methods
To adapt to concept drift, it is necessary to forget the outdated data or remove the effects on model parameters from the outdated data. In the signal processing community, many works have already been carried out for removing outdated data. The simplest form of such an algorithm is exponential decay [18,21], which applies an exponential decay factor at every recursive update. By using our notation, the recursive updates would be as follows.
This approach is simple and works well in many applications; however, there is a problem with non-stationary targets. As it applies the decay to the prior, it also forgets the prior with time. It is fine to forget the priors for a stationary target because we can set very close to 1.0, and it can make sufficiently good predictions once it receives enough data. However, if the target varies quickly, must be set to a small value in order to forget the outdated data quickly. In such a case, it will fail to achieve accurate predictions because the predictions only rely on a limited number of recently received data without its prior information.
Other more advanced methods, such as directional forgetting [22,23], which analyse the precision matrix and only apply forgetting on directions of their eigenvalues that are larger than a threshold. Essentially, it only forgets data in a direction that has enough information. As it does not forget in a direction that does not have enough data, it will prevent the failure from achieving accurate predictions due to the lack of training data. However, it is not appropriate to use here, as it would generate inaccurate predictions with wrongly high confidence due to using the outdated data.
4.3. Kalman Filter
Several of the ideas present in this paper can also be interpreted from a traditional filtering perspective. Particularly relevant is the Kalman filter [24,25], as an algorithm that estimates non-stationary unknown variables from a series of observations. Originally developed within system control, it is widely used in time series analysis for various applications, such as signal processing, social science and economics. It is possible to apply the Kalman filter to our task by considering the regression parameter as the non-stationary unknown variable and then derive similar recursive update equations as in CORAL. However, there are some key differences. First, how the Kalman filter maintains the priors for the estimating parameter differs from our method. CORAL uses online meta-learning to update the priors, whereas the Kalman filter implicitly computes the prior from the previous time step estimation and its evolution model. Secondly, the Kalman filter’s forgetting mechanism is different from CORAL’s and the other methods described in the previous subsection, as it adds the process noise covariance matrix to the target variable covariance matrix, whereas CORAL subtracts the old data contributions from the target variable precision matrix (Equation (7)). Although, under its assumptions, the Kalman filter approach is optimal, in practice, it requires knowing all the evolution model parameters, including the process noise covariance matrix. In many cases, this unrealistic, especially when the target variable is high dimensional. On the other hand, the CORAL approach does not require full knowledge of the evolution model. It has fewer parameters to tune—the sliding window length and online meta-learning learning rate—and it is easy to optimise even for the high-dimensional target variable cases. Extensions of the Kalman filter to adaptively estimate the model parameters, including the process noise covariance matrix, include [26,27,28,29,30,31]. As these should be discussed with a comparison to the sliding window adaptation algorithms, it is left as future work.
5. Evaluation
We evaluate CORAL on two non-stationary target regression tasks. One is a toy problem that involves a simple linear function model. The coefficients slowly change over time. The other task is more complex—predicting the blood glucose level (BGL) of a person with type 1 diabetes (T1D). We compare CORAL against the algorithm without the sliding window and also without offline/online meta-learning cases. The model without the sliding window and offline/online meta-learning corresponds to a Bayesian regression model. The model without the sliding window and online meta-learning (but with offline meta-learning) is equivalent to the ALPaCA algorithm.
5.1. Toy Problem
First, we test CORAL on a simple non-stationary task, which clearly shows how algorithms that do not consider the non-stationarity struggle and how our approach helps in such a scenario. The task is predicting from , and the model is simply , where a and b are coefficients and both in . x is sampled from a Gaussian distribution with mean zero and variance 100. At each time step, the algorithm receives the current and generates the prediction . It also receives the previous time step’s target value with some observation noise to update the prediction model. The observation noise is normally distributed with mean 0 and variance 2. We test the model while slowly varying the coefficients a and b as follows:
where t is the time step starting from zero. Hence, both coefficients oscillate with a sample period of 200 time steps and also slowly increase their baselines.
For the prediction model, we use as the basis function (features) to reproduce the target model. We test three models: (1) using neither the sliding window nor the online meta-learning, (2) with sliding window (length 5) and without online meta-learning, (3) with sliding window (length 5) and online meta-learning. We set the prediction stage period m equal to the sliding window size, which is five. In this evaluation, we do not use offline meta-learning because the target model is very simple (only two parameters to estimate). The priors are initially set to a standard normal distribution.
The posteriors of the coefficients (a and b) for the three models are shown in Figure 3 as well as their true values. The results without the sliding window (a) show that both a and b converge towards an average over the past true values. Furthermore, their variances are monotonically reduced to zero as it receives data. These behaviours are not favourable for the non-stationary target case, as they converge to wrong values, and they also become overconfident (underestimate its variances). The results of the model with a sliding window and without meta-learning (b) show that the posterior for a converges to the right value and variances. However, it struggles to achieve a good posterior for b, especially for later time steps. This is because the true b values at the later time steps are more apart from their prior distribution; hence, it fails to move the posterior to the true value with the limited number of data in the sliding window. The results (c) from the model with the sliding window and online meta-learning mitigate the problem in the parameter b posterior. This is because the model with online meta-learning updates its prior distributions to keep up with the long-term variation. These priors are shown in Figure 4, where (a) shows the priors of the parameters a and b with neither meta-learning nor the sliding window, and (b) shows the priors without meta-learning but with a sliding window. They both do not use online meta-learning; hence, the priors stay in their initial setting (normal distribution.) Additionally, (b) shows the priors with meta-learning. We can see that they adapt to the mean level drift (slow drift). It does not adapt to the oscillations (fast drift), but their variances correctly cover the range of oscillations.
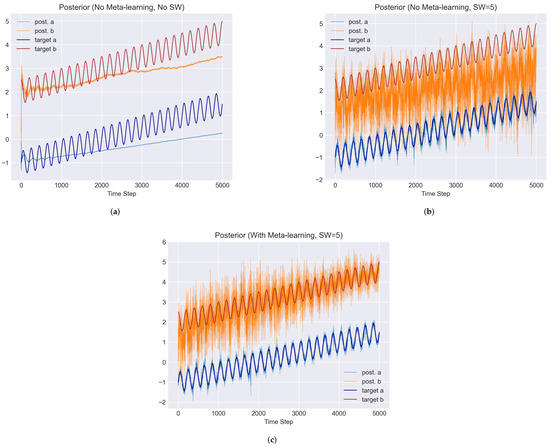
Figure 3.
Posterior distributions for parameters a and b over time steps. The dark blue and red lines are for the true a and b values. The light blue and orange lines show the mean of the posterior distributions, and shaded areas are for the std. range. (a) No meta-learning, no sliding window; (b) no meta-learning, sliding window = 5; (c) meta-learning, sliding window = 5.
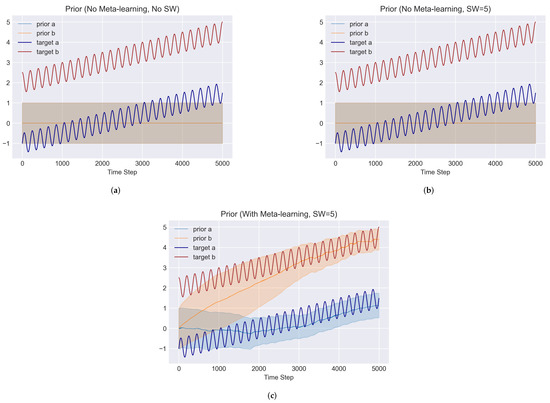
Figure 4.
Prior distributions for parameters a and b over time steps. The dark blue and red lines are for the true a and b values. The light blue and orange lines are for the mean of the prior distributions, and shaded areas are for the std. range. (a) No meta-learning, no sliding window; (b) no meta-learning, sliding window = 5; (c) meta-learning, sliding window = 5.
Figure 5 shows the mean squared error (MSE) with a 200 time step moving average for the three prediction models. It clearly shows that the model without the sliding window fails in this non-stationary task. With the sliding window, the prediction accuracy improves dramatically; however, the result without online meta-learning (orange line) slowly worsens as the true parameter value deviates from its prior distribution. By having the online meta-learning, it manages to update the priors to follow the long-term variation of the parameter; hence, the green line improves initially and then stays low.
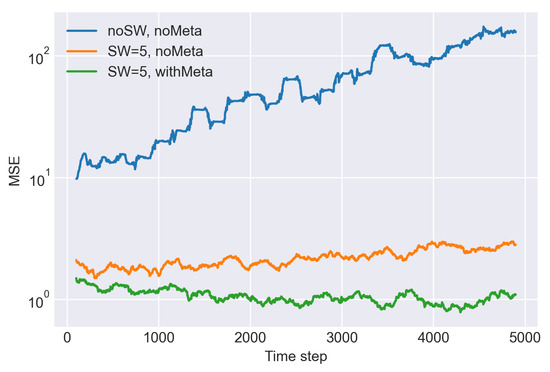
Figure 5.
The figure shows the mean squared error (MSE) with 200 time step moving average for the toy regression task. The coefficients of the linear generative model change their values over time to simulate the non-stationary target. Three lines are for the different prediction models. The blue line is the result of the model without meta-learning and without sliding window. The orange line is the result of the model without meta-learning and with sliding window. The green line is the result of the model with online meta-learning and sliding window.
Figure 6 shows the MSE when sweeping the sliding window length. The MSE is measured over the last 1000 time steps from the 5000 time steps simulation. The blue line is the results from the model without meta-learning. The orange line is the results from the model with meta-learning. We expected that the MSE increases for both short and long sliding window lengths. For the shorter sliding window, the model receives a smaller number of data to predict; hence, it degrades performance. For the longer sliding window side, it starts to fail due to the failure to adapt to the target variation. The results from the model without meta-learning shows such a shape. However, the results from the model with meta-learning does not degrade much for the short sliding window. It is because the meta-learning provides a better prior that compensates for the performance loss due to the lack of data in the sliding window. For the long sliding window side, the meta-learning cannot help because it is designed to track only slow long-term variations.
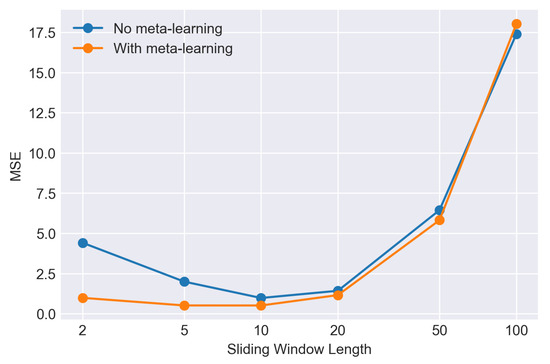
Figure 6.
The figure shows mean squared error (MSE) with sweeping the sliding window length. The MSE is calculated from the last 1k time steps of the total 5k time steps simulation. The blue line is the results from the model without meta-learning. The orange line is the results from the model with meta-learning.
5.2. Blood Glucose Level Prediction
We now evaluate the CORAL performance in a more complex prediction task—T1D BGL prediction. T1D is a chronic condition that is characterised by the lack of insulin secretion, resulting in uncontrolled BGL [32,33]. A person with T1D takes an insulin injection to control BGL. It is not easy to decide the timing and amount of insulin injection because how BGL reacts to the insulin varies for each individual and over time, even for the same individual. Machine learning algorithms can assist with such decisions. One of the possibilities of such a decision support system is predicting future BGL. Here, we predict the future BGL from the past insulin injection and meal information, and it allows the person with diabetes to see the consequences of various actions, e.g., different choices for insulin doses.
5.2.1. Data Generation
We use a simulator to generate the target BGL. UVa/Padova type 1 diabetes simulator is the first computer model accepted by the FDA as a substitute for preclinical trials of certain insulin treatments, including closed-loop algorithms [34]. Our simulator is based on an open-source implementation of the UVa/Padova type 1 diabetes simulator [35], which comes with 30 profiles for virtual people with diabetes—ten each for children, adolescents and adults.
UVa/Padova simulator is designed to simulate one meal event; hence, it does not simulate long-term parameter variations [34]. To evaluate the long-term parameter variations, we modified the simulator to drift from one profile to the other profile over time. The new simulator is given two profiles and how long it takes to move from one profile to the other. The simulator linearly changes the profiles over the given time period. Once it reaches the other profile, it starts going back to the original profile and repeats the cycle. In this evaluation, we set the drifting time to 5 days. This is motivated by previous work [36,37], which suggests that human insulin sensitivity variations due to exercises occur between 3 days to 5 days.
5.2.2. Predictor Model
The BGL prediction requires memory to remember the past insulin and meal information because the future BGL depends on these past inputs. To capture the past inputs, we employ a recurrent neural network (RNN) and form the basis function . More specifically, we use an echo state network (ESN) [38,39], which is one variant of RNN, and it has been successfully applied to the BGL prediction task [40]. One benefit of using ESN is that it does not require learning its recurrent layer weights. Instead, it uses randomly initialised, fixed weights for the recurrent layer, and only output layer weights are learned. To use ESN, the output layer is replaced with Bayesian linear regression. As ESN does not require learning its recurrent layer weights, there is no basis function parameter w to learn at the meta-learning stage. Thus, the meta-learning process only learns the prior distribution parameters, and it simplifies the overall learning process. For this evaluation, we set the sliding widow size 576 (2 days worth length) to handle the target model variation within the 5-day period. For further details about ESN, we refer interested readers to [41], which provides useful guidance for using an ESN.
5.2.3. Evaluation Procedure
In this evaluation, we assume that we have access to a lot of data from the general population (from the same age group) but no data from the target person. We can learn some prior knowledge from these data (offline meta-learning) first, and then the model updates its prior as it receives data from the actual target (online meta-learning).
First, we train the model priors with the virtual person profiles—adult#004, #005, #006, #007, #008, #009 and #010. We generate seven days worth of inputs (meal and insulin) and output (BGL) with 5 min time intervals for a randomly selected virtual person profile from the above list. The first 8 hours’ worth of data is supplied to the model to initialise the ESN’s internal state, and then the rest of the data is applied to train the prior parameters using the method described in Section 3.2. We repeat this process 250 times, then store the final prior parameter values to use for the test with a target profile.
After the offline meta-learning, we evaluate the models with target virtual person profiles. We carried out our evaluation with three target profiles: (1) stationary adult#001, (2) non-stationary varying between adult#001 and adult#003 and (3) non-stationary varying between adult#002 and adult#003. We evaluate six prediction models: two without a sliding window and four with a sliding window. For the model without the sliding window, we evaluate the models with and without offline meta-learning and both without online meta-learning. For the model with the sliding window, the models with and without offline meta-learning as well as with and without online meta-learning (in total, four combinations) are evaluated. In the case of the target profile the stationary adult#001, the model without the sliding window must perform the best; however, it is interesting to see how close the model with the sliding window and online meta-learning can perform. We run 100 days worth of data from the target profile through the prediction model, measure its root mean squared error (RMSE) over the last 20 days and report it. RMSE is a commonly used metric to evaluate the performance of the BGL predictions. Interestingly, there is a metric specific to the BGL predictions, such as glucose-specific MSE (gMSE) [42], which consider a clinical risk of a particular error. However, we use RMSE here as it is more generic and easier to interpret.
5.2.4. Results
The first set of results for the stationary target profile (adult#001) are summarised in Table 1. The results suggest that the offline meta-learning improves a lot in the RMSE measure in all cases. Although the improvements are smaller than with offline meta-learning, online meta-learning also improves the RMSE. The best result with the sliding window is worse than the result without it. This was expected as the target is stationary. The gap between them is reduced from 4.80 mg/dL to 1.57 mg/dL by enabling online meta-learning. It suggests that the online meta-learning mitigates the degradation due to the short window size and narrows the gap.

Table 1.
The summary of results for the BGL prediction task with the stationary target profile (adult#001). Numbers in the brackets are from the model without the sliding window, and the others are with the sliding window (length = 576). ML denotes meta-learning.
The next set of results is for the non-stationary targets varying between adult#001 and adult#003 profiles in Table 2. Without the sliding window, the results with and without offline meta-learning are similar to the previous results. It suggests that the errors are mainly due to failing to follow the target variation. With the sliding window, the results are improved except without meta-learning. It shows that the effectiveness of the sliding window approach and the meta-learning combination for the non-stationary targets and just the sliding window alone (or meta-learning alone) do not perform as well as the combination.

Table 2.
The summary of results for the BGL prediction task with the non-stationary target profile varying between adult#001 and adult#003. Numbers in the brackets are from the model without the sliding window, and the others are with the sliding window (length = 576). ML denotes meta-learning.
The third set of results is for the non-stationary targets again but between adult#002 and adult#003 in Table 3. The adult#002 profile is closer to adult#003 profile than adult#001 profile; hence, these tests do not have as many variations as the previous set of the test case. The results also indicate it, as the best results with and without the sliding window are similar.

Table 3.
The summary of results for the BGL prediction task with the non-stationary target profile varying between adult#002 and adult#003. Numbers in the brackets are from the model without the sliding window, and the others are with the sliding window (length = 576). ML denotes meta-learning.
Overall, the results are encouraging as in the non-stationary target case, the results with sliding window plus meta-learning are better than those without the sliding window. In the stationary target case, both results are similar. Ideally, the BGL would be controlled within a range of 70 to 180 mg/dL (this range would vary depending upon their age), and it could go up to over 300 mg/dL. Considering the ideal range of BGL, the evaluation results for our approach show acceptable performances. However, it still has much room for improvement.
Figure 7 shows the mean squared error (MSE) with a 20-day moving average length. The x-axis shows time steps in days. All of the results use the two-day sliding window. The simulation runs 100 days worth of data, and the plot shows up to 80 days because it is applied 20 days moving average. The dotted lines are for the model without offline meta-learning. The solid lines are for the model with offline meta-learning. The blue lines are for the model without online meta-learning. The orange lines are for the model with online meta-learning. The MSE at the beginning shows that the offline meta-learning improves MSE. As time progresses, the results with online meta-learning (orange lines) show improvements over the results without online meta-learning (blue lines).
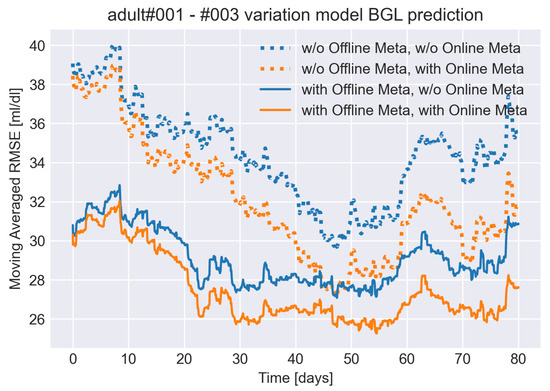
Figure 7.
The figure shows the mean squared error (MSE) with a 20-day moving average length. The x-axis shows time steps in days. All of the results use the two-day sliding window. The dotted lines are for the model without offline meta-learning. The solid lines are for the model with offline meta-learning. The blue lines are for the model without online meta-learning. The orange lines are for the model with online meta-learning. The MSE at the beginning shows the offline meta-learning improves MSE. As time progress, the model with online meta-learning results improves over the results without online meta-learning.
We also evaluate CORAL against other existing approaches—Recursive Least Square (RLS) with the exponential decay and the sliding window forgetting algorithms and ALPaCA with the exponential decay forgetting algorithm. RLS does not use meta-learning, whereas ALPaCA employs offline meta-learning, and CORAL exploits both offline and online meta-learning. The exponential decay algorithm is presented with the three decay factors: and , and the sliding window algorithm is also evaluated with the three sliding window sizes: and 1152, which are equivalent to one day, two days and four days. The results are shown in Figure 8 for the stationary target profile (adult#001) and Figure 9 for the non-stationary target profile (adult#001 and adult#003). These plots have the BGL prediction RMSE in the y-axis and the prediction time, which shows how far into the future it predicts in the x-axis.
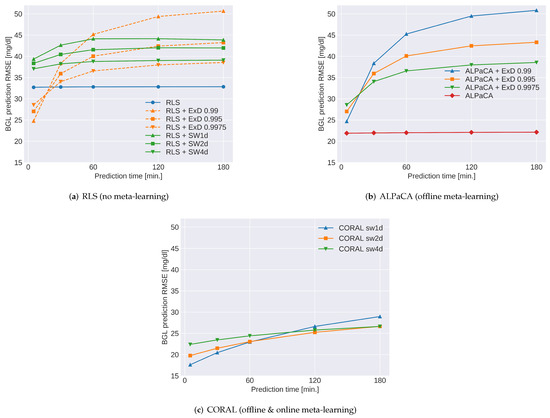
Figure 8.
Blood glucose level (BGL) prediction RMSE for the stationary target model (adult#001) with three base models—RLS, ALPaCA and CORAL. The x-axis shows its prediction time in minutes, which shows how far into the future it predicts.
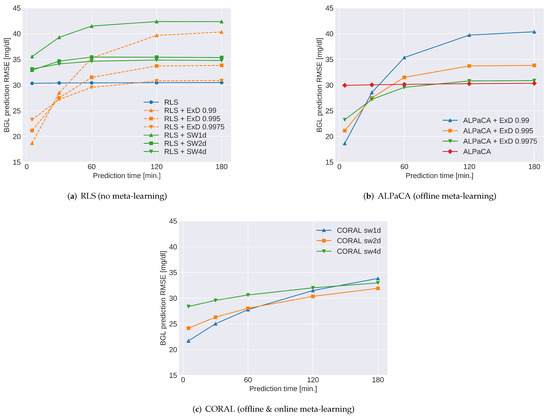
Figure 9.
Blood glucose level (BGL) prediction RMSE for the non-stationary target model (adult#001 ↔ adult#003) with three base models—RLS, ALPaCA and CORAL. The x-axis shows its prediction time in minutes, which shows how far into the future it predicts.
The RLS results for the stationary target Figure 8a shows that the RLS without any forgetting performs best, which is expected as the target is stationary. However, RLS with the exponential decay performs better for the shortest prediction time (5 min). We think this indicates that the prediction model is not yet fully trained to capture all the complex BGL behaviours, despite being trained with eighty days of data. The exponential decay algorithm forces the model to focus on the recently acquired data, and as a result, it does not generalise as well. Hence, the model becomes good at predicting the near future but not adequate for the more distant future predictions. The results of ALPaCA (b) show an excellent performance. It suggests that offline meta-learning helps learn the complex BGL behaviours. On the other hand, the results with the exponential decay algorithm do not show any benefit from offline meta-learning, and they are almost identical to the those for RLS with exponential decay. These results are expected as the exponential decay is also applied to the prior given by offline meta-learning, and it is lost after certain time steps (as discussed in Section 4.2). The results of CORAL (c) show good performance but not as well as ALPaCA without the forgetting algorithm. The target is stationary, and it requires neither online meta-learning nor a forgetting algorithm.
Figure 9 shows the results for the non-stationary target. The most relevant difference from the stationary target results is that the ALPaCA without the forgetting algorithm performs much worse as it requires a forgetting algorithm to follow the non-stationary target. CORAL performs well for a prediction time of up to two hours but worse than the RLS algorithm for a three-hour prediction time. Although this is unexpected, we think it is due to online meta-learning adjusting the prior suitable for the short time predictions, as the loss function for meta-learning (Equation (6)) uses the one time step (5 min) prediction. In summary, although CORAL does not outperform other models in all cases, CORAL with the one- or two-day sliding windows is the best model overall.
6. Conclusions
We proposed CORAL, a computationally efficient method to adapt to non-stationary targets. CORAL builds upon Bayesian linear regression with a sliding window in order to follow the target variation and online meta-learning to improve its prediction accuracy even for the non-stationary target scenario. We evaluated our method in two tasks. First, we studied a simple linear regression problem with varying generative model coefficients. Then, we tackled a more complex type 1 diabetes (T1D) blood glucose level (BGL) prediction task. The evaluation results showed the effectiveness of CORAL for non-stationary tasks and how the online meta-learning mitigates the performance loss due to short window sizes.
Regarding the limitations, CORAL assumes the sliding window size is known and fixed. Although the meta-learning mitigates the drawbacks of using a short window, we believe that an adaptive window size would perform better. Another aspect that requires attention is that the use of analytic recursive update formulas comes with the limitations of Gaussian models (and the predictive posterior is limited to a multivariate normal distribution). Finally, the non-stationary target adaptation is achieved by discarding (forgetting) old data and never utilising the discarded data in the future, even if it becomes relevant again. To recycle the past data, we might require a context detector to categorise and re-using the data when the current context matches with the data category.
For future work, we will address some of the limitations above by exploring algorithms for sliding window adaptation. In this work, we assumed the window size was given and fixed. However, the model will become much more flexible by having the ability for the size to be set in an adaptive manner. In a sense, this adaptation algorithm is related to the context detector mentioned above. We can view it as identifying how far the past data still belongs to the current context.
Author Contributions
T.Y.: Conceptualisation, methodology, software, validation, formal analysis, investigation, data curation, writing—original draft preparation, visualisation; R.S.-R.: Conceptualisation, validation, writing—review and editing, supervision; P.F.: writing—review and editing, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by SPHERE Next Steps Project funded by the U.K. Engineering, and Physical Sciences Research Council (EPSRC) under Grant EP/R005273/1. RSR is funded by the UKRI Turing AI Fellowship EP/V024817/1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study did not involve any underlying data.
Acknowledgments
Thanks are due to Yu Chen for providing useful comments on a draft of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gama, J.; Žliobaite, I.; Bifet, A.; Pechenizkiy, M.; Bouchachia, A. A survey on concept drift adaptation. ACM Comput. Surv. (CSUR) 2014, 46, 1–37. [Google Scholar] [CrossRef]
- Carmona-Cejudo, J.M.; Baena-Garcia, M.; del Campo-Avila, J.; Morales-Bueno, R.; Bifet, A. Gnusmail: Open Framework for On-Line Email Classification; IOS Press: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Bifet, A.; Frank, E. Sentiment knowledge discovery in twitter streaming data. In Proceedings of the International Conference on Discovery Science, Thessaloniki, Greece, 19–21 October 2010; pp. 1–15. [Google Scholar]
- Al-Shedivat, M.; Bansal, T.; Burda, Y.; Sutskever, I.; Mordatch, I.; Abbeel, P. Continuous adaptation via meta-learning in nonstationary and competitive environments. arXiv 2017, arXiv:1710.03641. [Google Scholar]
- Amit, R.; Meir, R. Meta-learning by adjusting priors based on extended PAC-Bayes theory. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 205–214. [Google Scholar]
- Ravi, S.; Beatson, A. Amortized Bayesian Meta-Learning. In Proceedings of the ICLR (Poster), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Grant, E.; Finn, C.; Levine, S.; Darrell, T.; Griffiths, T. Recasting gradient-based meta-learning as hierarchical bayes. arXiv 2018, arXiv:1801.08930. [Google Scholar]
- Morris, C.N. Parametric empirical Bayes inference: Theory and applications. J. Am. Stat. Assoc. 1983, 78, 47–55. [Google Scholar] [CrossRef]
- Bauer, M.; Rojas-Carulla, M.; Świkatkowski, J.B.; Schölkopf, B.; Turner, R.E. Discriminative k-shot learning using probabilistic models. arXiv 2017, arXiv:1706.00326. [Google Scholar]
- Patacchiola, M.; Turner, J.; Crowley, E.J.; O’Boyle, M.; Storkey, A. Bayesian Meta-Learning for the Few-Shot Setting via Deep Kernels. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 6–12 December 2020. [Google Scholar]
- Moreno-Torres, J.G.; Raeder, T.; Alaiz-Rodríguez, R.; Chawla, N.V.; Herrera, F. A unifying view on dataset shift in classification. Pattern Recognit. 2012, 45, 521–530. [Google Scholar] [CrossRef]
- Kull, M.; Flach, P. Patterns of dataset shift. In Proceedings of the First International Workshop on Learning over Multiple Contexts (LMCE) at ECML-PKDD, Nancy, France, 15–19 September 2014. [Google Scholar]
- Harrison, J.; Sharma, A.; Pavone, M. Meta-learning priors for efficient online bayesian regression. In International Workshop on the Algorithmic Foundations of Robotics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 318–337. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2013; Volume 3. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the 34th International Conference on Machine Learning—ICML 2017, Sydney, Australia, 6–11 August 2017; Volume 3, pp. 1856–1868. [Google Scholar]
- Yoon, J.; Kim, T.; Dia, O.; Kim, S.; Bengio, Y.; Ahn, S. Bayesian model-agnostic meta-learning. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 7343–7353. [Google Scholar]
- Finn, C.; Xu, K.; Levine, S. Probabilistic model-agnostic meta-learning. arXiv 2018, arXiv:1806.02817. [Google Scholar]
- Sayed, A.H. Adaptive Filters; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Harrison, J.; Sharma, A.; Finn, C.; Pavone, M. Continuous meta-learning without tasks. arXiv 2019, arXiv:1912.08866. [Google Scholar]
- Adams, R.P.; MacKay, D.J.C. Bayesian online changepoint detection. arXiv 2007, arXiv:0710.3742. [Google Scholar]
- Haykin, S.S. Introduction to Adaptive Filters; Macmillan: London, UK, 1984. [Google Scholar]
- Kulhavỳ, R.; Kárnỳ, M. Tracking of slowly varying parameters by directional forgetting. IFAC Proc. Vol. 1984, 17, 687–692. [Google Scholar] [CrossRef]
- Parkum, J.E.; Poulsen, N.K.; Holst, J. Recursive forgetting algorithms. Int. J. Control 1992, 55, 109–128. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems; The American Society of Mechanical Engineers: New York, NY, USA, 1960. [Google Scholar]
- Stepanov, O. Kalman filtering: Past and present. An outlook from Russia. (On the occasion of the 80th birthday of Rudolf Emil Kalman). Gyroscopy Navig. 2011, 2, 99–110. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Wu, Z.; Li, N.; Chambers, J. A novel adaptive Kalman filter with inaccurate process and measurement noise covariance matrices. IEEE Trans. Autom. Control 2017, 63, 594–601. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, A.; Schwarz, K. Adaptive Kalman filtering for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Sage, A.P.; Husa, G.W. Adaptive filtering with unknown prior statistics. Jt. Autom. Control Conf. 1969, 7, 760–769. [Google Scholar]
- Gao, X.; You, D.; Katayama, S. Seam tracking monitoring based on adaptive Kalman filter embedded Elman neural network during high-power fiber laser welding. IEEE Trans. Ind. Electron. 2012, 59, 4315–4325. [Google Scholar] [CrossRef]
- Sarkka, S.; Nummenmaa, A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations. IEEE Trans. Autom. Control 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Ardeshiri, T.; Özkan, E.; Orguner, U.; Gustafsson, F. Approximate Bayesian smoothing with unknown process and measurement noise covariances. IEEE Signal Process. Lett. 2015, 22, 2450–2454. [Google Scholar] [CrossRef] [Green Version]
- Alberti, K.G.M.M.; Zimmet, P.Z. Definition, diagnosis and classification of diabetes mellitus and its complications. Part 1: Diagnosis and classification of diabetes mellitus. Provisional report of a WHO consultation. Diabet. Med. 1998, 15, 539–553. [Google Scholar] [CrossRef]
- Davis, A.K.; DuBose, S.N.; Haller, M.J.; Miller, K.M.; DiMeglio, L.A.; Bethin, K.E.; Goland, R.S.; Greenberg, E.M.; Liljenquist, D.R.; Ahmann, A.J.; et al. Prevalence of detectable C-peptide according to age at diagnosis and duration of type 1 diabetes. Diabetes Care 2015, 38, 476–481. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dalla Man, C.; Micheletto, F.; Lv, D.; Breton, M.; Kovatchev, B.; Cobelli, C. The UVA/PADOVA type 1 diabetes simulator: New features. J. Diabetes Sci. Technol. 2014, 8, 26–34. [Google Scholar] [CrossRef] [Green Version]
- Xie, J. Simglucose v0.2.1. 2018. Available online: https://github.com/jxx123/simglucose (accessed on 28 December 2019).
- Mikines, K.J.; Sonne, B.; Farrell, P.A.; Tronier, B.; Galbo, H. Effect of physical exercise on sensitivity and responsiveness to insulin in humans. Am. J. Physiol. Endocrinol. Metab. 1988, 254, E248–E259. [Google Scholar] [CrossRef] [PubMed]
- Mikines, K.J.; Sonne, B.; Tronier, B.; Galbo, H. Effects of acute exercise and detraining on insulin action in trained men. J. Appl. Physiol. 1989, 66, 704–711. [Google Scholar] [CrossRef]
- Gürbilek, N. Real-Time Computing without Stable States: A New Framework for Neural Computation Based on Perturbations. J. Chem. Inf. Model. 2013, 53, 1689–1699. [Google Scholar] [CrossRef]
- Jaeger, H. The “Echo State” Approach to Analysing and Training Recurrent Neural Networks—With an Erratum Note 1; GMD Technical Report; German National Research Center for Information Technology: Bonn, Germany, 2010; pp. 1–47. [Google Scholar]
- Yamagata, T.; O’Kane, A.; Ayobi, A.; Katz, D.; Stawarz, K.; Marshall, P.; Flach, P.; Santos-Rodriguez, R. Model-based reinforcement learning for type 1 diabetes blood glucose control. CEUR Workshop Proc. 2020, 2820, 72–77. [Google Scholar]
- Lukoševičius, M. A practical guide to applying echo state networks. Lect. Notes Comput. Sci. 2012, 7700, 659–686. [Google Scholar] [CrossRef]
- Del Favero, S.; Facchinetti, A.; Cobelli, C. A glucose-specific metric to assess predictors and identify models. IEEE Trans. Biomed. Eng. 2012, 59, 1281–1290. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).