A Recursive Generative Adversarial Denoising Learning Method for Acoustic-Based Gear Fault Diagnosis Under Non-Stationary Noise Interference
Abstract
1. Introduction
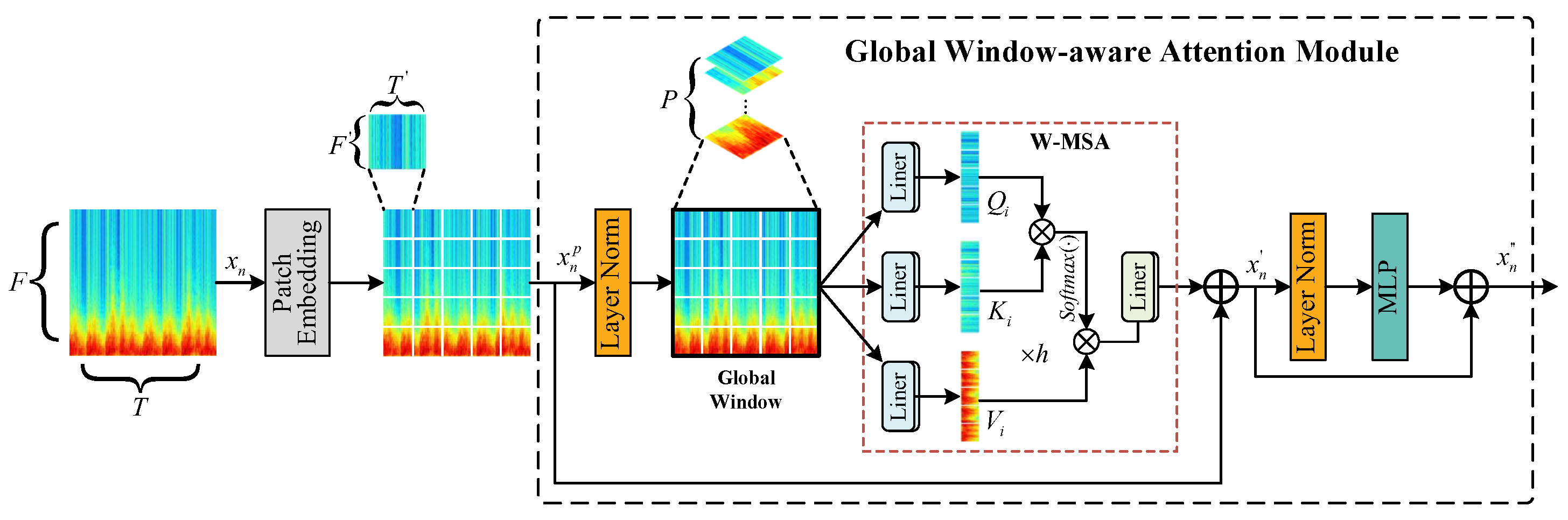
- A novel GWAM-based generator is first proposed to capture the periodic structure characteristics of gear acoustic signals under noise interference by adaptively representing non-stationary noise components and recursively modeling the global dependence of time–frequency features.
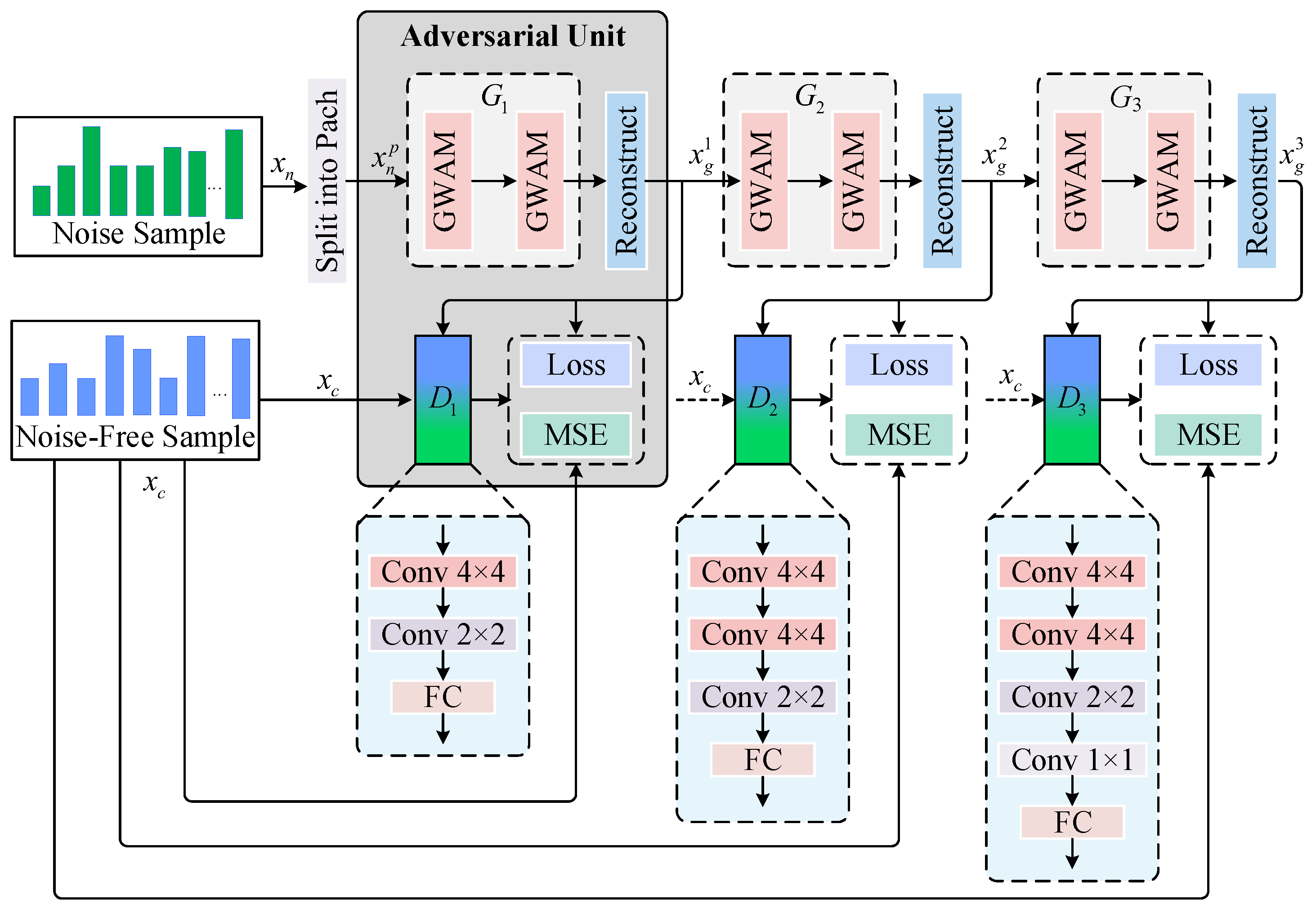
- A new adversarial mechanism is further developed by constructing a recursive discriminative architecture, which enables the model to effectively avoid the vanishing gradient problem and significantly refine the detail reconstruction quality of acoustic features from the noise condition.
- Building upon the above modules, a complete RGAD-based ABD framework is constructed to detect gear fault patterns in non-stationary noise conditions, which demonstrates the effectiveness of the proposed ABD framework in real industrial scenarios.
2. Background
2.1. Swin Transformer
2.2. Generative Adversarial Network
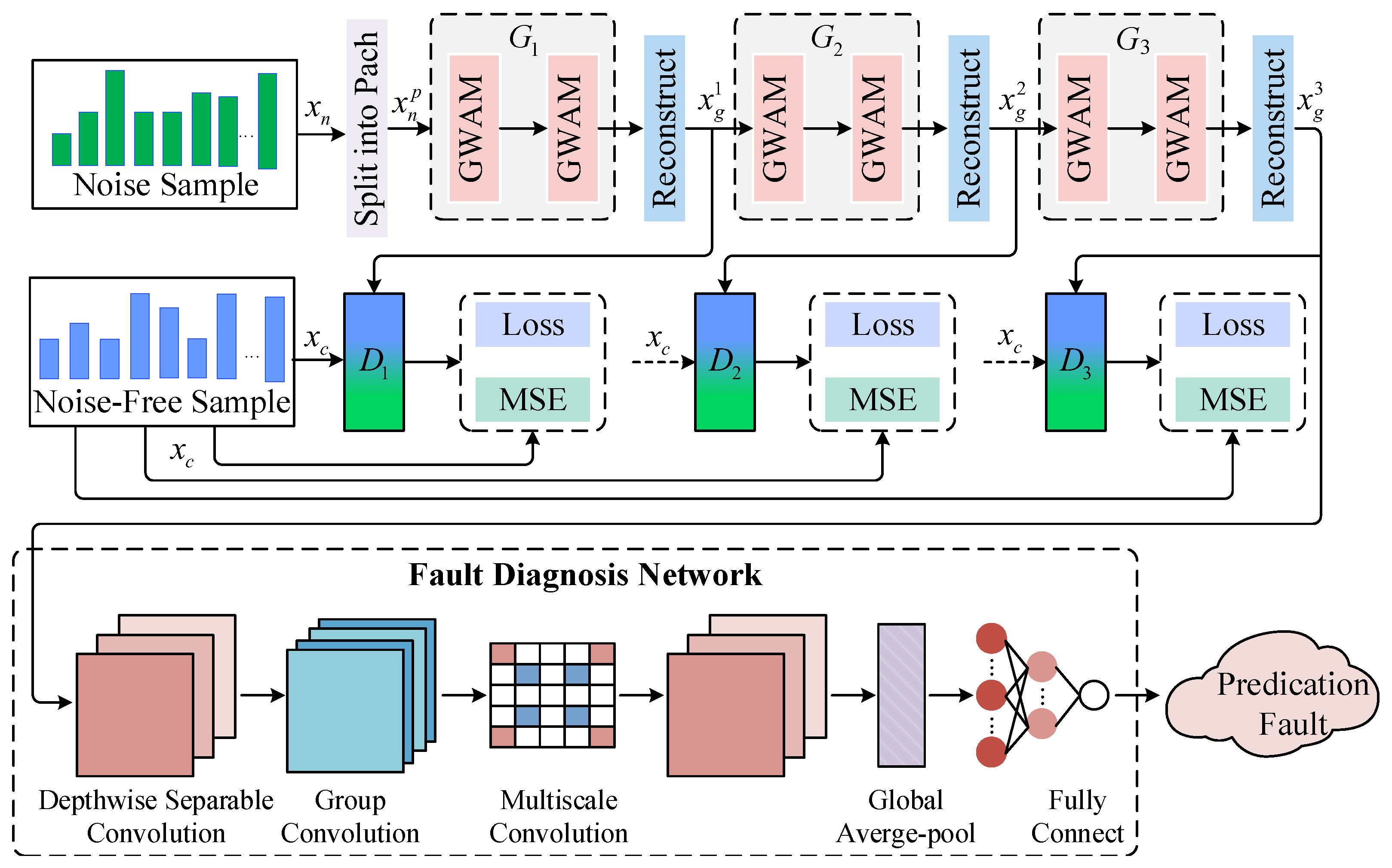
3. Methodology
3.1. Global Window-Aware Attention Module
3.2. Recursive Adversarial Mechanism
3.3. Loss Functions and Optimization Strategies
3.4. Overall RGAD-Based ABD Framework
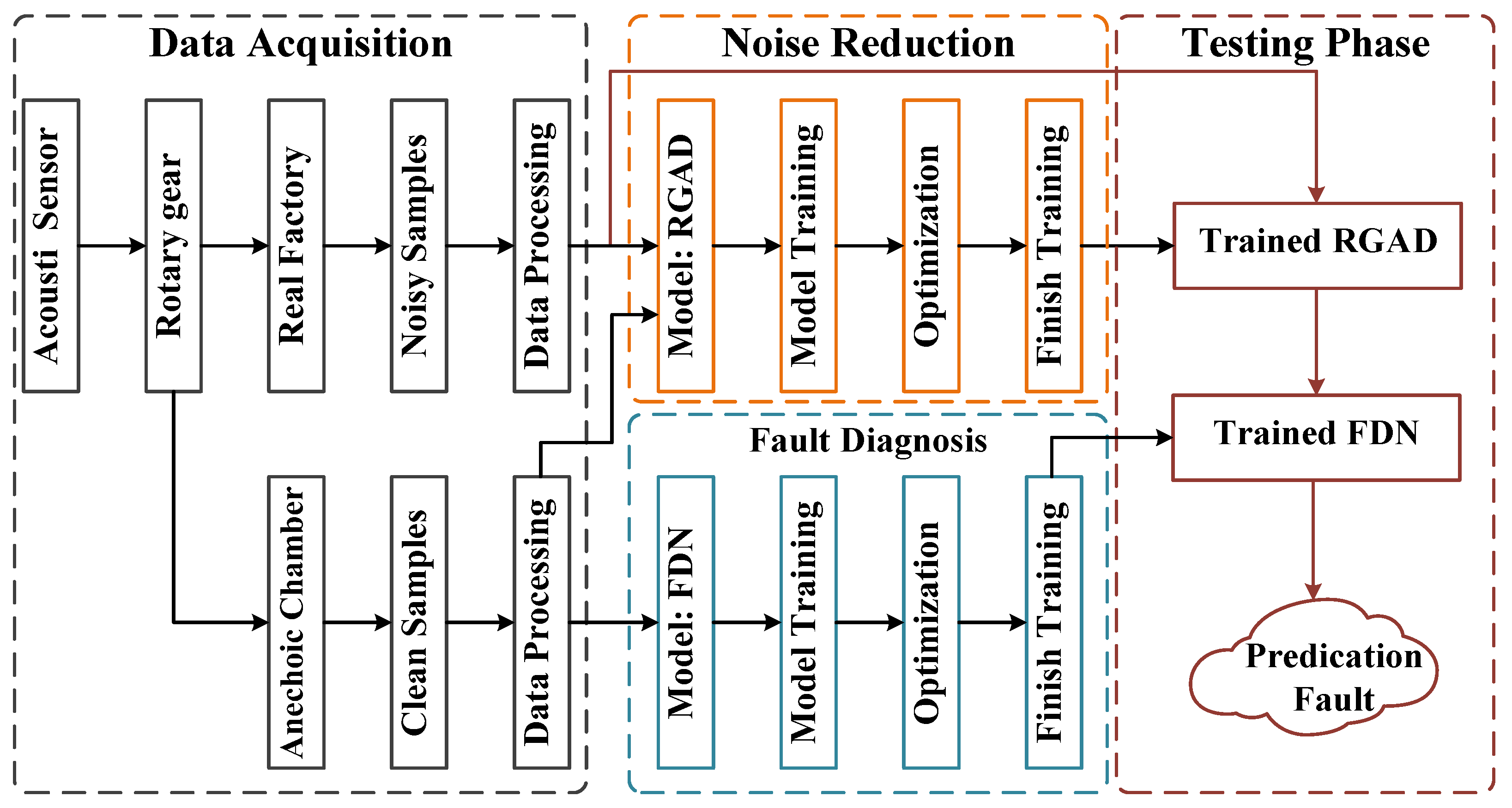
3.5. Fault Diagnosis Procedure of the Proposed Framework
4. Experiments
4.1. Experimental Setup
4.1.1. Experiment System
4.1.2. Data Preprocessing
4.1.3. Evaluation Metrics
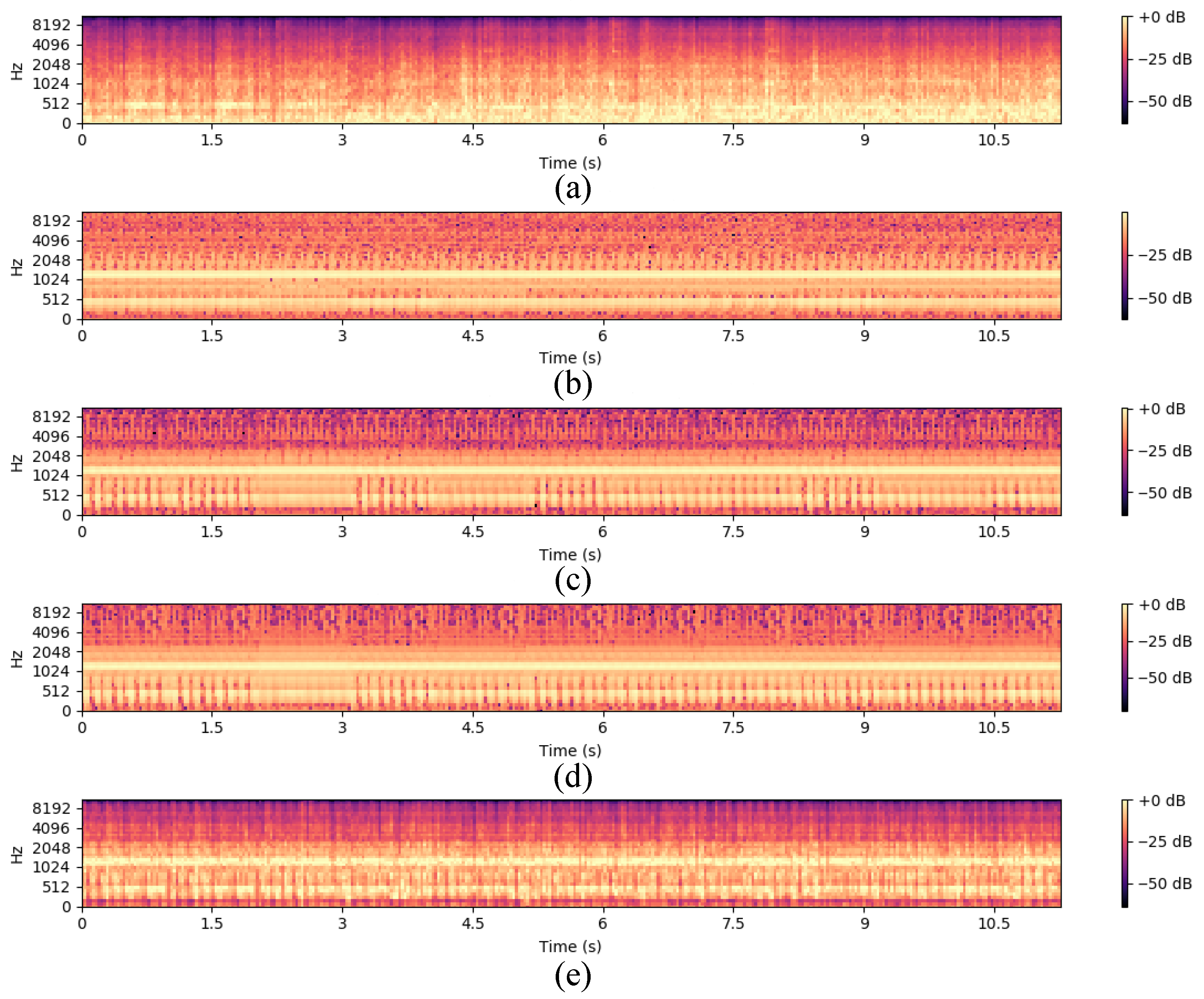
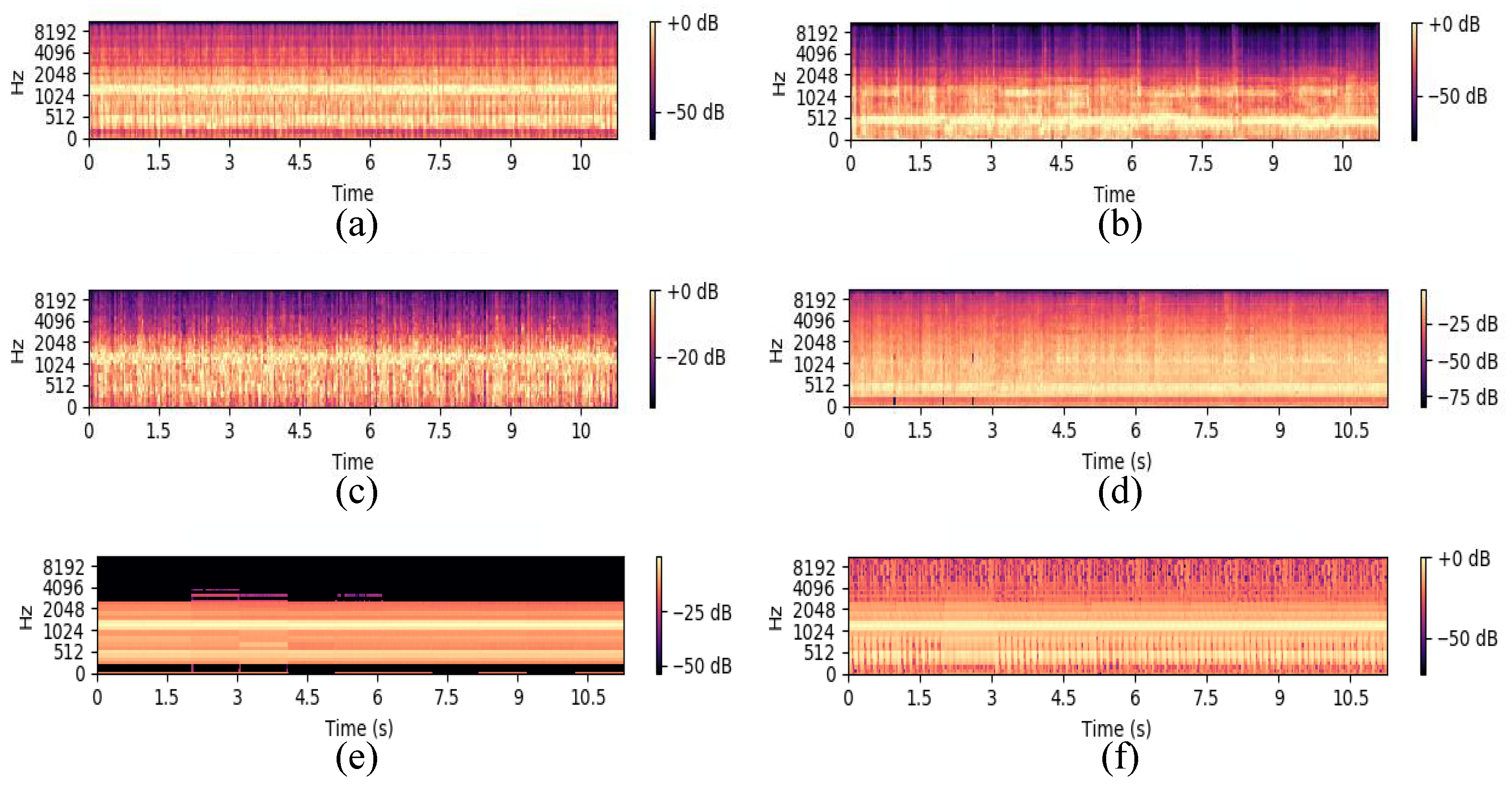
4.2. Analysis of RGAD
4.3. Ablation Experiments
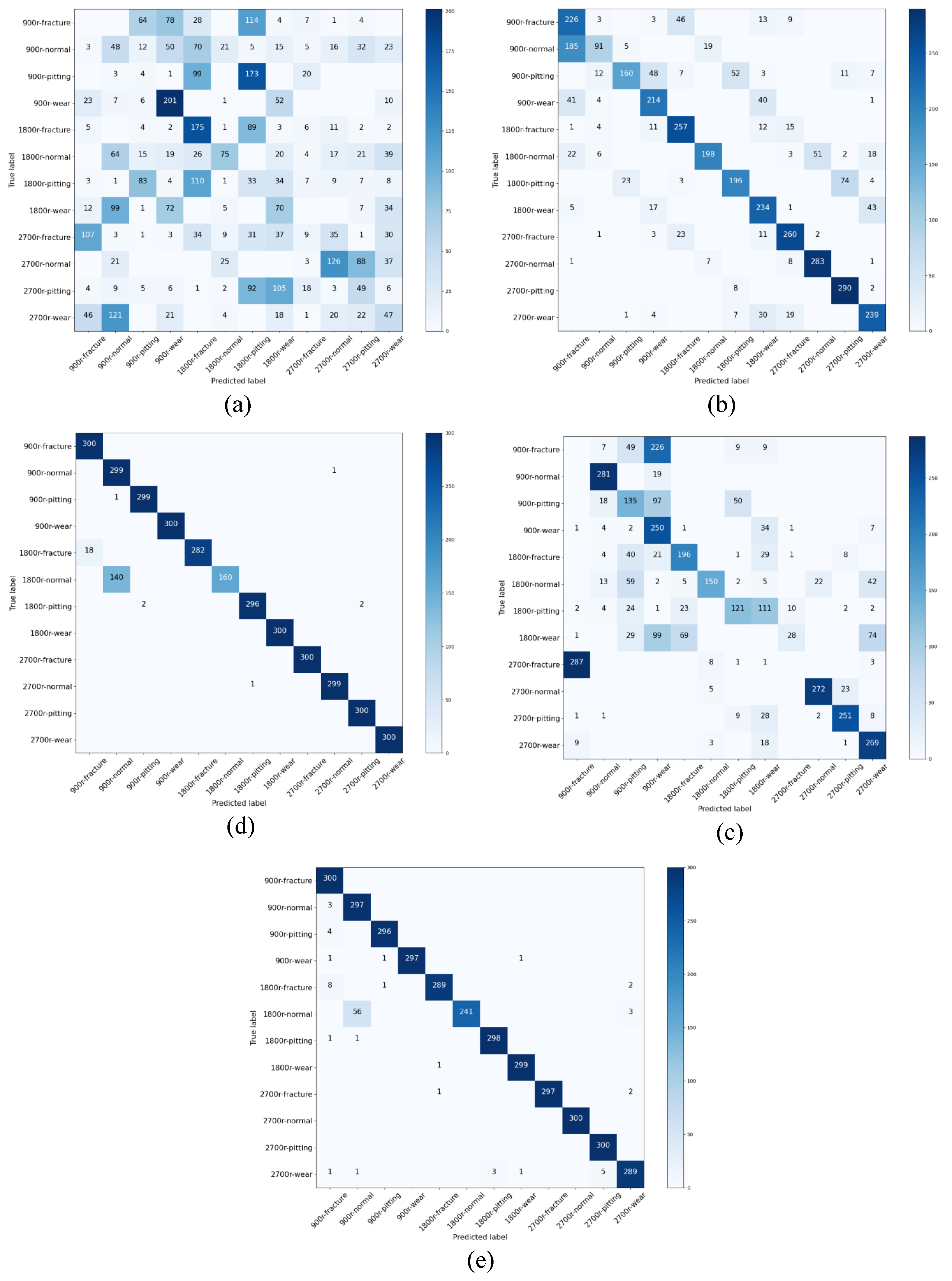
4.4. Compared with Other Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABD | Acoustic-Based Diagnosis |
| RGAD | Recursive Generative Adversarial Denoising |
| GWAM | Global Window-Aware Attention Module |
| FDN | Fault Diagnosis Network |
| IBM | Ideal Binary Mask |
| IRM | Ideal Ratio Mask |
| GAN | Generative Adversarial Network |
| W-MSA | Window-Based Multi-Head Self-Attention |
| LN | Layer Normalization |
| MSA | Multi-Head Self-Attention |
| MLP | Multi-Layer Perceptron |
| Swin Transformer | Shifted Window Transformer |
| SW-MSA | Shifted Window Multi-Head Self-Attention |
| LSGAN | Least-Squares Generative Adversarial Network |
| T-F | Time–Frequency |
| FC | Fully Connected |
| MSE | Mean Squared Error |
| BNC | Bayonet Nut Connector |
| WAV | Waveform Audio File Format |
| PSNR | Peak Signal-to-Noise Ratio |
| LMS | Least Mean Square |
| RLS | Recursive Least Squares |
| TF-Masking | Time–Frequency Masking |
| GAN- | Generative Adversarial Loss with Regularization Loss |
References
- Chen, C.; Shen, F.; Xu, J.; Yan, R. Probabilistic latent semantic analysis-based gear fault diagnosis under variable working conditions. IEEE Trans. Instrum. Meas. 2019, 69, 2845–2857. [Google Scholar] [CrossRef]
- Yao, Y.; Gui, G.; Yang, S.; Zhang, S. A recursive multi-head self-attention learning for acoustic-based gear fault diagnosis in real-industrial noise condition. Eng. Appl. Artif. Intell. 2024, 133, 108240. [Google Scholar] [CrossRef]
- Yao, Y.; Gui, G.; Yang, S.; Zhang, S. A recursive denoising learning for gear fault diagnosis based on acoustic signal in real industrial noise condition. IEEE Trans. Instrum. Meas. 2021, 70, 3524015. [Google Scholar] [CrossRef]
- Rezaei, A.; Dadouche, A.; Wickramasinghe, V.; Dmochowski, W. A comparison study between acoustic sensors for bearing fault detection under different speed and load using a variety of signal processing techniques. Tribol. Trans. 2011, 54, 179–186. [Google Scholar] [CrossRef]
- Peng, B.; Li, D.; Wang, K.I.K.; Abdulla, W.H. Acoustic-Based Industrial Diagnostics: A Scalable Noise-Robust Multiclass Framework for Anomaly Detection. Processes 2025, 13, 544. [Google Scholar] [CrossRef]
- Scanlon, P.; Kavanagh, D.F.; Boland, F.M. Residual life prediction of rotating machines using acoustic noise signals. IEEE Trans. Instrum. Meas. 2012, 62, 95–108. [Google Scholar] [CrossRef]
- Zhang, D.; Stewart, E.; Entezami, M.; Roberts, C.; Yu, D. Intelligent acoustic-based fault diagnosis of roller bearings using a deep graph convolutional network. Measurement 2020, 156, 107585. [Google Scholar] [CrossRef]
- Hassan, A.; Hashem, A.F.; Sayed, A.; Kayed, M. Physics-guided deep learning for acoustic-based fault diagnosis. Int. J. Engine Res. 2025. [Google Scholar] [CrossRef]
- Hou, J.; Jiang, W.; Lu, W. Application of a near-field acoustic holography-based diagnosis technique in gearbox fault diagnosis. J. Vib. Control 2013, 19, 3–13. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, S.; Yang, S.; Gui, G. Learning attention representation with a multi-scale CNN for gear fault diagnosis under different working conditions. Sensors 2020, 20, 1233. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, H.; Li, S.; Liu, Z.; Gui, G.; Dan, Y.; Hu, J. End-to-end convolutional neural network model for gear fault diagnosis based on sound signals. Appl. Sci. 2018, 8, 1584. [Google Scholar] [CrossRef]
- Glowacz, A. Acoustic based fault diagnosis of three-phase induction motor. Appl. Acoust. 2018, 137, 82–89. [Google Scholar] [CrossRef]
- Glowacz, A. Fault detection of electric impact drills and coffee grinders using acoustic signals. Sensors 2019, 19, 269. [Google Scholar] [CrossRef]
- Glowacz, A. Acoustic fault analysis of three commutator motors. Mech. Syst. Signal Process. 2019, 133, 106226. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Dubuc, B.; Salamone, S. A generalizable deep learning framework for localizing and characterizing acoustic emission sources in riveted metallic panels. Mech. Syst. Signal Process. 2019, 130, 248–272. [Google Scholar] [CrossRef]
- Boll, S. Suppression of acoustic noise in speech using spectral subtraction. IEEE Trans. Acoust. Speech Signal Process. 2003, 27, 113–120. [Google Scholar] [CrossRef]
- Scalart, P. Speech enhancement based on a priori signal to noise estimation. In Proceedings of the 1996 IEEE International Conference on Acoustics, Speech, and Signal Processing Conference Proceedings, Atlanta, GA, USA, 9 May 1996; Volume 2, pp. 629–632. [Google Scholar]
- Ephraim, Y.; Malah, D. Speech enhancement using a minimum-mean square error short-time spectral amplitude estimator. IEEE Trans. Acoust. Speech Signal Process. 2003, 32, 1109–1121. [Google Scholar] [CrossRef]
- Haykin, S.; Widrow, B. LEAST-MEAN-SQUARE ADAPTIVE FILTERS; Wiley Online Library: Hoboken, NJ, USA, 2003. [Google Scholar]
- Martinek, R.; Vanus, J.; Kelnar, M.; Bilik, P.; Zidek, J. Application of recursive least square algorithm to adaptive channel equalization. In Proceedings of the Measurement in Research and Industry, Shenzhen, China, 27–28 December 2015. [Google Scholar]
- Diniz, P.S. Adaptive Filtering; Springer: Berlin/Heidelberg, Germany, 1997; Volune 4. [Google Scholar]
- Shao, Y.; Srinivasan, S.; Jin, Z.; Wang, D. A computational auditory scene analysis system for speech segregation and robust speech recognition. Comput. Speech Lang. 2010, 24, 77–93. [Google Scholar] [CrossRef]
- Narayanan, A.; Wang, D. Investigation of speech separation as a front-end for noise robust speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 826–835. [Google Scholar] [CrossRef]
- Xu, Y.; Du, J.; Dai, L.R.; Lee, C.H. A regression approach to speech enhancement based on deep neural networks. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 23, 7–19. [Google Scholar] [CrossRef]
- Seltzer, M.L.; Yu, D.; Wang, Y. An investigation of deep neural networks for noise robust speech recognition. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 7398–7402. [Google Scholar]
- Pascual, S.; Bonafonte, A.; Serra, J. SEGAN: Speech enhancement generative adversarial network. arXiv 2017, arXiv:1703.09452. [Google Scholar] [CrossRef]
- Pandey, A.; Wang, D. On adversarial training and loss functions for speech enhancement. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 5414–5418. [Google Scholar]
- Fu, S.W.; Liao, C.F.; Tsao, Y.; Lin, S.D. Metricgan: Generative adversarial networks based black-box metric scores optimization for speech enhancement. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 2031–2041. [Google Scholar]
- Fu, S.W.; Yu, C.; Hsieh, T.A.; Plantinga, P.; Ravanelli, M.; Lu, X.; Tsao, Y. Metricgan+: An improved version of metricgan for speech enhancement. arXiv 2021, arXiv:2104.03538. [Google Scholar]
- Wang, D. Time-frequency masking for speech separation and its potential for hearing aid design. Trends Amplif. 2008, 12, 332–353. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2021; pp. 10012–10022. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Gogate, M.; Dashtipour, K.; Hussain, A. Robust real-time audio-visual speech enhancement based on dnn and gan. IEEE Trans. Artif. Intell. 2024, 6, 2860–2869. [Google Scholar] [CrossRef]
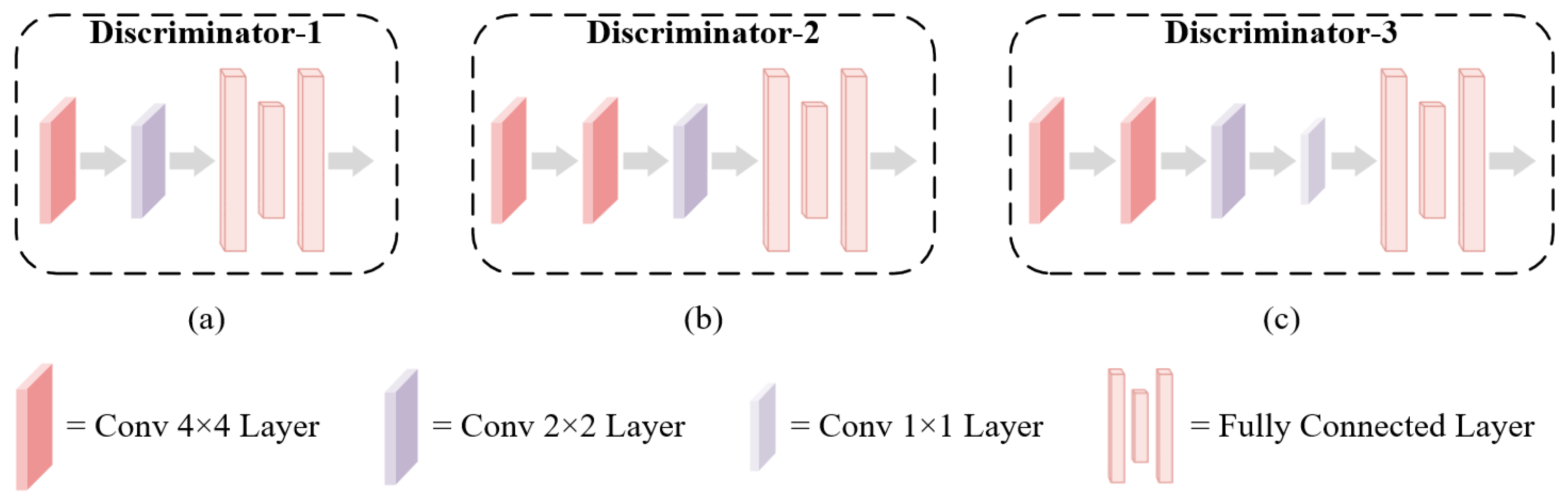
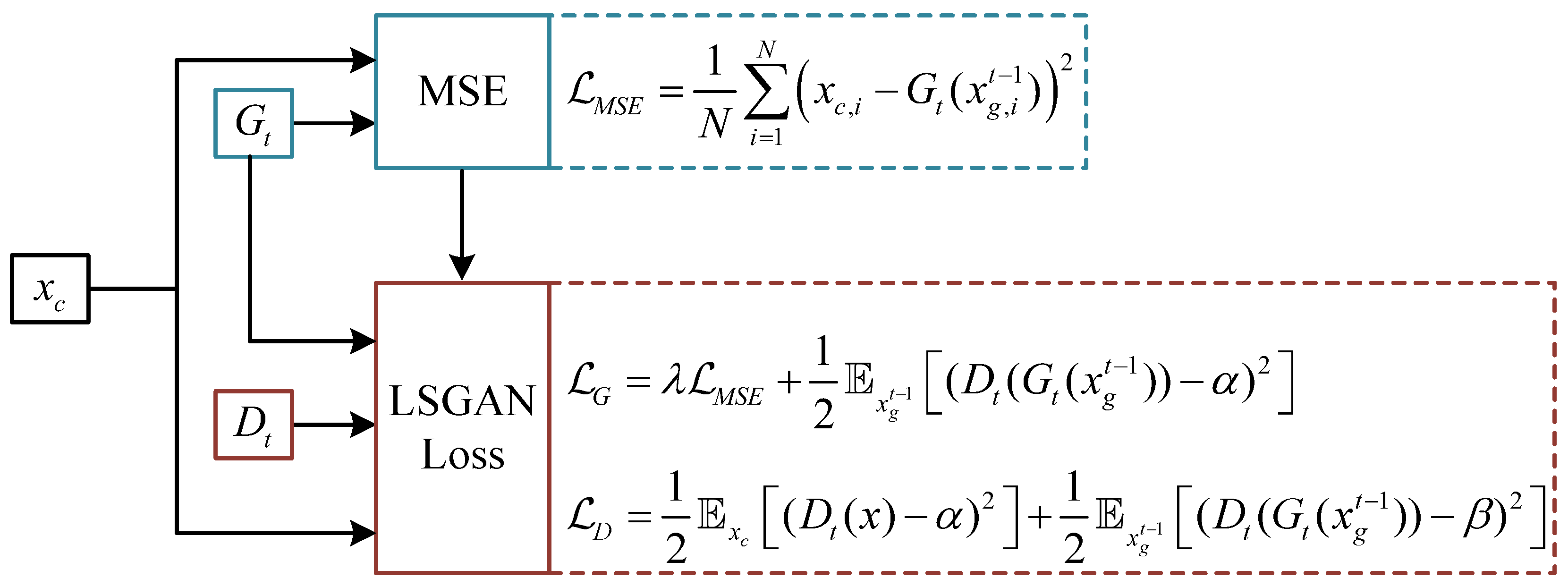


| Module | Structure | Hyperparameters |
|---|---|---|
| Discriminator-1 | Conv 4 × 4 | , , , |
| Conv 2 × 2 | , , , | |
| Fully Connected | ||
| Discriminator-2 | Conv 4 × 4 | , , , |
| Conv 4 × 4 | , , , | |
| Conv 2 × 2 | , , , | |
| Fully Connected | ||
| Discriminator-3 | Conv 4 × 4 | , , , |
| Conv 4 × 4 | , , , | |
| Conv 2 × 2 | , , , | |
| Conv 1 × 1 | , , , | |
| Fully Connected |
| Method | MSE | PSNR |
|---|---|---|
| Original | 0.07892 | 11.08 |
| Adversarial Unit 1 | 0.01734 | 17.61 |
| Adversarial Unit 2 | 0.01654 | 17.81 |
| Adversarial Unit 3 (final output) | 0.01644 | 17.84 |
| Method | Unit 1-MSE | Unit 2-MSE | Unit 3-MSE | PSNR | Accuracy |
|---|---|---|---|---|---|
| Regularization loss | 0.01785 | 0.01669 | 0.01651 | 17.82 | 95.28 |
| Equivalent discriminator | 0.01966 | 0.01821 | 0.01766 | 17.53 | 91.33 |
| Equivalent discriminator | 0.02529 | 0.02368 | 0.01655 | 17.81 | 94.86 |
| Equivalent discriminator | 0.01665 | 0.01647 | 0.01649 | 17.83 | 96.52 |
| RGAD (ours) | 0.01734 | 0.01654 | 0.01644 | 17.84 | 97.31 |
| Method | FLOPs | Parameters | Inference/Sample |
|---|---|---|---|
| Regularization loss | 1,569,138 | 2,341,718 | 0.30 ms |
| Equivalent discriminator | 1,569,138 | 2,344,972 | 0.30 ms |
| Equivalent discriminator | 1,569,138 | 2,420,524 | 0.30 ms |
| Equivalent discriminator | 1,569,138 | 2,496,172 | 0.30 ms |
| RGAD (ours) | 1,569,138 | 3,980,684 | 0.30 ms |
| Method | MSE | PSNR | Accuracy |
|---|---|---|---|
| LMS | 0.05559 | 12.55 | 31.99 |
| RLS | 0.04535 | 13.43 | 79.78 |
| TF-Masking | 0.03892 | 14.10 | 53.47 |
| GAN-L1 | 0.01766 | 17.53 | 95.41 |
| RGAD (ours) | 0.01644 | 17.84 | 97.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
E, Z.; Ma, X.; Yao, Y.; Sun, L. A Recursive Generative Adversarial Denoising Learning Method for Acoustic-Based Gear Fault Diagnosis Under Non-Stationary Noise Interference. Acoustics 2025, 7, 76. https://doi.org/10.3390/acoustics7040076
E Z, Ma X, Yao Y, Sun L. A Recursive Generative Adversarial Denoising Learning Method for Acoustic-Based Gear Fault Diagnosis Under Non-Stationary Noise Interference. Acoustics. 2025; 7(4):76. https://doi.org/10.3390/acoustics7040076
Chicago/Turabian StyleE, Zhiqun, Xingjiang Ma, Yong Yao, and Lei Sun. 2025. "A Recursive Generative Adversarial Denoising Learning Method for Acoustic-Based Gear Fault Diagnosis Under Non-Stationary Noise Interference" Acoustics 7, no. 4: 76. https://doi.org/10.3390/acoustics7040076
APA StyleE, Z., Ma, X., Yao, Y., & Sun, L. (2025). A Recursive Generative Adversarial Denoising Learning Method for Acoustic-Based Gear Fault Diagnosis Under Non-Stationary Noise Interference. Acoustics, 7(4), 76. https://doi.org/10.3390/acoustics7040076






