A Low-Cost Detection Method for Acoustic Defects in Building Components: Compressed Nearfield Acoustic Holography
Abstract
1. Introduction
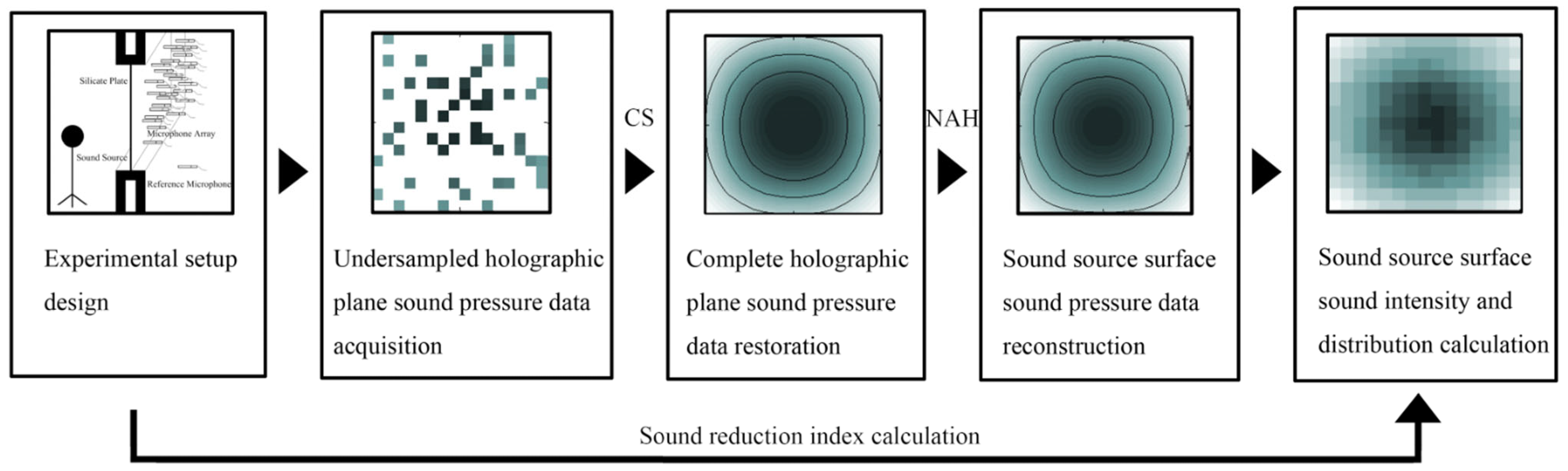
2. Method
2.1. Compressed Sensing
2.2. NAH Combined with CS
3. Simulation Methodology
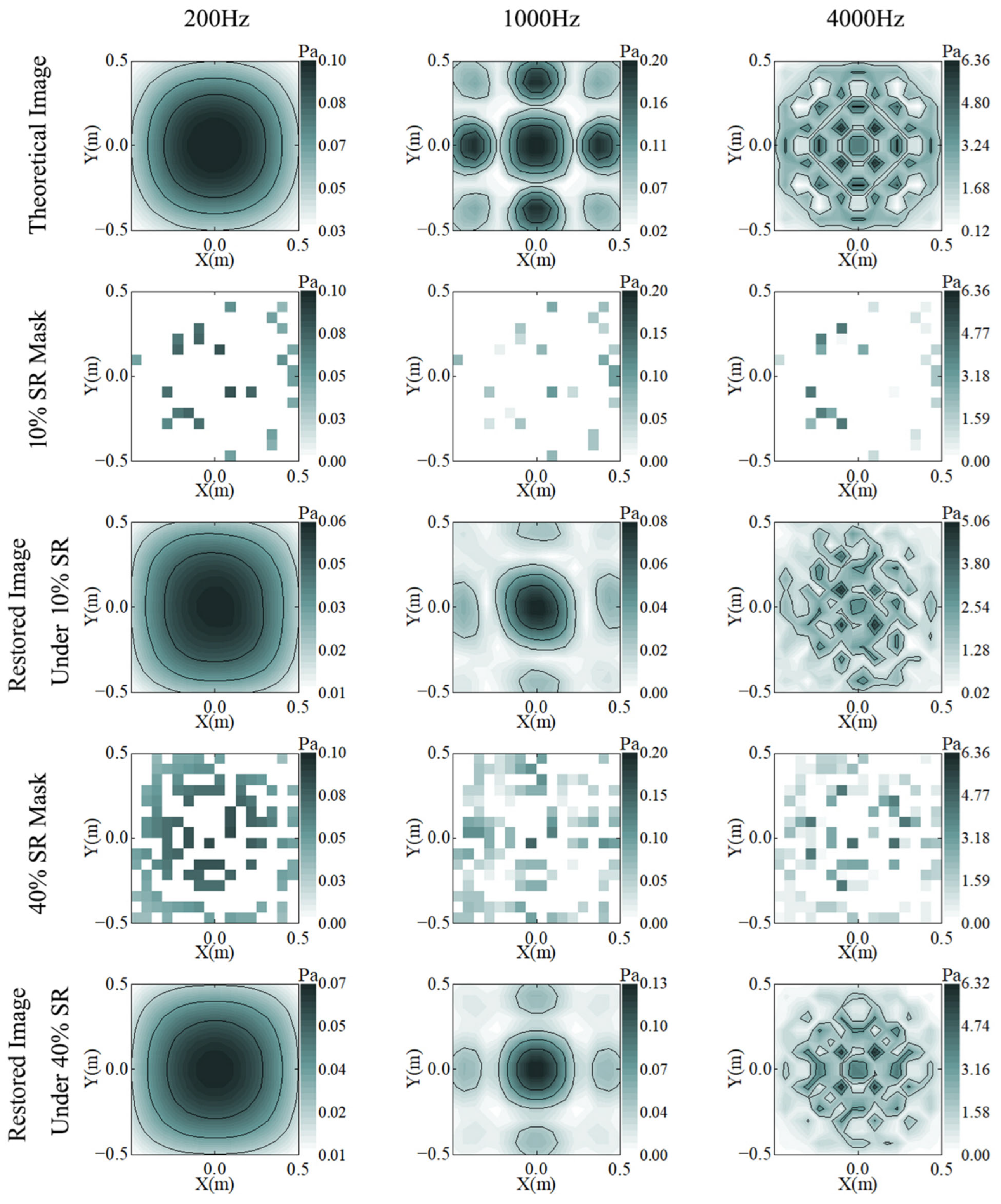
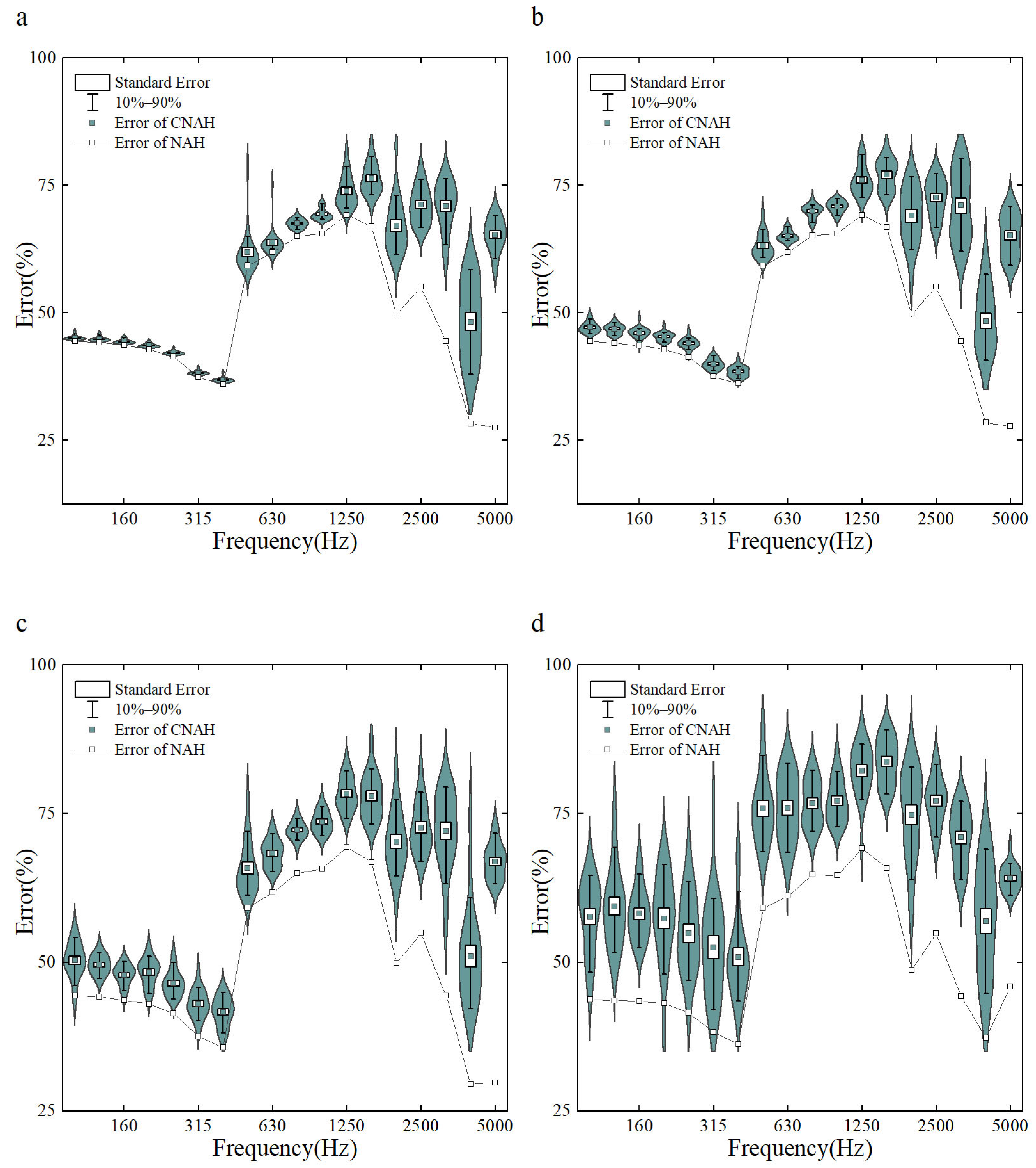
3.1. Reconstruction Under Varied Sampling Rates
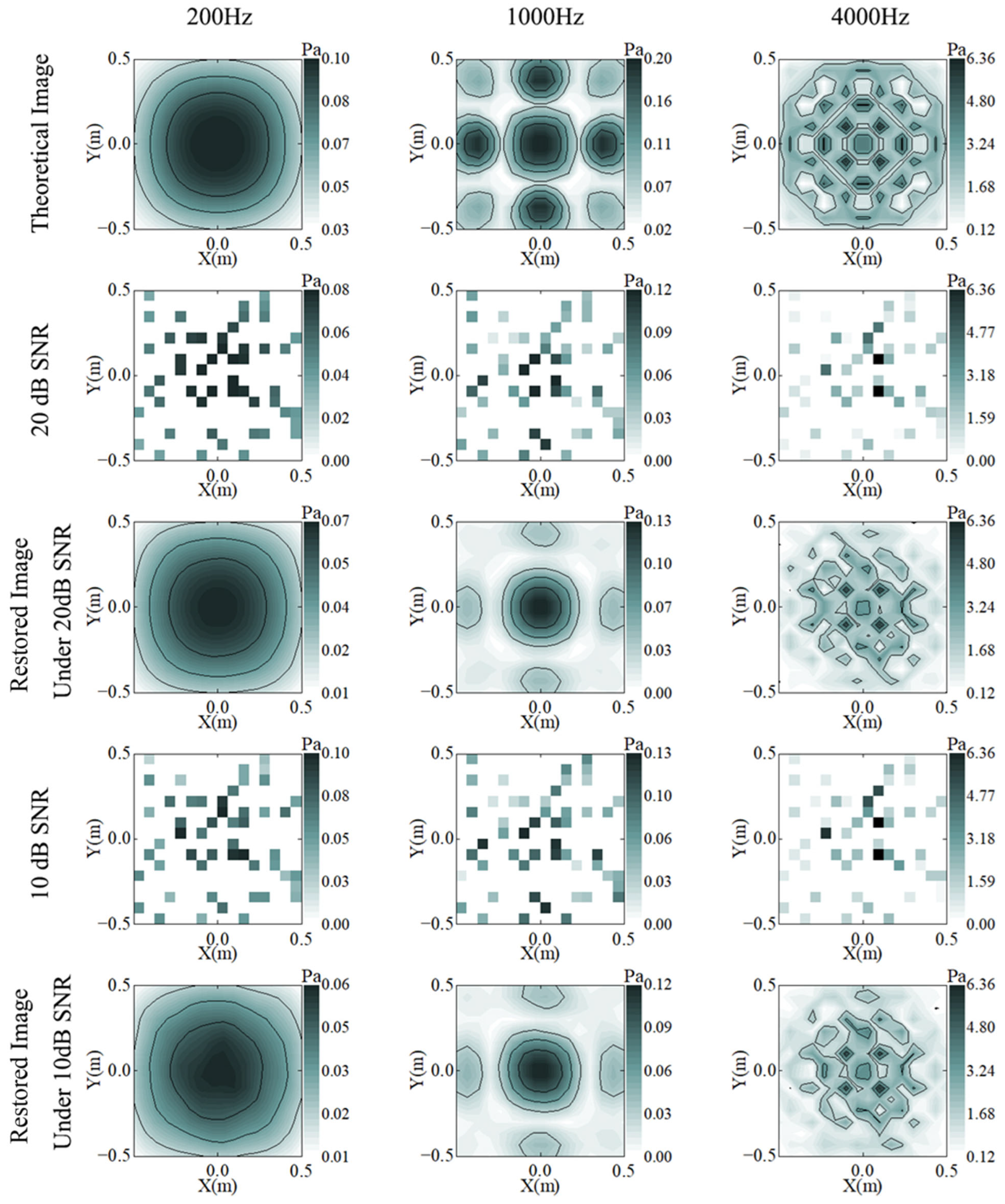
3.2. Reconstruction Under Varied Noise Levels
3.3. Influence of Mask
4. Experimental Data Processing
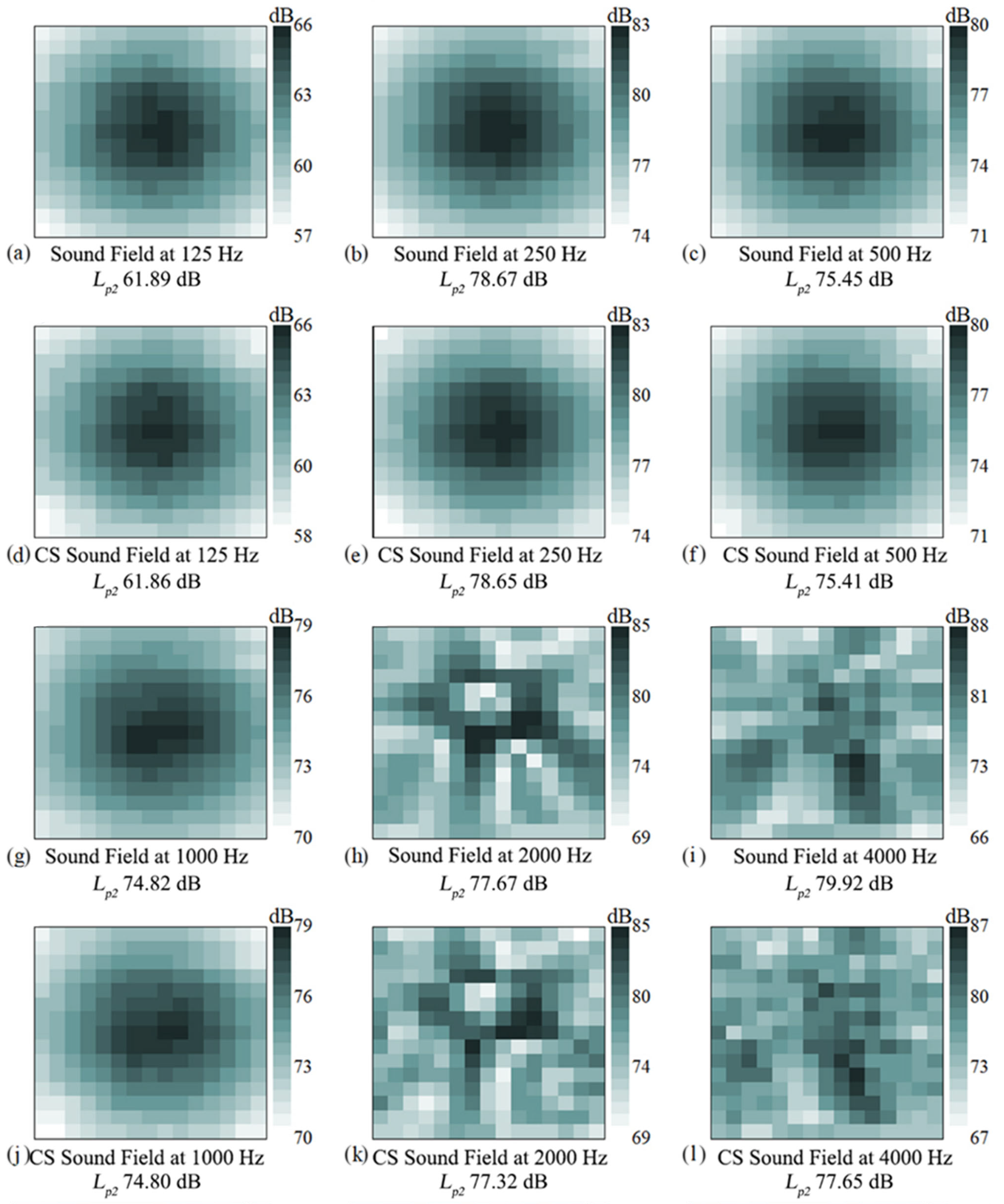
4.1. Anechoic Chamber Experiment
4.2. Reverberation Room Experiment
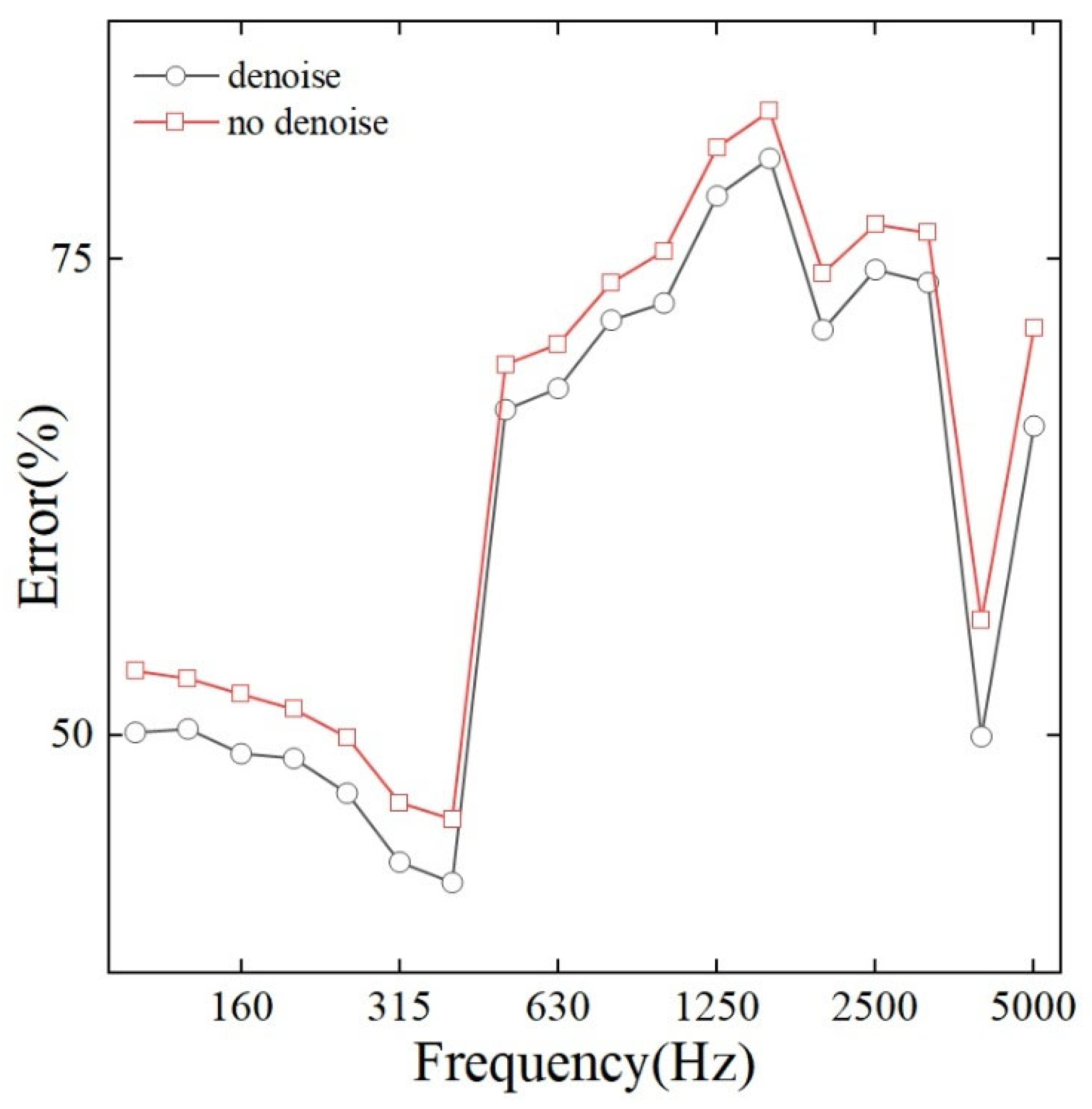
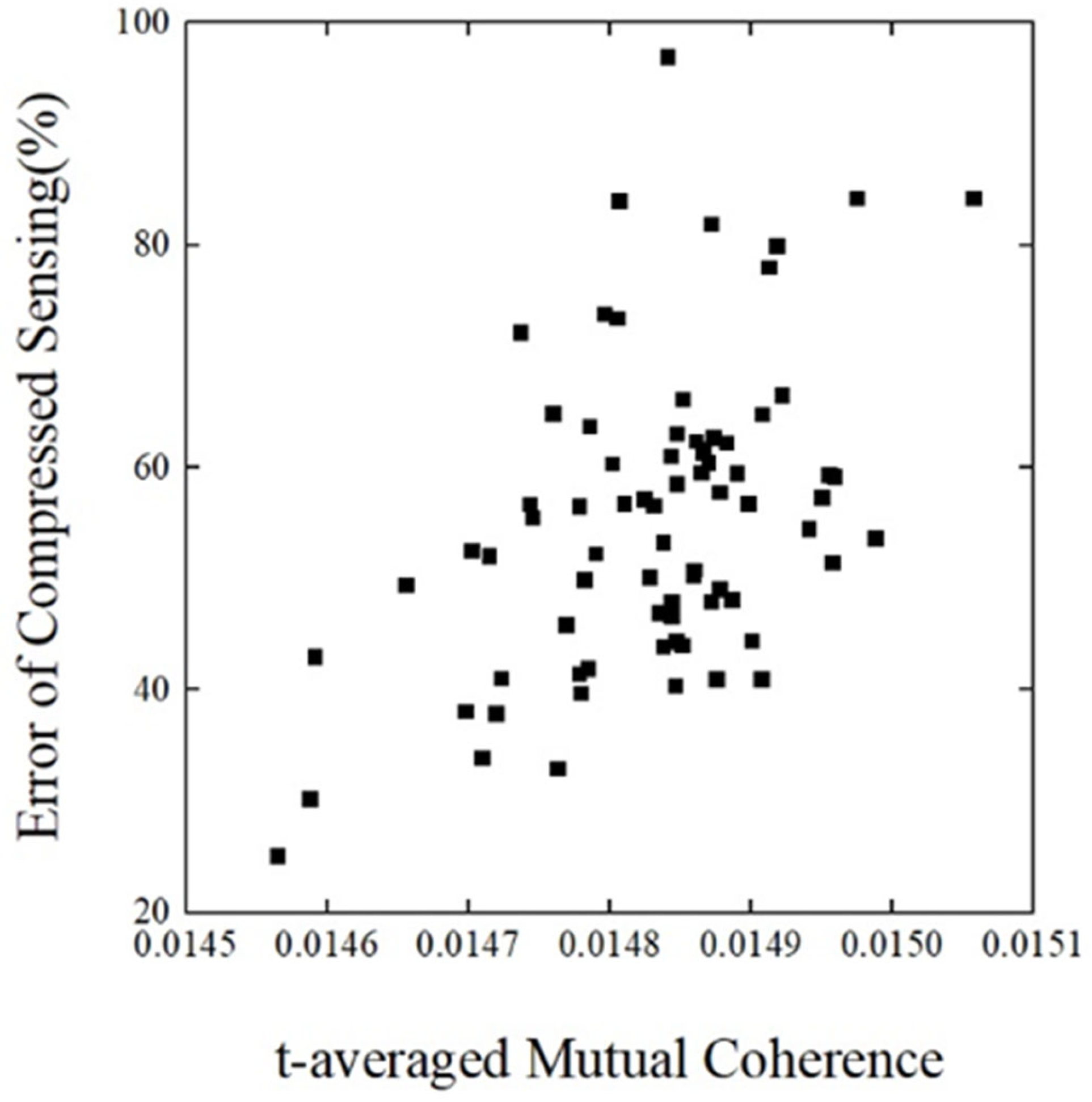
5. Discussion
6. Conclusions
- Introduce the theory of compression perception in sound insulation testing to realize higher accuracy surface sound pressure reconstruction as well as sound insulation measurement at sampling points below Nyquist’s theorem.
- Consider a noise-adapted basis pursuit algorithm to realize the robustness of reconstruction results in noisy environments.
- Provide and analyze a more stable observation matrix design strategy to reduce the error in sound insulation calculation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NAH | Nearfield acoustic holographic |
| CS | Compressed sensing |
| C-NAH | Compressed nearfield acoustic holographic |
| SR | Sample rate |
| SAR | Synthetic aperture radar |
References
- Maynard, J.D.; Williams, E.G.; Lee, Y. Nearfield acoustic holography: I. Theory of generalized holography and the development of NAH. J. Acoust. Soc. Am. 1985, 78, 1395–1413. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, N.; Zha, Y.; Gao, J.; Zhou, H.; Jiang, W. A hybrid nearfield acoustic holography based on the mapping relationship and boundary element method. Appl. Acoust. 2024, 216, 109823. [Google Scholar] [CrossRef]
- Wu, W.Y.; Zhang, X.Z.; Zhang, Y.B.; Bi, C.X. Real-time nearfield acoustic holography using particle velocity. J. Acoust. Soc. Am. 2024, 155, 3394–3409. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Xiong, W.; Wang, Q.; Yang, Y.; He, B. Sound insulation measurement of building components combining diffuse acoustic field excitation and near-field acoustic holography reconstruction. Shenxue Xuebao/Acta Acust. 2023, 48, 1021–1035. [Google Scholar] [CrossRef]
- Cheng, W.; Ni, J.; Song, C.; Ahsan, M.M.; Chen, X.; Nie, Z.; Liu, Y. Conical Statistical Optimal Near-Field Acoustic Holography with Combined Regularization. Sensors 2021, 21, 7150. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Hu, D.Y.; Yang, C.; Shi, W.; Liao, A.H. An improvement of the generalized discrete Fourier series based patch near-field acoustical holography. Appl. Acoust. 2021, 173, 107711. [Google Scholar] [CrossRef]
- Xie, S.H.; Ma, H.Y.; Cao, J.M.; Mo, F.S.; Cheng, Q.; Li, Y.; Hao, T. Refined acoustic holography via nonlocal metasurfaces. Sci. China Phys. Mech. Astron. 2024, 67, 239506. [Google Scholar] [CrossRef]
- Chai, K.; Lou, J.J.; Li, R.H.; Hu, J.B. Research and experiment on patch near-field acoustic holography based on two-level iteration. J. Ship Mech. 2024, 28, 1441–1450. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.L.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef]
- Usman, M.; Prieto, C.; Schaeffter, T.; Botnar, R.M. K-t group sparse: A method for accelerating dynamic MRI. Magn. Reson. Med. 2011, 66, 1163–1176. [Google Scholar] [CrossRef]
- Baraniuk, R.; Steeghs, P. Compressive radar imaging. In Proceedings of the IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007; pp. 128–133. [Google Scholar] [CrossRef]
- Coker, J.D.; Tewfik, A.H. Compressed sensing and multistatic SAR. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 1097–1100. [Google Scholar] [CrossRef]
- Stojanovic, I.; Karl, W.C. Imaging of Moving Targets with Multi-Static SAR Using an Overcomplete Dictionary. IEEE J. Sel. Top. Signal Process. 2010, 4, 164–176. [Google Scholar] [CrossRef]
- Gilles, C.; Laurent, D.; Antoine, P. Nearfield Acoustic Holography using sparsity and compressive sampling principles. J. Acoust. Soc. Am. 2012, 132, 1521–1534. [Google Scholar] [CrossRef]
- Xiao, Y.; Yuan, L.; Wang, J.; Hu, W.; Sun, R. Sparse Reconstruction of Sound Field Using Bayesian Compressive Sensing and Equivalent Source Method. Sensors 2023, 23, 5666. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Yuan, L.; Liu, Y.; Wang, J.; Hu, W.; Sun, R.; Liu, Y.; Ni, P. Sparse reconstruction of sound field using pattern-coupled Bayesian compressive sensing. J. Acoust. Soc. Am. 2024, 156, 548–559. [Google Scholar] [CrossRef] [PubMed]
- Zan, M.; Xu, Z.; He, J. A block bayesian compressive sensing method based on the equivalent source method for near-field acoustic holography. J. Vib. Control 2023, 29, 1303–1314. [Google Scholar] [CrossRef]
- Hu, D.Y.; Liu, X.Y.; Xiao, Y.; Fang, Y. Fast Sparse Reconstruction of Sound Field Via Bayesian Compressive Sensing. J. Vib. Acoust. 2019, 141, 041017. [Google Scholar] [CrossRef]
- He, Y.; Chen, L.; Xu, Z.; Zhang, Z. A compressed equivalent source method based on equivalent redundant dictionary for sound field reconstruction. Appl. Sci. 2019, 9, 808. [Google Scholar] [CrossRef]
- Geng, L.; Chen, X.G.; He, C.D.; Chen, W.; He, S.P. Compressive nonstationary near-field acoustic holography for reconstructing the instantaneous sound field. Mech. Syst. Signal Process. 2023, 204, 110779. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, F.; Xiao, Z.; Zhou, R.; Zhang, Y.; Bi, C. Multi-frequency equivalent source near-field acoustic holography method based on common sparse Bayesian learning. J. Vib. Shock 2024, 43, 260–267. [Google Scholar] [CrossRef]
- Wu, B.H.; Hsu, W.J. Application of compressive sensing to equivalent source method on near-field acoustic holography. Appl. Acoust. 2024, 223, 110075. [Google Scholar] [CrossRef]
- Chaitanya, S.K.; Srinivasan, K. Equivalent source method based near field acoustic holography using multipath orthogonal matching pursuit. Appl. Acoust. 2022, 187, 108501. [Google Scholar] [CrossRef]
- Shi, T.; Bolton, J.S.; Eberhardt, F. A hybrid compressive sensing approach to noise source visualization: Application to a diesel engine. J. Acoust. Soc. Am. 2023, 153, A55. [Google Scholar] [CrossRef]
- Topp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Iterative hard thresholding for compressed sensing. Appl. Comput. Harmon. Anal. 2009, 27, 265–274. [Google Scholar] [CrossRef]
- Gorodnitsky, I.F.; Rao, B.D. Sparse signal reconstruction from limited data using FOCUSS: A re-weighted minimum norm algorithm. IEEE Trans. Signal. Process. 1997, 45, 600–616. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient Projection for Sparse Reconstruction: Application to Compressed Sensing and Other Inverse Problems. IEEE J. Sel. Top Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, H.; Liu, F.; Wang, G. Bayesian Compressive Sensing with Variational Inference and Wavelet Tree Structure for Solving Inverse Scattering Problems. IEEE Trans. Antennas Propag. 2024, 72, 8750–8761. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Q.; Amin, M.G. Multi-Task Bayesian compressive sensing exploiting signal structures. Signal Process. 2021, 178, 107804. [Google Scholar] [CrossRef]
- Wang, R.; Bai, Y.; Yu, L.; Dong, G. Bayesian compressive sensing for identifying tonal acoustic modes of fan noise in the duct. Acta Acust. 2025, 50, 187–200. [Google Scholar] [CrossRef]
- Chen, S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Van den Berg, E.; Friedlander, M.P. Probing the Pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. 2008, 31, 890–918. [Google Scholar] [CrossRef]
- International Standard ISO 15186-2; Acoustics—Measurement of Sound Insulation in Buildings and of Building Elements Using Sound Intensity—Part 2: Field Measurements. ISO: Geneva, Switzerland, 2003.
- International Standard ISO 16283-1; Acoustics—Field Measurement of Sound Insulation in Buildings and of Building Elements-Part 1: Airborne Sound Insulation. ISO: Geneva, Switzerland, 2014.
- Jacobsen, F.; Tiana-Roig, E. Measurement of the sound power incident on the walls of a reverberation room with near field acoustic holography. Acta. Acust. United Acust. 2010, 96, 76–81. [Google Scholar] [CrossRef]
- Chen, X.Z.; Wang, Z.P.; Liu, Z.S.; Chen, X.D. Correcting the Phase Mismatch Errors of the Acoustic Intensity Measuring System by Transfer Function Method. Yiqi Yibiao Xuebao 1994, 4, 405–409. [Google Scholar]
- Xiong, W. Research on Measurement Method of Airborne Sound Insulation of Building Components Based on Nearfield Acoustic Holography. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2022. [Google Scholar]
- Cheng, W.; Bai, Y.; He, Y. Resolution enhanced statistically optimal cylindrical near-field acoustic holography based on equivalent source method. Meas. Sci. Technol. 2022, 33, 055015. [Google Scholar] [CrossRef]
- He, H.; Li, H.; Yan, J.; Wu, S. Application of equivalent source intensity density interpolation in near-field acoustic holography. Meas. Sci. Technol. 2023, 34, 115101. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Li, S.; Liu, B. Sub-wavelength focusing for low-frequency sound sources using an iterative time reversal method. Meas. Sci. Technol. 2022, 33, 125402. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Fang, J.; Xu, Z.; Zhang, B.; Hong, W.; Wu, Y. Fast compressed sensing SAR imaging based on approximated observation. IEEE J. Sel. Top Appl. Earth Obs. Remote Sens. 2014, 7, 352–363. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Wang, H.; Wang, Q.; Li, S. A Low-Cost Detection Method for Acoustic Defects in Building Components: Compressed Nearfield Acoustic Holography. Acoustics 2025, 7, 69. https://doi.org/10.3390/acoustics7040069
Yang C, Wang H, Wang Q, Li S. A Low-Cost Detection Method for Acoustic Defects in Building Components: Compressed Nearfield Acoustic Holography. Acoustics. 2025; 7(4):69. https://doi.org/10.3390/acoustics7040069
Chicago/Turabian StyleYang, Chenxi, Hongwei Wang, Qiaochu Wang, and Shujie Li. 2025. "A Low-Cost Detection Method for Acoustic Defects in Building Components: Compressed Nearfield Acoustic Holography" Acoustics 7, no. 4: 69. https://doi.org/10.3390/acoustics7040069
APA StyleYang, C., Wang, H., Wang, Q., & Li, S. (2025). A Low-Cost Detection Method for Acoustic Defects in Building Components: Compressed Nearfield Acoustic Holography. Acoustics, 7(4), 69. https://doi.org/10.3390/acoustics7040069





