A Model for the Dynamics of Stable Gas Bubbles in Viscoelastic Fluids Based on Bubble Volume Variation
Abstract
1. Introduction
2. Materials and Methods
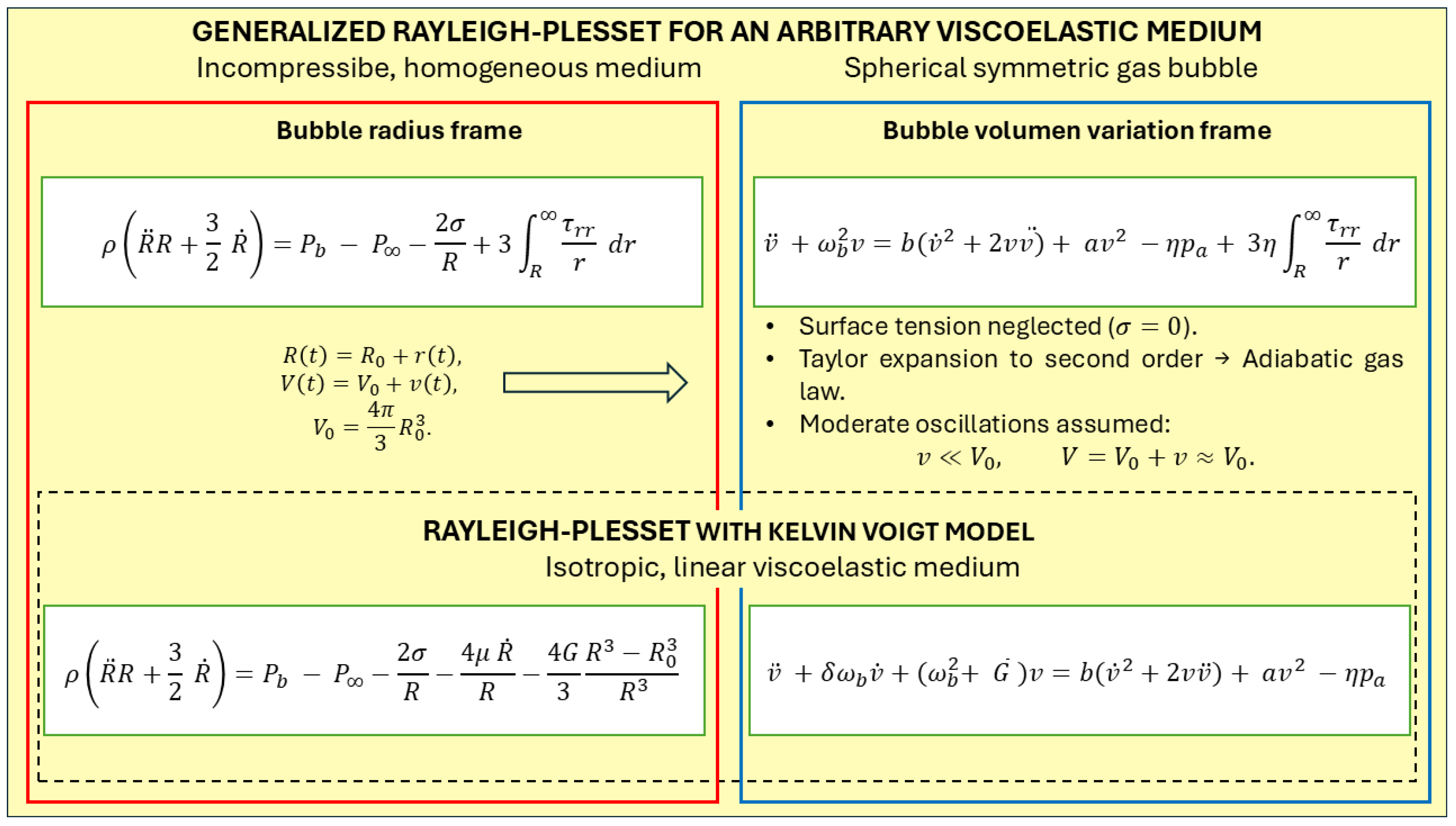
2.1. Governing Equations
2.1.1. Bubble Dynamics in an Arbitrary Viscoelastic Medium Written in the Volume Variation Framework
2.1.2. Bubble Dynamics in a Kelvin–Voigt Viscoelastic Medium Based on the Volume Variation Framework
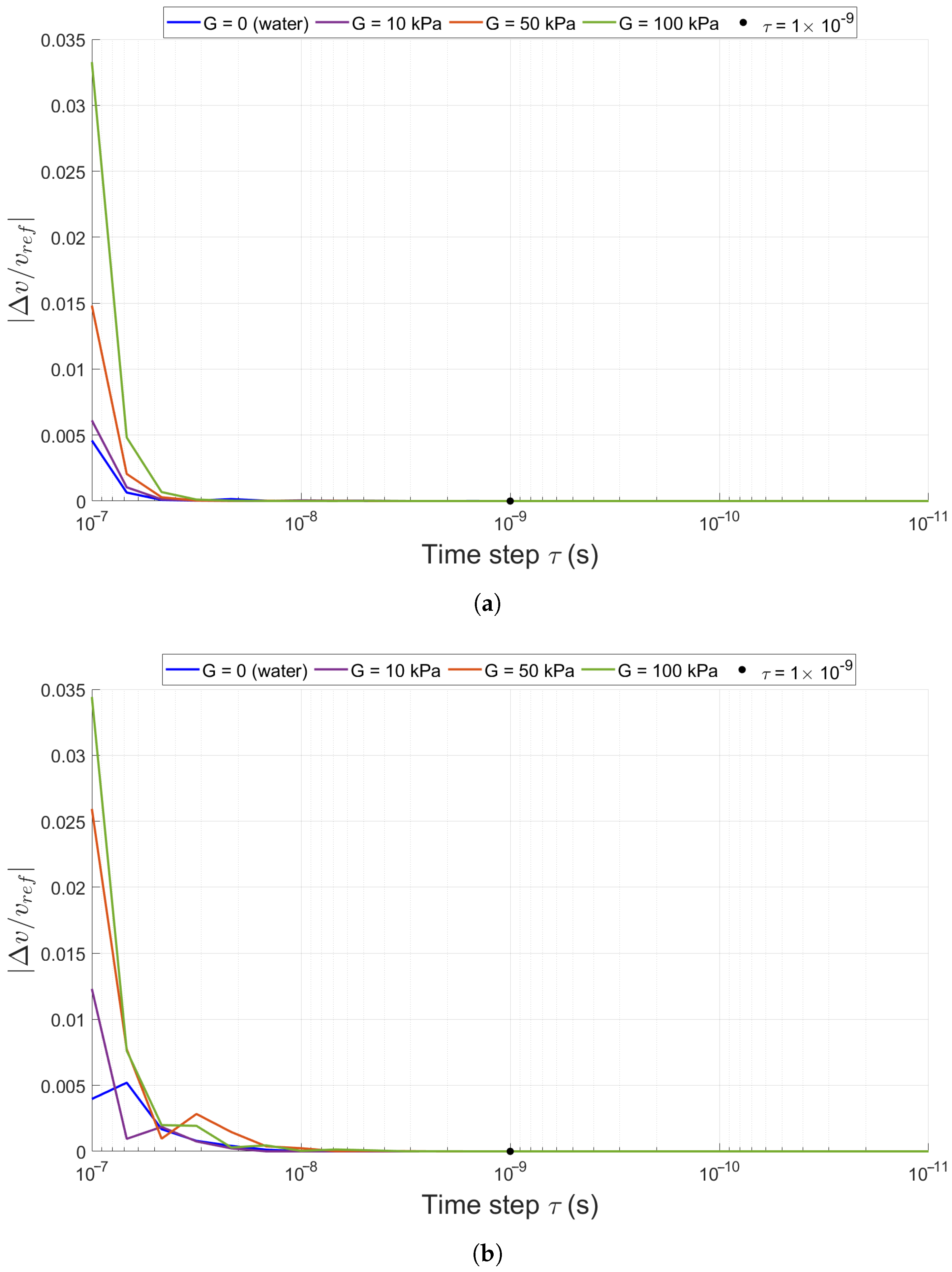
2.2. Numerical Solution of the Bubble Equation
3. Results
3.1. Validation of the Model
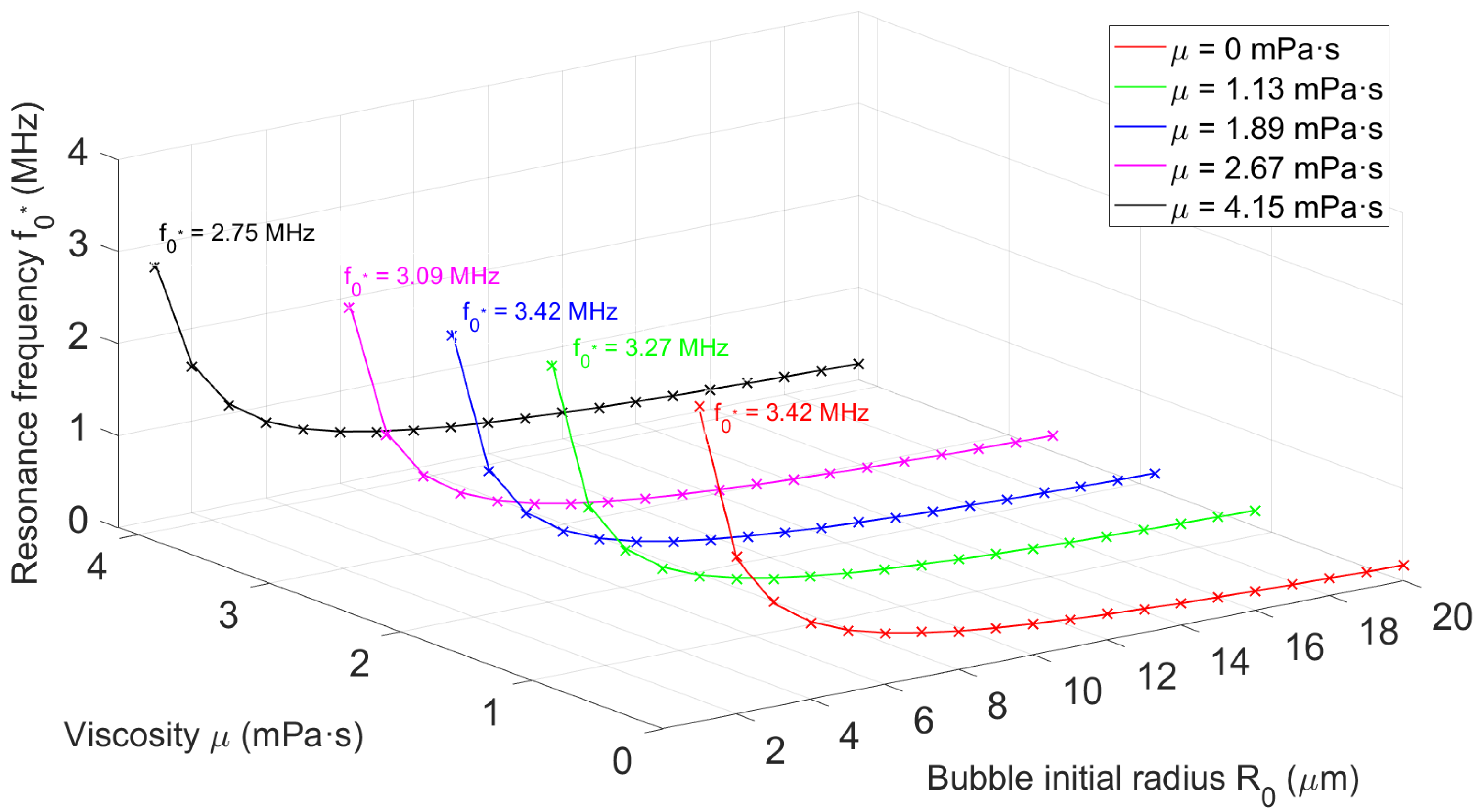
3.1.1. Effect of Elasticity and Viscosity on Bubble Resonance
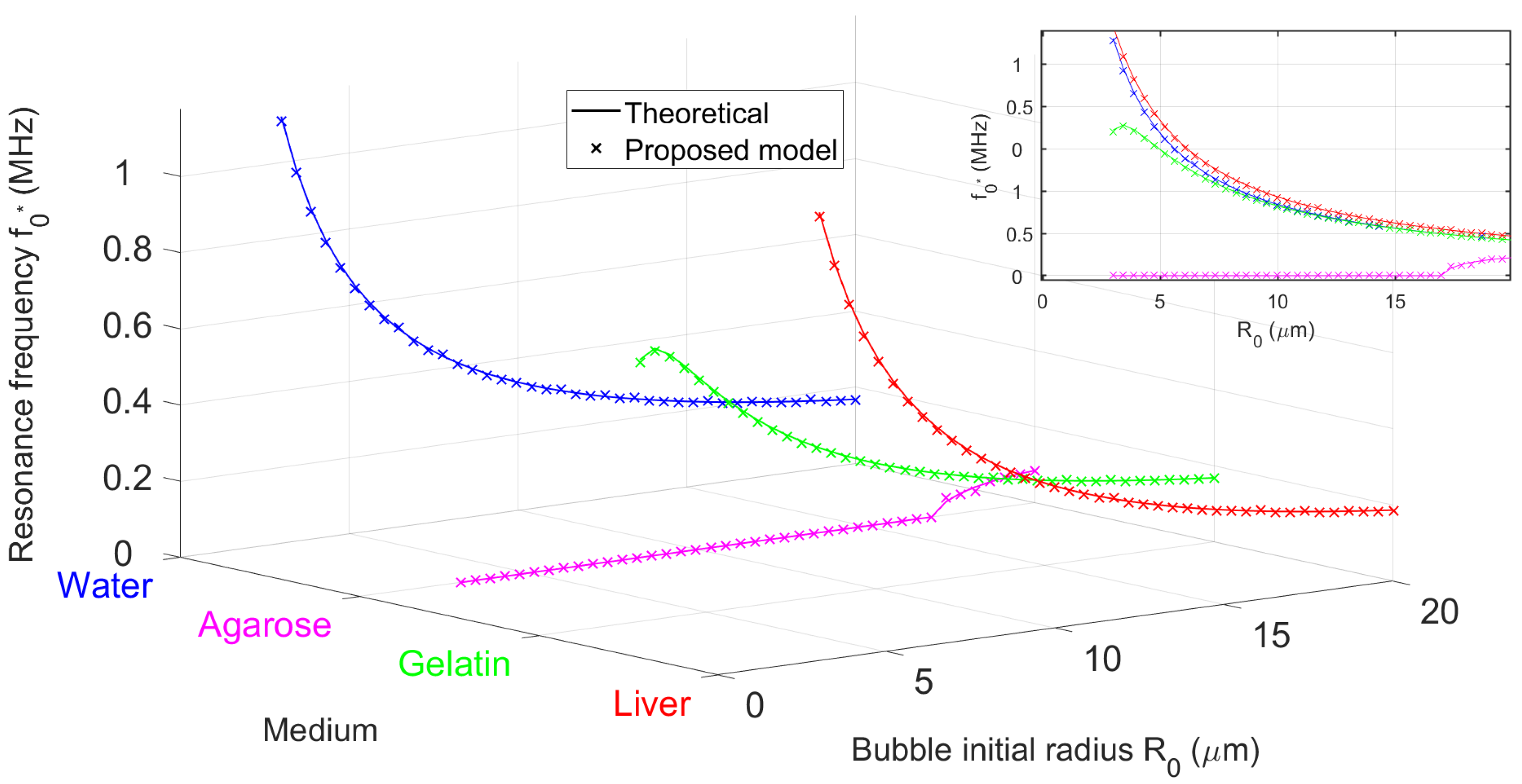
3.1.2. Bubble Resonance in Representative Soft Viscoelastic Media
3.1.3. Experimental Validation
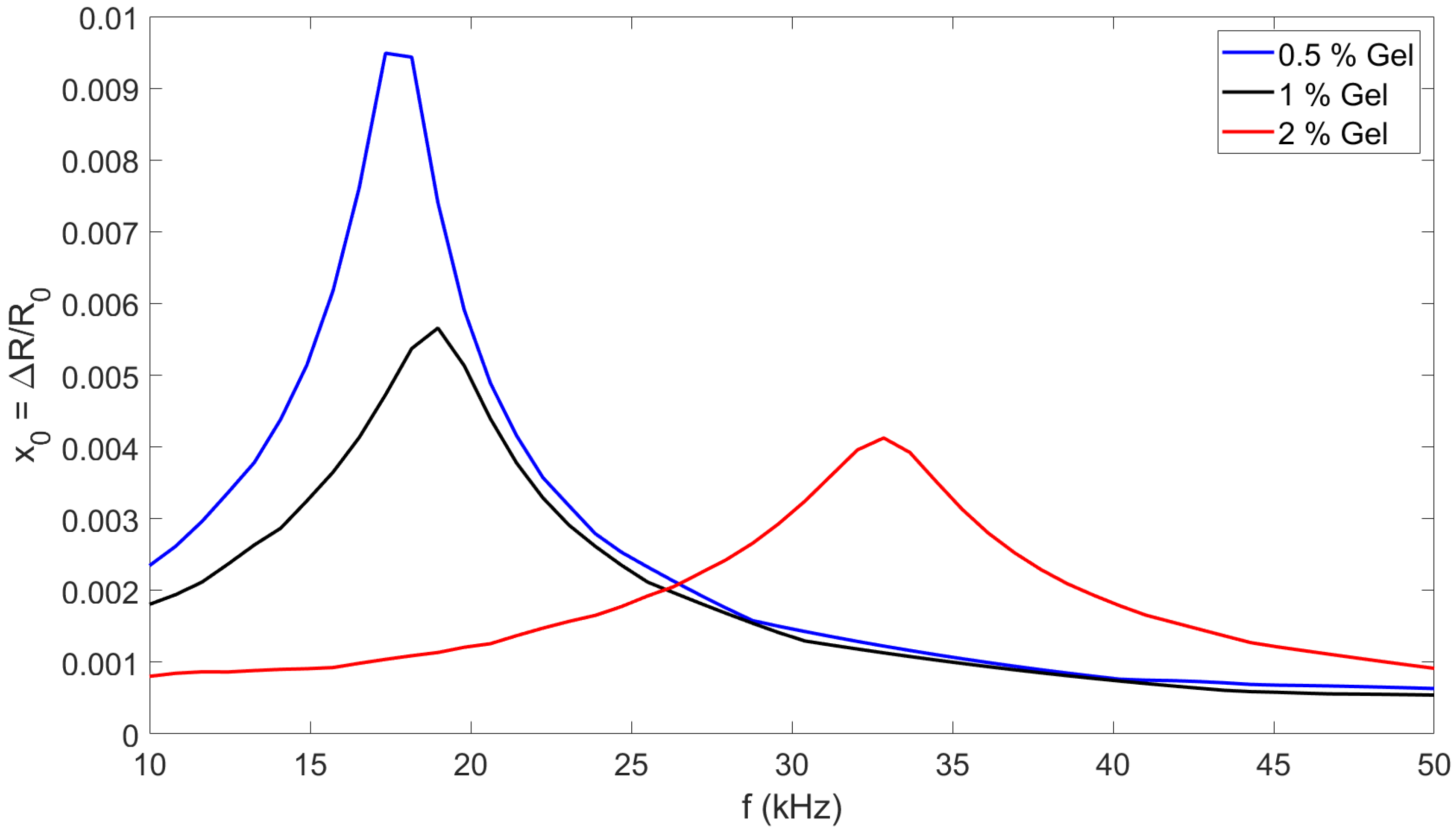
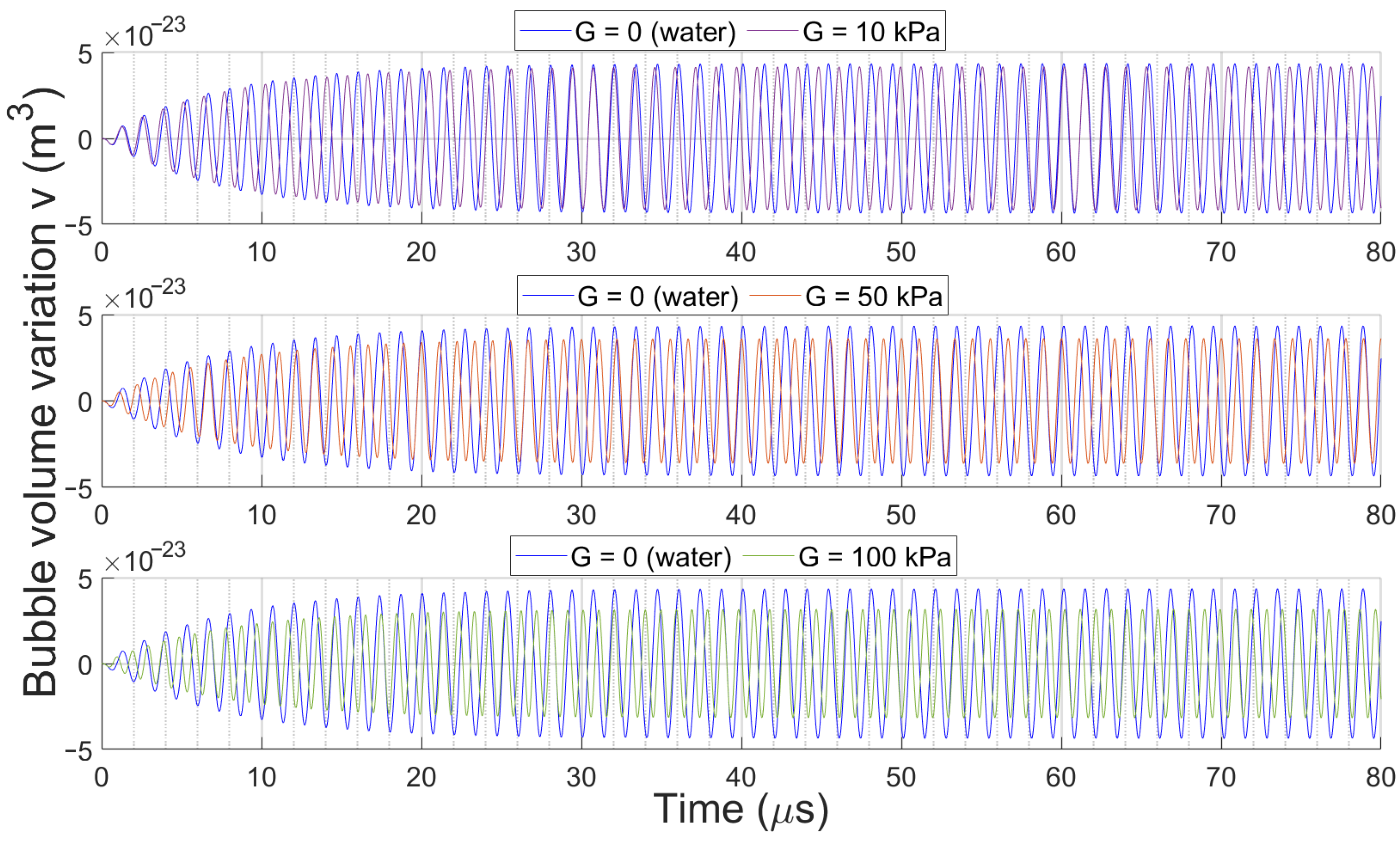
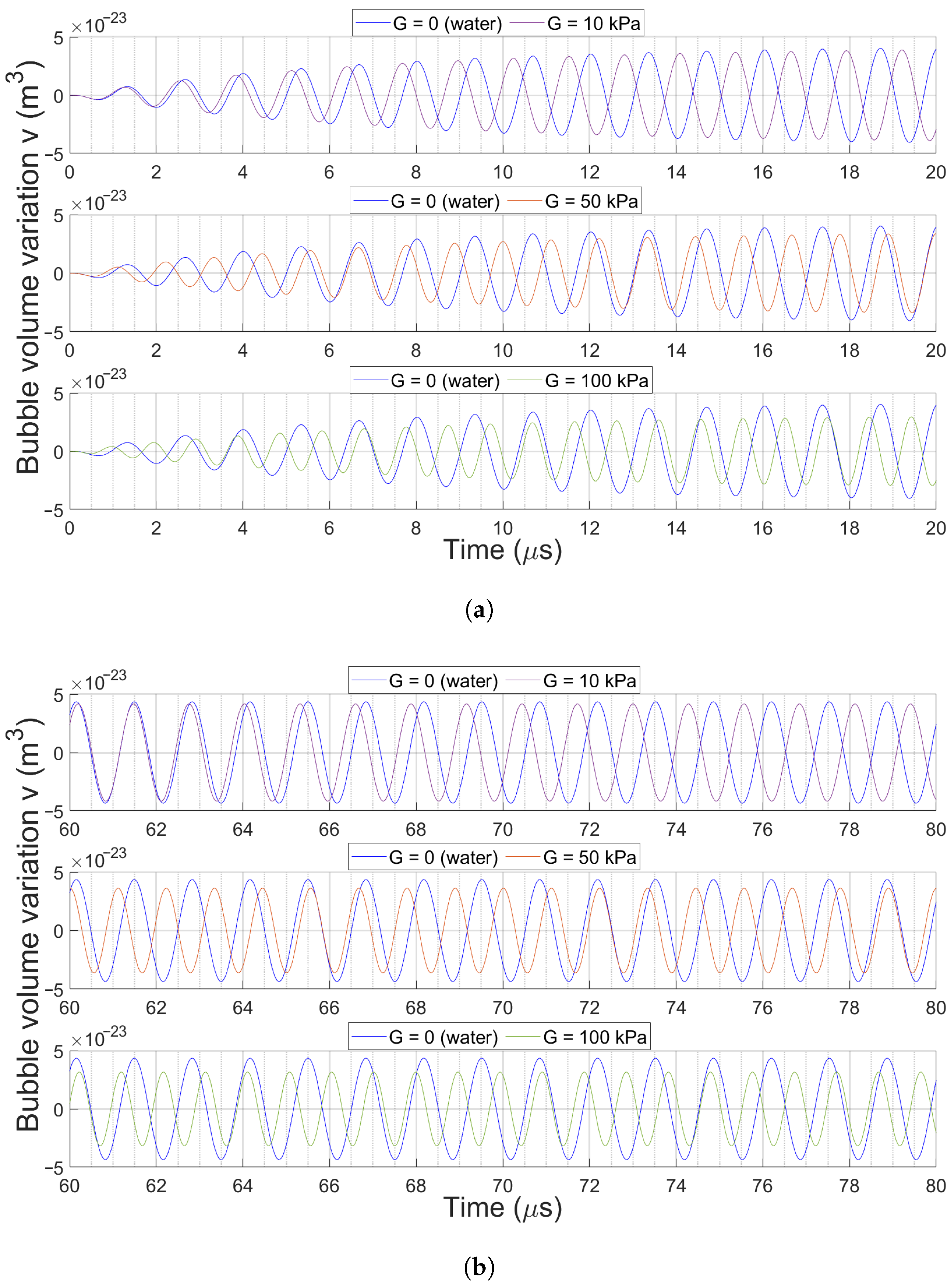
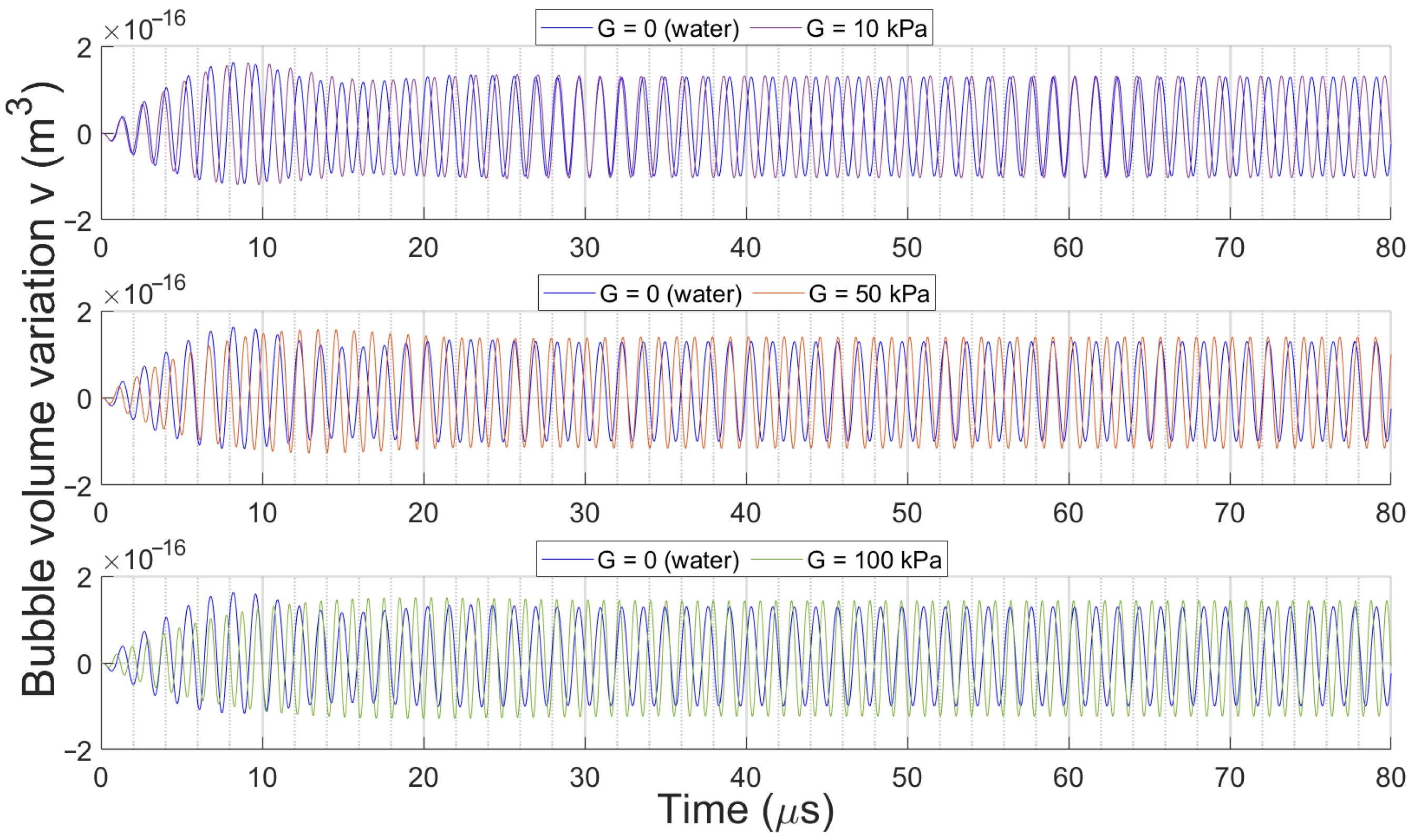
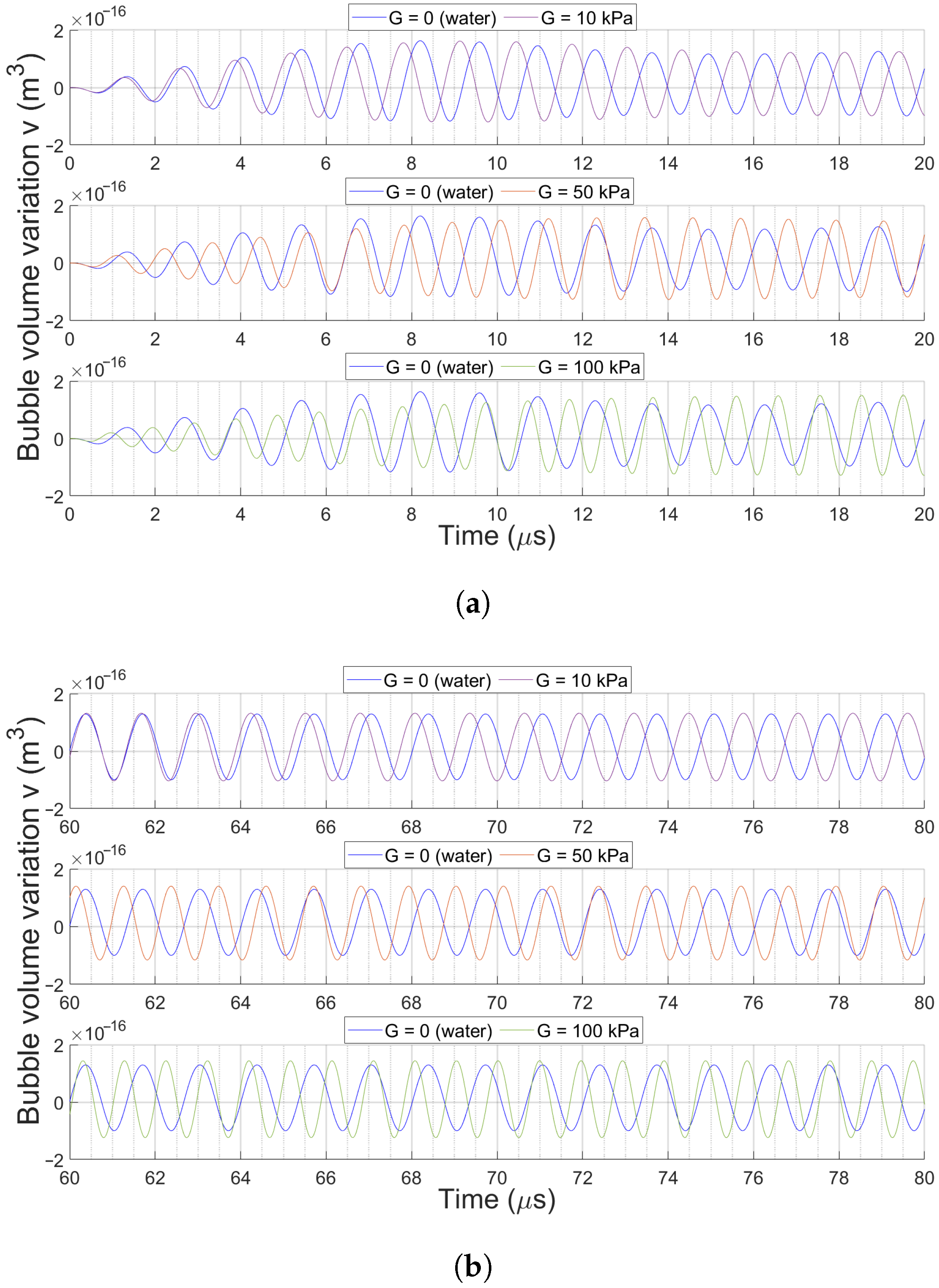
3.2. Bubble Volume Dynamics over Time
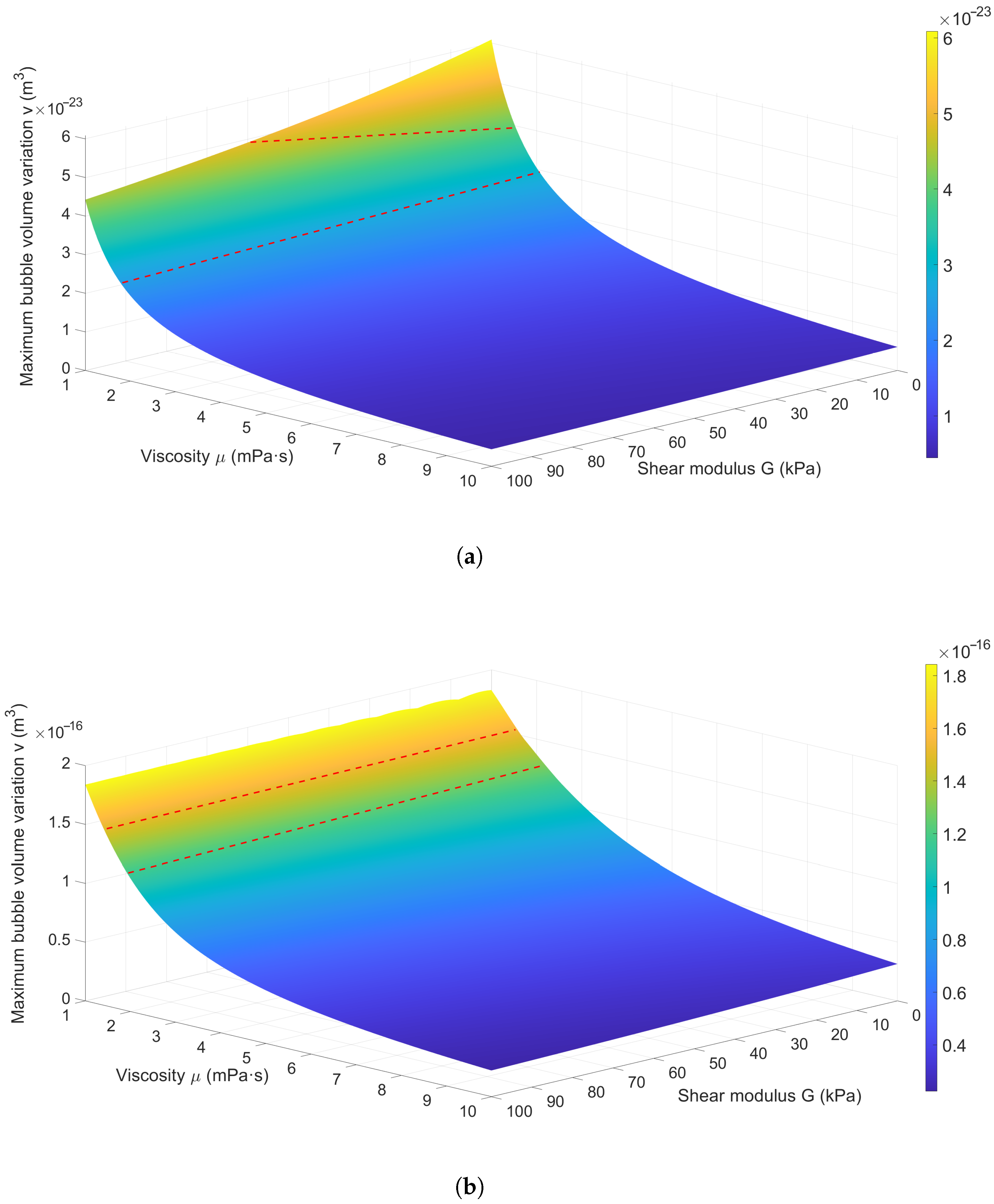
3.2.1. Bubble Volume Variation in Representative Soft Media
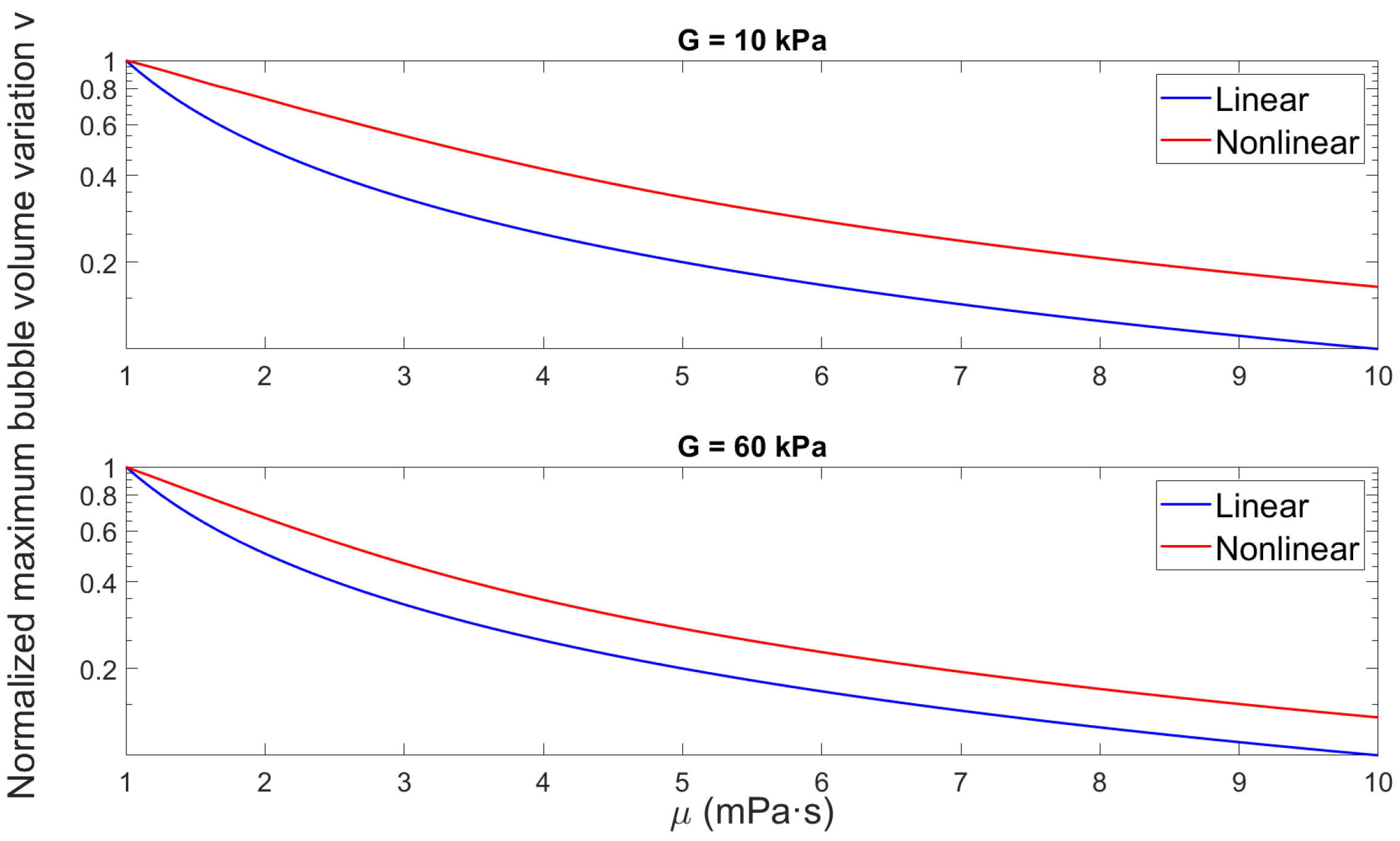
3.2.2. Effect of Medium Elasticity on Bubble Dynamics
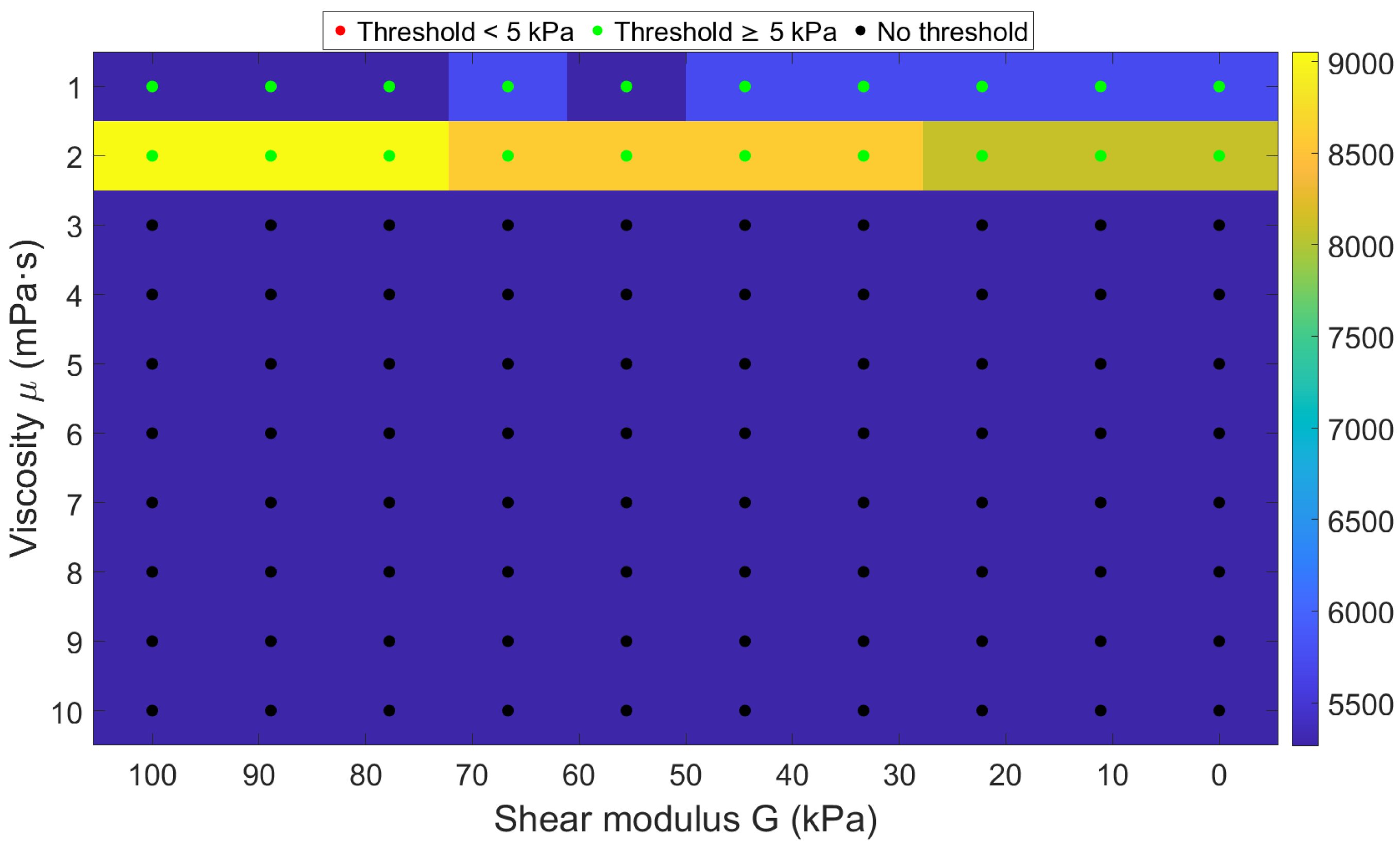
3.2.3. Bubble Behavior Across Shear Elasticity–Viscosity Parameter Space
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Coussios, C.; Roy, R. Applications of Acoustics and Cavitation to Noninvasive Therapy and Drug Delivery. Annu. Rev. Fluid Mech. 2008, 40, 395–420. [Google Scholar] [CrossRef]
- Tiong, T.; Chu, J.K.; Tan, K.W. Advancements in Acoustic Cavitation Modelling: Progress, Challenges, and Future Directions in Sonochemical Reactor Design. Ultrason. Sonochemistry 2025, 112, 107163. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, S.; Li, S.; Zhang, A.M. Application of the unified equation of bubble dynamics for simulating the large-scale air-gun bubble with migration effect. Phys. Fluids 2023, 35, 127125. [Google Scholar] [CrossRef]
- Ning, Y.C.; Zhang, S.; Qiu, Y.C.; Liu, Y.; Li, S.; Zhang, A.M. Study on the pressure wave characteristics of bubbles in low frequency, high pressure, and large capacity air guns. Sci. China Phys. Mech. Astron. 2024, 54, 124714. [Google Scholar] [CrossRef]
- Leighton, T. The Acoustic Bubble; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Allen, J.; Roy, R. Dynamics of gas bubbles in viscoelastic fluids. II. Nonlinear viscoelasticity. J. Acoust. Soc. Am. 2000, 108, 1640–1650. [Google Scholar] [CrossRef]
- Jamburidze, A.; De Corato, M.; Huerre, A.; Pommella, A.; Garbin, V. High-frequency linear rheology of hydrogels probed by ultrasound-driven microbubble dynamics. Soft Matter 2017, 13, 3946–3953. [Google Scholar] [CrossRef]
- Li, H.; Liu, H.; Zou, J. Minnaert Resonances for Bubbles in Soft Elastic Materials. SIAM J. Appl. Math. 2022, 82, 119–141. [Google Scholar] [CrossRef]
- Hwang, P.; Roy, R.; Crum, L. Artificial Bubble Cloud Targets for Underwater Acoustic Remote Sensing. J. Atmos. Ocean. Technol. 1995, 12, 1287–1302. [Google Scholar] [CrossRef]
- Keller, J.B.; Miksis, M. Bubble oscillations of large amplitude. J. Acoust. Soc. Am. 1980, 68, 628–633. [Google Scholar] [CrossRef]
- Fogler, H.; Goddard, J. Collapse of spherical cavities in viscoelastic fluids. Phys. Fluids 1970, 13, 1135–1141. [Google Scholar] [CrossRef]
- Tanasawa, I.; Yang, W.J. Dynamic behavior of a gas bubble in viscoelastic liquids. J. Appl. Phys. 1970, 41, 4526–4531. [Google Scholar] [CrossRef]
- Allen, J.; Roy, R. Dynamics of gas bubbles in viscoelastic fluids. I. Linear viscoelasticity. J. Acoust. Soc. Am. 2000, 107, 3167–3178. [Google Scholar] [CrossRef]
- Yang, X.; Church, C.C. A model for the dynamics of gas bubbles in soft tissue. J. Acoust. Soc. Am. 2005, 118, 3595–3606. [Google Scholar] [CrossRef]
- Hua, C.; Johnsen, E. Nonlinear oscillations following the Rayleigh collapse of a gas bubble in a linear viscoelastic (tissue-like) medium. Phys. Fluids 2013, 25, 083101. [Google Scholar] [CrossRef]
- Warnez, M.T.; Johnsen, E. Numerical modeling of bubble dynamics in viscoelastic media with relaxation. Phys. Fluids 2015, 27, 063103. [Google Scholar] [CrossRef] [PubMed]
- Zilonova, E.; Solovchuk, M.; Sheu, T. Bubble dynamics in viscoelastic soft tissue in high-intensity focal ultrasound thermal therapy. Ultrasonics Sonochemistry 2018, 40, 900–911. [Google Scholar] [CrossRef]
- Filonets, T.; Solovchuk, M. GPU-accelerated study of the inertial cavitation threshold in viscoelastic soft tissue using a dual-frequency driving signal. Ultrason. Sonochemistry 2022, 88, 106056. [Google Scholar] [CrossRef] [PubMed]
- Murakami, K.; Yamakawa, Y.; Zhao, J.; Johnsen, E.; Ando, K. Ultrasound-induced nonlinear oscillations of a spherical bubble in a gelatin gel. J. Fluid Mech. 2021, 924, A38. [Google Scholar] [CrossRef]
- Gaudron, R.; Warnez, M.T.; Johnsen, E. Bubble dynamics in a viscoelastic medium with nonlinear elasticity. J. Fluid Mech. 2015, 766, 54–75. [Google Scholar] [CrossRef]
- Shen, L.J. Fractional derivative models for viscoelastic materials at finite deformations. Int. J. Solids Struct. 2020, 190, 226–237. [Google Scholar] [CrossRef]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar] [CrossRef]
- Rayleigh, L. VIII. On the pressure developed in a liquid during the collapse of a spherical cavity. Philos. Mag. Ser. 1 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Prosperetti, A. A generalization of the Rayleigh–Plesset equation of bubble dynamics. Phys. Fluids 1982, 25, 409–410. [Google Scholar] [CrossRef]
- Zhang, A.M.; Li, S.M.; Xu, R.Z.; Pei, S.C.; Li, S.; Liu, Y.L. A theoretical model for compressible bubble dynamics considering phase transition and migration. J. Fluid Mech. 2024, 999, A58. [Google Scholar] [CrossRef]
- Preso, D.B.; Fuster, D.; Sieber, A.B.; Obreschkow, D.; Farhat, M. Vapor compression and energy dissipation in a collapsing laser-induced bubble. Phys. Fluids 2024, 36, 033342. [Google Scholar] [CrossRef]
- Lauterborn, W. Numerical investigation of nonlinear oscillations of gas bubbles in liquids. J. Acoust. Soc. Am. 1976, 59, 283–293. [Google Scholar] [CrossRef]
- Zabolotskaya, E.A.; Soluyan, S.I. A possible approach to amplification of sound waves. Sov. Phys. Acoust. 1967, 13, 254–256. [Google Scholar]
- Zabolotskaya, E.A.; Soluyan, S.I. Emission of Harmonic and Combination-Frequency Waves by Bubbles. Sov. Phys. Acoust. 1973, 18, 396–398. [Google Scholar]
- Ilinskii, Y.A.; Zabolotskaya, E.A. Cooperative radiation and scattering of acoustic waves by gas bubbles in liquids. J. Acoust. Soc. Am. 1992, 92, 2837–2841. [Google Scholar] [CrossRef]
- Vanhille, C. A fourth-order approximation Rayleigh-Plesset equation written in volume variation for an adiabatic-gas bubble in an ultrasonic field: Derivation and numerical solution. Results Phys. 2021, 25, 104193. [Google Scholar] [CrossRef]
- Leighton, T. The Rayleigh–Plesset equation in terms of volume with explicit shear losses. Ultrasonics 2008, 48, 85–90. [Google Scholar] [CrossRef]
- Hamilton, M.; Blackstock, D. Nonlinear Acoustics; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Vanhille, C.; Campos-Pozuelo, C. Numerical simulation of nonlinear ultrasonic standing waves in bubbly liquid. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 751–757. [Google Scholar] [CrossRef]
- Vanhille, C.; Campos-Pozuelo, C. Nonlinear ultrasonic standing waves: Two-dimensional simulations in bubbly liquids. Ultrason. Sonochemistry 2011, 18, 679–682. [Google Scholar] [CrossRef]
- Vanhille, C.; Campos-Pozuelo, C. Numerical simulations of three-dimensional nonlinear acoustic waves in bubbly liquids. Ultrason. Sonochemistry 2013, 20, 963–969. [Google Scholar] [CrossRef] [PubMed]
- Tejedor Sastre, M.T.; Vanhille, C. A numerical model for the study of the difference frequency generated from nonlinear mixing of standing ultrasonic waves in bubbly liquids. Ultrason. Sonochemistry 2017, 34, 881–888. [Google Scholar] [CrossRef] [PubMed]
- Spratt, K.S.; Lee, K.M.; Wilson, P.S.; Wochner, M.S. On the resonance frequency of an ideal arbitrarily-shaped bubble. Proc. Meet. Acoust. 2014, 20, 045004. [Google Scholar] [CrossRef]
- Dollet, B.; Marmottant, P.; Garbin, V. Bubble Dynamics in Soft and Biological Matter. Annu. Rev. Fluid Mech. 2019, 51, 331–355. [Google Scholar] [CrossRef]
- Catheline, S.; Gennisson, J.L.; Delon, G.; Fink, M.; Sinkus, R.; Abouelkaram, S.; Culioli, J. Measurement of viscoelastic properties of homogeneous soft solid using transient elastography: An inverse problem approach. J. Acoust. Soc. Am. 2004, 116, 3734–3741. [Google Scholar] [CrossRef]
- Mathews, J.H.; Fink, K.D. Numerical Methods Using MATLAB; Pearson Prentice Hall Upper: Saddle River, NJ, USA, 2004; Volume 4. [Google Scholar]
- Hasegawa, T.; Kanagawa, T. Effect of liquid elasticity on nonlinear pressure waves in a visco-elastic bubbly liquid. Phys. Fluids 2023, 35, 043309. [Google Scholar]
- Wang, Y.; Chen, D.; Wu, P. Multi-bubble scattering acoustic fields in viscoelastic tissues under dual-frequency ultrasound. Ultrason. Sonochemistry 2023, 99, 106585. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, D.; Li, J. Numerical studies of bubble pulsation in viscoelastic media under dual-frequency ultrasound. J. Phys. Conf. Ser. 2024, 2822, 012151. [Google Scholar] [CrossRef]
- Zilonova, E.; Solovchuk, M.; Sheu, T. Dynamics of bubble-bubble interactions experiencing viscoelastic drag. Phys. Rev. E 2019, 99, 023109. [Google Scholar] [CrossRef] [PubMed]
- Wells, P.; Liang, H. Medical ultrasound: Imaging of soft tissue strain and elasticity. J. R. Soc. Interface R. Soc. 2011, 8, 1521–1549. [Google Scholar] [CrossRef]
- Crha, J.; Orvalho, S.; Ruzicka, M.C.; Shirokov, V.; Jerhotová, K.; Pokorny, P.; Basařová, P. Bubble formation and swarm dynamics: Effect of increased viscosity. Chem. Eng. Sci. 2024, 288, 119831. [Google Scholar] [CrossRef]
- Kagami, S.; Kanagawa, T. Weakly nonlinear focused ultrasound in viscoelastic media containing multiple bubbles. Ultrason. Sonochemistry 2023, 97, 106455. [Google Scholar] [CrossRef]
- Qin, D.; Zou, Q.; Zhong, X.; Zhang, B.; Li, Z. Effects of medium viscoelasticity on bubble collapse strength of interacting polydisperse bubbles. Ultrason. Sonochemistry 2023, 95, 106375. [Google Scholar] [CrossRef] [PubMed]
- Qin, D.; Zou, Q.; Lei, S.; Wang, W.; Li, Z. Nonlinear dynamics and acoustic emissions of interacting cavitation bubbles in viscoelastic tissues. Ultrason. Sonochemistry 2021, 78, 105712. [Google Scholar] [CrossRef]
- Maxwell, A.D.; Cain, C.A.; Hall, T.L.; Fowlkes, J.B.; Xu, Z. Probability of Cavitation for Single Ultrasound Pulses Applied to Tissues and Tissue-Mimicking Materials. Ultrasound Med. Biol. 2013, 39, 449–465. [Google Scholar] [CrossRef] [PubMed]
- Aghayan, S.; Weinberg, K. Experimental and numerical investigation of dynamic cavitation in agarose gel as a soft tissue simulant. Mech. Mater. 2022, 175, 104486. [Google Scholar] [CrossRef]
- Husseini, G.A.; de la Rosa, M.A.D.; Richardson, E.S.; Christensen, D.A.; Pitt, W.G. The role of cavitation in acoustically activated drug delivery. J. Control. Release 2005, 107, 253–261. [Google Scholar] [CrossRef]
- Kaykanat, S.I.; Uguz, A.K. The role of acoustofluidics and microbubble dynamics for therapeutic applications and drug delivery. Biomicrofluidics 2023, 17, 021502. [Google Scholar] [CrossRef] [PubMed]
- Datta, S.; Coussios, C.C.; Ammi, A.Y.; Mast, T.D.; de Courten-Myers, G.M.; Holland, C.K. Ultrasound-enhanced thrombolysis using Definity as a cavitation nucleation agent. Ultrasound Med. Biol. 2008, 34, 1421–1433. [Google Scholar] [CrossRef]
- Rapoport, N.; Christensen, D.A.; Kennedy, A.M.; Nam, K.H. Cavitation Properties of Block Copolymer Stabilized Phase-Shift Nanoemulsions Used as Drug Carriers. Ultras. Med. Biol. 2010, 36, 419–429. [Google Scholar] [CrossRef]
- Chu, J.; Metcalfe, P.; Linford, H.V.; Zhao, S.; Goycoolea, F.M.; Chen, S.; Ye, X.; Holmes, M.; Orfila, C. Short-time acoustic and hydrodynamic cavitation improves dispersibility and functionality of pectin-rich biopolymers from citrus waste. J. Clean. Prod. 2022, 330, 129789. [Google Scholar] [CrossRef]
- Vanhille, C.; Campos-Pozuelo, C. An acoustic switch. Ultrason. Sonochem. 2014, 21, 50–52. [Google Scholar] [PubMed]
- Vanhille, C. Two-dimensonal numerical simulations of ultrasound in liquids with gas bubble agglomarates: Examples of bubbly-liquid-type acoustic metamaterials (BLAMMs). Sensors 2017, 17, 173. [Google Scholar] [CrossRef] [PubMed]
- Gallego-Juárez, J.; Graff, K. Power Ultrasonics: Applications of High-Intensity Ultrasound; Woodhead Publishing Series in Electronic and Optical Materials; Elsevier: Amsterdam, The Netherlands, 2015; Volume 66. [Google Scholar]
- Mason, T.J.; Lorimer, J.P. Applied Sonochemistry: The Uses of Power Ultrasound in Chemistry and Processing; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]



| Medium (Soft Biological Tissue) | Shear Modulus G (kPa) |
|---|---|
| Without shear elasticity | 0 |
| Fat | 3.3 |
| Liver | 4.3 |
| Muscle | 6.7 |
| Glandular breast | 11 |
| Medium | Viscosity () |
|---|---|
| GLY00 | 0.00 |
| GLY04 | 1.13 |
| GLY25 | 1.89 |
| GLY35 | 2.67 |
| GLY47 | 4.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carreras-Casanova, E.V.; Vanhille, C. A Model for the Dynamics of Stable Gas Bubbles in Viscoelastic Fluids Based on Bubble Volume Variation. Acoustics 2025, 7, 67. https://doi.org/10.3390/acoustics7040067
Carreras-Casanova EV, Vanhille C. A Model for the Dynamics of Stable Gas Bubbles in Viscoelastic Fluids Based on Bubble Volume Variation. Acoustics. 2025; 7(4):67. https://doi.org/10.3390/acoustics7040067
Chicago/Turabian StyleCarreras-Casanova, Elena V., and Christian Vanhille. 2025. "A Model for the Dynamics of Stable Gas Bubbles in Viscoelastic Fluids Based on Bubble Volume Variation" Acoustics 7, no. 4: 67. https://doi.org/10.3390/acoustics7040067
APA StyleCarreras-Casanova, E. V., & Vanhille, C. (2025). A Model for the Dynamics of Stable Gas Bubbles in Viscoelastic Fluids Based on Bubble Volume Variation. Acoustics, 7(4), 67. https://doi.org/10.3390/acoustics7040067







