Matched Filter for Acoustic Emission Monitoring in Noisy Environments: Application to Wire Break Detection
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.1.1. Long-Term AE Monitoring in an Operating Wind Turbine
2.1.2. Wire Break Events in Post-Tensioned Steel Tendons
2.1.3. Rebound Hammer Impacts on Post-Tensioned Steel Tendons
2.2. Methodology
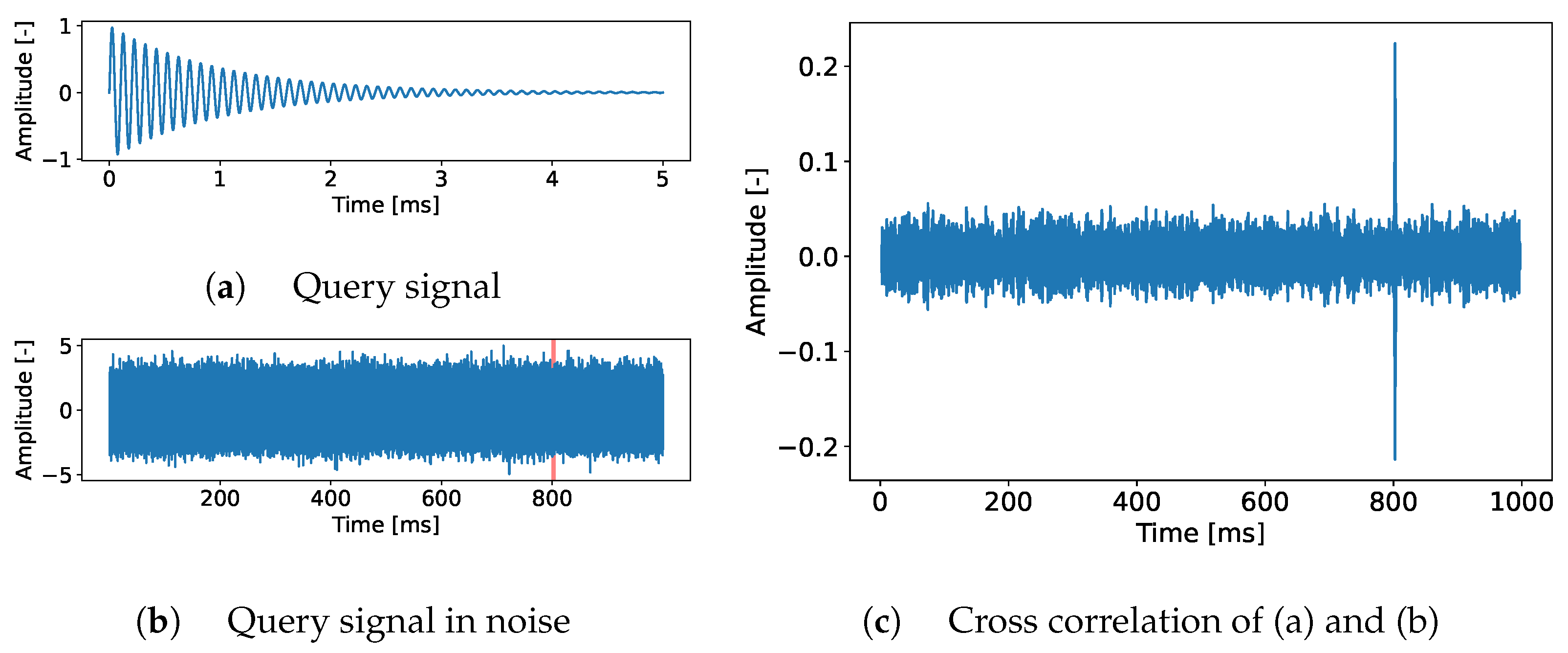
2.2.1. Matched Filter for Acoustic Emission Monitoring
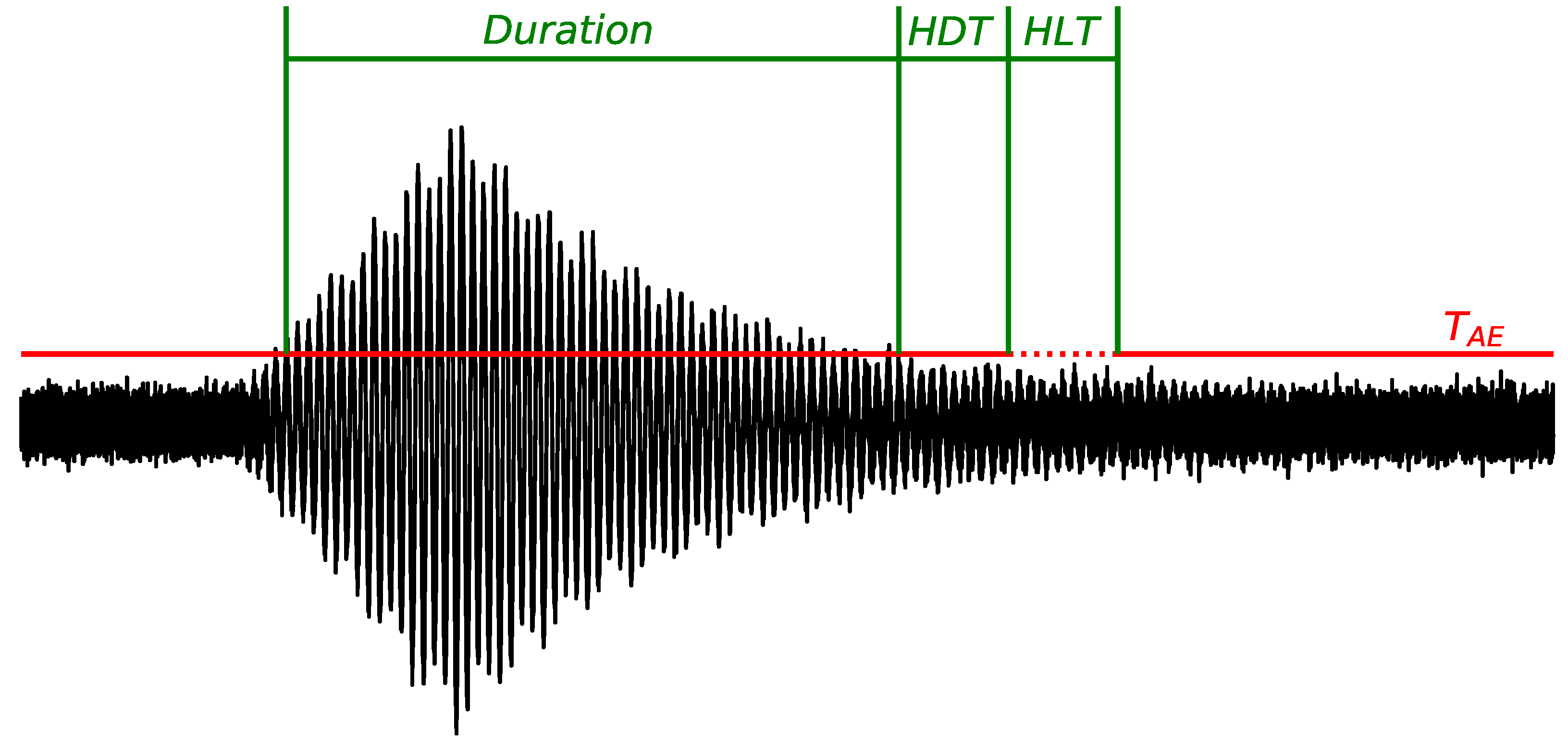
2.2.2. Amplitude-Based Detection
2.3. Evaluation
3. Results
3.1. Attenuation of Wire Break Signals & Environmental Noise Level
 24 installed on the transition piece replica (see Table 1). Even though we also observe an increase in amplitude for single wire break events here, an average decrease in the signal’s amplitude of approximately seven to eight dB is estimated for both, the wire break signals originating from the experiments on Tendon T3 and T2 as well as Tendon T2 and T1. Considering the observed background noise in the operating wind turbine summarized in Table 2, wire breaks occuring on the free span length of external tendons may indeed result in acoustic emission signals with a low SNR for sensors mounted on the footing or the transition piece of a wind turbine tower. Hence, the investigation of alternatives to conventional amplitude-based detection is of specific interest for acoustic emission monitoring applications on large civil infrastructures.
24 installed on the transition piece replica (see Table 1). Even though we also observe an increase in amplitude for single wire break events here, an average decrease in the signal’s amplitude of approximately seven to eight dB is estimated for both, the wire break signals originating from the experiments on Tendon T3 and T2 as well as Tendon T2 and T1. Considering the observed background noise in the operating wind turbine summarized in Table 2, wire breaks occuring on the free span length of external tendons may indeed result in acoustic emission signals with a low SNR for sensors mounted on the footing or the transition piece of a wind turbine tower. Hence, the investigation of alternatives to conventional amplitude-based detection is of specific interest for acoustic emission monitoring applications on large civil infrastructures.3.2. Evaluation of Matched Filter for Wire Break Detection
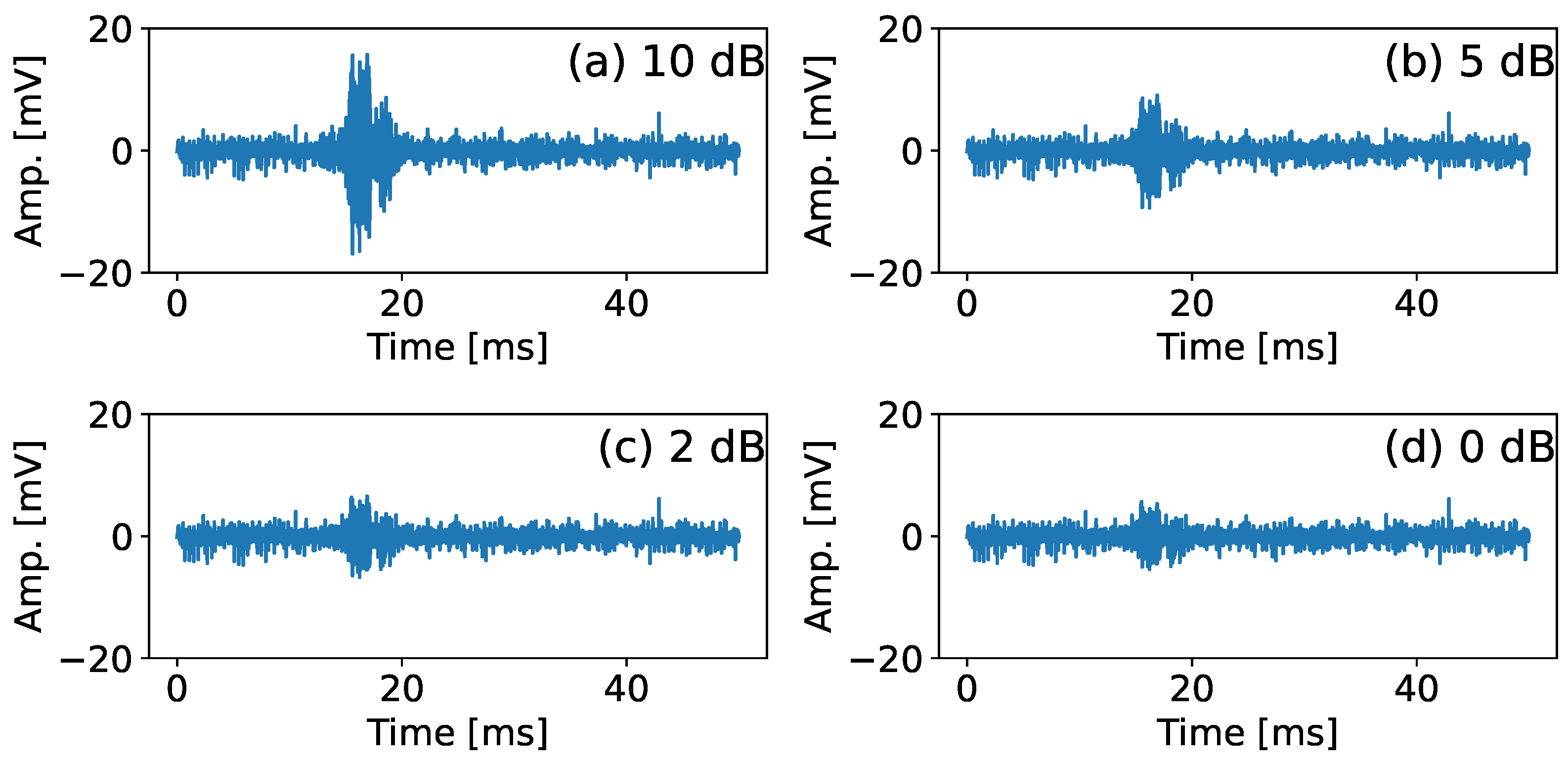
 5 installed in the wind turbine tower and the wire break signals recorded at the footing replica of the laboratory test frame. The different subfigures depict the results for the different query signals shown in Figure 7 and selected as described previously.
5 installed in the wind turbine tower and the wire break signals recorded at the footing replica of the laboratory test frame. The different subfigures depict the results for the different query signals shown in Figure 7 and selected as described previously.3.3. Comparison with Amplitude-Based Detection
 5 installed at the operating wind turbine and the wire break signals recorded at the footing replica during the laboratory experiments are also presented in Figure 8. For a more detailed comparison of the different detection techniques, the AUC values for both, the matched filter approach and the amplitude-based detection are presented in Table 3. The last column of these tables show the increase in AUC between the matched filter approach and the amplitude-based detection.
5 installed at the operating wind turbine and the wire break signals recorded at the footing replica during the laboratory experiments are also presented in Figure 8. For a more detailed comparison of the different detection techniques, the AUC values for both, the matched filter approach and the amplitude-based detection are presented in Table 3. The last column of these tables show the increase in AUC between the matched filter approach and the amplitude-based detection. 3,
3,  5 and sensor
5 and sensor  7. These significant differences can be attributed to single amplitude spikes within the raw measurements of sensor
7. These significant differences can be attributed to single amplitude spikes within the raw measurements of sensor  7, which causes high false positive rates using amplitude-based detection. The matched filter approach, however, seems to handle these kind of anomalies comparatively good, showing only a slight decrease in the AUC scores.
7, which causes high false positive rates using amplitude-based detection. The matched filter approach, however, seems to handle these kind of anomalies comparatively good, showing only a slight decrease in the AUC scores.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mishnaevsky, L., Jr.; Thomsen, K. Costs of repair of wind turbine blades: Influence of technology aspects. Wind Energy 2020, 23, 2247–2255. [Google Scholar] [CrossRef]
- Schacht, G.; Käding, M.; Bolle, G.; Marx, S. Konzepte für die Bewertung von Brücken mit Spannungsrisskorrosionsgefahr. Beton- und Stahlbetonbau 2019, 114, 85–94. [Google Scholar] [CrossRef]
- Nürnberger, U.; Beul, W. Untersuchungen an Verkehrsbauten aus Spannbeton zur Abschätzung des Gefährdungspotentials Infolge Spannungsrißkorrosion der Spannstähle. Teil 2-Untersuchungen der FMPA: Abschlußbericht zum BMV-Forschungsvorhaben FE 15.209 R91D (FMPA-Nr. 34-10566); Bundesanstalt für Materialforschung und-prüfung (BAM): Berlin, Germany, 1994. [Google Scholar]
- Scheerer, S.; Hampel, T.; Curbach, M. Überprüfung des Risikos der Spannungsrisskorrosion (SpRK) von Hennigsdorfer Spannstahl für den Produktionszeitraum bis 1993; Forschungsbericht; Institut für Massivbau und Otto-Mohr Laboratorium der TU Dresden: Dresden, Germany, 2012. [Google Scholar]
- Liu, W.; Hunsperger, R.; Folliard, K.; Chajes, M.; Barot, J.; Jhaveri, D.; Kunz, E. Detection and characterization of corrosion of bridge cables by time domain reflectometry. In Proceedings of the SPIE Conference on Nondestructive Evaluation Techniques for Aging Infrastructures and Manufacturing, Newport Beach, CA, USA, 3–5 March 1999; Volume 3587. [Google Scholar] [CrossRef]
- Furse, C.; Smith, P.; Diamond, M. Feasibility of Reflectometry for Nondestructive Evaluation of Prestressed Concrete Anchors. IEEE Sens. J. 2009, 9, 1322–1329. [Google Scholar] [CrossRef]
- Xu, F.; Jiang, Z.; Jiang, Q.; Wang, X.S. Damage Detection and Assessment of Broken Wires in Cables of a Bridge Based on Magnetic Flux Leakage. Exp. Tech. 2023, 47, 907–920. [Google Scholar] [CrossRef]
- Sun, L.; Wu, X.; Ouyang, Q.; Wang, J. A novel broken wire evaluation method for bridge cable magnetic flux leakage testing under lift-off uncertainty. J. Magn. Magn. Mater. 2023, 570, 170525. [Google Scholar] [CrossRef]
- Cullington, D.; MacNeil, D.; Paulson, P.; Elliott, J. Continuous acoustic monitoring of grouted post-tensioned concrete bridges. NDT & E Int. 2001, 34, 95–105. [Google Scholar] [CrossRef]
- Fricker, S.; Schechinger, B.; Vogel, T. Acoustic emission analysis as a monitoring method for prestressed concrete structures. In Proceedings of the 9th European Conference on NDT (ECNDT), Berlin, Germany, 25–29 September 2006. [Google Scholar]
- Fricker, S. Schallemissionsanalyse zur Erfassung von Spanndrahtbrüchen bei Stahlbetonbrücken. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2009. [Google Scholar] [CrossRef]
- Käding, M.; Schacht, G.; Marx, S. Acoustic Emission analysis of a comprehensive database of wire breaks in prestressed concrete girders. Eng. Struct. 2022, 270, 114846. [Google Scholar] [CrossRef]
- Sodeikat, C.; Groschup, R.; Knab, F.; Obermeier, P. Acoustic Emission in der Bauwerksüberwachung zur Feststellung von Spannstahlbrüchen. Beton- und Stahlbetonbau 2019, 114, 707–723. [Google Scholar] [CrossRef]
- Pirskawetz, S.M.; Schmidt, S. Detection of wire breaks in prestressed concrete bridges by Acoustic Emission analysis. Dev. Built Environ. 2023, 14, 100151. [Google Scholar] [CrossRef]
- Seidel, M. Experiences with two of the world’s largest wind turbine towers. In Proceedings of the 2003 EWEC European Wind Energy Conference and Exhibition, Madrid, Spain, 16–19 June 2003; pp. 16–19. [Google Scholar]
- Xu, R.; Käding, M.; Lange, A.; Ostermann, J.; Marx, S. Detection of impulsive signals on tendons for hybrid wind turbines using acoustic emission measurements. In Proceedings of the International Symposium on Non-Destructive Testing in Civil Engineering, Zurich, Switzerland, 16–18 August 2022. [Google Scholar]
- Turin, G.L. An introduction to matched filters. IRE Trans. Inf. Theory 1960, 6, 311–329. [Google Scholar] [CrossRef]
- Hamilton, P.; Tompkins, W. Adaptive matched filtering for QRS detection. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, New Orleans, LA, USA, 4–7 November 1988; pp. 147–148. [Google Scholar] [CrossRef]
- Mertins, A. Signaltheorie; Springer Vieweg: Wiesbaden, Germany, 2013. [Google Scholar] [CrossRef]
- Vallen Systeme GmbH. Amsy-6 System Description. 2021. Available online: https://www.vallen.de/zdownload/pdf/AMSY-6_Description.pdf (accessed on 24 January 2024).
- Unnþórsson, R. Hit Detection and Determination in AE Bursts. In Acoustic Emission—Research and Applications; InTech Open: London, UK, 2013. [Google Scholar]
- Muralidhara, S.; Prasad, B.R.; Eskandari, H.; Karihaloo, B. Fracture process zone size and true fracture energy of concrete using acoustic emission. Constr. Build. Mater. 2010, 24, 479–486. [Google Scholar] [CrossRef]
- Ch, G.; Ochtsu, M. Acoustic Emission Testing. Basics for Research-Applications in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Lange, A.; Käding, M.; Hinrichs, R.; Ostermann, J.; Marx, S. Wire Break Detection in Bridge Tendons Using Low-Frequency Acoustic Emissions. In Proceedings of the European Workshop on Structural Health Monitoring, Stanford, CA, USA, 12–14 September 2023; pp. 1024–1033. [Google Scholar]
- Xie, J.; Colonna, J.G.; Zhang, J. Bioacoustic signal denoising: A review. Artif. Intell. Rev. 2021, 54, 3575–3597. [Google Scholar] [CrossRef]
- Vaseghi, S.V. Advanced Digital Signal Processing and Noise Reduction; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
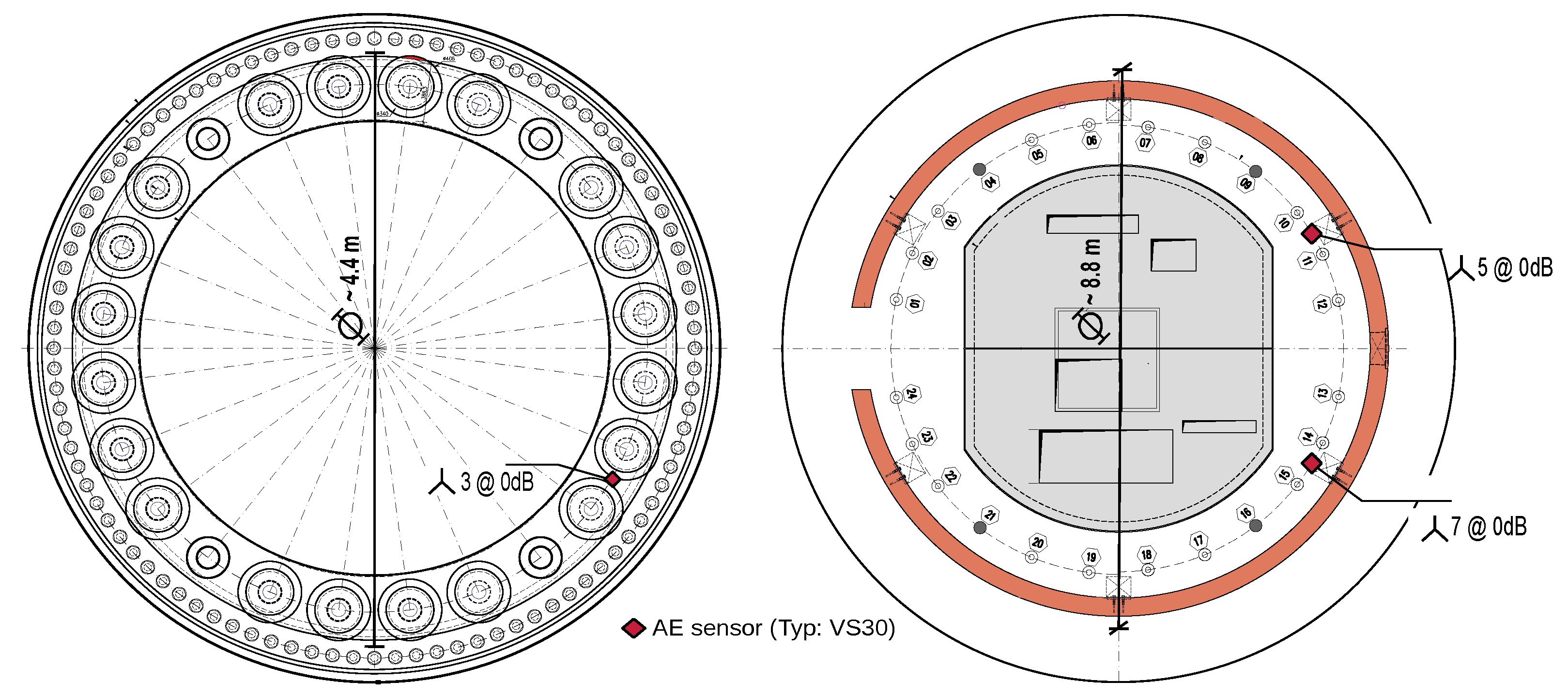
 1–8 were mounted on the tendon under test itself, so that these positions changed throughout the experiments as indicated by the superscripts (T2–T4). All other sensor positions remained unchanged. In this work, the sensors without preamplification (in red) mounted at the footing and the transition piece replica are in the focus of research.
1–8 were mounted on the tendon under test itself, so that these positions changed throughout the experiments as indicated by the superscripts (T2–T4). All other sensor positions remained unchanged. In this work, the sensors without preamplification (in red) mounted at the footing and the transition piece replica are in the focus of research.
 1–8 were mounted on the tendon under test itself, so that these positions changed throughout the experiments as indicated by the superscripts (T2–T4). All other sensor positions remained unchanged. In this work, the sensors without preamplification (in red) mounted at the footing and the transition piece replica are in the focus of research.
1–8 were mounted on the tendon under test itself, so that these positions changed throughout the experiments as indicated by the superscripts (T2–T4). All other sensor positions remained unchanged. In this work, the sensors without preamplification (in red) mounted at the footing and the transition piece replica are in the focus of research.
 13) and (b) the transition piece replica (sensor
13) and (b) the transition piece replica (sensor  24). The abscissa of the boxplots denotes, on which tendon the wire breaks were conducted. From left to right, the distance between wire break source and the anchor beam as well as the distance of the sensor to the anchor point of the tendon under test increases (see also Figure 2). The dotted lines and shaded areas indicate the mean noise amplitude and the 2 confidence interval (assuming normally distributed noise) from Table 2, respectively.
24). The abscissa of the boxplots denotes, on which tendon the wire breaks were conducted. From left to right, the distance between wire break source and the anchor beam as well as the distance of the sensor to the anchor point of the tendon under test increases (see also Figure 2). The dotted lines and shaded areas indicate the mean noise amplitude and the 2 confidence interval (assuming normally distributed noise) from Table 2, respectively.
 13) and (b) the transition piece replica (sensor
13) and (b) the transition piece replica (sensor  24). The abscissa of the boxplots denotes, on which tendon the wire breaks were conducted. From left to right, the distance between wire break source and the anchor beam as well as the distance of the sensor to the anchor point of the tendon under test increases (see also Figure 2). The dotted lines and shaded areas indicate the mean noise amplitude and the 2 confidence interval (assuming normally distributed noise) from Table 2, respectively.
24). The abscissa of the boxplots denotes, on which tendon the wire breaks were conducted. From left to right, the distance between wire break source and the anchor beam as well as the distance of the sensor to the anchor point of the tendon under test increases (see also Figure 2). The dotted lines and shaded areas indicate the mean noise amplitude and the 2 confidence interval (assuming normally distributed noise) from Table 2, respectively.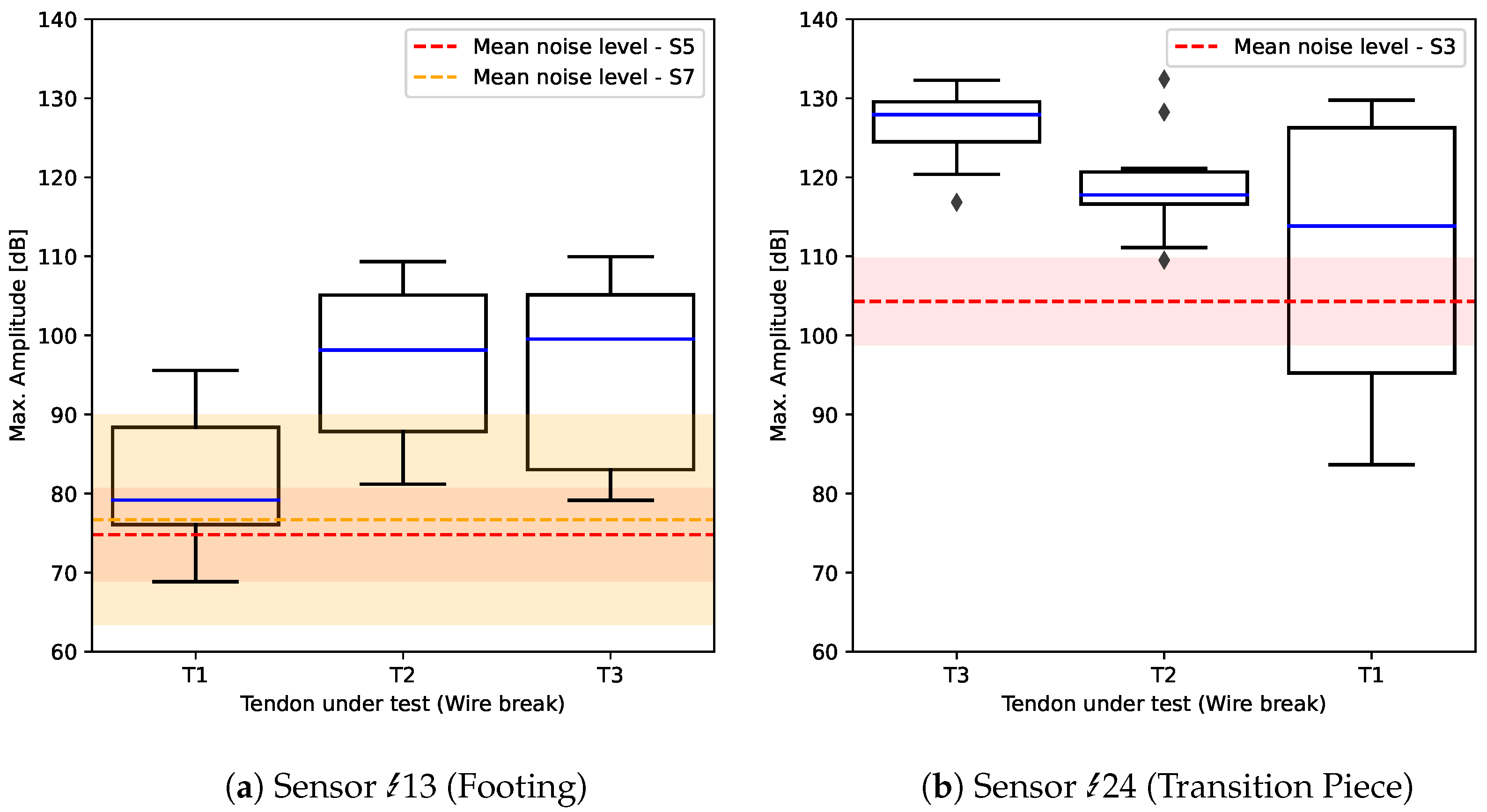

 24 during the laboratory experiments on Tendon T1–T3. and denote the arithmetic mean and the standard deviation, respectively.
24 during the laboratory experiments on Tendon T1–T3. and denote the arithmetic mean and the standard deviation, respectively.
 24 during the laboratory experiments on Tendon T1–T3. and denote the arithmetic mean and the standard deviation, respectively.
24 during the laboratory experiments on Tendon T1–T3. and denote the arithmetic mean and the standard deviation, respectively.| Tendon | Amp. Attenuation [] | |||
|---|---|---|---|---|
| max | min | |||
| T3 → T2 | 14.2 | −5.7 | 7.9 | 1.4 |
| T2 → T1 | 37.1 | −12.7 | 7.6 | 4.4 |
| T3 → T1 | 48.6 | −8.3 | 15.4 | 4.9 |
| Sensor | Amplitude [] | |||
|---|---|---|---|---|
| max | min | |||
 3 3 | 107.2 | 67.5 | 104.3 | 2.7 |
 5 5 | 80.8 | 65.6 | 74.8 | 2.9 |
 7 7 | 93.5 | 65.3 | 76.7 | 6.6 |
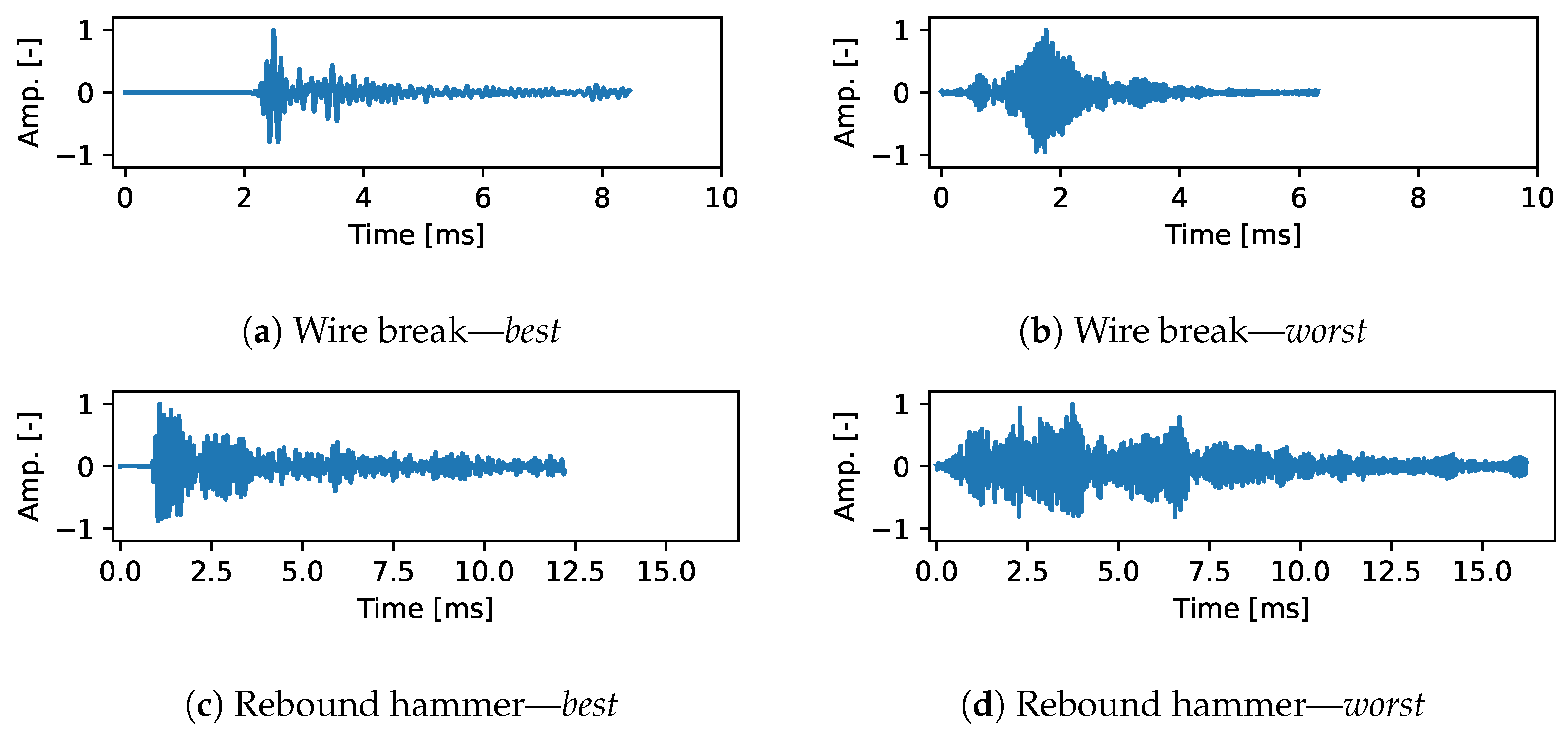
| (a) Wire Break (Best) | (b) Wire Break (Worst) | ||||||||||
| Operational Sensor 1 | Laboratory Sensors 2 | SNR | AUC [-] | ↑ AUC | Operational Sensor 1 | Laboratory Sensors 2 | SNR | AUC [-] | ↑ AUC | ||
| MF | Amp | MF | Amp | ||||||||
 3 3 |  13– 13– 16 16 | Unscaled | 1.0000 | 0.9848 | 0.0152 |  3 3 |  13– 13– 16 16 | Unscaled | 0.9943 | 0.9848 | 0.0095 |
| SNR 10 dB | 1.0000 | 1.0000 | 0.0000 | SNR 10 dB | 0.9941 | 1.0000 | −0.0059 | ||||
| SNR 5 dB | 1.0000 | 0.9643 | 0.0357 | SNR 5 dB | 0.9953 | 0.9643 | 0.0310 | ||||
| SNR 2 dB | 1.0000 | 0.7202 | 0.2798 | SNR 2 dB | 0.9954 | 0.7202 | 0.2752 | ||||
| SNR 0 dB | 1.0000 | 0.4537 | 0.5463 | SNR 0 dB | 0.9950 | 0.4537 | 0.5413 | ||||
 5 5 |  21– 21– 24 24 | Unscaled | 0.9999 | 0.9712 | 0.0287 |  5 5 |  21– 21– 24 24 | Unscaled | 0.9941 | 0.9712 | 0.0229 |
| SNR 10 dB | 1.0000 | 0.9978 | 0.0022 | SNR 10 dB | 0.9938 | 0.9978 | −0.0040 | ||||
| SNR 5 dB | 0.9999 | 0.7850 | 0.2149 | SNR 5 dB | 0.9903 | 0.7850 | 0.2053 | ||||
| SNR 2 dB | 0.9997 | 0.3969 | 0.6028 | SNR 2 dB | 0.9820 | 0.3969 | 0.5851 | ||||
| SNR 0 dB | 0.9992 | 0.2206 | 0.7786 | SNR 0 dB | 0.9746 | 0.2206 | 0.7540 | ||||
 7 7 |  21– 21– 24 24 | Unscaled | 1.0000 | 0.7530 | 0.2470 |  7 7 |  21– 21– 24 24 | Unscaled | 0.9864 | 0.7530 | 0.2334 |
| SNR 10 dB | 1.0000 | 0.5453 | 0.4547 | SNR 10 dB | 0.9854 | 0.5453 | 0.4401 | ||||
| SNR 5 dB | 1.0000 | 0.4580 | 0.5420 | SNR 5 dB | 0.9783 | 0.4580 | 0.5203 | ||||
| SNR 2 dB | 0.9999 | 0.3488 | 0.6511 | SNR 2 dB | 0.9595 | 0.3488 | 0.6107 | ||||
| SNR 0 dB | 0.9993 | 0.2379 | 0.7614 | SNR 0 dB | 0.9420 | 0.2379 | 0.7041 | ||||
| (c) Rebound Hammer (Worst) | (d) Rebound Hammer (Worst) | ||||||||||
| Operational Sensor 1 | Laboratory Sensors 2 | SNR | AUC [-] | ↑ AUC | Operational Sensor 1 | Laboratory Sensors 2 | SNR | AUC [-] | ↑ AUC | ||
| MF | Amp | MF | Amp | ||||||||
 3 3 |  13– 13– 16 16 | Unscaled | 1.0000 | 0.9848 | 0.0152 |  3 3 |  13– 13– 16 16 | Unscaled | 1.0000 | 0.9848 | 0.0152 |
| SNR 10 dB | 1.0000 | 1.0000 | 0.0000 | SNR 10 dB | 1.0000 | 1.0000 | 0.0000 | ||||
| SNR 5 dB | 1.0000 | 0.9643 | 0.0357 | SNR 5 dB | 1.0000 | 0.9643 | 0.0357 | ||||
| SNR 2 dB | 1.0000 | 0.7202 | 0.2798 | SNR 2 dB | 1.0000 | 0.7202 | 0.2798 | ||||
| SNR 0 dB | 1.0000 | 0.4537 | 0.5463 | SNR 0 dB | 1.0000 | 0.4537 | 0.5463 | ||||
 5 5 |  21– 21– 24 24 | Unscaled | 0.9999 | 0.9712 | 0.0287 |  5 5 |  21– 21– 24 24 | Unscaled | 0.9961 | 0.9712 | 0.0249 |
| SNR 10 dB | 1.0000 | 0.9978 | 0.0022 | SNR 10 dB | 0.9961 | 0.9978 | −0.0017 | ||||
| SNR 5 dB | 1.0000 | 0.7850 | 0.2150 | SNR 5 dB | 0.9896 | 0.7850 | 0.2046 | ||||
| SNR 2 dB | 1.0000 | 0.3969 | 0.6031 | SNR 2 dB | 0.9849 | 0.3969 | 0.5880 | ||||
| SNR 0 dB | 0.9999 | 0.2206 | 0.7793 | SNR 0 dB | 0.9781 | 0.2206 | 0.7575 | ||||
 7 7 |  21– 21– 24 24 | Unscaled | 1.0000 | 0.7530 | 0.2470 |  7 7 |  21– 21– 24 24 | Unscaled | 0.9897 | 0.7530 | 0.2367 |
| SNR 10 dB | 1.0000 | 0.5453 | 0.4547 | SNR 10 dB | 0.9901 | 0.5453 | 0.4448 | ||||
| SNR 5 dB | 1.0000 | 0.4580 | 0.5420 | SNR 5 dB | 0.9785 | 0.4580 | 0.5205 | ||||
| SNR 2 dB | 1.0000 | 0.3488 | 0.6512 | SNR 2 dB | 0.9640 | 0.3488 | 0.6152 | ||||
| SNR 0 dB | 1.0000 | 0.2379 | 0.7621 | SNR 0 dB | 0.9404 | 0.2379 | 0.7025 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lange, A.; Xu, R.; Kaeding, M.; Marx, S.; Ostermann, J. Matched Filter for Acoustic Emission Monitoring in Noisy Environments: Application to Wire Break Detection. Acoustics 2024, 6, 204-218. https://doi.org/10.3390/acoustics6010011
Lange A, Xu R, Kaeding M, Marx S, Ostermann J. Matched Filter for Acoustic Emission Monitoring in Noisy Environments: Application to Wire Break Detection. Acoustics. 2024; 6(1):204-218. https://doi.org/10.3390/acoustics6010011
Chicago/Turabian StyleLange, Alexander, Ronghua Xu, Max Kaeding, Steffen Marx, and Joern Ostermann. 2024. "Matched Filter for Acoustic Emission Monitoring in Noisy Environments: Application to Wire Break Detection" Acoustics 6, no. 1: 204-218. https://doi.org/10.3390/acoustics6010011
APA StyleLange, A., Xu, R., Kaeding, M., Marx, S., & Ostermann, J. (2024). Matched Filter for Acoustic Emission Monitoring in Noisy Environments: Application to Wire Break Detection. Acoustics, 6(1), 204-218. https://doi.org/10.3390/acoustics6010011







