Abstract
The frequency-difference and frequency-sum autoproducts, quadratic products of complex acoustic field amplitudes at two frequencies, may mimic genuine acoustic fields at the difference and sum frequencies of the constituent fields, respectively. Autoproducts have proven useful in extending the useable frequency range for acoustic remote sensing to frequencies outside a recorded field’s bandwidth. In array signal processing applications, the spatial coherence of the field often sets performance limits. This paper presents results for the spatial coherence of the genuine field, the frequency-difference autoproduct, and the frequency-sum autoproduct as determined from data collected during the Cascadia Open-Access Seismic Transects (COAST 2012) experiment. In this experiment, an airgun array providing a 10 to 200 Hz signal was repeatedly fired off the coast of Washington state, and the resulting acoustic fields were recorded by a nominal 8 km long, 636-element towed horizontal array. Based on hundreds of airgun firings from a primarily shore-parallel transect, both autoproducts were found to extend field coherence to frequencies outside the genuine field’s bandwidth and to produce longer coherence lengths than genuine fields, in most cases. When used for matched-field processing, the same data illustrate the benefits of the autoproducts’ extended coherence.
1. Introduction
Array signal processing techniques are used in a wide variety of underwater acoustic applications, including both active and passive remote sensing. Coherence between separated receivers is commonly needed for success in such applications, with increased coherence leading to better outcomes. In general, the coherence between two points in space depends on the locations of the two points, the signal frequency, and the characteristics of the environment between the sound source and the two points. Coherence commonly increases with decreasing receiver separation and decreasing frequency, as well as with decreased environmental variability and complexity [1], although coherence in the presence of certain environmental characteristics has been shown to exhibit unintuitive behavior [2]. In addition, coherence measurements may be degraded when noise is present.
The distance over which a field exhibits coherence is known as the coherence length. Limited coherence length can be problematic for acoustic array signal processing in the ocean, especially for long arrays, when the array aperture exceeds the field’s coherence length at the frequencies of interest. Coherence length is directly related to array gain [3,4], and thus has important implications in beamforming [5,6] and matched-field processing applications [7]. When an array is nominally shorter than the field’s coherence length, all of its elements should contribute positively to the achievable array gain; conversely, adding array elements that extend the array’s aperture beyond the coherence length generally does not provide performance improvements and can potentially reduce the performance of array signal processing techniques. In particular, prior work has shown that for shallow water environments, spatial coherence length is a primary factor in predicting array performance [8]. For a known finite coherence length, the theoretical limitations of conventional beamforming methods with a linear array are understood and readily calculated [5,6]. Coherence length has been studied in a variety of simulation and experimental geometries and scenarios, including with both vertical and horizontal arrays [9], in the presence of internal waves [10,11,12], with varying channel depth [4], in the presence of multipath propagation [3], and at long ranges [13,14], to understand the influence of various ocean environmental characteristics. The coherence of acoustic waves scattered from the ocean surface [15,16,17] and floor sediment [18,19] has also been investigated.
A shared characteristic of all existing work on coherence is the limitation to in-band signal frequencies, a typical feature of conventional signal processing methods. Interestingly, recent work has considered surrogate fields, the frequency-difference and frequency-sum autoproducts, as possible replacements for genuine acoustic fields at frequencies not broadcast by the source [20,21]. Use of the autoproducts has been successful for beamforming [22,23,24,25] and matched-field processing [26,27,28] at frequencies outside the broadcast signal’s bandwidth. However, the coherence of autoproducts has yet to be directly examined, despite its importance in signal processing applications. Thus, the primary purpose of this paper is to report the spatial coherence properties of autoproducts computed from bottom-reflected acoustic recordings made during the Cascadia Open-Access Seismic Transects (COAST) experiment [29], conducted off the coast of Washington state on a varying bathymetry in July 2012. In particular, this manuscript presents results for spatial coherence and coherence lengths, as a function of frequency, for the frequency-difference and frequency-sum autoproducts and compares them to those of the genuine acoustic field—from which they are derived—in the same environment.
The autoproducts provide a means for processing signals at frequencies below and above the signal recording’s bandwidth; thus, the coherence of the autoproducts relative to that of genuine in-band fields is critical for understanding their performance for various applications. In addition to signal processing at frequencies unavailable in the genuine field, information at in-band frequencies that is masked by low SNR, or other undesired features, can potentially be recovered by utilizing the autoproducts.
The remainder of this manuscript is divided into five sections. Section 2 details the mathematical formulations for coherence, coherence length, and autoproducts, and overviews the COAST 2012 experiment and the specific data used for this study. Section 3 presents the coherence and matched-field processing results for the genuine field, and for the frequency-difference and -sum autoproducts. The final section discusses this effort and presents the conclusions drawn from it.
2. Materials and Methods
The mathematical formulas for coherence, autoproducts, and matched-field processing (MFP) used herein are described first, followed by an overview of the COAST 2012 experiment and the dataset used.
2.1. Coherence and Coherence Length
In general, for independent field samples recorded at locations and , the complex coherence, , of the field at temporal frequency between these locations can be estimated from an ensemble-average (indicated by -brackets) of a product of normalized field amplitudes:
where the asterisk indicates complex conjugation, is the location of the reference receiver, is the receiver a distance away from the reference receiver, and is the field sample at angular frequency from the receiver located at [30]. The normalization in (1) ensures that the coherence value is bounded by the unit circle in the complex plane. The variance in phase of for controls the coherence magnitude. Magnitudes of near one indicate highly coherent fields, while magnitudes near zero indicate poor coherence.
In this investigation, equally spaced sample locations in the horizontal direction pointing away from a known-location source are of interest, so , where is the sample location index relative to the reference receiver, is the separation between neighboring receivers, is the horizontal range unit vector pointing away from the source, and is the total horizontal separation between any two receiver locations. The assumption of spatial homogeneity across the receiving array admits the following simplification to (1):
where the spatial dependence is modified to receiver separation only. Approximate spatial homogeneity justification for a different ocean experiment is provided in Andrew et al. [14]. Here, a further simplification is permitted as the coherence phase is not of interest. Thus,
defines the genuine acoustic field coherence function. The highest possible value of is unity (perfect coherence between field samples separated by ), while the minimum magnitude of is zero (complete lack of coherence between field samples separated by ).
The coherence length is the distance over which a predetermined level of coherence is maintained, though the exact mathematical definition of coherence length varies between scientific areas, applications, and authors. For the present purposes, the coherence length is determined from the decay of with increasing receiver-separation distance . The normalization in (1) requires and typically decreases monotonically with increasing . Thus, the coherence length, ), may then be defined as the receiver separation where falls below a specified threshold. No strict rules exist for this threshold value, but (≈ 0.368) is a common choice [4,11] and is used here as well.
2.2. Autoproducts
In prior work, coherence lengths have been determined from analysis, simulated data, and experimental measurements in a variety of acoustic environments and with a variety of signals. However, all such results consider only in-band signal frequencies. Recent work [20] has shown that the frequency-difference and frequency-sum autoproducts constructed from nonzero-bandwidth acoustic field recordings may mimic genuine acoustic fields at (user-selectable) frequencies below and above, respectively, the recorded signal’s bandwidth. Further, the autoproducts can be used to obtain unique results in acoustic remote sensing [31]. The frequency-difference autoproduct, , and frequency-sum autoproduct, , are defined from two frequencies of the acoustic recording at the element of a receiving array as
where denote the pair of recorded acoustic frequencies. Prior work has shown that and may mimic genuine acoustic fields at the difference, , and sum, , frequencies [20]. Equations (4) and (5) may be averaged through the recorded field’s bandwidth, , to determine the bandwidth-averaged autoproducts:
where is the in-band center frequency. The signal bandwidths available to average and are given by and , respectively. The bandwidth averaging of (6) and (7) is advantageous in multipath environments, because it suppresses cross terms incurred from the quadratic construction of the autoproducts and enhances their mimicry of genuine difference- or sum-frequency acoustic fields [20,21]. The implementation here differs slightly from bandwidth averages in previous work. Due to imperfect knowledge of the source spectrum, autoproduct samples are averaged directly in (6) and (7), without explicit removal of the source spectrum.
The coherence definitions of the frequency-difference and frequency-sum autoproducts follow directly from (1)–(3), with the bandwidth-averaged autoproducts replacing the genuine acoustic field:
Coherence lengths, and , for and , respectively, were then determined from the spatial decay of and in an equivalent manner to the calculation of from .
Uncertainty estimates for the ’s and ’s are included to facilitate quantitative comparisons between acoustic field coherence and autoproduct coherence. The 95% confidence interval [32] for the coherence random error, , reported here is:
These approximate error bounds rely exclusively on the number of field samples, , and the mean coherence value, . As such, (10) and (11) are used to generate error estimates for the genuine acoustic field coherence calculated from (3), and the frequency-difference and frequency-sum autoproduct coherence calculated from (8) and (9). The error estimates of (10) and (11) have been used previously in ocean acoustic coherence studies [16,17] and are expected to be a good approximation of the true variance for a large ensemble, [30]. More exact confidence bound formulations exist [30,33], as well as iterative algorithms for confidence bound generation [34,35]. However, (10) and (11) were used in favor of these alternatives because of their relative simplicity and the sufficiently large ensemble number, , provided by the COAST 2012 experiment.
2.3. Matched-Field Processing
A field’s coherence length has significant implications in array signal processing, and this is examined herein for the specific case of matched-field processing (MFP) of the in-band field and its autoproducts. Previous work has considered the autoproducts for out-of-band MFP and has shown that they may provide improvements over conventional MFP when signal processing at in-band frequencies is problematic [26,27,28]. Specifically, frequency-difference methods can suppress the negative impacts of array sparseness, random scattering, and wavefront mismatch, while frequency-sum methods can enhance resolution.
MFP is a common scheme to identify an unknown source location, in both range and direction, from a measured field. Computed replica fields (also known as replicas), based on a modeled acoustic propagation environment, are generated for many potential source locations. The location of the source is then selected such that the replica field exhibits the highest correlation with the measured field at the recording locations. The first development of MFP in underwater acoustics can be found in Bucker [36] and an overview of MFP is available in Jensen et al. [37].
The MFP strategy implemented is the Bartlett processor, which is a frequency domain spatial correlation between the measured field and computed replicas. Mathematically,
where is the number of array elements informed by the coherence length of the field, is the search coordinate, and is the weight vector based on the modeled propagation between and the receiving location, . The replicas here implement image theory for the surface and bottom reflections, which has been used recently in underwater shallow target localization using MFP [38]. When plotted as a function of the search coordinate , is normalized by its maximum value and presented as a decibel value: .
The out-of-band MFP formulation is identical to (12) with replaced by or :
with the weight vector evaluated at the difference or sum frequency, as appropriate.
2.4. COAST 2012 Experiment
The Cascadia Open-Access Seismic Transects (COAST) experiment [29] was conducted off the coast of Washington state in July 2012. The goal of this experiment was to collect two-dimensional seismic reflection profiles and other geophysical data. In this experiment, the R/V Marcus G. Langseth towed an approximately 8 km long streamer at 9 m depth that contained a receiver array with 636 hydrophone channels spaced 12.5 m apart. To minimize contributions from purely horizontal-traveling energy, the recorded acoustic signal of each channel was an average of 14 hydrophones located along the horizontal array [39]. Herein, receiving groups are referred to as elements or individual hydrophones for simplicity. A further discussion of receiver subtleties exists in Abadi and Freneau [40] or Diebold et al. [39]. The output of the receiver nearest to the source exhibited behavior (low amplitude) inconsistent with neighboring receivers, and thus was removed from the data analysis, so that = 635 for the purposes of this manuscript.
An array of 36 airguns, towed 240 m behind the ship at either 9 m (used here) or 15 m depth [41], was used as a single directional acoustic source with a total volume of 6600 cubic inches. The wideband impulsive signal was preferentially broadcast toward the ocean floor and contained frequency content from below 10 Hz to above 200 Hz. The ship towed the airgun and receiving arrays at 4.5 knots along 11 separate transects, during which the airgun array was fired approximately every 50 m while the receiving array recorded for 16.384 s with a 500 Hz sampling rate. The timing of the source broadcasts and receiving array recording window provided ample time to record direct-path and multiple-reflected-path sounds at both the closest and furthest receivers. For the present study, the direct path is time-gated out and replaced with zeros in the time domain to emphasize reflected-path coherence. Further, no corrections for ship motion during the data recording interval were made in the data processing.
Figure 1a shows the layout of the experiment, with solid bold lines indicating each of the 11 transects. For the current study, data from the primarily shore-parallel transect number 10 (indicated in Figure 1a by a white arrow) were used, since the depth variation along this track was the smallest of the 11 available and the number of usable signal samples was far greater than the other primarily shore-parallel transect, number 11. Figure 1b shows the bathymetry of transect 10, which was traversed from north to south. To ensure array curvature and significantly distinct bathymetry did not influence the results, the first 200 and the last 483 airgun signal pulses along this track were not used in the analysis. The airgun was powered down for an additional 172 pulses due to marine life in the area. Hence, of the total 1684 airgun pulses on this transect, 829 pulses were utilized here in this study. These data were collected on July 22, 2012, between 01:30:30 and 07:57:23 Greenwich Mean Time (GMT). The ship location, shown in Figure 1b, traversed 50 km from the first (10 km) to the last (60 km) analyzed signal pulses. The average water depth along the analyzed portion of the transect was slightly more than 1.9 km and varied by less than 200 m from this value.
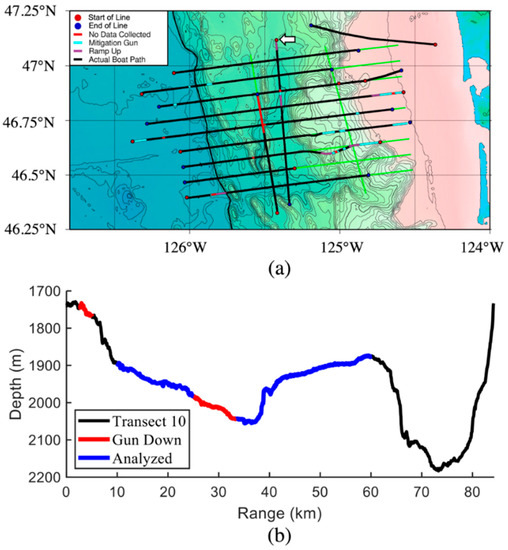
Figure 1.
(a) Layout of the COAST experiment from Holbrook et al. [29], conducted off the coast of Washington state in July 2012. Each line represents the ship’s path while towing an ~8 km streamer with 636 receivers spaced 12.5 m and a source array of 36 airguns at 4.5 knots. The white arrow indicates the beginning of the analyzed transect. Data were collected by coordinated firing of the airgun array approximately every 50 m and recording for 16.384 s. (b) The bathymetry of transect 10 is shown here as a function of the ship location with blue indicating the ship location for the analyzed signal pulses.
The airgun array was designed so that acoustic energy was primarily directed towards the ocean floor. Figure 2 shows a range–depth schematic with the nominal horizontal and vertical dimensions, corresponding to the experimental data used here. The bottom-reflected (solid line) and bottom-surface-reflected (dashed line) propagation paths to a single receiver are shown. These two paths convey most of the signal energy from the airgun array to the receivers. Although the nominal bathymetric depth is known along the transect, the actual reflection of bottom-reflected sound may include contributions from below the bathymetric depth. Reflection strength and phase is dependent on the geoacoustic properties of the ocean bottom and may contribute to coherence loss in the recorded sound along with the noted variations in bathymetry. As the receiving array was towed along transect 10, additional reductions in measured coherence arose from the varying bathymetry, ocean floor and surface roughness, and other propagation fluctuations along these paths.
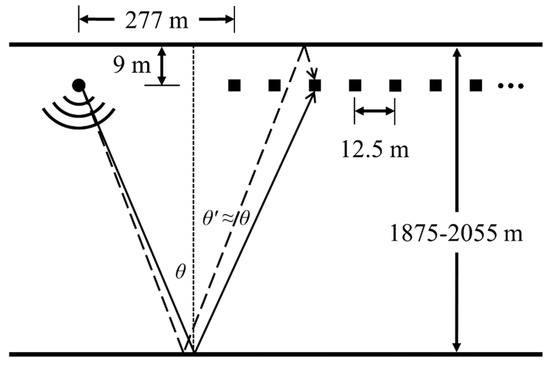
Figure 2.
The approximate layout of COAST 2012 transect 10. The solid circle indicates the airgun array. The solid squares indicate receivers. The first bottom reflection (solid line) and bottom-surface reflection (dashed line) account for most of the signal energy recorded by each receiver of the array.
Figure 3a shows a waterfall plot of the receiver array output for one signal pulse taken at 06:36:16 GMT (only every 10th recorded waveform is shown for clarity), when the depth at the ship was roughly 1906 m. Here, receiver number 1 is closest to the airgun array and receiver number 635 is furthest from it. The strong signal arriving at the various receivers between 2.5 and 6.0 s is the first bottom reflection. A second bottom reflection and a faint third reflection are also evident in the recordings. The direct path is visible in the measurements of the nearest 50 receivers as a small-amplitude pulse arriving before the prominent reflections. Due to the absence of significant direct-path energy further along the array, a half-second time-gate is applied herein to remove the expected direct-path arrival at all receivers. Spectrograms for receivers 1 and 635 of the field sample in Figure 3a are shown with a 256 ms Hamming window and 128 ms window overlap in Figure 3b and Figure 3c, respectively. In the spectrogram for the closest receiver, the first reflected path is visible (uneven red vertical stripe) near 2.5 s, followed by several bottom reflections with a time spacing of 2.5–3 s. For the farthest receiver, two bottom reflections are clearly apparent, with a possible third path indicated as well. In both spectrograms, the vertical blue bars are the result of the time-gated direct path.
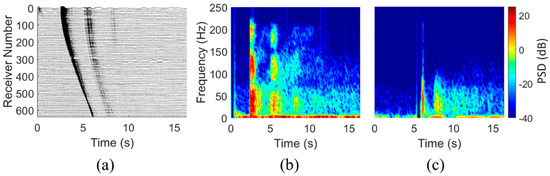
Figure 3.
(a) Waterfall plot showing the time-series output of every 10th receiver for the ping recorded at 06:36:16 GMT on 22 July 2012. Spectrogram outputs with time-gated direct path, 256 ms Hamming window and 128 ms window overlap for the receivers closest to (b) and furthest from (c) the source.
The spectrograms demonstrate that substantial signal energy exists across most of the available frequency range, with noise being more prominent at lower frequencies. Additional dips in signal amplitude are apparent in Figure 3b around 80 and 160 Hz. Spectrograms from other positions along the array are similar, and show the variations expected with increasing source-to-receiver range and variations in water column depth.
The dips in signal amplitude around 80 Hz and 160 Hz in Figure 3b are predictable based on the experimental geometry and receiving array depth below the pressure-release ocean surface. Upward-propagating sea-floor-reflected sound destructively interferes with downward-propagating sea-surface reflected sound in these frequency ranges, and this phenomenon causes variation in SNR across the frequencies of interest for this experiment. Figure 4 shows the measured SNR for the nearest receiver to the source (Figure 4a) and at a location halfway along the receiving array (Figure 4b) as a function of frequency. In Figure 4c, the SNR is indicated for all frequencies and receiving locations. The SNR was calculated for each receiver at each frequency, , as the average recorded signal variance, , divided by the average noise variance, , for the 829 airgun pulses:
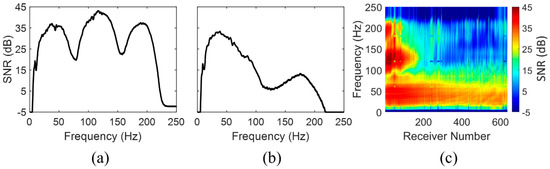
Figure 4.
Signal-to-noise ratio (SNR) from (15) for the closest receiver (a) and halfway along the receiving array (b) for 829 signal pulses. SNR, plotted against both receiver number and frequency, is shown in panel (c). The dips in SNR, particularly for the nearest receiver, occur at the frequencies predicted for destructive interference of upward- and downward-propagating sounds at the depth of the receiver array.
The ‘’ within the logarithm ensures that tends to the appropriate limit when the recorded complex field amplitudes, , which contain signal and noise, become increasingly dominated by noise. Additionally, each value in Figure 4 was averaged over multiple frequency samples with a 1 Hz sliding window to increase smoothness. To evaluate (15), the complex field amplitudes, , were determined from a 1.5 s time segment within each recording that started at the beginning of the first bottom reflection’s arrival, while the noise-only amplitudes, , were determined from a 1.5 s time segment at the end of each recording when no signal was apparent.
The dips in SNR seen in Figure 4, particularly for the closest receiver, occur at the frequencies expected to produce destructive interference between bottom-reflected upward-propagating sound and bottom-surface-reflected downward-propagating sound for the COAST 2012 experimental geometry. A reduction in coherence length is expected at these SNR dips as well. In addition, the SNR drops below 0 dB for frequencies below roughly 5 Hz. Thus, at the lowest frequencies considered here, the genuine field’s coherence is obscured by noise. A notable comparison between Figure 4a,b is the prominence of the first major dip. For the further receiver, this SNR dip occurs at a frequency that is approximately 35 Hz higher than that for the close receiver and is much less prominent. This SNR–dip frequency variation arises from propagation angle variations in the experimental geometry that occur as receiver range increases. Additionally, in Figure 4c, the following receivers have been removed for poor SNR: 47, 53, 75, 188, 287, 415, 495, 539, 544, 606, and 626, resulting in = 624 herein. This noise contamination was discussed in the cruise report, with most of these specific receivers identified as problematic for a different transect [29].
3. Results
3.1. Coherence
The coherence was calculated from the frequency domain data of COAST 2012 transect 10, as described in Section 2. Given that the results for in-band, frequency-difference, and frequency-sum coherence all come from exactly the same data, and that comparisons are the primary topic of this manuscript, no geometrical or environmental corrections based on the known experimental parameters were made to improve or alter any of the measured coherences. Furthermore, no signal-spectrum adjustments or frequency-dependent sea floor reflection coefficient corrections were made to the data or the replicas. In all cases, the nearest receiver was used as the reference receiver. Additional reference receivers and reference receiver coherence averaging was not included, but similar results are expected if other reference receivers are chosen. Based on the sampling rate and time record duration, each signal pulse nominally provides 0.061 Hz frequency resolution. Herein, unless otherwise noted, the closest resolved frequency to the specified integer frequency was considered.
For simplicity and consistency, the signal bandwidth limits were defined as = 10 Hz and = 200 Hz for all the results provided here. Thus, the bandwidth-averaged frequency-difference autoproduct calculated from (4) and (6) can probe difference frequencies from 0–190 Hz. Analogously, the frequency-sum autoproduct can achieve sum frequencies from 20–400 Hz. These three bandwidths overlap for 20–190 Hz, where coherences can be directly compared.
Figure 5 shows the three possible coherence curves for 60 Hz (Figure 5a), 80 Hz (Figure 5b), and 120 Hz (Figure 5c). The in-band coherence from (3) is shown in black, frequency-difference coherence from (8) in red, and frequency-sum coherence from (9) in blue. The confidence bounds from (10) and (11) are shown as semitransparent regions of the same color surrounding each coherence curve. The horizontal axis for all panels is the scaled receiver spacing, , with limits of 0 and 40 wavelengths. Wavelengths were computed from the given frequency and a reference sound speed (1480 m/s) determined from the average of the sound speed profiles recorded during the transect. The vertical axes are bounded from 0 to 1 and the horizontal dotted black line indicates the coherence length threshold. Figure 5b,c correspond to frequencies expected to exhibit destructive interference for the acoustic field and the autoproduct, respectively.
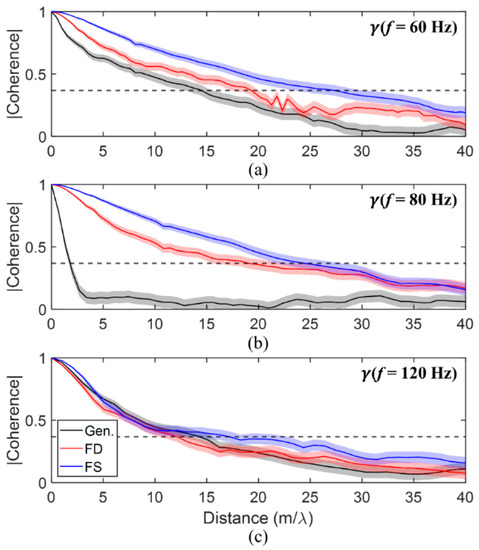
Figure 5.
Coherence vs. distance (normalized by wavelength) comparison for frequencies obtainable by all three fields. The genuine in-band field is shown in black, the frequency-difference autoproduct is shown in red, and the frequency-sum autoproduct is shown in blue. The horizontal dotted black line is the threshold value for coherence length. Confidence intervals estimated from (10) and (11) are indicated as semitransparent regions, and the frequency used is displayed in the upper right of each panel for 60 Hz (a), 80 Hz (b), and 120 Hz (c).
The three panels in Figure 5 indicate that more coherence may be available from the autoproduct when the genuine field and both autoproducts can all be obtained at the same frequency. At 60 Hz, displayed in Figure 5a, the frequency-difference and frequency-sum autoproduct coherence exceeds the genuine field coherence by more than the estimated uncertainty. At 80 Hz, displayed in Figure 5b, the destructive interference pattern discussed in Section 2 significantly decreases the in-band field’s coherence, but for the frequency-difference (frequency-sum) autoproduct, significant coherence is maintained for a horizontal receiver separation of nearly 20 (25). This occurs because the quadratic character of the autoproducts causes them to respond to the ocean surface’s pressure-release boundary as if it were a hard boundary (see [20]). As a result, destructive interference occurs for autoproducts at 120 Hz, which is shown in Figure 5c. Interestingly, the effect of the destructive interference on the autoproducts’ coherence is not as significant and can be attributed to the benefits of the bandwidth averaging in (6) and (7). Within uncertainties, all three fields exhibit similar coherences at this frequency.
Either the frequency-difference or the frequency-sum autoproduct shares a bandwidth with the genuine acoustic field in two other regions. Difference frequencies from 10–19 Hz and sum frequencies from 191–200 Hz overlap with the signal bandwidth. Figure 6 compares the genuine acoustic coherence to autoproduct coherence for 19 Hz (Figure 6a) and 191 Hz (Figure 6b). Again, the coherence determined from the genuine acoustic field is shown in black, the frequency-difference autoproduct in red, and the frequency-sum autoproduct in blue. The confidence bounds are again indicated as semitransparent regions. For 19 Hz, the curves shown in Figure 6a indicate that the frequency-difference autoproduct provides a significantly greater coherence for 5 to 35. For the 191 Hz curves shown in Figure 6b, the frequency-sum autoproduct coherence and the acoustic field coherence are nearly identical. This is similar to the results shown in Figure 5c, as 191 Hz is expected to exhibit destructive interference for the frequency-sum autoproduct.
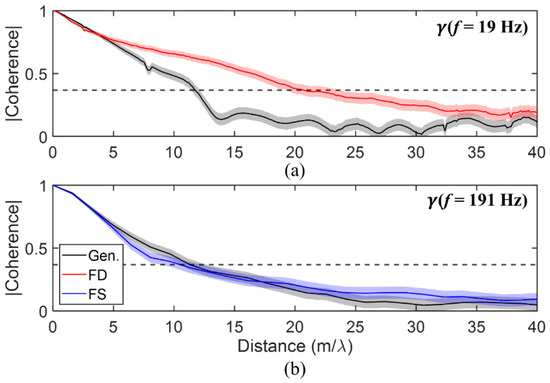
Figure 6.
Coherence vs. distance (normalized by wavelength) comparison for frequencies within the signal bandwidth and obtainable by either the frequency-difference or frequency-sum autoproduct. Results for the genuine in-band field are shown in black, results for the frequency-difference autoproduct are shown in red, and results for the frequency-sum autoproduct are shown in blue. The horizontal dotted black line is the threshold value for coherence length. Confidence intervals determined from (10) and (11) are indicated as semitransparent regions, and the frequency is displayed in the upper right of each panel for 19 Hz (a) and 191 Hz (b).
Finally, the autoproduct constructions allow for coherence calculation at frequencies both below and above the recorded signal bandwidth. For the data used here, the frequencies available to the frequency-difference (frequency-sum) autoproduct but unavailable to the in-band field are 1–9 Hz (201–400 Hz). Notably, the frequency-sum autoproduct provides coherence results above the signal bandwidth and above the Nyquist frequency limit (250 Hz) dictated by the experimental sampling rate. Coherence curves for two such frequencies, 1 Hz and 315 Hz, are shown in Figure 7a,b. The vertical axes are bounded from 0 to 1. The wavelength-scaled receiver-spacing horizontal axis in Figure 7a spans the entire 8 km receiving array, while the horizontal axis of Figure 7b is limited to 40. Hence, for sufficiently low difference frequencies, the frequency-difference autoproduct is coherent along the entire receiving array, even if the constituent fields were not coherent themselves. Additionally, the frequency-sum autoproduct is coherent across a significant number of wavelengths, even at sum frequencies exceeding the Nyquist limit for the genuine acoustic field.
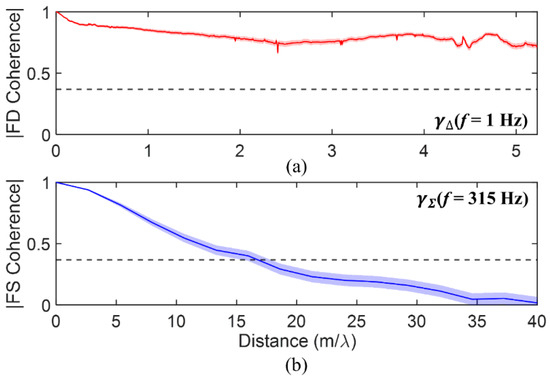
Figure 7.
Coherence vs. distance (normalized by wavelength) comparison for frequencies obtainable only by the frequency-difference or frequency-sum autoproduct. The frequency-difference autoproduct is shown in red in (a) and the frequency-sum autoproduct is shown in blue in (b). The horizontal dotted black line is the threshold value for coherence length. Confidence intervals using (10) and (11) are indicated as semitransparent regions, and the frequency used is displayed in the upper right of each panel.
3.2. Coherence Length
As described in Section 2, in-band, frequency-difference, and frequency-sum coherence lengths, , , and , were determined from identifying the length from the measured coherences, , , and , respectively. Although the experiment provides a 0.061 Hz frequency resolution, coherence lengths as functions of cyclic frequency () are reported here in 1 Hz increments. This was accomplished by averaging the coherence lengths for all resolved frequencies that round to the same integer-Hz frequency value. The upper and lower confidence-interval bounds of (10) and (11) (shown in Figure 5, Figure 6 and Figure 7) were processed analogously to the mean coherences to provide confidence bounds on the coherence lengths at each resolved frequency. These upper and lower confidence bounds were then combined to produce an average bound for integer-Hz-averaged coherence lengths [42].
Complete results for the three coherence lengths (divided by the nominal wavelength) are plotted vs. frequency in logarithmic coordinates in Figure 8. Here, black dots indicate , red dots indicate , blue dots indicate , and the dashed black line represents the receiving array length. The error bars, shown between 5 Hz and 20 Hz for the three coherence lengths, represent the 95th percentile of the integer-Hz confidence-interval bounds.
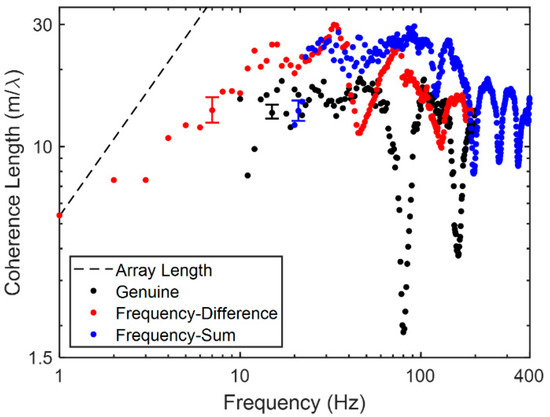
Figure 8.
Coherence length (normalized by wavelength) vs. frequency comparison for the genuine and autoproduct fields on logarithmic axes. Genuine acoustic field coherence lengths are indicated by black dots for = 10–200 Hz while frequency-difference (-sum) coherence lengths are displayed in red (blue) for = 1–190 Hz ( = 20–400 Hz). The receiving array length is indicated by a dashed black line and nominal error bars representing the 95th percentile for each data type are indicated between 5 and 20 Hz.
For the in-band frequency range (10 to 200 Hz), both autoproduct coherence lengths generally exceed that of the in-band field and are less suppressed at the coherence dips seen at frequencies corresponding to destructive interference at the array depth. When averaged through their respective frequency ranges (provided in parentheses), the frequency-difference autoproduct’s coherence length is 16.7 wavelengths (1 Hz 190 Hz), the genuine field’s coherence length is 12.0 wavelengths (10 Hz 200 Hz), and the frequency-sum autoproduct’s coherence length is 17.6 wavelengths (20 Hz 400 Hz). In the below-band (1 Hz 10 Hz) and above-band (200 Hz 400 Hz) frequency ranges, where the in-band coherence is either based on noise or cannot be calculated, the autoproducts provide coherence lengths of 5 to 18 wavelengths. Taken together, these results strongly suggest that the autoproducts might enhance coherent array signal processing when they can be calculated at in-band frequencies, and that they can extend coherent array signal processing to out-of-band frequencies. As a final note, at the lowest difference frequency, 1 Hz, the coherence length is compromised by the finite length (8 km) of the COAST 2012 array, as the coherence does not dip below the threshold.
As mentioned previously, the coherence length dips seen in the various curves on Figure 8 are caused by destructive interference of upward- and downward-traveling sound at the depth of the receiving array. However, the frequencies of these dips differ between the genuine field and the autoproducts because of the modified boundary condition arising from the autoproducts’ construction [20]. In addition, the depth of these coherence length dips is reduced for the autoproducts because they benefit from the bandwidth averaging specified in (6) and (7) that does not appear in (1). A related phenomenon causes the coherence lengths from the lowest sum frequencies, near 20 Hz, to be reduced due to the minimal frequency averaging available from (7) in that sum frequency range.
For comparative purposes, an overview of coherence length results from several experiments is provided in Table 1. This summary highlights the variability in the environments, experiments, and geometries in which coherence length has been studied. As a result of this variation, measured coherence lengths differ substantially across these studies, from less than 10 wavelengths to over 400. All of these results utilize sub-1 kHz signals, and some utilize frequencies or frequency ranges that overlap with the frequency range considered in this study. Both shallow and deep ocean results are provided, typically using horizontal line arrays (HLAs). Several notable differences exist between these experiments and the COAST 2012 experiment, inhibiting a direct comparison. First, the horizontal distance between the source and the receiving elements is generally much shorter in the COAST 2012 experiment, ranging from 277 m to over 8 km, while in the experiments summarized in Table 1, much larger ranges were often investigated. Second, no experiments summarized in this table were designed such that a near-surface source was broadcasting sound towards the ocean floor to measure the reflected path, which is expected to have significant impact on coherence length results. Third, the COAST 2012 experiment utilized a towed array, meaning the physical location of each snapshot was different, which is only true for one of the referenced results in Table 1. Interestingly, even though these experiments differ substantially from COAST 2012, many of these studies provide coherence lengths of the same order as those obtained here, with the experimental and environmental differences likely accounting for much of the coherence length differences.

Table 1.
Summary of coherence lengths from a collection of other studies.
3.3. Extension to Matched-Field Processing
MFP is a well-known array signal processing technique for remote unknown source localization that is beneficially impacted by increased coherence length. Thus, it was chosen to illustrate the extended coherence afforded by the autoproducts. The results provided in the prior subsections suggest that the autoproducts typically provide longer coherence lengths than in-band fields, while also providing useful coherence at above- and below-band frequencies. Therefore, the autoproducts may also provide a way to improve signal processing outcomes at low-coherence and low-SNR frequencies within and outside the signal bandwidth. However, the COAST 2012 experiment was not designed as a spatial coherence or source localization experiment; thus, some adjustments to the standard MFP implementation are needed. Nevertheless, the results presented here illustrate the benefits of the greater coherence possible with the autoproducts, particularly outside of the ordinary field’s bandwidth.
To properly implement MFP within the COAST 2012 experimental scenario, the replica weight vector specified in (12)–(14) must account for the bottom-reflected and bottom-surface-reflected arrivals, as well as the endfire location of the source with respect to the nominally straight and horizontal array. The weight vector used herein took the following form:
where is the search coordinate in range from the endfire array, is the bottom-reflected distance at receiver from a source at , is the bottom-surface-reflected distance at receiver from a source at , and the negative (positive) surface reflection coefficient is chosen for in-band (out-of-band) MFP. Here, the reflected-path distances are calculated by using the depth of the ocean at the location of the tow vessel, which may not be the ocean depth where the acoustic reflection occurs, so (16) introduces some mismatch. The and amplitude factor specified in (16) could have been changed to and when correlating with the autoproducts to compensate for their quadratic nature, but this change was not made for simplicity.
The final adjustment made to the standard MFP processor is a coherent average over five pings. Hence, replaces in (12) and the reflected-path distances in (16) are calculated from the average depth at tow vessel for the five pings. Equations (13) and (14) are adjusted identically for the frequency-difference and frequency-sum autoproducts. Although coherent ping-averaging is uncommon, its implementation here directly reflects the coherence formulation defined in Section 2.
The MFP plots for single frequencies utilize an illustrative set of five pings sampled throughout the duration of the transect: 271, 777, 872, 1065, and 1183. The first set of results are for the in-band frequency of 80 Hz. At this frequency, three receivers reside within the coherence length of the genuine field. Meanwhile, 29 and 37 receivers reside within coherence lengths of the frequency-difference and frequency-sum autoproduct coherence lengths, respectively. MFP results are shown in Figure 9a for the genuine field in black, the frequency-difference autoproduct in red, and the frequency-sum autoproduct in blue. The plotted curves show the MFP output vs. search range (distance) at the depth of the source along the line of the array. The vertical dashed black line indicates the true source range. The results directly reflect the improved coherence of the autoproducts. Both the frequency-difference and frequency-sum approaches exhibit good source range estimation, whereas the three-receiver MFP approach of the in-band field is unable to confidently localize the source. Meanwhile, in Figure 9b, the number of receivers included in the calculation for each field is 37. As expected, increasing the number of receivers significantly beyond the genuine field’s coherence length results in spurious peaks, while the autoproduct-based results are largely unchanged.
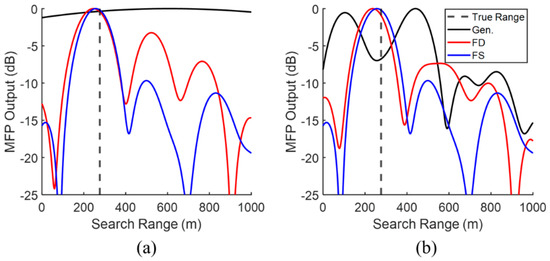
Figure 9.
Matched-field processing results at 80 Hz for all three fields at the depth of the source along the line of the array. The genuine in-band field is shown in black, the frequency-difference autoproduct is shown in red, and the frequency-sum autoproduct is shown in blue. The vertical dashed black line indicates the true source range. (a) MFP calculations include receivers informed by each field’s coherence length; (b) MFP calculations include receivers informed by the maximum coherence length.
The second set of MFP results are for frequencies below and above the signal bandwidth. Figure 10 shows frequency-difference MFP at 5 Hz and frequency-sum MFP at 315 Hz for the same set of pings. Both approaches exhibit good source range estimation, even though neither frequency was in the original broadcast signal’s bandwidth. Further, the difference in the widths of the main lobes of each approach supports the unconventional claim that the frequency-difference and frequency-sum autoproducts are coherent at below- and above-band frequencies, respectively.
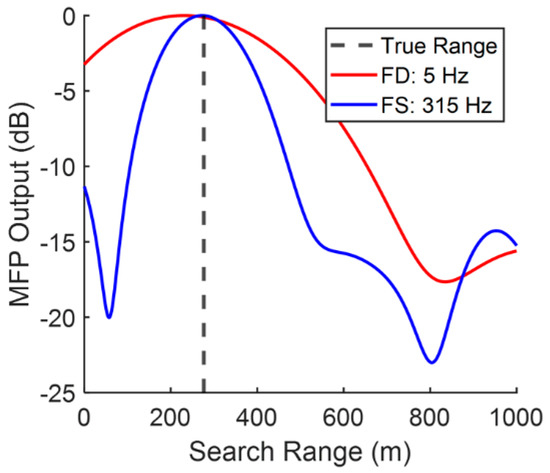
Figure 10.
Matched-field processing results as in Figure 9 for frequencies outside of the signal bandwidth. The vertical dashed black line indicates the true source range. The frequency-difference autoproduct at 5 Hz is shown in red, while the frequency-sum autoproduct at 315 Hz is shown in blue.
In-band, frequency-difference, and frequency-sum source range estimates were determined at each frequency by identifying the maximum MFP output across the search coordinates. Although there is 0.061 Hz frequency resolution in the experiment, only the closest resolved frequency to each integer frequency is considered for simplicity. This calculation was conducted for 100 randomly selected five-ping ensembles. Source range estimates within 100 m of the true target are deemed successful, and the success fraction across the 100 trials is recorded in Figure 11. Here, black dots indicate the in-band success fraction, red dots indicate the frequency-difference success fraction, and blue dots indicate the frequency-sum success fraction. In all cases, the MFP calculations include receivers informed by the maximum coherence length across the three methods.
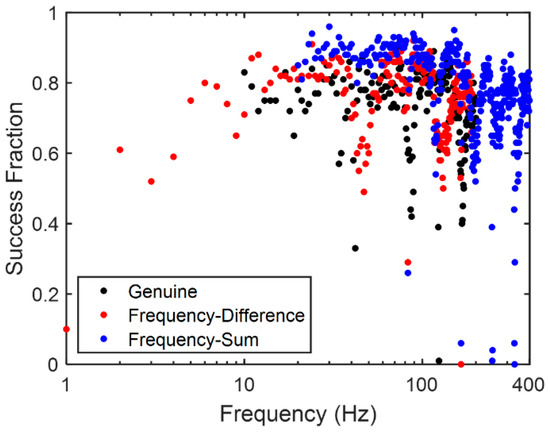
Figure 11.
Source range estimation success fraction (across 100 trials) vs. frequency comparison for the genuine and autoproduct fields on logarithmic horizontal axes. Genuine acoustic field success fractions are indicated by black dots for = 10–200 Hz while frequency-difference (-sum) coherence lengths are displayed in red (blue) for = 1–190 Hz ( = 20–400 Hz).
The complete results support the coherence length findings shown in Figure 8. For the frequencies obtainable by all three methods (20 to 190 Hz), frequency-difference and in-band field approaches perform similarly, and frequency-sum outperforms them both. Within this frequency range, the frequency-difference autoproduct’s average success fraction was 0.76, the genuine field’s average success fraction was 0.74, and the frequency-sum autoproduct’s average success fraction was 0.84. Further, successful source range localization can be obtained at frequencies both below and above the signal bandwidth.
There exist a few unexpectedly low success fractions for the autoproducts in Figure 11. The poor localization at 1 Hz is directly attributed to the large main lobe widths that results from processing at very low frequencies. Additionally, the destructive interference of upward- and downward-traveling sound at the depth of the receiving array is reflected in the dips of the various curves in Figure 11, matching the coherence length dips in Figure 8. Interestingly, a few blue and red dots with low success fraction occur at 80 and 160 Hz, frequencies of constructive interference for autoproducts. Since the autoproducts are coherent at these frequencies, poor localization success suggests that the MFP processor could be improved by adjusting the weight vectors for autoproduct processing. Systematically altering the weight vectors is outside of the scope of the paper, but replica field adjustments have recently been undertaken to improve performance in long-range ocean source localization using autoproducts [28,43].
4. Discussion
Prior work has shown that autoproduct-based methods can be effective for mitigating array signal processing problems associated with array sparseness, unknown random scattering, and wavefront mismatch [31]. Given that such improvements require coherent fields, the goals of this investigation were to determine and compare the spatial coherences of the acoustic field, its frequency-difference autoproduct, and its frequency-sum autoproduct from ocean recordings collected on a north-to-south transect during the COAST 2012 experiment. In particular, this investigation considered 829 airgun pulses recorded by 624 receivers (nearly) uniformly spaced along an 8 km long horizontal array towed at a depth of 9 m, where the ocean depth was approximately 1.9 km. Variations in water depth, surface reflections, and acoustic propagation along the 50 km long tow path led to coherence loss between the first and any subsequent receiver along the array. The nominal frequency range of the airgun signals was 10 Hz to 200 Hz. Nevertheless, coherence results were obtained for frequencies from 1 Hz to 400 Hz, including a substantial range (20 to 190 Hz) where all three types of coherence and coherence lengths could be determined. The claims of coherence were then illustrated with a simple matched-field processing approach to source range estimation.
The work presented here supports five conclusions. First, the frequency-difference autoproduct has substantial coherence at frequencies below the signal band, where signal energy is insignificant, and noise dominates the recorded field. In the current investigation, the frequency-difference autoproduct provided coherence lengths of 5.4 to 30 difference frequency wavelengths, , for 1 Hz 190 Hz. Second, the frequency-sum autoproduct is similarly coherent at frequencies above the signal band and above the Nyquist frequency set by the sampling rate. In the current investigation, the frequency-sum autoproduct provided coherence lengths of 7.8 to 30 sum frequency wavelengths, , for 20 Hz 400 Hz. Third, destructive interference from surface reflections at the 9 m depth of the receiving array in the COAST 2012 experiment reduced coherence lengths for all three fields at predictable frequencies, but more modest coherence suppression occurred for the autoproducts. Fourth, the autoproducts maintained coherence at frequencies where the genuine field suffers from destructive interference and reduced coherence length. This happens because the quadratic nature of the autoproducts rectifies the ocean surface reflection coefficient so that the ocean surface appears as a rigid boundary, and this alters the autoproducts’ interference pattern at the COAST 2012 receiver depth. However, to successfully localize in these interference patterns, an alternate replica field scheme may be required in matched-field applications. Fifth, and perhaps most important, the coherence lengths of the autoproducts are generally greater than that of the corresponding genuine acoustic field from which they are derived and can support coherent array signal processing. In this investigation, the frequency-averaged coherence lengths were 12.0, 16.7, and 17.6 wavelengths for the genuine field, frequency-difference autoproduct, and frequency-sum autoproduct, respectively. The increased coherence lengths possible with the autoproducts are believed to result from utilizing the full signal bandwidth for frequency averaging to produce each autoproduct sample prior to determining coherence.
Author Contributions
Conceptualization, A.S.D. and D.R.D.; methodology, N.J.J., A.S.D., and D.R.D.; software, N.J.J. and A.S.D.; validation, N.J.J. and A.S.D.; formal analysis, N.J.J., A.S.D., and D.R.D.; investigation, N.J.J., A.S.D., and D.R.D.; resources, D.R.D.; data curation, N.J.J. and A.S.D.; writing—original draft preparation, N.J.J., A.S.D., and D.R.D.; writing—review and editing, N.J.J., A.S.D., and D.R.D.; visualization, N.J.J., A.S.D., and D.R.D.; supervision, D.R.D.; project administration, D.R.D.; funding acquisition, N.J.J. and D.R.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Office of Naval Research (ONR), grant number N00014-19-1-2459, and the US Department of Defense through the National Defense Science and Engineering Graduate (NDSEG) Fellowship.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The COAST 2012 [29] dataset can be accessed at https://www.marine-geo.org/tools/entry/MGL1212#datasets, accessed on 19 October 2020.
Acknowledgments
The authors would like to thank Shima Abadi for providing code to read the COAST 2012 data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Urick, R.J. Principles of Underwater Sound, 3rd ed.; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Heaney, K.D. Shallow Water Narrowband Coherence Measurements in the Florida Strait. J. Acoust. Soc. Am. 2011, 129, 2026–2041. [Google Scholar] [CrossRef] [PubMed]
- Carey, W.M.; Moseley, W.B. Space-Time Processing Environmental-Acoustic Effects. IEEE J. Ocean. Eng. 1991, 16, 285–301. [Google Scholar] [CrossRef]
- Carey, W.M. Determination of Signal Coherence Length Based on Signal Coherence and Gain Measurements in Deep and Shallow Water. J. Acoust. Soc. Am. 1998, 104, 831–837. [Google Scholar] [CrossRef]
- Cox, H. Line Array Performance When the Signal Coherence Is Spatially Dependent. J. Acoust. Soc. Am. 1973, 54, 1743–1746. [Google Scholar] [CrossRef]
- Morgan, D.R.; Smith, T.M. Coherence Effects on the Detection Performance of Quadratic Array Processors, with Applications to Large-Array Matched-Field Beamforming. J. Acoust. Soc. Am. 1990, 87, 737–747. [Google Scholar] [CrossRef]
- Baggeroer, A.B.; Kuperman, W.A.; Mikhalevsky, P.N. An Overview of Matched Field Methods in Ocean Acoustics. IEEE J. Ocean. Eng. 1993, 18, 401–424. [Google Scholar] [CrossRef]
- Rolt, K.D.; Abbot, P.A. Littoral Coherence Limitations on Acoustic Arrays. In Acoustical Imaging; Lees, S., Ferrari, L.A., Eds.; Springer: Boston, MA, USA, 1997; pp. 537–542. [Google Scholar]
- Wan, L.; Zhou, J.X.; Rogers, P.H.; Knobles, D.P. Spatial Coherence Measurements from Two L-Shape Arrays in Shallow Water. Acoust. Phys. 2009, 55, 383–392. [Google Scholar] [CrossRef]
- Finette, S.; Oba, R. Horizontal Array Beamforming in an Azimuthally Anisotropic Internal Wave Field. J. Acoust. Soc. Am. 2003, 114, 131–144. [Google Scholar] [CrossRef]
- Duda, T.F.; Collis, J.M.; Lin, Y.-T.; Newhall, A.E.; Lynch, J.F.; DeFerrari, H.A. Horizontal Coherence of Low-Frequency Fixed-Path Sound in a Continental Shelf Region with Internal-Wave Activity. J. Acoust. Soc. Am. 2012, 131, 1782–1797. [Google Scholar] [CrossRef]
- Lunkov, A.A.; Petnikov, V.G. The Coherence of Low-Frequency Sound in Shallow Water in the Presence of Internal Waves. Acoust. Phys. 2014, 60, 61–71. [Google Scholar] [CrossRef]
- Gorodetskaya, E.Y.; Malekhanov, A.I.; Sazontov, A.G.; Vdovicheva, N.K. Deep-Water Acoustic Coherence at Long Ranges: Theoretical Prediction and Effects on Large-Array Signal Processing. IEEE J. Oceanic Eng. 1999, 24, 156–171. [Google Scholar] [CrossRef]
- Andrew, R.K.; Howe, B.M.; Mercer, J.A. Transverse Horizontal Spatial Coherence of Deep Arrivals at Megameter Ranges. J. Acoust. Soc. Am. 2005, 117, 1511–1526. [Google Scholar] [CrossRef]
- Dowling, D.R.; Jackson, D.R. Coherence of Acoustic Scattering from a Dynamic Rough Surface. J. Acoust. Soc. Am. 1993, 93, 3149–3157. [Google Scholar] [CrossRef]
- Dahl, P.H. Forward Scattering from the Sea Surface and the van Cittert–Zernike Theorem. J. Acoust. Soc. Am. 2004, 115, 589–599. [Google Scholar] [CrossRef]
- Dahl, P.H. Observations and Modeling of Angular Compression and Vertical Spatial Coherence in Sea Surface Forward Scattering. J. Acoust. Soc. Am. 2010, 127, 96–103. [Google Scholar] [CrossRef]
- Berkson, J.M. Measurements of Coherence of Sound Reflected from Ocean Sediments. J. Acoust. Soc. Am. 1980, 68, 1436–1441. [Google Scholar] [CrossRef]
- Brown, D.C.; Brownstead, C.F.; Lyons, A.P.; Gabrielson, T.B. Measurements of Two-Dimensional Spatial Coher-ence of Normal-Incidence Seafloor Scattering. J. Acoust. Soc. Am. 2018, 144, 2095–2108. [Google Scholar] [CrossRef]
- Worthmann, B.M.; Dowling, D.R. The Frequency-Difference and Frequency-Sum Acoustic-Field Autoproducts. J. Acoust. Soc. Am. 2017, 141, 4579–4590. [Google Scholar] [CrossRef]
- Lipa, J.E.; Worthmann, B.M.; Dowling, D.R. Measurement of Autoproduct Fields in a Lloyd’s Mirror Environment. J. Acoust. Soc. Am. 2018, 143, 2419–2427. [Google Scholar] [CrossRef] [PubMed]
- Abadi, S.H.; Song, H.C.; Dowling, D.R. Broadband Sparse-Array Blind Deconvolution Using Frequen-cy-Difference Beamforming. J. Acoust. Soc. Am. 2012, 132, 3018–3029. [Google Scholar] [CrossRef] [Green Version]
- Abadi, S.H.; van Overloop, M.J.; Dowling, D.R. Frequency-Sum Beamforming in an Inhomogeneous Environment. In Proceedings of the Meetings on Acoustics ICA2013, Montreal, QC, Canada, 2–7 June 2013; Volume 19, p. 055080. [Google Scholar]
- Douglass, A.S.; Song, H.C.; Dowling, D.R. Performance Comparisons of Frequency-Difference and Conventional Beamforming. J. Acoust. Soc. Am. 2017, 142, 1663–1673. [Google Scholar] [CrossRef] [PubMed]
- Abadi, S.H.; Haworth, K.J.; Mercado-Shekhar, K.P.; Dowling, D.R. Frequency-Sum Beamforming for Passive Cav-itation Imaging. J. Acoust. Soc. Am. 2018, 144, 198–209. [Google Scholar] [CrossRef] [PubMed]
- Worthmann, B.M.; Song, H.C.; Dowling, D.R. High Frequency Source Localization in a Shallow Ocean Sound Channel Using Frequency Difference Matched Field Processing. J. Acoust. Soc. Am. 2015, 138, 3549–3562. [Google Scholar] [CrossRef] [PubMed]
- Worthmann, B.M.; Song, H.C.; Dowling, D.R. Adaptive Frequency-Difference Matched Field Processing for High Frequency Source Localization in a Noisy Shallow Ocean. J. Acoust. Soc. Am. 2017, 141, 543–556. [Google Scholar] [CrossRef]
- Geroski, D.J.; Dowling, D.R. Long-Range Frequency-Difference Source Localization in the Philippine Sea. J. Acoust. Soc. Am. 2019, 146, 4727–4739. [Google Scholar] [CrossRef] [PubMed]
- Holbrook, S.; Kent, G.; Keranen, K.; Johnson, P.; Trehu, A.; Tobin, H.; Caplan-Auerbach, J.; Beeson, J. COAST: Cascadia Open-Access Seismic Transects. In Proceedings of the AGU Fall Meeting Abstracts 2012, San Francisco, CA, USA, 3–7 December 2012; Volume 2012, pp. 11–12. [Google Scholar]
- Carter, G.C.; Knapp, C.H.; Nuttall, A.H. Statistics of the Estimate of the Magnitude-Coherence Function. IEEE Trans Audio Electroacoust. 1973, 21, 388–389. [Google Scholar] [CrossRef]
- Dowling, D.R. Revealing Hidden Information with Quadratic Products of Acoustic Field Amplitudes. Phys. Rev. Fluids 2018, 3, 110506. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Engineering Applications of Correlation and Spectral Analysis; Wiley and Sons: New York, NY, USA, 1980. [Google Scholar]
- Carter, G.C. Coherence and Time Delay Estimation. Proc. IEEE 1987, 75, 236–255. [Google Scholar] [CrossRef]
- Wang, S.Y.; Tang, M.X. Exact Confidence Interval for Magnitude-Squared Coherence Estimates. IEEE Signal Process. Lett. 2004, 11, 326–329. [Google Scholar] [CrossRef]
- Zoubir, A.M. On Confidence Intervals for the Coherence Function. In Proceedings of the ICASSP, IEEE International Conference Acoustics, Speech, and Signal Process, Philadelphia, PA, USA, 23 March 2005; Volume 4. [Google Scholar]
- Bucker, H.P. Use of Calculated Sound Fields and Matched-Field Detection to Locate Sound Sources in Shallow Water. J. Acoust. Soc. Am. 1976, 59, 368–373. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Hotkani, M.M.; Bousquet, J.F.; Seyedin, S.A.; Martin, B.; Malekshahi, E. Underwater Target Localization Using Opportunistic Ship Noise Recorded on a Compact Hydrophone Array. Acoustics 2021, 3, 611–629. [Google Scholar] [CrossRef]
- Diebold, J.B.; Tolstoy, M.; Doermann, L.; Nooner, S.L.; Webb, S.C.; Crone, T.J. R/V Marcus G. Langseth Seismic Source: Modeling and Calibration. Geochem. Geophys. Geosyst. 2010, 11, Q12012. [Google Scholar] [CrossRef]
- Abadi, S.H.; Freneau, E. Short-Range Propagation Characteristics of Airgun Pulses during Marine Seismic Reflection Surveys. J. Acoust. Soc. Am. 2019, 146, 2430–2442. [Google Scholar] [CrossRef] [PubMed]
- Tolstoy, M.; Diebold, J.; Doermann, L.; Nooner, S.; Webb, S.C.; Bohnenstiehl, D.R.; Crone, T.J.; Holmes, R.C. Broadband Calibration of the R/V Marcus G. Langseth Four-String Seismic Sources. Geochem. Geophys. Geosyst. 2009, 10, Q08011. [Google Scholar] [CrossRef]
- Taylor, J.R. An Introduction to Error Analysis, 2nd ed.; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Geroski, D.J.; Dowling, D.R. Robust Long-Range Source Localization in the Deep Ocean Using Phase-Only Matched Autoproduct Processing. J. Acoust. Soc. Am. 2021, 150, 171–182. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).