Dual-Axis MEMS Resonant Scanner Using 128∘Y Lithium Niobate Thin-Film
Abstract
:1. Introduction
2. Principle and Structure
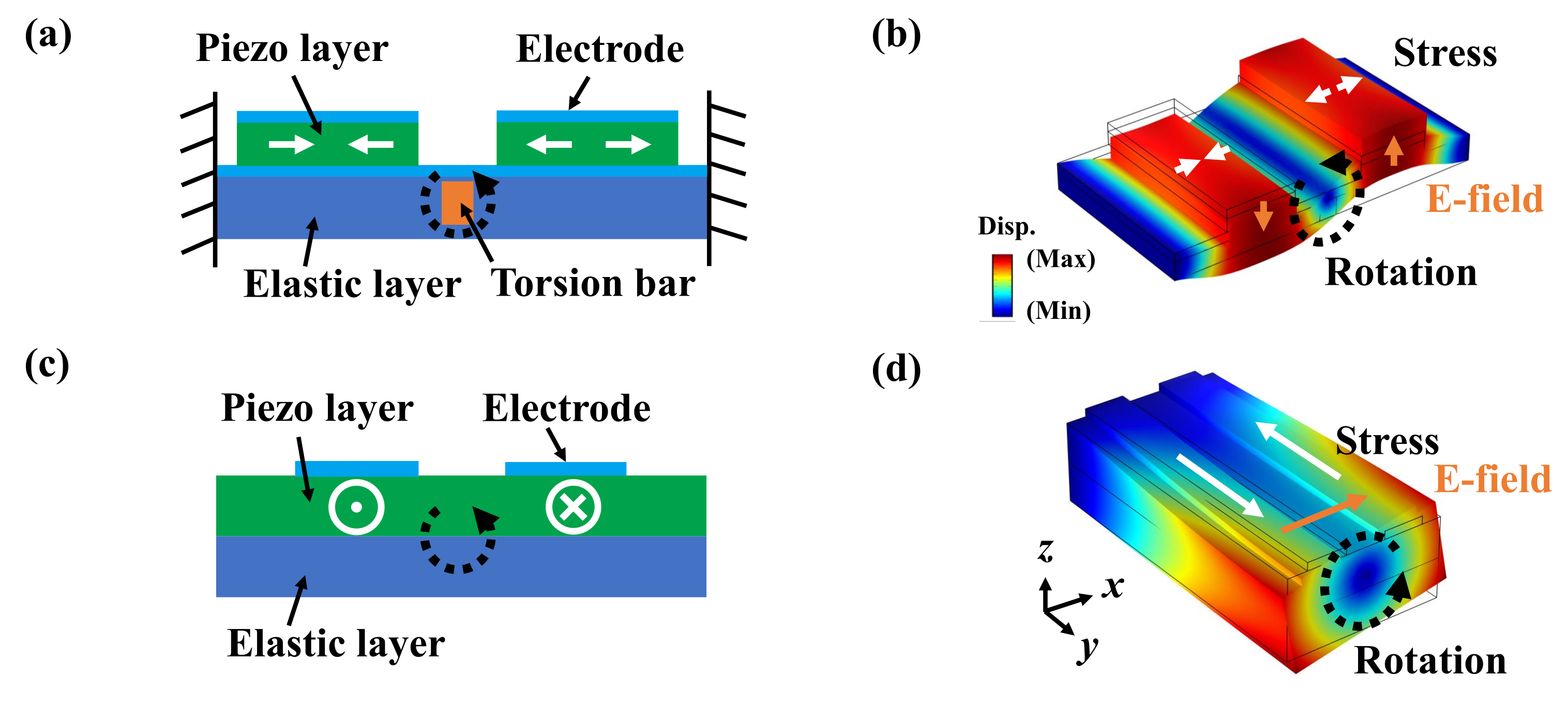
2.1. Principle of Torsional Actuator
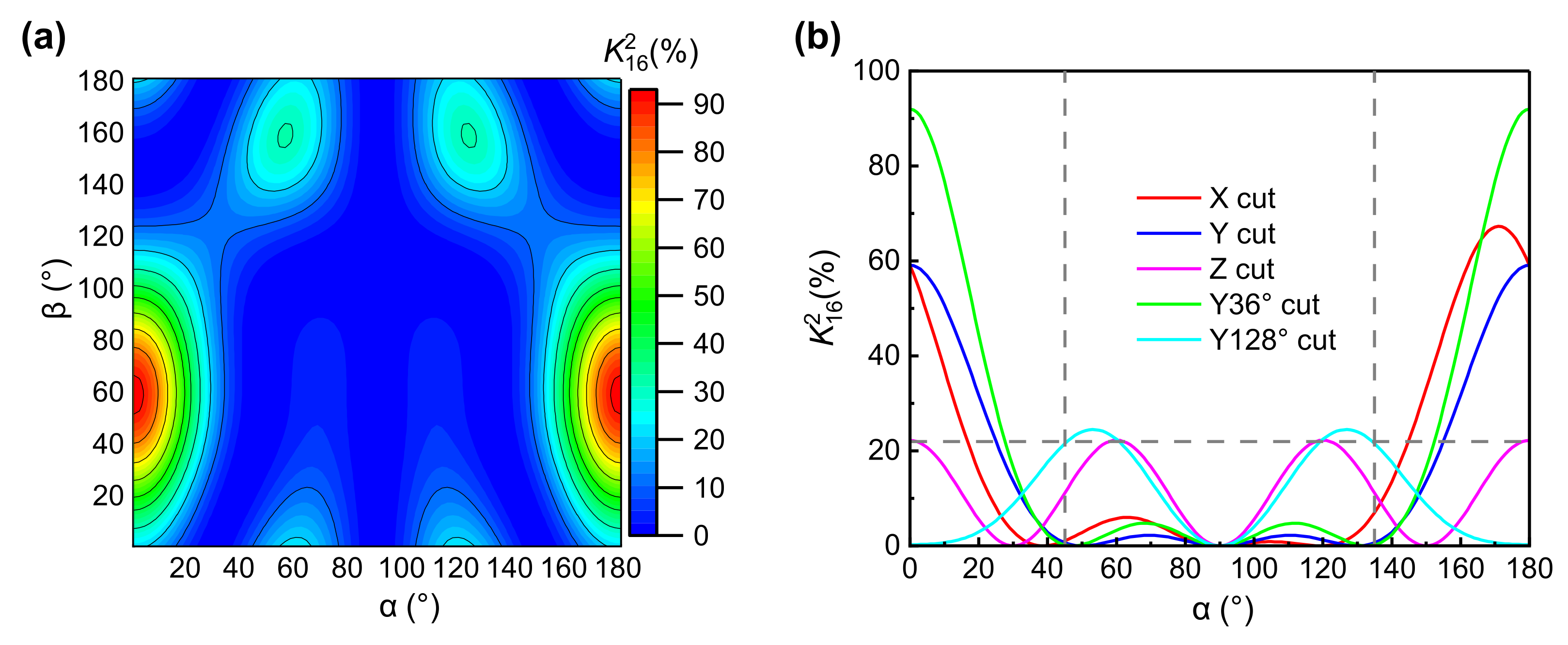
2.2. Euler Angle for LN
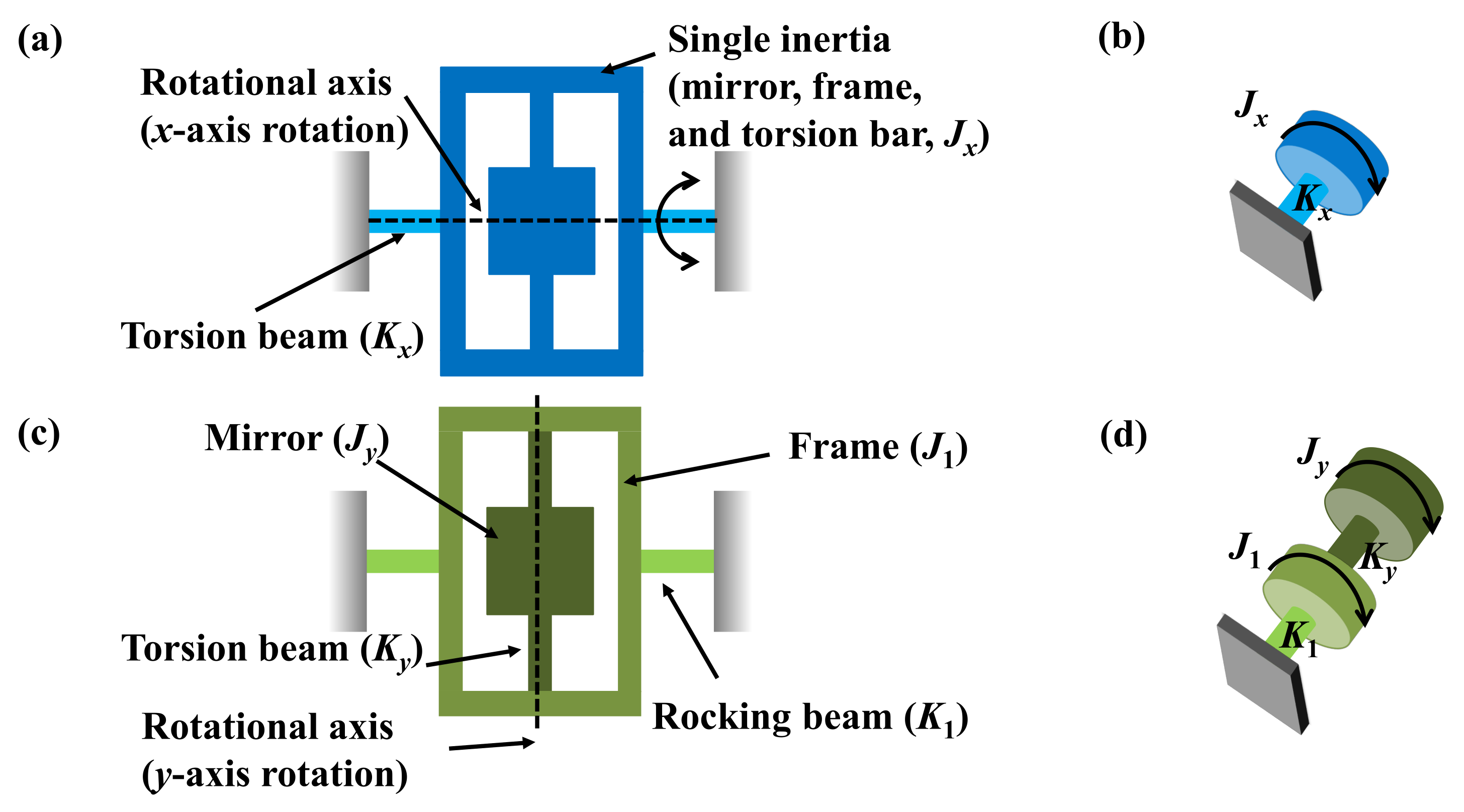
2.3. Structure
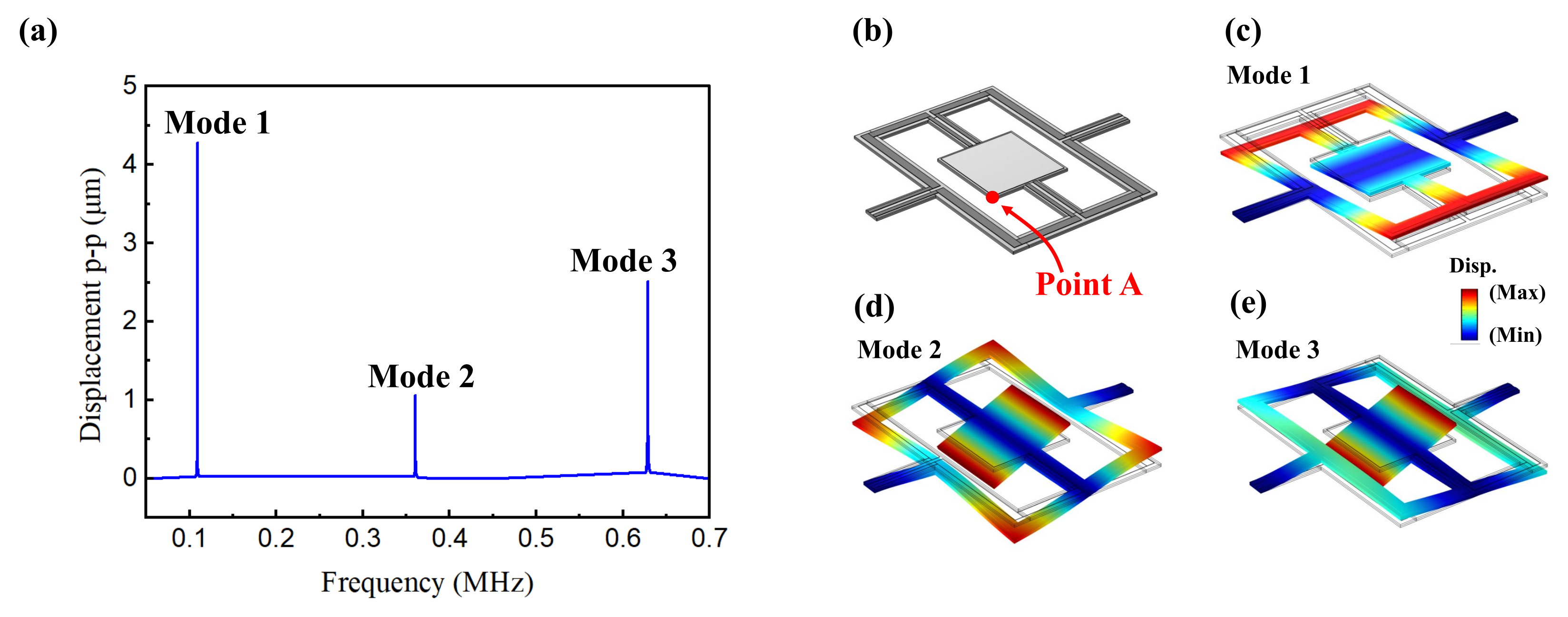
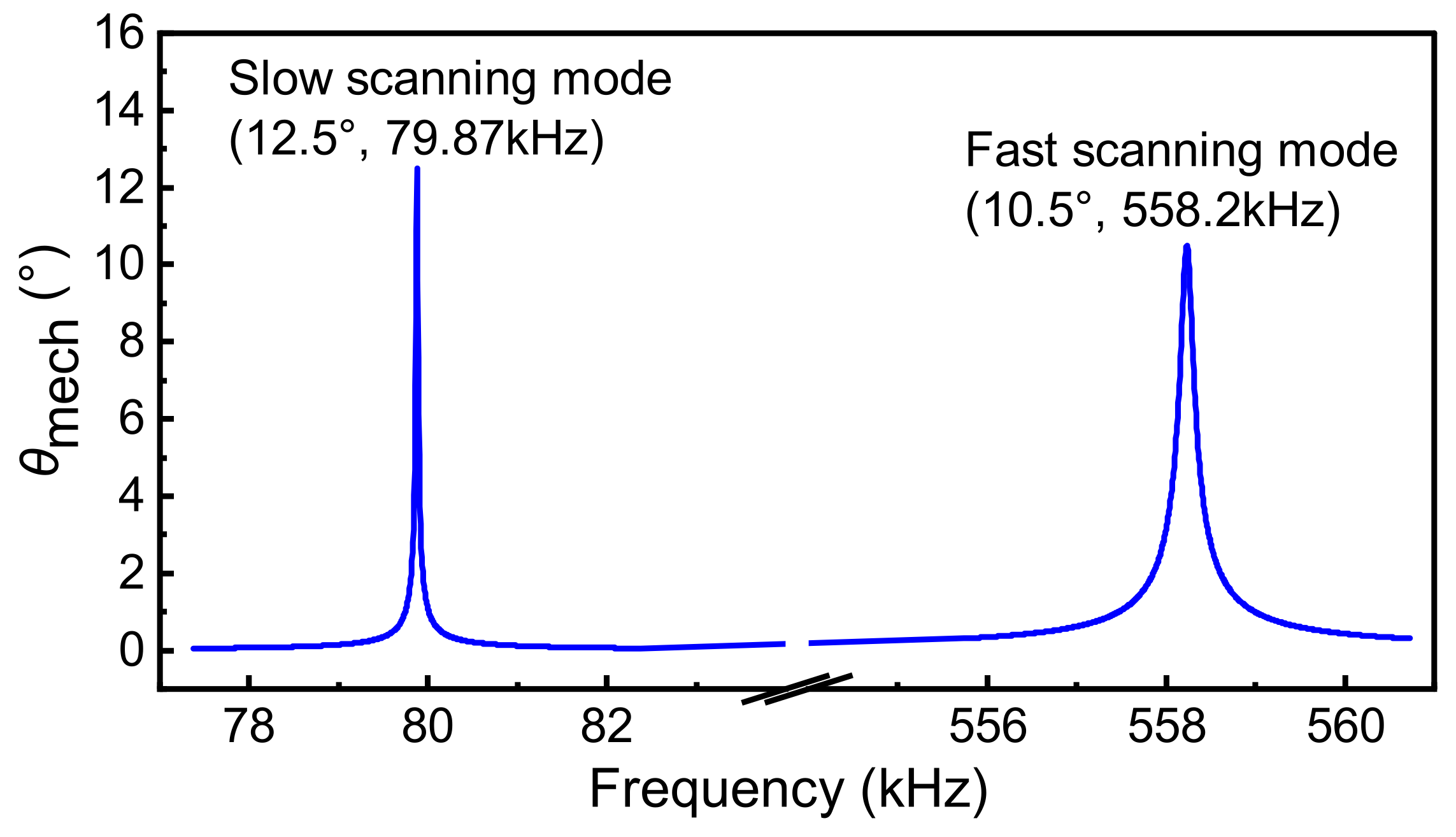
2.4. Frequency Response and Mode Shapes
3. Analytical Modeling
3.1. Resonant Frequency
3.2. Angular Deflection
3.3. Figure of Merit
4. Simulation Results
4.1. Simulation Setup
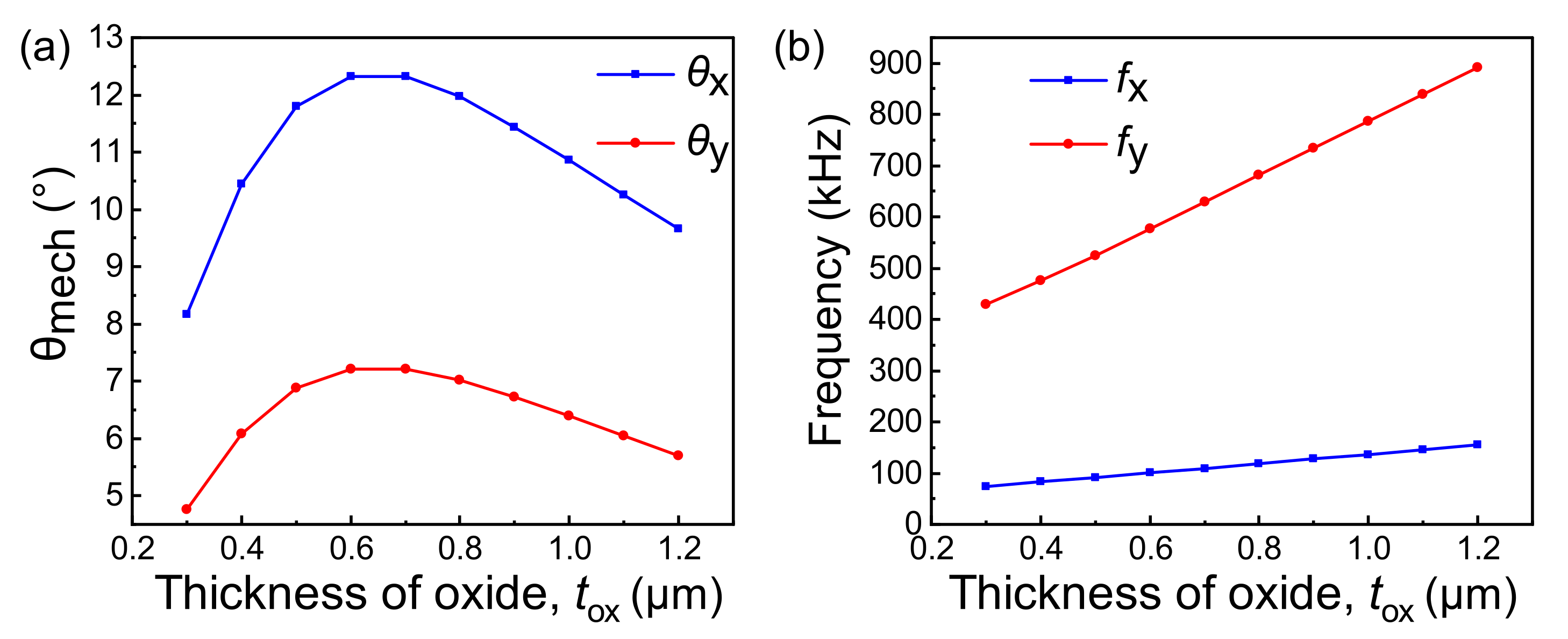
4.2. Layer Thickness
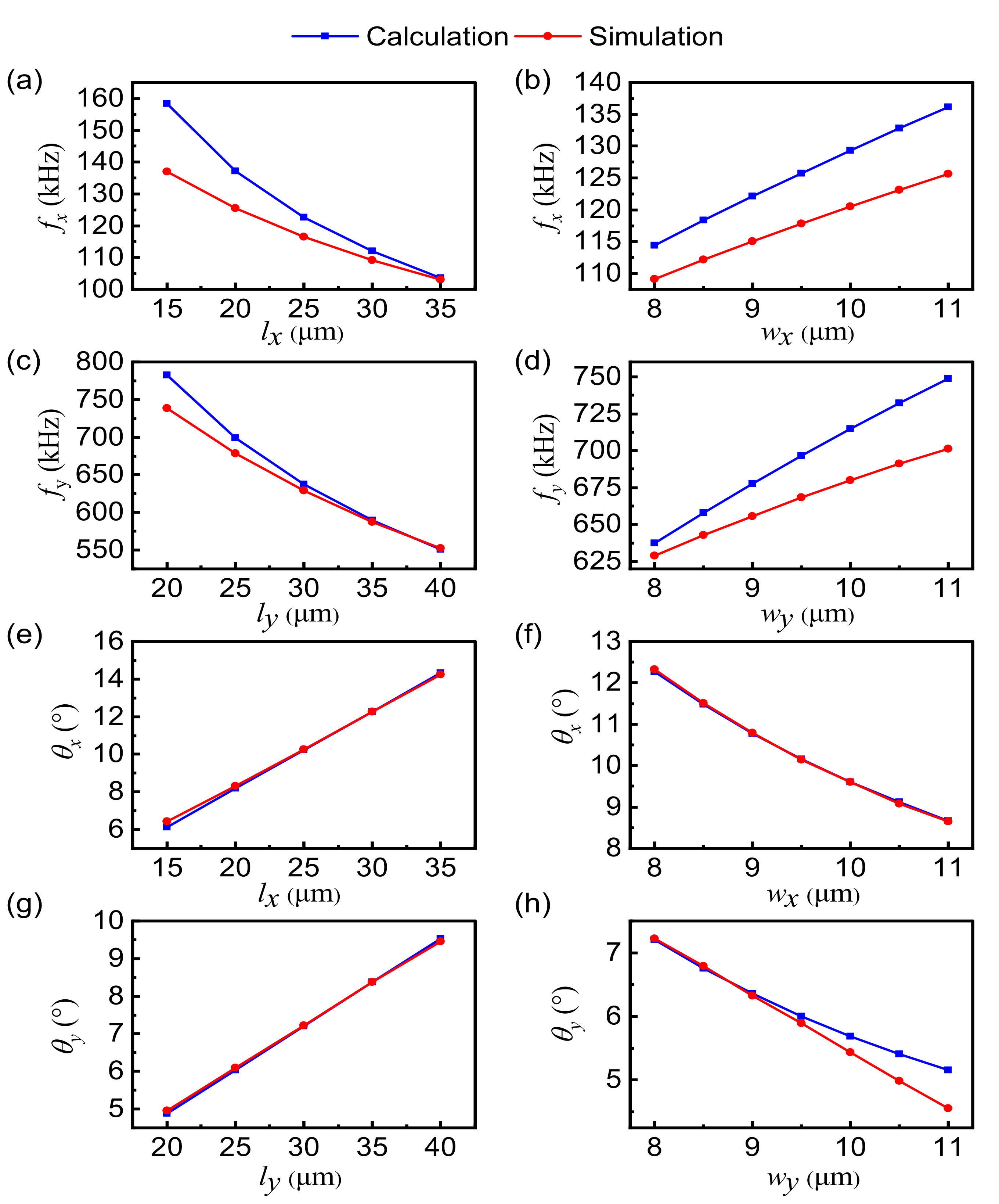
4.3. Geometry Parameters
5. Conclusions
- The Lithium niobate on insulation (LNOI) can be a novel and promising platform to design MEMS scanner/actuator. The transferred LN crystal provides high piezoelectricity that is much higher than AlN, with ZnO comparable to PZT, and a high quality factor, smooth surface and high strength.
- A novel principle of the torsional actuator, the electric field is directly applied to the torsion bar. With transduction, the torsion bar is driven directly, resulting in high deflection.
- The unique bimodal of of Y128-cut LN can be utilized in the 2D scanner. The proposed scanner performs 2D scanning with a single port reducing the complexity of the control circuit.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- An, Y.; Sun, B.; Wang, P.; Xiao, L.; Liu, H.; Xie, H. A 1 × 20 MEMS mirror array with large scan angle and low driving voltage for optical wavelength-selective switches. Sens. Actuators A Phys. 2021, 324, 112689. [Google Scholar] [CrossRef]
- Petrak, O.; Schwarz, F.; Pohl, L.; Reher, M.; Janicke, C.; Przytarski, J.; Senger, F.; Albers, J.; Giese, T.; Ratzmann, L.; et al. Laser beam scanning based AR-display applying resonant 2D MEMS mirrors. In Optical Architectures for Displays and Sensing in Augmented, Virtual, and Mixed Reality (AR, VR, MR) II; International Society for Optics and Photonics: Bellingham, WA, USA, 2021; Volume 11765, p. 1176503. [Google Scholar]
- Druml, N.; Maksymova, I.; Thurner, T.; van Lierop, D.; Hennecke, M.; Foroutan, A. 1D MEMS micro-scanning LiDAR. In Proceedings of the Conference on Sensor Device Technologies and Applications, Venice, ltaly, 16 September 2018; Volume 9. [Google Scholar]
- Kasturi, A.; Milanovic, V.; Atwood, B.H.; Yang, J. UAV-borne lidar with MEMS mirror-based scanning capability. In Laser Radar Technology and Applications XXI; SPIE: Bellingham, WA, USA, 2016; Volume 9832, pp. 206–215. [Google Scholar] [CrossRef]
- Pengwang, E.; Rabenorosoa, K.; Rakotondrabe, M.; Andreff, N. Scanning micromirror platform based on MEMS technology for medical application. Micromachines 2016, 7, 24. [Google Scholar] [CrossRef] [PubMed]
- Holmström, S.T.; Baran, U.; Urey, H. MEMS laser scanners: A review. J. Microelectromech. Syst. 2014, 23, 259–275. [Google Scholar] [CrossRef]
- Wang, D.; Watkins, C.; Xie, H. MEMS Mirrors for LiDAR: A review. Micromachines 2020, 11, 456. [Google Scholar] [CrossRef]
- Wang, D.; Xie, H.; Thomas, L.; Koppal, S.J. A Miniature LiDAR with a Detached MEMS Scanner for Micro-Robotics. IEEE Sens. J. 2021, 21, 21941–21946. [Google Scholar] [CrossRef]
- Luetzenburg, G.; Kroon, A.; Bjørk, A.A. Evaluation of the Apple iPhone 12 Pro LiDAR for an Application in Geosciences. Sci. Rep. 2021, 11, 22221. [Google Scholar] [CrossRef]
- Gupta, S.; Lohani, B. Augmented reality system using lidar point cloud data for displaying dimensional information of objects on mobile phones. In ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences; Copernicus GmbH: Göttingen, Germany, 2014; Volume II-5, pp. 153–159. [Google Scholar] [CrossRef] [Green Version]
- Baran, U.; Brown, D.; Holmstrom, S.; Balma, D.; Davis, W.O.; Muralt, P.; Urey, H. Resonant PZT MEMS Scanner for High-Resolution Displays. J. Microelectromech. Syst. 2012, 21, 1303–1310. [Google Scholar] [CrossRef] [Green Version]
- Urey, H. Torsional MEMS scanner design for high-resolution scanning display systems. In Optical Scanning 2002; International Society for Optics and Photonics: Bellingham, WA, USA, 2002; Volume 4773, pp. 27–37. [Google Scholar]
- Wang, Q.; Wang, W.; Zhuang, X.; Zhou, C.; Fan, B. Development of an Electrostatic Comb-Driven MEMS Scanning Mirror for Two-Dimensional Raster Scanning. Micromachines 2021, 12, 378. [Google Scholar] [CrossRef]
- Li, H.; Duan, X.; Li, G.; Oldham, K.R.; Wang, T.D. An Electrostatic MEMS Translational Scanner with Large Out-of-Plane Stroke for Remote Axial-Scanning in Multi-Photon Microscopy. Micromachines 2017, 8, 159. [Google Scholar] [CrossRef] [Green Version]
- Hung, A.C.L.; Lai, H.Y.H.; Lin, T.W.; Fu, S.G.; Lu, M.S.C. An electrostatically driven 2D micro-scanning mirror with capacitive sensing for projection display. Sens. Actuators A Phys. 2015, 222, 122–129. [Google Scholar] [CrossRef]
- Sun, C.; Liu, Y.; Li, B.; Su, W.; Luo, M.; Du, G.; Wu, Y. Modeling and Optimization of a Novel ScAlN-Based MEMS Scanning Mirror with Large Static and Dynamic Two-Axis Tilting Angles. Sensors 2021, 21, 5513. [Google Scholar] [CrossRef] [PubMed]
- Hung, E.; Senturia, S. Extending the travel range of analog-tuned electrostatic actuators. J. Microelectromech. Syst. 1999, 8, 497–505. [Google Scholar] [CrossRef]
- Yu, H.; Zhou, P.; Shen, W. Fast-scan MOEMS Mirror for HD Laser Projection Applications. In Proceedings of the 2021 IEEE 16th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Xiamen, China, 25–29 April 2021; pp. 265–269. [Google Scholar]
- Kim, S.; Lee, C.; Kim, J.Y.; Kim, J.; Lim, G.; Kim, C. Two-axis polydimethylsiloxane-based electromagnetic microelectromechanical system scanning mirror for optical coherence tomography. J. Biomed. Opt. 2016, 21, 106001. [Google Scholar] [CrossRef] [PubMed]
- Ju, S.; Jeong, H.; Park, J.H.; Bu, J.U.; Ji, C.H. Electromagnetic 2D scanning micromirror for high definition laser projection displays. IEEE Photonics Technol. Lett. 2018, 30, 2072–2075. [Google Scholar] [CrossRef]
- Zhou, Y.; Wen, Q.; Wen, Z.; Huang, J.; Chang, F. An electromagnetic scanning mirror integrated with blazed grating and angle sensor for a near infrared micro spectrometer. J. Micromech. Microeng. 2017, 27, 125009. [Google Scholar] [CrossRef] [Green Version]
- Seo, Y.H.; Hwang, K.; Park, H.C.; Jeong, K.H. Electrothermal MEMS fiber scanner for optical endomicroscopy. Opt. Express 2016, 24, 3903–3909. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Yu, X.; Feng, P.X.L.; Li, J.; Xie, H. A MEMS lens scanner based on serpentine electrothermal bimorph actuators for large axial tuning. Opt. Express 2020, 28, 23439–23453. [Google Scholar] [CrossRef]
- Tanguy, Q.A.; Gaiffe, O.; Passilly, N.; Cote, J.M.; Cabodevila, G.; Bargiel, S.; Lutz, P.; Xie, H.; Gorecki, C. Real-time Lissajous imaging with a low-voltage 2-axis MEMS scanner based on electrothermal actuation. Opt. Express 2020, 28, 8512–8527. [Google Scholar] [CrossRef]
- Karpelson, M.; Wei, G.Y.; Wood, R.J. A review of actuation and power electronics options for flapping-wing robotic insects. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 779–786. [Google Scholar] [CrossRef]
- Uchino, K. Piezoelectric actuators 2006. J. Electroceramics 2008, 20, 301–311. [Google Scholar] [CrossRef]
- Eom, C.B.; Trolier-McKinstry, S. Thin-film piezoelectric MEMS. MRS Bull. 2012, 37, 1007–1017. [Google Scholar] [CrossRef] [Green Version]
- Shkir, M.; Arif, M.; Ganesh, V.; Manthrammel, M.; Singh, A.; Yahia, I.; Maidur, S.R.; Patil, P.S.; AlFaify, S. Investigation on structural, linear, nonlinear and optical limiting properties of sol-gel derived nanocrystalline Mg doped ZnO thin films for optoelectronic applications. J. Mol. Struct. 2018, 1173, 375–384. [Google Scholar] [CrossRef]
- Shao, J.; Li, Q.; Feng, C.; Li, W.; Yu, H. AlN based piezoelectric micromirror. Opt. Lett. 2018, 43, 987–990. [Google Scholar] [CrossRef]
- Tang, J.; Niu, D.; Tai, Z.; Hu, X. Deposition of highly c-axis-oriented ScAlN thin films at different sputtering power. J. Mater. Sci. Mater. Electron. 2017, 28, 5512–5517. [Google Scholar] [CrossRef]
- Yuan, J.R.; Jiang, X.; Snook, K.; Rehrig, P.W.; Shrout, T.R.; Hackenberger, W.S.; Cheng, A.; Cao, P.; Lavalelle, G.; Geng, X. 5I-1 Microfabrication of Piezoelectric Composite Ultrasound Transducers (PC-MUT). In Proceedings of the 2006 IEEE Ultrasonics Symposium, Vancouver, BC, Canada, 2–6 October 2006; pp. 922–925. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Chen, X.; Bertrand, M.; Shams-Ansari, A.; Chandrasekhar, S.; Winzer, P.; Lončar, M. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 2018, 562, 101–104. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Hu, H. Analysis of Waveguides on Lithium Niobate Thin Films. Crystals 2018, 8, 191. [Google Scholar] [CrossRef] [Green Version]
- Jagatpal, N.; Mercante, A.J.; Ahmed, A.N.R.; Prather, D.W. Thin Film Lithium Niobate Electro-Optic Modulator for 1064 nm Wavelength. IEEE Photonics Technol. Lett. 2021, 33, 271–274. [Google Scholar] [CrossRef]
- Kourani, A.; Yang, Y.; Gong, S. A Ku-Band Oscillator Utilizing Overtone Lithium Niobate RF-MEMS Resonator for 5G. IEEE Microw. Wirel. Components Lett. 2020, 30, 681–684. [Google Scholar] [CrossRef]
- Link, S.; Lu, R.; Yang, Y.; Hassanien, A.E.; Gong, S. An A1 Mode Resonator at 12 GHz using 160nm Lithium Niobate Suspended Thin Film. In Proceedings of the 2021 IEEE International Ultrasonics Symposium (IUS), Xi’an, China, 11–16 September 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Sun, D.; Zhang, Y.; Wang, D.; Song, W.; Liu, X.; Pang, J.; Geng, D.; Sang, Y.; Liu, H. Microstructure and domain engineering of lithium niobate crystal films for integrated photonic applications. Light. Sci. Appl. 2020, 9, 197. [Google Scholar] [CrossRef]
- Emad, A.; Lu, R.; Li, M.H.; Yang, Y.; Wu, T.; Gong, S. Resonant Torsional Micro-Actuators Using Thin-Film Lithium Niobate. In Proceedings of the 2019 IEEE 32nd International Conference on Micro Electro Mechanical Systems (MEMS), Seoul, Korea, 27–31 January 2019; pp. 282–285. [Google Scholar]
- Ballas, R.G. Piezoelectric Beam Bending Actuators and Hamilton’s Principle. In Piezoelectric Multilayer Beam Bending Actuators: Static and Dynamic Behavior and Aspects of Sensor Integration; Microtechnology and Mems; Springer: Berlin/Heidelberg, Germany, 2007; pp. 77–102. [Google Scholar] [CrossRef]
- Wang, Q.M.; Du, X.H.; Xu, B.; Cross, L. Electromechanical coupling and output efficiency of piezoelectric bending actuators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 638–646. [Google Scholar] [CrossRef] [PubMed]
- Rosenbaum, J.F. Bulk Acoustic Wave Theory and Devices; Artech House Inc.: Boston, MA, USA, 1988; Available online: https://zbmath.org/?q=an%3A00042444 (accessed on 10 February 2022).
- Qin, L.; Wang, Q.M. Mass sensitivity of thin film bulk acoustic resonator sensors based on polar c-axis tilted zinc oxide and aluminum nitride thin film. J. Appl. Phys. 2010, 108, 104510. [Google Scholar] [CrossRef]
- Mizutaui, K.; Toda, K. Analysis of lamb wave propagation characteristics in rotated Y-cut X-propagation LiNbO3 plates. Electron. Commun. Jpn. (Part I Commun.) 1986, 69, 47–55. [Google Scholar] [CrossRef]
- Janin, P.; Bauer, R.; Griffin, P.; Riis, E.; Uttamchandani, D. Fast piezoelectric scanning MEMS mirror for 1D ion addressing. In Proceedings of the 2019 International Conference on Optical MEMS and Nanophotonics (OMN), Daejeon, Korea, 28 July–1 August 2019; pp. 220–221. [Google Scholar] [CrossRef] [Green Version]
- Piot, A.; Pribošek, J.; Maufay, J.; Schicker, J.; Tortschanoff, A.; Matloub, R.; Muralt, P.; Moridi, M. Optimization of Resonant PZT MEMS Mirrors by Inverse Design and Electrode Segmentation. J. Microelectromech. Syst. 2021, 30, 216–223. [Google Scholar] [CrossRef]
- Boni, N.; Carminati, R.; Mendicino, G.; Merli, M.; Terzi, D.; Lazarova, B.; Fusi, M. Piezoelectric MEMS mirrors for the next generation of small form factor AR glasses. In MOEMS and Miniaturized Systems XXI; SPIE: Bellingham, WA, USA, 2022; Volume 12013, pp. 30–46. [Google Scholar] [CrossRef]
- Urey, H.; Kan, C.; Davis, W.O. Vibration mode frequency formulae for micromechanical scanners. J. Micromech. Microeng. 2005, 15, 1713. [Google Scholar] [CrossRef]
- Chen, S.H.; Michael, A.; Kwok, C.Y. Design and Modeling of Piezoelectrically Driven Micro-Actuator With Large Out-of-Plane and Low Driving Voltage for Micro-Optics. J. Microelectromech. Syst. 2019, 28, 919–932. [Google Scholar] [CrossRef]
- Fraga, M.A.; Furlan, H.; Pessoa, R.S.; Massi, M. Wide bandgap semiconductor thin films for piezoelectric and piezoresistive MEMS sensors applied at high temperatures: An overview. Microsyst. Technol. 2014, 20, 9–21. [Google Scholar] [CrossRef]
- Guy, I.L.; Muensit, S.; Goldys, E.M. Extensional piezoelectric coefficients of gallium nitride and aluminum nitride. Appl. Phys. Lett. 1999, 75, 4133–4135. [Google Scholar] [CrossRef]
- Lu, R.; Yang, Y.; Link, S.; Gong, S. A1 Resonators in 128° Y-cut Lithium Niobate with Electromechanical Coupling of 46.4%. J. Microelectromech. Syst. 2020, 29, 313–319. [Google Scholar] [CrossRef]
- Ye, L.; Zhang, G.; You, Z. 5 V Compatible Two-Axis PZT Driven MEMS Scanning Mirror with Mechanical Leverage Structure for Miniature LiDAR Application. Sensors 2017, 17, 521. [Google Scholar] [CrossRef] [Green Version]
- Piot, A.; Pribošek, J.; Moridi, M. Dual-axis resonant scanning mems mirror with pulsed-laser-deposited barium-doped PZT. In Proceedings of the 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS), Gainesville, FL, USA, 25–29 January 2021; pp. 89–92. [Google Scholar]
- Gu-Stoppel, S.; Stenchly, V.; Kaden, D.; Quenzer, H.; Wagner, B.; Hofmann, U.; Dudde, R. New designs for MEMS-micromirrors and micromirror packaging with electrostatic and piezoelectric drive. TechConnect Briefs 2016, 4, 87–91. [Google Scholar]
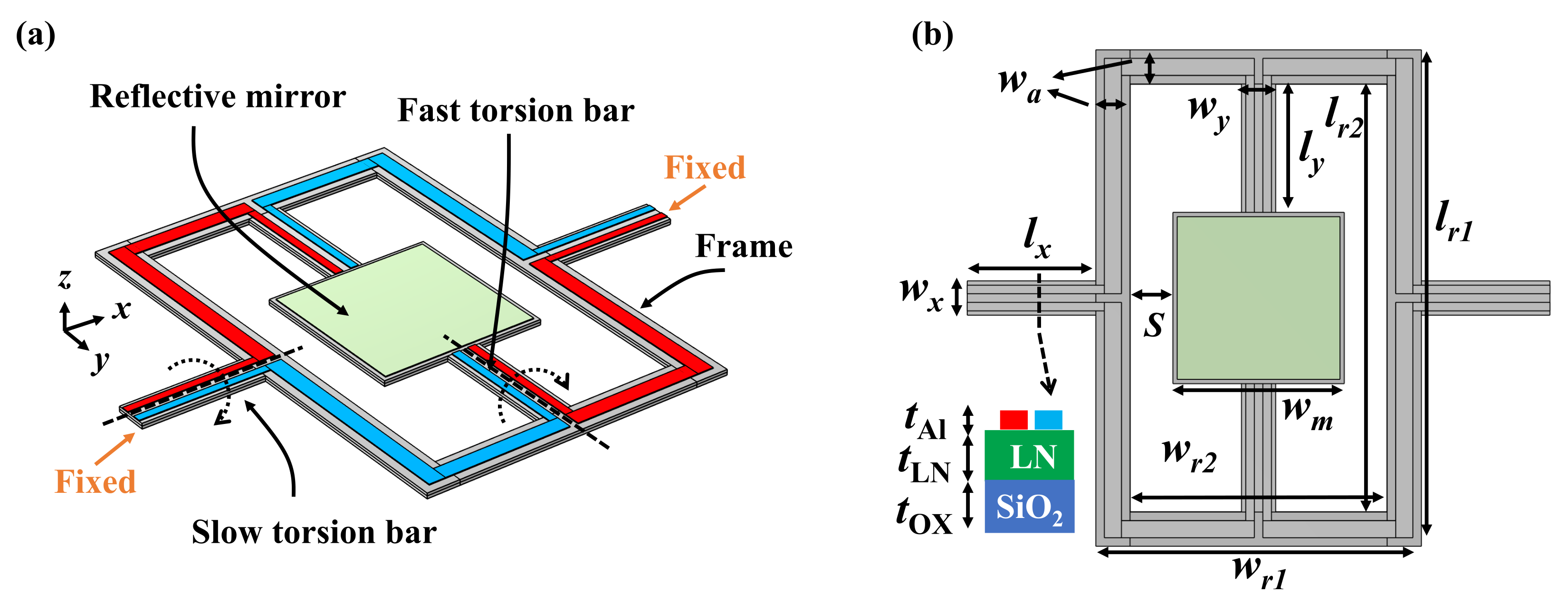
| Parameter | Description | Default Value |
|---|---|---|
| Width of reflective mirror | 40 m | |
| Length of reflective mirror | 40 m | |
| Width of fast torsion bar | 8 m | |
| Length of fast torsion bar | 30 m | |
| Width of slow torsion bar | 8 m | |
| Length of slow torsion bar | 30 m | |
| Width of frame | 10 m | |
| S | Space between mirror and frame | 10 m |
| Thickness of LN thin film | 0.55 m | |
| Thickness of SiO layer | 0.7 m | |
| Thickness of Al electrode | 0.2 m | |
| t | 1.2 m | |
| 80 m | ||
| 120 m |
| Material | Driving Voltage (V) | (°) | (kHz) | (°) | (kHz) | FoM () | Mirror Size (mm) | Deflection (°/V) | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| PZT | 2 | 40° | 0.95 | 42° | 1.46 | 122.6 | 2 | 20°\21° | [52] |
| PZT | 5 | 15.5° | 0.49 | 5.9° | 25.1 | 147.9 | 1 | 3.1°\1.18° | [53] |
| PZT | 20 | 31.3° | 1.5 | 21.4° | 29.9 | 639.9 | 1 | 1.56°\1.495° | [54] |
| AIN | 20 | 6.8° | 183.1 | 11.6° | 360.2 | 835.7 | 0.2 | 0.34°\0.58° | [44] |
| LN | 1 | 50.0° | 79.87 | 42.0° | 558.2 | 937.8 | 0.04 | 50.0°\42.0° | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Liu, K.; Wu, T. Dual-Axis MEMS Resonant Scanner Using 128∘Y Lithium Niobate Thin-Film. Acoustics 2022, 4, 313-328. https://doi.org/10.3390/acoustics4020019
Lu Y, Liu K, Wu T. Dual-Axis MEMS Resonant Scanner Using 128∘Y Lithium Niobate Thin-Film. Acoustics. 2022; 4(2):313-328. https://doi.org/10.3390/acoustics4020019
Chicago/Turabian StyleLu, Yaoqing, Kangfu Liu, and Tao Wu. 2022. "Dual-Axis MEMS Resonant Scanner Using 128∘Y Lithium Niobate Thin-Film" Acoustics 4, no. 2: 313-328. https://doi.org/10.3390/acoustics4020019
APA StyleLu, Y., Liu, K., & Wu, T. (2022). Dual-Axis MEMS Resonant Scanner Using 128∘Y Lithium Niobate Thin-Film. Acoustics, 4(2), 313-328. https://doi.org/10.3390/acoustics4020019






