Plane and Surface Acoustic Waves Manipulation by Three-Dimensional Composite Phononic Pillars with 3D Bandgap and Defect Analysis
Abstract
1. Introduction
2. Phononic Crystal and Theoretical Background
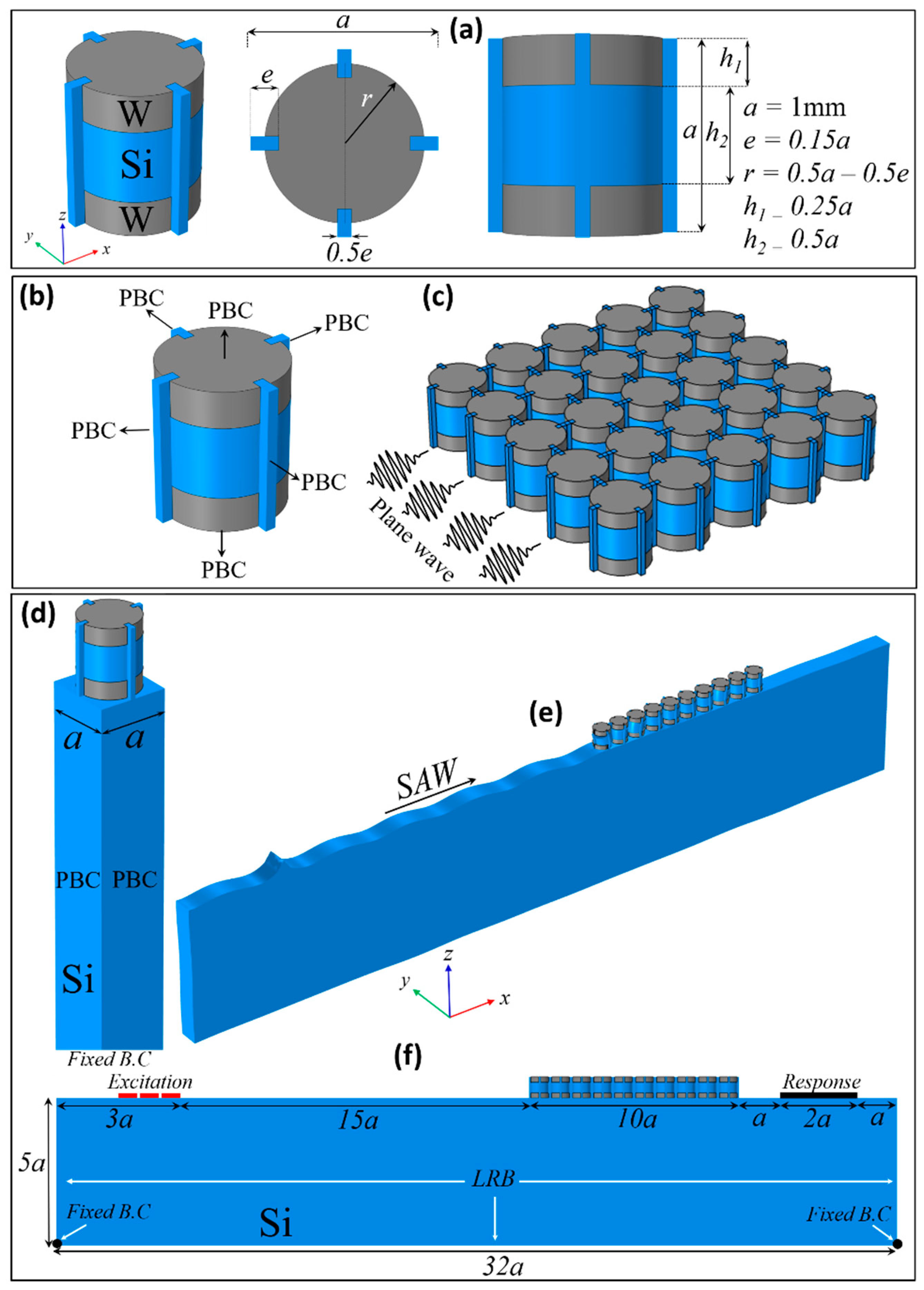
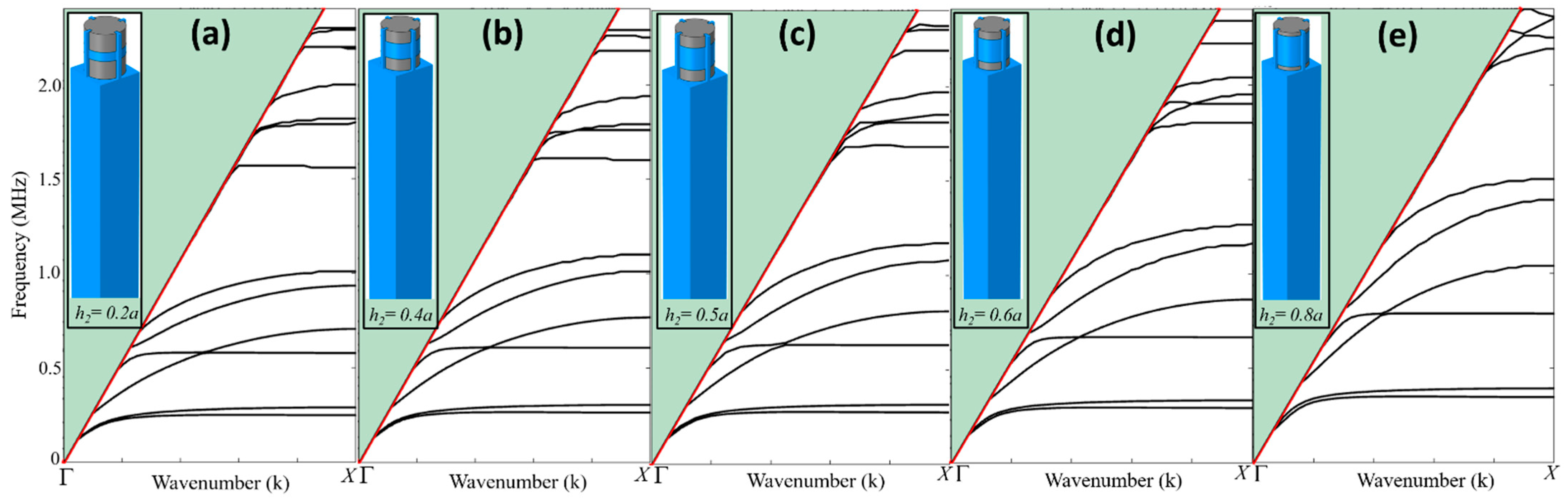
2.1. Unit Cell Structure
2.2. Theory and Mathematical Framework
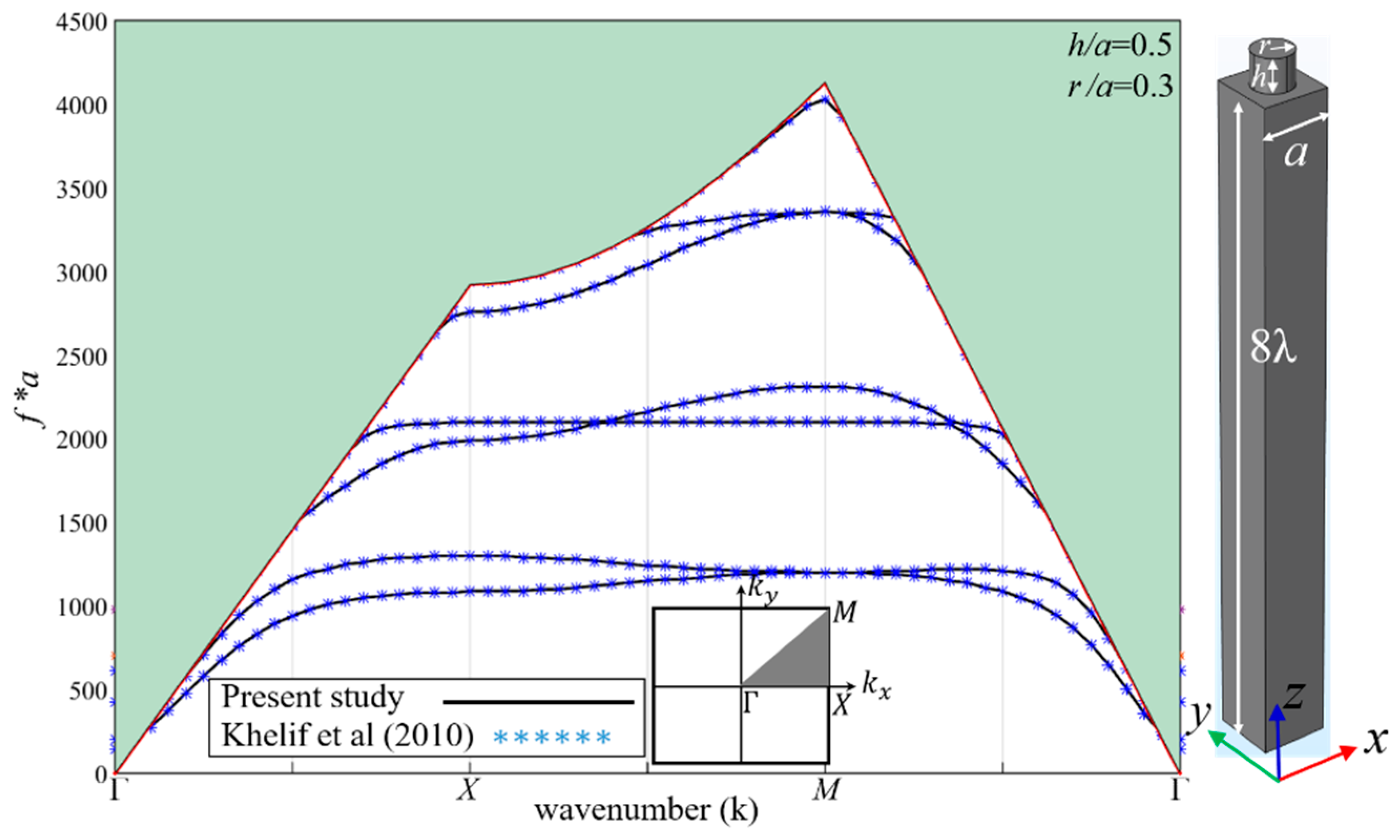
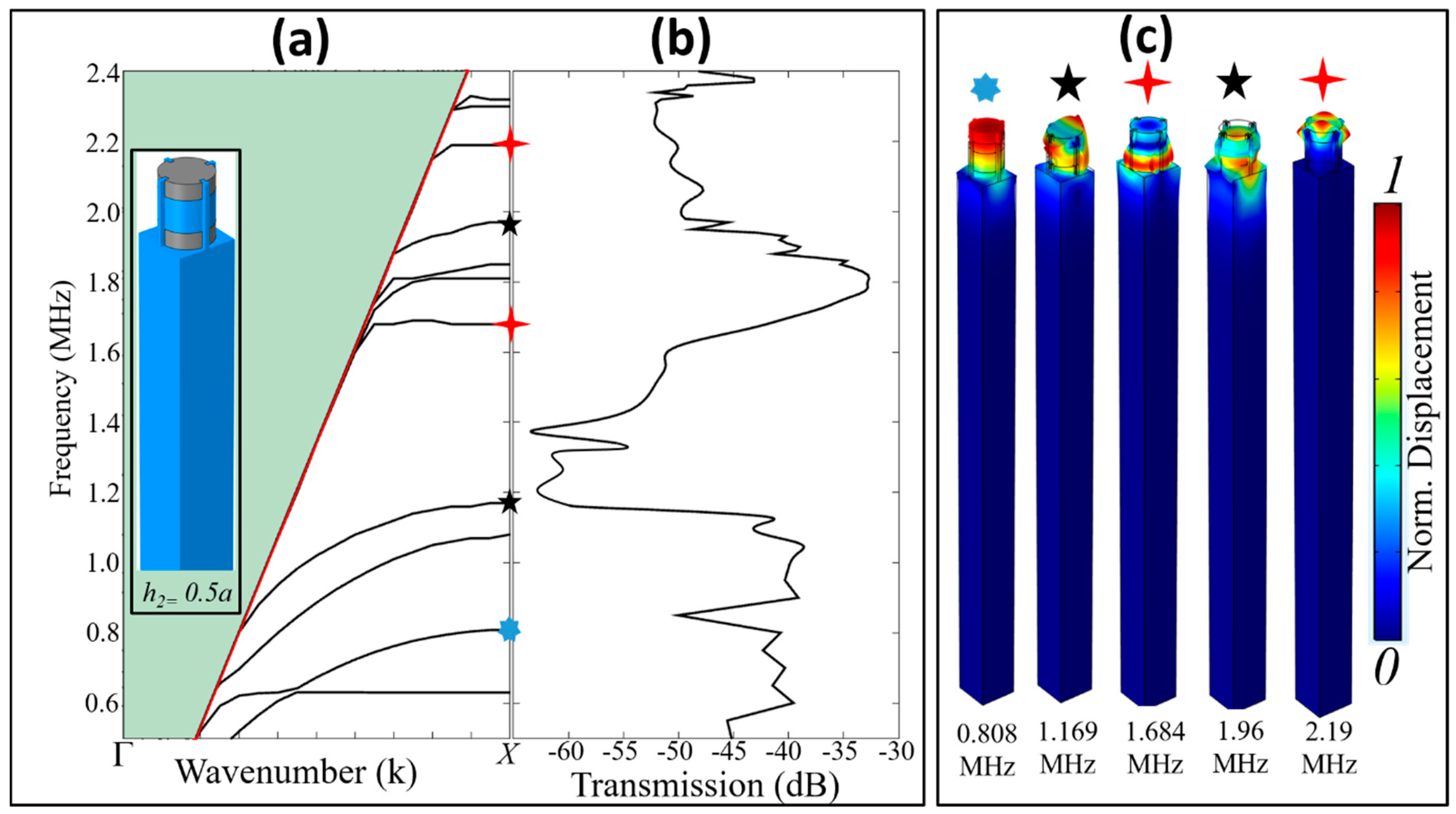
2.3. Model Validation
3. Results and Discussion
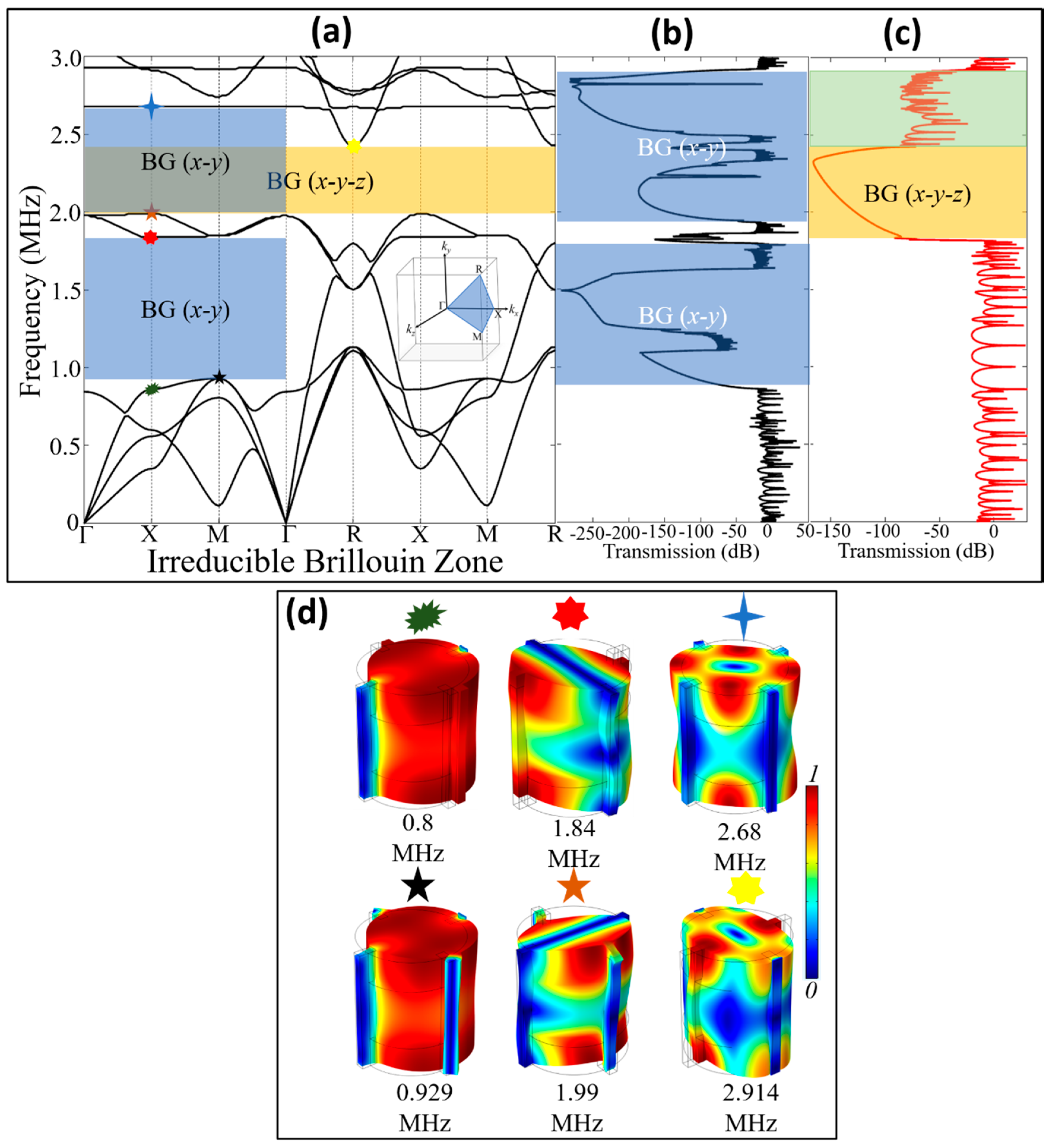
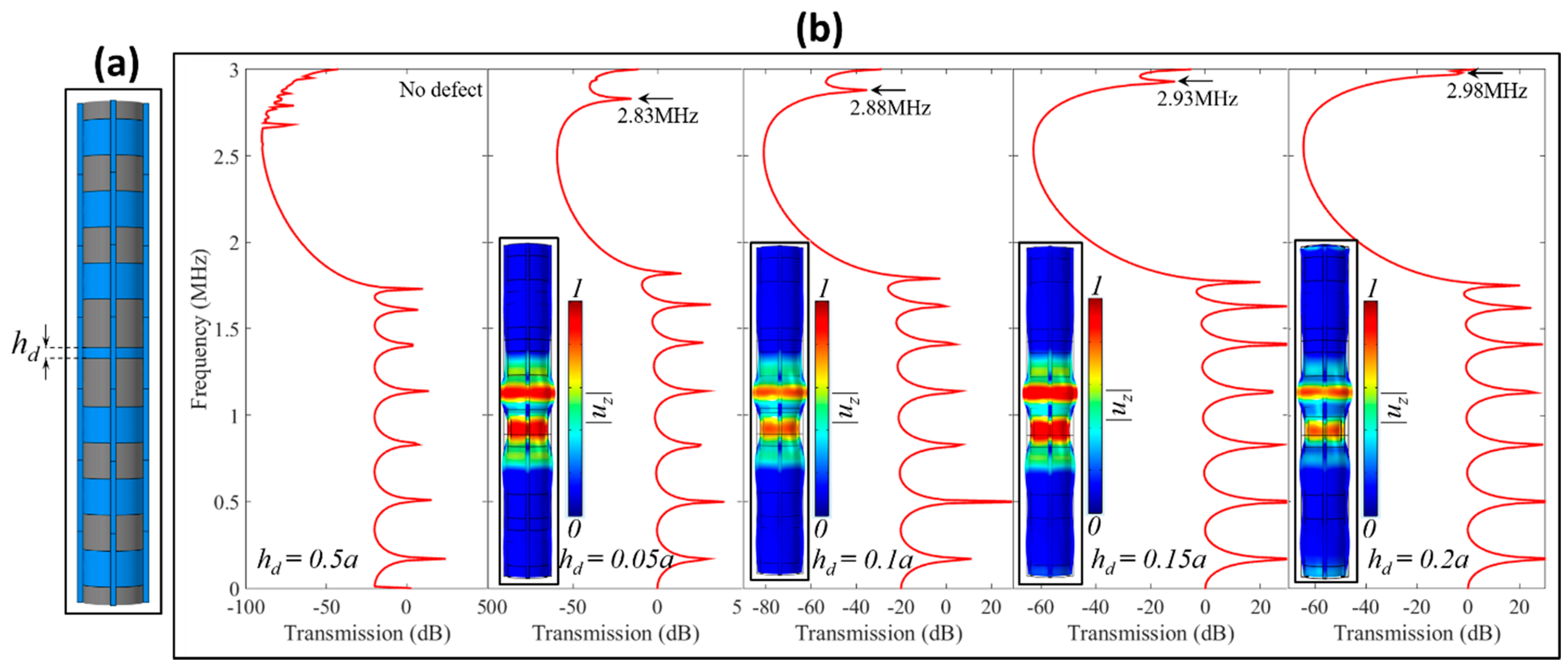
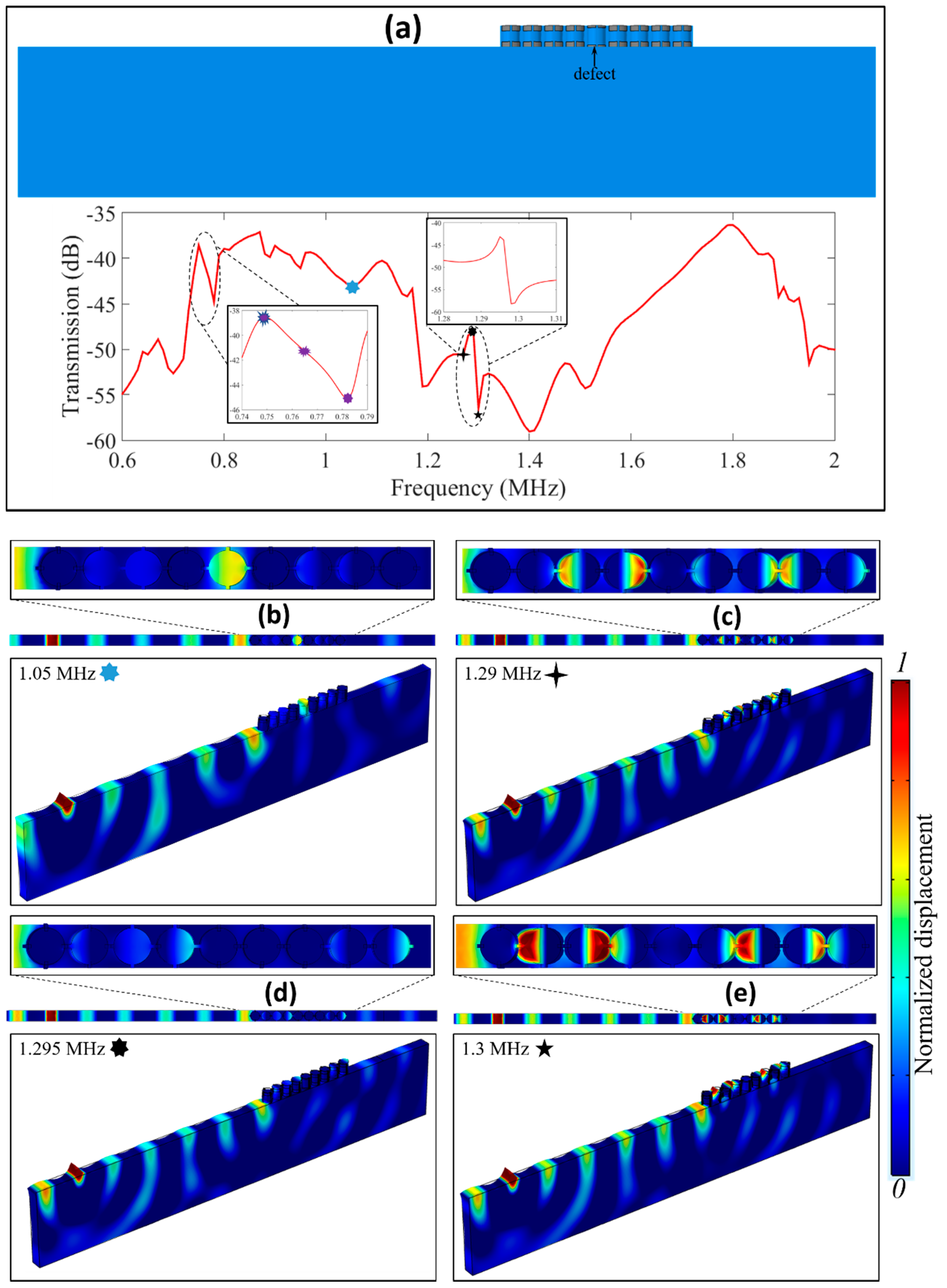
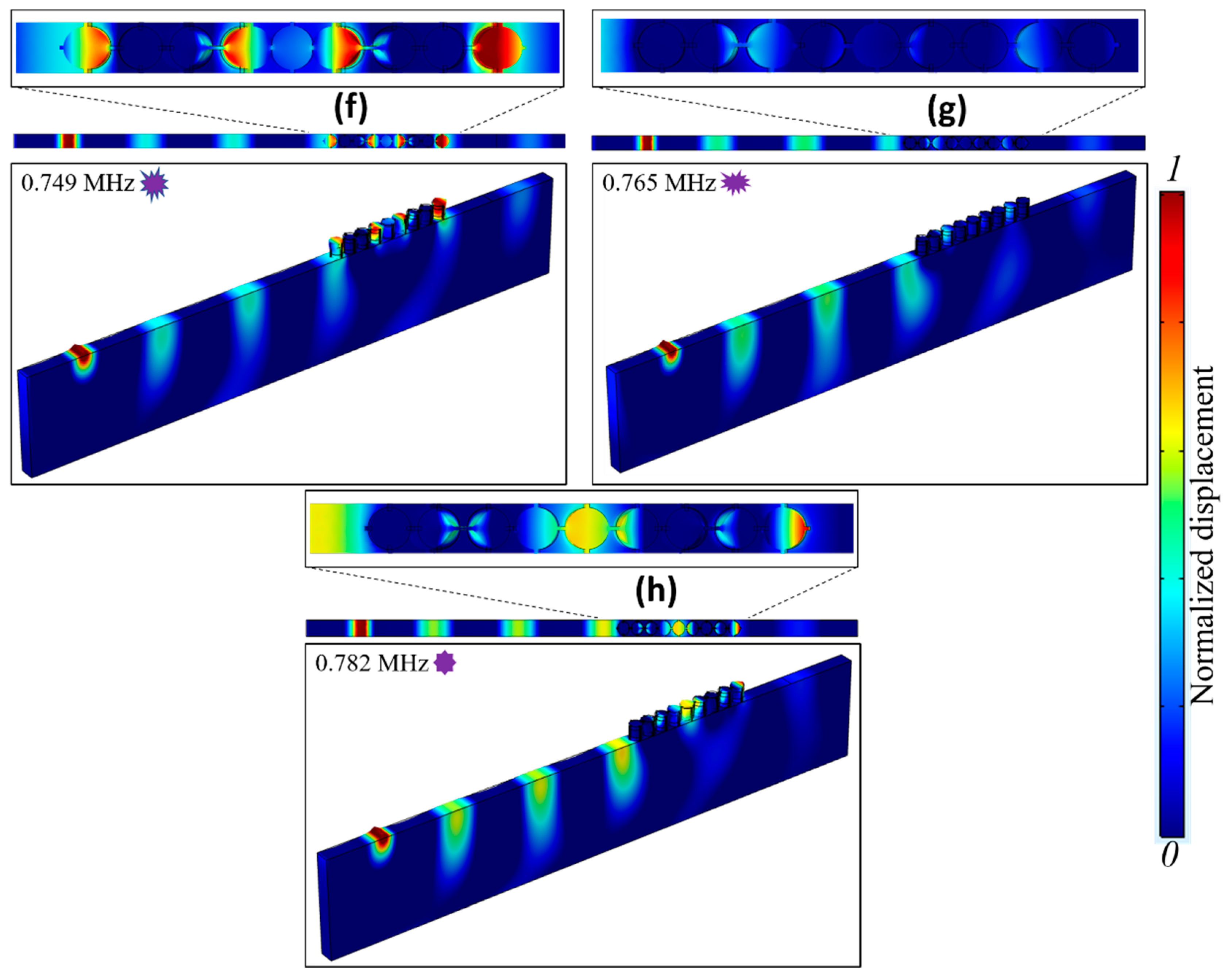
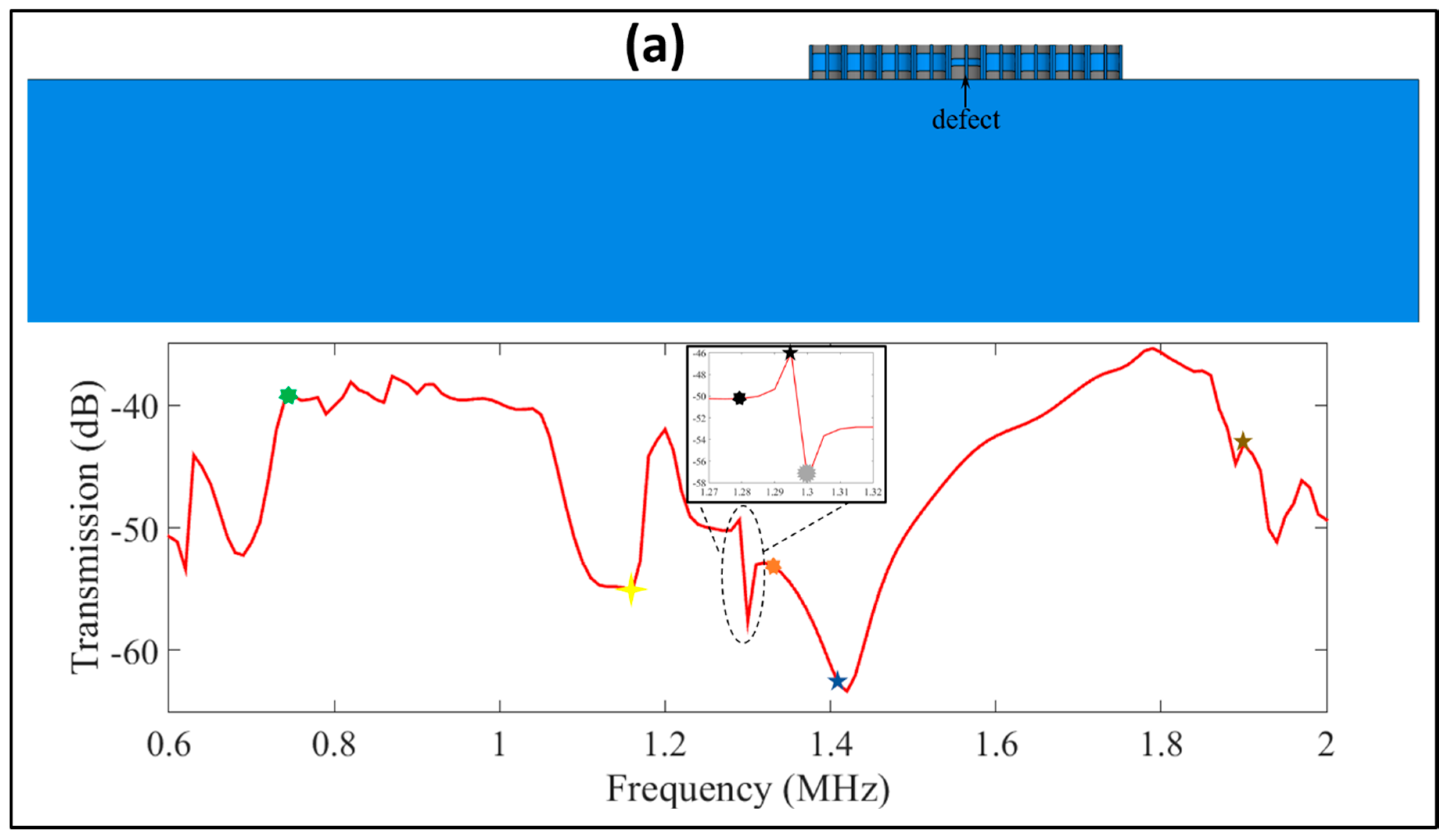
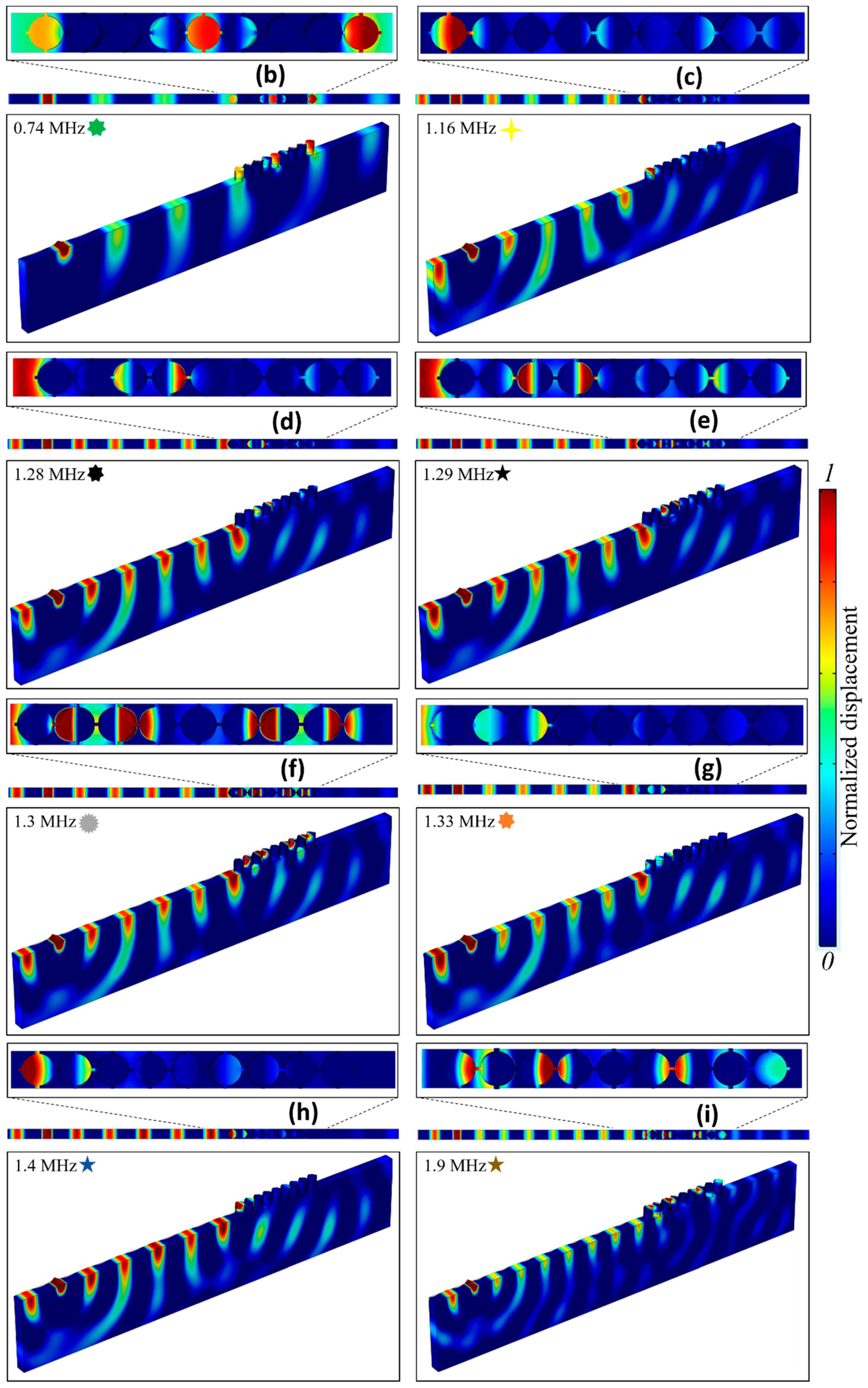
3.1. Plane Wave Propagation and Defect Analysis
3.2. SAW Propagation and Defect Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pennec, Y.; Djafari-Rouhani, B.; Vasseur, J.O.; Khelif, A.; Deymier, P.A. Tunable filtering and demultiplexing in phononic crystals with hollow cylinders. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004, 69, 046608. [Google Scholar] [CrossRef] [PubMed]
- Qiu, C.Y.; Liu, Z.Y.; Mei, J.; Shi, J. Mode-selecting acoustic filter by using resonant tunneling of two-dimensional double phononic crystals. Appl. Phys. Lett. 2005, 87, 104101. [Google Scholar] [CrossRef]
- Kumar, S.; Lee, H.P. The present and future role of acoustic metamaterials for architectural and urban noise mitigations. In Proceedings of Acoustics; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2019; pp. 590–607. [Google Scholar]
- Ang, L.Y.L.; Koh, Y.K.; Lee, H.P. Plate-type acoustic metamaterials: Experimental evaluation of a modular large-scale design for low-frequency noise control. In Proceedings of Acoustics; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2019; pp. 354–368. [Google Scholar]
- Zhang, X.; Liu, Z. Superlenses to overcome the diffraction limit. Nat. Mater. 2008, 7, 435–441. [Google Scholar] [CrossRef] [PubMed]
- De Ponti, J.M.; Colombi, A.; Ardito, R.; Braghin, F.; Corigliano, A.; Craster, R.V. Graded metasurface for enhanced sensing and energy harvesting. arXiv 2019, arXiv:1907.09297. [Google Scholar]
- Jin, Y.B.; Fernez, N.; Pennec, Y.; Bonello, B.; Moiseyenko, R.P.; Hemon, S.; Pan, Y.D.; Djafari-Rouhani, B. Tunable waveguide and cavity in a phononic crystal plate by controlling whispering-gallery modes in hollow pillars. Phys. Rev. B 2016, 93, 054109. [Google Scholar] [CrossRef]
- Lim, C.W.; Reddy, J.N.; Carrera, E.; Xu, X.; Zhou, Z. Surface elastic waves whispering gallery modes based subwavelength tunable waveguide and cavity modes of the phononic crystals. Mech. Adv. Mater. Struct. 2020, 27, 1053–1064. [Google Scholar] [CrossRef]
- Craster, R.V.; Guenneau, S. Acoustic Metamaterials: Negative Refraction, Imaging, Lensing and Cloaking; Springer Science & Business Media: Berlin, Germany, 2012; Volume 166. [Google Scholar]
- Cummer, S.A.; Schurig, D. One path to acoustic cloaking. New J. Phys. 2007, 9, 45. [Google Scholar] [CrossRef]
- Ning, L.; Wang, Y.-Z.; Wang, Y.-S. Active control cloak of the elastic wave metamaterial. Int. J. Solids Struct. 2020, 202, 126–135. [Google Scholar] [CrossRef]
- Lim, C.W. Analytical modeling and computation on topological properties of protected interface state of 1-d phononic crystal in elastic media. J. Mech. Mater. Struct. 2020, 15, 15–35. [Google Scholar] [CrossRef]
- Zhou, W.; Lim, C.W. Topological edge modeling and localization of protected interface modes in 1D phononic crystals for longitudinal and bending elastic waves. Int. J. Mech. Sci. 2019, 159, 359–372. [Google Scholar] [CrossRef]
- Zhou, W.; Su, Y.; Chen, W.; Lim, C.W. Voltage-controlled quantum valley Hall effect in dielectric membrane-type acoustic metamaterials. Int. J. Mech. Sci. 2020, 172, 105368. [Google Scholar] [CrossRef]
- Zhou, W.J.; Chen, W.Q.; Lim, C.W. Surface effect on the propagation of flexural waves in periodic nano-beam and the size-dependent topological properties. Compos. Struct. 2019, 216, 427–435. [Google Scholar] [CrossRef]
- Zhou, W.J.; Chen, W.Q.; Chen, Z.Y.; Lim, C.W. Actively controllable flexural wave band gaps in beam-type acoustic metamaterials with shunted piezoelectric patches. Eur. J. Mech. Solid 2019, 77, 103807. [Google Scholar] [CrossRef]
- Brule, S.; Javelaud, E.H.; Enoch, S.; Guenneau, S. Experiments on seismic metamaterials: Molding surface waves. Phys. Rev. Lett. 2014, 112, 133901. [Google Scholar] [CrossRef] [PubMed]
- Lim, C.W. Wide Rayleigh waves bandgap engineered metabarriers for seismic shielding of civil infrastructures. J. Eng. Mech. 2020, in press. [Google Scholar]
- Lim, C.W. Elastic waves propagation in thin plate metamaterials and evidence of low frequency pseudo and local resonance bandgaps. Phys. Lett. A 2019, 383, 2789–2796. [Google Scholar] [CrossRef]
- Lim, C.W.; Reddy, J.N. Built-up structural steel sections as seismic metamaterials for surface wave attenuation with low frequency wide bandgap in layered soil medium. Eng. Struct. 2019, 188, 440–451. [Google Scholar] [CrossRef]
- Wu, T.; Lim, C.W. Forest trees as naturally available seismic metamaterials: Low frequency Rayleigh waves with extremely wide bandgaps. Int. J. Struct. Stab. Dyn. 2020, 2043014. [Google Scholar] [CrossRef]
- Zhou, W.J.; Wu, B.; Du, Q.J.; Huang, G.L.; Lu, C.F.; Chen, W.Q. Actively tunable transverse waves in soft membrane-type acoustic metamaterials. J. Appl. Phys. 2018, 123, 165304. [Google Scholar] [CrossRef]
- Huang, H.H.; Sun, C.T.; Huang, G.L. On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar] [CrossRef]
- Park, J.; Park, B.; Kim, D.; Park, J. Determination of effective mass density and modulus for resonant metamaterials. J. Acoust. Soc. Am. 2012, 132, 2793–2799. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- Yu, K.; Fang, N.X.; Huang, G.; Wang, Q. Magnetoactive Acoustic Metamaterials. Adv. Mater. 2018, 30, 1706348. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- An, N.; Domel, A.G.; Zhou, J.; Rafsanjani, A.; Bertoldi, K. Programmable Hierarchical Kirigami. Adv. Funct. Mater. 2020, 30, 1906711. [Google Scholar] [CrossRef]
- Barnhart, M.V.; Xu, X.C.; Chen, Y.Y.; Zhang, S.; Song, J.Z.; Huang, G.L. Experimental demonstration of a dissipative multi-resonator metamaterial for broadband elastic wave attenuation. J. Sound Vib. 2019, 438, 1–12. [Google Scholar] [CrossRef]
- Lim, C.W. Dissipative multiresonant pillared and trampoline metamaterials with amplified local resonance bandgaps and broadband vibration attenuation. J. Vib. Acoust. 2020, 142, 061012. [Google Scholar] [CrossRef]
- Lim, C.W.; Li, J.T.H.; Zhao, Z. Lightweight architected lattice phononic crystals with broadband and multiband vibration mitigation characteristics. Extrem. Mech. Lett. 2020, 41, 100994. [Google Scholar] [CrossRef]
- Ang, L.Y.L.; Koh, Y.K.; Lee, H.P. Acoustic Metamaterials: A Potential for Cabin Noise Control in Automobiles and Armored Vehicles. Int. J. Appl. Mech. 2016, 8, 1650072. [Google Scholar] [CrossRef]
- Vyas, N.S.; Lim, C.W. A Novel Application of Multi-Resonant Dissipative Elastic Metahousing For Bearings. SAGE J. Vib. Control 2020. under review. [Google Scholar]
- Liu, Y.; Du, J.; Cheng, L. Bandgap formation under temperature-induced quasi-periodicity in an acoustic duct with flexible walls. J. Sound Vib. 2020, 486, 115615. [Google Scholar] [CrossRef]
- Huang, Z.; Zhao, S.; Su, M.; Yang, Q.; Li, Z.; Cai, Z.; Zhao, H.; Hu, X.; Zhou, H.; Li, F.; et al. Bioinspired Patterned Bubbles for Broad and Low-Frequency Acoustic Blocking. ACS Appl. Mater. Interfaces 2020, 12, 1757–1764. [Google Scholar] [CrossRef] [PubMed]
- Allam, A.; Sabra, K.; Erturk, A. 3D-Printed Gradient-Index Phononic Crystal Lens for Underwater Acoustic Wave Focusing. Phys. Rev. Appl. 2020, 13, 064064. [Google Scholar] [CrossRef]
- Lim, C.W. From photonic crystals to seismic metamaterials: A review via phononic crystals and acoustic metamaterials. Appl. Mech. Rev. 2020. under review. [Google Scholar]
- Wang, Y.-F.; Wang, Y.-Z.; Wu, B.; Chen, W.; Wang, Y.-S. Tunable and active phononic crystals and metamaterials. Appl. Mech. Rev. 2020, 72, 040801. [Google Scholar] [CrossRef]
- Meseguer, F.; Holgado, M.; Caballero, D.; Benaches, N.; Sanchez-Dehesa, J.; Lopez, C.; Llinares, J. Rayleigh-wave attenuation by a semi-infinite two-dimensional elastic-band-gap crystal. Phys. Rev. B 1999, 59, 12169–12172. [Google Scholar] [CrossRef]
- Khelif, A.; Achaoui, Y.; Benchabane, S.; Laude, V.; Aoubiza, B. Locally resonant surface acoustic wave band gaps in a two-dimensional phononic crystal of pillars on a surface. Phys. Rev. B 2010, 81, 1–7. [Google Scholar] [CrossRef]
- Williams, E.G.; Roux, P.; Rupin, M.; Kuperman, W.A. Theory of multiresonant metamaterials forA0Lamb waves. Phys. Rev. B 2015, 91, 104307. [Google Scholar] [CrossRef]
- Oudich, M.; Djafari-Rouhani, B.; Bonello, B.; Pennec, Y.; Sarry, F. Phononic Crystal Made of Multilayered Ridges on a Substrate for Rayleigh Waves Manipulation. Crystals 2017, 7, 372. [Google Scholar] [CrossRef]
- Oudich, M.; Djafari-Rouhani, B.; Bonello, B.; Pennec, Y.; Hemaidia, S.; Sarry, F.; Beyssen, D. Rayleigh Waves in Phononic Crystal Made of Multilayered Pillars: Confined Modes, Fano Resonances, and Acoustically Induced Transparency. Phys. Rev. Appl. 2018, 9, 034013. [Google Scholar] [CrossRef]
- Hussein, M.I.; Leamy, M.J.; Ruzzene, M. Dynamics of Phononic Materials and Structures: Historical Origins, Recent Progress, and Future Outlook. Appl. Mech. Rev. 2014, 66, 040802. [Google Scholar] [CrossRef]
- Zhou, X.; Assouar, M.B.; Oudich, M. Acoustic superfocusing by solid phononic crystals. Appl. Phys. Lett. 2014, 105, 233506. [Google Scholar] [CrossRef]
- Siddiqi, M.; Lee, J. Wide acoustic bandgap solid disk-shaped phononic crystal anchoring boundaries for enhancing quality factor in AlN-on-Si MEMS resonators. Micromachines 2018, 9, 413. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Chen, Y.; Zhu, X.; Garcia-Vidal, F.J.; Yin, X.; Zhang, W.; Zhang, X. Acoustic rainbow trapping. Sci. Rep. 2013, 3, 1728. [Google Scholar] [CrossRef]
- Bilal, O.R.; Hussein, M.I. Trampoline metamaterial: Local resonance enhancement by springboards. Appl. Phys. Lett. 2013, 103, 111901. [Google Scholar] [CrossRef]
- Achaoui, Y.; Laude, V.; Benchabane, S.; Khelif, A. Local resonances in phononic crystals and in random arrangements of pillars on a surface. J. Appl. Phys. 2013, 114, 104503. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari Rouhani, B.; Larabi, H.; Akjouj, A.; Gillet, J.N.; Vasseur, J.O.; Thabet, G. Phonon transport and waveguiding in a phononic crystal made up of cylindrical dots on a thin homogeneous plate. Phys. Rev. B 2009, 80, 144302. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari-Rouhani, B.; Larabi, H.; Vasseur, J.O.; Hladky-Hennion, A.C. Low-frequency gaps in a phononic crystal constituted of cylindrical dots deposited on a thin homogeneous plate. Phys. Rev. B 2008, 78, 104105. [Google Scholar] [CrossRef]
- Wu, T.-C.; Wu, T.-T.; Hsu, J.-C. Waveguiding and frequency selection of Lamb waves in a plate with a periodic stubbed surface. Phys. Rev. B 2009, 79, 104306. [Google Scholar] [CrossRef]
- Wu, T.T.; Huang, Z.G.; Tsai, T.C.; Wu, T.C. Evidence of complete band gap and resonances in a plate with periodic stubbed surface. Appl. Phys. Lett. 2008, 93, 98–101. [Google Scholar] [CrossRef]
- Oudich, M.; Senesi, M.; Assouar, M.B.; Ruzenne, M.; Sun, J.-H.; Vincent, B.; Hou, Z.; Wu, T.-T. Experimental evidence of locally resonant sonic band gap in two-dimensional phononic stubbed plates. Phys. Rev. B 2011, 84, 165136. [Google Scholar] [CrossRef]
- Oudich, M.; Zhou, X.; Assouar, M.B. General analytical approach for sound transmission loss analysis through a thick metamaterial plate. J. Appl. Phys. 2014, 116, 193509. [Google Scholar] [CrossRef]
- Jin, Y.; Pennec, Y.; Pan, Y.; Djafari-Rouhani, B. Phononic crystal plate with hollow pillars connected by thin bars. J. Phys. D Appl. Phys. 2016, 50, 035301. [Google Scholar] [CrossRef]
- Jin, Y.; Pennec, Y.; Pan, Y.; Djafari-Rouhani, B. Phononic Crystal Plate with Hollow Pillars Actively Controlled by Fluid Filling. Crystals 2016, 6, 64. [Google Scholar] [CrossRef]
- Achaoui, Y.; Khelif, A.; Benchabane, S.; Robert, L.; Laude, V. Experimental observation of locally-resonant and Bragg band gaps for surface guided waves in a phononic crystal of pillars. Phys. Rev. B 2011, 83, 1–5. [Google Scholar] [CrossRef]
- Robillard, J.F.; Devos, A.; Roch-Jeune, I. Time-resolved vibrations of two-dimensional hypersonic phononic crystals. Phys. Rev. B 2007, 76, 092301. [Google Scholar] [CrossRef]
- Giannetti, C.; Revaz, B.; Banfi, F.; Montagnese, M.; Ferrini, G.; Cilento, F.; Maccalli, S.; Vavassori, P.; Oliviero, G.; Bontempi, E.; et al. Thermomechanical behavior of surface acoustic waves in ordered arrays of nanodisks studied by near-infrared pump-probe diffraction experiments. Phys. Rev. B 2007, 76, 125413. [Google Scholar] [CrossRef]
- Yudistira, D.; Boes, A.; Graczykowski, B.; Alzina, F.; Yeo, L.Y.; Sotomayor Torres, C.M.; Mitchell, A. Nanoscale pillar hypersonic surface phononic crystals. Phys. Rev. B 2016, 94, 094304. [Google Scholar] [CrossRef]
- Colombi, A.; Roux, P.; Guenneau, S.; Gueguen, P.; Craster, R.V. Forests as a natural seismic metamaterial: Rayleigh wave bandgaps induced by local resonances. Sci. Rep. 2016, 6, 19238. [Google Scholar] [CrossRef]
- De Ponti, J.M.; Colombi, A.; Ardito, R.; Braghin, F.; Corigliano, A.; Craster, R.V. Graded elastic metasurface for enhanced energy harvesting. New J. Phys. 2020, 22, 013013. [Google Scholar] [CrossRef]
- Chaplain, G.J.; De Ponti, J.M.; Colombi, A.; Fuentes-Dominguez, R.; Dryburg, P.; Pieris, D.; Smith, R.J.; Clare, A.; Clark, M.; Craster, R.V. Tailored elastic surface to body wave Umklapp conversion. Nat. Commun. 2020, 11, 3267. [Google Scholar] [CrossRef] [PubMed]
- D’Alessandro, L.; Belloni, E.; Ardito, R.; Braghin, F.; Corigliano, A. Mechanical low-frequency filter via modes separation in 3D periodic structures. Appl. Phys. Lett. 2017, 111, 231902. [Google Scholar] [CrossRef]
- Lim, C.W. Ultrawide 3D phononic bandgap metastructures as broadband low frequency filter. Sci. Rep. 2020. submitted. [Google Scholar]
- Lim, C.W. Ultrawide bandgap by 3D monolithic mechanical metastructure for vibration and noise control. Arch. Civ. Mech. Eng. 2020. submitted. [Google Scholar]
- Maurel, A.; Marigo, J.-J.; Pham, K.; Guenneau, S. Conversion of Love waves in a forest of trees. Phys. Rev. B 2018, 98, 134311. [Google Scholar] [CrossRef]
- Hofstadter, D.R. Energy-Levels and Wave-Functions of Bloch Electrons in Rational and Irrational Magnetic-Fields. Phys. Rev. B 1976, 14, 2239–2249. [Google Scholar] [CrossRef]
| Young Modulus E (GPa) | Density ρ (kg/m3) | ||
|---|---|---|---|
| Silicon (Si) | 166 | 2330 | 0.28 |
| Tungsten (W) | 400 | 19,270 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammad; Lim, C.W.; Leung, A.Y.T. Plane and Surface Acoustic Waves Manipulation by Three-Dimensional Composite Phononic Pillars with 3D Bandgap and Defect Analysis. Acoustics 2021, 3, 25-41. https://doi.org/10.3390/acoustics3010004
Muhammad, Lim CW, Leung AYT. Plane and Surface Acoustic Waves Manipulation by Three-Dimensional Composite Phononic Pillars with 3D Bandgap and Defect Analysis. Acoustics. 2021; 3(1):25-41. https://doi.org/10.3390/acoustics3010004
Chicago/Turabian StyleMuhammad, C.W. Lim, and Andrew Y. T. Leung. 2021. "Plane and Surface Acoustic Waves Manipulation by Three-Dimensional Composite Phononic Pillars with 3D Bandgap and Defect Analysis" Acoustics 3, no. 1: 25-41. https://doi.org/10.3390/acoustics3010004
APA StyleMuhammad, Lim, C. W., & Leung, A. Y. T. (2021). Plane and Surface Acoustic Waves Manipulation by Three-Dimensional Composite Phononic Pillars with 3D Bandgap and Defect Analysis. Acoustics, 3(1), 25-41. https://doi.org/10.3390/acoustics3010004







