Handclap for Acoustic Measurements: Optimal Application and Limitations
Abstract
1. Introduction
- The sound source shall be as close to omnidirectional as possible. A maximum deviation of directivity of source in decibels for excitation with octave bands of pink noise and measured in free field is expected (a table of maximum deviation per frequency is featured in ISO 3382-1);
- The sound source shall produce a sound pressure level sufficient to provide decay curves with the required minimum dynamic range, without contamination by background noise. In the case of measurements of impulse responses using pseudo-random sequences (e.g., maximum-length sequence [8]), the required sound pressure level might be quite low because a strong improvement of the signal-to-noise ratio by means of synchronous averaging is possible. In the case of measurements which do not use a synchronous averaging (or other) technique to augment the decay range, a source level will be required that gives at least 45 dB above the background level in the corresponding frequency band (also an alternative source level above the background level is provided in ISO 3382-1 which is discussed in the Methods, Section 2).
- To the best of our knowledge, this is the first study that suggests the optimal hand configuration (among 11) for acoustic measurements. Previous studies have either identified the hand configurations (e.g., [26]) or performed measurements without considering the optimal hand configuration [32,33,34,35];
- Another contribution of this study is that it suggests the expected measurement accuracy utilizing a handclap as a sound source for some of the most common acoustic parameters (i.e., reverberation time, early decay time, clarity);
- No known empirical research has focused on comparing measurements performed with a handclap as a sound source and measurements performed with a dodecahedron speaker following the recommendations of ISO 3382-1;
- Three new hand configurations were suggested and measured;
- Practical steps for measurements with a handclap as an acoustic source are suggested.
2. Methods
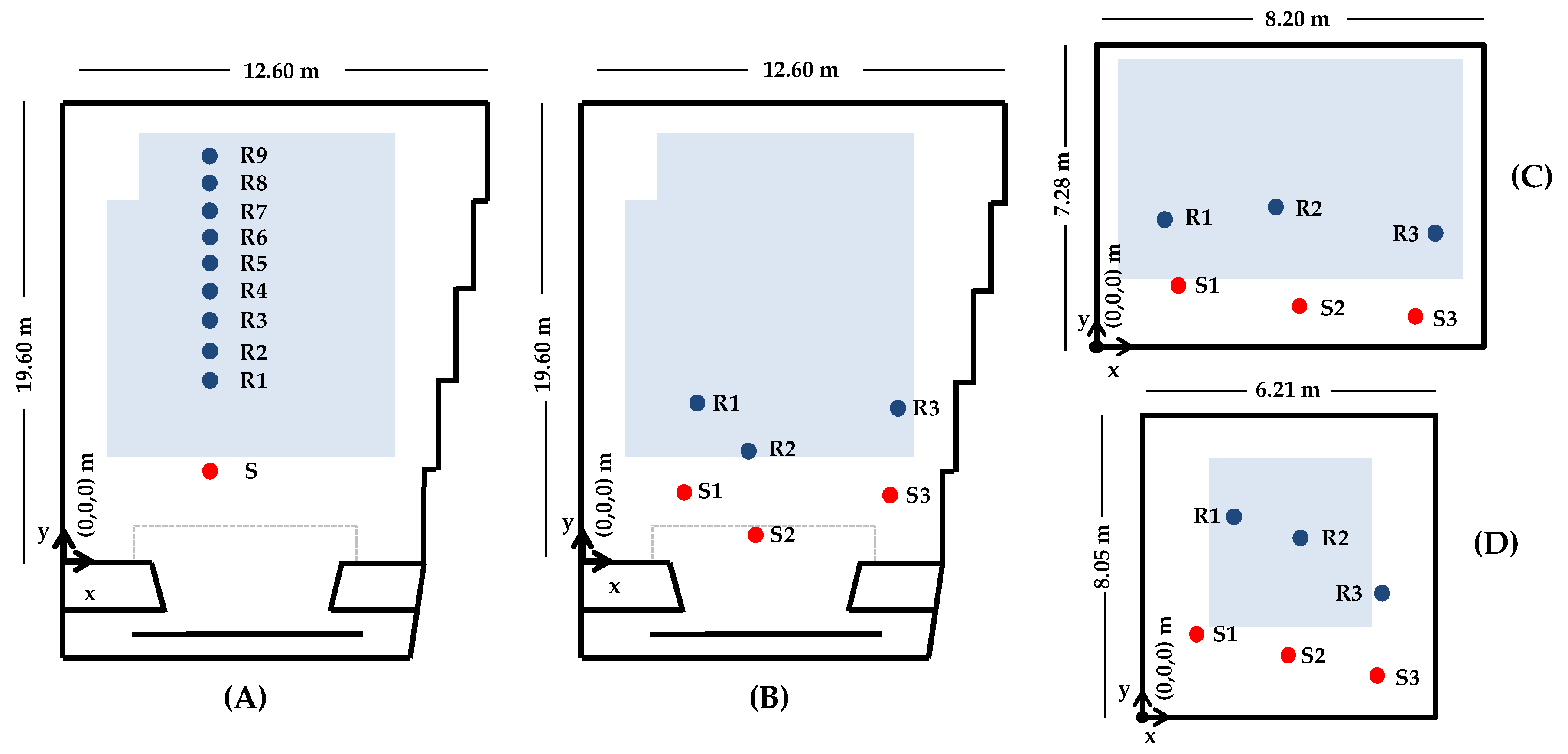
2.1. Measurements with A Handclap as A Sound Source
- Measurements to investigate optimal hand configuration;
- Measurements at different source–receiver distances;
- Measurements in different spaces.
2.1.1. Measurements to Investigate Optimal Hand Configuration
2.1.2. Measurements at Different Source–Receiver Distances
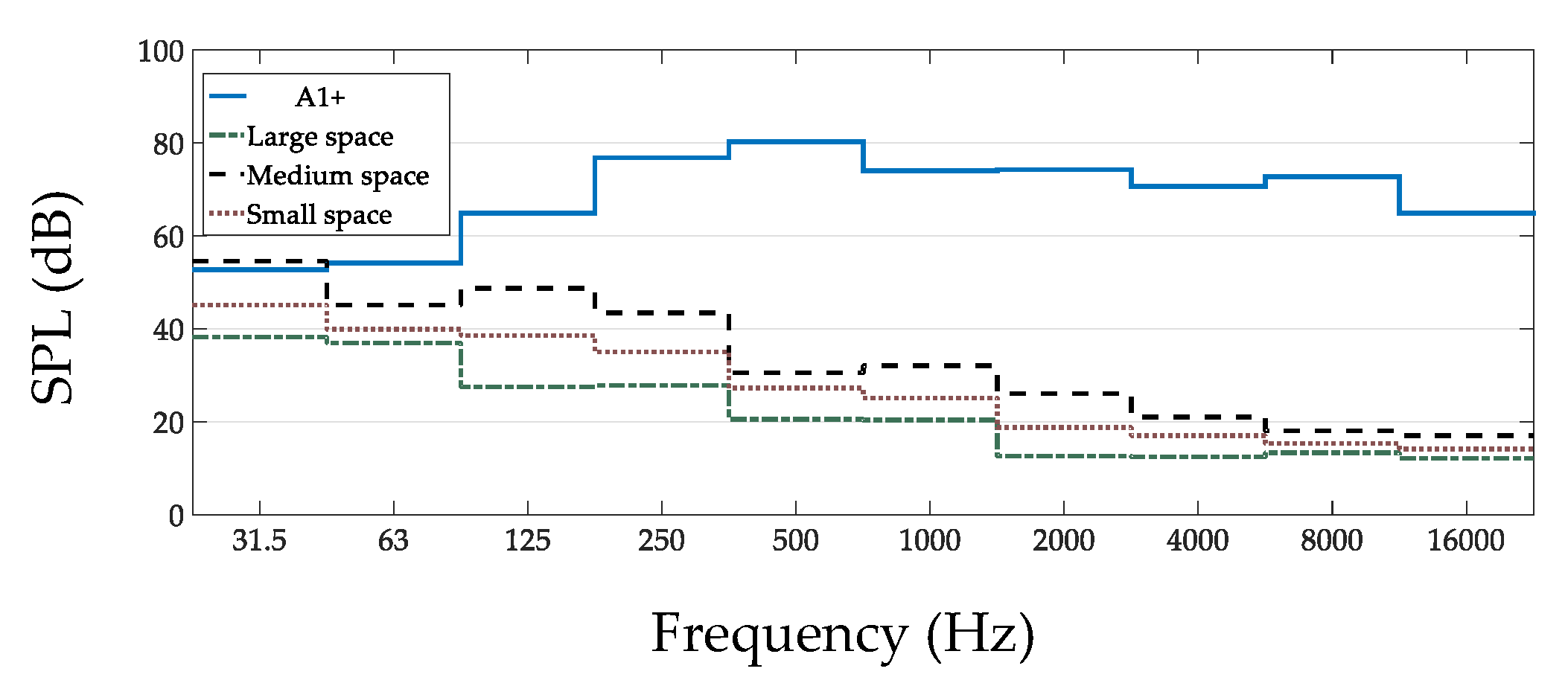
2.1.3. Measurements at Different Spaces
2.2. Measurements with A Dodecahedron Speaker
2.3. Acoustic Parameters-Compensation Method
3. Results
- Measurements to Investigate Optimum Hand Configuration
- Measurements at Different Source–Receiver Distances
- Measurements at Different Spaces
3.1. Measurements to Investigate Optimum Hand Configuration
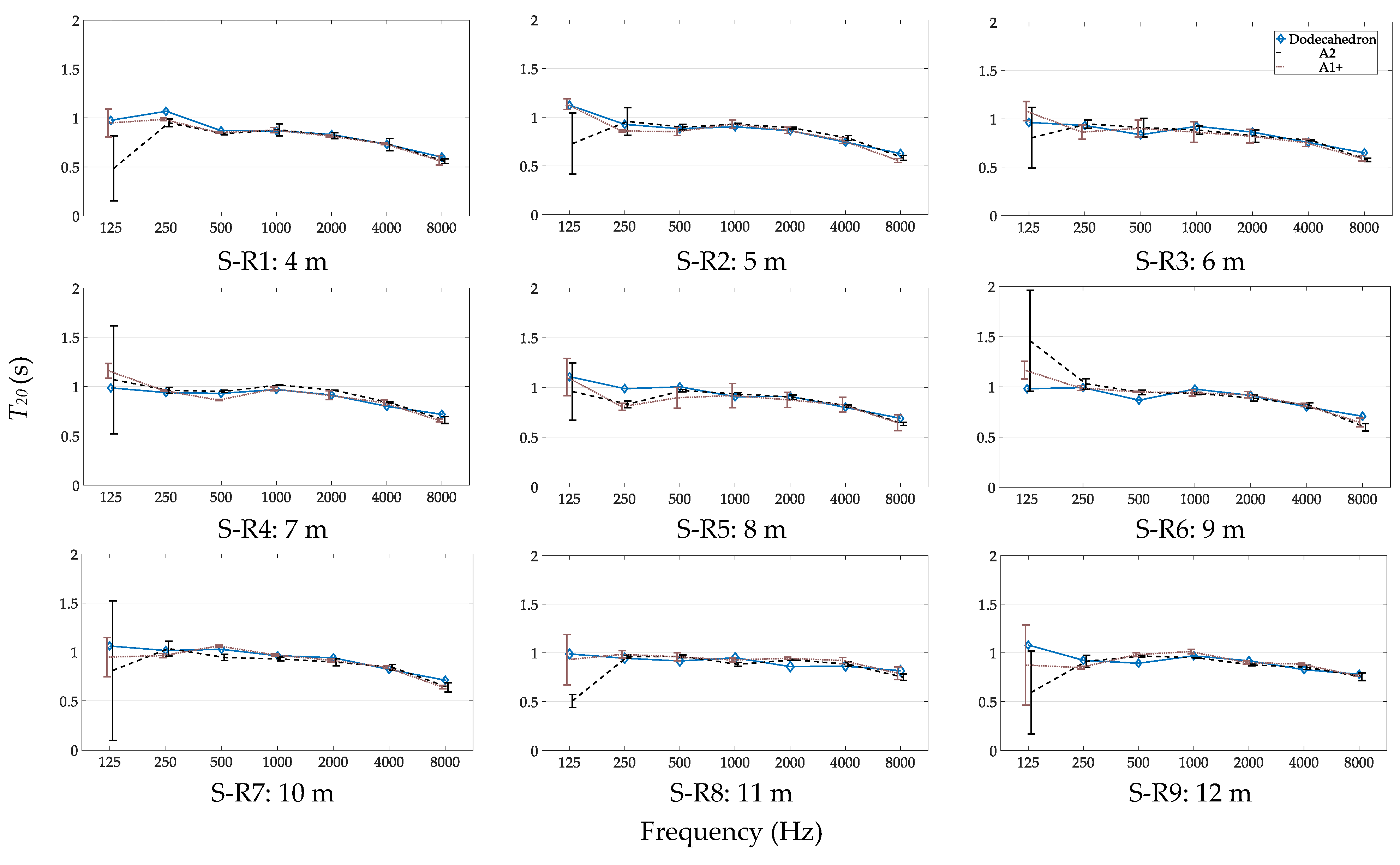
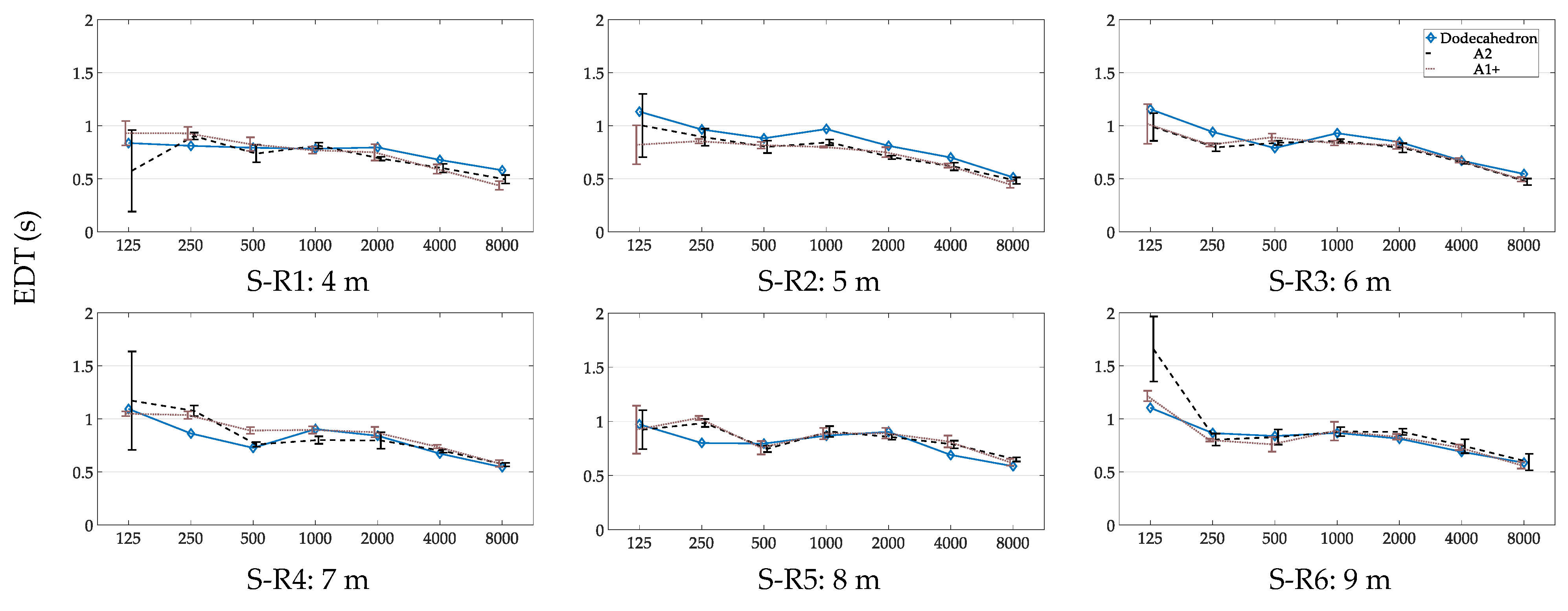
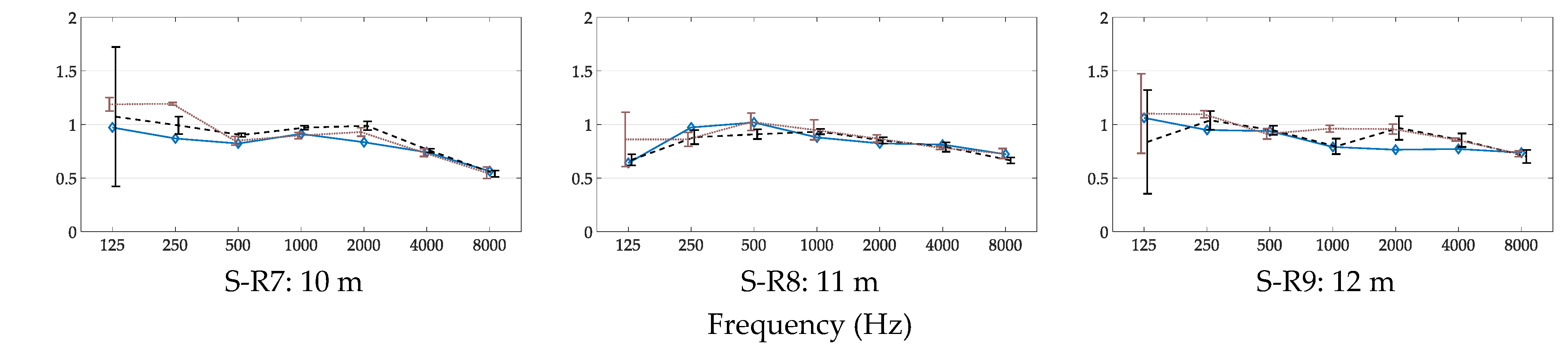
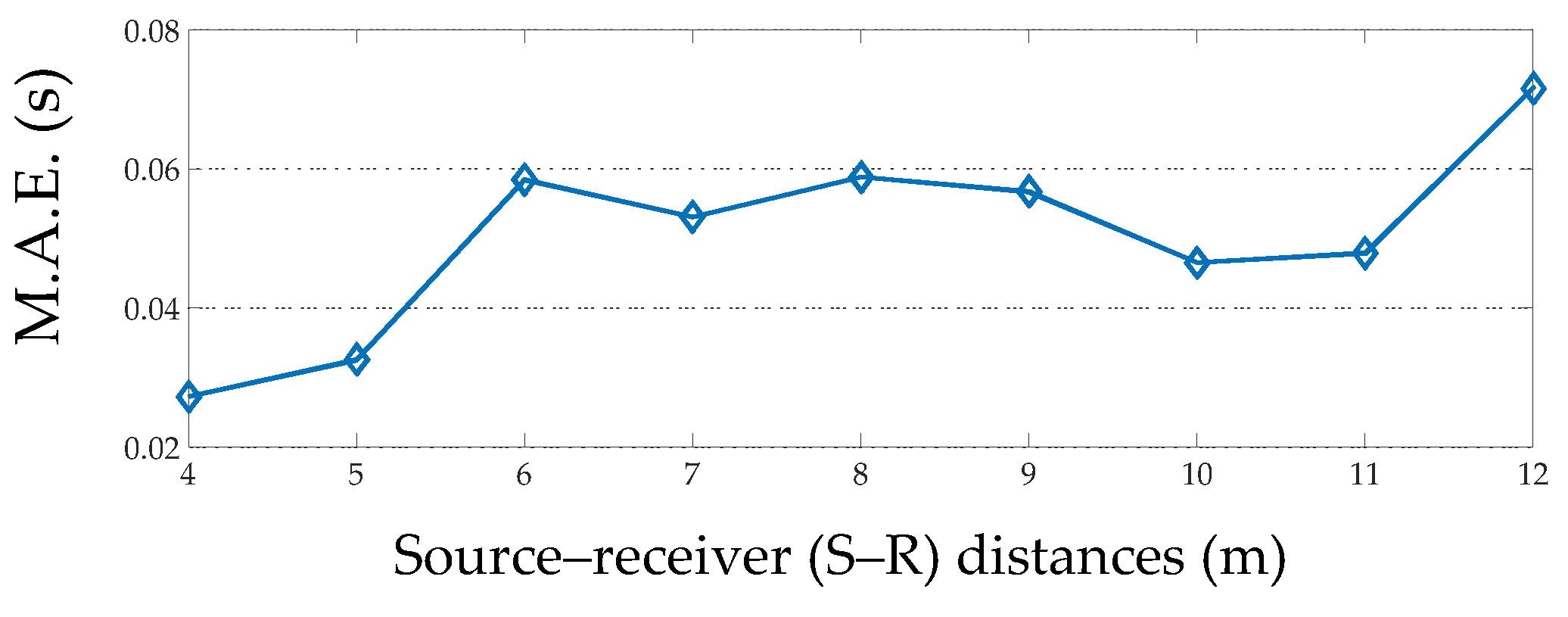
3.2. Measurements at Different Source–Receiver Distances
3.2.1. T20 for Different Source–Receiver Distances
3.2.2. EDT for Different Source–Receiver Distances
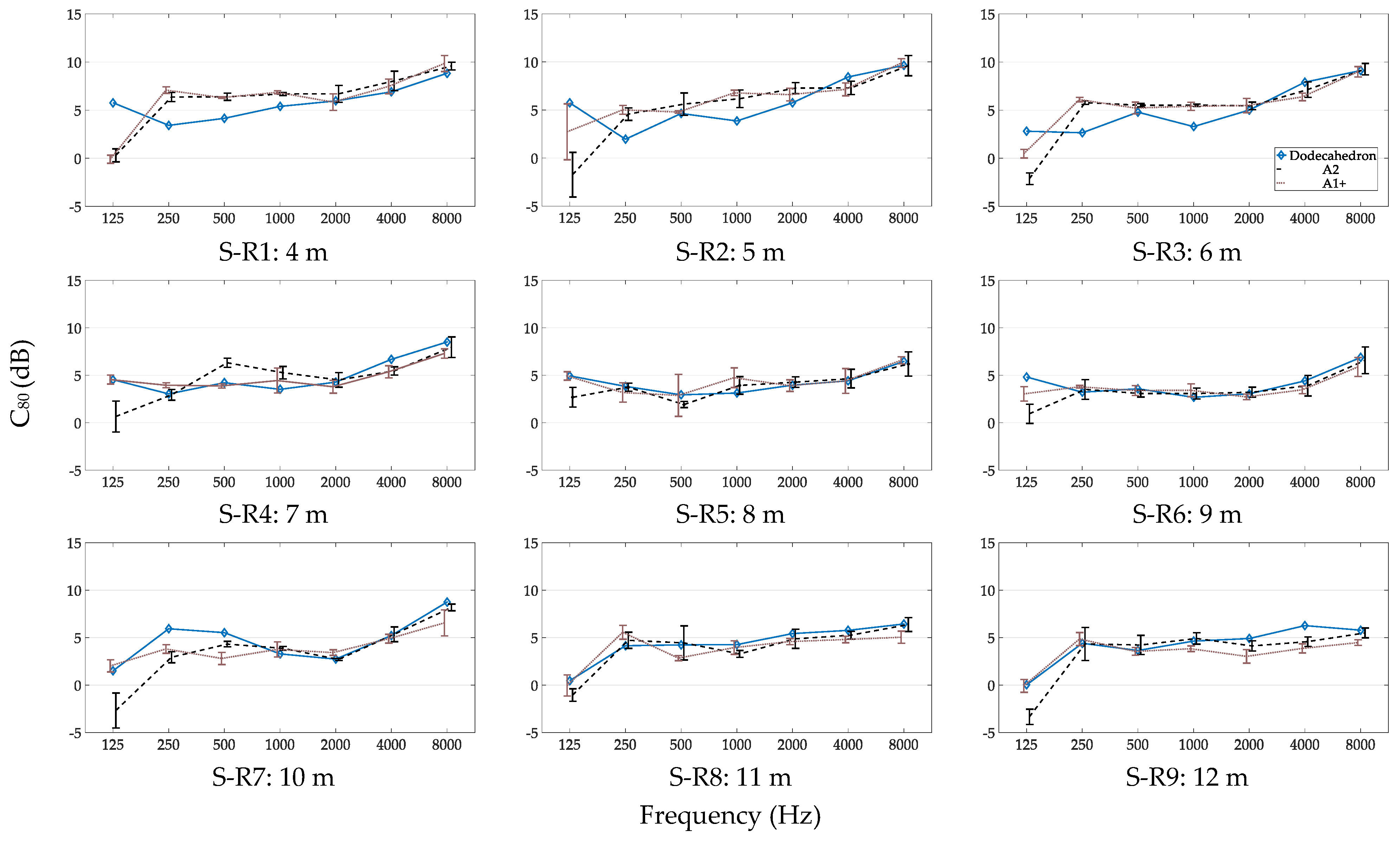
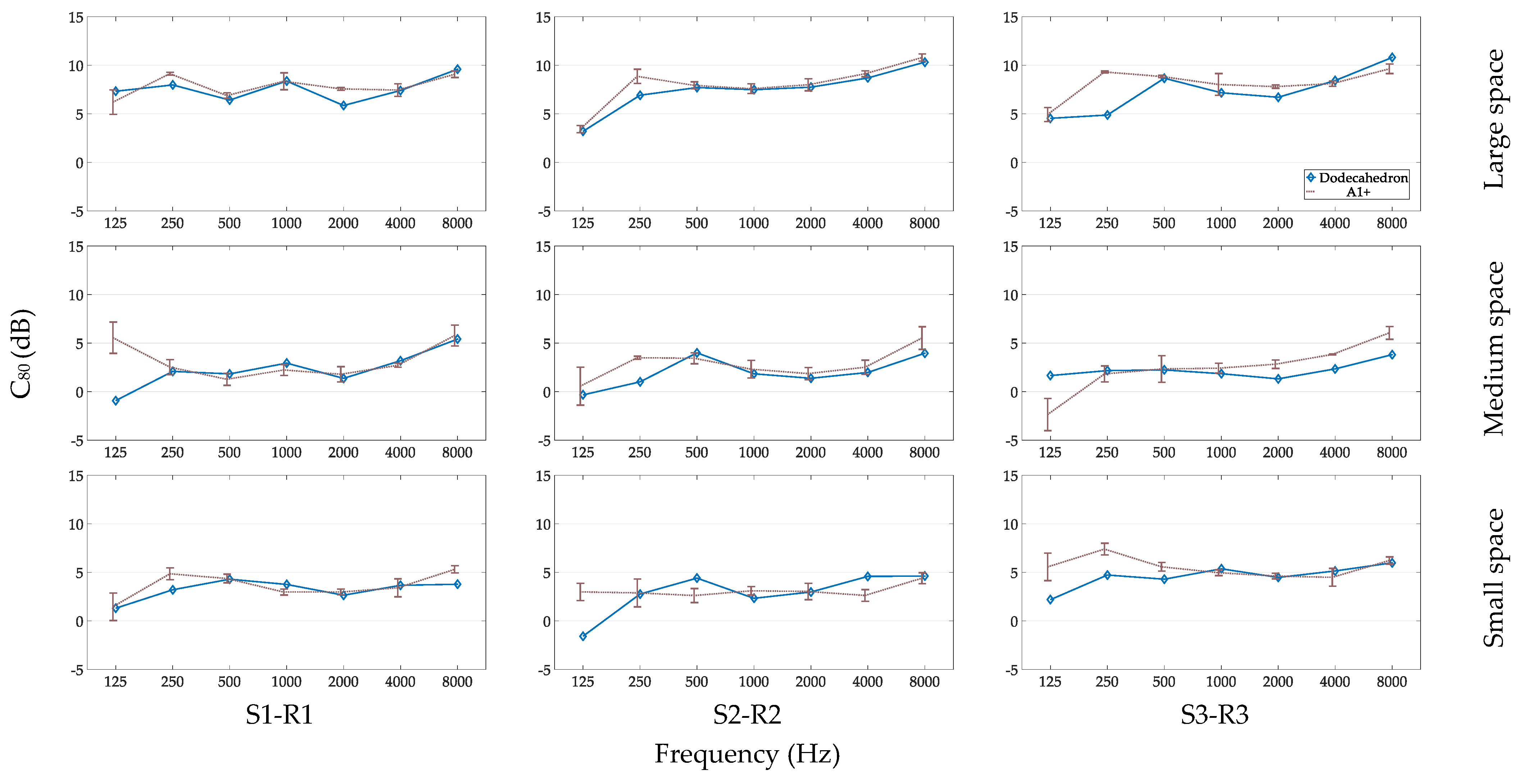
3.2.3. C80 for Different Source–Receiver Distances
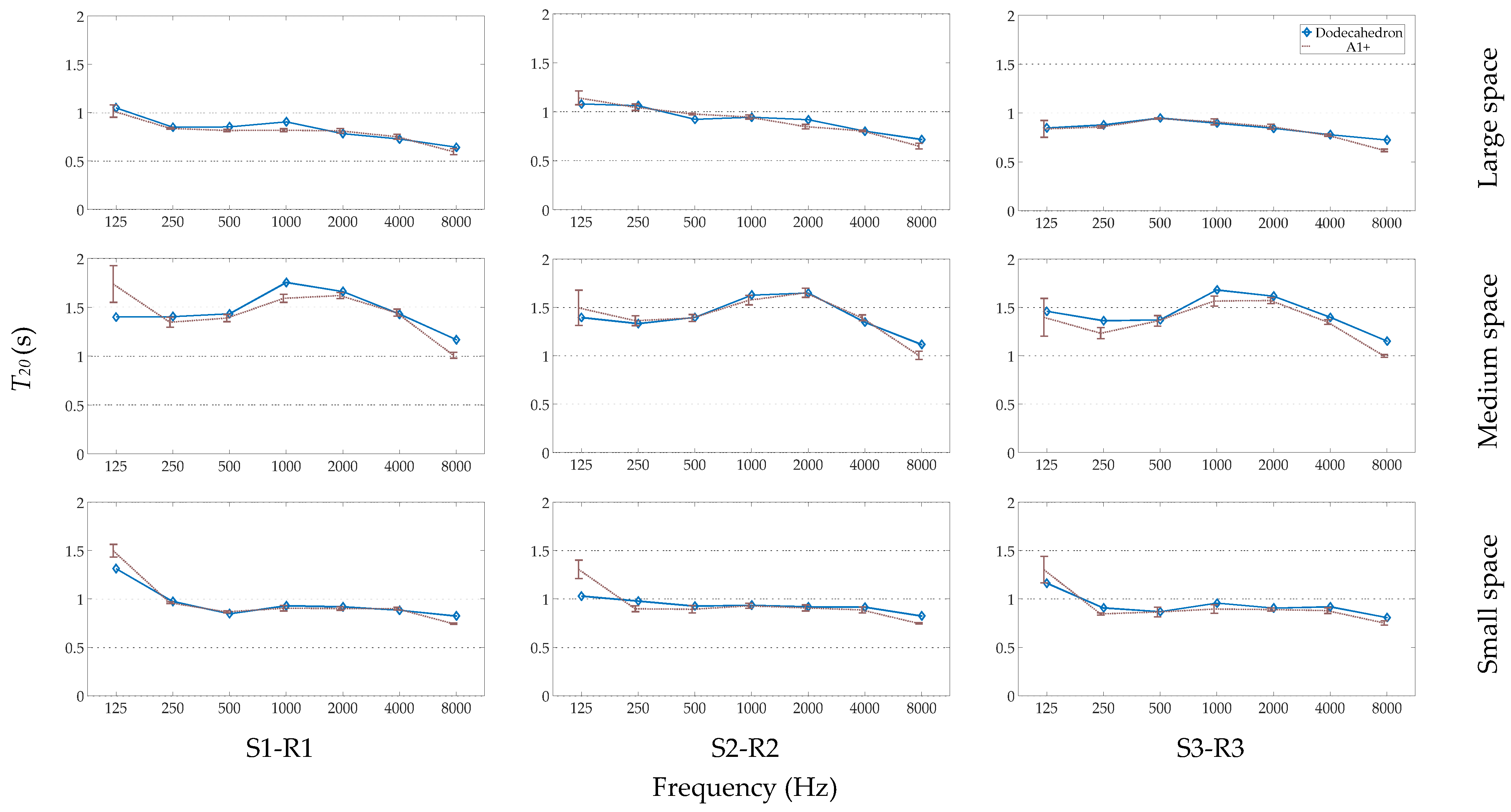
3.3. Measurements at Different Spaces
3.3.1. T20 for Different Spaces
3.3.2. EDT for Different Spaces
3.3.3. C80 for Different Spaces
4. Discussion
- Suggested Hand Configuration for Acoustic Measurements
- Measurement of T with a Handclap
- Measurement of EDT with a Handclap
- Measurement of C80 with a Handclap
- Suggested Steps for Measurements with a Handclap as an Acoustic Source
4.1. Suggested Hand Configuration for Acoustic Measurements
4.2. Measurement of T with A Handclap
4.3. Measurement of EDT with a Handclap
4.4. Measurement of C80 with a Handclap
4.5. Suggested Steps for Measurements with A Handclap as An Acoustic Source
- Utilization of hand configuration A1+ for acoustic measurements (Figure 1). This study has shown that this hand configuration will provide the best possible signal-to-noise levels for most frequency bands in typical spaces and will yield the best results (more on this on Section 4.1);
- Training of hand configuration A1+ to optimize results is recommended. Training of measurements with a handclap has shown to result in better repeatability of the measurements [26];
- Source–receiver distance in measurements should be near minimum distance, dmin, (Equation (2)) suggested by the ISO 3382-2 [48]. At shorter source–receiver distance, the signal-to-noise ratio is higher, therefore better measurements can be achieved (more on this on Section 4.2);
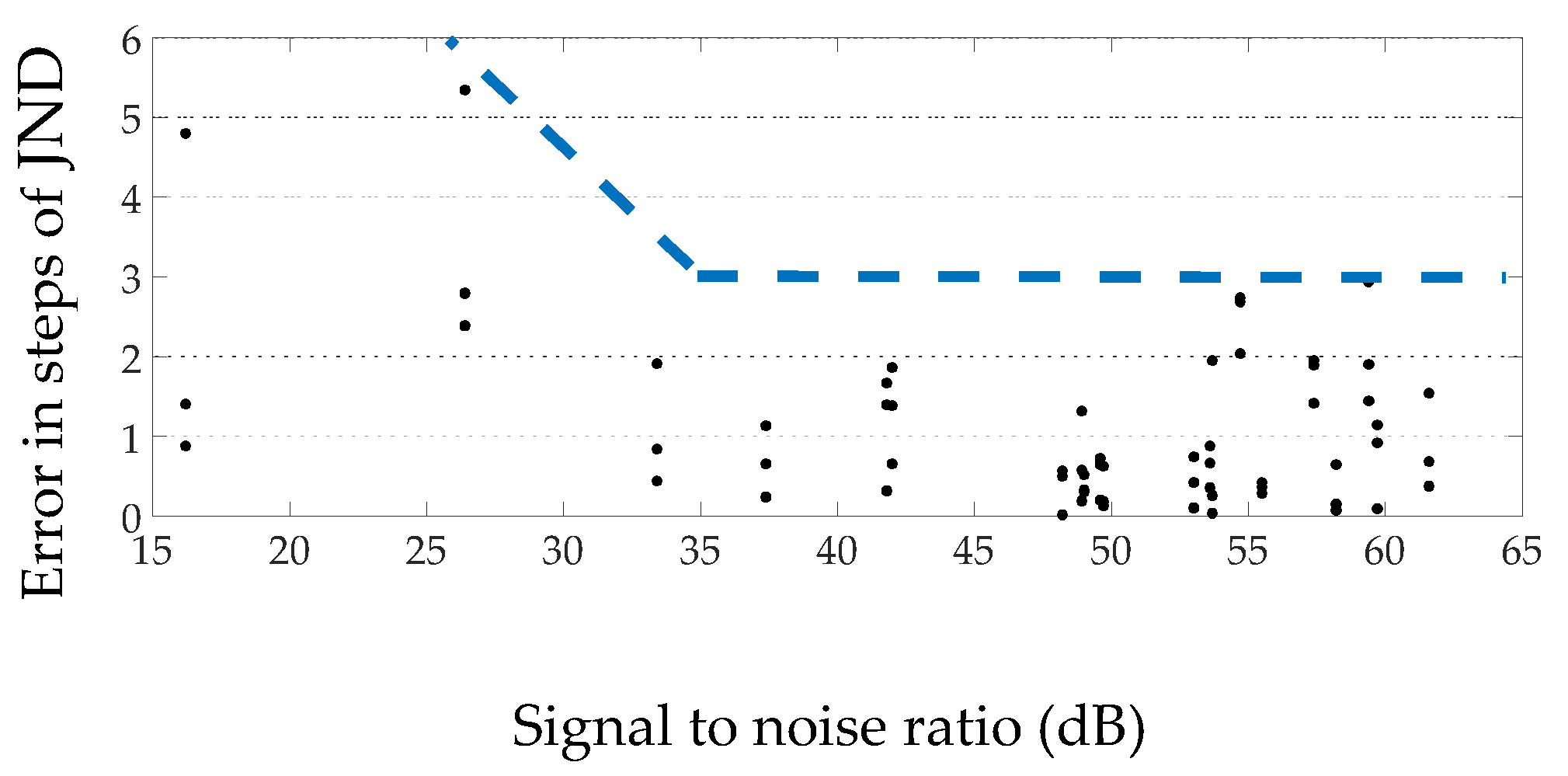
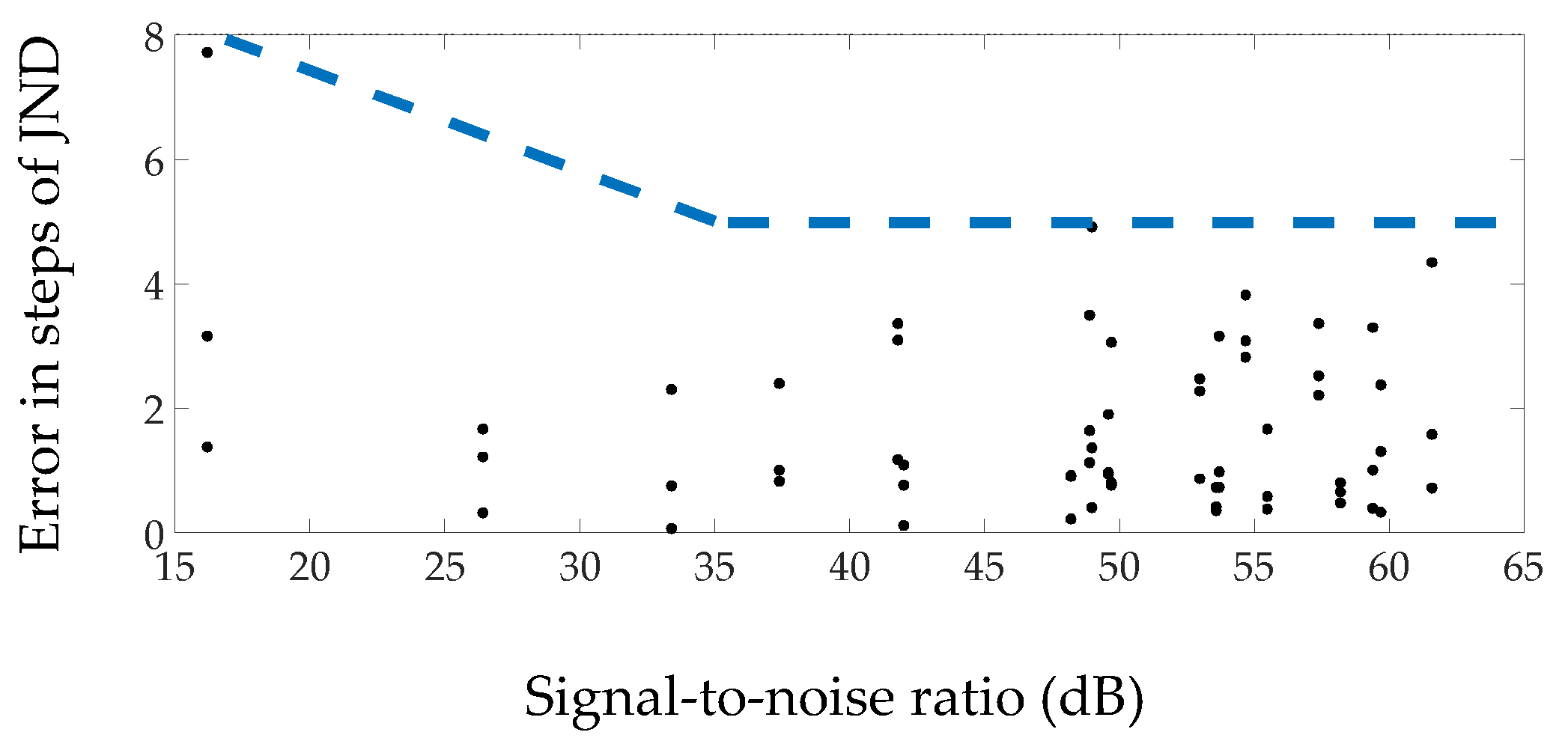
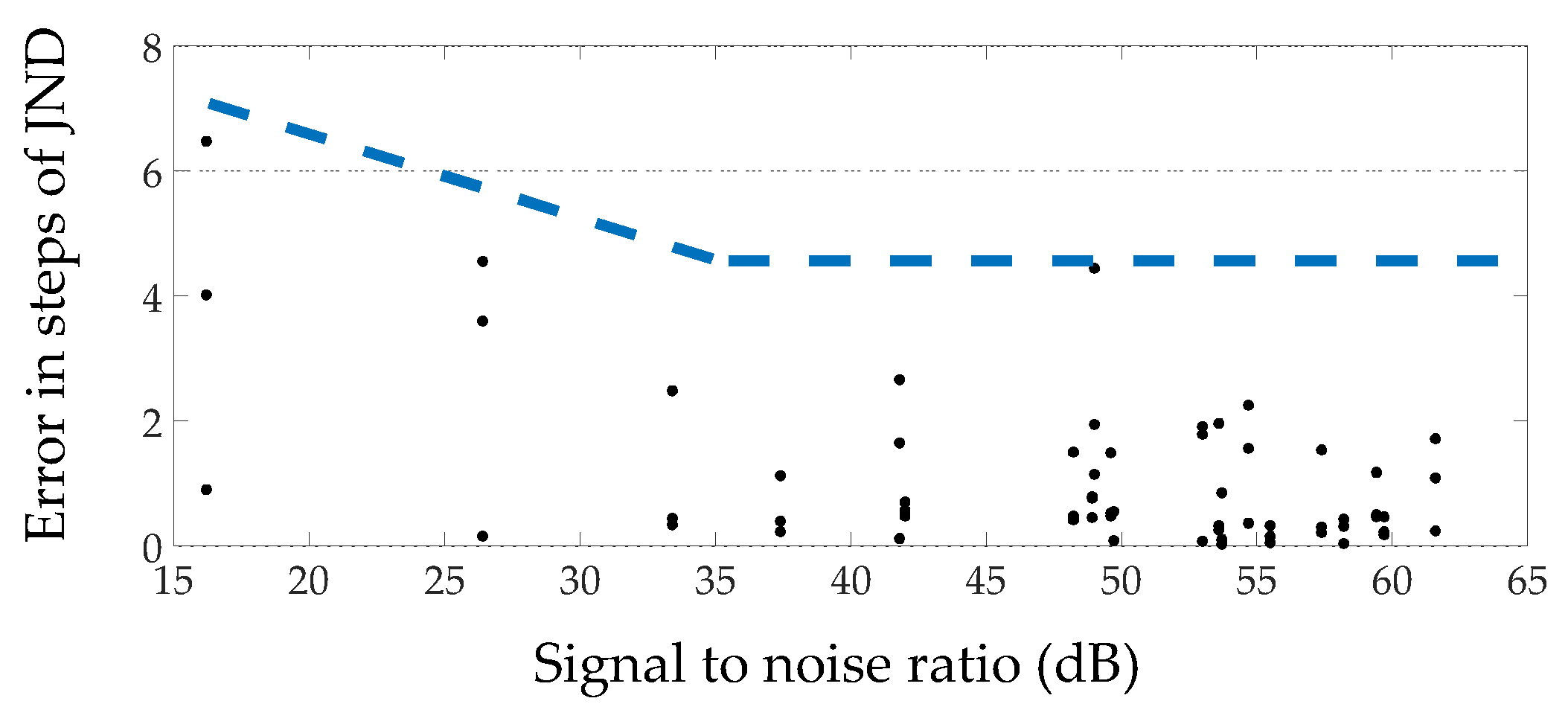
- If available, background noise levels should be measured in order to evaluate the accuracy of the results according to the signal-to-noise ratio. The results indicating probable measurement accuracy according to the signal-to-background noise level provided in this paper (more on this on Section 4.2, Section 4.3, Section 4.4);
- Measurements for the same source–receiver positions should be performed at least four times and averaged;
- A compensation method for the background noise should be applied in the processing of measurements; Background noise affects the decay range of the impulse response decay curves and the evaluation of the acoustic parameters (more on this on Section 2.3). Available software for acoustics measurements that provides compensation methods can be found in Reference [62].
- If possible, measurements with a mobile phone should be avoided. Measurements of T with a handclap and different cellphones as sound recorders were found to provide different results [34], while in another study, differences of T were within +/−0.2 s compared to measurements with a sound level meter [35]. Measurements with a cellphone have been studied mainly for the measurements of SPL [63]. Differences were found across operating systems (iOS and Android), across different versions of the operating system as well as applications (apps) for those systems. Difference in measurements can be attributed to factors such as small dynamic range, internal filters applied in the low frequency range as well as input gain control applied by (some of) the operating systems. In conclusion, measurements with a mobile phone depend on many factors and the expected accuracy is not easy to predict. However external microphones can be used for better results [64].
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A# | Aligned (hand configuration) |
| C80 | Clarity |
| EDT | Early Decay Time |
| ESS | Exponential Sine Sweep |
| ISO | International Organization for Standardization |
| JND | Just Noticeable Difference |
| MEMS | Micro-Electromechanical Systems |
| MLS | Maximum Length Sequence |
| O# | Opposite (hand configuration) |
| P# | Parallel (hand configuration) |
| SD | Standard Deviation |
| SNR | Sound-to-Noise Ratio |
| SPLs | Sound Pressure Levels |
| T | Reverberation Time |
| T20 | Reverberation Time (based on a 20 dB dynamic range) |
| T30 | Reverberation Time (based on a 30 dB dynamic range) |
| Ts | Centre Time |
Appendix A
| Source Position | Receiver Positions | ||||
|---|---|---|---|---|---|
| S(4.58, 4.63, 1.30) | R1(4.58, 8.62, 1.53) | R2(4.58, 9.62, 1.66) | R3(4.58, 10.61, 1.80) | R4(4.58, 11.60, 1.94) | R5(4.58, 12.59, 2.09) |
| R6(4.58, 13.58, 2.24) | R7(4.58, 14.57, 2.38) | R8(4.58, 15.56, 2.53) | R9(4.58, 16.55, 2.68) | ||
| Large Space | Medium Space | Small Space | |||
|---|---|---|---|---|---|
| S1(3.36, 3.64, 1.30) | R1(3.57, 7.71, 1.42) | S1(2.55, 2.20, 1.30) | R1(2.03, 3.78, 1.20) | S1(1.40, 3.15, 1.30) | R1(2.16, 5.76, 1.20) |
| S2(5.92, 1.82, 2.20) | R2(5.78, 5.77, 1.20) | S2(4.70, 1.55, 1.30) | R2(3.85, 3.98, 1.20) | S2(3.15, 2.53, 1.30) | R2(3.57, 4.98, 1.20) |
| S3(8.80, 3.30, 1.30) | R3(9.24, 7.27, 1.36) | S3(5.62, 1.17, 1.30) | R3(6.57, 3.02, 1.20) | S3(4.20, 1.40, 1.30) | R3(4.31, 3.35, 1.20) |
References
- Crocker, M.J. Encyclopedia of Acoustics; John Wiley: Hoboken, NJ, USA, 1997; p. 107. [Google Scholar]
- Kuttruff, H. Acoustics, an Introduction; Taylor and Francis: New York, NY, USA, 2007; p. 84. [Google Scholar]
- Papadakis, N.M.; Stavroulakis, G.E. Review of Acoustic Sources Alternatives to a Dodecahedron Speaker. Appl. Sci. 2019, 9, 3705. [Google Scholar] [CrossRef]
- Leishman, T.W.; Rollins, S.; Smith, H.M. An experimental evaluation of regular polyhedron loudspeakers as omnidirectional sources of sound. J. Acoust. Soc. Am. 2006, 120, 1411–1422. [Google Scholar] [CrossRef]
- ISO. ISO 3382-1: 2009. In Measurement of Room Acoustic Parameters—Part 1: Performance Spaces; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- ISO. ISO 16283-1:2014. In Acoustics—Field Measurement of Sound Insulation in Buildings and of Building Elements—Part 1: Airborne Sound Insulation; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- ISO. 10140-5. Acoustics—Laboratory Measurement of Sound Insulation of Building Elements—Part 5: Requirements for Test Facilities and Equipment; ISO: Geneva, Switzerland, 2014. [Google Scholar]
- Schroeder, M.R. Integrated impulse method measuring sound decay without using impulses. J. Acoust. Soc. Am. 1979, 66, 497–500. [Google Scholar] [CrossRef]
- Farina, A. Simultaneous measurement of impulse response and distortion with a swept-sine technique. In Proceedings of Audio Engineering Society Convention 108; Audio Engineering Society: Paris, France, 2000. [Google Scholar]
- ISO. ISO 18233-2006 Acoustics—Application of New Measurement Methods in Building and Room Acoustics; ISO: Geneva, Switzerland, 2006. [Google Scholar]
- Stan, G.-B.; Embrechts, J.-J.; Archambeau, D. Comparison of different impulse response measurement techniques. J. Audio Eng. Soc. 2002, 50, 249–262. [Google Scholar]
- Guidorzi, P.; Barbaresi, L.; D’Orazio, D.; Garai, M. Impulse responses measured with MLS or Swept-Sine signals applied to architectural acoustics: An in-depth analysis of the two methods and some case studies of measurements inside theaters. Energy Procedia 2015, 78, 1611–1616. [Google Scholar] [CrossRef]
- Antoniadou, S.; Papadakis, N.M.; Stavroulakis, G.E. Measuring Acoustic Parameters with ESS and MLS: Effect of Artificially Varying Background Noises. In Proceedings of the Euronoise 2018, Heraclion, Greece, 27–31 May 2018. [Google Scholar]
- Pätynen, J.; Katz, B.F.; Lokki, T. Investigations on the balloon as an impulse source. J. Acoust. Soc. Am. 2011, 129, EL27–EL33. [Google Scholar] [CrossRef]
- Lamothe, M.R.; Bradley, J. Acoustical characteristics of guns as impulse sources. Can. Acoust. 1985, 13, 16–24. [Google Scholar]
- Arana, M.; Vela, A.; San Martin, L. Calculating the impulse response in rooms using pseudo-impulsive acoustic sources. Acta Acust. United Acust. 2003, 89, 377–380. [Google Scholar]
- Polack, J.-D.; Christensen, L.S.; Juhl, P.M. An innovative design for omnidirectional sound sources. Acta Acust. United Acust. 2001, 87, 505–512. [Google Scholar]
- Sumarac-Pavlovic, D.; Mijic, M.; Kurtovic, H. A simple impulse sound source for measurements in room acoustics. Appl. Acoust. 2008, 69, 378–383. [Google Scholar] [CrossRef]
- Papadakis, N.M.; Stavroulakis, G.E. Low Cost Omnidirectional Sound Source Utilizing a Common Directional Loudspeaker for Impulse Response Measurements. Appl. Sci. 2018, 8, 1703. [Google Scholar] [CrossRef]
- Sayin, U.; Artís, P.; Guasch, O. Realization of an omnidirectional source of sound using parametric loudspeakers. J. Acoust. Soc. Am. 2013, 134, 1899–1907. [Google Scholar] [CrossRef] [PubMed]
- Kruse, R.; Häußler, A.; van de Par, S. An omnidirectional loudspeaker based on a ring-radiator. Appl. Acoust. 2013, 74, 1374–1377. [Google Scholar] [CrossRef]
- San Martín, R.; Arana, M.; Machín, J.; Arregui, A. Impulse source versus dodecahedral loudspeaker for measuring parameters derived from the impulse response in room acoustics. J. Acoust. Soc. Am. 2013, 134, 275–284. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Agustina, L.; Barnard, J. Practical and technical suitability perceptions of sound sources and test signals used in room acoustic testing. In INTER-NOISE and NOISE-CON Congress and Conference Proceedings; Institute of Noise Control Engineering: Madrid, Spain, 2019. [Google Scholar]
- Fletcher, N.H. Shock waves and the sound of a hand-clap–a simple model. Acoust. Aust. 2013, 41, 165–168. [Google Scholar]
- Hargather, M.J.; Settles, G.S.; Madalis, M.J. Schlieren imaging of loud sounds and weak shock waves in air near the limit of visibility. Shock Waves 2010, 20, 9–17. [Google Scholar] [CrossRef]
- Repp, B.H. The sound of two hands clapping: An exploratory study. J. Acoust. Soc. Am. 1987, 81, 1100–1109. [Google Scholar] [CrossRef]
- Jylhä, A.; Erkut, C. Inferring the Hand Configuration from Hand Clapping Sounds. In Proceedings of the 11th International Conference Digital Audio Effects Workshop (DAFx’08), Espoo, Finland, 1–4 September 2008; pp. 301–304. [Google Scholar]
- Peltola, L.; Erkut, C.; Cook, P.R.; Valimaki, V. Synthesis of hand clapping sounds. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 1021–1029. [Google Scholar] [CrossRef]
- Griesinger, D. Beyond MLS-Occupied hall measurement with FFT techniques. In Proceedings of Audio Engineering Society Convention 101; Audio Engineering Society: New York, NY, USA, 1996. [Google Scholar]
- San Martín, R.; Arana, M. Uncertainties caused by source directivity in room-acoustic investigations. J. Acoust. Soc. Am. 2008, 123, EL133–EL138. [Google Scholar] [CrossRef]
- Knüttel, T.; Witew, I.B.; Vorländer, M. Influence of “omnidirectional” loudspeaker directivity on measured room impulse responses. J. Acoust. Soc. Am. 2013, 134, 3654–3662. [Google Scholar] [CrossRef]
- Rizzi, L.; Ghelfi, G.; Campanini, S.; Rosati, A. Rapid Room Acoustics Parameters Measurements with Smartphones. In Proceedings of the ISCV22, Florence, Italy, 12–16 July 2019. [Google Scholar]
- Seetharaman, P.; Tarzia, S.P. The hand clap as an impulse source for measuring room acoustics. In Proceedings of Audio Engineering Society Convention 132; Audio Engineering Society: New York, NY, USA, 2012. [Google Scholar]
- Huang, K. Impulse response of the Bayreuth Festspielhaus. arXiv 2017, arXiv:1703.07080. [Google Scholar]
- Brown, R.; Evans, L. Acoustics and the Smartphone. In Proceedings of the ACOUSTICS 2011, Gold Coast, Australia, 2–4 November 2011. [Google Scholar]
- Halmrast, T. When source is also receiver. Build. Acoust. 2013, 20, 403–421. [Google Scholar] [CrossRef]
- Shukla, A.; Patil, P.; Nanaware, K.; Salve, S. Clap Pattern Based Electrical Appliance Control. IJSRD 2017, 5, 902–905. [Google Scholar]
- Olokede, S.S. Design of a clap activated switch. Leonardo J. Sci. 2008, 7, 44–58. [Google Scholar]
- Kilis, N.; Mitianoudis, N. A Novel Scheme for Single-Channel Speech Dereverberation. Acoustics 2019, 1, 711–725. [Google Scholar] [CrossRef]
- Zäh, U.; Riedhammer, K.; Bocklet, T.; Nöth, E. Clap Your Hands! Calibrating Spectral Subtraction for Dereverberation. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 4226–4229. [Google Scholar]
- Tsilfidis, A.; Georganti, E.; Kokkinis, E.K.; Mourjopoulos, J. Speech Dereverberation Based on a Recorded Handclap. In Proceedings of the 2011 17th International Conference on Digital Signal Processing (DSP), Corfu, Greece, 6–8 July 2011; pp. 1–6. [Google Scholar]
- Malik, H.; Mahmood, H. Acoustic environment identification using unsupervised learning. Secur. Inform. 2014, 3, 11. [Google Scholar] [CrossRef]
- Jylhä, A.; Erkut, C. Sonic interactions with hand clap sounds. Proc. Audio Most. 2008, 2008, 93–100. [Google Scholar]
- Jylhä, A.; Erkut, C. A hand clap interface for sonic interaction with the computer. In Proceedings of CHI’09 Extended Abstracts on Human Factors in Computing Systems; Association for Computing Machinery: New York, NY, USA, 2009; pp. 3175–3180. [Google Scholar]
- Hanahara, K.; Tada, Y.; Muroi, T. Human-robot communication by means of hand-clapping (preliminary experiment with hand-clapping language). In Proceedings of the 2007 IEEE International Conference on Systems, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2007; pp. 2995–3000. [Google Scholar]
- Almahdi, R.; Diharjo, K.; Hidayat, R.L.G.; Suharty, N.S. In situ test: Acoustic performance of eco-absorber panel based albizia wood and sugar palm fiber on meeting room in UNS Inn Hotel. In Proceedings of IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; p. 012033. [Google Scholar]
- Lee, Y.; Cha, H. A Light-weight and Scalable Localization Technique Using Mobile Acoustic Source. In Proceedings of the Sixth IEEE International Conference on Computer and Information Technology (CIT’06), Seoul, Korea, 20–22 September 2006; p. 235. [Google Scholar]
- ISO. ISO 3382-2: 2008. In Measurement of Room Acoustic Parameters—Part 2: Reverberation Time in Ordinary Rooms; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- Hak, C.; Wenmaekers, R.; Van Luxemburg, L. Measuring room impulse responses: Impact of the decay range on derived room acoustic parameters. Acta Acust. United Acust. 2012, 98, 907–915. [Google Scholar] [CrossRef]
- Rossing, T.D. Springer Handbook of Acoustics; Springer: Berlin, Germany, 2007; p. 323. [Google Scholar]
- Reichardt, W.; Alim, O.A.; Schmidt, W. Abhängigkeit der Grenzen zwischen brauchbarer und unbrauchbarer Durchsichtigkeit von der Art des Musikmotives, der Nachhallzeit und der Nachhalleinsatzzeit. Appl. Acoust. 1974, 7, 243–264. [Google Scholar] [CrossRef]
- Kuttruff, H. Room Acoustics; CRC Press: Boca Raton, FL, USA, 2016; p. 169. [Google Scholar]
- Guski, M.; Vorländer, M. Comparison of noise compensation methods for room acoustic impulse response evaluations. Acta Acust. United Acust. 2014, 100, 320–327. [Google Scholar] [CrossRef]
- Chu, W.T. Comparison of reverberation measurements using Schroeder’s impulse method and decay-curve averaging method. J. Acoust. Soc. Am. 1978, 63, 1444–1450. [Google Scholar] [CrossRef]
- Guski, M. Influences of External Error Sources on Measurements of Room Acoustic Parameters; Logos Verlag Berlin GmbH: Berlin, Germany, 2015; Volume 24. [Google Scholar]
- Bies, D.A.; Scharton, T. Relation between Near Field and Far Field Acoustic Measurements; National Aeronautics and Space Administration (NASA), Ames Research Center: Mountain View, CA, USA, 1974. [Google Scholar]
- Hosoe, S.; Nishino, T.; Itou, K.; Takeda, K. Measurement of head-related transfer functions in the proximal region. In Proceedings of Forum Acusticum; European Acoustics Association: Budapest, Hungary, 2005; pp. 2539–2542. [Google Scholar]
- Weisser, A.; Buchholz, J.M. Conversational speech levels and signal-to-noise ratios in realistic acoustic conditions. J. Acoust. Soc. Am. 2019, 145, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.M.; Vigeant, M.C. Evaluations of output from room acoustic computer modeling and auralization due to different sound source directionalities. Appl. Acoust. 2008, 69, 1281–1293. [Google Scholar] [CrossRef]
- Wenmaekers, R.; Hak, C.; Hornikx, M.; Kohlrausch, A. Sensitivity of stage acoustic parameters to source and receiver directivity: Measurements on three stages and in two orchestra pits. Appl. Acoust. 2017, 123, 20–28. [Google Scholar] [CrossRef]
- Vorländer, M.; Guski, M. Suggestions for Revision of ISO 3382. In Proceedings of the DAGA 2016, 42nd Annual Conference on Acoustics, Aachen, Germany, 14–17 March 2016. [Google Scholar]
- Dietrich, P.; Guski, M.; Pollow, M.; Masiero, B.; Müller-Trapet, M.; Scharrer, R.; Vorländer, M. ITA-toolbox-An open source MATLAB toolbox for acousticians. Fortschr. Akust. DAGA 2012, 12, 151–152. [Google Scholar]
- Kardous, C.A.; Shaw, P.B. Evaluation of smartphone sound measurement applications. J. Acoust. Soc. Am. 2014, 135, EL186–EL192. [Google Scholar] [CrossRef] [PubMed]
- Kardous, C.A.; Shaw, P.B. Evaluation of smartphone sound measurement applications (apps) using external microphones—A follow-up study. J. Acoust. Soc. Am. 2016, 140, EL327–EL333. [Google Scholar] [CrossRef]

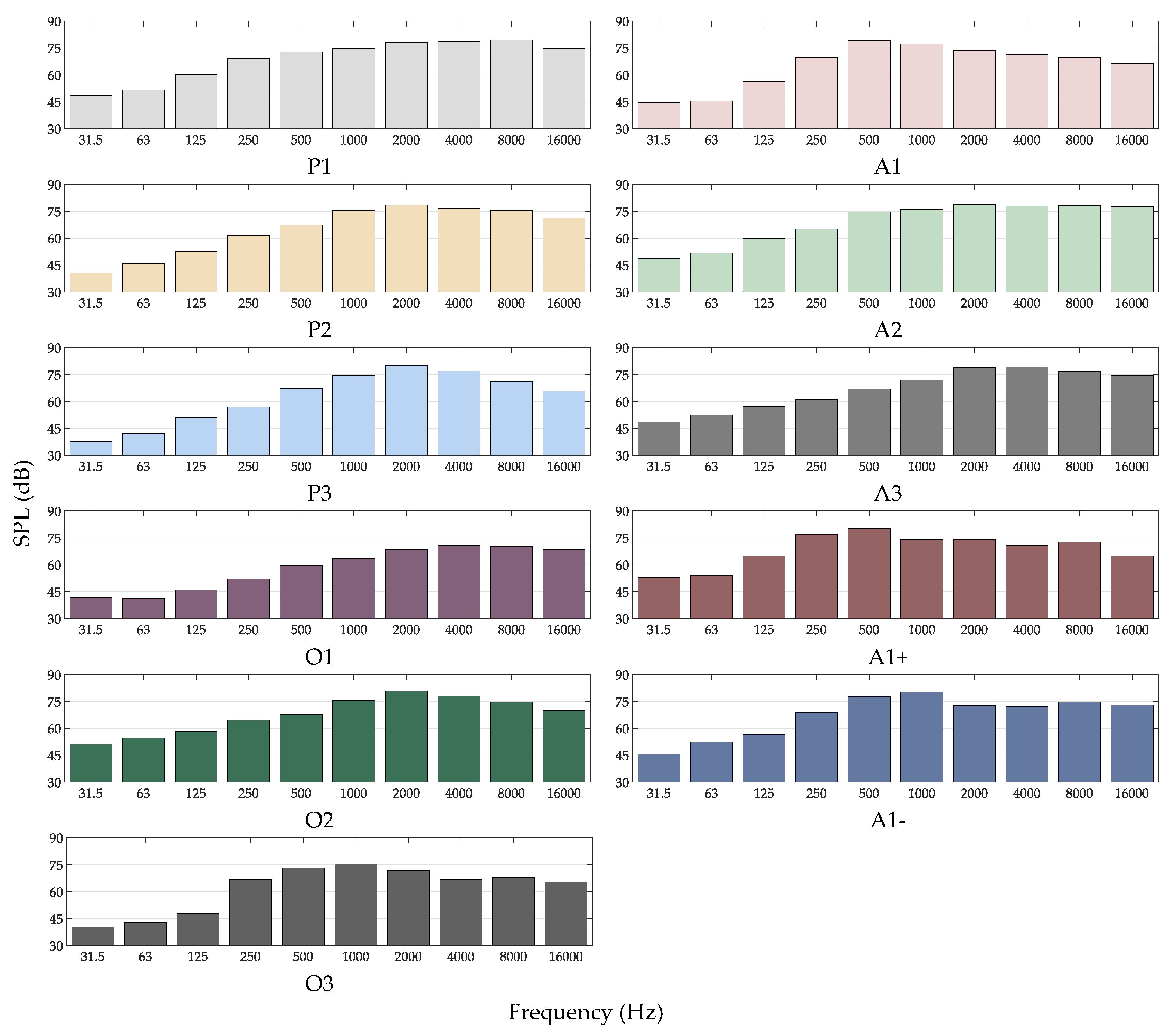



| Hand Configuration | P1 | P2 | P3 | A1 | A2 | A3 | A1+ | A1− | O1 | O2 | O3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SPL (dB) | 84.2 | 83.2 | 83.0 | 83.0 | 85.2 | 84.1 | 83.8 | 84.1 | 76.0 | 84.3 | 79.5 |
| Standard Deviation (dB) | 5.61 | 7.48 | 6.43 | 5.90 | 6.28 | 7.05 | 4.47 | 5.55 | 5.69 | 7.39 | 4.49 |
| Maximum SPL (dB) | 95.4 | 97.0 | 95.8 | 97.0 | 96.3 | 95.5 | 89.8 | 91.8 | 86.8 | 95.3 | 86.1 |
| Natural Configuration (%) | 4.54 | 18.2 | 0.00 | 9.00 | 63.6 | 0.00 | 4.54 | 0.00 | 0.00 | 0.00 | 0.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadakis, N.M.; Stavroulakis, G.E. Handclap for Acoustic Measurements: Optimal Application and Limitations. Acoustics 2020, 2, 224-245. https://doi.org/10.3390/acoustics2020015
Papadakis NM, Stavroulakis GE. Handclap for Acoustic Measurements: Optimal Application and Limitations. Acoustics. 2020; 2(2):224-245. https://doi.org/10.3390/acoustics2020015
Chicago/Turabian StylePapadakis, Nikolaos M., and Georgios E. Stavroulakis. 2020. "Handclap for Acoustic Measurements: Optimal Application and Limitations" Acoustics 2, no. 2: 224-245. https://doi.org/10.3390/acoustics2020015
APA StylePapadakis, N. M., & Stavroulakis, G. E. (2020). Handclap for Acoustic Measurements: Optimal Application and Limitations. Acoustics, 2(2), 224-245. https://doi.org/10.3390/acoustics2020015






