Influence of Sound-Absorbing Material Placement on Room Acoustical Parameters
Abstract
1. Introduction
2. Background and Related Research
3. Methods to Study Absorption Placement
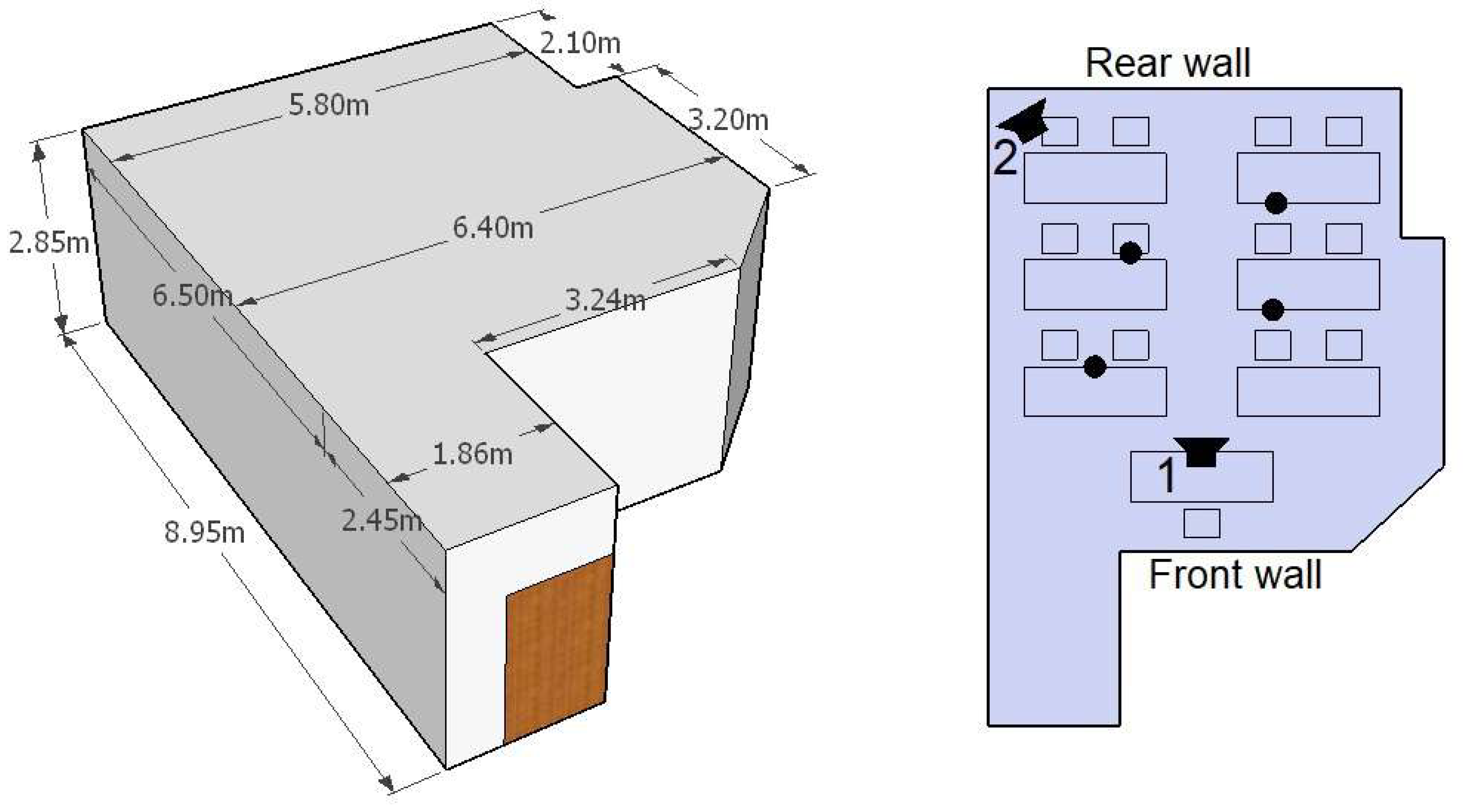
3.1. Reverberation Room
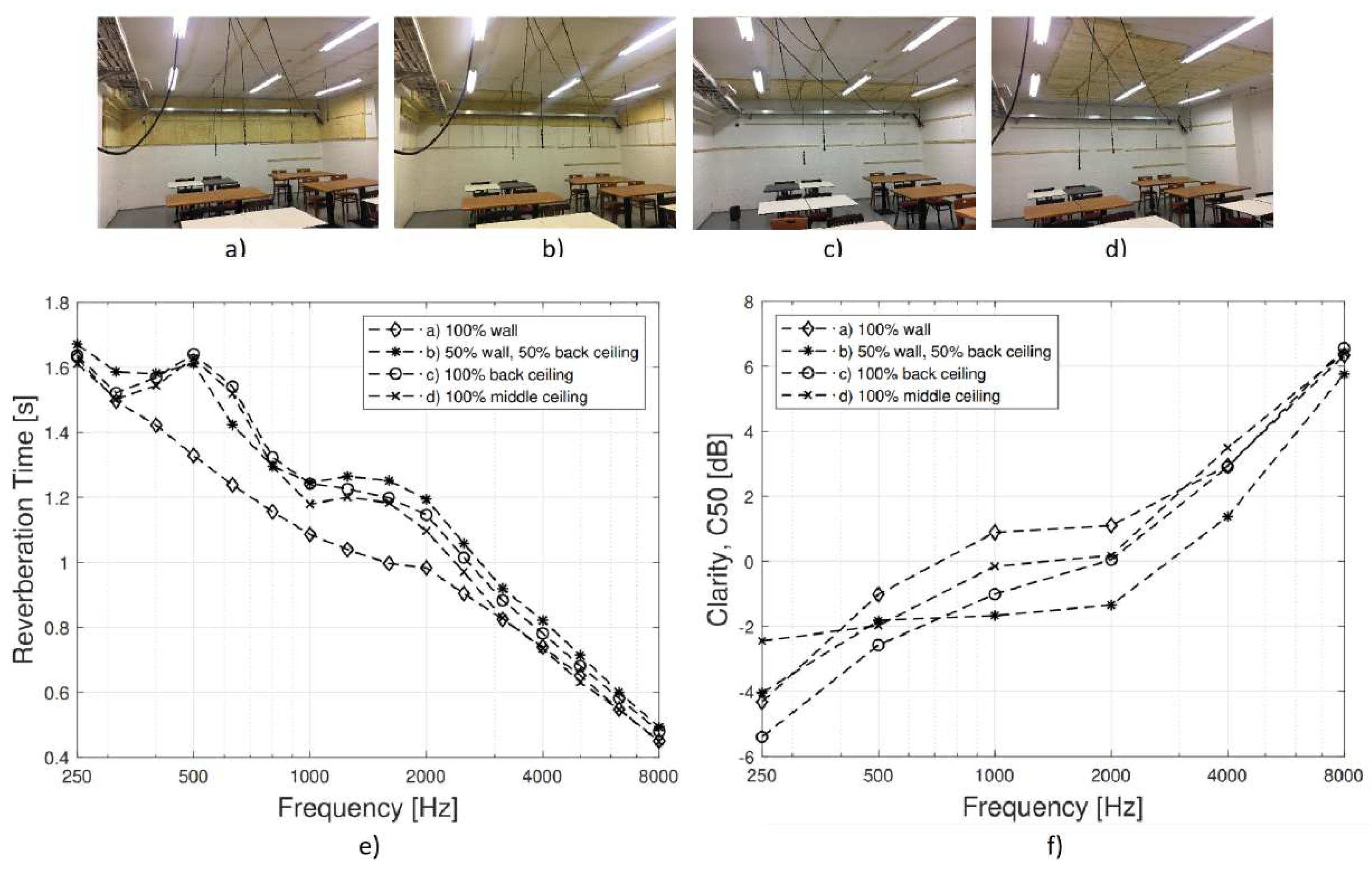
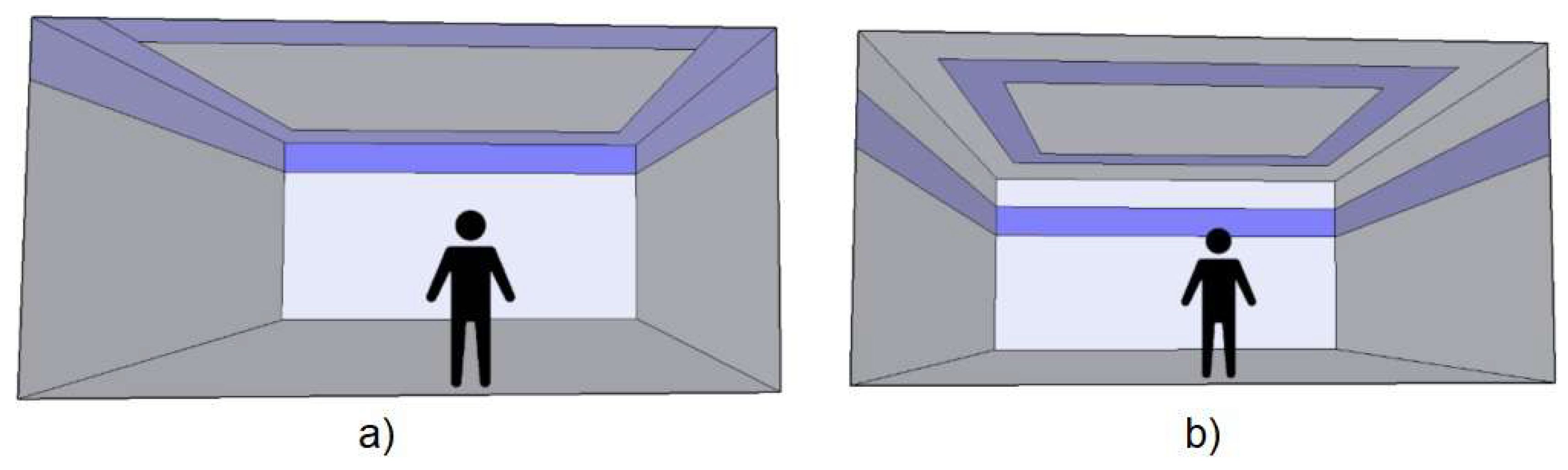
3.2. Mockup Classroom
- (a)
- 100% at the upper part of the rear and back side walls.
- (b)
- 50% at the upper part of the rear and back side walls and 50% at the back part of the ceiling.
- (c)
- 100% at the back part of the ceiling.
- (d)
- 100% at the middle of the ceiling.
4. Results
4.1. Measurements of Absorption Coefficients
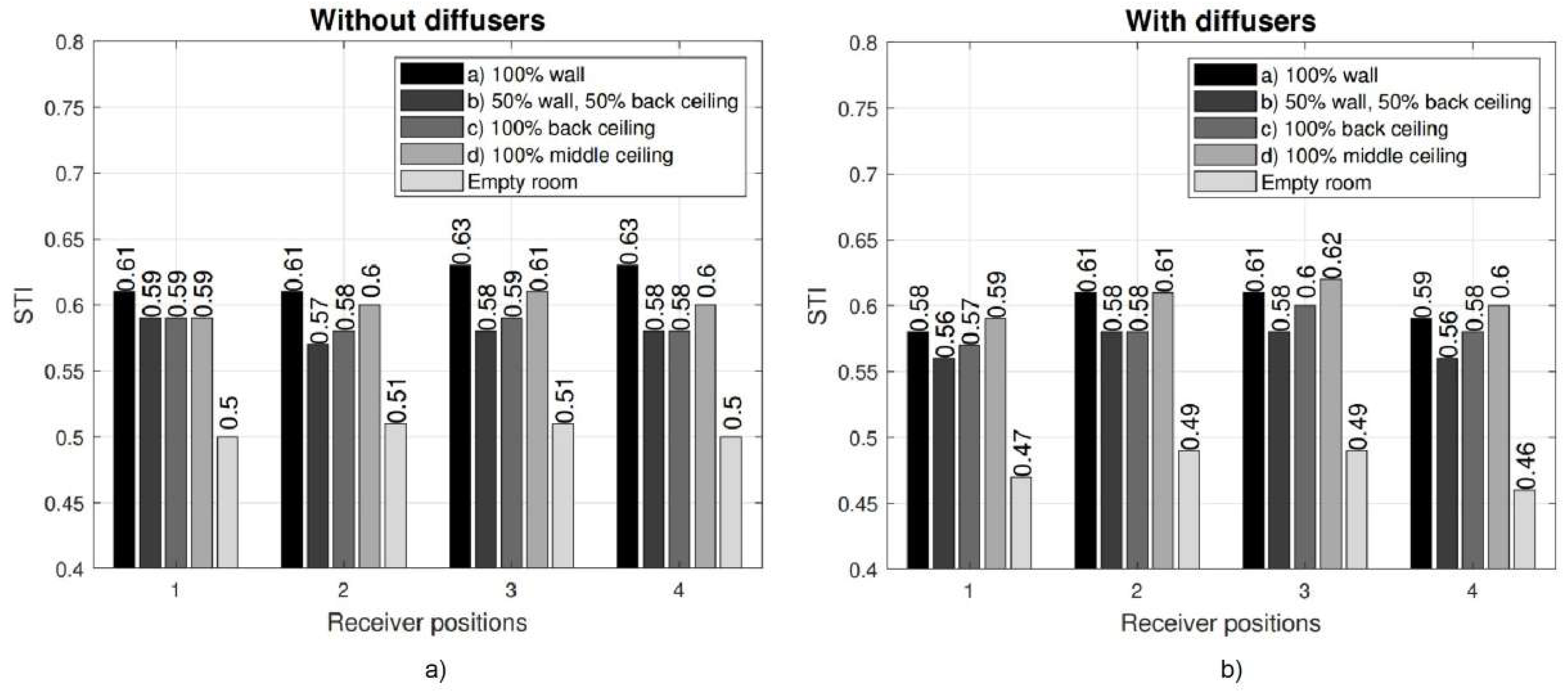
4.2. Measurements of , and STI
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
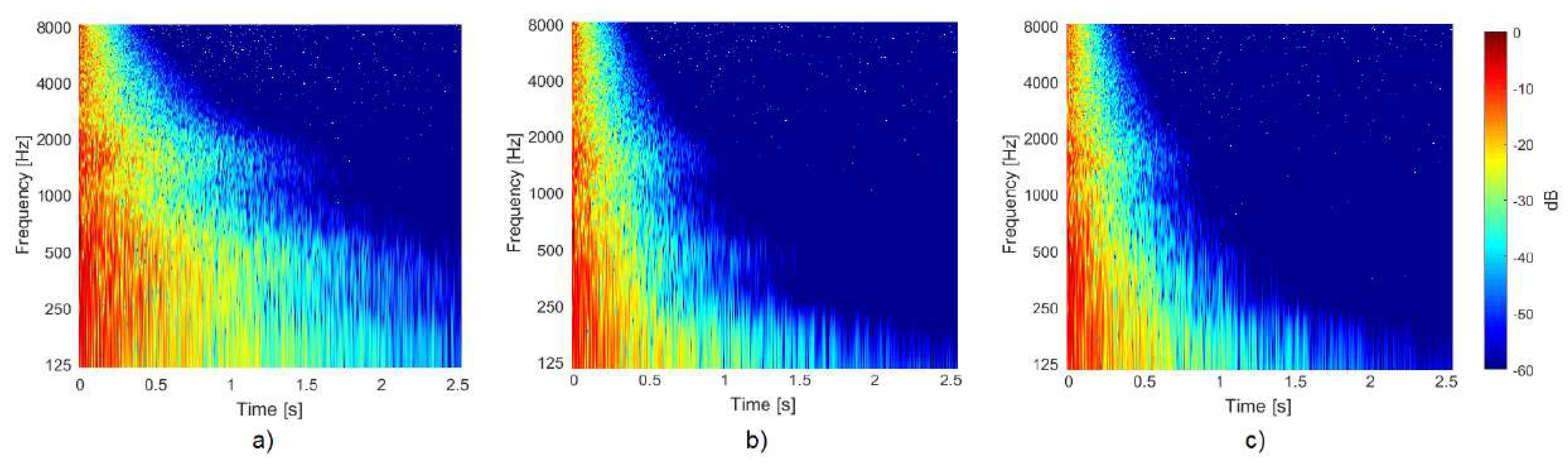
Appendix A. Effect of the Directivity of the Loudspeaker on Sound Absorption Coefficient Measurements
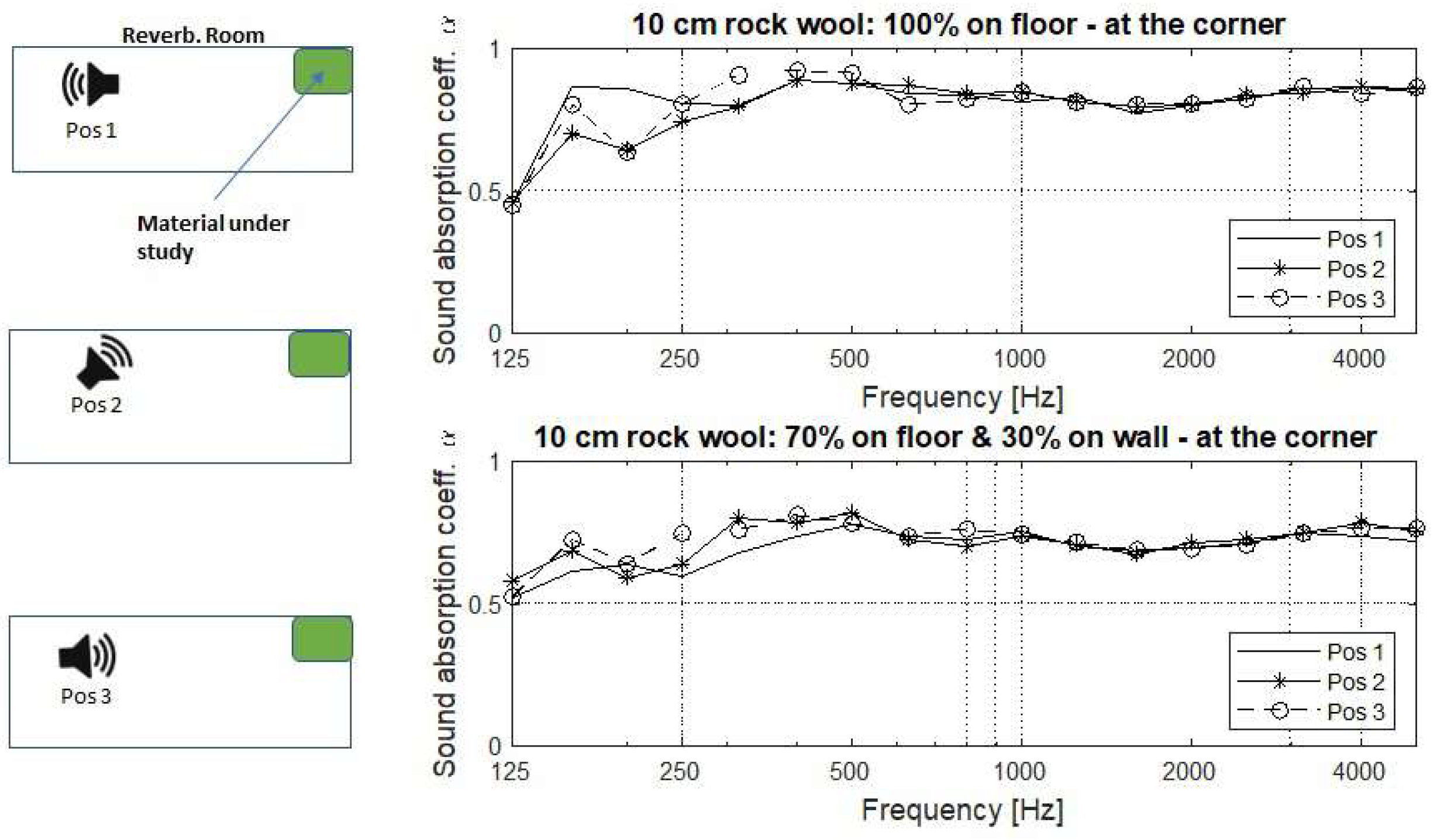
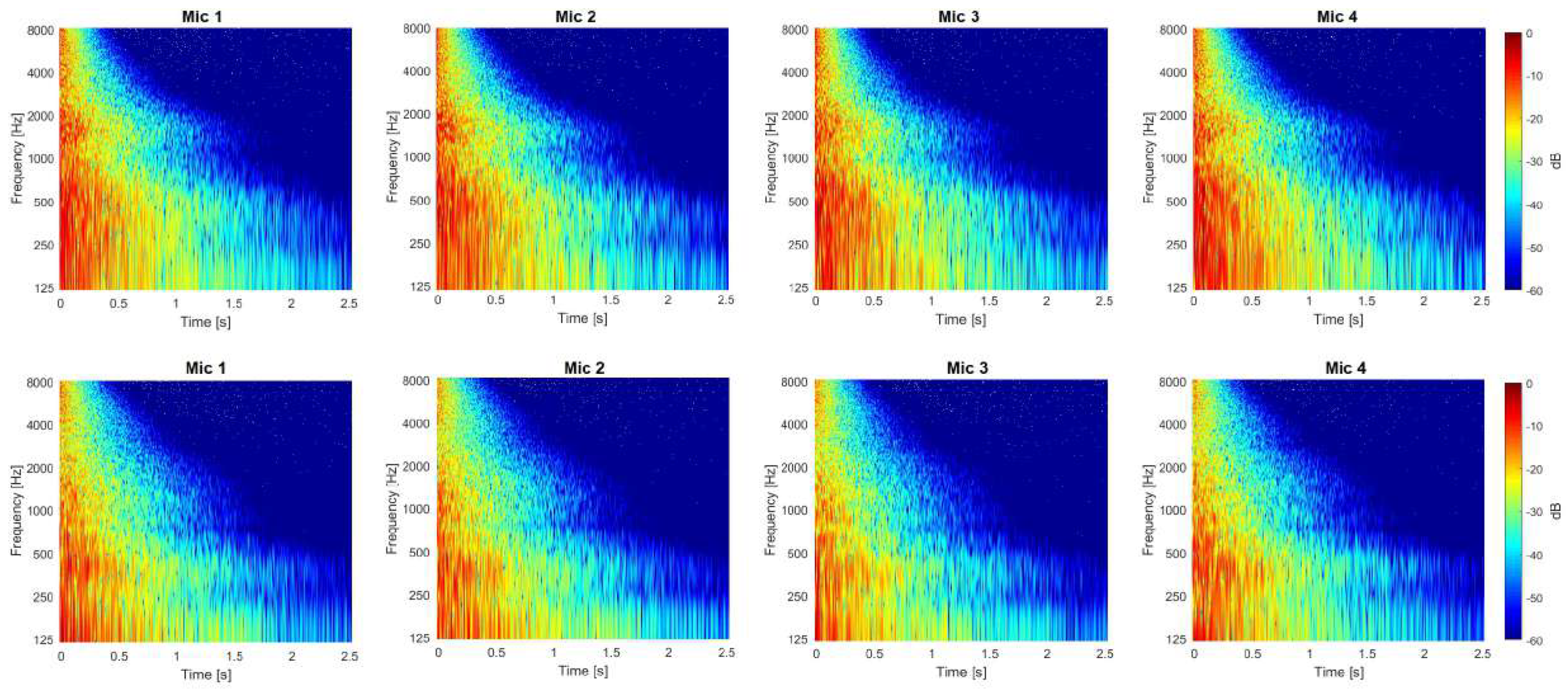
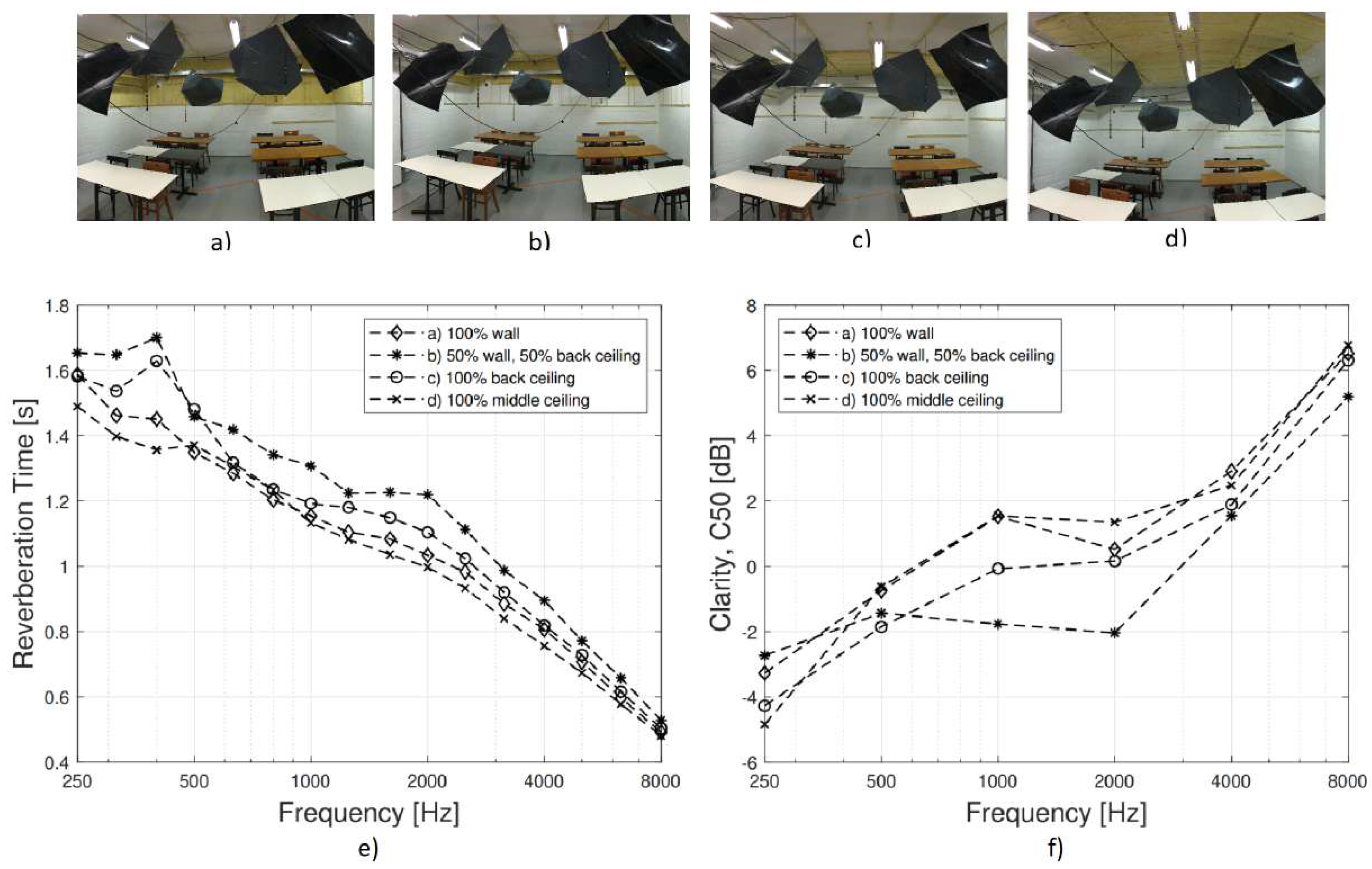
Appendix B. Effect of Hanging Diffusive Elements on Room Modes and Diffuseness
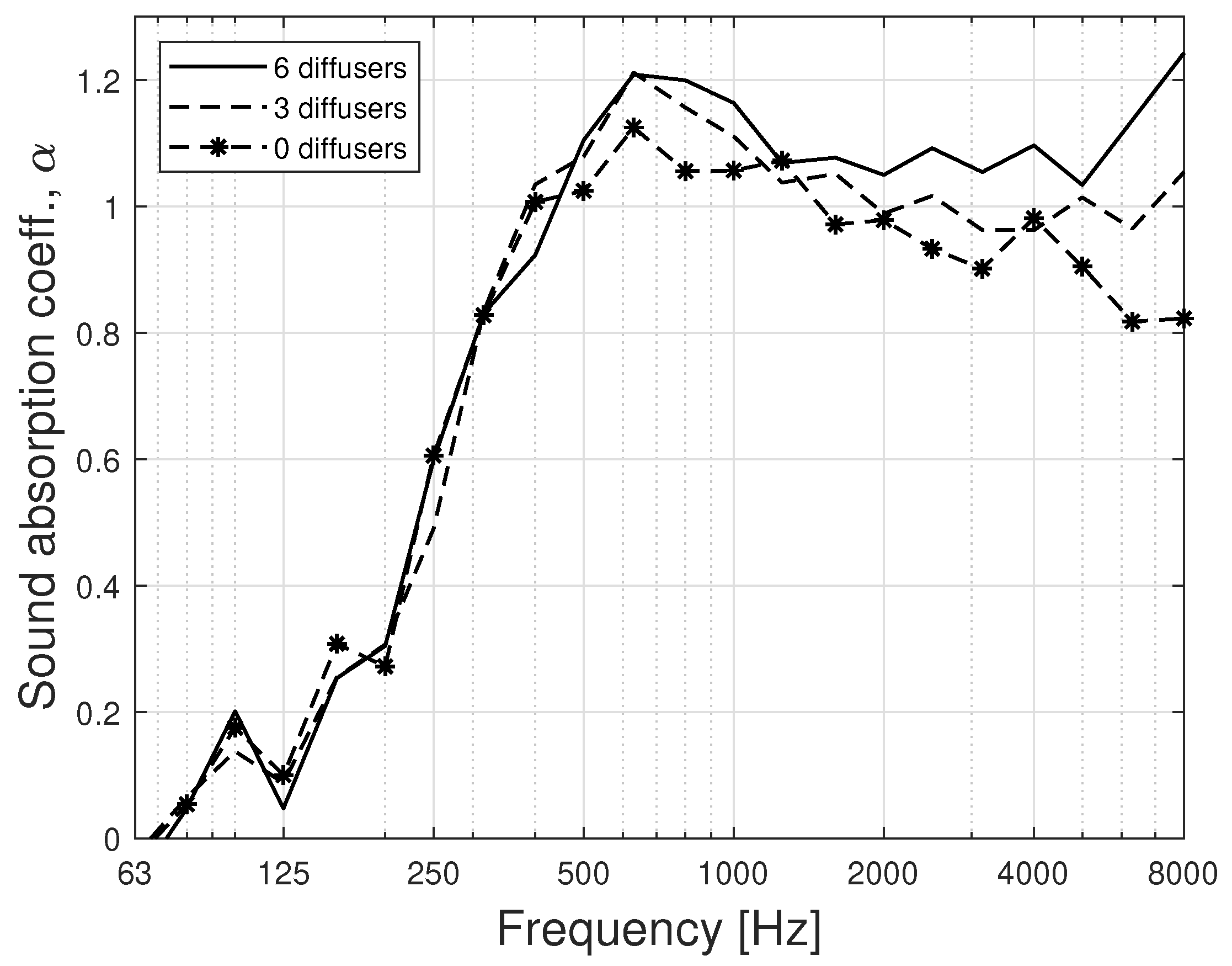
References
- Shield, B.M.; Dockrell, J.E. The effects of noise on children at school: A review. Build. Acoust. 2003, 10, 97–116. [Google Scholar] [CrossRef]
- Lubman, D.; Sutherland, L.C. Classroom acoustics for the 21st century. In Proceedings of the 19th International Congress on Acoustics, Madrid, Spain, 2–7 September 2007. [Google Scholar]
- Bradley, J.S.; Sato, H. The intelligibility of speech in elementary school classrooms. J. Acoust. Soc. Am. 2008, 123, 2078–2086. [Google Scholar] [CrossRef] [PubMed]
- Shield, B.; Conetta, R.; Dockrell, J.; Connolly, D.; Cox, T.; Mydlarz, C. A survey of acoustic conditions and noise levels in secondary school classrooms in England. J. Acoust. Soc. Am. 2015, 137, 177–188. [Google Scholar] [CrossRef] [PubMed]
- Tiesler, G.; Machner, R.; Brokmann, H. Classroom acoustics and impact on health and social behaviour. Energy Procedia 2015, 78, 3108–3113. [Google Scholar] [CrossRef]
- Campbell, C.; Svensson, C.; Nilsson, E. Classroom acoustic research on speech behaviour of teachers and students. In Proceedings of the 42nd International Congress and Exposition on Noise Control Engineering (Internoise), Innsbruck, Austria, 15–18 September 2013. [Google Scholar]
- Rossing, T. Springer Handbook of Acoustics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Shtrepi, L.; Astolfi, A.; D’Antonio, G.; Guski, M. Objective and perceptual evaluation of distance-dependent scattered sound effects in a small variable-acoustics hall. J. Acoust. Soc. Am. 2016, 140, 3651–3662. [Google Scholar] [CrossRef] [PubMed]
- Ryu, J.K.; Jeon, J.Y. Subjective and objective evaluations of a scattered sound field in a scale model opera house. J. Acoust. Soc. Am. 2008, 124, 1538–1549. [Google Scholar] [CrossRef] [PubMed]
- Bradley, J.S.; Sato, H.; Picard, M. On the importance of early reflections for speech in rooms. J. Acoust. Soc. Am. 2003, 113, 3233–3244. [Google Scholar] [CrossRef] [PubMed]
- Campbell, C.; Nilsson, E.; Svensson, C. The same reverberation time in two identical rooms does not necessarily mean the same levels of speech clarity and sound levels when we look at impact of different ceiling and wall absorbers. Energy Procedia 2015, 78, 1635–1640. [Google Scholar] [CrossRef]
- Bradley, J.; Reich, R.; Norcross, S. On the combined effects of signal-to-noise ratio and room acoustics on speech intelligibility. J. Acoust. Soc. Am. 1999, 106, 1820–1828. [Google Scholar] [CrossRef]
- Smirnowa, J.; Ossowski, A. A method for optimising absorptive configurations in classrooms. Acta Acust. United Acust. 2005, 91, 103–109. [Google Scholar]
- Nijs, L.; Rychtáriková, M. Calculating the optimum reverberation time and absorption coefficient for good speech intelligibility in classroom design using U50. Acta Acust. United Acust. 2011, 97, 93–102. [Google Scholar] [CrossRef]
- Choi, Y.J. Effects of periodic type diffusers on classroom acoustics. Appl. Acoust. 2013, 74, 694–707. [Google Scholar] [CrossRef]
- Picard, M.; Bradley, J.S. Revisiting Speech Interference in Classrooms: Revisando la interferencia en el habla dentro del salón de clases. Audiology 2001, 40, 221–244. [Google Scholar] [CrossRef] [PubMed]
- Hodgson, M.; Nosal, E.M. Effect of noise and occupancy on optimal reverberation times for speech intelligibility in classrooms. J. Acoust. Soc. Am. 2002, 111, 931–939. [Google Scholar] [CrossRef] [PubMed]
- Pelegrín-García, D.; Smits, B.; Brunskog, J.; Jeong, C.H. Vocal effort with changing talker-to-listener distance in different acoustic environments. J. Acoust. Soc. Am. 2011, 129, 1981–1990. [Google Scholar] [CrossRef] [PubMed]
- Sala, E.; Viljanen, V. Improvement of acoustic conditions for speech communication in classrooms. Appl. Acoust. 1995, 45, 81–91. [Google Scholar] [CrossRef]
- Bistafa, S.R.; Bradley, J.S. Predicting reverberation times in a simulated classroom. J. Acoust. Soc. Am. 2000, 108, 1721–1731. [Google Scholar] [CrossRef]
- Sabine, W. Reverberation. The American Architect and the Engineering Record; Sabine WC Prefaced by Beranek LL (1992) Collected Papers on Acoustics. Peninsula Publishing: Los Altos, CA, USA, 1900; Chapter 1. [Google Scholar]
- Eyring, C.F. Reverberation time in “dead” rooms. J. Acoust. Soc. Am. 1930, 1, 217–241. [Google Scholar] [CrossRef]
- Millington, G. A modified formula for reverberation. J. Acoust. Soc. Am. 1932, 4, 69–82. [Google Scholar] [CrossRef]
- Cremer, L.; Müller, H.A. Principles and applications of room acoustics. Appl. Sci. 1982, 2, 434. [Google Scholar] [CrossRef]
- Kuttruff, H. Sound decay in enclosures with non-diffuse sound field. In Proceedings of the Wallace Clement Sabine Centennial Symposium, Cambridge, MA, USA, 5–7 June 1994; pp. 5–7. [Google Scholar]
- Fitzroy, D. Reverberation formula which seems to be more accurate with nonuniform distribution of absorption. J. Acoust. Soc. Am. 1959, 31, 893–897. [Google Scholar] [CrossRef]
- Arau-Puchades, H. An improved reverberation formula. Acta Acust. United Acust 1988, 65, 163–180. [Google Scholar]
- Kuttruff, H. A simple iteration scheme for the computation of decay constants in enclosures with diffusely reflecting boundaries. J. Acoust. Soc. Am. 1995, 98, 288–293. [Google Scholar] [CrossRef]
- Schroeder, M.; Gerlach, R. Diffusion, room shape and absorber location-influence on reverberation time. J. Acoust. Soc. Am. 1974, 56, 1300. [Google Scholar] [CrossRef]
- Schultz, T. Diffusion in reverberation rooms. J. Sound Vib. 1971, 16, 17–28. [Google Scholar] [CrossRef]
- Hodgson, M. When is diffuse-field theory applicable? Appl. Acoust. 1996, 49, 197–207. [Google Scholar] [CrossRef]
- Abdou, A.; Guy, R. A review of objective descriptors for sound diffuseness. Can. Acoust. 1994, 22, 43–44. [Google Scholar]
- Vér, I.L.; Beranek, L.L. Noise and Vibration Control Engineering-Principles and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Jeong, C.H.; Nolan, M.; Balint, J. Difficulties in comparing diffuse sound field measures and data/code sharing for future collaboration. In Proceedings of the 11th European Congress and Exposition on Noise Control Engineering (Euronoise), Crete, Greece, 27 May 2018. [Google Scholar]
- Epain, N.; Jin, C.T.; Epain, N.; Jin, C.T.; Epain, N.; Jin, C.T. Spherical harmonic signal covariance and sound field diffuseness. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 1796–1807. [Google Scholar] [CrossRef]
- ISO. 354 Acoustics—Measurement of Sound Absorption in a Reverberation Room; ISO: Geneva, Switzerland, 2003. [Google Scholar]
- Schroeder, M.R.; Kuttruff, K. On frequency response curves in rooms. Comparison of experimental, theoretical, and Monte Carlo results for the average frequency spacing between maxima. J. Acoust. Soc. Am. 1962, 34, 76–80. [Google Scholar] [CrossRef]
- Vercammen, M. Improving the accuracy of sound absorption measurement according to ISO 354. In Proceedings of the International Symposium on Room Acoustics (ISRA) 2010, Melbourne, Australia, 29–31 August 2010. [Google Scholar]
- Pompoli, F.; Bonfiglio, P.; Horoshenkov, K.V.; Khan, A.; Jaouen, L.; Bécot, F.X.; Sgard, F.; Asdrubali, F.; D’Alessandro, F.; Hübelt, J.; et al. How reproducible is the acoustical characterization of porous media? J. Acoust. Soc. Am. 2017, 141, 945–955. [Google Scholar] [CrossRef]
- ISO 17497-1. Acoustics—Sound-Scattering Properties of Surfaces—Part 1: Measurement of the Random-Incidence Scattering Coefficient in a Reverberation Room; ISO: Geneva, Switzerland, 2004. [Google Scholar]
- ISO 3741. Acoustics-Determination of Sound Power Levels and Sound Energy Levels of Noise Sources Using Sound Pressure-Precision Methods for Reverberation Test Rooms; ISO: Geneva, Switzerland, 2010. [Google Scholar]
- De Bruijn, A. A mathematical analysis concerning the edge effect of sound absorbing materials. Acta Acust. United Acust. 1973, 28, 33–44. [Google Scholar]
- ARTA Software. Available online: www.artalabs.hr/ (accessed on 29 June 2019).
- Farina, A. Simultaneous Measurement of impulse response and distortion with a swept-sine technique. In Proceedings of the 108th Audio Engineering Society (AES) Convention, Paris, France, 19–22 February 2000. [Google Scholar]
- Jambrosic, K.; Horvat, M.; Domitrovic, H. Reverberation time measuring methods. In Proceedings of the Acoustics’08, ASA, EAA and SFA, Paris, France, 29 June–4 July 2008. [Google Scholar]
- Schroeder, M.R. The “Schroeder frequency” revisited. J. Acoust. Soc. Am. 1996, 99, 3240–3241. [Google Scholar] [CrossRef]
- ISO 3382-1. Acoustics. Measurement of Room Acoustic Parameters—Part 1: Performance Spaces; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- IEC 60268-16. Sound System Equipment—Part 16: Objective Rating of Speech Intelligibility by Speech Transmission Index; ISO: Geneva, Switzerland, 2011. [Google Scholar]
- Angus, J.A. The effect of diffusers on frequency dependent room mode decay. In Proceedings of the 107th Convention of the Audio Engineering Society, York, UK, 1 September 1999. [Google Scholar]
- Halmrast, T. Flutter echoes; timbre and possible use as sound effect. In Proceedings of the 18th International Conference on Digital Audio Effects (DAFx-15), Trondheim, Norway, 30 November–3 December 2015. [Google Scholar]
- Bolt, R.H. Note on normal frequency statistics for rectangular rooms. J. Acoust. Soc. Am. 1946, 18, 130–133. [Google Scholar] [CrossRef]
- Bradley, J.S.; Reich, R.; Norcross, S. A just noticeable difference in C50 for speech. Appl. Acoust. 1999, 58, 99–108. [Google Scholar] [CrossRef]
- Hongisto, V.; Keränen, J.; Larm, P. Simple model for the acoustical design of open-plan offices. Acta Acust. United Acust. 2004, 90, 481–495. [Google Scholar]
- SFS 5907. Acoustic Classification of Spaces in Buildings; Finnish Standard Association (FSA): Helsinki, Finland, 2004. [Google Scholar]

| Frequency (Hz) | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 |
| (dB) | 40.6 | 30.4 | 30.7 | 27.5 | 20 | 12.3 | 12.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cucharero, J.; Hänninen, T.; Lokki, T. Influence of Sound-Absorbing Material Placement on Room Acoustical Parameters. Acoustics 2019, 1, 644-660. https://doi.org/10.3390/acoustics1030038
Cucharero J, Hänninen T, Lokki T. Influence of Sound-Absorbing Material Placement on Room Acoustical Parameters. Acoustics. 2019; 1(3):644-660. https://doi.org/10.3390/acoustics1030038
Chicago/Turabian StyleCucharero, Jose, Tuomas Hänninen, and Tapio Lokki. 2019. "Influence of Sound-Absorbing Material Placement on Room Acoustical Parameters" Acoustics 1, no. 3: 644-660. https://doi.org/10.3390/acoustics1030038
APA StyleCucharero, J., Hänninen, T., & Lokki, T. (2019). Influence of Sound-Absorbing Material Placement on Room Acoustical Parameters. Acoustics, 1(3), 644-660. https://doi.org/10.3390/acoustics1030038





