A High-Frequency Model of a Circular Beam with a T-Shaped Cross Section
Abstract
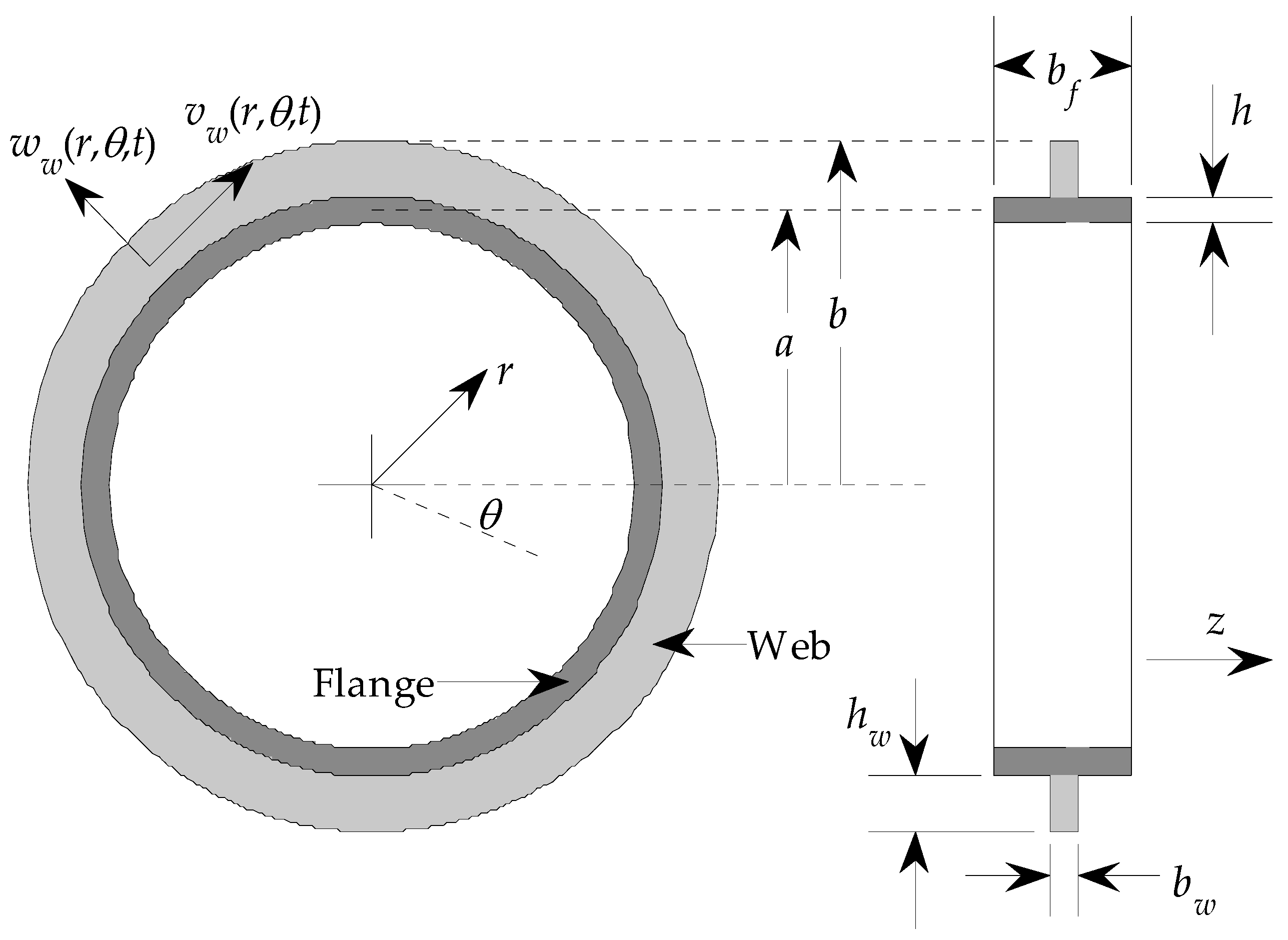
1. Introduction
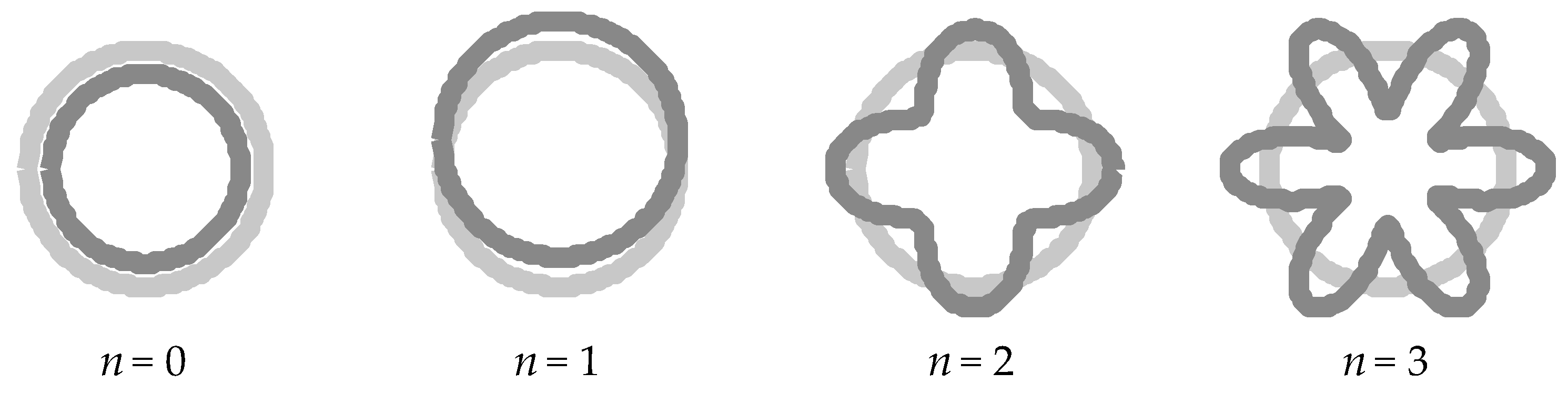
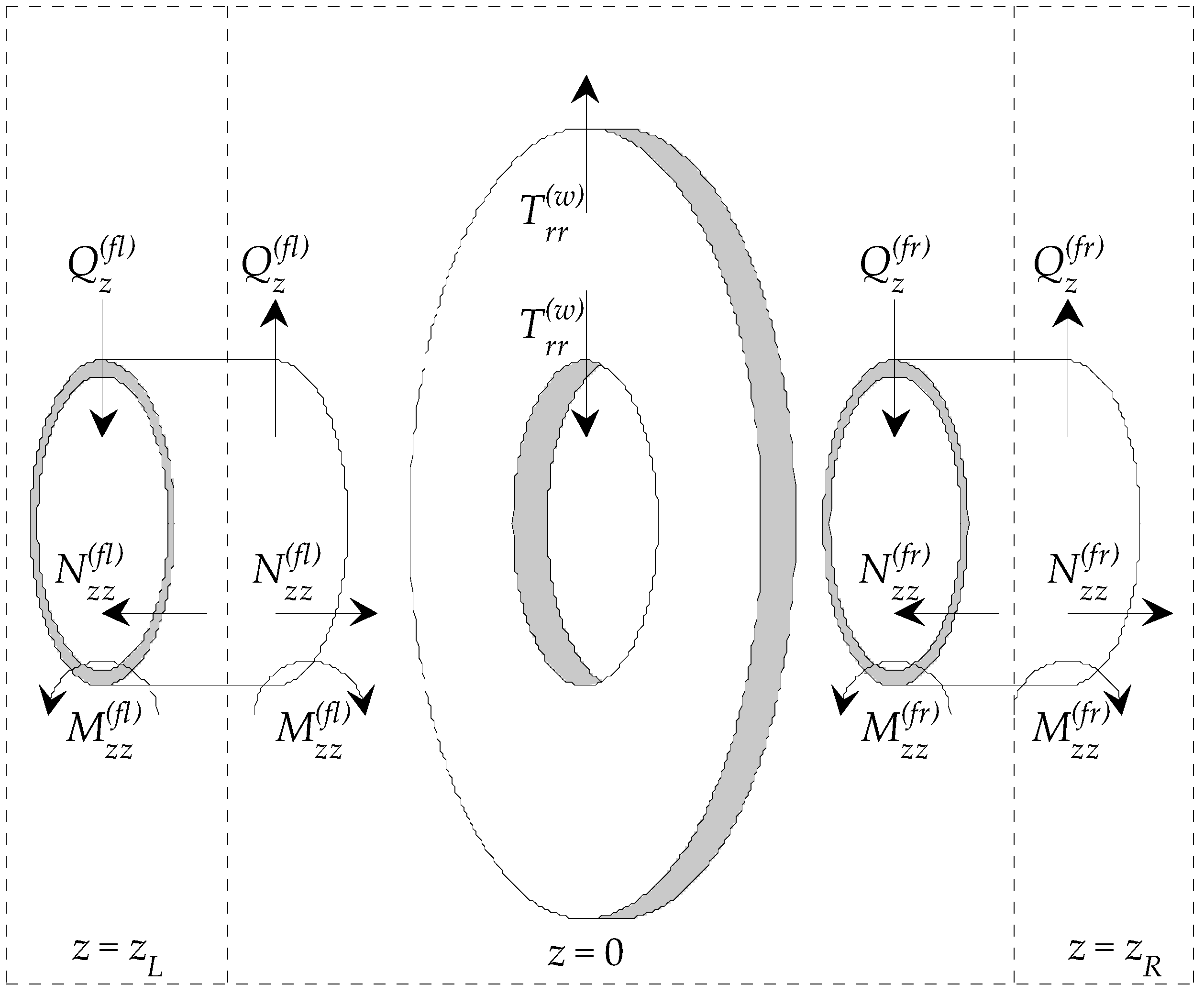
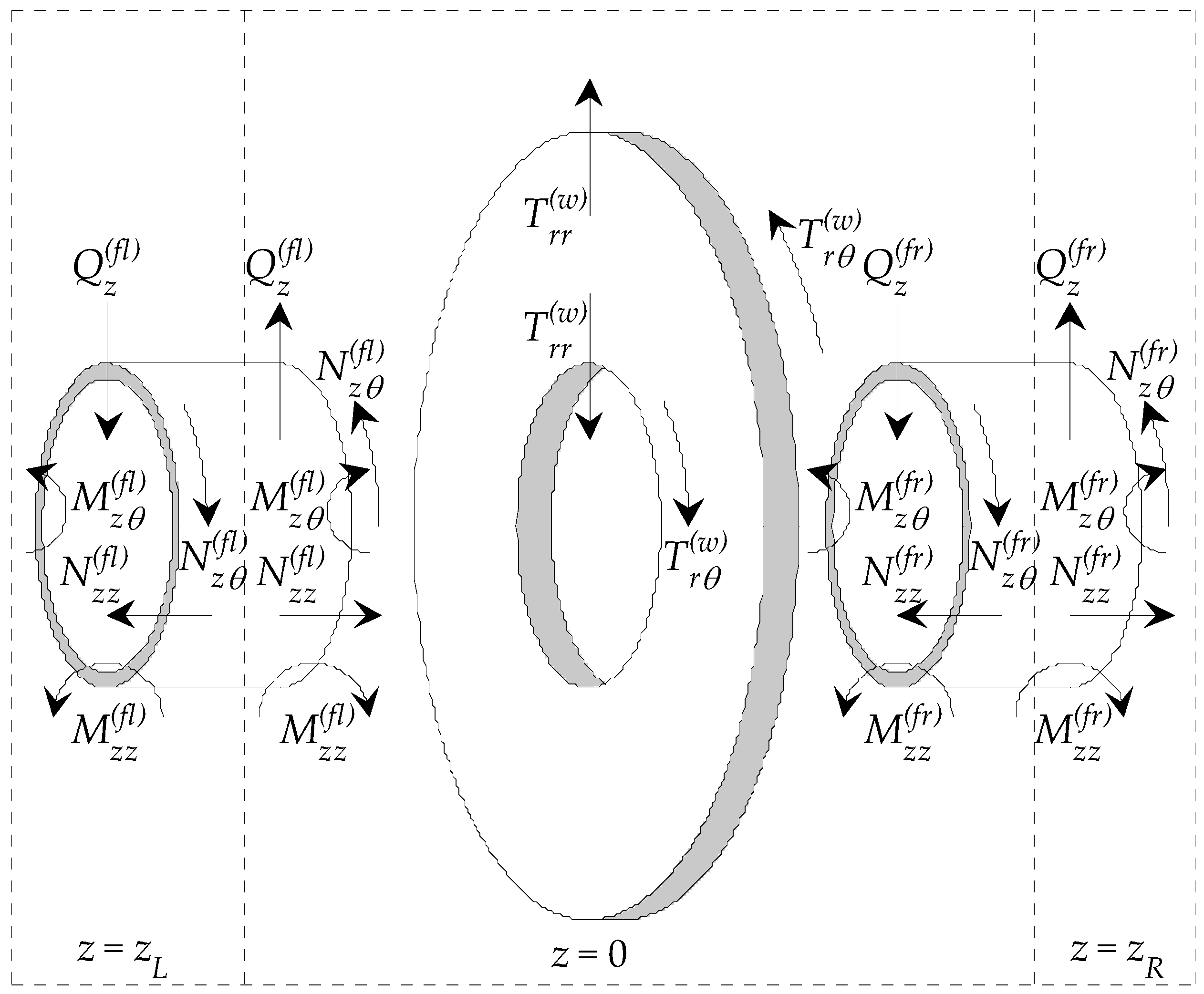
2. Methods
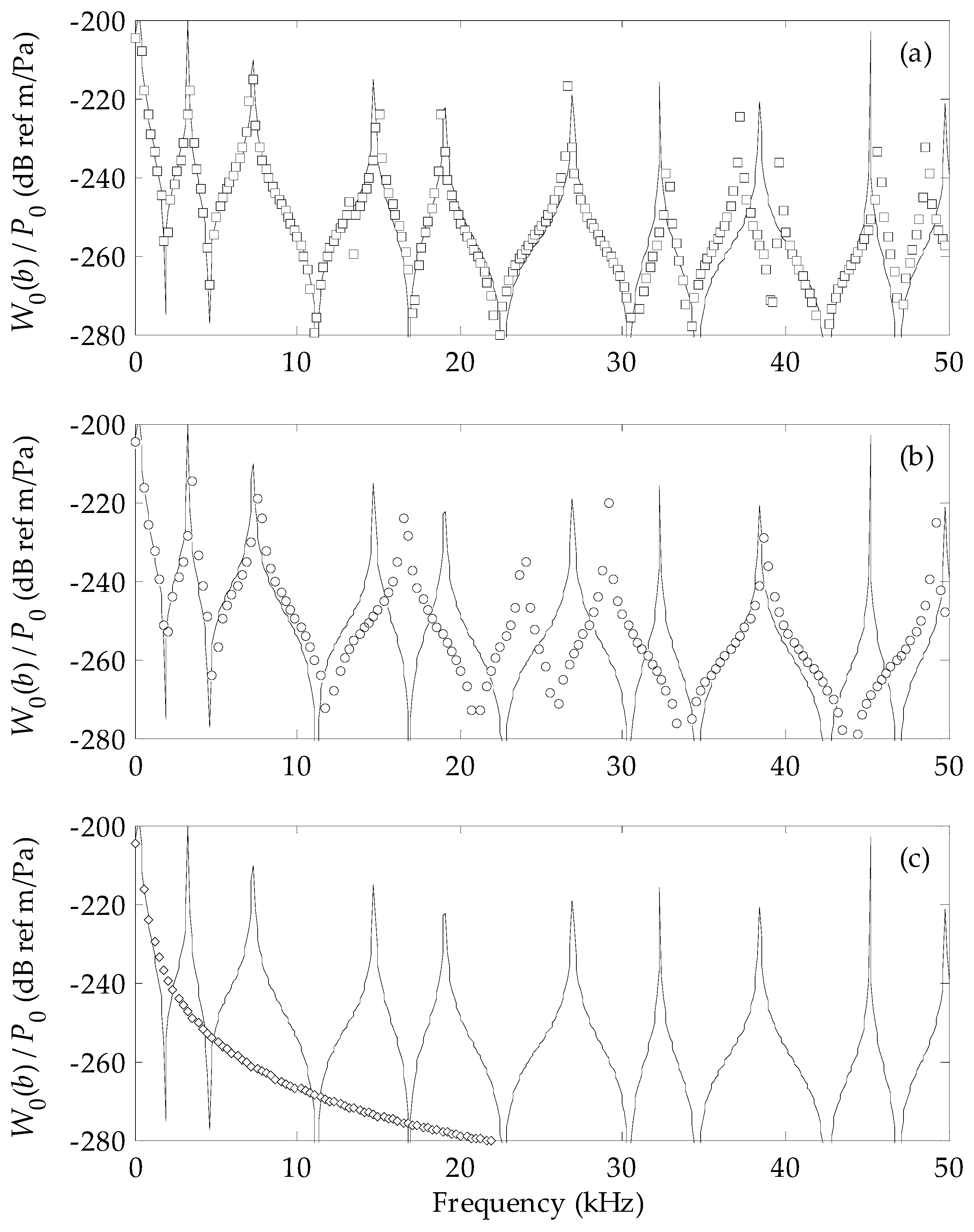
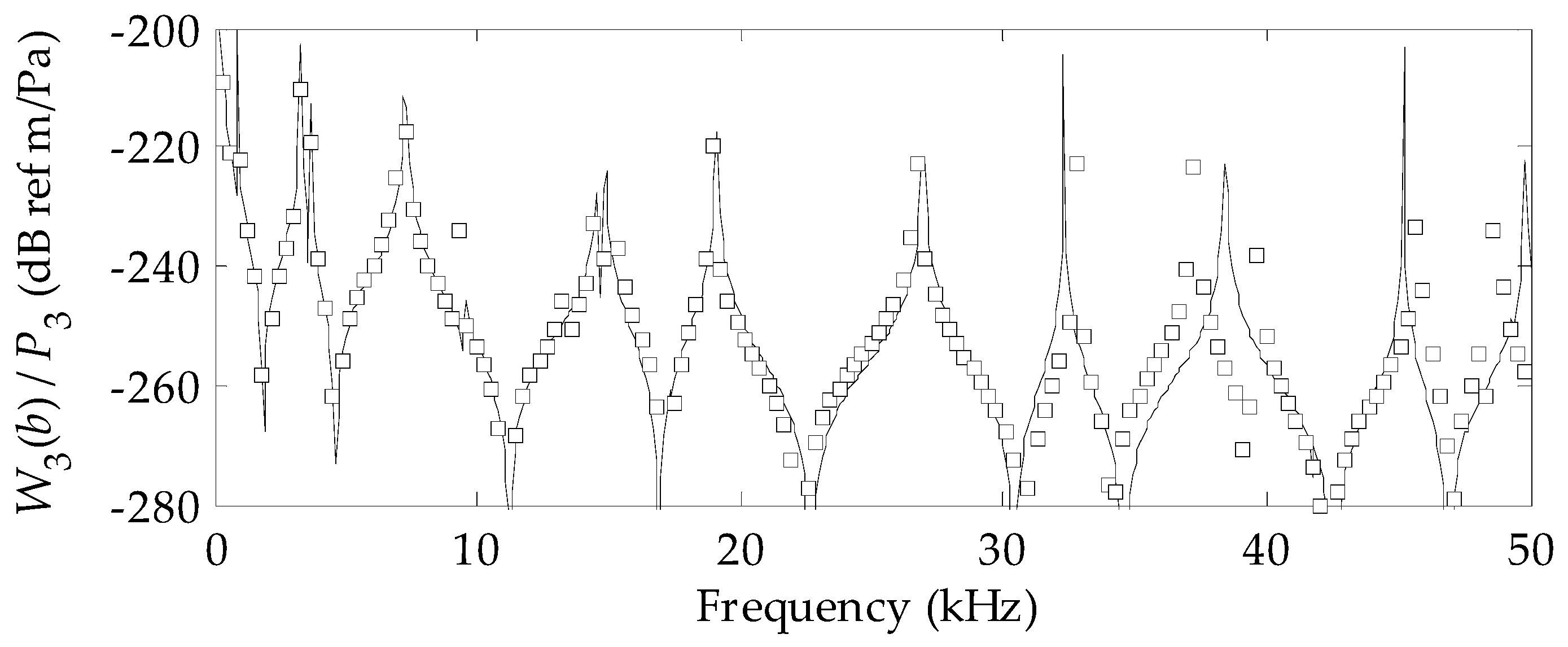
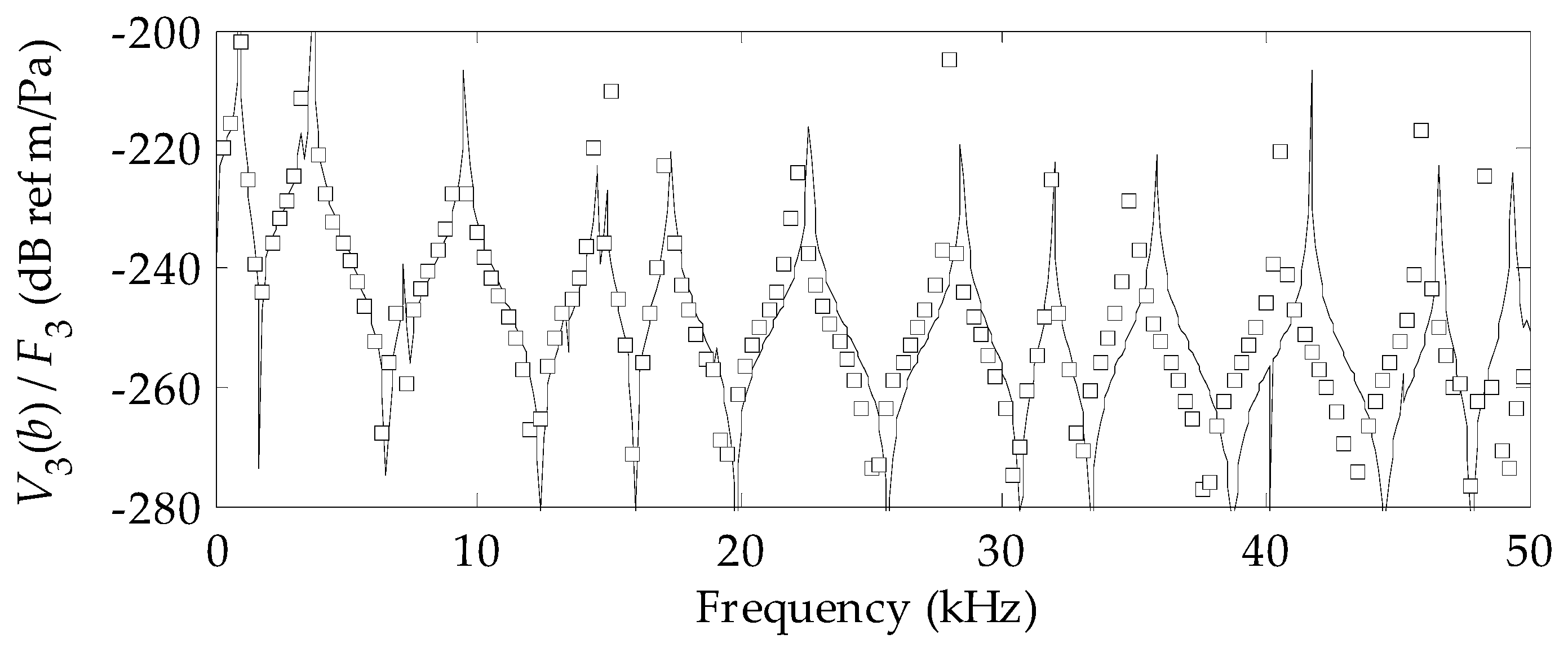
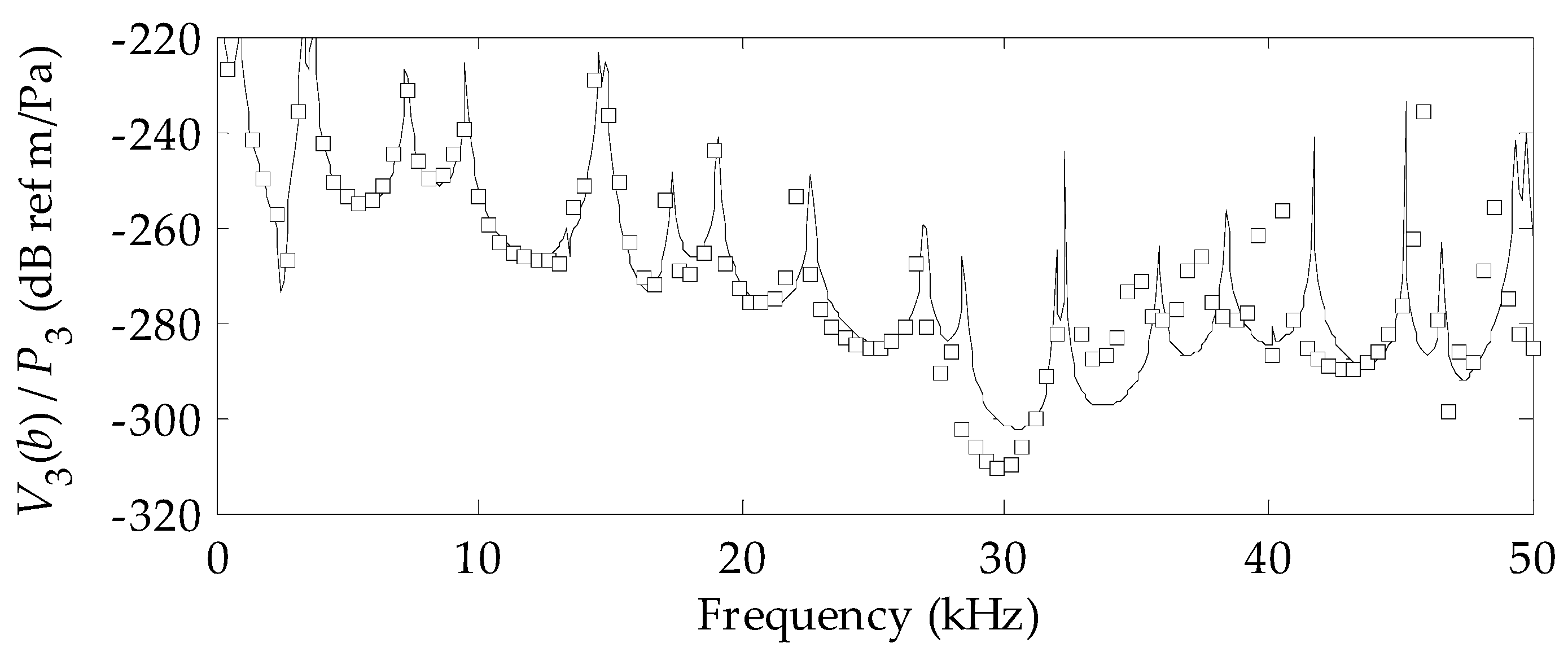
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Hull, A.J.; Perez, D.; Cox, D.L. An Analytical Model of a Curved Beam with a T-Shaped Cross Section; NUWC-NPT Technical Memorandum 17-054; Naval Undersea Warfare Center Division: Newport, RI, USA, 13 June 2017. [Google Scholar]
- Hull, A.J.; Perez, D.; Cox, D.L. An analytical model of a curved beam with a T-shaped cross section. J. Sound Vib. 2018, 416, 29–54. [Google Scholar] [CrossRef]
- Donnell, L.H. Stability of Thin-Walled Tubes Under Torsion; National Advisory Committee for Aeronautics (NACA) Report Number 479; NACA: Washington, DC, USA, 1933. [Google Scholar]
- Mirsky, I.; Herrmann, G. Nonaxially symmetric motions of cylindrical shells. J. Acoust. Soc. Am. 1957, 29, 1116–1123. [Google Scholar] [CrossRef]
- Han, S.M.; Benaroya, H.; Wei, T. Dynamics of transversely vibrating beams using four engineering theories. J. Sound Vib. 1999, 225, 935–988. [Google Scholar] [CrossRef]
- Timoshenko, S.P. On the transverse vibrations of bars of uniform cross-section. Philos. Mag. 1922, 43, 125–131. [Google Scholar] [CrossRef]
- Bickford, W.B. A Consistent Higher Order Beam Theory. In Proceedings of the 11th Southeastern Conference on Theoretical and Applied Mechanics, Huntsville, AL, USA, 8–9 April 1982; pp. 137–150. [Google Scholar]
- Karama, M.; Afaq, K.S.; Mistou, S. Mechanical behavior of laminated composite beam by new multi-layered laminated composite structures model with transverse shear stress continuity. Int. J. Solids Struct. 2003, 40, 1525–1546. [Google Scholar] [CrossRef]
- Ambati, G.; Bell, J.F.W.; Sharp, J.C.K. In-plane vibrations of annular rings. J. Sound Vib. 1976, 47, 415–432. [Google Scholar] [CrossRef]
- Kirkhope, J. In-plane vibration of a thick circular ring. J. Sound Vib. 1977, 50, 219–227. [Google Scholar] [CrossRef]
- Hawkings, D.L. A generalized analysis of the vibration of circular rings. J. Sound Vib. 1977, 54, 67–74. [Google Scholar] [CrossRef]
- Kirkhope, J.; Bell, R.; Olmstead, J.L.D. The vibration of rings of unsymmetrical cross-section. J. Sound Vib. 1984, 96, 495–504. [Google Scholar] [CrossRef]
- Bhimaraddi, A. Generalized analysis of shear deformable rings and curved beams. Int. J. Solids Struct. 1988, 24, 363–373. [Google Scholar] [CrossRef]
- Lin, S.M.; Lee, S.Y. Closed-form solutions for dynamic analysis of extensional circular Timoshenko beams with general elastic boundary conditions. Int. J. Solids Struct. 2001, 38, 227–240. [Google Scholar] [CrossRef]
- Konovalyuk, I.P. Diffraction of a plane sound wave by a plate reinforced with stiffness members. Sov. Phys. Acoust. 1969, 14, 465–469. [Google Scholar]
- Graff, K.F.; Klein, C.A.; Kouyoumjian, R.G. On the Effect of Mass Loading on a Stiffening Rib; The Ohio State University Research Foundation Technical Report, Project 4409-A1, Report Number 1; The Ohio State University: Columbus, OH, USA, 10 January 1977. [Google Scholar]
- Woolley, B.L. Acoustic scattering from a submerged plate. I. one reinforcing rib. J. Acoust. Soc. Am. 1980, 67, 1642–1653. [Google Scholar] [CrossRef]
- Woolley, B.L. Acoustic scattering from a submerged plate. II. finite number of reinforcing ribs. J. Acoust. Soc. Am. 1980, 67, 1654–1658. [Google Scholar] [CrossRef]
- Marcus, M.H.; Sarkissian, A. Rib resonances resent in the scattering response of a ribbed cylindrical shell. J. Acoust. Soc. Am. 1998, 103, 1864–1866. [Google Scholar] [CrossRef]
- Tran-Van-Nhieu, M. Scattering from a ribbed finite cylindrical shell. J. Acoust. Soc. Am. 2001, 110, 2858–2866. [Google Scholar] [CrossRef]
- Cauchy, A.-L. On the pressure or tension in a solid body. Exerc. Math. 1827, 2, 42–56. [Google Scholar]
- Graf, K.F. Wave Motion in Elastic Solids; Dover Publications, Inc.: Mineola, NY, USA, 1975; pp. 464–480. ISBN 0-486-66745-6. [Google Scholar]
- Vinson, J.R. The Behavior of Shells Composed of Isotropic and Composite Materials; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993; pp. 65–80. [Google Scholar]
- Mindlin, R.D.; Deresiewicz, H. Thickness-shear and flexural vibrations of a circular disk. J. Appl. Phys. 1954, 25, 1329–1332. [Google Scholar] [CrossRef]
- Rao, S.S.; Prasad, A.S. Vibrations of annular plates including the effects of rotary inertia and transverse shear deformation. J. Sound Vib. 1975, 21, 305–324. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hull, A.J.; Perez, D. A High-Frequency Model of a Circular Beam with a T-Shaped Cross Section. Acoustics 2019, 1, 295-336. https://doi.org/10.3390/acoustics1010017
Hull AJ, Perez D. A High-Frequency Model of a Circular Beam with a T-Shaped Cross Section. Acoustics. 2019; 1(1):295-336. https://doi.org/10.3390/acoustics1010017
Chicago/Turabian StyleHull, Andrew J., and Daniel Perez. 2019. "A High-Frequency Model of a Circular Beam with a T-Shaped Cross Section" Acoustics 1, no. 1: 295-336. https://doi.org/10.3390/acoustics1010017
APA StyleHull, A. J., & Perez, D. (2019). A High-Frequency Model of a Circular Beam with a T-Shaped Cross Section. Acoustics, 1(1), 295-336. https://doi.org/10.3390/acoustics1010017



