Chemical Equilibrium Fracture Mechanics—Hydrogen Embrittlement Application
Abstract
:1. Introduction
2. Materials and Methods
2.1. Areas of Hydrogen in Solid Solution
2.2. Areas of Hydride Precipitation
3. Results and Discussion
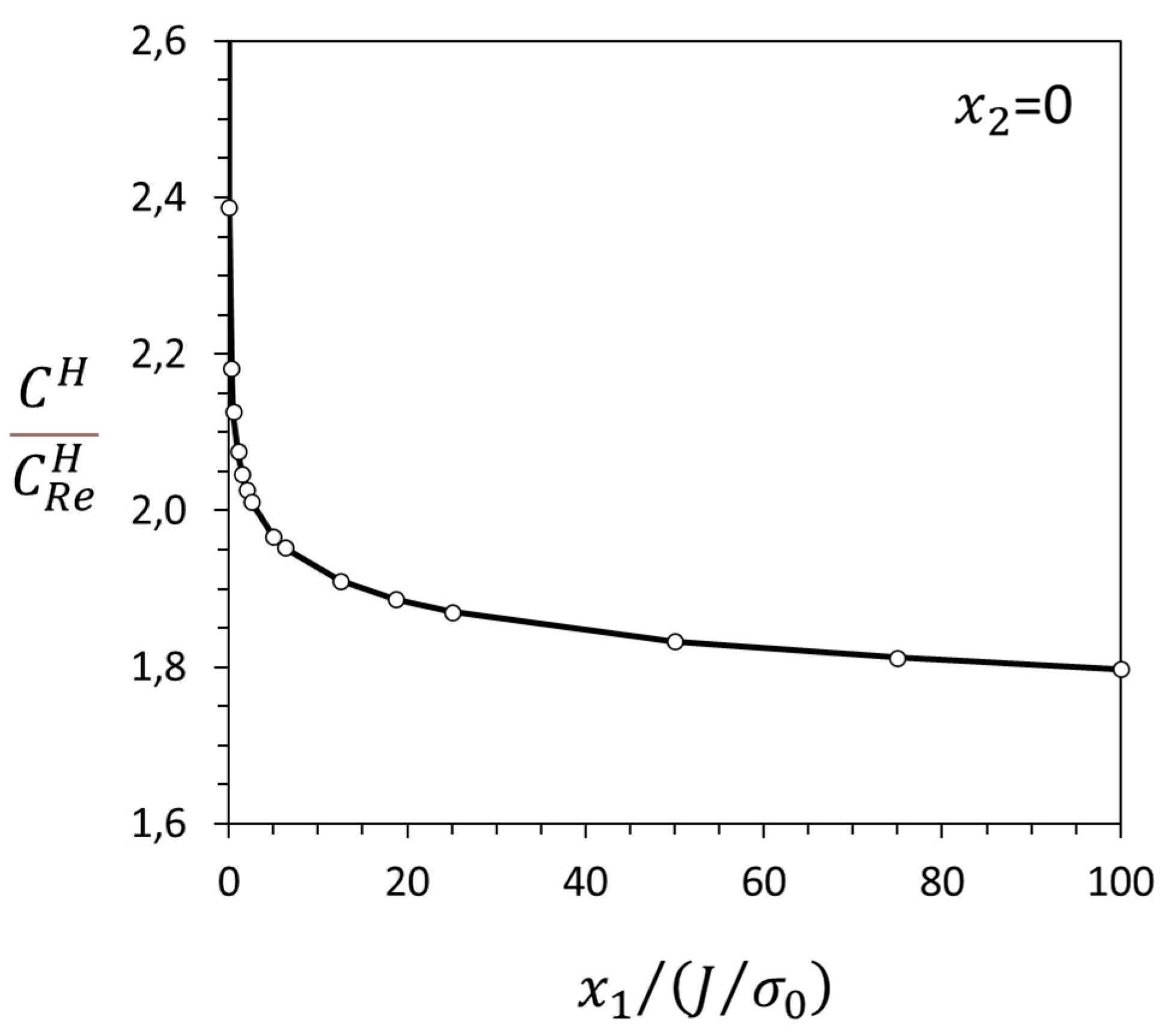
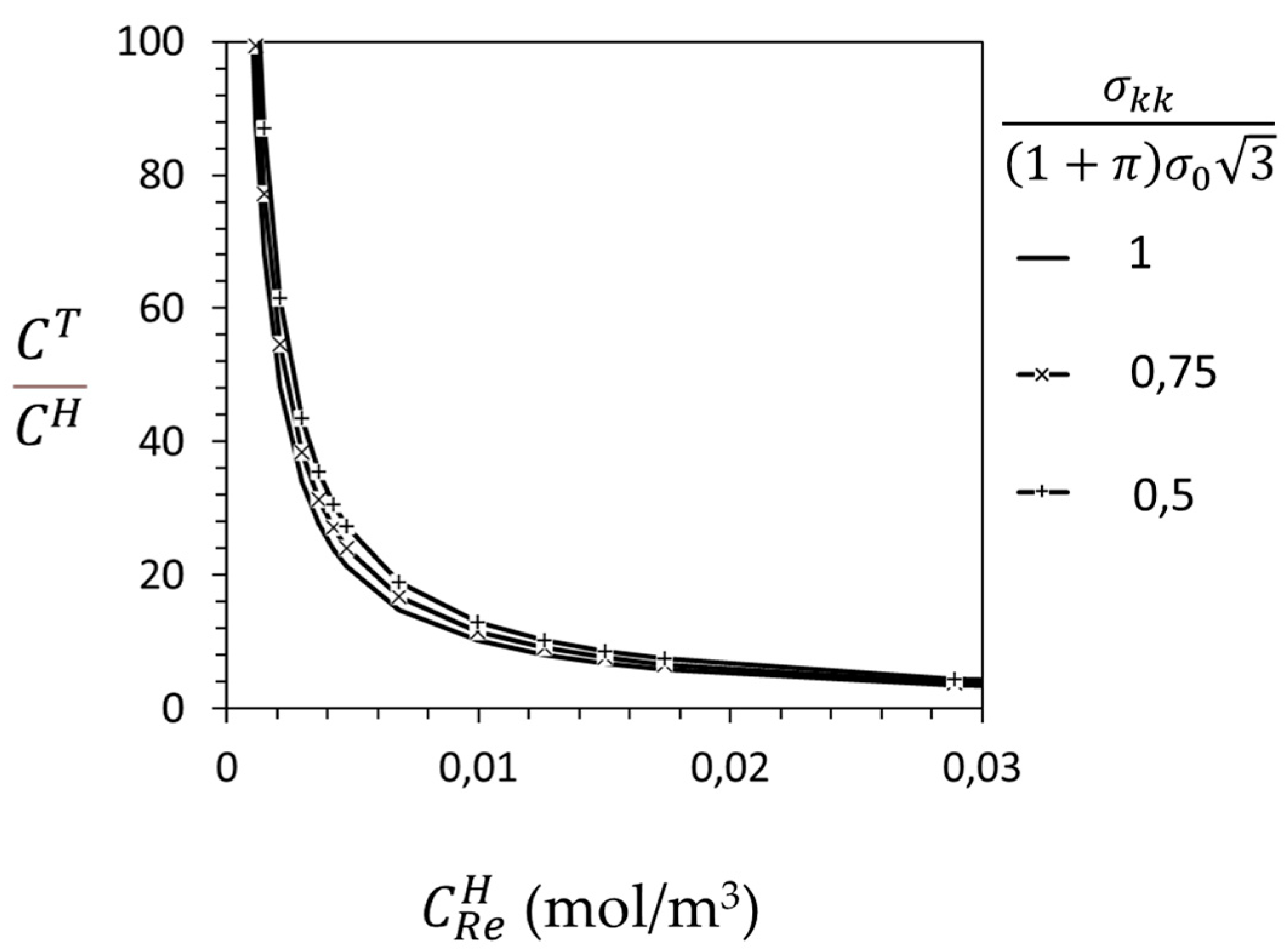
3.1. Crack-Tip Fields for Hydrogen in Solid Solution
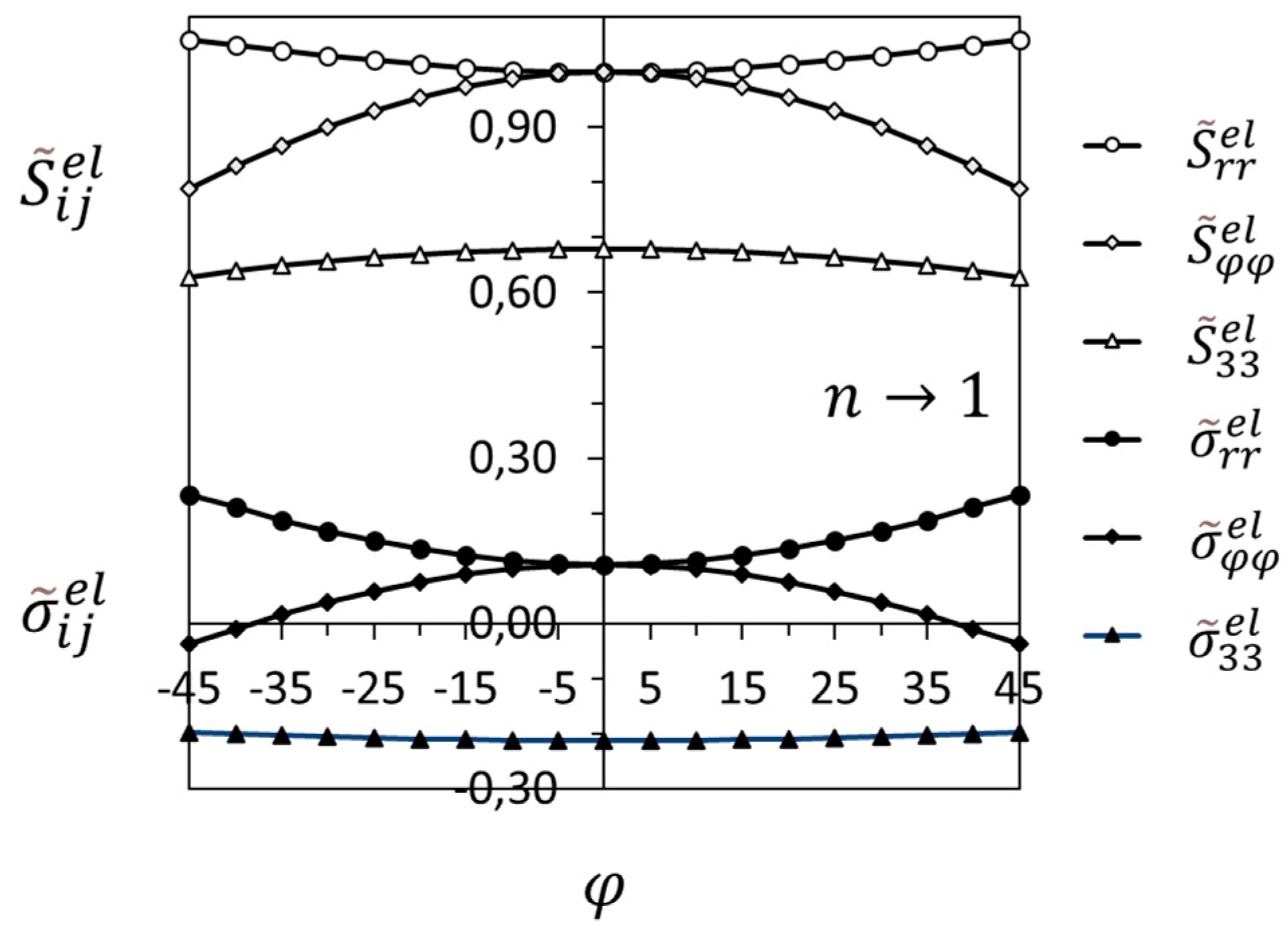
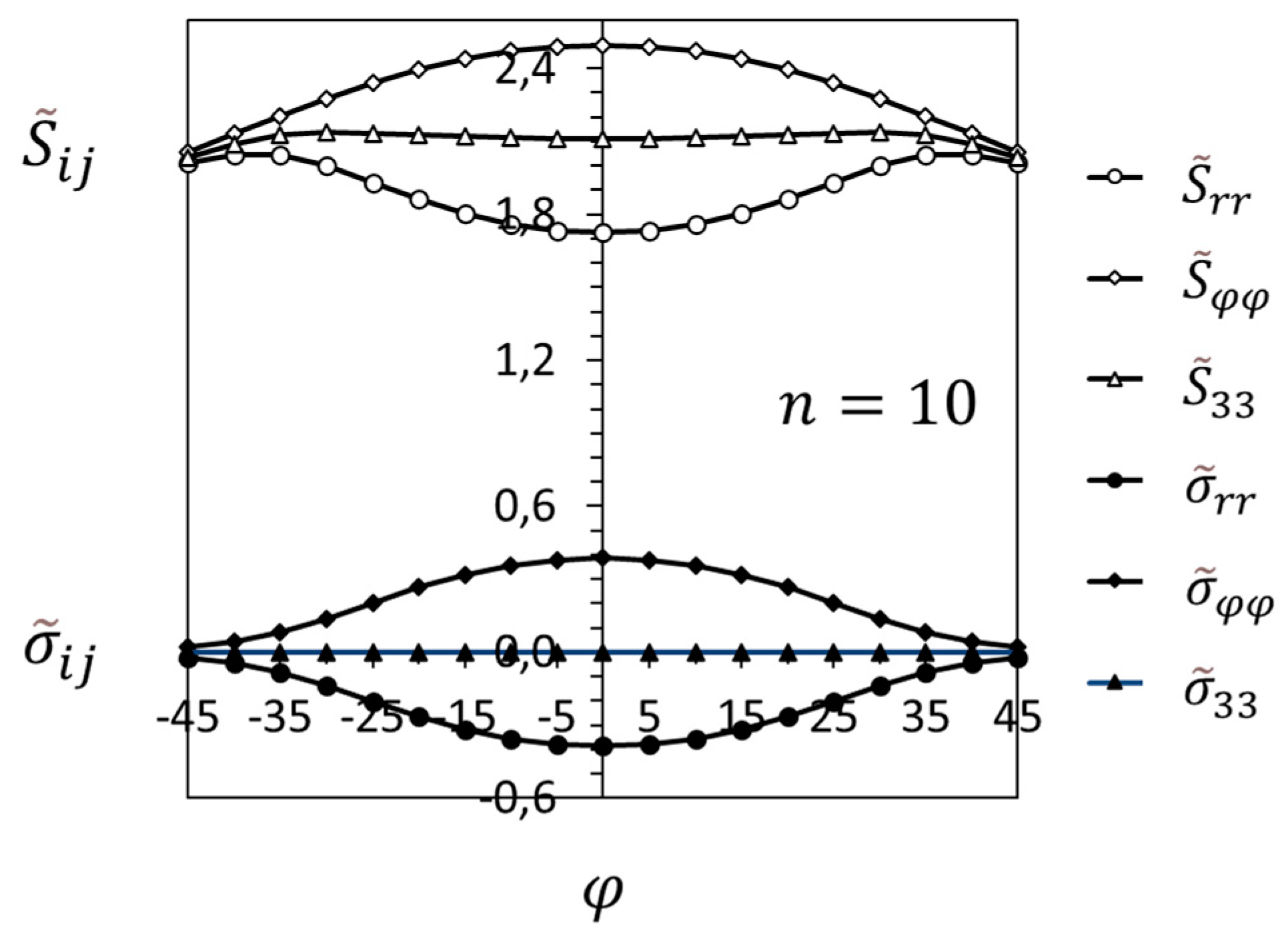
3.2. Crack-Tip Fields in the Hydride Precipitation Zone
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brewer, T. Climate Change: An Interdisciplinary Introduction; Springer Nature: Cham, Switzerland, 2023. [Google Scholar]
- Nuttal, W.J.; Powel, J.B.; Anaya-Stucchi, K.L.; Bakenne, A.T.; Wilson, A. Insights into the New Hydrogen Economy; Springer Nature: Cham, Switzerland, 2025. [Google Scholar]
- Barrera, O.; Bombac, D.; Chen, Y.; Daff, T.D.; Galindo-Nava, E.; Gong, P.; Haley, D.; Horton, R.; Katzarov, I.; Kermode, J.R.; et al. Understanding and mitigating hydrogen embrittlement of steels: A review of experimental, modelling and design progress from atomistic to continuum. J. Mater. Sci. 2018, 53, 6251–6290. [Google Scholar] [CrossRef] [PubMed]
- Coleman, C.E. Cracking of hydride-forming metals and alloys. Compr. Struct. Integr. 2003, 6, 103–161. [Google Scholar]
- Takano, S.; Suzuki, T. An electron-optical study of β-hydride and hydrogen embrittlement of vanadium. Acta Metall. 1974, 22, 265–274. [Google Scholar] [CrossRef]
- Birnbaum, H.K.; Grossbeck, M.L.; Amano, M. Hydride precipitation in Nb and some properties of NbH. J. Less-Common Met. 1976, 49, 357–370. [Google Scholar] [CrossRef]
- Northwood, D.O.; Kosasih, U. Hydrides and delayed hydrogen cracking in zirconium and its alloys. Int. Met. Rev. 1983, 28, 92–121. [Google Scholar] [CrossRef]
- Shih, D.S.; Robertson, I.M.; Birnbaum, H.K. Hydrogen embrittlement of α titanium: In situ TEM studies. Acta Metall. 1988, 36, 111–124. [Google Scholar] [CrossRef]
- Lufrano, J.; Sofronis, P.; Birnbaum, H.K. Modeling of hydrogen transport and elastically accommodated hydride formation near a crack tip. J. Mech. Phys. Solids 1996, 44, 179–205. [Google Scholar] [CrossRef]
- Lufrano, J.; Sofronis, P.; Birnbaum, H.K. Elastoplastically accommodated hydride formation and embrittlement. J. Mech. Phys. Solids 1998, 46, 1497–1520. [Google Scholar] [CrossRef]
- Varias, A.G.; Massih, A.R. Simulation of hydrogen embrittlement in zirconium alloys under stress and temperature gradients. J. Nucl. Mater. 2000, 279, 273–285. [Google Scholar] [CrossRef]
- Varias, A.G.; Massih, A.R. Hydride-induced embrittlement and fracture in metals—Effect of stress and temperature distribution. J. Mech. Phys. Solids 2002, 50, 1469–1510. [Google Scholar] [CrossRef]
- Varias, A.G.; Feng, J.L. Simulation of hydride-induced steady-state crack growth in metals—Part I: Growth near hydrogen chemical equilibrium. Comput. Mech. 2004, 34, 339–356. [Google Scholar] [CrossRef]
- Varias, A.G.; Feng, J.L. Simulation of hydride-induced steady-state crack growth in metals—Part II: General near-tip field. Comput. Mech. 2004, 34, 357–376. [Google Scholar] [CrossRef]
- Winzer, N.; Atrens, A.; Dietzel, W.; Song, G.; Kainer, K.U. Evaluation of the delayed hydride cracking mechanism for transgranular stress corrosion cracking of magnesium alloys. Mater. Sci. Eng. A 2007, 466, 18–31. [Google Scholar] [CrossRef]
- Courty, O.; Motta, A.T.; Hales, J.D. Modeling and simulation of hydrogen behavior in Zircaloy-4 fuel cladding. J. Nucl. Mater. 2014, 452, 311–320. [Google Scholar] [CrossRef]
- Jernkvist, L.O.; Massih, A.R. Multi-field modelling of hydride forming metals Part I: Model formulation and validation. Comput. Mater. Sci. 2014, 85, 363–382. [Google Scholar] [CrossRef]
- Jernkvist, L.O. Multi-field modelling of hydride forming metals Part II: Application to fracture. Comput. Mater. Sci. 2014, 85, 383–401. [Google Scholar] [CrossRef]
- Abdolvand, H. Progressive modelling and experimentation of hydrogen diffusion and precipitation in anisotropic polycrystals. Int. J. Plast. 2019, 116, 39–61. [Google Scholar] [CrossRef]
- Xia, Z.; Zang, J.; Tong, Q.; Ding, S. Multi-physics modeling of delayed hydride cracking in zirconium alloys. J. Mech. Phys. Solids 2019, 132, 103677. [Google Scholar] [CrossRef]
- Ding, G.; Xia, Z.; Zhang, J.; Ding, S.; Pang, H.; Song, X.; Chen, L. Effects of irradiation on the multi-field coupling delayed hydride cracking behavior of zirconium alloys. J. Nucl. Mater. 2022, 563, 153605. [Google Scholar] [CrossRef]
- Varias, A.G. Elastic crack-tip field in hydride forming metals under hydrogen chemical equilibrium. Int. J. Fract. 2024, 245, 183–194. [Google Scholar] [CrossRef]
- Varias, A.G. Elastic-plastic crack-tip field in hydride forming metals under hydrogen chemical equilibrium. Int. J. Fract. 2024, 246, 47–57. [Google Scholar] [CrossRef]
- Varias, A.G. Hydride induced embrittlement and fracture of non-hardening metals under hydrogen chemical equilibrium. Int. J. Solids Struct. 2024, 305, 113073. [Google Scholar] [CrossRef]
- Voisey, K.T. The Engineer’s Guide to Materials. An Applications-Focused Introduction to Materials Science; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Joshi, S.; Martukanitz, R.P.; Nassar, A.R.; Michaleris, P. Additive manufacturing with Metals. Design, Processes, Materials, Quality Assurance, and Applications; Springer Nature: Cham, Switzerland, 2023. [Google Scholar]
- Coleman, C.E. The Metallurgy of Zirconium; International Atomic Energy Agency: Vienna, Austria, 2022; Volume 3. [Google Scholar]
- Teter, D.F.; Robertson, I.M.; Birnbaum, H.K. The effect of hydrogen on the deformation and fracture of β-Titanium. Acta Mater. 2001, 49, 4313–4323. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Fu, Q.; Akiyama, E.; Song, X.; Wang, Y.; Li, Q.; Zou, N. Tensile mechanical properties and fracture behaviors of nickel-based superalloy 718 in the presence of hydrogen. Int. J. Hydrog. Energy 2018, 43, 20118–20132. [Google Scholar] [CrossRef]
- Martin, M.L.; Dadfarnia, M.; Nagao, A.; Wang, S.; Sofronis, P. Enumeration of the hydrogen-enhanced localized plasticity mechanism for hydrogen embrittlement in structural materials. Acta Mater. 2019, 165, 734–750. [Google Scholar] [CrossRef]
- Troiano, A.R. The role of hydrogen and other interstitials in the mechanical behavior of metals. Trans. ASM 1960, 52, 54–80. [Google Scholar] [CrossRef]
- Oriani, R.A.; Josephic, P.H. Equilibrium aspects of hydrogen-induced cracking of steels. Acta Metall. 1974, 22, 1065–1074. [Google Scholar] [CrossRef]
- Oriani, R.A.; Josephic, P.H. Equilibrium and kinetic studies of hydrogen assisted cracking of steel. Acta Metall. 1977, 25, 979–988. [Google Scholar] [CrossRef]
- Birenis, D.; Ogawa, Y.; Matsunaga, H.; Takakuwa, O.; Yamabe, J.; Prytz, Ø.; Thøgersen, A. Hydrogen-assisted crack propagation in α-iron during elasto-plastic fracture toughness tests. Mater. Sci. Eng. A 2019, 756, 396–404. [Google Scholar] [CrossRef]
- Symons, D.M.; Thompson, A.W. The effect of hydrogen on the fracture of alloy X-750. Metall. Mater. Trans. A 1996, 27A, 101–110. [Google Scholar] [CrossRef]
- Beachem, C.D. A new model for hydrogen assisted cracking (hydrogen embrittlement). Metall. Trans. 1972, 3, 437–451. [Google Scholar] [CrossRef]
- Birnbaum, H.K.; Sofronis, P. Hydrogen enhanced localized plasticity—A mechanism for hydrogen related fracture. Mater. Sci. Eng. 1994, A176, 191–202. [Google Scholar] [CrossRef]
- Zhang, Z.; Obasi, G.; Morana, R.; Preuss, M. In-situ observation of hydrogen induced crack initiation in a nickel-based superalloy. Scr. Mater. 2017, 140, 40–44. [Google Scholar] [CrossRef]
- Robertson, I.M.; Birnbaum, H.K. An HVEM study of hydrogen effects on the deformation and fracture of nickel. Acta Metall. 1986, 34, 353–366. [Google Scholar] [CrossRef]
- Lynch, S.P. Environmentally assisted cracking: Overview of evidence for an adsorption-induced localized-slip process. Acta Metall. 1988, 36, 2639–2661. [Google Scholar] [CrossRef]
- Sofronis, P.; McMeeking, R.M. Numerical analysis of hydrogen transport near a blunting crack tip. J. Mech. Phys. Solids 1989, 37, 317–350. [Google Scholar] [CrossRef]
- Lufrano, J.; Sofronis, P.; Symons, D. Hydrogen transport and large strain elastoplasticity near a notch in alloy X-750. Eng. Fract. Mech. 1998, 59, 827–845. [Google Scholar] [CrossRef]
- Krom, A.H.M.; Koers, R.W.J.; Bakker, A. Hydrogen transport near a blunting crack tip. J. Mech. Phys. Solids 1999, 47, 971–992. [Google Scholar] [CrossRef]
- Varias, A.G.; Warren, R. Distribution of Hydrogen in Interstitial Lattice Sites and Saturable Traps, Ahead of a Steadily Growing Crack—Mathematical Model and Numerical Algorithm; Malmö University: Malmö, Sweden, 2001; PA-06-12-01. [Google Scholar] [CrossRef]
- Kanayama, H.; Ndong-Mefane, S.; Ogino, M.; Miresmaeili, R. Reconsideration of the Hydrogen Diffusion Model Using the McNabb-Foster Formulation; Memoirs of the Faculty of Engineering, Kyushu University: Fukuoka, Japan, 2009; Volume 69, pp. 149–161. [Google Scholar]
- Di Leo, C.V.; Anand, L. Hydrogen in metals: A coupled theory for species diffusion and large elastic–plastic deformations. Int. J. Plast. 2013, 43, 42–69. [Google Scholar] [CrossRef]
- Dadfarnia, M.; Martin, M.L.; Nagao, A.; Sofronis, P.; Robertson, I.M. Modeling hydrogen transport by dislocations. J. Mech. Phys. Solids 2015, 78, 511–525. [Google Scholar] [CrossRef]
- Zhang, Z.; Peeters, J.; Popovich, V.; Ayas, C. Combined effects of stress and temperature on hydrogen diffusion in non-hydride forming alloys applied in gas turbines. Int. J. Hydrog. Energy 2022, 47, 30687–30706. [Google Scholar] [CrossRef]
- Varias, A.G. Hydrogen Distribution in Metals Under Chemical Equilibrium and Steady-State Heat Conduction; EH-29122022; Euro Harmonization and Engineering: N. Iraklio, Greece, 2022. [Google Scholar] [CrossRef]
- Denbigh, K.G. The Thermodynamics of the Steady State; Methuen & CO.: London, UK, 1951. [Google Scholar]
- Shewmon, P. Diffusion in Solids; The Minerals, Metals & Materials Society: Warrendale, PA, USA, 1989. [Google Scholar]
- Nagumo, M. Fundamentals of Hydrogen Embrittlement; Springer Nature: Singapore, 2023. [Google Scholar]
- Johnson, H.H.; Quick, N.; Kumnick, A.J. Hydrogen trapping mechanisms by permeation techniques. Scr. Metall. 1979, 13, 67–72. [Google Scholar] [CrossRef]
- Oriani, R.A. The diffusion and trapping of hydrogen in steel. Acta Metall. 1970, 18, 147–157. [Google Scholar] [CrossRef]
- Krom, A.H.M.; Bakker, A.D. Hydrogen trapping models in steel. Metall. Mater. Trans. B 2000, 31B, 1475–1482. [Google Scholar] [CrossRef]
- Shi, R.; Nie, Z.; Fan, Q.; Wang, F.; Zhou, Y.; Liu, X. Correlation between dislocation-density-based strain hardening and microstructural evolution in dual phase TC6 titanium alloy. Mater. Sci. Eng. A 2018, 715, 101–107. [Google Scholar] [CrossRef]
- Nabarro, F.R.N. The strains produced by precipitation in alloys. Proc. R. Soc. 1940, A175, 519–538. [Google Scholar]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. 1957, A241, 376–396. [Google Scholar]
- Lee, J.K.; Earmee, Y.Y.; Aaronson, H.I.; Russell, K.C. Plastic relaxation of the transformation strain energy of a misfitting spherical precipitate: Ideal plastic behavior. Metall. Trans. A 1980, 11A, 1837–1847. [Google Scholar] [CrossRef]
- Earmee, Y.Y.; Johnson, W.C.; Lee, J.K. Plastic relaxation of the transformation strain energy of a misfitting spherical precipitate: Linear and power-law strain hardening. Metall. Trans. A 1981, 12A, 1521–1530. [Google Scholar]
- Broberg, K.B. Cracks and Fracture; Academic Press: London, UK, 1999. [Google Scholar]
- Ashby, M.F.; Jones, D.R.H. Engineering Materials 2: An Introduction to Microstructures, Processing and Design; Pergamon: Oxford, UK, 1986. [Google Scholar]
- Hertzberg, R.W. Deformation and Fracture Mechanics of Engineering Materials; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Hirth, J.P. Effects of hydrogen on the properties of iron and steel. Metall. Trans. A 1980, 11A, 861–890. [Google Scholar] [CrossRef]
- Kumnick, A.J.; Johnson, H.H. Deep trapping states for hydrogen in deformed iron. Acta Metall. 1980, 28, 33–39. [Google Scholar] [CrossRef]
- Special Metals Alloy Technical Bulletins. Available online: https://www.specialmetals.com/documents/technical-bulletins/inconel/inconel-alloy-x-750.pdf (accessed on 31 October 2024).
- Baranowski, B.; Majchrzak, S.; Flanagan, T.B. The volume increase of fcc metals and alloys due to interstitial hydrogen over a wide range of hydrogen contents. J. Phys. F Met. Phys. 1971, 1, 258–261. [Google Scholar] [CrossRef]
- Senkov, O.N.; Dubois, M.; Jonas, J.J. Elastic moduli of titanium-hydrogen alloys in the temperature range 20 °C to 1100 °C. Metall. Mater. Trans. A 1996, 27A, 3963–3970. [Google Scholar] [CrossRef]
- Alvarez, A.M.; Robertson, I.M.; Birnbaum, H.K. Hydrogen embrittlement of a metastable β-titanium alloy. Acta Mater. 2004, 52, 4161–4175. [Google Scholar] [CrossRef]
- Waisman, J.L.; Sines, G.; Robinson, L.B. Diffusion of hydrogen in titanium alloys due to composition, temperature, and stress gradients. Metall. Trans. 1973, 4, 291–302. [Google Scholar] [CrossRef]
- Vitt, R.S.; Ono, K. Hydrogen solubility in alpha titanium. Metall. Trans. 1971, 2, 608–609. [Google Scholar] [CrossRef]
- Pardee, W.J.; Paton, N.E. Model of sustained load cracking by hydride growth in Ti alloys. Metall. Trans. A 1980, 11A, 1391–1400. [Google Scholar] [CrossRef]
- Chen, C.Q.; Li, S.X.; Zheng, H.; Wang, L.B.; Lu, K. An investigation on structure, deformation and fracture of hydrides in titanium with a large range of hydrogen contents. Acta Mater. 2004, 52, 3697–3706. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Singular behaviour at the end of a tensile crack in a hardening material. J. Mech. Phys. Solids 1968, 16, 13–31. [Google Scholar] [CrossRef]
- Rice, J.R.; Rosengren, G.F. Plane strain deformation near a crack tip in a power-law hardening material. J. Mech. Phys. Solids 1968, 16, 1–12. [Google Scholar] [CrossRef]
- San Marchi, C.; Somerday, B.P.; Robinson, S.L. Permeability, solubility and diffusivity of hydrogen isotopes in stainless steels at high gas pressures. Int. J. Hydrog. Energy 2007, 32, 100–116. [Google Scholar] [CrossRef]
- Symington, M.; Shih, C.F.; Ortiz, M. Tables of Plane Strain Mixed-Mode Plastic Crack Tip Fields; Brown University: Providence, RI, USA, 1988; MRG/DMR-8714665/1. [Google Scholar]
- Rice, J.R. A path independent integral and the approximate analysis of strain concentration by notches and cracks. J. Appl. Mech. 1968, 35, 379–387. [Google Scholar] [CrossRef]
- Williams, M.L. On the stress distribution at the base of a stationary crack. J. Appl. Mech. 1957, 24, 109–114. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Plastic stress and strain fields at a crack tip. J. Mech. Phys. Solids 1968, 16, 337–347. [Google Scholar] [CrossRef]




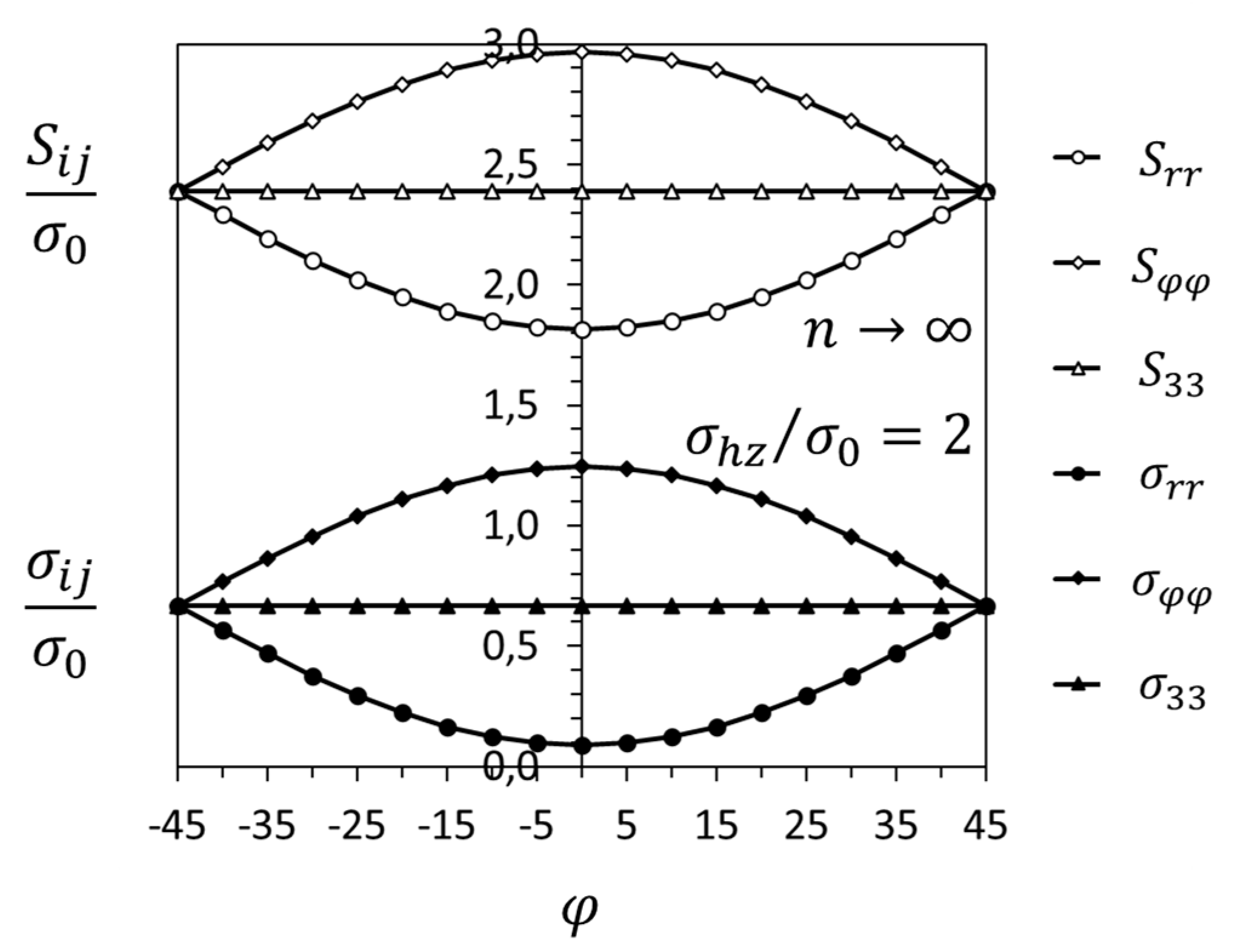
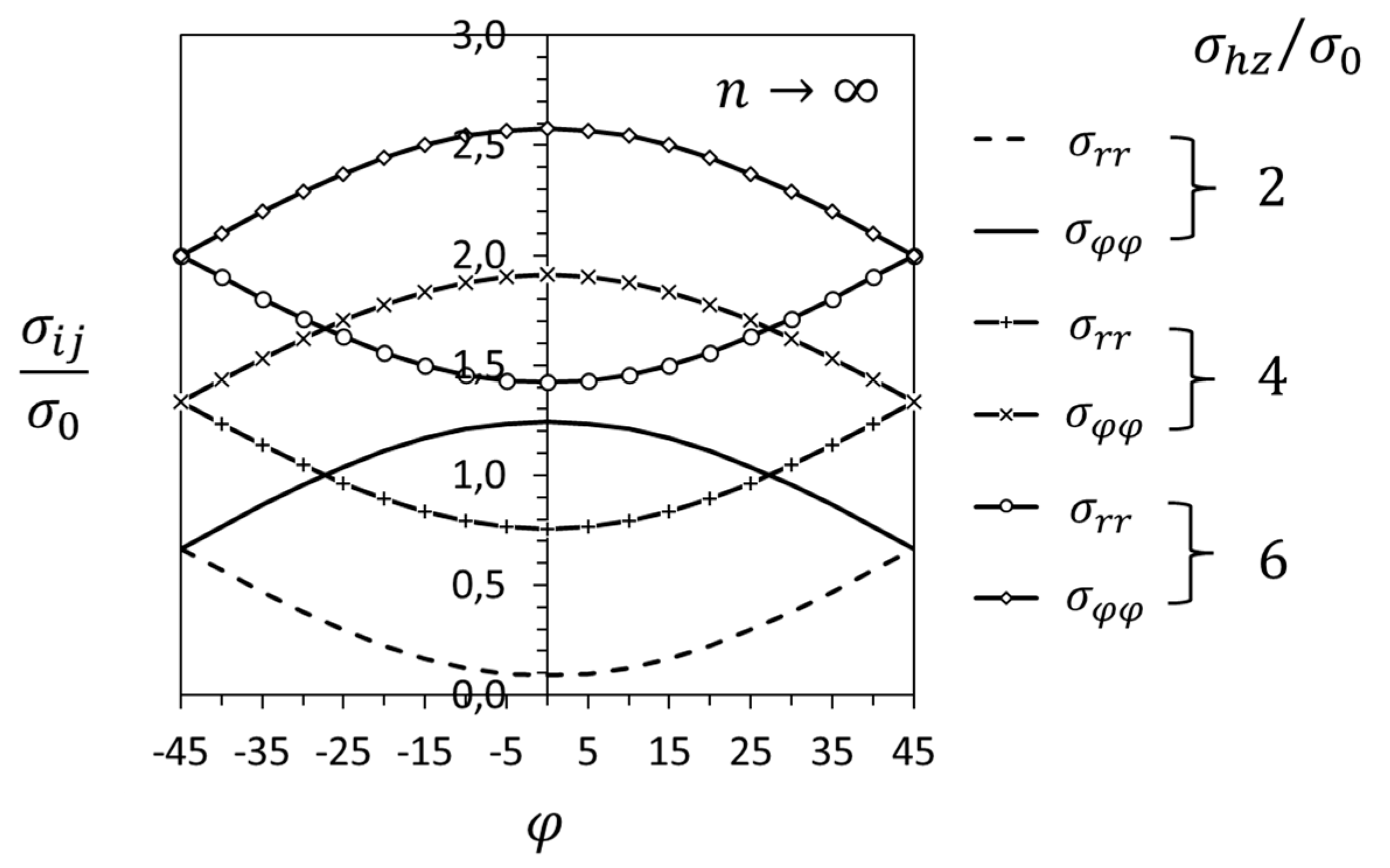
| Material Property (Units) | Reference | |
|---|---|---|
| E (GPa) | 210 | [62] |
| ν | 0.3 | [63] |
| (MPa) | 250 | |
| 20 | calculation | |
| (m3/mol) | 2 × 10−6 | [64] |
| (m3/mol) | 7.1 × 10−6 | calculation |
| (kJ/mol) | 59.9 | [65] |
| (m−3 · mol−1) | [65] | |
| β | 6 | [55] |
| Material Property (Units) | Reference | |
|---|---|---|
| E (GPa) | 214 (at 25 °C) 196 (at 285 °C) | [66] |
| ν | 0.29 | [66] |
| (MPa) | 810 (at 25 °C) 735 (at 285 °C) | [35] |
| 15 | calculation | |
| (m3/mol) | 1.72 × 10−6 | [35,42,67] |
| (m3/mol) | 6.87 × 10−6 | [42] |
| (kJ/mol) | 15.1 | [35,42] |
| (m−3 · mol−1) | [42] | |
| β | 1 | [42,55] |
| Material Property (Units) | Reference | |
|---|---|---|
| E (GPa) | 110 | [68] |
| ν | 0.34 | [68] |
| (MPa) | 140 1 | |
| (m3/mol) | 1.7 × 10−6 | [69,70] |
| (m3/mol) | 10.62 × 10−6 | calculation |
| (mol/m3) | 3.8478 × 105 exp(−20,951.28/RT) | [71] |
| (m3/mol) | 13.17 × 10−6 | calculation |
| 0.24 | [72] | |
| 1.5 2 | e.g., [73] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varias, A.G. Chemical Equilibrium Fracture Mechanics—Hydrogen Embrittlement Application. Corros. Mater. Degrad. 2025, 6, 5. https://doi.org/10.3390/cmd6010005
Varias AG. Chemical Equilibrium Fracture Mechanics—Hydrogen Embrittlement Application. Corrosion and Materials Degradation. 2025; 6(1):5. https://doi.org/10.3390/cmd6010005
Chicago/Turabian StyleVarias, Andreas G. 2025. "Chemical Equilibrium Fracture Mechanics—Hydrogen Embrittlement Application" Corrosion and Materials Degradation 6, no. 1: 5. https://doi.org/10.3390/cmd6010005
APA StyleVarias, A. G. (2025). Chemical Equilibrium Fracture Mechanics—Hydrogen Embrittlement Application. Corrosion and Materials Degradation, 6(1), 5. https://doi.org/10.3390/cmd6010005






