The PARC_CL 2.1 Crack Model for NLFEA of Reinforced Concrete Elements Subjected to Corrosion Deterioration
Abstract
:1. Introduction
2. Materials and Methods
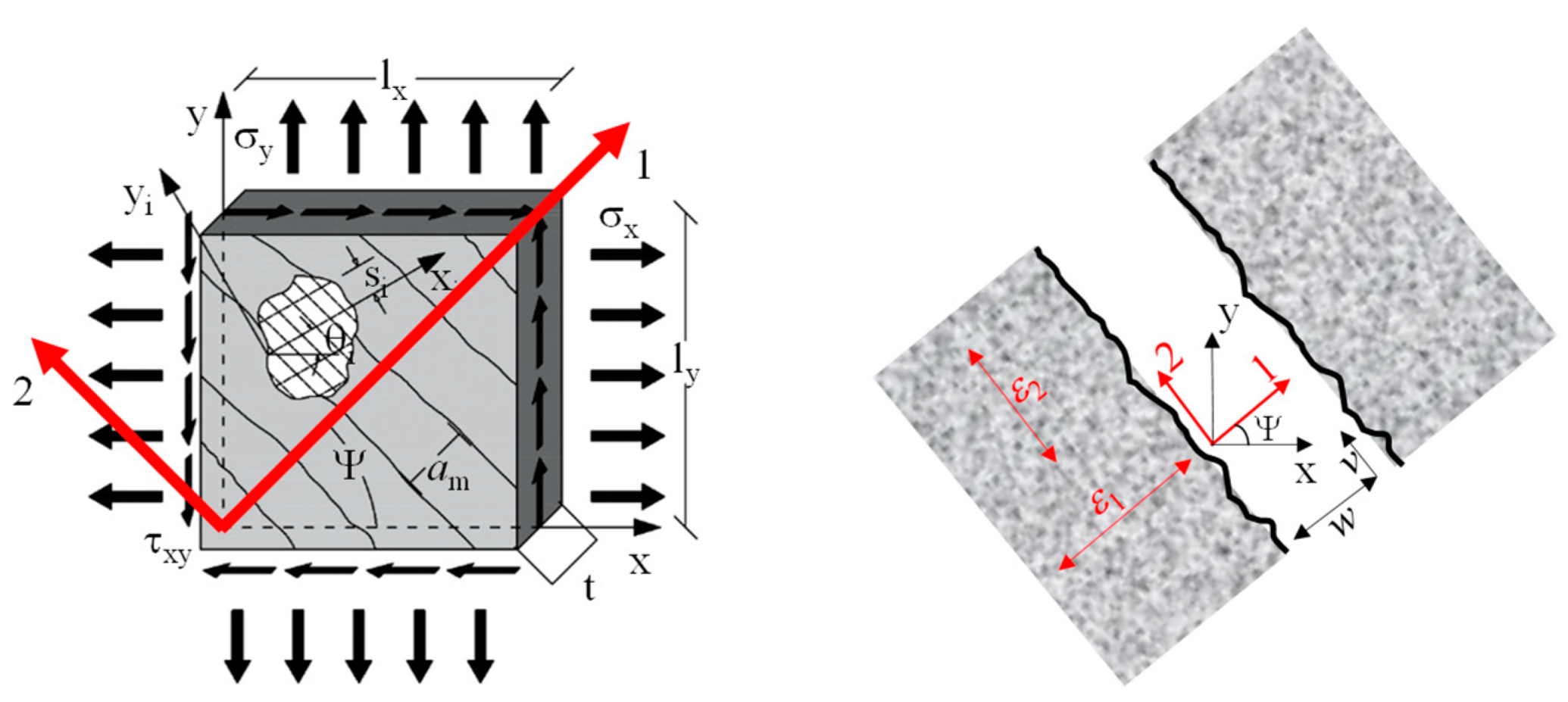
2.1. The PARC_CL 2.1 Crack Model
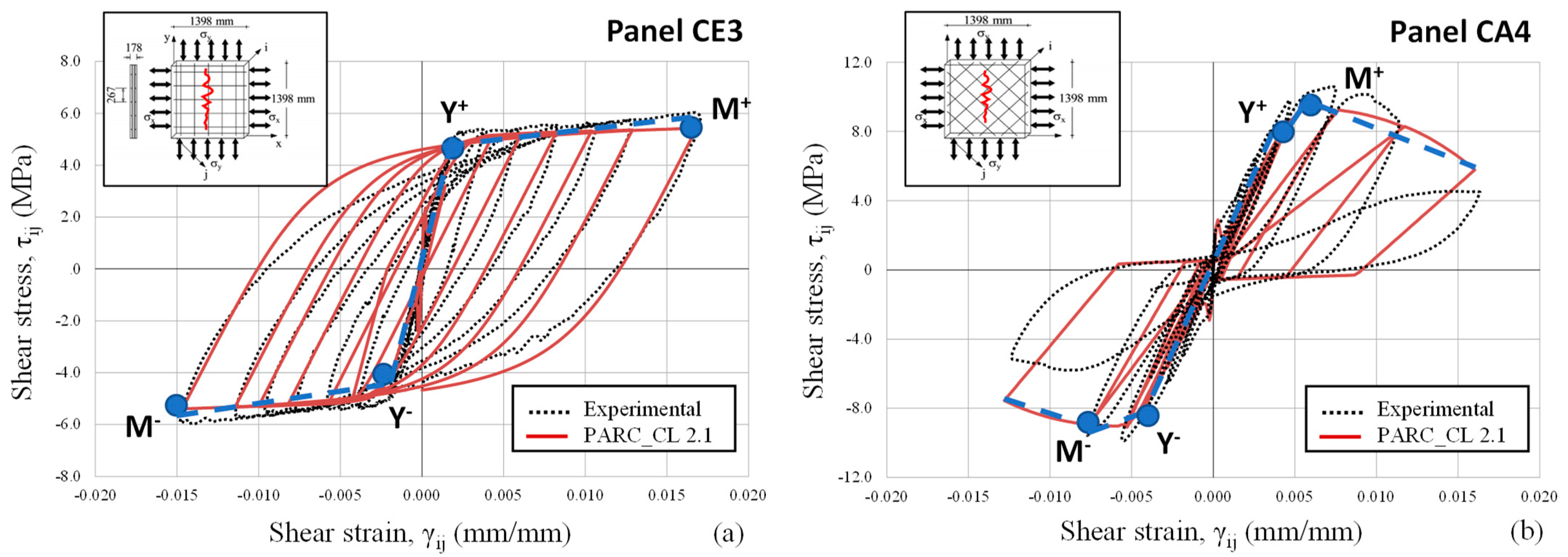
2.2. Validation of the Model
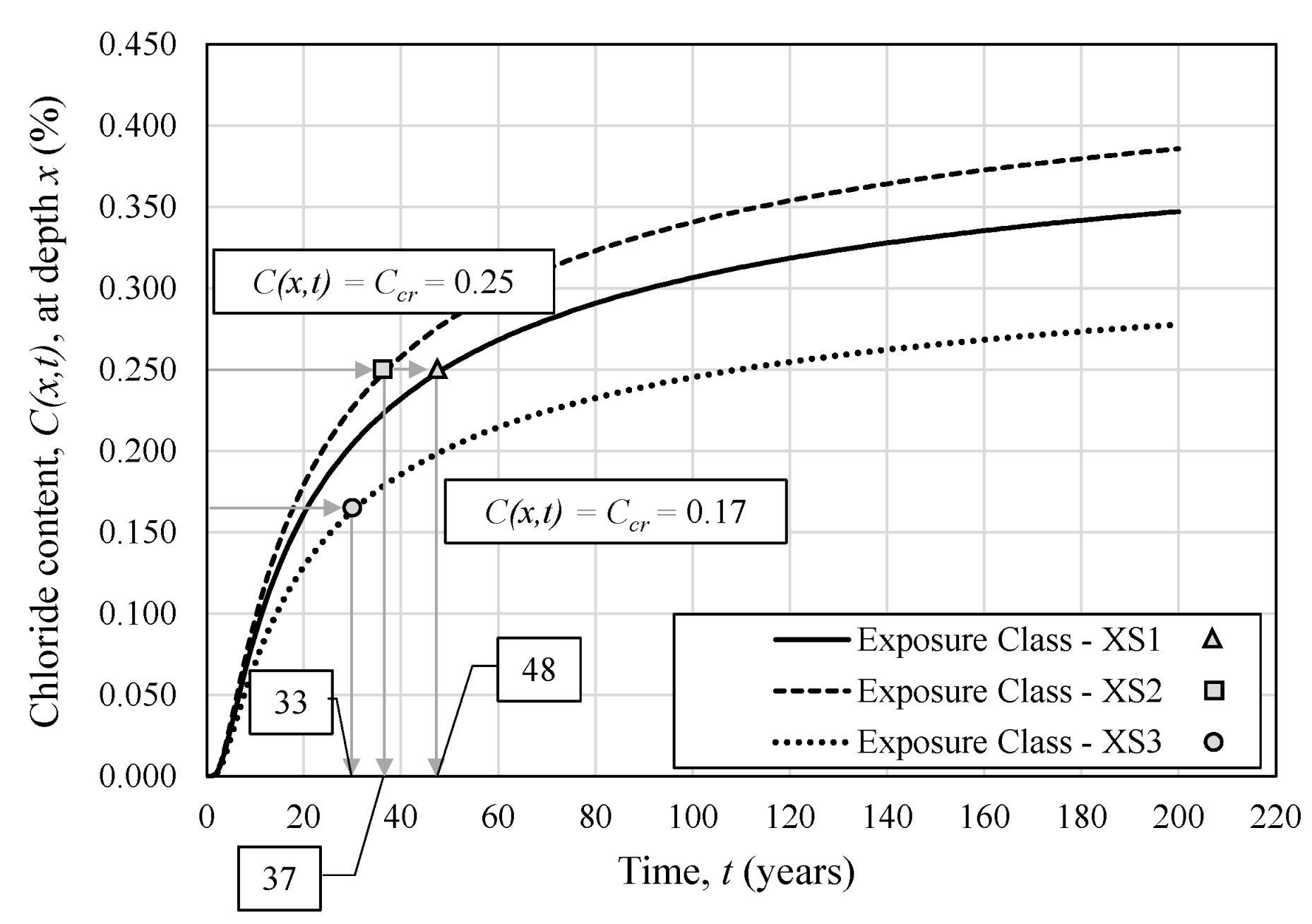
2.3. Prediction of Corrosion Deterioration
2.4. Mechanical Properties
2.4.1. Steel
2.4.2. Concrete
3. Results and Discussion
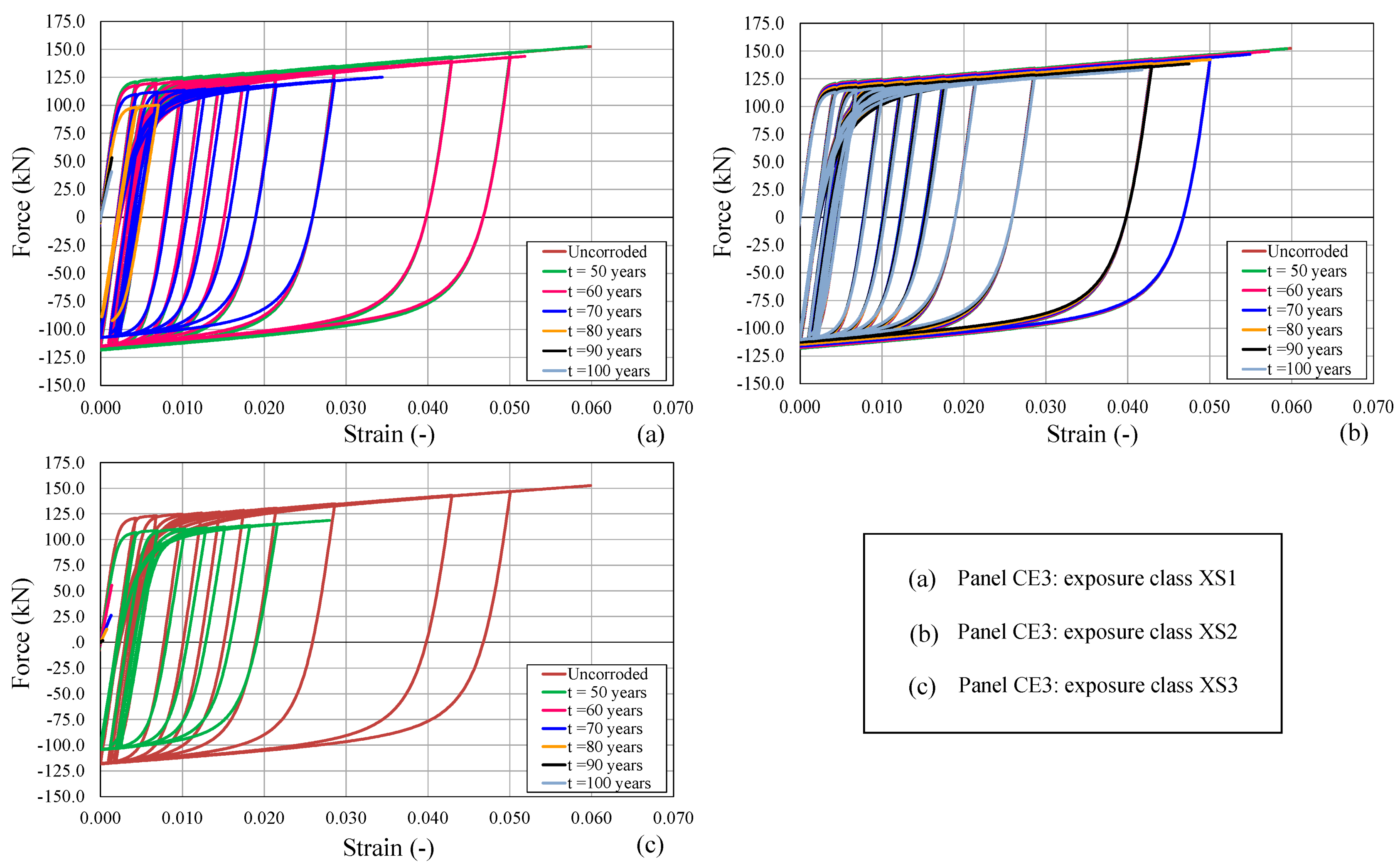
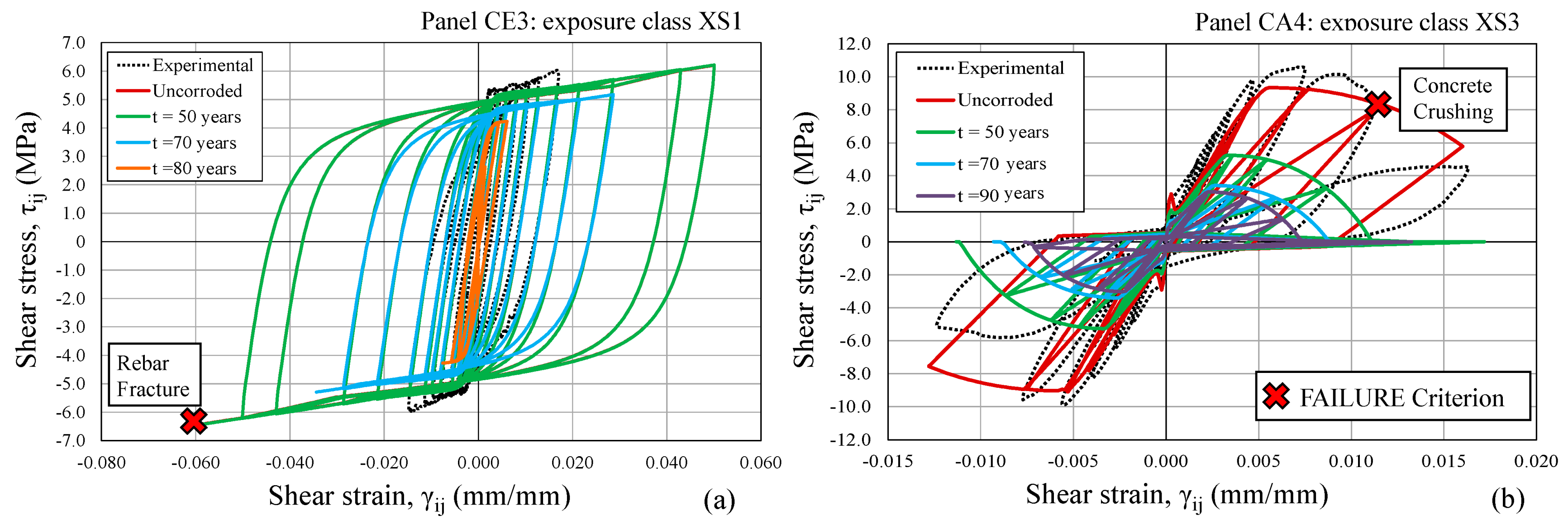
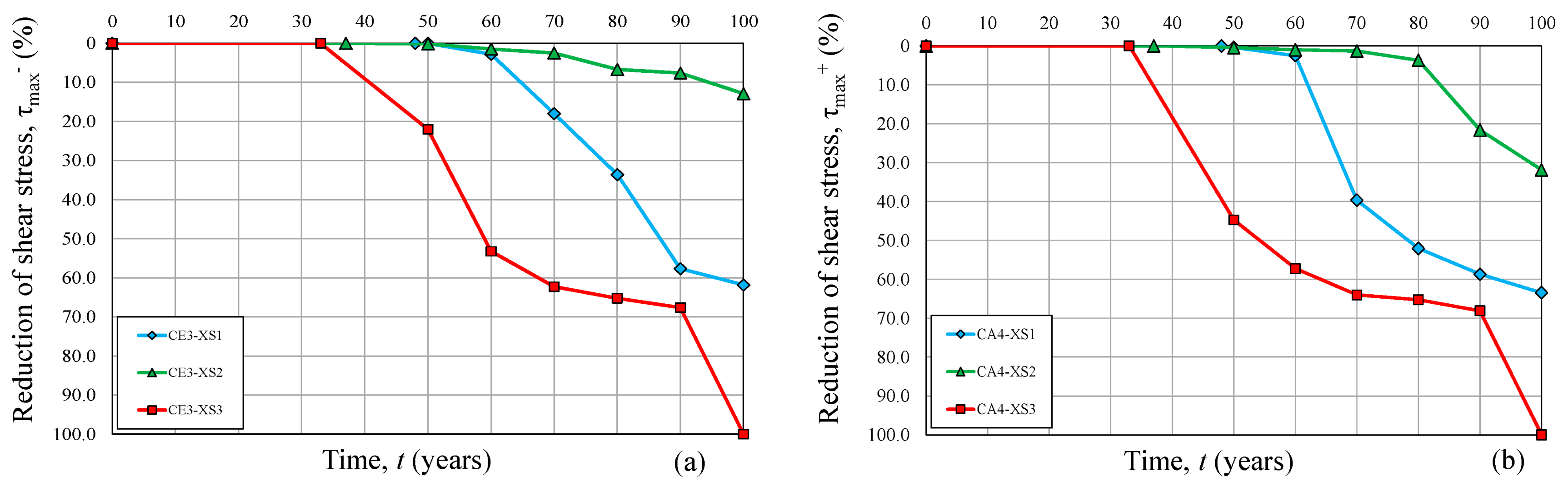
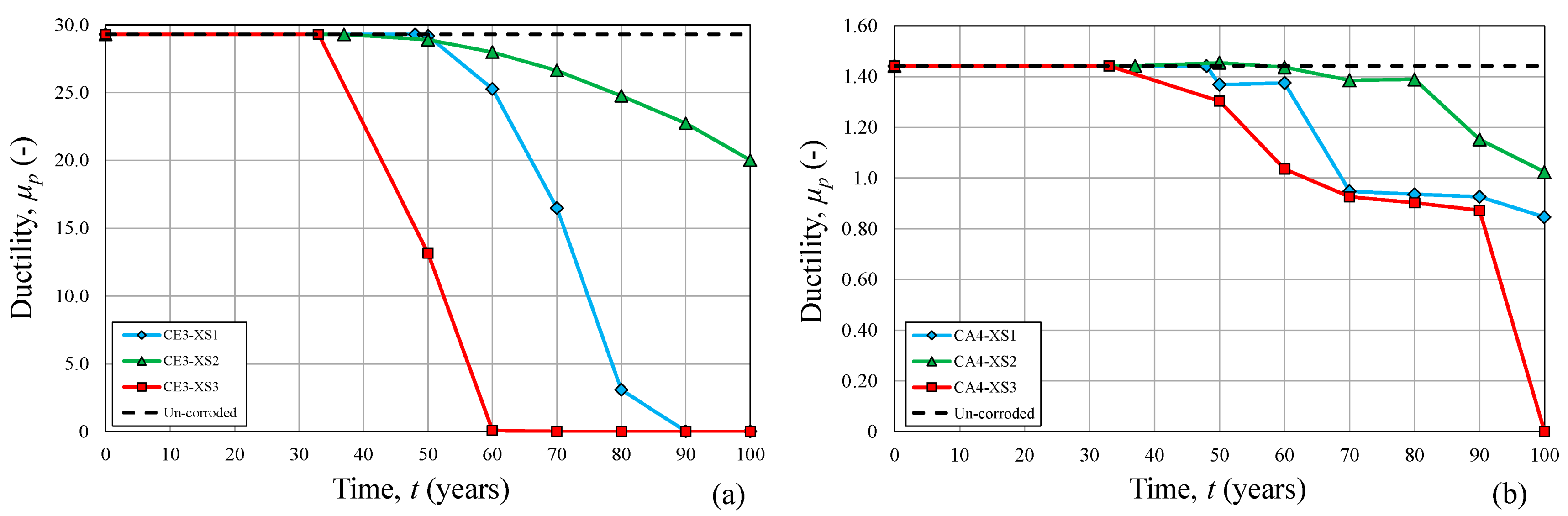
3.1. Shear Stress–Shear Strain Response Reduction
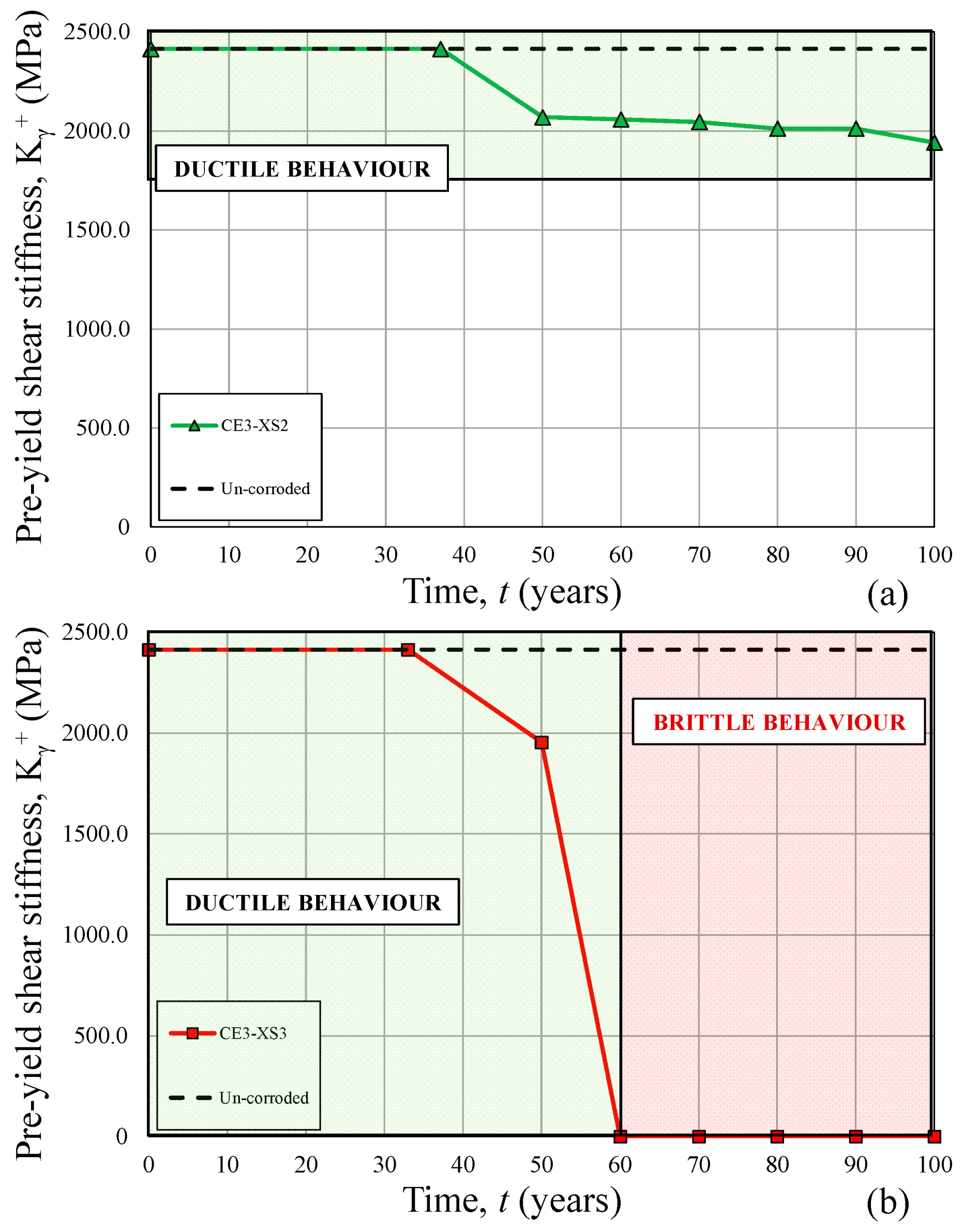
3.2. Pre-Yield Shear Stiffness Effect
4. Conclusions
- Generally, the PARC_CL 2.1 crack model can be used as a powerful and useful tool for the prediction of the cyclic response of existing corroded RC structures.
- As expected, the corroded RC panels present lower maximum resistance and ductility than the uncorroded one. In this regard, considering the severe reduction of mechanical properties of both steel and concrete over time, brittle failures characterized by absence of ductility occur.
- Over time, a significant reduction in terms of maximum shear stress, τmax, ductility, μp, and pre-yield shear stiffness, Kγ, was observed, especially for the exposure class XS3, which results in being the worst environmental condition analyzed. On the other hand, a significant lower reduction was noticed in the case of exposure class XS2, except for panel CA4.
- As highlighted by NLFEA results, the failure of each panel occurred after a different exposure time as a function of both the reduction of the mechanical properties of steel and concrete and the type of exposure class considered. As a general statement, panel CE3 fails due to the rupture of reinforcement, while the failure of panel CA4 is induced by concrete crushing. In particular, with the decrease of mechanical properties induced by the corrosion deterioration process, the failure mode characterizing each RC panel analyzed does not vary over time.
- To carry out reliable calculations of existing RC structures over time, particular attention must be addressed to the estimation of important parameters, such as critical chloride content, chloride diffusion coefficient, and corrosion rate. These values may be obtained by means of in situ measurement, when possible, or through probabilistic and statistical analyses. On this research topic, further studies need to be carried out.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Corroded RC Panels | Parameter | Time of Analysis (Years) | |||||
|---|---|---|---|---|---|---|---|
| 50 | 60 | 70 | 80 | 90 | 100 | ||
| Exposure Class: XS1 | |||||||
| CE3 | τmax+ (MPa) | 6.22 | 6.20 | 5.17 | 4.27 | 3.50 | 3.48 |
| τmax– (MPa) | –6.45 | –6.27 | –5.29 | –4.28 | –2.73 | –2.46 | |
| γmax+ (-) | 0.0501 | 0.0500 | 0.0285 | 0.0063 | 0.0014 | 0.0013 | |
| γmax− (-) | –0.0598 | –0.0520 | –0.0346 | –0.0081 | –0.0019 | –0.0003 | |
| CA4 | τmax+ (MPa) | 9.47 | 9.26 | 5.73 | 4.55 | 3.93 | 3.47 |
| τmax− (MPa) | –9.36 | –9.00 | –5.70 | –4.50 | –3.94 | –3.47 | |
| γmax+ (-) | 0.0057 | 0.0056 | 0.0038 | 0.0031 | 0.0027 | 0.0026 | |
| γmax− (-) | –0.0057 | –0.0055 | –0.0038 | –0.0030 | –0.0028 | –0.0025 | |
| Exposure Class: XS2 | |||||||
| CE3 | τmax+ (MPa) | 6.20 | 6.16 | 6.15 | 5.86 | 5.84 | 5.33 |
| τmax– (MPa) | –6.44 | –6.36 | –6.29 | –6.02 | –5.96 | –5.62 | |
| γmax+ (-) | 0.0498 | 0.0496 | 0.0494 | 0.0429 | 0.0425 | 0.0285 | |
| γmax− (-) | –0.0592 | –0.0574 | –0.0547 | –0.0510 | –0.0470 | –0.0416 | |
| CA4 | τmax+ (MPa) | 9.46 | 9.41 | 9.37 | 9.15 | 7.44 | 6.47 |
| τmax– (MPa) | –9.28 | –9.22 | –9.21 | –8.97 | –7.42 | –6.49 | |
| γmax+ (-) | 0.0056 | 0.0054 | 0.0054 | 0.0053 | 0.0044 | 0.0040 | |
| γmax– (-) | –0.0058 | –0.0057 | –0.0056 | –0.0055 | –0.0045 | –0.0041 | |
| Exposure Class: XS3 | |||||||
| CE3 | τmax+ (MPa) | 4.87 | 3.30 | 3.16 | 2.22 | 2.07 | - |
| τmax– (MPa) | –5.03 | –3.02 | –2.44 | –2.24 | –2.09 | - | |
| γmax+ (-) | 0.0213 | 0.0014 | 0.0014 | 0.0002 | 0.0002 | - | |
| γmax− (-) | –0.0280 | –0.0021 | –0.0003 | –0.0003 | –0.0003 | - | |
| CA4 | τmax+ (MPa) | 5.25 | 4.06 | 3.42 | 3.30 | 3.03 | - |
| τmax− (MPa) | –5.27 | –4.07 | –3.41 | –3.30 | –3.03 | - | |
| γmax+ (-) | 0.0035 | 0.0028 | 0.0025 | 0.0023 | 0.0003 | 0.0003 | |
| γmax− (-) | –0.0034 | –0.0028 | –0.0026 | –0.0023 | –0.0020 | - | |
| Corroded RC Panels | Parameter | Time of Analysis (Years) | |||||
|---|---|---|---|---|---|---|---|
| 50 | 60 | 70 | 80 | 90 | 100 | ||
| Exposure Class: XS1 | |||||||
| CE3 | Kγ+ (MPa) | 2074.4 | 2059.1 | 1888.2 | 1698.6 | - | - |
| Kγ− (MPa) | 2449.5 | 2303.0 | 2121.2 | 1787.9 | - | - | |
| CA4 | Kγ+ (MPa) | 1660.5 | 1653.6 | 1508.5 | 1468.8 | 1453.7 | 1334.9 |
| Kγ− (MPa) | 1642.1 | 1636.4 | 1499.2 | 1451.6 | 1405.7 | 1386.3 | |
| Exposure Class: XS2 | |||||||
| CE3 | Kγ+ (MPa) | 2069.4 | 2057.9 | 2045.4 | 2011.5 | 2005.6 | 1941.4 |
| Kγ− (MPa) | 2449.5 | 2419.2 | 2363.6 | 2333.3 | 2287.9 | 2166.7 | |
| CA4 | Kγ+ (MPa) | 1701.4 | 1672.7 | 1669.7 | 1666.7 | 1596.6 | 1517.2 |
| Kγ− (MPa) | 1582.5 | 1575.6 | 1568.4 | 1555.7 | 1524.5 | 1483.3 | |
| Exposure Class: XS3 | |||||||
| CE3 | Kγ+ (MPa) | 1954.5 | - | - | - | - | - |
| Kγ− (MPa) | 2050.5 | 1482.4 | - | - | - | - | |
| CA4 | Kγ+ (MPa) | 1590.0 | 1374.9 | 1266.7 | 1188.2 | 1174.5 | - |
| Kγ− (MPa) | 1548.9 | 1452.3 | 1310.6 | 1304.7 | 1273.6 | - | |
References
- Di Prisco, M. Critical infrastructures in Italy: State of the art, case studies, rational approaches to select the intervention priorities. In Proceedings of the Fib Symposium 2019: Concrete—Innovations in Materials, Design and Structures, Kraków, Poland, 27–29 May 2019; pp. 49–58. [Google Scholar]
- Sanchez, J.; Fullea, J.; Andrade, C. Corrosion-induced brittle failure in reinforcing steel. Theor. Appl. Fract. Mech. 2017, 92, 229–232. [Google Scholar] [CrossRef]
- Coronelli, D.; Hanjari, K.Z.; Lundgren, K. Severely Corroded RC with Cover Cracking. J. Struct. Eng. 2013, 139, 221–232. [Google Scholar] [CrossRef] [Green Version]
- Coronelli, D.; François, R.; Dang, H.; Zhu, W. Strength of Corroded RC Beams with Bond Deterioration. J. Struct. Eng. 2019, 145, 04019097. [Google Scholar] [CrossRef]
- Andrade, C.; Alonso, C.; Molina, F.J. Cover Cracking as a function of bar corrosion: Experimental test. Mater. Struct. 1993, 26, 453–464. [Google Scholar] [CrossRef]
- Torres-Acosta, A.A.; Castro-Borges, P. Corrosion-induced Cracking of Concrete Elements Exposed to a Natural Marine Environment for Five Years. Corrosion 2013, 69, 1122–1131. [Google Scholar] [CrossRef]
- Rodriguez, J.; Ortega, L.M.; Casal, J. Load carrying capacity of concrete structures with corroded reinforcement. Constr. Build. Mater. 1997, 11, 239–248. [Google Scholar] [CrossRef]
- Torres-Acosta, A.A.; Fabela-Gallegos, M.; Munoz-Noval, A.; Vazquez-Vega, D.; Hernandez-Jimenez, J.R.; Martinez-Madrid, M. Influence of corrosion on the Structural Stiffness of Reinforced Concrete Beams. Corrosion 2004, 60, 862–872. [Google Scholar] [CrossRef]
- Torres-Acosta, A.A.; Navarro-Gutierrez, S.; Teran-Guillen, J. Residual Flexure Capacity of Corroded Reinforced Concrete Beams. Eng. Struct. 2007, 29, 1145–1152. [Google Scholar] [CrossRef]
- Ahmad, S. Reinforcement corrosion in concrete structures, its monitoring and service life prediction—A review. Cem. Concr. Compos. 2003, 25, 459–471. [Google Scholar] [CrossRef]
- Ranjith, A.; Rao, K.B.; Manjunath, K. Evaluating the effect of corrosion on service life prediction of RC structures—A parametric review. Int. J. Sustain. Built Environ. 2016, 5, 587–603. [Google Scholar] [CrossRef] [Green Version]
- Imperatore, S.; Rinaldi, Z. Strength decay of RC sections for chloride attack. Int. J. Struct. Integr. 2016, 7, 194–212. [Google Scholar] [CrossRef]
- ABAQUS-6. 12-1 Standard User’s Manual; Hibbitt, Karlsson and Sorensen, Inc: Providence, RI, USA, 2012.
- Belletti, B.; Scolari, M.; Vecchi, F. PARC_CL 2.0 crack model for NLFEA of reinforced concrete structures under cyclic loadings. Comput. Struct. 2017, 191, 165–179. [Google Scholar] [CrossRef]
- Belletti, B.; Stocchi, A.; Scolari, M.; Vecchi, F. Validation of the PARC_CL 2.0 crack model for the assessment of the nonlinear behaviour of RC structures subjected to seismic action: SMART 2013 sharing table test simulation. Eng. Struct. 2017, 150, 759–773. [Google Scholar] [CrossRef]
- Belletti, B.; Muttoni, A.; Ravasini, S.; Vecchi, F. Parametric analysis on punching shear resistance of reinforced concrete continuous slab. Mag. Concr. Res. 2018, 71, 1083–1096. [Google Scholar] [CrossRef]
- Mansour, M.; Hsu, T.T.C. Behavior of Reinforced Concrete Elements under Cyclic Shear. I: Experiments. J. Struct. Eng. 2005, 131, 44–53. [Google Scholar] [CrossRef]
- Tuutti, K. Corrosion of Steel in Concrete; Swedish Cement and Concrete Research Institute: Stockholm, Sweden, 1982. [Google Scholar]
- Crete, D. Probabilistic Performance Based Durability Design of Concrete Structures: Statistical Quantification of the Variables in the Limit State Functions; Report No. BE 95-1347; The European Union—Brite EuRam III: Brussels, Belgium, 2000; pp. 62–63. [Google Scholar]
- Fluge, F. Marine Chlorides–A probabilistic approach to drive provisions for EN 206-1. In Proceedings of the Duranet 3rd Workshop-Service Life Design of Concrete Structures—From Theory to Standardization, Tromsø, Norway, Tromsø, Norway, 10–12 June 2001. [Google Scholar]
- Contecvet IN30902I. A Validated User’s Manual for Assessing the Residual Life of Concrete Structures; DG Enterprise, CEC: Tokyo, Japan, 2001.
- Chen, E.; Berrocal, C.G.; Fernandez, I.; Löfgren, I.; Lundgren, K. Assessment of the mechanical behaviour of reinforcement bars with localised pitting corrosion by Digital Image Correlation. Eng. Struct. 2020, 219, 110936. [Google Scholar] [CrossRef]
- Coronelli, D.; Gambarova, P. Compressive Behavior of Unconfined and Confined Clay Brick Masonry Compressive Behavior of Unconfined and Confined Clay. J. Struct. Eng. 2004, 130, 1214–1224. [Google Scholar] [CrossRef]
- He, W.; Wu, Y.F.; Liew, K.M. A fracture energy based constitutive model for the analysis of reinforced concrete structures under cyclic loading. Comput. Methods Appl. Mech. Eng. 2008, 197, 4745–4762. [Google Scholar] [CrossRef]
- Gambarova, P. Sulla trasmissione del taglio in elementi bidimensionali piani di c.a. fessurati. In Proceedings of the Giornate AICAP, Bari, Italy, 26–29 May 1983; pp. 141–156. (In Italian). [Google Scholar]
- Vecchio, F.J.; Collins, M.P. Compression Response of Cracked Reinforced Concrete. J. Struct. Eng. 1993, 119, 3590–3610. [Google Scholar] [CrossRef]
- Menegotto, M.; Pinto, P.E. Method of Analysis for Cyclically Loaded R. C. Plane Frames Including Changes in Geometry and Non-Elastic Behavior of Elements under Combined Normal Force and Bending. In Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads; IABSE: Lisbon, Portugal, 1973; pp. 15–22. [Google Scholar]
- Monti, G.; Nuti, C. Nonlinear Cyclic Behavior of Reinforcing Bars Including Buckling. J. Struct. Eng. 1992, 118, 3268–3284. [Google Scholar] [CrossRef]
- Kashani, M.M.; Lowes, L.N.; Crewe, A.J.; Alexander, N.A. Phenomenological hysteretic model for corroded reinforcing bars including inelastic buckling and low-cycle fatigue degradation. Comput. Struct. 2015, 156, 58–71. [Google Scholar] [CrossRef] [Green Version]
- Belletti, B.; Damoni, C.; Gasperi, A. Modeling approaches suitable for pushover analyses of RC structural wall buildings. Eng. Struct. 2013, 57, 327–338. [Google Scholar] [CrossRef]
- Belletti, B.; Esposito, R.; Walraven, J. Shear Capacity of Normal, Lightweight, and High-Strength Concrete Beams according to Model Code 2010. II: Experimental Results versus Nonlinear Finite Element Program Results. J. Struct. Eng. 2013, 139, 1600–1607. [Google Scholar] [CrossRef]
- Belletti, B.; Cerioni, R.; Iori, I. Physical Approach for Reinforced-Concrete (PARC) Membrane Elements. J. Struct. Eng. 2001, 127, 1412–1426. [Google Scholar] [CrossRef]
- Walraven, J.; Belletti, B.; Esposito, R. Shear Capacity of Normal, Lightweight, and High-Strength Concrete Beams according to Model Code 2010. I: Experimental Results versus Analytical Model Results. J. Struct. Eng. 2013, 139, 1593–1599. [Google Scholar] [CrossRef]
- CEN. European Standard: EN-206: Concrete-Specification, Performance, Production and Conformity; CEN: Brussels, Belgium, 2014. [Google Scholar]
- Collepardi, M.; Marcialis, A.; Turriziani, R. Penetration of Chloride Ions into Cement Pastes and Concretes. J. Am. Ceram. Soc. 1972, 55, 534–535. [Google Scholar] [CrossRef]
- Alonso, C.; Andrade, C.; Castellote, M.; Castro, P. Chloride threshold values to depassivate reinforcing bars embedded in a standardized OPC mortar. Cem. Concr. Res. 2000, 30, 1047–1055. [Google Scholar] [CrossRef]
- Val, D.V.; Melchers, E.R. Reliability of Deteriorating RC Slab Bridges. J. Struct. Eng. 1997, 123, 1638–1644. [Google Scholar] [CrossRef]
- Val, D.V. Deterioration of Strength of RC Beams due to Corrosion and Its Influence on Beam Reliability. J. Struct. Eng. 2007, 133, 1297–1306. [Google Scholar] [CrossRef]
- Xia, J.; Jin, W.L. Prediction of corrosion-induced crack width of corroded reinforced concrete structures. In Proceedings of the 4th International Conference on the Durability of Concrete Structures, Purdue University, West Lafayette, IN, USA, 24–26 July 2014; pp. 146–154. [Google Scholar] [CrossRef] [Green Version]
- Vidal, T.; Castel, A.; François, R. Analyzing crack width to predict corrosion in reinforced concrete. Cem. Concr. Res. 2004, 34, 165–174. [Google Scholar] [CrossRef]
- Jiang, C.; Wu, Y.F.; Dai, M.J. Degradation of steel-to-concrete bond due to corrosion. Constr. Build. Mater. 2018, 158, 1073–1080. [Google Scholar] [CrossRef]
- Li, D.; Wei, R.; Li, L.; Guan, X.; Mi, X. Pitting corrosion of reinforcing steel bars in chloride contaminated concrete. Constr. Build. Mater. 2019, 199, 359–368. [Google Scholar] [CrossRef]

| Rebar Diameter, D0 (mm) | fy0 (MPa) | εy0 (-) | fu0 (MPa) | εu0 (-) |
| 19.00 | 425.40 | 0.002127 | 541.15 | 0.06 |
| 25.00 | 453.40 | 0.002267 | 568.87 | 0.06 |
| Panel | CE3 | CA4 | ||
| Ratio of longitudinal tension reinforcement, ρ | 0.012 | 0.027 | ||
| Cylinder compressive strength of concrete, fc0 | 50.00 | 45.00 | ||
| Concrete strain at maximum compressive stress, εc0 | 0.0024 | 0.0028 |
| Exposure Classes | XS1 | XS2 | XS3 |
|---|---|---|---|
| Achieved surface chloride content, Csa (%), [19,20] | 0.45 | 0.50 | 0.36 |
| Critical chloride content, Ccr (%) | 0.25 | 0.25 | 0.17 |
| Initiation period–Depassivation time, ti (years) | 48 | 37 | 33 |
| Exposure Class | Parameters | Time of Analysis (Years) | |||||
|---|---|---|---|---|---|---|---|
| 50 | 60 | 70 | 80 | 90 | 100 | ||
| XS1 | Ppit(tp) (mm) | 0.39 | 2.37 | 4.34 | 6.31 | 8.28 | 10.25 |
| μmax (%) (D0 = 19 mm) | 0.09 | 2.93 | 9.40 | 18.88 | 30.78 | 44.41 | |
| μmax (%) (D0 = 25 mm) | 0.05 | 1.66 | 5.37 | 10.94 | 18.12 | 26.65 | |
| XS2 | Ppit(tp) (mm) | 0.75 | 1.33 | 1.91 | 2.49 | 3.07 | 3.65 |
| μmax (%) (D0 = 19 mm) | 0.31 | 0.95 | 1.94 | 3.25 | 4.87 | 6.78 | |
| μmax (%) (D0 = 25 mm) | 0.17 | 0.54 | 1.09 | 1.83 | 2.76 | 3.86 | |
| XS3 | Ppit(tp) (mm) | 4.93 | 7.83 | 10.73 | 13.63 | 16.50 | 19.43 |
| μmax (%) (D0 = 19 mm) | 11.95 | 27.87 | 47.87 | 69.67 | 89.57 | 100.00 | |
| μmax (%) (D0 = 25 mm) | 6.86 | 16.35 | 28.87 | 43.54 | 59.32 | 78.71 | |
| Exposure Class | Corroded RC Panels | Time of Analysis (Years) | |||||
|---|---|---|---|---|---|---|---|
| 50 | 60 | 70 | 80 | 90 | 100 | ||
| XS1 | CE3 | 50.00 | 49.71 | 45.10 | 42.75 | 41.28 | 40.29 |
| CA4 | 45.00 | 45.00 | 24.33 | 18.94 | 16.39 | 14.89 | |
| XS2 | CE3 | 50.00 | 50.00 | 50.00 | 49.27 | 47.59 | 46.30 |
| CA4 | 45.00 | 45.00 | 45.00 | 42.85 | 33.23 | 28.06 | |
| XS3 | CE3 | 44.26 | 41.57 | 40.09 | 39.24 | 38.90 | 37.30 |
| CA4 | 22.15 | 16.85 | 14.61 | 13.38 | 12.63 | 12.12 | |
| Sample ID | τmax+ (MPa) | γmax+ (mm/mm) | τmax− (MPa) | γmax− (mm/mm) | Kγ + (MPa) | Kγ − (MPa) |
|---|---|---|---|---|---|---|
| CE3 | 6.22 | 0.0501 | −6.45 | −0.0600 | 2414 | 2576 |
| CA4 | 10.54 | 0.0075 | −10.2 | −0.0077 | 1791 | 1804 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franceschini, L.; Vecchi, F.; Belletti, B. The PARC_CL 2.1 Crack Model for NLFEA of Reinforced Concrete Elements Subjected to Corrosion Deterioration. Corros. Mater. Degrad. 2021, 2, 474-492. https://doi.org/10.3390/cmd2030025
Franceschini L, Vecchi F, Belletti B. The PARC_CL 2.1 Crack Model for NLFEA of Reinforced Concrete Elements Subjected to Corrosion Deterioration. Corrosion and Materials Degradation. 2021; 2(3):474-492. https://doi.org/10.3390/cmd2030025
Chicago/Turabian StyleFranceschini, Lorenzo, Francesca Vecchi, and Beatrice Belletti. 2021. "The PARC_CL 2.1 Crack Model for NLFEA of Reinforced Concrete Elements Subjected to Corrosion Deterioration" Corrosion and Materials Degradation 2, no. 3: 474-492. https://doi.org/10.3390/cmd2030025
APA StyleFranceschini, L., Vecchi, F., & Belletti, B. (2021). The PARC_CL 2.1 Crack Model for NLFEA of Reinforced Concrete Elements Subjected to Corrosion Deterioration. Corrosion and Materials Degradation, 2(3), 474-492. https://doi.org/10.3390/cmd2030025







