Probabilistic Corrosion Initiation Model for Coastal Concrete Structures
Abstract
1. Introduction
2. Corrosion of Reinforcing Steel in Concrete Structures
3. Probabilistic Corrosion Initiation Model: Methods
3.1. Diffusion-Based Probabilistic Model
3.2. Model Parameter Estimation: Bayesian Methods
3.3. Experimental Data
3.4. Model Selection Criteria
4. Probabilistic Corrosion Initiation Model: Application
4.1. Probabilistic Modeling: Reference Case and Additional Correction Parameters
4.2. Model Selection Results: Model A, B, and C
5. Corrosion Reliability and Sensitivity Measurement
5.1. Uncertainties and Model Parameters
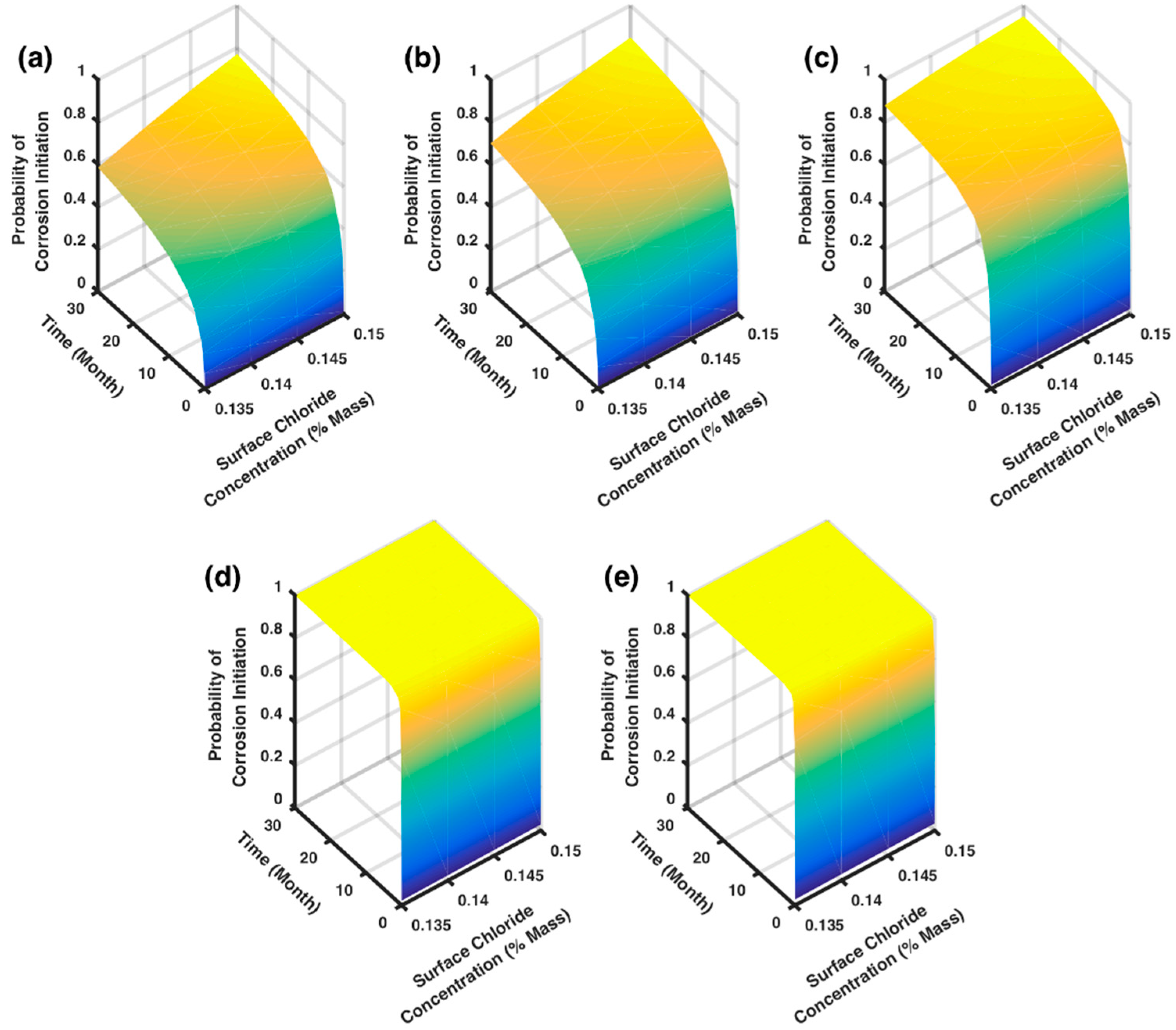
5.2. Conditional Probability of Corrosion Initiation
5.3. Probability of Corrosion Initiation
5.4. Parameter Sensitivity
5.5. Importance of the Variability
6. Conclusions
- Model selection criteria of and were used and selected Model A as the statistically most efficient model among the developed models reflecting the prediction results. Model A dropped w/c as an explicit parameter. However, w/c is inexplicitly considered in Model A as a parameter to determine the critical threshold of the chloride concentration. The model variability and parameter uncertainties were estimated for the given set of experimental data. The Bayesian updating method used for the research allows further updating of the model upon the availability of future data.
- Based on the developed model, the corrosion reliability was estimated in terms of the conditional probability of the corrosion initiation under given surface chloride concentration for example structures. The developed model predicts the probability of the corrosion initiation of any other RC structures within the range shown in Table 2, which is the range of the parameters of data sets used for this model. Further, the framework and methods presented in the paper can be generally used for outside of the range upon any future availability of new sets of data.
- The sensitivity analyses showed that the critical threshold of chloride concentration, , the surface chloride concentration, , and the cover depth of the concrete structures, , are the most effective parameters to increase the reliability of corrosion initiation. The importance measure showed that controlling of the uncertainties of the surface chloride concentration, , is the most efficient to increase the corrosion reliability out of the entire set of parameters.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Koch, G.H.; Brongers, M.P.; Thompson, N.G.; Virmani, Y.P.; Payer, J.H. Corrosion Cost and Preventive Strategies in the United States; Federal Highway Administration: Washington, DC, USA, 2002.
- Irie, H.; Yoshida, Y.; Sakurada, Y.; Ito, T. Non-destructive-testing methods for concrete structures. NTT Tech. Rev. 2008, 6, 1–8. [Google Scholar]
- Thanapol, Y.; Akiyama, M.; Frangopol, D.M. Updating the Seismic Reliability of Existing RC Structures in a Marine Environment by Incorporating the Spatial Steel Corrosion Distribution: Application to Bridge Piers. J. Bridge Eng. 2016, 21, 04016031. [Google Scholar] [CrossRef]
- Kim, J.; Gucunski, N.; Dinh, K. Similarities and differences in bare concrete deck deterioration curves from multi NDE technology surveys. In Proceedings of the Health Monitoring of Structural and Biological Systems 2016; International Society for Optics and Photonics, Las Vegas, NV, USA, 21–24 March 2016; Volume 9805, p. 98052H. [Google Scholar]
- Castro, P.; De Rincon, O.; Pazini, E. Interpretation of chloride profiles from concrete exposed to tropical marine environments. Cem. Concr. Res. 2001, 31, 529–537. [Google Scholar] [CrossRef]
- Sandberg, P.; Tang, L.; Andersen, A. Recurrent studies of chloride ingress in uncracked marine concrete at various exposure times and elevations. Cem. Concr. Res. 1998, 28, 1489–1503. [Google Scholar] [CrossRef]
- Castro-Borges, P.; Balancán-Zapata, M.; López-González, A. Analysis of Tools to Evaluate Chloride Threshold for Corrosion Onset of Reinforced Concrete in Tropical Marine Environment of Yucatán, México. J. Chem. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Oh, B.H.; Jang, S.Y.; Shin, Y.S. Experimental investigation of the threshold chloride concentration for corrosion initiation in reinforced concrete structures. Mag. Concr. Res. 2003, 55, 117–124. [Google Scholar] [CrossRef]
- Ann, K.Y.; Ahn, J.H.; Ryou, J.S. The importance of chloride content at the concrete surface in assessing the time to corrosion of steel in concrete structures. Constr. Build. Mater. 2009, 23, 239–245. [Google Scholar] [CrossRef]
- Val, D.V.; Trapper, P.A. Probabilistic evaluation of initiation time of chloride-induced corrosion. Reliab. Eng. Syst. Saf. 2008, 93, 364–372. [Google Scholar] [CrossRef]
- Bastidas-Arteaga, E.; Chateauneuf, A.; Sánchez-Silva, M.; Bressolette, P.; Schoefs, F. A comprehensive probabilistic model of chloride ingress in unsaturated concrete. Eng. Struct. 2011, 33, 720–730. [Google Scholar] [CrossRef]
- Arora, P.; Popov, B.N.; Haran, B.; Ramasubramanian, M.; Popova, S.; White, R.E. Corrosion initiation time of steel reinforcement in a chloride environment—A one dimensional solution. Corros. Sci. 1997, 39, 739–759. [Google Scholar] [CrossRef]
- Engelund, S.; Sørensen, J.D. A probabilistic model for chloride-ingress and initiation of corrosion in reinforced concrete structures. Struct. Saf. 1998, 20, 69–89. [Google Scholar] [CrossRef]
- Castaneda, H.; Karsilaya, A.; Okeil, A.; Taha, M.R. A Comprehensive Reliability-Based Framework for Corrosion Damage Monitoring and Repair Design of Reinforced Concrete Structures. TranSet Data 2018, 26, 65. [Google Scholar]
- Bertolini, L.; Elsener, B.; Pedeferri, P.; Redaelli, E.; Polder, R.B. Corrosion of Steel in Concrete: Prevention, Diagnosis, Repair; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 978-3-527-65171-9. [Google Scholar]
- Freire, L.; Nóvoa, X.R.; Montemor, M.F.; Carmezim, M.J. Study of passive films formed on mild steel in alkaline media by the application of anodic potentials. Mater. Chem. Phys. 2009, 114, 962–972. [Google Scholar] [CrossRef]
- Nagayama, M.-I.; Cohen, M. The Anodic Oxidation of Iron in a Neutral Solution I. The Nature and Composition of the Passive Film. J. Electrochem. Soc. 1962, 109, 781–795. [Google Scholar] [CrossRef]
- Sánchez, M.; Takenouti, H.; García-Jareño, J.J.; Vicente, F.; Alonso, C. A theoretical approach of impedance spectroscopy during the passivation of steel in alkaline media. Electrochim. Acta 2009, 54, 7222–7226. [Google Scholar] [CrossRef]
- El Haleem, S.A.; El Aal, E.E.A.; El Wanees, S.A.; Diab, A. Environmental factors affecting the corrosion behaviour of reinforcing steel: I. The early stage of passive film formation in Ca(OH)2 solutions. Corros. Sci. 2010, 52, 3875–3882. [Google Scholar] [CrossRef]
- Tuutti, K. Corrosion of Steel in Concrete. Ph.D. Thesis, Lund University, Swedish Cement and Concrete Research Institute, Stockholm, Sweden, 1982. [Google Scholar]
- Böhni, H. Corrosion in Reinforced Concrete Structures; Woodland Publishing: Chelmsford, UK, 2005; ISBN 978-1-84569-043-4. [Google Scholar]
- Broomfield, J.P. Corrosion of Steel in Concrete: Understanding, Investigation and Repair; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Luping, T. Chloride Transport in Concrete—Measurement and Prediction. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 1996. [Google Scholar]
- Mangat, P.S.; Molloy, B.T. Prediction of long term chloride concentration in concrete. Mater. Struct. 1994, 27, 338–346. [Google Scholar] [CrossRef]
- Choe, D.-E.; Gardoni, P.; Rosowsky, D.; Haukaas, T. Probabilistic capacity models and seismic fragility estimates for RC columns subject to corrosion. Reliab. Eng. Syst. Saf. 2008, 93, 383–393. [Google Scholar] [CrossRef]
- DuraCrete. Statistical Quantification of the Variables in the Limit State Functions; The European Union-Brite EuRam III-Contract BRPR-CT95-0132-Project BE95-1347/R9; European Union: Brussels, Belgium, 2000. [Google Scholar]
- Choe, D.-E.; Gardoni, P.; Rosowsky, D.; Haukaas, T. Seismic fragility estimates for reinforced concrete bridges subject to corrosion. Struct. Saf. 2009, 31, 275–283. [Google Scholar] [CrossRef]
- Box, G.E.P.; Tiao, G.C. Bayesian Inference in Statistical Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-1-118-03144-5. [Google Scholar]
- Gardoni, P.; Der Kiureghian, A.; Mosalam, K.M. Probabilistic Capacity Models and Fragility Estimates for Reinforced Concrete Columns based on Experimental Observations. J. Eng. Mech. 2002, 128, 1024–1038. [Google Scholar] [CrossRef]
- Castro, P.; Veleva, L.; Balancán, M. Corrosion of reinforced concrete in a tropical marine environment and in accelerated tests. Constr. Build. Mater. 1997, 11, 75–81. [Google Scholar] [CrossRef]
- Castro, P.; Sanjuán, M.A.; Genesca, J. Carbonation of concretes in the Mexican Gulf. Build. Environ. 2000, 35, 145–149. [Google Scholar] [CrossRef]
- Choe, D.-E.; Gardoni, P.; Rosowsky, D. Fragility Increment Functions for Deteriorating Reinforced Concrete Bridge Columns. J. Eng. Mech. 2010, 136, 969–978. [Google Scholar] [CrossRef]
- Akaike, H. A Bayesian analysis of the minimum AIC procedure. Ann. Inst. Stat. Math. 1978, 30, 9–14. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the Bayes procedure. Biometrika 1978, 65, 53–59. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003; ISBN 978-0-387-95364-9. [Google Scholar]
- Der Kiureghian, A. Measures of Structural Safety Under Imperfect States of Knowledge. J. Struct. Eng. 1989, 115, 1119–1140. [Google Scholar] [CrossRef]
- Hohenbichler, M.; Rackwitz, R. First-order concepts in system reliability. Struct. Saf. 1982, 1, 177–188. [Google Scholar] [CrossRef]
- Zhang, J.; Lounis, Z. Sensitivity analysis of simplified diffusion-based corrosion initiation model of concrete structures exposed to chlorides. Cem. Concr. Res. 2006, 36, 1312–1323. [Google Scholar] [CrossRef]
- Der Kiureghian, A.; Ke, J.B. Finite-element based reliability analysis of frame structures. In Proceedings of the Proc. 4th Int. Conference on Structural Safety and Reliability, Kobe, Japan, 27–29 May 1985; pp. 395–404. [Google Scholar]







| Concrete Conditions | (% Concrete Mass) |
|---|---|
| 0.101 | |
| 0.095 | |
| 0.083 | |
| 0.053 | |
| 0.049 |
| Variable | Symbol | Range |
|---|---|---|
| Concrete Strength | 14.7–34.3 MPa | |
| Curing days | 1–7 days | |
| Water-to-Cement ratio | 0.46–0.76 | |
| Distance from shore | - | 50–100 m |
| Mean | St. Dev. | Correlation Coefficient | ||||
|---|---|---|---|---|---|---|
| 500.0 | 1.000 | 1 | - | - | - | |
| 30.01 | 1.002 | 0.0002 | 1 | - | - | |
| 0.590 | 0.063 | −0.0056 | −0.0566 | 1 | - | |
| 0.263 | 0.053 | −0.0028 | −0.0526 | 0.0093 | 1 | |
| Concrete Conditions | Distribution | St. Dev. | Concrete Conditions | Distribution | |||
|---|---|---|---|---|---|---|---|
| Normal | 1.846 | 0.582 | Normal | 1.735 | 0.379 | ||
| Normal | 3.310 | 0.896 | |||||
| Normal | 2.063 | 0.386 | Normal | 0.887 | 0.166 | ||
| Normal | 0.951 | 0.197 | |||||
| Normal | 1.430 | 0.376 | Normal | 0.728 | 0.119 | ||
| Model | AIC | BIC | MAPE (%) | |||
|---|---|---|---|---|---|---|
| A: | 3 | 129.4 | 17.6 | 140.3 | 10.2 | 5.63 |
| B: | 4 | 119.9 | 8.1 | 134.5 | 4.4 | 5.61 |
| C: | 5 | 111.8 | 0 | 130.1 | 0 | 5.53 |
| Mean | St. Dev. | Correlation Coefficient | ||||
|---|---|---|---|---|---|---|
| 500.0 | 1.000 | 1 | - | - | - | |
| 29.99 | 1.084 | 0.0073 | 1 | - | - | |
| 0.667 | 0.021 | −0.0303 | −0.4203 | 1 | - | |
| 0.301 | 0.013 | −0.0122 | −0.0522 | 0.0105 | 1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.; Choe, D.-E.; Castro-Borges, P.; Castaneda, H. Probabilistic Corrosion Initiation Model for Coastal Concrete Structures. Corros. Mater. Degrad. 2020, 1, 328-344. https://doi.org/10.3390/cmd1030016
Kim C, Choe D-E, Castro-Borges P, Castaneda H. Probabilistic Corrosion Initiation Model for Coastal Concrete Structures. Corrosion and Materials Degradation. 2020; 1(3):328-344. https://doi.org/10.3390/cmd1030016
Chicago/Turabian StyleKim, Changkyu, Do-Eun Choe, Pedro Castro-Borges, and Homero Castaneda. 2020. "Probabilistic Corrosion Initiation Model for Coastal Concrete Structures" Corrosion and Materials Degradation 1, no. 3: 328-344. https://doi.org/10.3390/cmd1030016
APA StyleKim, C., Choe, D.-E., Castro-Borges, P., & Castaneda, H. (2020). Probabilistic Corrosion Initiation Model for Coastal Concrete Structures. Corrosion and Materials Degradation, 1(3), 328-344. https://doi.org/10.3390/cmd1030016







