Microcalorimetry Techniques for Studying Interactions at Solid–Liquid Interface: A Review
Abstract
1. Introduction
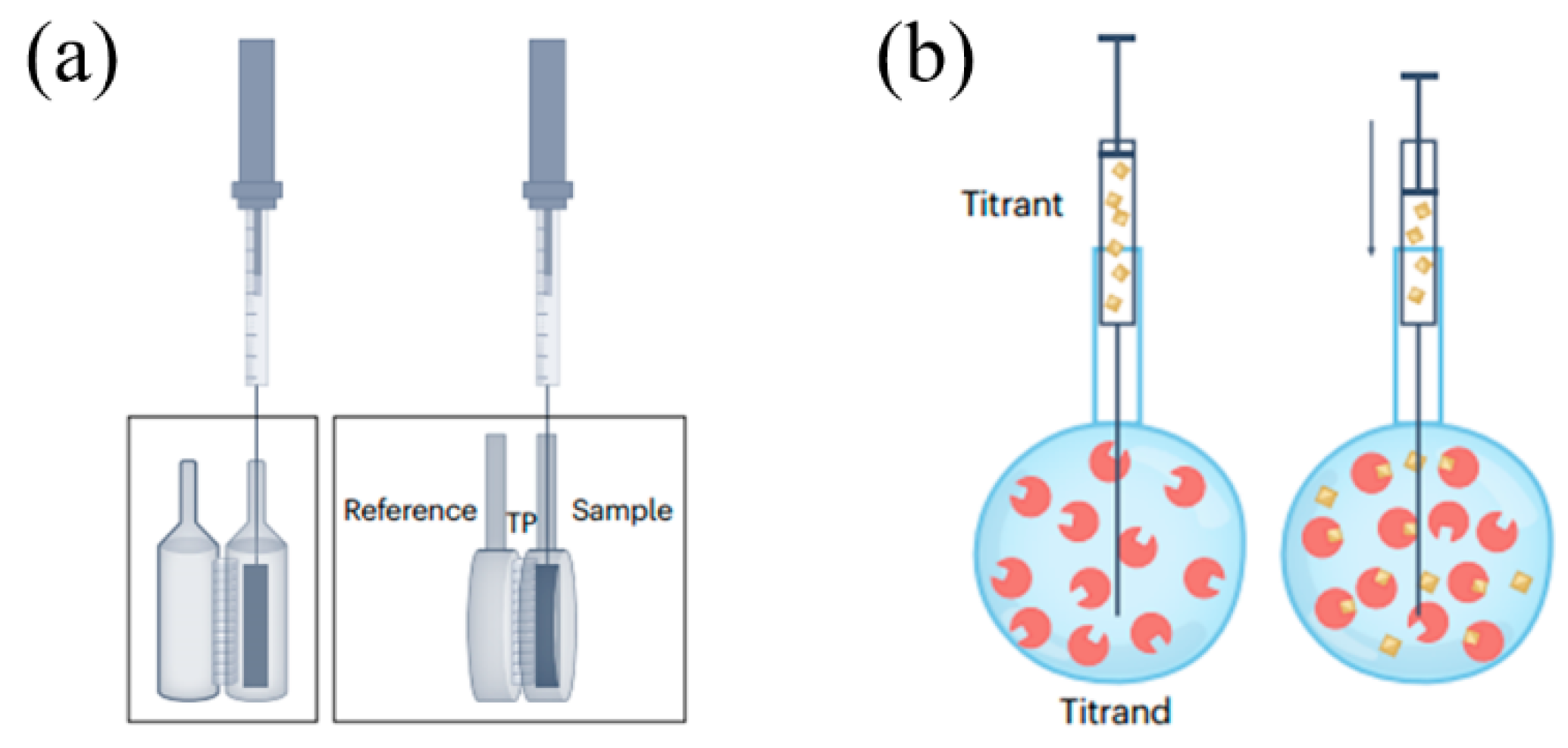
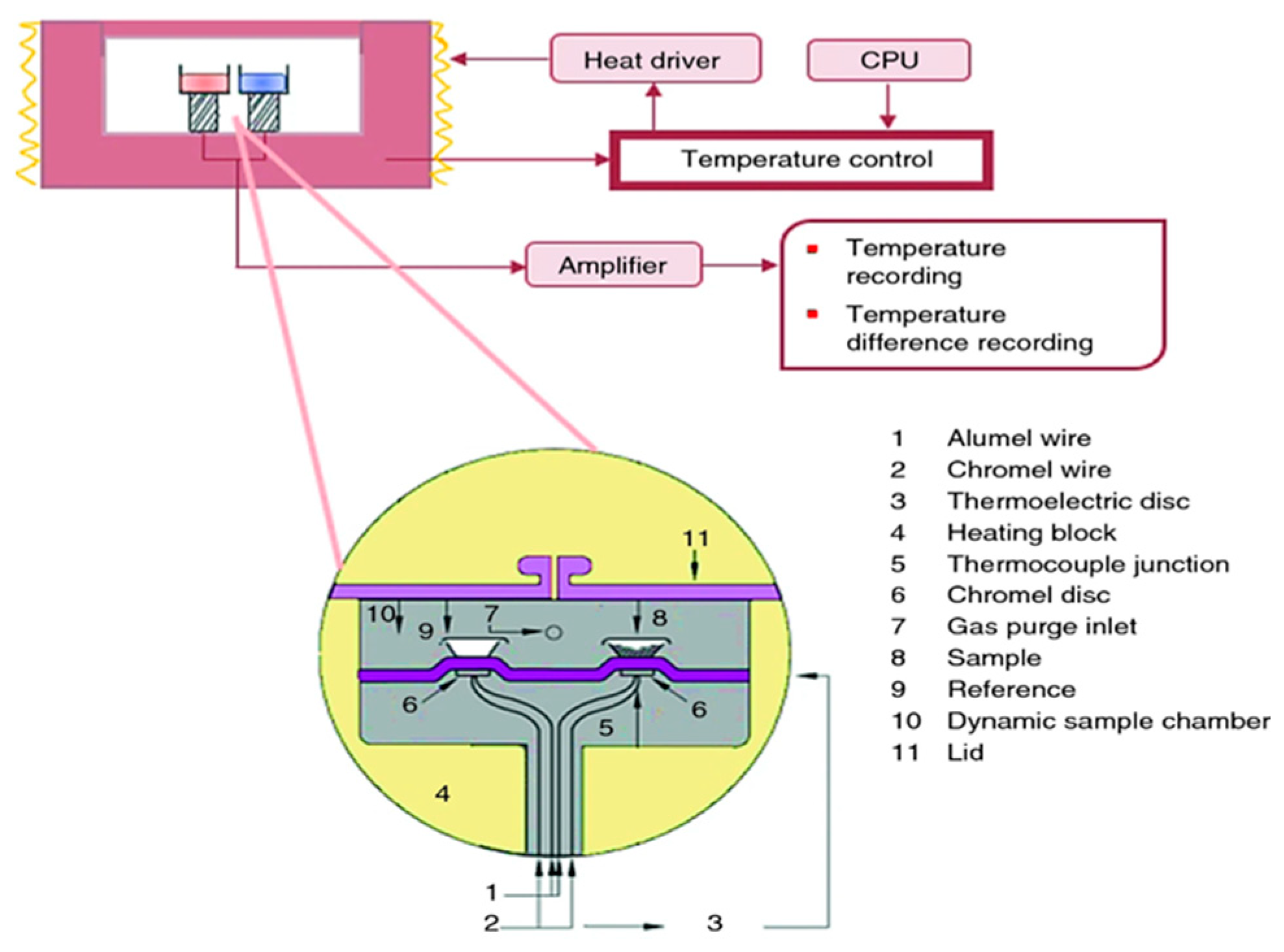
2. Fundamental Principles of ITC and DSC
3. Calorimetric Insights into Enthalpy Changes during Solid–Liquid Immersion Processes
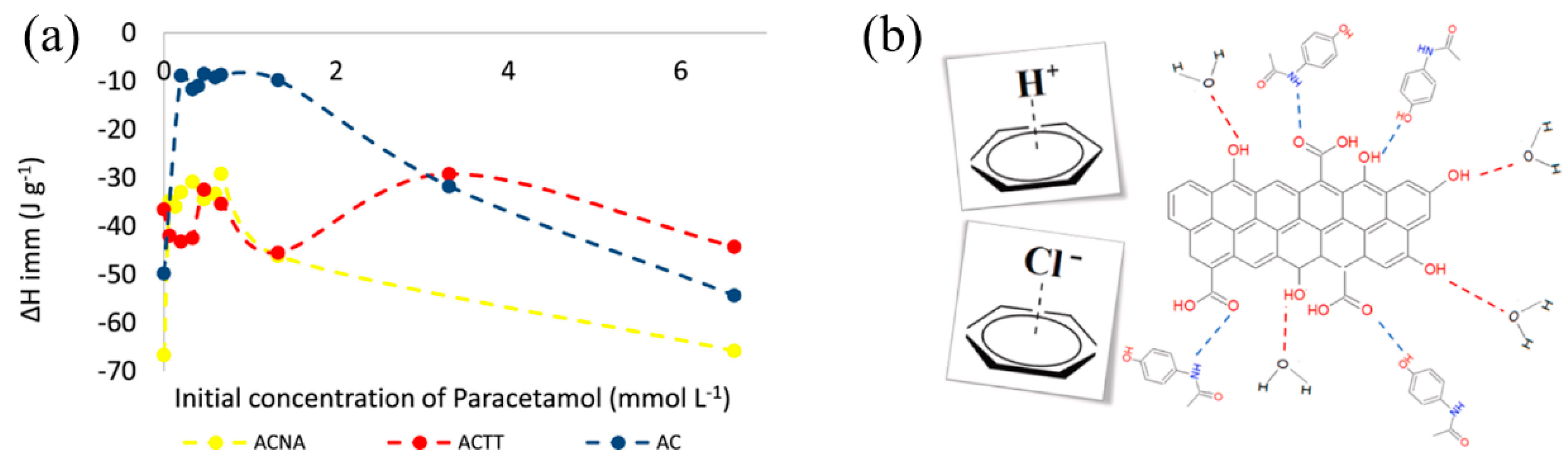
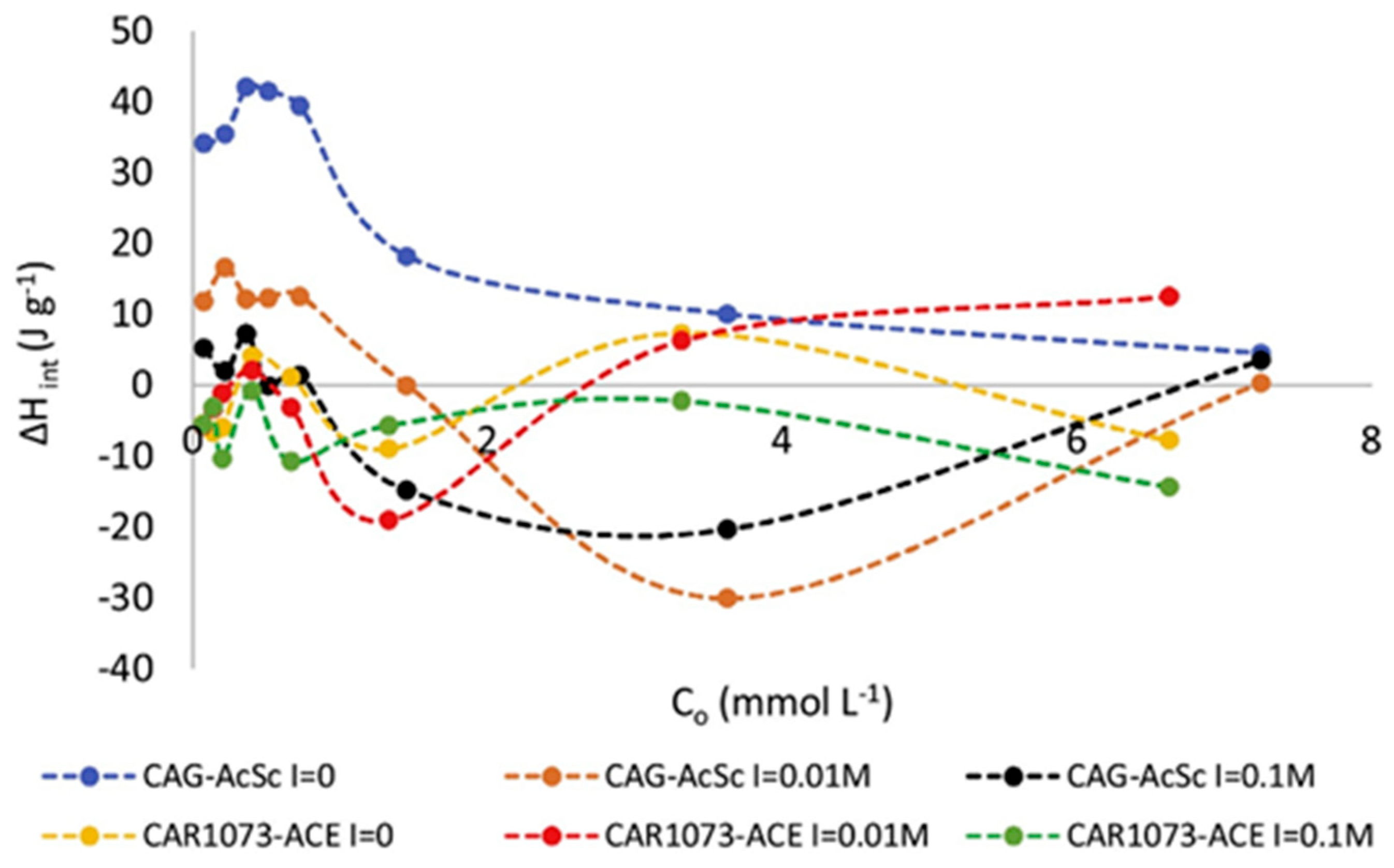
3.1. The Influence of Non-Covalent Interactions between Liquid Molecules and Solid Interface Molecules on Immersion Enthalpy
3.2. Influence of Liquid-Accessible Surface Area on the Immersion Enthalpy at Solid Surfaces
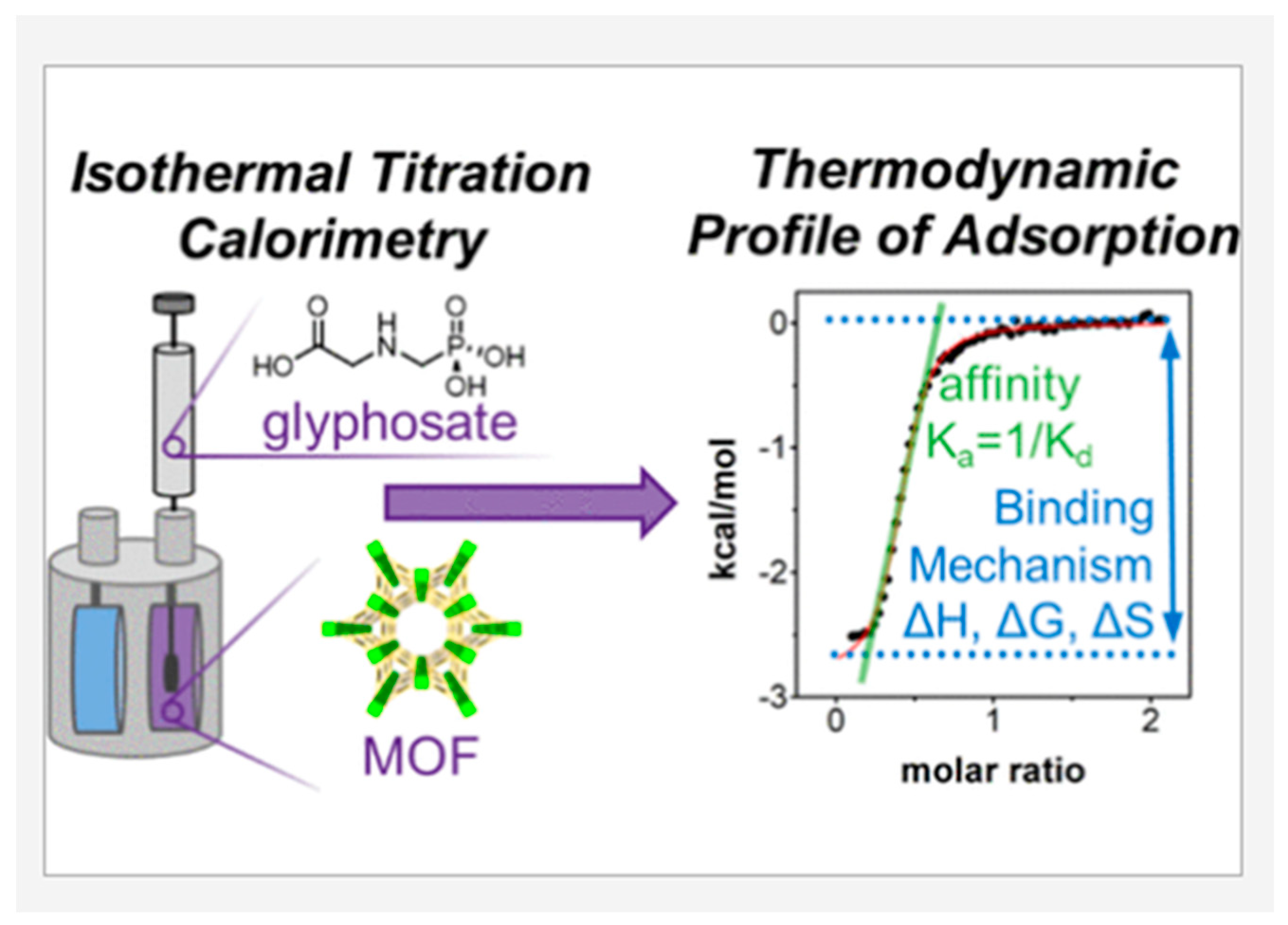
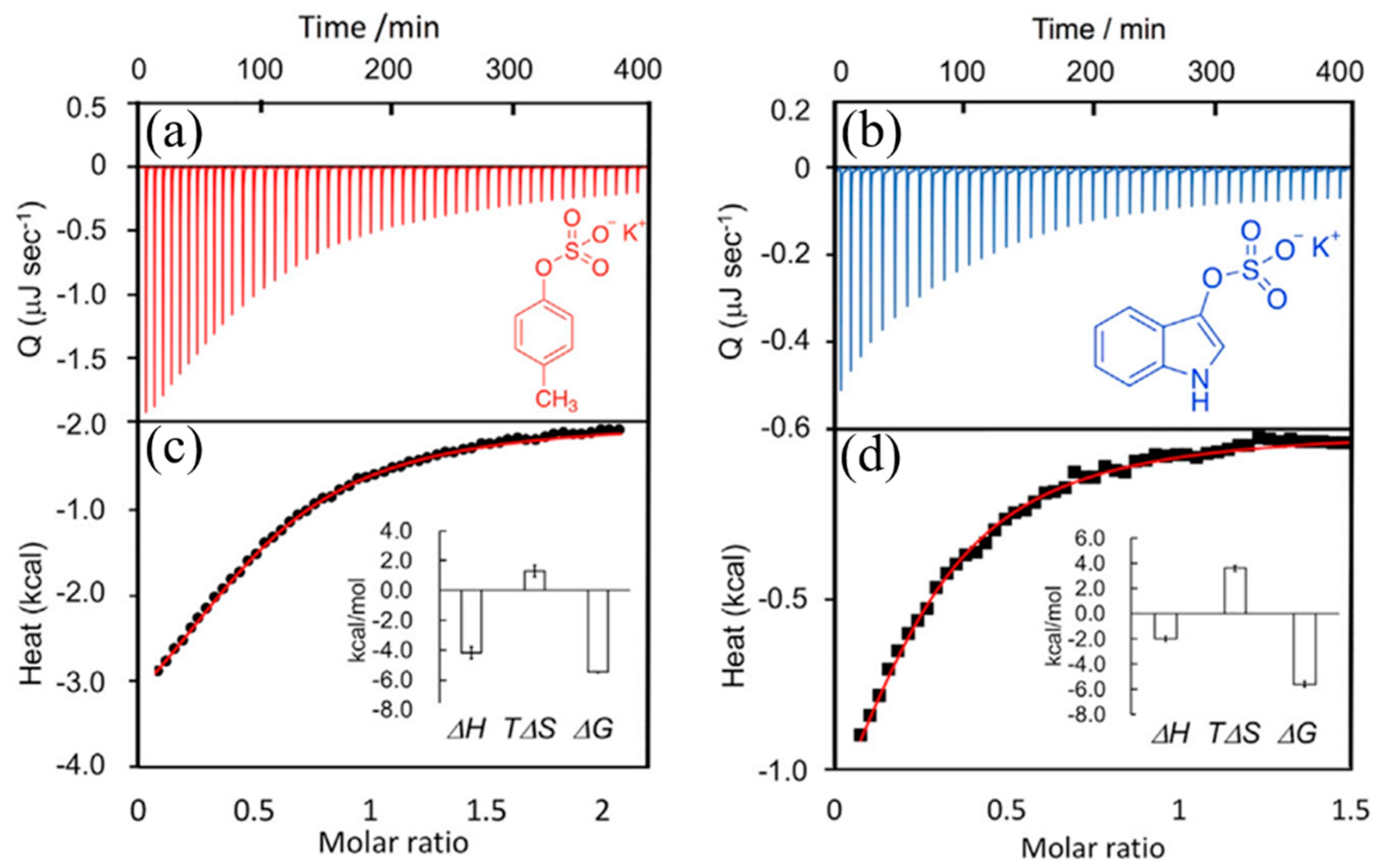
4. Application of Calorimetry in the Study of Specific Solid–Liquid Interaction Processes
4.1. Calorimetry in Investigating Adhesion and Adsorption Behavior during Solid–Liquid Immersion
4.2. Immersion Calorimetry as a Quantitative Method for Assessing Solid Particle Wettability
4.2.1. Theoretical Derivation of the Contact Angle and Immersion Heat
4.2.2. Practical Examples of Quantifying Solid Particle Wettability Using Immersion Calorimetry
4.3. Characterization of Super-Hydrophobic Materials Using DSC
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yamada, Y.; Ichii, T.; Utsunomiya, T.; Sugimura, H. Visualizing polymeric liquid/solid interfaces by atomic force microscopy utilizing quartz tuning fork sensors. Jpn. J. Appl. Phys. 2020, 59, SN1009. [Google Scholar] [CrossRef]
- Bowles, A.P.; Honig, C.D.; Ducker, W.A. No-slip boundary condition for weak solid–liquid interactions. J. Phys. Chem. C 2011, 115, 8613–8621. [Google Scholar] [CrossRef]
- Shi, Z.; Ran, B.; Liu, L. Determining the interaction energy of a quartz–kaolinite system at different pH levels by atomic force microscopy and extended DLVO theory. Powder Technol. 2022, 409, 117842. [Google Scholar] [CrossRef]
- Ferreira, Q.; Delfino, C.L.; Morgado, J.; Alcácer, L. Bottom-Up Self-Assembled Supramolecular Structures Built by STM at the Solid/Liquid Interface. Materials 2019, 12, 382. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Kim, Y.J.; Park, J.Y. Scanning tunneling microscopy under chemical reaction at solid–liquid and solid–gas interfaces. Chem. Phys. Rev. 2023, 4, 031303. [Google Scholar] [CrossRef]
- Ngo, D.; He, X.; Luo, H.; Qu, J.; Kim, S.H. Competitive adsorption of lubricant base oil and ionic liquid additives at air/liquid and solid/liquid interfaces. Langmuir 2020, 36, 7582–7592. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, D.; Marquez, M.D.; Zenasni, O.; Han, L.T.; Baldelli, S.; Lee, T.R. Surface dipoles induce uniform orientation in contacting polar liquids. Chem. Mater. 2020, 32, 7832–7841. [Google Scholar] [CrossRef]
- Su, H.; Zhou, W.; Zhang, H.; Zhou, W.; Zhao, X.; Li, Y.; Liu, M.; Cheng, W.; Liu, Q. Dynamic evolution of solid–liquid electrochemical interfaces over single-atom active sites. J. Am. Chem. Soc. 2020, 142, 12306–12313. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, J.; Mao, B.; An, T.; Wang, J.; Cao, M. Inside solid-liquid interfaces: Understanding the influence of the electrical double layer on alkaline hydrogen evolution reaction. Appl. Catal. B 2021, 293, 120220. [Google Scholar] [CrossRef]
- Maillet, B.; Dittrich, G.; Huber, P.; Coussot, P. Diffusionlike drying of a nanoporous solid as revealed by magnetic resonance imaging. Phys. Rev. Appl. 2022, 18, 054027. [Google Scholar] [CrossRef]
- Verma, R.K.; Hill, J.O.; Niinistö, L.; Mojumdar, S.; Kumar, D.D. A curriculum framework for education in calorimetry. J. Mater. Educ. 2012, 34, 161–174. [Google Scholar]
- Bastos, M.; Abian, O.; Johnson, C.M.; Ferreira-da-Silva, F.; Vega, S.; Jimenez-Alesanco, A.; Ortega-Alarcon, D.; Velazquez-Campoy, A. Isothermal titration calorimetry. Nat. Rev. Methods. Prim. 2023, 3, 17. [Google Scholar] [CrossRef]
- Freire, E.; Mayorga, O.L.; Straume, M. Isothermal titration calorimetry. Anal. Chem. 1990, 62, 950A–959A. [Google Scholar] [CrossRef]
- Barranco-Medina, S.; Kakorin, S.; Lázaro, J.J.; Dietz, K.-J. Thermodynamics of the dimer−decamer transition of reduced human and plant 2-Cys peroxiredoxin. Biochemistry 2008, 47, 7196–7204. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Larson, J.D.; Bottoms, C.A.; Arturo, E.C.; Henzl, M.T.; Jenkins, J.L.; Nix, J.C.; Becker, D.F.; Tanner, J.J. Structural basis of the transcriptional regulation of the proline utilization regulon by multifunctional PutA. J. Mol. Biol. 2008, 381, 174–188. [Google Scholar] [CrossRef] [PubMed]
- Alegre-Cebollada, J.; Cunietti, M.; Herrero-Galán, E.; Gavilanes, J.G.; Martínez-del-Pozo, Á. Calorimetric scrutiny of lipid binding by sticholysin II toxin mutants. J. Mol. Biol. 2008, 382, 920–930. [Google Scholar] [CrossRef]
- Penn, C.J.; Gonzalez, J.M.; Chagas, I. Investigation of atrazine sorption to biochar with titration calorimetry and flow-through analysis: Implications for design of pollution-control structures. Front. Chem. 2018, 6, 307. [Google Scholar] [CrossRef]
- Agostoni, V.; Anand, R.; Monti, S.; Hall, S.; Maurin, G.; Horcajada, P.; Serre, C.; Bouchemal, K.; Gref, R. Impact of phosphorylation on the encapsulation of nucleoside analogues within porous iron (iii) metal–organic framework MIL-100 (Fe) nanoparticles. J. Mater. Chem. B 2013, 1, 4231–4242. [Google Scholar] [CrossRef]
- Aykaç, A.; Noiray, M.; Malanga, M.; Agostoni, V.; Casas-Solvas, J.M.; Fenyvesi, E.; Gref, R.; Vargas-Berenguel, A. A non-covalent “click chemistry” strategy to efficiently coat highly porous MOF nanoparticles with a stable polymeric shell. Biochim. Biophys. Acta Gen. Subj. 2017, 1861, 1606–1616. [Google Scholar] [CrossRef]
- Kato, S.; Drout, R.J.; Farha, O.K. Isothermal titration calorimetry to investigate uremic toxins adsorbing onto metal-organic frameworks. Cell Rep. Phys. Sci. 2020, 1, 100006. [Google Scholar] [CrossRef]
- Wanhala, A.K.; Doughty, B.; Bryantsev, V.S.; Wu, L.; Mahurin, S.M.; Jansone-Popova, S.; Cheshire, M.C.; Navrotsky, A.; Stack, A.G. Adsorption mechanism of alkyl hydroxamic acid onto bastnäsite: Fundamental steps toward rational collector design for rare earth elements. J. Colloid Interface Sci. 2019, 553, 210–219. [Google Scholar] [CrossRef] [PubMed]
- Holdgate, G.A. Making cool drugs hot: Isothermal titration calorimetry as a tool to study binding energetics. Biotechniques 2001, 31, 164–166, 168, 170 passim. [Google Scholar]
- Geschwindner, S.; Ulander, J.; Johansson, P. Ligand binding thermodynamics in drug discovery: Still a hot tip? J. Med. Chem. 2015, 58, 6321–6335. [Google Scholar] [CrossRef]
- Klebe, G. Broad-scale analysis of thermodynamic signatures in medicinal chemistry: Are enthalpy-favored binders the better development option? Drug Discov. Today 2019, 24, 943–948. [Google Scholar] [CrossRef]
- Varghese, N.; Mogera, U.; Govindaraj, A.; Das, A.; Maiti, P.K.; Sood, A.K.; Rao, C. Binding of DNA nucleobases and nucleosides with graphene. ChemPhysChem 2009, 10, 206–210. [Google Scholar] [CrossRef]
- Lever, T.; Haines, P.; Rouquerol, J.; Charsley, E.L.; Van Eckeren, P.; Burlett, D.J. ICTAC nomenclature of thermal analysis (IUPAC Recommendations 2014). Pure. Appl. Chem. 2014, 86, 545–553. [Google Scholar] [CrossRef]
- Dołęga, A.; Juszyńska-Gałązka, E.; Deptuch, A.; Jaworska-Gołąb, T.; Zieliński, P.M. Thermoanalytical studies of a cytotoxic derivative of carbamazepine: Iminostilbene. J. Therm. Anal. Calorim. 2021, 146, 2151–2160. [Google Scholar] [CrossRef]
- Kumar, R.; Nirwan, A.; Mondal, B.; Kumar, R. Study on thermophysical properties of pentadecane and its composites with thermally expanded graphite as shape-stabilized phase change materials. J. Therm. Anal. Calorim. 2022, 147, 8689–8697. [Google Scholar] [CrossRef]
- Basko, A.V.; Pochivalov, K.V.; Chalykh, T.I.; Shandryuk, G.A.; Ezhov, A.A.; Artemov, V.V.; Kudryavtsev, Y.V. Combining optical microscopy, turbidimetry, and DSC to study structural transformations in the mixtures of semicrystalline polymers with low-molar-mass crystallizable substances. Thermochim. Acta 2020, 690, 178671. [Google Scholar] [CrossRef]
- Wang, C.; Wang, T.; Hu, Z.; Cai, Z. Facile synthesis and thermal performance of cety palmitate/nickel foam composite phase change materials for thermal energy storage. J. Energy Storage 2020, 28, 101179. [Google Scholar] [CrossRef]
- Leyva-Porras, C.; Cruz-Alcantar, P.; Espinosa-Solís, V.; Martínez-Guerra, E.; Piñón-Balderrama, C.I.; Martínez, I.C.; Saavedra-Leos, M.Z. Application of differential scanning calorimetry (DSC) and modulated differential scanning calorimetry (MDSC) in food and drug industries. Polymers 2019, 12, 5. [Google Scholar] [CrossRef]
- Rodríguez-Estupiñán, P.; Miranda-Carvajal, I.; Campos, P.C.; Guerrero-Fajardo, C.A.; Giraldo, L.; Moreno-Piraján, J.C. Graphene-based materials: Analysis through calorimetric techniques. J. Therm. Anal. Calorim. 2022, 147, 9301–9351. [Google Scholar] [CrossRef]
- Rouquerol, J.; Rouquerol, F.; Llewellyn, P.; Maurin, G.; Sing, K. Adsorption by Powders and Porous Solids: Principles, Methodology and Applications; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Di Iorio, J.R.; Johnson, B.A.; Román-Leshkov, Y. Ordered hydrogen-bonded alcohol networks confined in Lewis acid zeolites accelerate transfer hydrogenation turnover rates. J. Am. Chem. Soc. 2020, 142, 19379–19392. [Google Scholar] [CrossRef]
- Giraldo, L.; Moreno-Piraján, J.C. Relation between immersion enthalpies of activated carbons in different liquids, textural properties, and phenol adsorption. J. Therm. Anal. Calorim. 2014, 117, 1517–1523. [Google Scholar] [CrossRef]
- Blanco-Martinez, D.; Giraldo, L.; Moreno-Pirajan, J. Effect of the pH in the adsorption and in the immersion enthalpy of monohydroxylated phenols from aqueous solutions on activated carbons. J. Hazard. Mater. 2009, 169, 291–296. [Google Scholar] [CrossRef]
- Moreno-Piraján, J.C.; Blanco, D.; Giraldo, L. Relation between the adsorbed quantity and the immersion enthalpy and the immersion enthalpy in catechol aqueous solutions on activated carbons. Int. J. Mol. Sci. 2011, 13, 44–55. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, G.; Giraldo, L.; Moreno, J. Calorimetric study of the immersion enthalpies of activated carbon cloths in different solvents and aqueous solutions. J. Therm. Anal. Calorim. 2009, 96, 547–552. [Google Scholar] [CrossRef]
- Rodríguez-Estupiñán, P.; Giraldo, L.; Moreno-Piraján, J.C. Modified surface chemistry of activated carbons: Correlation with immersion enthalpy. J. Therm. Anal. Calorim. 2013, 114, 245–251. [Google Scholar] [CrossRef]
- Hernández-Monje, D.; Giraldo, L.; Moreno-Piraján, J.C. Immersion enthalpy of benzene/cyclohexane and toluene/cyclohexane binary mixtures into modified activated carbons. J. Therm. Anal. Calorim. 2019, 138, 2565–2575. [Google Scholar] [CrossRef]
- Bernal, V.; Giraldo, L.; Moreno-Piraján, J.C. Understanding the solid-liquid equilibria between paracetamol and activated carbon: Thermodynamic approach of the interactions adsorbent-adsorbate using equilibrium, kinetic and calorimetry data. J. Hazard. Mater. 2021, 419, 126432. [Google Scholar] [CrossRef]
- Rodriguez-Reinoso, F.; Molina-Sabio, M.; Gonzalez, M. Effect of oxygen surface groups on the immersion enthalpy of activated carbons in liquids of different polarity. Langmuir 1997, 13, 2354–2358. [Google Scholar] [CrossRef]
- Acevedo, S.; Giraldo, L.; Moreno-Piraján, J.C. Adsorption of CO2 on activated carbons prepared by chemical activation with cupric nitrate. ACS Omega 2020, 5, 10423–10432. [Google Scholar] [CrossRef]
- Barroso-Bogeat, A.; Alexandre-Franco, M.; Fernández-González, C.; Gómez-Serrano, V. Physico-chemical characterization of activated carbon–metal oxide photocatalysts by immersion calorimetry in benzene and water. J. Therm. Anal. Calorim. 2016, 125, 65–74. [Google Scholar] [CrossRef]
- Hernandez-Monje, D.; Gutiérrez, L.G.; Moreno-Piraján, J.C. Immersion enthalpy of activated carbons with different oxygen content in toluene-hexane mixtures. J. Mol. Liq. 2020, 310, 113140. [Google Scholar] [CrossRef]
- Carvajal-Bernal, A.M.; Gómez-Granados, F.; Giraldo, L.; Moreno-Piraján, J.C. A study of the interactions of activated carbon-phenol in aqueous solution using the determination of immersion enthalpy. Appl. Sci. 2018, 8, 843. [Google Scholar] [CrossRef]
- Giraldo, L.; Moreno-Piraján, J. Immersion enthalpy variation of surface-modified mineral activated carbon in lead (II) aqueous solution adsorption: The relation between immersion enthalpy and adsorption capacity. Eclet. Quim. 2006, 31, 15–21. [Google Scholar] [CrossRef]
- Castillejos, E.; Bachiller-Baeza, B.; Rodríguez-Ramos, I.; Guerrero-Ruiz, A. An immersion calorimetry study of the interaction of organic compounds with carbon nanotube surfaces. Carbon 2012, 50, 2731–2740. [Google Scholar] [CrossRef]
- Barton, S.; Boulton, G.; Harrison, B. Surface studies on graphite: An estimation of the average polarity of the oxygen complexes. Carbon 1972, 10, 391–393. [Google Scholar] [CrossRef]
- Barton, S.; Harrison, B. Surface studies on carbon: Immersional energetics of spheron 6 in water. Carbon 1975, 13, 47–50. [Google Scholar] [CrossRef]
- Stoeckli, F.; Hugi-Cleary, D.; Centeno, T. The characterisation of solids by adsorption and immersion techniques and by AFM/STM. J. Eur. Ceram. Soc. 1998, 18, 1177–1185. [Google Scholar] [CrossRef][Green Version]
- Bernal, V.; Giraldo, L.; Moreno-Piraján, J.C. Thermodynamic analysis of acetaminophen and salicylic acid adsorption onto granular activated carbon: Importance of chemical surface and effect of ionic strength. Thermochim. Acta 2020, 683, 178467. [Google Scholar] [CrossRef]
- Young, G.; Bursh, T. Immersion calorimetry studies of the interaction of water with silica surfaces. J. Colloid Sci. 1960, 15, 361–369. [Google Scholar] [CrossRef]
- Atkinson, D.; Mcleod, A.I.; Sing, K.; Capon, A. Physical adsorption and heat of immersion studies of microporous carbons. Carbon 1982, 20, 339–343. [Google Scholar] [CrossRef]
- Stoeckli, H.; Kraehenbuehl, F. The enthalpies of immersion of active carbons, in relation to the Dubinin theory for the volume filling of micropores. Carbon 1981, 19, 353–356. [Google Scholar] [CrossRef]
- Olson, D.; Haag, W.; Borghard, W. Use of water as a probe of zeolitic properties: Interaction of water with HZSM-5. Microporous Mesoporous Mater. 2000, 35, 435–446. [Google Scholar] [CrossRef]
- Sano, T.; Kasuno, T.; Takeda, K.; Arazaki, S.; Kawakami, Y. Sorption of water vapor on HZSM-5 type zeolites. Stud. Surf. Sci. Catal. 1997, 105, 1771–1778. [Google Scholar]
- Berke, C.H.; Kiss, A.; Kleinschmit, P.; Weitkamp, J. Der Hydrophobizitäts-Index: Eine neue Methode zur Charakterisierung der Oberflächeneigenschaften zeolithischer Adsorbentien. Chem. Ing. Tech. 1991, 63, 623–625. [Google Scholar] [CrossRef]
- Silvestre-Albero, J.; De Salazar, C.G.; Sepúlveda-Escribano, A.; Rodrıguez-Reinoso, F. Characterization of microporous solids by immersion calorimetry. Colloids Surf. A 2001, 187, 151–165. [Google Scholar] [CrossRef]
- Vargas, D.P.; Giraldo, L.; Moreno-Piraján, J.C. Characterisation of granular activated carbon prepared by activation with CaCl2 by means of gas adsorption and immersion calorimetry. Adsorption 2016, 22, 717–723. [Google Scholar] [CrossRef]
- Madani, S.H.; Silvestre-Albero, A.; Biggs, M.J.; Rodríguez-Reinoso, F.; Pendleton, P. Immersion calorimetry: Molecular packing effects in micropores. ChemPhysChem 2015, 16, 3984–3991. [Google Scholar] [CrossRef]
- Guerrero-Fajardo, C.A.; Giraldo, L.; Moreno-Piraján, J.C. Graphene oxide: Study of pore size distribution and surface chemistry using immersion calorimetry. Nanomaterials 2020, 10, 1492. [Google Scholar] [CrossRef]
- Harvey, O.R.; Herbert, B.E.; Rhue, R.D.; Kuo, L.-J. Metal interactions at the biochar-water interface: Energetics and structure-sorption relationships elucidated by flow adsorption microcalorimetry. Environ. Sci. Technol. 2011, 45, 5550–5556. [Google Scholar] [CrossRef]
- Fritah, Z.; Drouet, C.; Salles, F.; Marsan, O.; Aufray, M. Influence of water on an epoxy/amine-metal interphase: A combined DFT and mixing calorimetry approach. ACS Appl. Mater. Interfaces 2023, 15, 11342–11352. [Google Scholar] [CrossRef]
- Yan, L.; Low, P.F.; Roth, C.B. Enthalpy changes accompanying the collapse of montmorillonite layers and the penetration of electrolyte into interlayer space. J. Colloid Interface Sci. 1996, 182, 417–424. [Google Scholar] [CrossRef]
- Haouzi, A.; Salles, F.; Henry, M.; Douillard, J.-M. Thermodynamic analysis of the immersion of a smectite substituted with Na or Ca: Heat effect due to the cation. J. Colloid Interface Sci. 2007, 307, 531–542. [Google Scholar] [CrossRef]
- GSharma; Muthuswamy, E.; Naguib, M.; Gogotsi, Y.; Navrotsky, A.; Wu, D. Calorimetric study of alkali metal ion (K+, Na+, Li+) exchange in a clay-like Mxene. J. Phys. Chem. C 2017, 121, 15145–15153. [Google Scholar]
- Drout, R.J.; Kato, S.; Chen, H.; Son, F.A.; Otake, K.-I.; Islamoglu, T.; Snurr, R.Q.; Farha, O.K. Isothermal titration calorimetry to explore the parameter space of organophosphorus agrochemical adsorption in MOFs. J. Am. Chem. Soc. 2020, 142, 12357–12366. [Google Scholar] [CrossRef]
- Bernal, V.; Giraldo, L.; Moreno-Piraján, J.C. A new methodology to determine the effect of the adsorbate-adsorbent interactions on the analgesic adsorption onto activated carbon using kinetic and calorimetry data. Environ. Sci. Pollut. Res. 2020, 27, 36639–36650. [Google Scholar] [CrossRef]
- Wang, N.; Sasaki, M.; Yoshida, T.; Kotanigawa, T. Estimation of coal hydrophilicity by flow microcalorimetry. Colloids Surf. A 1998, 135, 11–18. [Google Scholar] [CrossRef]
- Hansford, D.T.; Grant, D.J.; Newton, J.M. Surface energetics of the wetting of a hydrophobic powder. J. Chem. Soc. Faraday Trans. 1980, 76, 2417–2431. [Google Scholar] [CrossRef]
- Spagnolo, D.A.; Maham, Y.; Chuang, K.T. Calculation of contact angle for hydrophobic powders using heat of immersion data. J. Phys. Chem. 1996, 100, 6626–6630. [Google Scholar] [CrossRef]
- Yan, N.; Masliyah, J.H. Characterization and demulsification of solids-stabilized oil-in-water emulsions Part 1. Partitioning of clay particles and preparation of emulsions. Colloids Surf. A 1995, 96, 229–242. [Google Scholar] [CrossRef]
- Young, T. An essay on the cohesion of fluids. In Abstracts of the Papers Printed in the Philosophical Transactions of the Royal Society of London; The Royal Society: London, UK, 1832; pp. 171–172. [Google Scholar]
- Fowkes, F.M. Additivity of intermolecular forces at interfaces. i. determination of the contribution to surface and interfacial tensions of dispersion forces in various liquids1. J. Phys. Chem. 1963, 67, 2538–2541. [Google Scholar] [CrossRef]
- Fowkes, F.M. Determination of interfacial tensions, contact angles, and dispersion forces in surfaces by assuming additivity of intermolecular interactions in surfaces. J. Phys. Chem. 1962, 66, 382. [Google Scholar] [CrossRef]
- Owens, D.K.; Wendt, R. Estimation of the surface free energy of polymers. J. Appl. Polym. Sci. 1969, 13, 1741–1747. [Google Scholar] [CrossRef]
- Jie-Rong, C.; Wakida, T. Studies on the surface free energy and surface structure of PTFE film treated with low temperature plasma. J. Appl. Polym. Sci. 1997, 63, 1733–1739. [Google Scholar] [CrossRef]
- Park, S.-M.; Roy, R.; Kweon, J.-H.; Nam, Y. Strength and failure modes of surface treated CFRP secondary bonded single-lap joints in static and fatigue tensile loading regimes. Compos. Part A 2020, 134, 105897. [Google Scholar] [CrossRef]
- Kaelble, D. Dispersion-polar surface tension properties of organic solids. J. Adhes. 1970, 2, 66–81. [Google Scholar] [CrossRef]
- Wu, S. Polar and nonpolar interactions in adhesion. J. Adhes. 1973, 5, 39–55. [Google Scholar] [CrossRef]
- van Oss, C.J.; Chaudhury, M.; Good, R.J. Monopolar surfaces. Adv. Colloid Interface. Sci. 1973, 5, 39–55. [Google Scholar] [CrossRef]
- Della Volpe, C.; Siboni, S. Acid–base surface free energies of solids and the definition of scales in the Good–van Oss–Chaudhury theory. J. Adhes. Sci. Technol. 2000, 14, 235–272. [Google Scholar] [CrossRef]
- Schultz, J.; Nardin, M. Determination of the Surface Energy of Solids by the Two-Liquid-Phase Method, Modern Approaches to Wettability: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 1992; pp. 73–100. [Google Scholar]
- Shi, B.; Wang, Y.; Jia, L. Comparison of Dorris-Gray and Schultz methods for the calculation of surface dispersive free energy by inverse gas chromatography. J. Chromatogr. A 2011, 1218, 860–862. [Google Scholar] [CrossRef]
- Girifalco, L.; Good, R.J. A theory for the estimation of surface and interfacial energies. I. Derivation and application to interfacial tension. J. Phys. Chem. 1957, 61, 904–909. [Google Scholar] [CrossRef]
- Altay, B.N.; Ma, R.; Fleming, P.D.; Joyce, M.J.; Anand, A.; Chen, T.; Keskin, B.; Maddipatla, D.; Turkani, V.S.; Kotkar, P.R. Surface free energy estimation: A new methodology for solid surfaces. Adv. Mater. Interfaces 2020, 7, 1901570. [Google Scholar] [CrossRef]
- Li, D.; Neumann, A. Contact angles on hydrophobic solid surfaces and their interpretation. J. Colloid Interface. Sci. 1992, 148, 190–200. [Google Scholar] [CrossRef]
- Zhang, D. An Equation-of-State approach to measure the surface free energy (SFE) of bituminous binders. Measurement 2020, 158, 107715. [Google Scholar] [CrossRef]
- Weston, J.; Jentoft, R.; Grady, B.; Resasco, D.; Harwell, J. Silica nanoparticle wettability: Characterization and effects on the emulsion properties. Ind. Eng. Chem. Res. 2015, 54, 4274–4284. [Google Scholar] [CrossRef]
- Yan, N.; Maham, Y.; Masliyah, J.H.; Gray, M.R.; Mather, A.E. Measurement of contact angles for fumed silica nanospheres using enthalpy of immersion data. J. Colloid Interface Sci. 2000, 228, 1–6. [Google Scholar] [CrossRef]
- Xu, B. Further Exploration of Heat of Immersion as a Method to Quantify Wettability for Particulates: Effect of Temperature. Master’s Thesis, University of Oklahoma Graduate College, Norman, OK, USA, 2023. [Google Scholar]
- Taguta, J.; O’Connor, C.; McFadzean, B. The relationship between enthalpy of immersion and flotation response. Colloids Surf. A 2018, 558, 263–270. [Google Scholar] [CrossRef]
- Wang, H.; Sun, F.; Wang, C.; Zhu, Y.; Wang, H. A simple drop-casting approach to fabricate the super-hydrophobic PMMA-PSF-CNFs composite coating with heat-, wear-and corrosion-resistant properties. Colloid Polym. Sci. 2016, 294, 303–309. [Google Scholar] [CrossRef]
- Wu, C.; Tang, W.; Zhang, J.; Liu, S.; Wang, Z.; Wang, X.; Lu, X. Preparation of super-hydrophobic PVDF membrane for MD purpose via hydroxyl induced crystallization-phase inversion. J. Membrane Sci. 2017, 543, 288–300. [Google Scholar] [CrossRef]
- Wu, G.; Liu, D.; Chen, J.; Liu, G.; Kong, Z. Preparation and properties of super hydrophobic films from siloxane-modified two-component waterborne polyurethane and hydrophobic nano SiO2. Prog. Org. Coat. 2019, 127, 80–87. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Cao, Q.; Wang, C.; Yang, C.; Li, Y.; Zhou, J. Novel porous oil-water separation material with super-hydrophobicity and super-oleophilicity prepared from beeswax, lignin, and cotton. Sci. Total Environ. 2020, 706, 135807. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Wu, J.; Zhang, M. Microcalorimetry Techniques for Studying Interactions at Solid–Liquid Interface: A Review. Surfaces 2024, 7, 265-282. https://doi.org/10.3390/surfaces7020018
Hu H, Wu J, Zhang M. Microcalorimetry Techniques for Studying Interactions at Solid–Liquid Interface: A Review. Surfaces. 2024; 7(2):265-282. https://doi.org/10.3390/surfaces7020018
Chicago/Turabian StyleHu, Heshu, Jiazhong Wu, and Minghui Zhang. 2024. "Microcalorimetry Techniques for Studying Interactions at Solid–Liquid Interface: A Review" Surfaces 7, no. 2: 265-282. https://doi.org/10.3390/surfaces7020018
APA StyleHu, H., Wu, J., & Zhang, M. (2024). Microcalorimetry Techniques for Studying Interactions at Solid–Liquid Interface: A Review. Surfaces, 7(2), 265-282. https://doi.org/10.3390/surfaces7020018







