Surface Interactions of Transonic Shock Waves with Graphene-Like Nanoribbons

Abstract

Graphene-like nanoribbons (GLNRs) were fabricated (length—20 μm; width—2 μm) and subjected to blast-like pulsed pressure >1.5 GPa (pulse speed ≈1 Mach, impulse duration, ≈µs) to examine the amount of absorption. GLNRs prepared by the chemical vapor deposition technique via controlled biomass combustion were subjected to investigate the structure–property characteristics using microspectroscopic techniques. Following this, GLNRs were employed to high strain rate (HSR) studies with the help of the technique known as split Hopkinson pressure bar (SHPB) to evaluate numerous dynamic parameters. The parameters were extracted from variations in the stress and strain rates. Their analysis provided insight into the damping response of blast energy within GLNRs. By and large, the impact generated modified the microstructure, exhibiting modifications in the number of layers, conjugated loops, and dynamic disorder. Signal processing analysis carried out for incident and transmitted impulse pressure revealed an interaction mechanism of shock wave with GLNR. Details are presented.

1. Introduction

Any pressure impulse exceeding the magnitude of GPa is treated as an explosion [1]. It causes the generation of energy in the form of transient heat (2000–4000 K), sound (>20 kdB), and intense light flashes with the simultaneous emergence of shock waves [2] that consequently lead to a dynamic deformation in structure [3]. It is a mechanical disturbance propagating in a medium [4] at peculiar shear velocities and broadly classified into elastic, plastic, shock, blast, and explosion waves with non-linearly peaking amplitudes. The nature of the pressure impulse and mechanical stability of the medium chiefly decide the level of catastrophe. On imparting high strain rate (HSR) deformation, there is a transient temperature and rapid pressure rise in a material that may lead to a complex scenario that depends on numerous structural aspects such as surfaces, interfaces, microstructures, porosity, direction of flow of heat and material, etc., causing fragmentation, perforation, and spall. The cause beneath such an extreme result is a shock wave [5]. It is catastrophic, lethal, and devastating. However, in the strategic sector, the damping of such an impact [6], explosive detonation, and dynamic deformation could be understood to a certain extend by a thorough understanding of the HSR deformation mechanism and dynamic response of the damping material. An explosion is an uncontrollable phenomenon; however, the same could be realized at the laboratory scale using shock wave tube [7], stand off/contact explosion [8], and split Hopkinson pressure bar (SHPB) [9] techniques. Among them, SHPB is an inexpensive, time-effective, safe measurement route to generate shock waves to realize an explosion scenario off the field [10]. Mechanical parameters of aluminum alloys were investigated, both at room [11] and high temperature [12] using the SHPB technique. Furthermore, tensile, force-displacement behavior, and compressive strength data were analyzed for shock mitigation in carbon nanotube/polymer composites [13,14,15]. However, most of the reported studies are on quasi-static measurements rather than HSR and focused onto enhancement into reinforcing properties of alloys and composites [16], including deformation in graphene [17].

Herein, we have examined shock mitigation in graphene-like nanoribbons (GLNR). Particularly, we address fundamental questions such as how shock waves interact with GLNR, what happens to its morphology and microstructure with dynamic pressure, how inherent disorder and defects factor into the resulting various microscopic failures such as slip, twinning, etc. GLNRs, after fabrication by chemical vapor deposition (CVD), were subjected to SHPB for the extraction of parameters such as stress, strain, and strain rates. The samples were further investigated using optical and field emission scanning electron microscopy (FESEM), as well as Raman, Fourier Transform infrared (FTIR), and UV-visible spectroscopy. The transmitted and reflected shock wave signals were signal processed for damage feature extraction in GLNR. Broadly, the shock wave/GLNR interaction process involved microstructure modifications related to glissile dynamics, flow hardening, transient phase transformation, physicochemical modifications, phonon drag, and importantly, shock damping. Details are presented.

2. Experimental

GLNR were obtained by following the synthesis protocols reported in [9,18], whereas SHPB measurements were performed as per the procedures in the reference [9]. GLNR samples subjected to SHPB were termed HSR GLNR samples. The loading scheme is shown in Figure 1 indicating an incident bar, GLNR, and transmission bar in SHPB. Both GLNR and HSR GLNR were examined using a number of characterization tools such as optical microscopy, Raman spectroscopy (Horiba HR800 Jobin Vyon, India) (wavelength ≈532 nm, scan range ≈200–3000 cm⁻¹), confocal imaging (Horiba HR800 Jobin Vyon, India), field emission microscopy (FESEM) (Carl Zeiss, India) at a beam potential of 5 kV, and dark field transmission electron microscopy (HRTEM) (Techni, India) at 200 kV at numerous magnifications. In some cases, the selective area electron diffraction pattern (SAED) was recorded.

3. Results and Discussion

For analyzing mechanical properties, we assumed that deformation in GLNRs is uniform and maintaining stress equilibrium while impact, frictional, and other dynamic effects were neglected, including linear variations in particle velocity (volume strain) with shock velocity.

3.1. Mechanical Analysis

In a quasi-static and dynamic range when the magnitude of stress exceeds the elastic limit, a plastic deformation sets in GLNRs. A decomposed component of elastic and plastic waves propagates in the form of impulse in which the built-up hydrostatic stress component exceeds dynamic flow stress by several orders of magnitude. As a first approximation, we have assumed that GLNRs offered no impedance to the developed shear, and calculated shock parameters are obtained by Lagrange–Rankine–Hugoniot formulism [19,20,21]. The progressing stress disturbance is characterized by $\frac{{\partial }^{2}u}{\partial t^2}=\frac{\raisebox{1ex}{$d\sigma $}\!\left/ \!\raisebox{-1ex}{$dϵ$}\right.}{{\rho }_0} (\frac{{\partial }^{2}u}{\partial x^2})$ at a constant strain, ε, with $V_o={(\frac{d\sigma /dϵ}{{\rho }_o})}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ and $\frac{d\sigma }{dϵ}=E$ (in an elastic limit), in which, u is the volume strain speed, ${\rho }_o$ is the density of nanocarbon, i.e., GLNR ≈ 0.02 kg/m³, and E is the elastic energy (measured in GPa). The boundary conditions are u = $V_o$t at $x_i=0$ and any t > 0; u = 0 at $x_f=\infty$. The position, $x$, and time, t, variations are given by $\frac{x}{t}=\frac{\dot{\sigma }}{{\rho }_0}$. The variable strePss rate, $\dot{\sigma }$, is explained while analyzing the stress (σ)–strain (ε) curve and other derived quantities. By and large, the structural strength of a GLNR in a dynamic region depends on the strain, ε, and the first dispersion derivative of strain i.e., the strain rate, $\frac{d\epsilon }{dt}$ (denoted by ἑ). 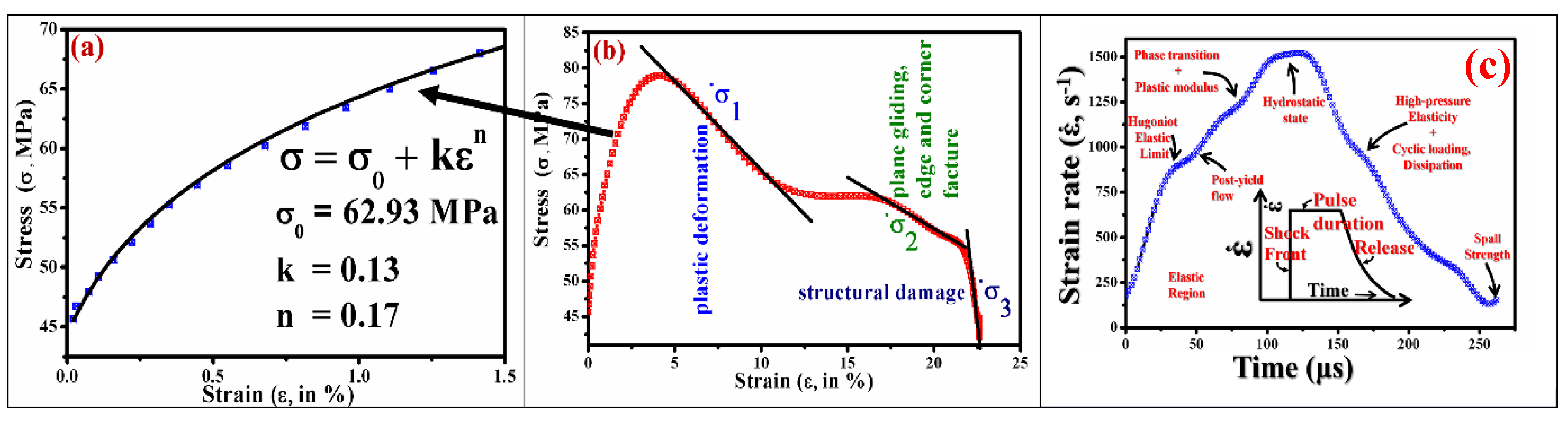Figure 2a shows the σ–ε curve for GLNR fitted by a bilinear function in the first stage, which is elastic in nature. The power function is fitted of the type $\sigma ={\sigma }_0+k {ϵ}^n$; here, k is a pre-exponential factor (0.13), and the work-hardening coefficient n = 0.17. The velocity, $V_S$, with which the shock wave incident is $~3.5\times {10}^3\mathrm{m}/\mathrm{s}$, is given as above. The GLNR departs from its elastic limit with large dispersion in $V_o$. The characteristic time parameter $t_c$ involved in the phase transformation from the elastic to plastic region, is given by $t_c= \frac{\partial \sigma /\partial \dot{\epsilon }}{\partial \sigma /\partial \epsilon }$ and estimated to be ≈10⁻⁵ s⁻¹, as given in Figure 2b.

The gradual decrease in σ is indicative of ε propagation in a GLNR matrix, which has experienced the strain flow hardening. The change has occurred in three stages. The ${\dot{\sigma }}_1$ is attributed to the strain impediment offered by GLNRs in the form of interparticle plastic deformation. The ${\dot{\sigma }}_2$ is attributed to the plane gliding of conjugated ribbon stacks (evident prominently in subsequent Raman and microscopy analysis). The ${\dot{\sigma }}_3$ causes damage to the ribbon structure terminally. The impact has cascading consequences. For an ideal shock wave, a discontinuous shear wave front follows a plateau at the top and the gradual decay of impulse, which is shown as an inset in Figure 2c. In contrast, shock waves imprinted onto a material have distinctly peculiar features that are pressure- and medium-dependent. In the case of GLNRs, the volumetric stress rise rate is much higher under elastic conditions, which yield to the Hugoniot elastic limit (HEL) around about 8 GPa. The flow strength of any medium depends on the pressure employed. It can be independent (Hugoniot) of pressure or change, causing a softening or hardening of material. In plot Figure 2c, at HEL, elastic and plastic wave components get separated. The elastic fraction within HEL propagates with higher velocity than the plastic wave. After crossing the HEL, the rise in pressure is steady until the approach of the top plateau region due to the continuous plastic wave front nature, and mainly, such pressure rise is governed by the constitutive parameters attributed to the mechanical properties of GLNRs. The observed phase change is not prominent in the obtained wave profile due to a significant amount of elastic and plastic wave front separation. The plateau zone is observed at the top of the recorded profile. The pressure-unloading region in GLNRs suggests elastic deformation followed by plastic deformation and identical to shock loading subsequent to HEL. The short tail shows the fracture of GLNRs.

3.2. Fractographic Analysis

Both GLNRs and HSR GLNRs were examined and analyzed using electron and optical microscopy. For optical microscopy, magnification was kept at 100×, and several sites were surveyed. A few representative micrographic images are shown in Figure 3.

Optical micrography was used to obtain more insights into the nature, shape, and size of pre and post-impacted GLNR. For better imaging, suspended GLNR (HSR GLNR) solution was drop-casted onto a silicon wafer and dried. The optical imaging was carried out at several sites in a raster scan-line fashion to collect statistics on ribbons.

Figure 3a shows GLNRs and Figure 3b shows HSR GLNRs. The images were processed for their contrast with optimum brightness and sharpness to reveal features of the ribbons. The GLNR were mostly seen with sharp edges and a prominent rectangular shape. Even smaller ribbons carried similar structural features; however, these are not provided here. The ribbons were thick and may have several conjugated graphene layers within them. Figure 3b is a typical HSR GLNR, which is observed to be different in its morphology. It seems that after impact size, the shape is changed with a bit of elongation and loss of conjugated layers. Figure 3c,d shows representative FESEM images of GLNRs and fractured HSR GLNRs. The resemblances of optical images can be seen in FESEM imaging in terms of the shape, sharp edges, and rectangular shape of the ribbon geometry. Further, fractographic analysis provides important clues for the underlining mechanisms of deformation, fracture, and spall due to the shock experienced by GLNRs. Figure 3e,f shows HRTEM images recorded for HSR GLNRs. In FESEM, it is quite evident that the individual surface of the ribbon is acting as a stress concentration zone. The warps that are visible on the surface of the GLNRs, in moderate fashion, is indicative of the flow of the stress wave front within the GLNRs, which may have undergone breakage of the entire ribbon structure. The effect of shock onto local structure modifications such as dislocation, slip, and disorder can be revealed in depth in TEM investigations. By and large, the images showed a detailed change in the morphology of the ribbon and the effect of impact.

The HSR GLNR has displayed typical two/three step-like features in the Figure 3e inset. The arrow connected to the inset shows the existence of microcracking that originated in one of the steps. The crack tip is located around the junction of two nearly orthogonal cut sides of the step. The track of the crack is almost straight and narrows toward the termination. The approximate track length is ≈3–3.5 µm with a width of roughly 150–200 nm. It seems that the crack ends with a generating stacking fault in the overlayer graphene ribbon. Figure 3f displays more features such as a circular bend in the end of the track of the crack followed by warp-like exfoliation. Startlingly, in another step, a crack is not seen. The blur rings recorded in the SAED pattern are indicative of a lower degree of crystallinity in GLNRs. Broadly, the degree of crystallinity is not changed, even after impact.

3.3. Raman Spectroscopic Investigations

In general, the amount of sp² and sp³ content and their proportion in the ribbon offers peculiar physical properties and variety to the obtained nanocarbons. Raman spectroscopy fundamentally extracts information on sp² ordering directly and sp³ indirectly. Raman scattering is a proprietary probe to examine structure and dynamics at the molecular level by extracting numerous parameters such as dynamic force constant, k_q, crystalline, L_a, disordered length, L_D, areal defect density, n_D, electron–phonon coupling, EPC, and Fermi velocity, V_F. Figure 4 shows recorded Raman spectra for (a) GLNRs and (b) HSR GLNRs at 532 nm photo excitation; the corresponding confocal Raman imaging is seen in (c) and (d). For GLNR, D and G peaks appeared, respectively, at ≈1333 and 1593 cm⁻¹. The estimates for k_q are approximately given by the relation ${\omega }_{q=}\sqrt{k_q/\mu }$, where k_q is the dynamical variable of the force constant, and μ is the reduced atomic mass of carbon. For GLNR, the values estimated were ≈460 and ≈650 N/m, respectively, for D and G. The corresponding bond lengths of –C–C– and –C=C– were ≈1.60 and 1.20 Å, respectively. Post-impact analysis revealed that at D sites, the force constant is down-shifted to ≈410, and at G, it is reduced to 600 N/m compounded to bond deformation at 2.85 and 3.50 Å, respectively. The plastic deformation in GLNR cannot be explained by applying a specific theory. The challenges come due to the formulism having numerous deformation mechanisms such as dislocation glide, mechanical twinning, and phase transformations. Raman analysis can quantify information about dislocation movement as the agent for plastic deformation by treating k_q at the footy of shear stress, τ. The assumption made here is that dislocations produce shear strain, γ, by movement. The dislocation moves under the action of shear stresses, τ. The force on the dislocation per unit length, under this ideal orientation arrangement, is given by $F=\tau b$; here, $b$ is the offset (Burger) vector. There are frictional forces resisting the movement of a dislocation; thus, a force is required to make it move. At the sp³ site, such force movement, i.e., estimated $F_D$, is ≈0.3 nN, whereas at sp², $F_G$ ≈ 0.6 nN. In-plane shear stress is 33% high compared to out-plane shear stress.

Some of the Raman features are similar to those recorded for graphene-like nanoflakes [9]. For GLNRs, D-peak deconvolutions were composed of two prominent components: one at ≈1200 cm⁻¹ attributed to an amorphous (a-C–O) carboxyl phase and another broad at 616 cm⁻¹ quasi-crystalline carbon (qc-C). There was a significant upshift in vibration modes on impact. The D was shifted to ≈1326 cm⁻¹, whereas G was shifted to 1583 cm⁻¹ for HSR GLNR. The a-C is also blue-shifted by ≈90 cm⁻¹ with a total disappearance of qc-C component. The upshifted D and G show strain and frustration at molecular levels of HSR GLNRs. For 532 nm excitation, the value of I_D/I_G for GLNRs was 1.55 and reduced by 0.44 after impact. The ratio is connected to crystalline length, L_a, by relation $L_a(nm)=(2.4\times {10}^{-10}) {\lambda }_L^4\frac{I_D}{I_G},$ where λ_L represents the laser excitation. L_a was found to be ≈17 nm for GLNRs and 7 nm for HSR GLNRs. The change was attributed to the lowering sp² content and increasing sp³ zone by impact. In addition, I_D/I_G is correlated to the inter-defect distance, L_D, by a modified Tuinstra–Koienig relationship $\frac{I_D}{I_G}=\frac{C({\lambda }_L)}{L_D^2}$, where $C(\lambda )$ is the phenomenological parameter ≈102 nm² (at 532 nm) and for L_D, in terms of defect density n_D, one can write $n_D(c{m}^{-2})=\frac{{10}^{-14}}{L_D^2}$. For GLNRs, L_D and n_D were ≈15 nm and ≈10⁻¹³/cm², respectively, whereas for HSR GLNRs, these values were ≈10 nm and ≈10⁻¹²/cm², respectively. In particular, the derived values of L_a, L_D, and n_D are connected to the shear strain, γ. The movement of chiral dislocations in GLNRs may produce an elastic shear strain, γ_E, with an assumption that dislocations are interacting within the elastic limit. The relation among n_D, γ_E, and L_D is given by γ_E = n_D × b × L_D; that yields to a value >10⁻⁹, whereas in the plastic regime, γ_P is >10⁻⁹ for GLNRs. The disorder speed, ν, is given by $\dot{\gamma }=n_D\times b\times \nu$, and ν is found to be more than 1000 cm-s⁻¹.

Further, the width of the D peak in a 2D nanocarbon system is connected with EPC having an acoustic longitudinal and transverse branch. The width amounts to inter-phonon interaction compounded with other elementary excitations; however, anharmonic, elementary excitations can be ignored. The degree of phonon interactions can be quantified by measuring the FWHM of the D peak. The FWHM for GLNR was 165 and 205 cm⁻¹ for HSR GLNR. The corresponding estimated EPC was 5 and 35 N/m. Moreover, EPC has a relation with Fermi velocity, V_F, which is measured in ms⁻¹ and given by $EPC=\frac{\sqrt{3}}{4}\frac{a_0^2}{\mu }\frac{EPC{\mathsf{\Gamma }}^2}{{\nu }_F^2}$ where $EPC{\mathsf{\Gamma }}^2$ is the hypothetical Γ-phonon-branching parameter (47 (eV/Å)²), a_o is 3.14 Å, and μ, is the reduced mass of the carbon molecule. The value of V_F for GLNR and HSR GLNR was, respectively, ≈1 × 10⁶ and 5 × 10⁵ ms⁻¹ [22,23,24].

Interestingly, there was no 2D peak recorded for GLNRs. However, for HSR GLNRs, a prominent 2D band was observed that extended 2000–2750 cm⁻¹. This shows the longitudinal effect of the impulse, which has exfoliated the conjugated layers of GLNRs, introducing stacking faults.

Further, spectral confocal mapping is a promising technique that has been successfully used previously to evaluate the nanofiller dispersion in a polymer matrix [22]. We adopted a similar technique to assess our post-impacted GLNRs. The Raman spectral features collected from each specific spatial coordinate within the selected scan area are used as pixels for final imaging of the specific zone. The typical Raman spectra were recorded in the range of 1000–1800 cm⁻¹. However, the spectral variation over the range 1200–1600 cm⁻¹ (range covering the D and G peaks of GLNRs) were used to map the modifications in the post-impacted nanocomposites. The obtained images consisted of a topology of sp³ and sp² zones, which are shown in Figure 4c,d. The color contrast between the sp³ and sp² zone is seen in both the images. The spectral image was taken in large areas (50 × 50 µm²). The sp³ phase in Figure 4c was distributed homogeneously with uniform spread within the planer sp² network. At some places, the degree of disorder in the sp³ zone was seen to be higher and appeared as a distinctly dark region. In the planer region, no such peculiarities have been observed. They were mostly smooth and flat. The features seen in Figure 4d are significantly different. There are two important observations: first, the sp³ zone is redistributed in a systematic pattern and, secondly, it shows small warps in the sp² zone. Perhaps, it seems to be the imprint of the propagated shock impulse, which sequentially stressed the sp³ zone (indicated by a horizontal arrow). The vertical arrows show its relative strength, which is enhanced at the boundary layers of GLNR. After impact, the trail of the damaged zone is seen.

3.4. Signal Processing Studies: Impulse Interaction with GLNR

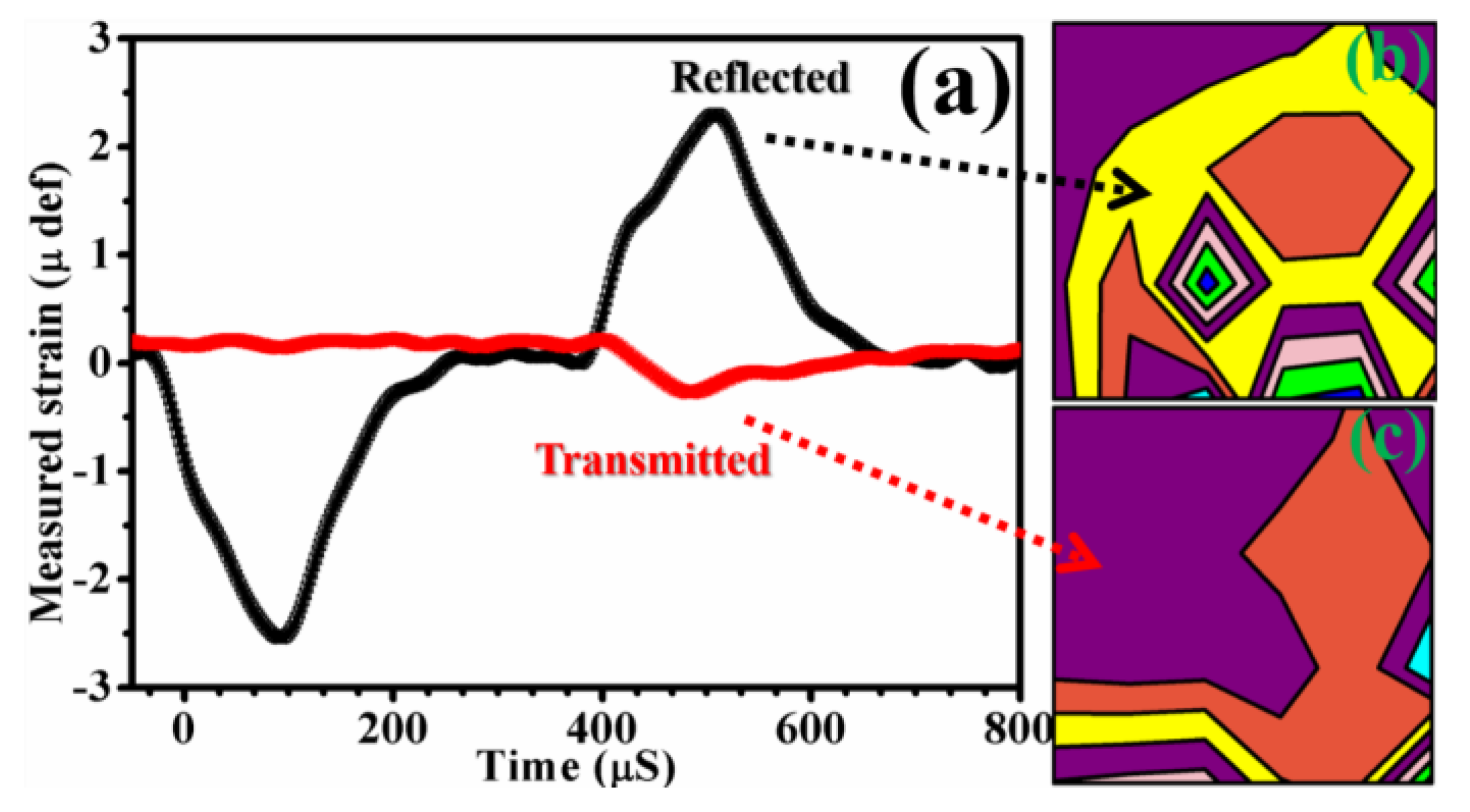
In SHPB, the GLNR samples were sandwiched between the two elastic pressure bars. The striker bar, also termed as a projectile, becomes propelled with the help of a gas gun toward the incident bar. Striking onto the incident bar, an elastic compression wave sets in, and impact travels through this input bar. Since the GLNR samples are mounted onto the input bar at the interface, part of the impact wave gets reflected and part of the wave gets transmitted through the specimen to the input bar. Following this, the reflected wave travels back as a tensile wave. The resulting time-dependent strains were calculated from the voltage signals, which were measured by semiconductor strain gauge sensors attached to the incident bar. The reflected signals will be received by the same sensor attached to this bar. In similar fashion, the output bar collects the transmitted signal. The signals received are shown in Figure 5a. These signals were processed further to extract information about how the strain energy is propagated in GLNRs. For this, signal-processing studies were performed using the short-term Fourier transform (STFT) technique to investigate the flow of strain energy in the time and frequency domain. Figure 5b,c respectively shows the reflected and transmitted strain in the GLNRs.

The STFT functional is given by $x(\left[n\right],\omega )=X(m,\omega )=\sum _{m=0}^{m=\infty }x\left[n\right]•\omega \left[n-m\right]e^{-j\omega n}.$ The operation was performed on a time sequence, where x [n] is the data array variable of time, $\omega$ is the continuous signal frequency, and m is the discrete time locality. The equation shows the DTFT of the signal with the window function described below. The STFT was computed by adopting the following procedure: (a) a finite number of signal data points (N) were taken from the input shock signal, where these N points were equal to the window size; (b) the window of the chosen type was used to multiply the extracted data, point-by-point; (c) zeros were padded on both sides of the window. The provision was made in case the window width becomes smaller than the size of the FFT, and (d) FFT were computed. Furthermore, the following steps were performed to compute STFT with the following settings: (i) sampling interval as 1, (ii) FFT length as 256, (iii) window length as 256, (iv) overlap as 128, and (v) type of window as rectangle. The window function is given by $\omega \left[n\right]=1, \mathrm{if} 0\le n\le N-1;=0$, otherwise. The output results are the complex valued data matrix (N × M) with the following conditions: $N=\frac{F_w}{2}+1, \mathrm{if}\mathrm{input}\mathrm{signal}\mathrm{data}\mathrm{real};\mathrm{else};=F_w \mathrm{complex}$ and $M=f(\frac{D_s-W_s}{W_s-O_s})+1$. Here, $F_w$ is the transform width, $D_s$ is the size of the data, $W_s$ is the width of the window, $O_s$ is the overlap function, and $f$ is the floor function. In addition, one can analyze the frequency content of the signal as well as the variations in frequency with time. The segments on the signal apply the discrete Fourier transform to slide the window onto the entire signal to get the coefficients of the transform. The spectral content of the signal can be obtained using ${\left|X(m,\omega )\right|}^2$, i.e., by squaring the coefficients and plotting the two-dimensional contour plots. The spectrograph shows temporal variations in the shock rate of recurrence. The blocks represent how the power is dispersed within the GLNRs. Each colored area covered represents the corresponding energy dissipation and the size of the contour represents the amount of energy loss. The propagation of the shock wave through the GLNRs causes the dissipation of impact energy within ribbons and leads to a number of deformations of chemical and physical origins, as discussed below.

Impulse pressure can be imaged as a kind of excitation perturbation, in the form of a δ-function. In the GLNR, the impulse pressure exerts negligibly small shear compared to the compressive hydrostatic component and induces disturbance, moving isentropically, which is given by an approximate relation: $\sqrt{\raisebox{1ex}{$\frac{d\sigma }{d\epsilon }$}\!\left/ \!\raisebox{-1ex}{$\rho $}\right.}$ is equivalent to $\sqrt{\raisebox{1ex}{$dP$}\!\left/ \!\raisebox{-1ex}{$dV$}\right.}$, (where, ρ is the density of the GLNRs, while P and V are the change in the pressure and volume, respectively). The subjected mechanical disturbance varies with time and enhances in its peak strength as it propagates over the GLNRs, resulting in disorder activation [23]. The inherent defect is a key component for the dynamic flow strength in the GLNRs. Regarding shock travel, there emerges a mismatch in the material flow of the GLNRs and the speed of the shock wave front. This results in a distortion in the GLNR beyond its elastic limit, leading to plastic deformation and finally fracture (spall region). The plastic deformation would build residual internal stresses, leading to the separation of conjugated layers. The gliding ribbon layers could be modeled by a Peierls–Nabarro stress mechanism. At the gliding interface, conjugated layers experience two resultant forces: first, compression due to the extra plane present leading to edge dislocation, and second, a missing plane to neutralize the compressive force due to the short fall of the dislocated edge. It is a balancing phenomenon and dislocation extension depends on the Poisson’s ratio. The slip dislocation starts moving in response to the applied shear stress, and the ratio of the in-plane to out-of-plane stress sets the critical stress limit [25,26,27]. The slip ratio is given by $\frac{{\sigma }_{\parallel }}{{\sigma }_{\perp }}=\frac{4\pi }{(\sigma -1)}\times \left\{5.8+\log (\sigma -1)\right\}\times e^{\frac{4\pi }{(\sigma -1)}}$, in which ${\sigma }_{\perp }$ and ${\sigma }_{\parallel }$ are respectively the out-plane and in-plane stress components. For GLNRs (0.07) and HSR GLNRs (0.1), the estimated values of σ are provided in parentheses. 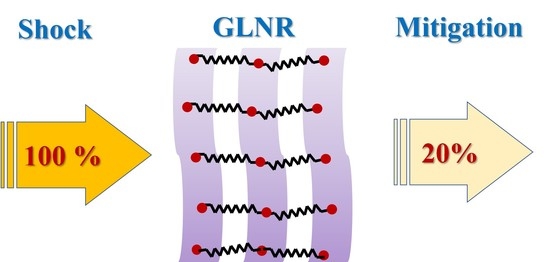The estimated slip ratio $\frac{{\sigma }_{\parallel }}{{\sigma }_{\perp }}$ is ≈10⁻⁴ for GLNRs, which is as low as 10⁻⁶ after impact. Broadly, the incident transonic impulse of speed with a Mach number more than 1.0 damps almost more than 80% of its shock energy within GLNR, transmitting a small fraction ≈5%, and the rest is subject to spall/fracture, as shown in Figure 6, schematically.

Table 1. Estimated dynamic mechanical parameters for the GLNRs from Hugoniot formalism.

Sr. No.	Parameter (SI Unit)	GLNR	HSR GLNR
1	Young’s modulus	>60 MPa	-
2	Elastoplastic time constant, $t_c$	≈10−4 s−1 (metal-like)	-
3	Hugoniot elastic limit (GPa)	-	≈8 (ceramic-like)
4	Force constant, (–C–C–) (N/m)	460	410
5	Force constant, (–C=C–) (N/m)	650	600
6	Bond length (Å)	1.60	2.85
7	Bond deformation (Å)	1.20	3.50
8	Disorder velocity (cm/s)	-	1300

shows other mechanical parameters obtaind for GLNR.

Thus, in certain situations, energy storage in a medium becomes an unimportant characteristic of a material compared with its ability to dissipate energy within. Specifically, it is important when designing and building armor blocks, bulletproof armors, bunkers, etc., where shock, acceleration, and jerk need to be damped efficiently and effectively. The study performed herein develops a fundamental insight into the shock wave interaction with GLNRs that provides an important clue for designing body armors using nanocarbons.

4. Conclusions

We have investigated shock waves mitigation in graphene-like nanoribbons (GLNRs). GLNRs were synthesized using the chemical vapor deposition method. The impulse pressure of GPa magnitude and microsecond duration having a speed >1 Mach were created using the split Hopkinson pressure bar technique and delivered onto GLNRs. Data have been collected for the strain, stress, and their time-varying components. The number of mechanical parameters was extracted such as the strain (ε)–stress (σ) constitutive conjugate, elastoplastic transformation rate, work-hardening factor, compressive force, ultimate elastic limit, slip movement rate, shock dissipation constant, Peierls–Nabarro stress, etc. The bilinear σ–ε behavior of the curve revealed the non-linear (parabolic) nature of work hardening with an exponent value, n, ≈0.17. The elastic-to-plastic transformation factor was estimated to be ≈10⁻⁵ s⁻¹. The strain rate of stress, $\dot{\sigma }$ (i.e., $\frac{d\sigma }{dϵ}$), with strain was seen, typically, of three stages in the plastic region. It was comprised of conjugated ribbon separation, layer exfoliation, and corner/edge fracture at the spall stage. Under the elastic conditions, the volumetric stress rise was higher, which resulted in an ultimate (Hugoniot) elastic limit (HEL) of ≈8 GPa. GLNRs departed significantly in the elastic zone and closely resemble an ideal Rankian–Hugoniot model in the plastic region. Shear waves have three folds of in-plane impact compared with out-of-plane impact, resulting in stacking faults in conjugated layers. Raman analysis extracted information on the dynamics of slip disorder due to shear stresses. It showed a compressive force movement, $F_D,$ of ≈0.3 nN at sp³ and a ≈0.9 nN at sp² site with a dislocation speed $>1000 \mathrm{cm}/\mathrm{s}.$ Imaging by Raman technique indicated a redistribution of sp³ content and emergence of strain@sp³, imprinting a shock trail compounded with warps into sp² planes. The incident impulse velocity is reduced almost by 80% showing the effective shock mitigation characteristics of GLNR. Analysis revealed a multifaceted hydrodynamic response of the GLNR material suitable for shock absorbent application in a strategic sector.