The Work Function of TiO2
Abstract
:1. Introduction
2. Materials and Methods
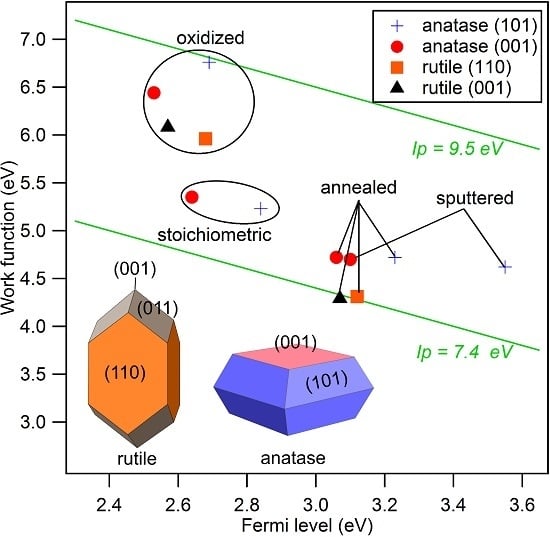
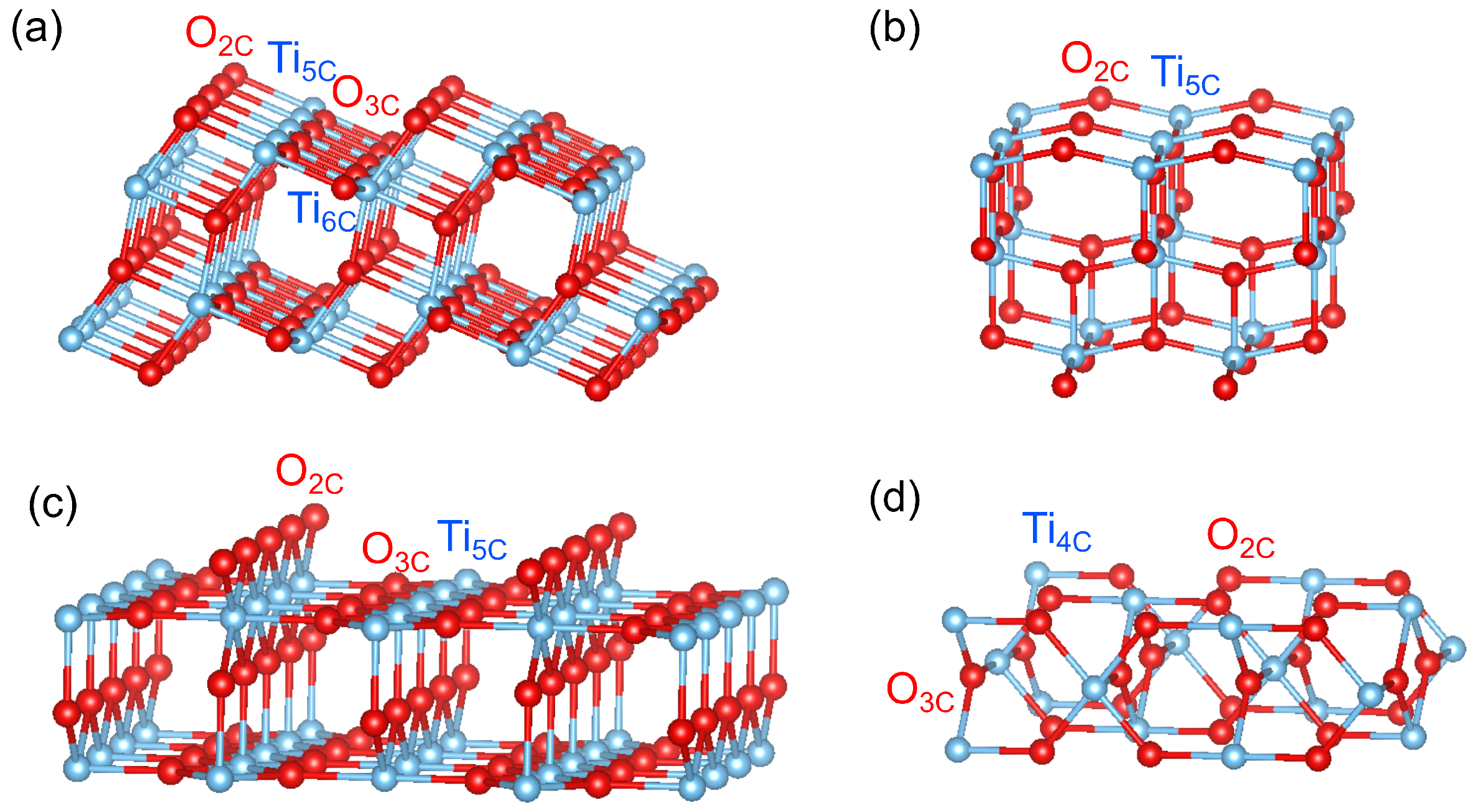
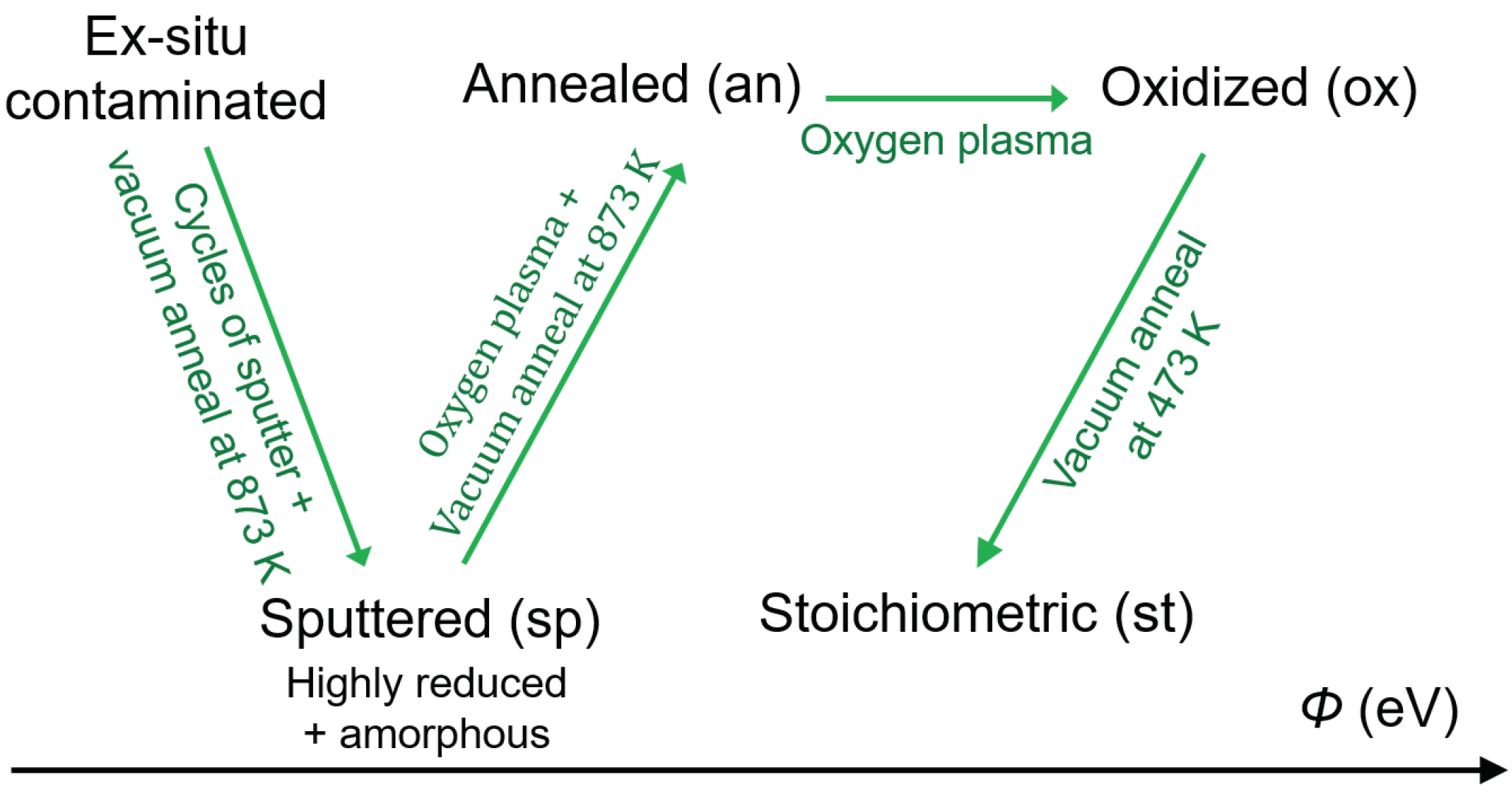
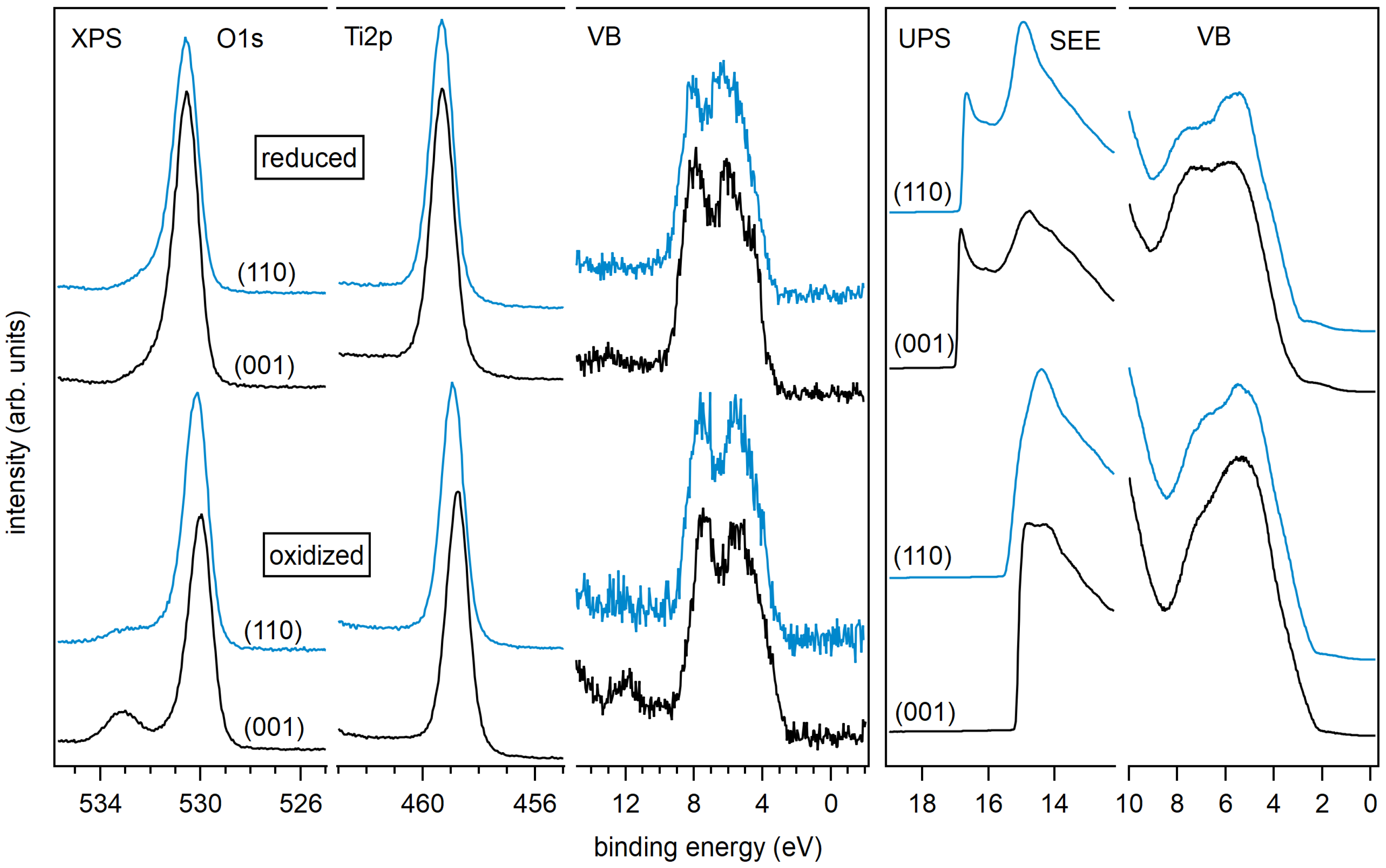
3. Results and Discussion
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| XPS | X-ray photoelectron spectroscopy |
| UPS | ultraviolet photoelectron spectroscopy |
| UHV | ultra-high vacuum |
| LEED | low-energy electron diffraction |
Appendix A. LEED Pattern for Annealed Anatase Surfaces

Appendix B. Further Work Function Data
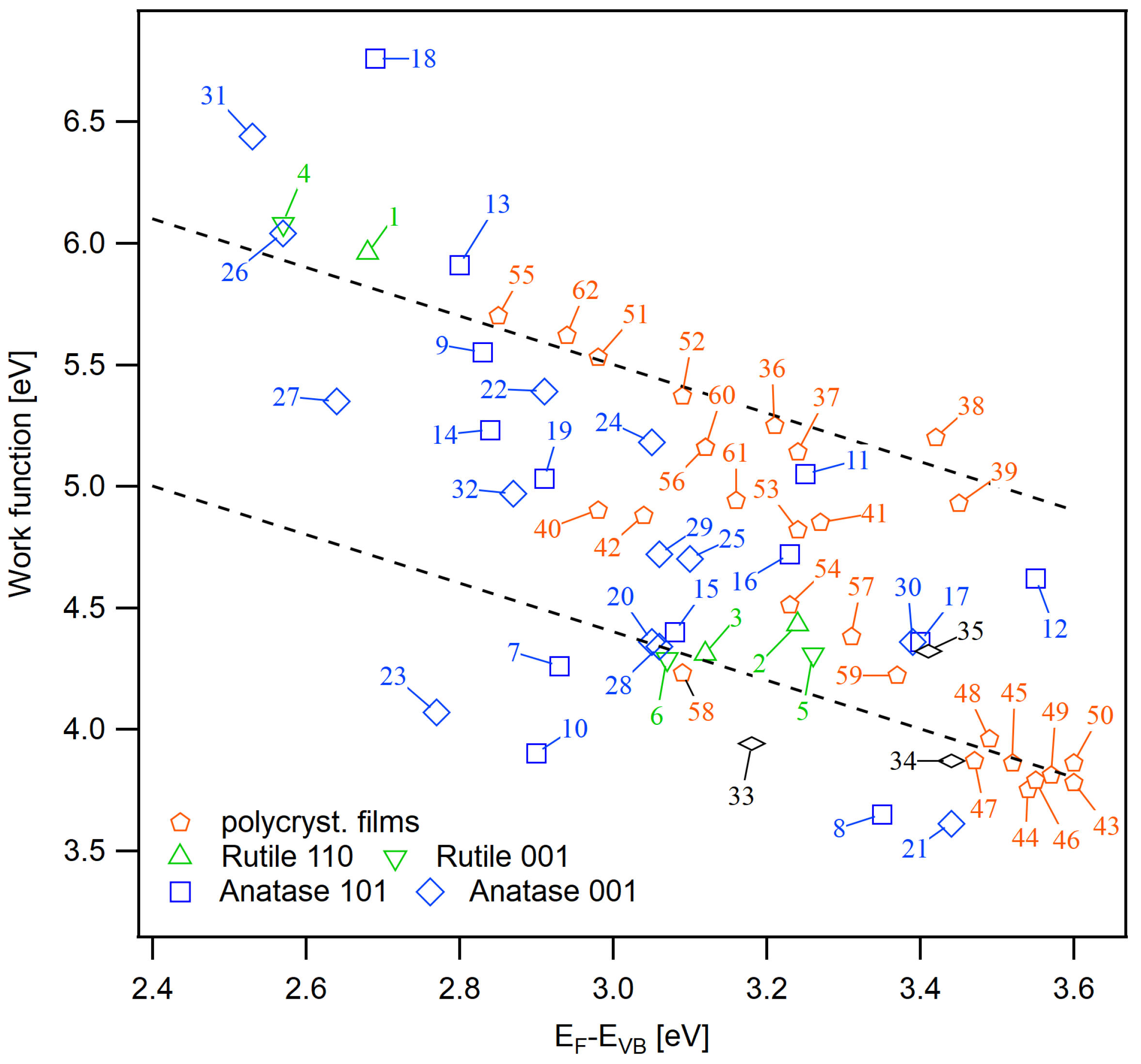
| No. | Sample | Description | |||
|---|---|---|---|---|---|
| 1 | rutile (110) | (i) same as #2; (ii) O plasma, RT, 15 min | 2.68 | 5.96 | 8.64 |
| 2 | rutile (110) | (i) 500 C, 0.5 Pa O, 2h; (ii) 600 C, Pa, 1 h | 3.24 | 4.43 | 7.67 |
| 3 | rutile (110) | same as #2 | 3.12 | 4.31 | 7.43 |
| 4 | rutile (001) | same as #1 | 2.57 | 6.08 | 8.65 |
| 5 | rutile (001) | same as #2 | 3.26 | 4.31 | 7.57 |
| 6 | rutile (001) | same as #2 | 3.07 | 4.29 | 7.36 |
| 7 | anatase (101) | same as #2 | 2.93 | 4.26 | 7.19 |
| 8 | anatase (101) | same as #2 + air exposure | 3.35 | 3.65 | 7.00 |
| 9 | anatase (101) | O plasma, RT, 15 min | 2.83 | 5.55 | 8.38 |
| 10 | anatase (101) | same as #9 + air exposure | 2.90 | 3.90 | 6.80 |
| 11 | anatase (101) | (i) same as #12; (ii) O plasma, RT, 15 min; (iii) annealing in Pa, 200 C, 20 min | 3.25 | 5.05 | 8.30 |
| 12 | anatase (101) | cycles of sputtering + annealing 600 C, Pa, 1 h | 3.55 | 4.62 | 8.17 |
| 13 | anatase (101) | (i) same as #12; (ii) O plasma, RT, 15 min | 2.80 | 5.91 | 8.71 |
| 14 | anatase (101) | stoichiometric as in manuscript | 2.84 | 5.23 | 8.07 |
| 15 | anatase (101) | (i) same as #14; (ii) HO adsorption | 3.08 | 4.40 | 7.48 |
| 16 | anatase (101) | reduced as in manuscript | 3.23 | 4.72 | 7.95 |
| 17 | anatase (101) | (i) same #16; (ii) HO adsorption | 3.4 | 4.36 | 7.76 |
| 18 | anatase (101) | oxidized as in manuscript | 2.69 | 6.76 | 9.45 |
| 19 | anatase (101) | (i) same as #18; (ii) HO adsorption | 2.91 | 5.03 | 7.94 |
| 20 | anatase (001) | same as #7 | 3.05 | 4.36 | 7.41 |
| 21 | anatase (001) | same as #8 | 3.44 | 3.61 | 7.05 |
| 22 | anatase (001) | same as #9 | 2.83 | 5.55 | 8.38 |
| 23 | anatase (001) | same as #10 | 2.90 | 3.90 | 6.80 |
| 24 | anatase (001) | same as #11 | 3.25 | 5.05 | 8.30 |
| 25 | anatase (001) | same as #12 | 3.55 | 4.62 | 8.17 |
| 26 | anatase (001) | same as #13 | 2.80 | 5.91 | 8.71 |
| 27 | anatase (001) | same as #14 | 2.84 | 5.23 | 8.07 |
| 28 | anatase (001) | same as #15 | 3.08 | 4.4 | 7.48 |
| 29 | anatase (001) | same as #16 | 3.23 | 4.72 | 7.95 |
| 30 | anatase (001) | same as #17 | 3.40 | 4.36 | 7.76 |
| 31 | anatase (001) | same as #18 | 2.69 | 6.76 | 9.45 |
| 32 | anatase (001) | same as #19 | 2.91 | 5.03 | 7.94 |
| 33 | powder | sol-gel, as prepared | 3.18 | 3.94 | 7.12 |
| 34 | powder | hydrothermal, as prepared | 3.44 | 3.87 | 7.31 |
| 35 | nanocrystals | (101) facetted | 3.41 | 4.32 | 7.73 |
| 36 | sprayed film | 0.5 Pa O, 400 C, 12 h | 3.21 | 5.25 | 8.46 |
| 37 | sprayed film | 0.5 Pa Ar, 400 C, 12 h | 3.24 | 5.14 | 8.38 |
| 38–42 | sprayed film | same as #36 | – | – | – |
| 43–50 | sprayed film | as received | – | – | – |
| 51 | thin film | (i) in situ magnetron sputtering at RT; (ii) 0.5 Pa O, 600 C, 1 h | 2.98 | 5.53 | 8.51 |
| 52 | thin film | (i) in situ magnetron sputtering at RT; (ii) 0.5 Pa O, 400 C, 1 h | 3.09 | 5.37 | 8.46 |
| 53 | sprayed film | same as #11 | 3.24 | 4.82 | 8.06 |
| 54 | sprayed film | same as #12 | 3.23 | 4.51 | 7.74 |
| 55 | sprayed film | same as #13 | 2.85 | 5.70 | 8.55 |
| 56 | sprayed film | stoichiometric as in manuscript | 3.12 | 5.16 | 8.28 |
| 57 | sprayed film | (i) same as #58; (ii) HO adsorption | 3.31 | 4.23 | 7.32 |
| 58 | sprayed film | reduced as in manuscript | 3.09 | 4.23 | 7.32 |
| 59 | sprayed film | (i) same as #60; (ii) HO adsorption | 3.37 | 4.22 | 7.59 |
| 60 | sprayed film | stoichiometric as in manuscript | 3.12 | 5.16 | 8.28 |
| 61 | sprayed film | (i) same as #62; (ii) HO adsorption | 3.16 | 4.94 | 8.10 |
| 62 | sprayed film | oxidized as in manuscript | 2.94 | 5.62 | 8.56 |
References
- Linsebigler, A.L.; Lu, G.; Yates, J.T. Photocatalysis on TiO2 Surfaces: Principles, Mechanisms, and Selected Results. Chem. Rev. 1995, 95, 735–758. [Google Scholar] [CrossRef]
- Grätzel, M. Solar Energy Conversion by Dye-Sensitized Photovoltaic Cells. Inorg. Chem. 2005, 44, 6841–6851. [Google Scholar] [CrossRef] [PubMed]
- Selcuk, S.; Selloni, A. Facet-dependent trapping and dynamics of excess electrons at anatase TiO2 surfaces and aqueous interfaces. Nat. Mater. 2016, 15, 1107. [Google Scholar] [CrossRef] [PubMed]
- Diebold, U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar] [CrossRef]
- Herman, G.S.; Gao, Y. Growth of epitaxial anatase (001) and (101) films. Thin Solid Films 2001, 397, 157–161. [Google Scholar] [CrossRef]
- Setvin, M.; Daniel, B.; Mansfeldova, V.; Kavan, L.; Scheiber, P.; Fidler, M.; Schmid, M.; Diebold, U. Surface preparation of TiO2 anatase (101): Pitfalls and how to avoid them. Surf. Sci. 2014, 626, 61–67. [Google Scholar] [CrossRef]
- Yang, H.G.; Sun, C.H.; Qiao, S.Z.; Zou, J.; Liu, G.; Smith, S.C.; Cheng, H.M.; Lu, G.Q. Anatase TiO2 single crystals with a large percentage of reactive facets. Nature 2008, 453, 638. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Kuang, Q.; Wang, Q.; Xie, Z. Engineering a high energy surface of anatase TiO2 crystals towards enhanced performance for energy conversion and environmental applications. RSC Adv. 2015, 5, 20396–20409. [Google Scholar] [CrossRef]
- Liu, G.; Yu, J.C.; Lu, G.Q.M.; Cheng, H.M. Crystal facet engineering of semiconductor photocatalysts: motivations, advances and unique properties. Chem. Commun. 2011, 47, 6763–6783. [Google Scholar] [CrossRef] [PubMed]
- Scheiber, P.; Fidler, M.; Dulub, O.; Schmid, M.; Diebold, U.; Hou, W.; Aschauer, U.; Selloni, A. (Sub)Surface Mobility of Oxygen Vacancies at the TiO2 Anatase (101) Surface. Phys. Rev. Lett. 2012, 109, 136103. [Google Scholar] [CrossRef] [PubMed]
- Reckers, P.; Dimamay, M.; Klett, J.; Trost, S.; Zilberberg, K.; Riedl, T.; Parkinson, B.A.; Brötz, J.; Jaegermann, W.; Mayer, T. Deep and Shallow TiO2 Gap States on Cleaved Anatase Single Crystal (101) Surfaces, Nanocrystalline Anatase Films, and ALD Titania Ante and Post Annealing. J. Phys. Chem. C 2015, 119, 9890–9898. [Google Scholar] [CrossRef]
- Baldini, E.; Chiodo, L.; Dominguez, A.; Palummo, M.; Moser, S.; Yazdi-Rizi, M.; Auböck, G.; Mallett, B.P.; Berger, H.; Magrez, A. Strongly bound excitons in anatase TiO2 single crystals and nanoparticles. Nat. Commun. 2017, 8, 13. [Google Scholar] [CrossRef] [PubMed]
- Moser, S.; Moreschini, L.; Jaćimović, J.; Barišić, O.S.; Berger, H.; Magrez, A.; Chang, Y.J.; Kim, K.S.; Bostwick, A.; Rotenberg, E.; et al. Tunable Polaronic Conduction in Anatase TiO2. Phys. Rev. Lett. 2013, 110, 196403. [Google Scholar] [CrossRef] [PubMed]
- Emori, M.; Sakino, A.; Ozawa, K.; Sakama, H. Polarization-dependent ARPES measurement for valence band of anatase TiO2. Solid State Commun. 2014, 188, 15–18. [Google Scholar] [CrossRef]
- Sandell, A.; Sanyal, B.; Walle, L.; Richter, J.; Plogmaker, S.; Karlsson, P.; Borg, A.; Uvdal, P. Probing and modifying the empty-state threshold of anatase TiO2: Experiments and ab initio theory. Phys. Rev. B 2008, 78, 075113. [Google Scholar] [CrossRef]
- Tuan, A.C.; Kaspar, T.C.; Droubay, T.; Rogers, J.W., Jr.; Chambers, S.A. Band offsets for the epitaxial TiO2/SrTiO3/Si(001) system. Appl. Phys. Lett. 2003, 83, 3734–3736. [Google Scholar] [CrossRef]
- Thomas, A.G.; Flavell, W.R.; Kumarasinghe, A.R.; Mallick, A.K.; Tsoutsou, D.; Smith, G.C.; Stockbauer, R.; Patel, S.; Grätzel, M.; Hengerer, R. Resonant photoemission of anatase TiO2 (101) and (001) single crystals. Phys. Rev. B 2003, 67, 035110. [Google Scholar] [CrossRef]
- Thomas, A.G.; Flavell, W.R.; Mallick, A.K.; Kumarasinghe, A.R.; Tsoutsou, D.; Khan, N.; Chatwin, C.; Rayner, S.; Smith, G.C.; Stockbauer, R.L.; et al. Comparison of the electronic structure of anatase and rutile TiO2 single-crystal surfaces using resonant photoemission and X-ray absorption spectroscopy. Phys. Rev. B 2007, 75, 035105. [Google Scholar] [CrossRef]
- Pfeifer, V.; Erhart, P.; Li, S.; Rachut, K.; Morasch, J.; Brötz, J.; Reckers, P.; Mayer, T.; Rühle, S.; Zaban, A.; et al. Energy Band Alignment Between Anatase and Rutile TiO2. J. Phys. Chem. Lett. 2013, 4, 4182–4187. [Google Scholar] [CrossRef]
- Schwanitz, K.; Weiler, U.; Hunger, R.; Mayer, T.; Jaegermann, W. Synchrotron-induced photoelectron spectroscopy of the dye-sensitized nanocrystalline TiO2/electrolyte interface: Band gap states and their interaction with dye and solvent molecules. J. Phys. Chem. C 2007, 111, 849–854. [Google Scholar] [CrossRef]
- Liu, G.; Schulmeyer, T.; Thissen, A.; Klein, A.; Jaegermann, W. In situ preparation and interface characterization of TiO2/Cu2S heterointerface. Appl. Phys. Lett. 2003, 82, 2269–2271. [Google Scholar] [CrossRef]
- Henrich, V.E.; Dresselhaus, G.; Zeiger, H.J. Observation of Two-Dimensional Phases Associated with Defect States on the Surface of TiO2. Phys. Rev. Lett. 1976, 36, 1335–1339. [Google Scholar] [CrossRef]
- Thompson, T.L.; Diwald, O.; Yates, J.T. CO2 as a Probe for Monitoring the Surface Defects on TiO2(110)Temperature-Programmed Desorption. J. Phys. Chem. B 2003, 107, 11700–11704. [Google Scholar] [CrossRef]
- Borodin, A.; Reichling, M. Characterizing TiO2(110) surface states by their work function. Phys. Chem. Chem. Phys. 2011, 13, 15442–15447. [Google Scholar] [CrossRef] [PubMed]
- Klein, A.; Körber, C.; Wachau, A.; Säuberlich, F.; Gassenbauer, Y.; Schafranek, R.; Harvey, S.P.; Mason, T.O. Surface Potentials of Magnetron Sputtered Transparent Conducting Oxides. Thin Solid Films 2009, 518, 1197–1203. [Google Scholar] [CrossRef]
- Goniakowski, J.; Finocchi, F.; Noguera, C. Polarity of oxide surfaces and nanostructures. Rep. Prog. Phys. 2008, 71, 016501. [Google Scholar] [CrossRef]
- Ishii, H.; Sugiyama, K.; Ito, E.; Seki, K. Energy Level Alignment and Interfacial Electronic Structures at Organic/Metal and Organic/Organic Interfaces. Adv. Mater. 1999, 11, 605–625. [Google Scholar] [CrossRef]
- Batzill, M.; Diebold, U. The surface and materials science of tin oxide. Prog. Surf. Sci. 2005, 79, 47–154. [Google Scholar] [CrossRef]
- Klein, A.; Körber, C.; Wachau, A.; Säuberlich, F.; Gassenbauer, Y.; Harvey, S.P.; Proffit, D.E.; Mason, T.O. Transparent Conducting Oxides for Photovoltaics: Manipulation of Fermi Level, Work Function, and Energy Band Alignment. Materials 2010, 3, 4892–4914. [Google Scholar] [CrossRef] [PubMed]
- Hohmann, M.V.; Ágoston, P.; Wachau, A.; Bayer, T.J.M.; Brötz, J.; Albe, K.; Klein, A. Orientation Dependent Ionization Potential of In2O3: A Natural Source for Inhomogeneous Barrier Formation at Electrode Interfaces in Organic Electronics. J. Phys. Condens. Matter 2011, 23, 334203. [Google Scholar] [CrossRef] [PubMed]
- Wardenga, H.; Klein, A. Surface Potentials of (111), (110) and (100) oriented CeO2-x thin films. Appl. Surf. Sci. 2016, 377, 1–8. [Google Scholar] [CrossRef]
- Morgan, B.J.; Watson, G.W. A Density Functional Theory + U Study of Oxygen Vacancy Formation at the (110), (100), (101), and (001) Surfaces of Rutile TiO2. J. Phys. Chem. C 2009, 113, 7322–7328. [Google Scholar] [CrossRef]
- Cheng, H.; Selloni, A. Surface and subsurface oxygen vacancies in anatase TiO2 and differences with rutile. Phys. Rev. B 2009, 79, 092101. [Google Scholar] [CrossRef]
- Li, H.; Guo, Y.; Robertson, J. Calculation of TiO2 Surface and Subsurface Oxygen Vacancy by the Screened Exchange Functional. J. Phys. Chem. C 2015, 119, 18160–18166. [Google Scholar] [CrossRef]
- He, Y.; Dulub, O.; Cheng, H.; Selloni, A.; Diebold, U. Evidence for the Predominance of Subsurface Defects on Reduced Anatase TiO2(101). Phys. Rev. Lett. 2009, 102, 106105. [Google Scholar] [CrossRef] [PubMed]
- Bahnemann, D. Photocatalytic water treatment: solar energy applications. Solar Energy 2004, 77, 445–459. [Google Scholar] [CrossRef]
- Fujishima, A.; Zhang, X.; Tryk, D.A. TiO2 photocatalysis and related surface phenomena. Surf. Sci. Rep. 2008, 63, 515–582. [Google Scholar] [CrossRef]
- De Angelis, F.; Valentin, C.D.; Fantacci, S.; Vittadini, A.; Selloni, A. Theoretical Studies on Anatase and Less Common TiO2 Phases: Bulk, Surfaces, and Nanomaterials. Chem. Rev. 2014, 114, 9708–9753. [Google Scholar] [CrossRef] [PubMed]
- Bourikas, K.; Kordulis, C.; Lycourghiotis, A. Titanium Dioxide (Anatase and Rutile): Surface Chemistry, Liquid-Solid Interface Chemistry, and Scientific Synthesis of Supported Catalysts. Chem. Rev. 2014, 114, 9754–9823. [Google Scholar] [CrossRef] [PubMed]
- Pang, C.L.; Lindsay, R.; Thornton, G. Chemical reactions on rutile TiO2(110). Chem. Soc. Rev. 2008, 37, 2328–2353. [Google Scholar] [CrossRef] [PubMed]
- Hussain, H.; Tocci, G.; Woolcot, T.; Torrelles, X.; Pang, C.L.; Humphrey, D.S.; Yim, C.M.; Grinter, D.C.; Cabailh, G.; Bikondoa, O.; et al. Structure of a model TiO2 photocatalytic interface. Nat. Mater. 2017, 16, 461. [Google Scholar] [CrossRef] [PubMed]
- Vittadini, A.; Selloni, A.; Rotzinger, F.P.; Grätzel, M. Structure and Energetics of Water Adsorbed at TiO2 Anatase (101) and (001) Surfaces. Phys. Rev. Lett. 1998, 81, 2954–2957. [Google Scholar] [CrossRef]
- Aschauer, U.; He, Y.; Cheng, H.; Li, S.C.; Diebold, U.; Selloni, A. Influence of Subsurface Defects on the Surface Reactivity of TiO2: Water on Anatase (101). J. Phys. Chem. C 2010, 114, 1278–1284. [Google Scholar] [CrossRef]
- Li, Y.; Gao, Y. Interplay between Water and TiO2 Anatase (101) Surface with Subsurface Oxygen Vacancy. Phys. Rev. Lett. 2014, 112, 206101. [Google Scholar] [CrossRef]
- Jackman, M.J.; Thomas, A.G.; Muryn, C. Photoelectron Spectroscopy Study of Stoichiometric and Reduced Anatase TiO2(101) Surfaces: The Effect of Subsurface Defects on Water Adsorption at Near-Ambient Pressures. J. Phys. Chem. C 2015, 119, 13682–13690. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, H.; Andino, J.M.; Li, Y. Photocatalytic CO2 Reduction with H2O on TiO2 Nanocrystals: Comparison of Anatase, Rutile, and Brookite Polymorphs and Exploration of Surface Chemistry. ACS Catal. 2012, 2, 1817–1828. [Google Scholar] [CrossRef]
- Duncan, D.; Allegretti, F.; Woodruff, D. Water does partially dissociate on the perfect TiO2 (110) surface: A quantitative structure determination. Phys. Rev. B 2012, 86, 045411. [Google Scholar] [CrossRef]
- Walle, L.E.; Borg, A.; Uvdal, P.; Sandell, A. Experimental evidence for mixed dissociative and molecular adsorption of water on a rutile TiO2 (110) surface without oxygen vacancies. Phys. Rev. B 2009, 80, 235436. [Google Scholar] [CrossRef]
- Mu, R.; Zhao, Z.J.; Dohnálek, Z.; Gong, J. Structural motifs of water on metal oxide surfaces. Chem. Soc. Rev. 2017, 46, 1785–1806. [Google Scholar] [CrossRef] [PubMed]
- Patrick, C.E.; Giustino, F. Structure of a water monolayer on the anatase TiO2 (101) surface. Phys. Rev. Appl. 2014, 2, 014001. [Google Scholar] [CrossRef]
- Henrion, O.; Klein, A.; Pettenkofer, C.; Jaegermann, W. Low temperature adsorption of water on cleaved GaAs(110) surfaces. Surf. Sci. Lett. 1996, 366, L685. [Google Scholar] [CrossRef]
- Klein, A. Interface Properties of Dielectric Oxides. J. Am. Ceram. Soc. 2016, 99, 369–387. [Google Scholar] [CrossRef]
- Wendt, S.; Sprunger, P.T.; Lira, E.; Madsen, G.K.H.; Li, Z.; Hansen, J.O.; Matthiesen, J.; Blekinge-Rasmussen, A.; Lægsgaard, E.; Hammer, B.; et al. The Role of Interstitial Sites in the Ti3d Defect State in the Band Gap of Titania. Science 2008, 320, 1755–1759. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, M.; Hebenstreit, W.; Gross, L.; Diebold, U.; Henderson, M.A.; Jennison, D.R.; Schultz, P.A.; Sears, M.P. Oxygen-induced restructuring of the TiO2(110) surface: A comprehensive study. Surf. Sci. 1999, 437, 173–190. [Google Scholar] [CrossRef]
- Wu, C.C.; Wu, C.I.; Sturm, J.C.; Kahn, A. Surface modification of indium tin oxide by plasma treatment: An effective method to improve the efficiency, brightness, and reliability of organic light emitting devices. Appl. Phys. Lett. 1997, 70, 1348. [Google Scholar] [CrossRef]
- Klissurski, D.; Hadjiivanov, K.; Kantcheva, M.; Gyurova, L. Study of peroxide-modified titanium dioxide (anatase). J. Chem. Soc. Faraday Trans. 1990, 86, 385–388. [Google Scholar] [CrossRef]
- Iwamoto, M.; Yoda, Y.; Yamazoe, N.; Seiyama, T. Study of metal oxide catalysts by temperature programmed desorption. 4. Oxygen adsorption on various metal oxides. J. Phys. Chem. 1978, 82, 2564–2570. [Google Scholar] [CrossRef]
- Bayer, T.J.M.; Wachau, A.; Fuchs, A.; Deuermeier, J.; Klein, A. Atomic layer deposition of Al2O3 onto Sn-doped In2O3: Absence of self-limited adsorption during initial growth by oxygen diffusion from the substrate and band offset modification by Fermi level pinning in Al2O3. Chem. Mater. 2012, 24, 4503–4510. [Google Scholar] [CrossRef]
- Klein, A. Transparent Conducting Oxides: Electronic Structure - Property Relationship from Photoelectron Spectroscopy with in-situ Sample Preparation. J. Am. Ceram. Soc. 2013, 96, 331–345. [Google Scholar] [CrossRef]
- Idriss, H.; Barteau, M.A. Characterization of TiO2 surfaces active for novel organic syntheses. Catal. Lett. 1994, 26, 123–139. [Google Scholar] [CrossRef]
- Moulder, J.F.; Stickle, W.F.; Sobol, P.E.; Bomben, K.D. Handbook of X-ray Photoelectron Spectroscopy; Physical Electronics, Inc.: Eden Prairie, MN, USA, 1995. [Google Scholar]
- Yesodharan, E.; Grätzel, M. Photodecomposition of Liquid Water with TiO2? Supported Noble Metal Clusters. Helv. Chim. Acta 1983, 66, 2145–2153. [Google Scholar] [CrossRef]
- Kodaira, S.; Sakisaka, Y.; Maruyama, T.; Haruyama, Y.; Aiura, Y.; Kato, H. Angle-resolved photoemission study of an in-gap state in TiO2. Solid State Commun. 1994, 89, 9–12. [Google Scholar] [CrossRef]
- Finazzi, E.; Valentin, C.D.; Pacchioni, G.; Selloni, A. Excess electron states in reduced bulk anatase TiO2: Comparison of standard GGA, GGA+U, and hybrid DFT calculations. J. Chem. Phys. 2008, 129, 154113. [Google Scholar] [CrossRef] [PubMed]
- Ohno, T.; Sarukawa, K.; Matsumura, M. Crystal faces of rutile and anatase TiO2 particles and their roles in photocatalytic reactions. New J. Chem. 2002, 26, 1167–1170. [Google Scholar] [CrossRef]
- Yu, J.; Low, J.; Xiao, W.; Zhou, P.; Jaroniec, M. Enhanced Photocatalytic CO2-Reduction Activity of Anatase TiO2 by Coexposed 001 and 101 Facets. J. Am. Chem. Soc. 2014, 136, 8839–8842. [Google Scholar] [CrossRef] [PubMed]
- Dette, C.; Pérez-Osorio, M.A.; Kley, C.S.; Punke, P.; Patrick, C.E.; Jacobson, P.; Giustino, F.; Jung, S.J.; Kern, K. TiO2 Anatase with a Bandgap in the Visible Region. Nano Lett. 2014, 14, 6533–6538. [Google Scholar] [CrossRef] [PubMed]
- King, P.D.C.; Veal, T.D.; Fuchs, F.; Wang, C.Y.; Payne, D.J.; Bourlange, A.; Zhang, H.; Bell, G.R.; Cimalla, V.; Ambacher, O.; et al. Band gap, electronic structure, and surface electron accumulation of cubic and rhombohedral In2O3. Phys. Rev. B 2009, 79, 205211. [Google Scholar] [CrossRef]
- Berthold, T.; Rombach, J.; Stauden, T.; Polyakov, V.; Cimalla, V.; Krischok, S.; Bierwagen, O.; Himmerlich, M. Consequences of plasma oxidation and vacuum annealing on the chemical properties and electron accumulation of In2O3 surfaces. J. Appl. Phys. 2016, 120, 245301. [Google Scholar] [CrossRef]
- Vasheghani Farahani, S.K.; Veal, T.D.; Mudd, J.J.; Scanlon, D.O.; Watson, G.W.; Bierwagen, O.; White, M.E.; Speck, J.S.; McConville, C.F. Valence-band density of states and surface electron accumulation in epitaxial SnO2 films. Phys. Rev. B 2014, 90, 155413. [Google Scholar] [CrossRef]
- Körber, C.; Ágoston, P.; Klein, A. Surface and Bulk Properties of Sputter Deposited Intrinsic and Doped SnO2 Thin Films. Sens. Actuators B 2009, 139, 665–672. [Google Scholar] [CrossRef]
- Rachut, K.; Körber, C.; Brötz, J.; Klein, A. Growth and Surface Properties of Epitaxial SnO2. Phys. Stat. Sol. (A) 2014, 211, 1997–2004. [Google Scholar] [CrossRef]
- Batzill, M.; Katsiev, K.; Burst, J.M.; Diebold, U.; Chaka, A.M.; Delley, B. Gas-phase-dependent properties of SnO2 (110), (100), and (101) single-crystal surfaces: Structure, composition, and electronic properties. Phys. Rev. B 2005, 72, 165414. [Google Scholar] [CrossRef]
- Cox, D.F.; Fryberger, T.B.; Semancik, S. Oxygen vacancies and defect electronic states on the SnO2(110)-1×1 surface. Phys. Rev. B 1988, 38, 2072–2083. [Google Scholar] [CrossRef]
- Ágoston, P.; Albe, K. Disordered reconstructions of the reduced SnO2-(110) surface. Surf. Sci. 2011, 605, 714–722. [Google Scholar] [CrossRef]
- Deák, P.; Aradi, B.; Frauenheim, T. Band Lineup and Charge Carrier Separation in Mixed Rutile-Anatase Systems. J. Phys. Chem. C 2011, 115, 3443–3446. [Google Scholar] [CrossRef]
- Scanlon, D.O.; Dunnill, C.W.; Buckeridge, J.; Shevlin, S.A.; Logsdail, A.J.; Woodley, S.M.; Catlow, C.R.A.; Powell, M.J.; Palgrave, R.G.; Parkin, I.P.; et al. Band alignment of rutile and anatase TiO2. Nat. Mater. 2013, 12, 798. [Google Scholar] [CrossRef] [PubMed]
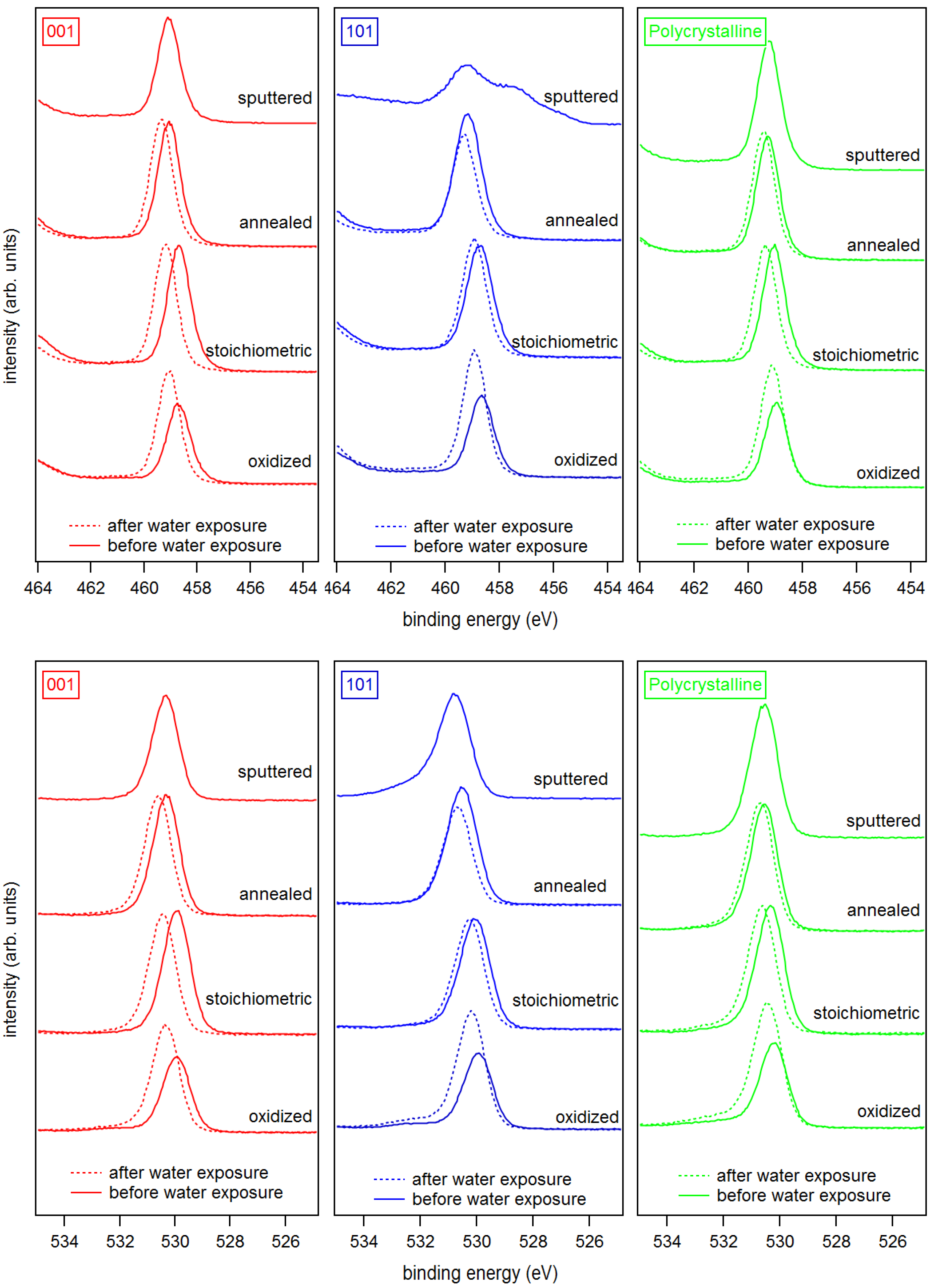
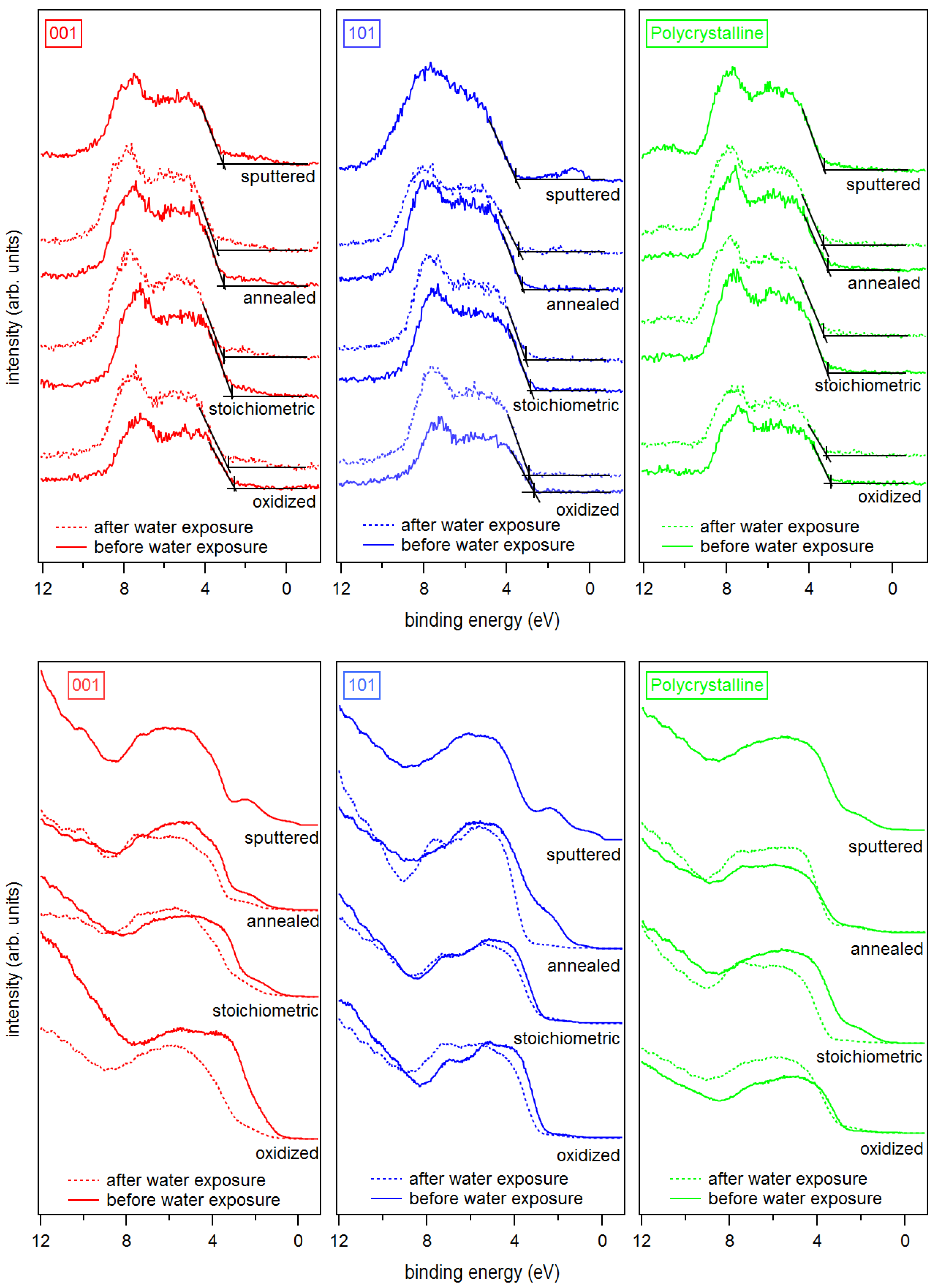
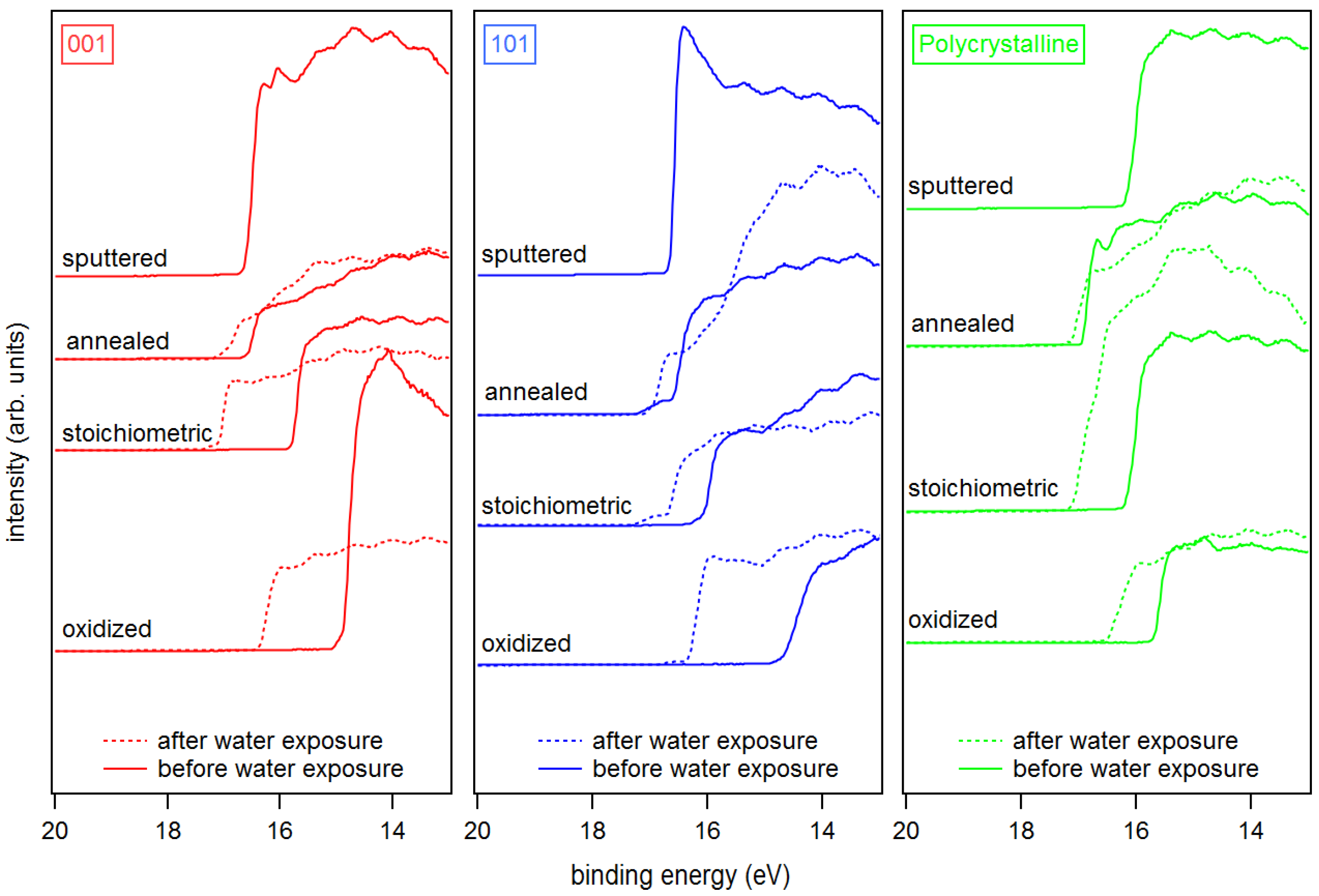
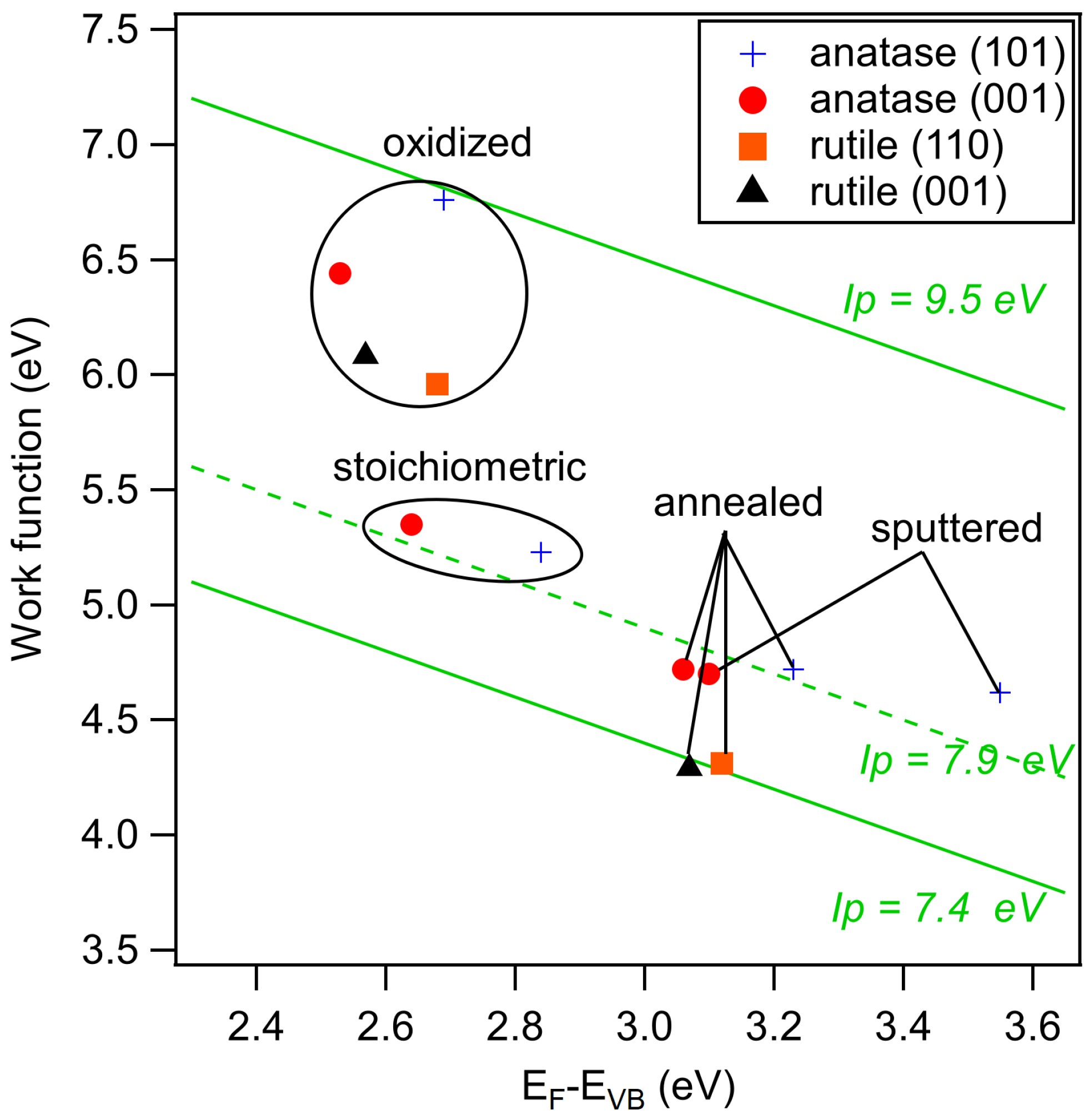
| Sputtered | Annealed | Stoichiometric | Oxidized | Ex-Situ | |
|---|---|---|---|---|---|
| Ti 2p (eV) | |||||
| a-(001) | 459.08 | 459.07 (459.36) | 458.70 (459.20) | 458.64 (459.06) | 459.27 |
| a-(101) | 459.21 | 459.17 (459.31) | 458.73 (458.93) | 458.69 (458.91) | 459.28 |
| a-poly | 459.25 | 459.28 (459.44) | 459.06 (459.37) | 458.95 (459.09) | |
| r-(001) | 459.38 | 458.78 | |||
| r-(110) | 459.35 | 458.95 | |||
| O 1s (eV) | |||||
| a-(001) | 530.35 | 530.33 (530.62) | 529.95 (530.47) | 529.93 (530.32) | 530.60 |
| a-(101) | 530.81 | 530.52 (530.68) | 530.07 (530.27) | 529.93 (530.19) | 530.62 |
| a-poly | 530.57 | 530.56 (530.71) | 530.35 (530.64) | 530.20 (530.44) | |
| r-(001) | 530.69 | 530.04 | |||
| r-(110) | 530.62 | 530.21 | |||
| (eV) | |||||
| a-(001) | 3.10 | 3.06 (3.39) | 2.64 (3.06) | 2.53 (2.87) | 3.44 |
| a-(101) | 3.55 | 3.23 (3.40) | 2.84 (3.08) | 2.69 (2.91) | 3.35 |
| a-poly | 3.23 | 3.09 (3.37) | 3.12 (3.31) | 2.94 (3.16) | |
| r-(001) | 3.07 | 2.57 | |||
| r-(110) | 3.12 | 2.68 | |||
| in (eV) | |||||
| a-(001) | 4.70 | 4.72 (4.36) | 5.35 (4.34) | 6.44 (4.97) | 3.61 |
| a-(101) | 4.62 | 4.72 (4.36) | 5.23 (4.40) | 6.76 (5.03) | 3.65 |
| a-poly | 4.51 | 4.23 (4.22) | 5.16 (4.38) | 5.62 (4.94) | |
| r-(001) | 4.29 | 6.08 | |||
| r-(110) | 4.31 | 5.96 | |||
| (eV) | |||||
| a-(001) | 7.80 | 7.78 (7.75) | 7.99 (7.40) | 8.97 (7.84) | 7.05 |
| a-(101) | 8.17 | 7.95 (7.76) | 8.07 (7.48) | 9.45 (7.94) | 7.00 |
| a-poly | 7.74 | 7.32 (7.59) | 8.28 (7.69) | 8.56 (8.10) | |
| r-(001) | 7.36 | 8.65 | |||
| r-(110) | 7.43 | 8.64 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kashiwaya, S.; Morasch, J.; Streibel, V.; Toupance, T.; Jaegermann, W.; Klein, A. The Work Function of TiO2. Surfaces 2018, 1, 73-89. https://doi.org/10.3390/surfaces1010007
Kashiwaya S, Morasch J, Streibel V, Toupance T, Jaegermann W, Klein A. The Work Function of TiO2. Surfaces. 2018; 1(1):73-89. https://doi.org/10.3390/surfaces1010007
Chicago/Turabian StyleKashiwaya, Shun, Jan Morasch, Verena Streibel, Thierry Toupance, Wolfram Jaegermann, and Andreas Klein. 2018. "The Work Function of TiO2" Surfaces 1, no. 1: 73-89. https://doi.org/10.3390/surfaces1010007
APA StyleKashiwaya, S., Morasch, J., Streibel, V., Toupance, T., Jaegermann, W., & Klein, A. (2018). The Work Function of TiO2. Surfaces, 1(1), 73-89. https://doi.org/10.3390/surfaces1010007