Determining the Thickness of Gold Leaf in Post-Byzantine Religious Panel Paintings Using Imaging μ-XRF
Abstract
1. Introduction
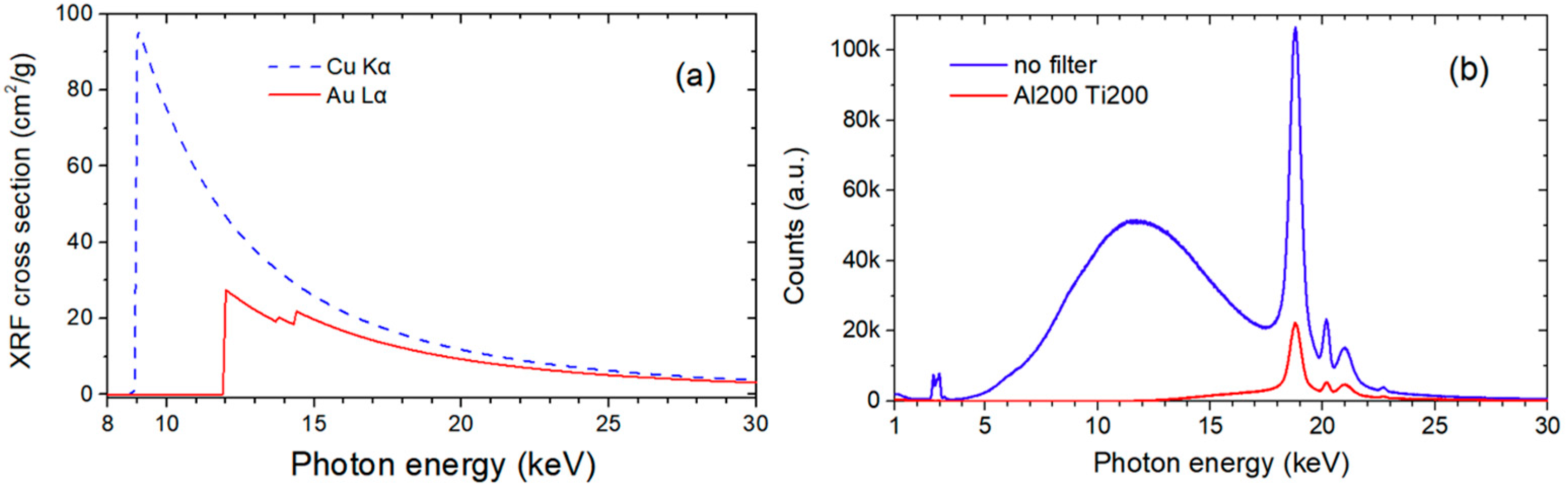
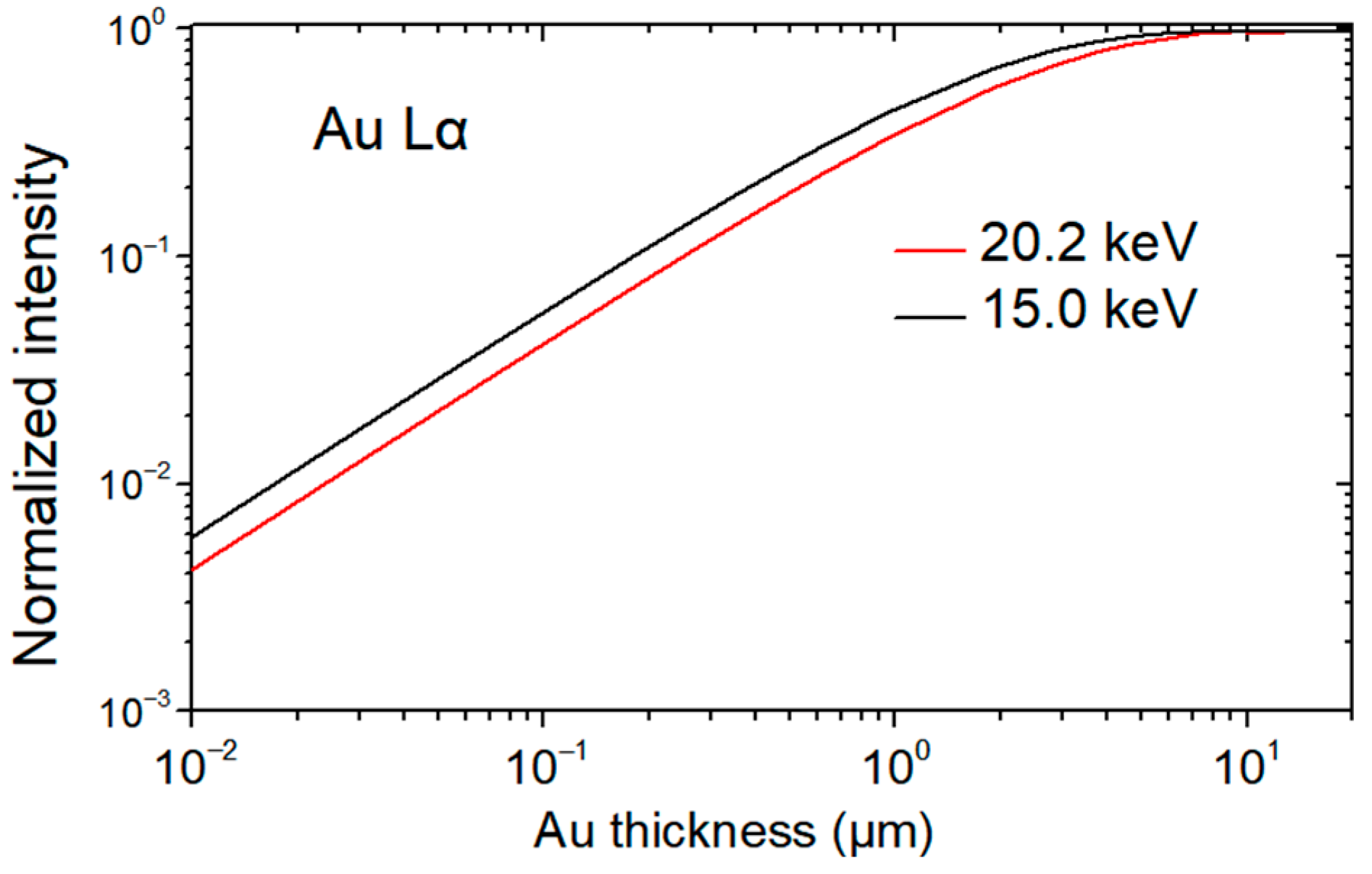
2. Theory
3. Materials and Methods
3.1. The Mock-Up
3.2. Experimental Setup
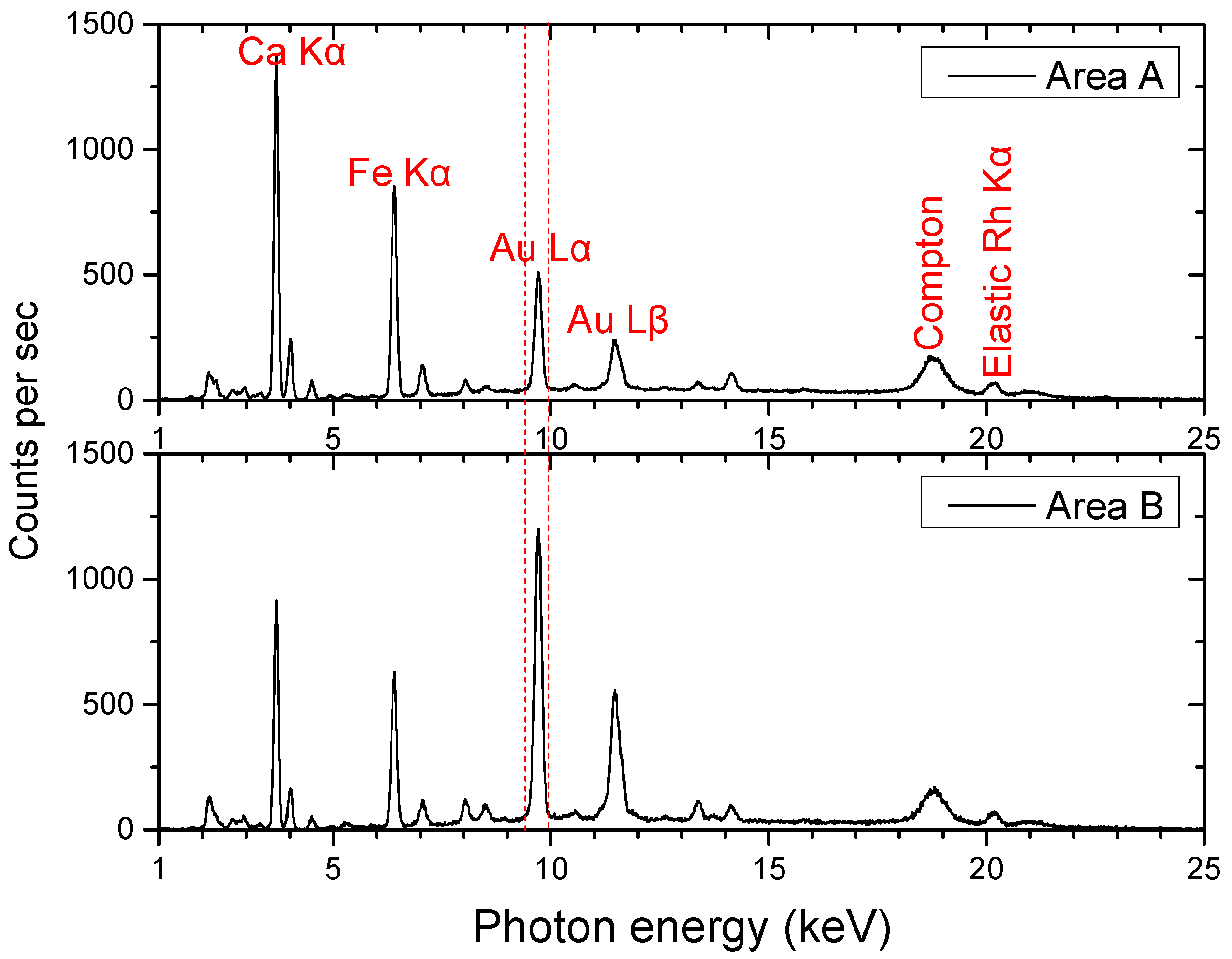
4. Results and Discussion
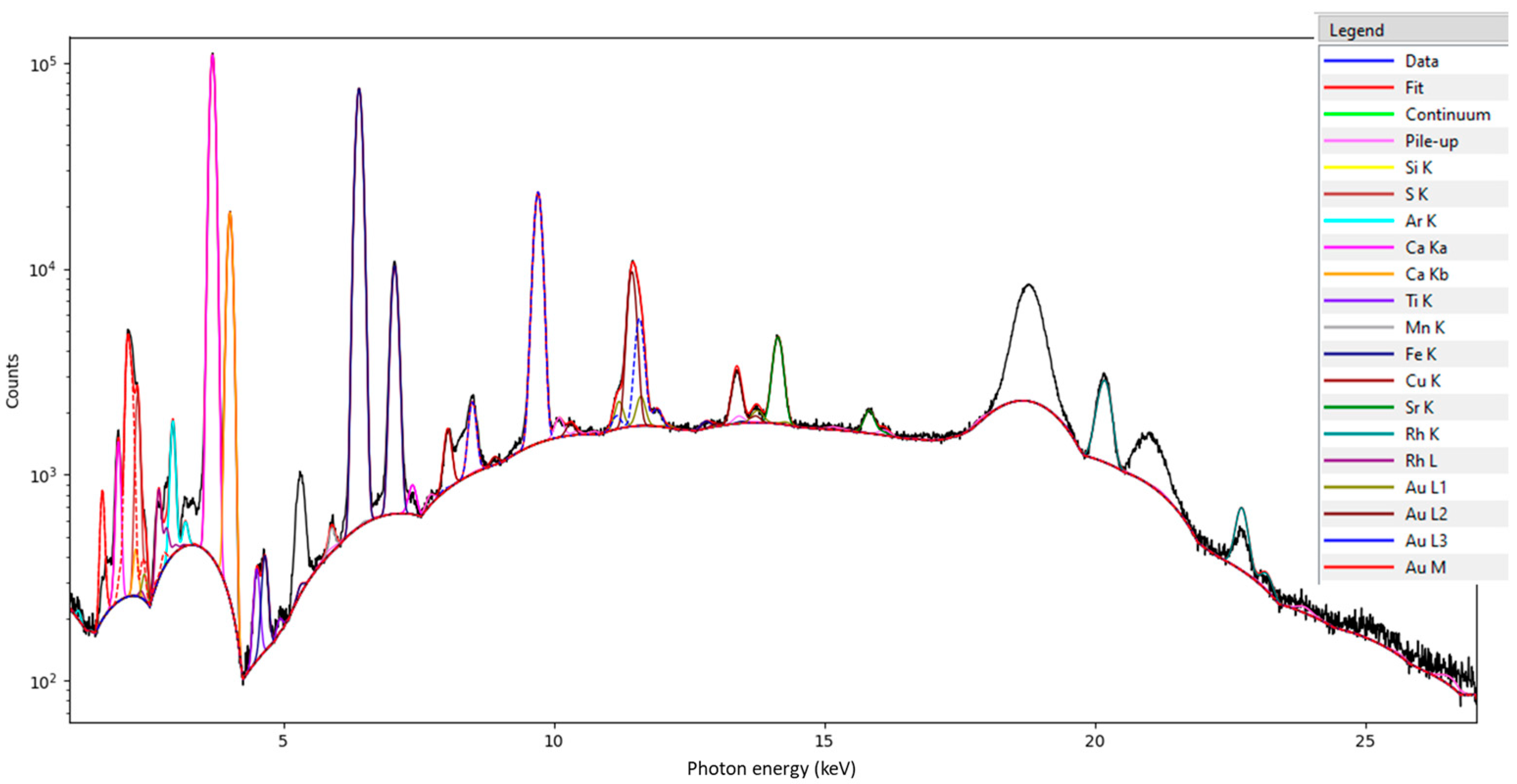
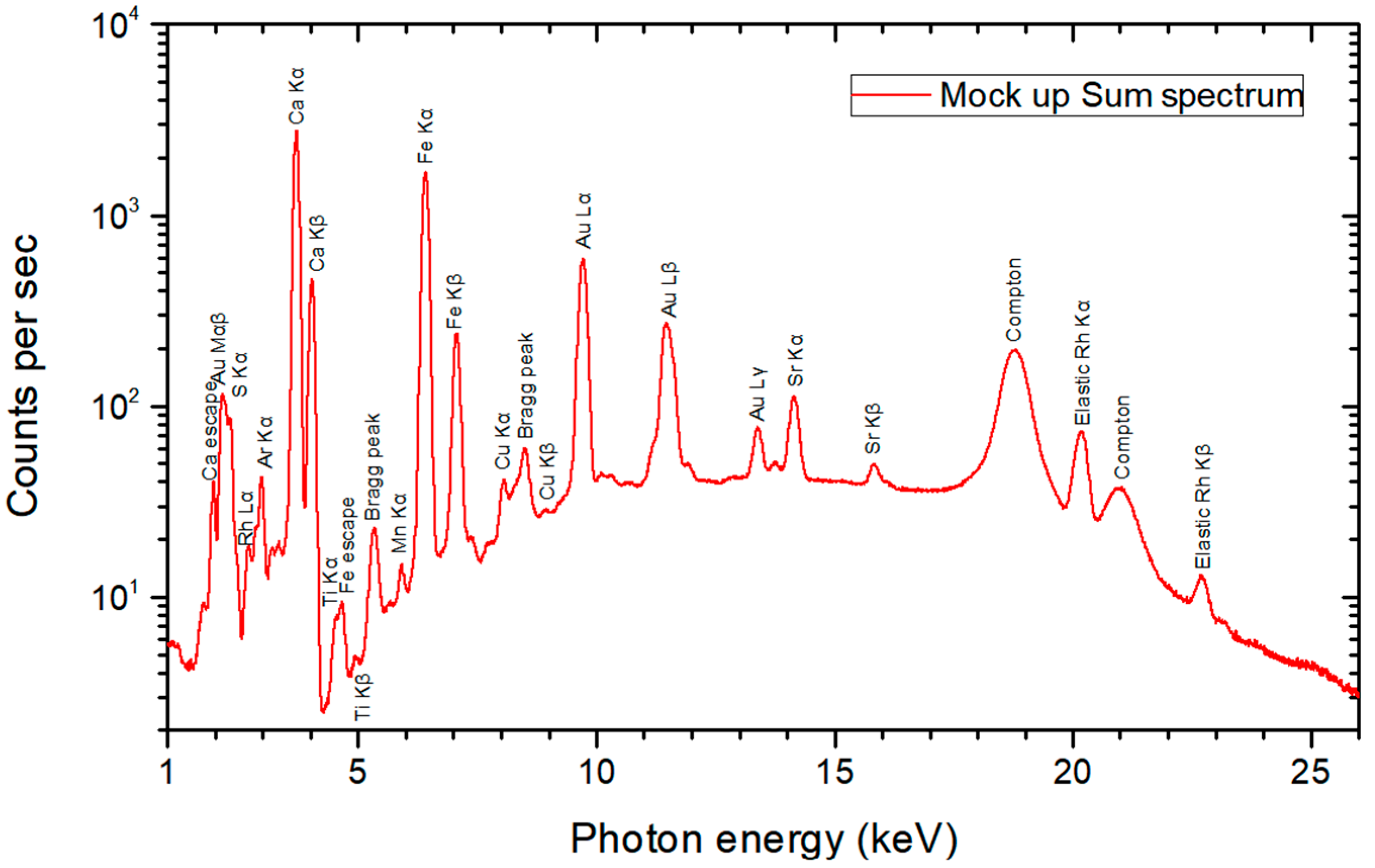
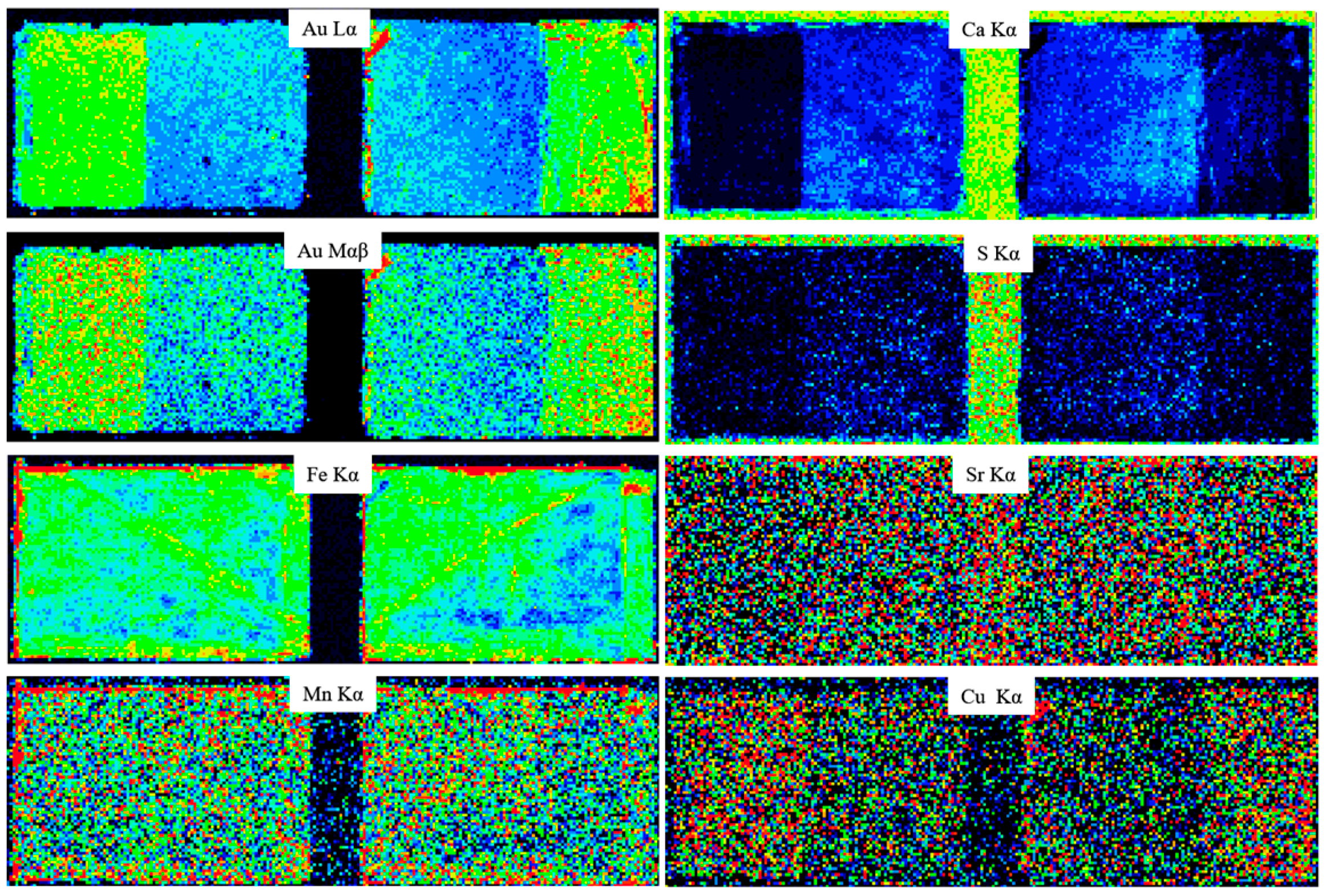
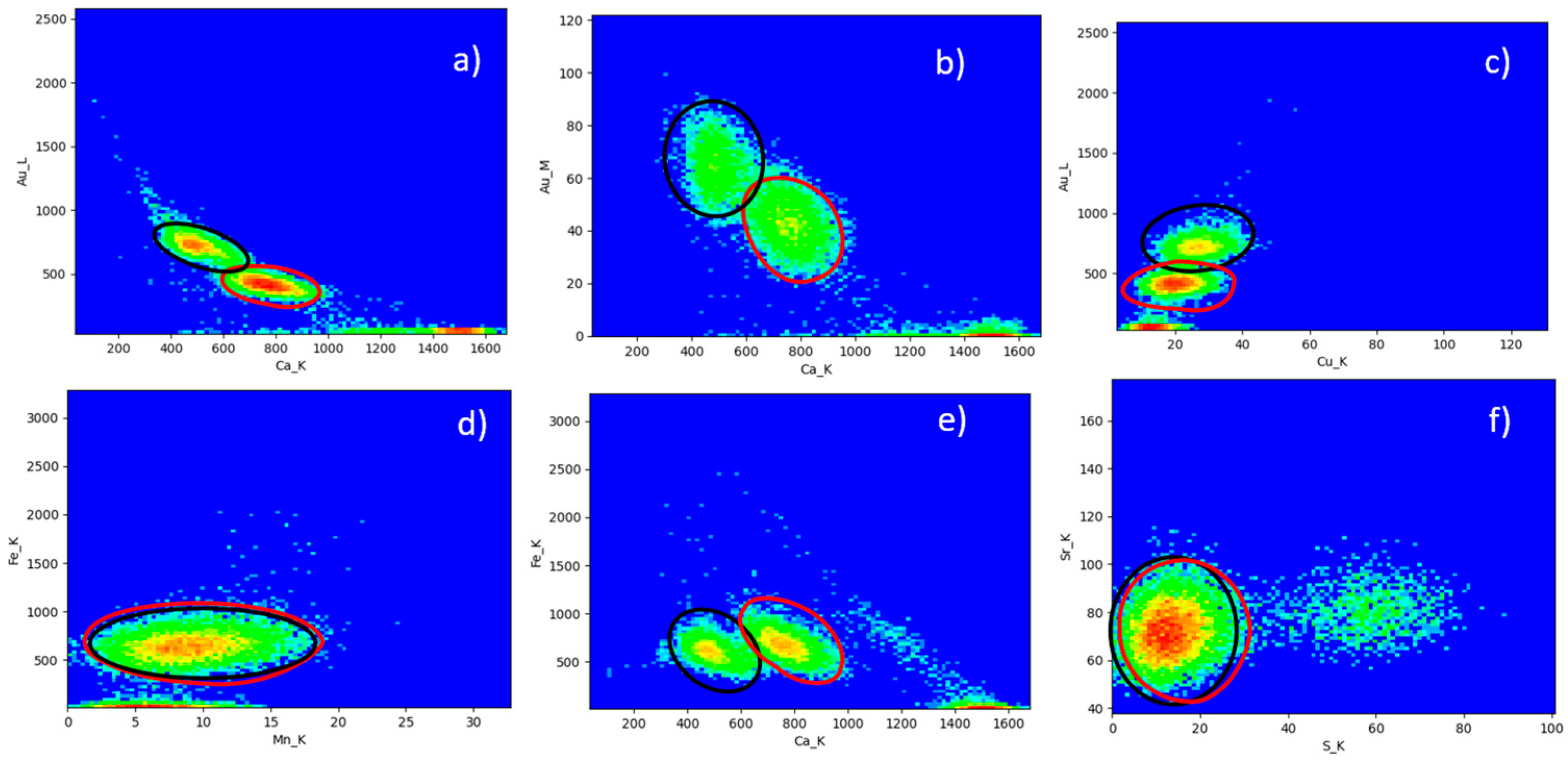
4.1. Mock-Up μ-XRF Imaging

4.2. Thickness of the Gilded Areas on the Mock-Up
4.3. The Thickness of the Gilded Areas on the “Virgin Mary, Odigitria” Icon
4.4. The Thickness of the Gilded Areas on “St John the Forerunner with Scenes from His Life” Icon
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Mantler, M.; Schreiner, M. X-ray fluorescence spectrometry in art and archaeology. X-Ray Spectrom. 2000, 29, 3–17. [Google Scholar] [CrossRef]
- Alfeld, M.; Pedroso, J.V.; van Eikema Hommes, M.; Van der Snickt, G.; Tauber, G.; Blaas, J.; Haschke, M.; Erler, K.; Dik, J.; Janssens, K. A Mobile Instrument for in Situ Scanning Macro-XRF Investigation of Historical Paintings. J. Anal. At. Spectrom. 2013, 28, 760. [Google Scholar] [CrossRef]
- Romano, F.P.; Caliri, C.; Nicotra, P.; Di Martino, S.; Pappalardo, L.; Rizzo, F.; Santos, H.C. Real-Time Elemental Imaging of Large Dimension Paintings with a Novel Mobile Macro X-Ray Fluorescence (MA-XRF) Scanning Technique. J. Anal. At. Spectrom. 2017, 32, 773–781. [Google Scholar] [CrossRef]
- Alfeld, M. MA-XRF for Historical Paintings: State of the Art and Perspective. Microsc. Microanal. 2020, 26, 72–75. [Google Scholar] [CrossRef]
- Mazzinghi, A.; Ruberto, C.; Castelli, L.; Czelusniak, C.; Giuntini, L.; Mandò, P.A.; Taccetti, F. Ma-Xrf for the Characterisation of the Painting Materials and Technique of the Entombment of Christ by Rogier van Der Weyden. Appl. Sci. 2021, 11, 6151. [Google Scholar] [CrossRef]
- dos Santos, H.C.; Caliri, C.; Pappalardo, L.; Catalano, R.; Orlando, A.; Rizzo, F.; Romano, F.P. Real-Time MA-XRF Imaging Spectroscopy of the Virgin with the Child Painted by Antonello de Saliba in 1497. Microchem. J. 2018, 140, 96–104. [Google Scholar] [CrossRef]
- Walczak, M.; Tarsińska-Petruk, D.; Płotek, M.; Goryl, M.; Kruk, M.P.; Tarsińska-Petruk, D.; Płotek, M.; Goryl, M.; Kruk, M.P.; Tarsińska-Petruk, D.; et al. MA-XRF Study of 15th–17th Century Icons from the Collection of the National Museum in Krakow, Poland. X-Ray Spectrom. 2019, 48, 303–310. [Google Scholar] [CrossRef]
- Mastrotheodoros, G.P.; Asvestas, A.; Gerodimos, T.; Tzima, A.; Papadopoulou, V.; Anagnostopoulos, D.F. MA-XRF Investigation of a 17th Century Icon by the Renowned Painter Theodoros Poulakis. J. Archaeol. Sci. Rep. 2024, 53, 104313. [Google Scholar] [CrossRef]
- Nikolaidou, N.V.; Asvestas, A.; Kaminari, A.A.; Panou, T.; Sampatakos, A.; Anagnostopoulos, D.F.; Alexopoulou, A.G.; Mastrotheodoros, G.P. Seeking the Unseen: A Multimodal Non-Invasive Investigation of a Post-Byzantine Overpainted Icon. Heritage 2025, 8, 377. [Google Scholar] [CrossRef]
- Gerodimos, T.; Asvestas, A.; Mastrotheodoros, G.P.; Chantas, G.; Liougos, I.; Likas, A.; Anagnostopoulos, D.F. Scanning X-ray Fluorescence Data Analysis for the Identification of Byzantine Icons’ Materials, Techniques, and State of Preservation: A Case Study. J. Imaging 2022, 8, 147. [Google Scholar] [CrossRef]
- Broecke, L. Cennino Cennini’s il Libro Dell’arte: A New English Language Translation and Commentary with Italian Transcription, 1st ed.; Archetype Publisher: London, UK, 2015. [Google Scholar]
- Atrei, A.; Scala, A.; Giamello, M.; Uva, M.; Pulselli, R.M.; Marchettini, N. Chemical Composition and Micro Morphology of Golden Laminae in the Wall Painting. “La Maestà” by Simone Martini: A Study by Optical Microscopy, XRD, FESEM-EDS and ToF-SIMS. Appl. Sci. 2019, 9, 3452. [Google Scholar] [CrossRef]
- Osticioli, I.; Capozzoli, L.; Salvadori, B.; Banchelli, M.; Lavacchi, A.; Matteini, P.; Siano, S.; Gallo, L. The “oro di metà” Gilding in the Fifteenth-Century: A Multi-Analytical Investigation. Heritage 2019, 2, 1166–1175. [Google Scholar] [CrossRef]
- Mastrotheodoros, G.P.; Anagnostopoulos, D.F.; Beltsios, K.G.; Filippaki, E.; Bassiakos, Y. Glittering on the Wall: Gildings on Greek Post-Byzantine Wall Paintings. In Transdisciplinary Multispectral Modeling and Cooperation for the Preservation of Cultural Heritage; Communications in Computer and Information Science, Volume 962; Springer: Cham, Switzerland, 2019; pp. 397–404. [Google Scholar] [CrossRef]
- Wu, Q.; Döbeli, M.; Lombardo, T.; Schmidt-Ott, K.; Watts, B.; Nolting, F.; Ganz, D. Does Substrate Colour Affect the Visual Appearance of Gilded Medieval Sculptures? Part II: SEM–EDX Observations on Gold Leaf Samples Taken from Medieval Wooden Sculptures. Herit. Sci. 2020, 8, 119. [Google Scholar] [CrossRef]
- Fourdrin, C.; Pagès Camagna, S.; Pacheco, C.; Radepont, M.; Lemasson, Q.; Moignard, B.; Pichon, L.; Bourgeois, B.; Jeammet, V. Characterization of Gold Leaves on Greek Terracotta Figurines: A PIXE-RBS Study. Microchem. J. 2016, 126, 446–453. [Google Scholar] [CrossRef]
- Cesareo, R.; Castellano, A.; Buccolieri, G.; Quarta, S.; Marabelli, M. Giotto in the Chapel of the Scrovegni: EDXRF Analysis of the Golden Haloes with Portable Equipment. X-Ray Spectrom. 2004, 33, 289–293. [Google Scholar] [CrossRef]
- Karydas, A.G.; Brekoulaki, H.; Bourgeois, B.; Jockey, P. In-situ X-Ray Fluorescence analysis of raw pigments and traces of polychromy on Hellenistic sculpture at the archaeological museum of Delos, ASMOSIA VII. In Proceedings of the 7th International Conference of Association for the Study of Marble and Other Stones in Antiquity, Thassos, Greece, 15–20 September 2003; pp. 811–829. [Google Scholar]
- Theophilus. In On Divers Arts; Hawthorne, J.G.; Smith, C.S., Translators; Dover: New York, NY, USA, 1979. [Google Scholar]
- Mastrotheodoros, G.P.; Beltsios, K.G.; Bassiakos, Y.; Papadopoulou, V. On the Metal-Leaf Decorations of Post-Byzantine Greek Icons. Archaeometry 2018, 60, 269–289. [Google Scholar] [CrossRef]
- Pessanha, S.; Queralt, I.; Carvalho, M.L.; Sampaio, J.M. Determination of gold leaf thickness using X-ray fluorescence spectrometry: Accuracy comparison using analytical methodology and Monte Carlo simulations. Appl. Radiat. Isot. 2019, 152, 6–10. [Google Scholar] [CrossRef]
- Cesareo, R.; Lins, S.A.B.; Ridolfi, S.; Brunetti, A. Thin Thickness Gilding Determined by X-Rays Ratios from EDXRF-Spectra. X-Ray Spectrom. 2022, 51, 170–177. [Google Scholar] [CrossRef]
- Pessanha, S.; Manso, M.; Antunes, V.; Carvalho, M.L.; Sampaio, J.M. Monte Carlo Simulation of Portable XRF Setup: Non-Invasive Determination of Gold Leaf Thickness in Indo-Portuguese Panel Paintings. Spectrochim. Acta—Part B At. Spectrosc. 2019, 156, 1–6. [Google Scholar] [CrossRef]
- Lins, S.A.B.; Gigante, G.E.; Cesareo, R.; Ridolfi, S.; Brunetti, A. Testing the Accuracy of the Calculation of Gold Leaf Thickness by MC Simulations and MA-XRF Scanning. Appl. Sci. 2020, 10, 3582. [Google Scholar] [CrossRef]
- Mantler, M. Quantitative Analysis. In Handbook of Practical X-Ray Fluorescence Analysis; Beckhoff, B., Kanngießer, B., Langhoff, N., Wedell, R., Wolff, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 317–321. [Google Scholar]
- Schoonjans, T.; Brunetti, A.; Golosio, B.; Del Rio, M.S.; Solé, V.A.; Ferrero, C.; Vincze, L. The xraylib library for X-ray-matter interactions. Recent developments, Spectrochim. Acta—Part B At. Spectrosc. 2011, 66, 776–784. [Google Scholar] [CrossRef]
- Dionysios of Fourna. In Ερμηνεία της ζωγραφικής Τέχνης [Hermeneia of the Art of Painting]; Spanos: Athens, Greece, 1997.
- Mactaggart, P.; Mactaggart, A. Practical Gilding; Archetype: London, UK, 2002. [Google Scholar]
- Solé, V.A.; Papillon, E.; Cotte, M.; Walter, P.; Susini, J. A multiplatform code for the analysis of energy-dispersive X-ray fluorescence spectra, Spectrochim. Acta Part B At. Spectrosc. 2007, 62, 63–68. [Google Scholar] [CrossRef]
- Franceschi, E.; Locardi, F. Strontium, a new marker of the origin of gypsum in cultural heritage? J. Cult. Herit. 2014, 15, 522–527. [Google Scholar] [CrossRef]
- X-ray Interactions with Matter, Center for X-Ray Optics at Lawrence Berkeley National Laboratory. Available online: https://henke.lbl.gov/optical_constants/ (accessed on 15 July 2025).
- Gerodimos, T.; Georvasilis, I.; Asvestas, A.; Mastrotheodoros, G.P.; Likas, A.; Anagnostopoulos, D.F. MA-XRF Datasets Analysis Based on Convolutional Neural Network: A Case Study on Religious Panel Paintings. Chemom. Intell. Lab. Syst. 2024, 250, 105138. [Google Scholar] [CrossRef]
- MICROMATTER, Technologies Inc. Available online: https://www.micromatter.com/XRFCalibrationStandards.aspx (accessed on 15 July 2025).
- Brunetti, A.; Golosio, B.; Schoonjans, T.; Oliva, P. Use of Monte Carlo simulations for cultural heritage X-ray fluorescence analysis. Spectrochim. Acta Part B At. Spectrosc. 2015, 108, 15–20. [Google Scholar] [CrossRef]



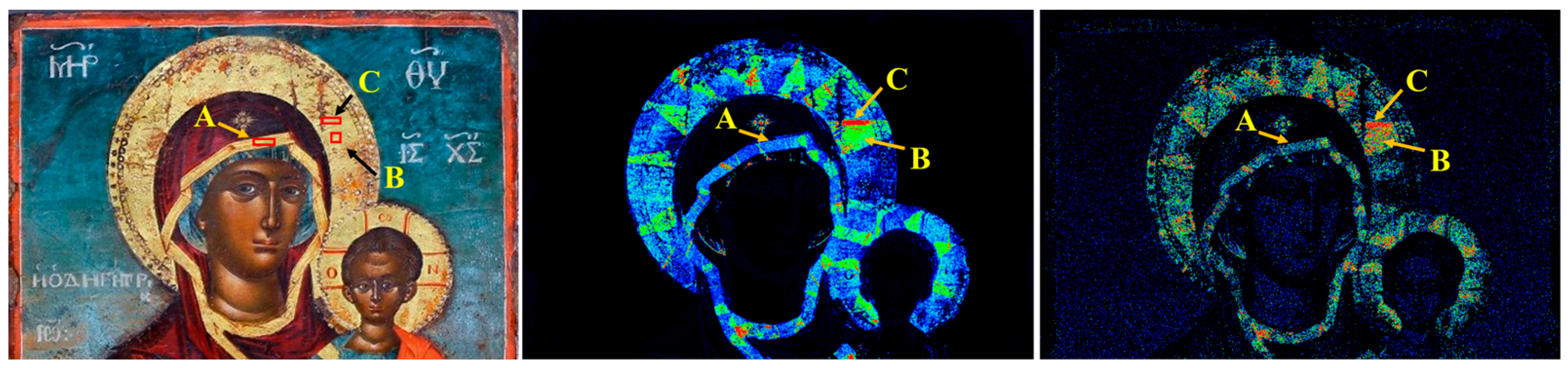
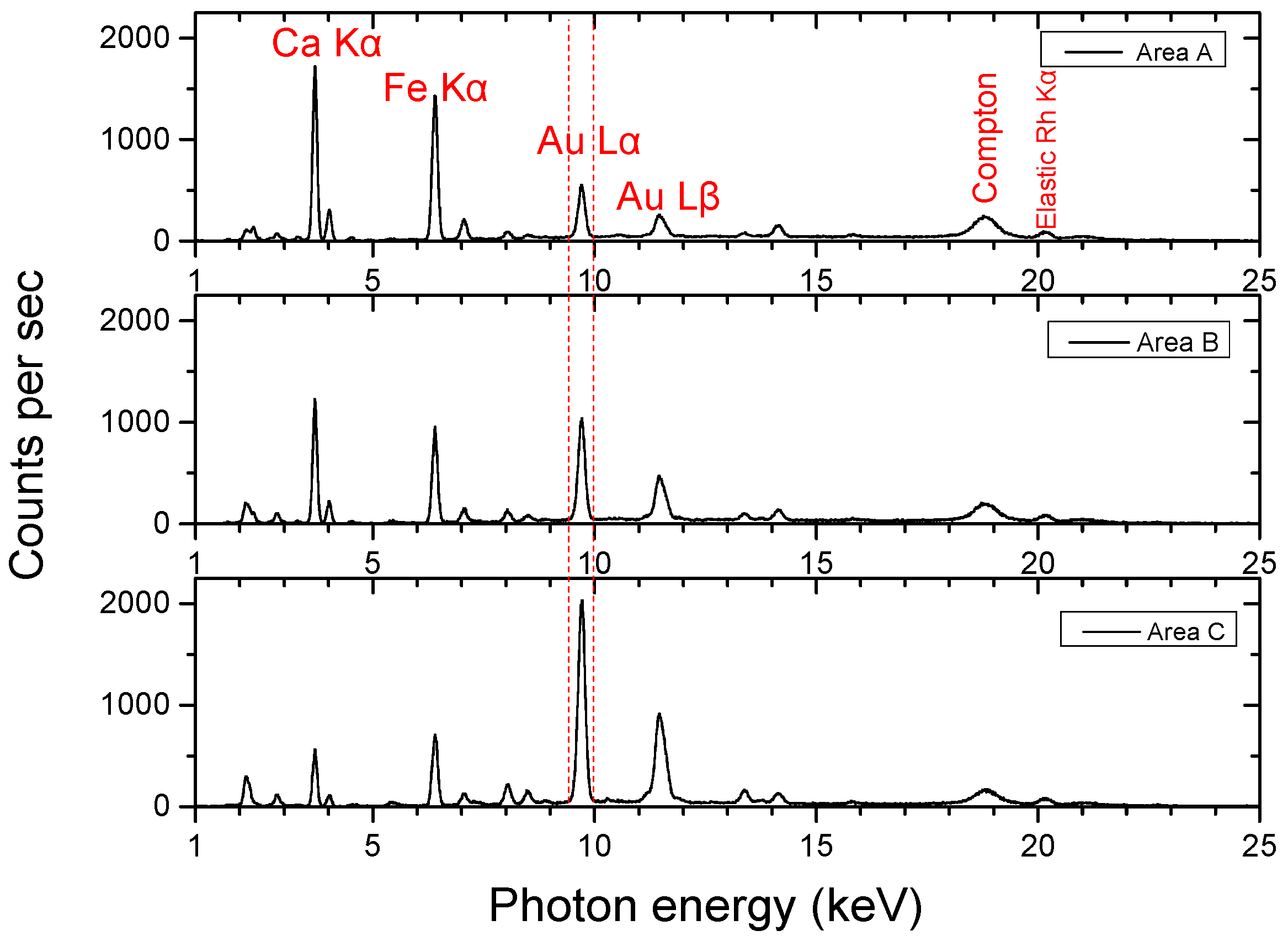

| Area | Dimensions (mm2) | Number of Pixels | Live Time (s) | Lα Intensity (104 c/s) | Surface Density (μg/cm2) | Thickness (nm) |
|---|---|---|---|---|---|---|
| A | 17.0 × 21.5 | 1462 | 28.47 | 1.83 ± 0.03 | 458 ± 70 | 237 ± 36 |
| B | 22.5 × 24.0 | 2160 | 42.06 | 1.01 ± 0.02 | 253 ± 38 | 131 ± 20 |
| C | 12.5 × 13.5 | 675 | 13.17 | 1.71 ± 0.05 | 427 ± 64 | 221 ± 33 |
| D | 18.5 × 28.0 | 2027 | 40.35 | 0.91 ± 0.02 | 227 ± 34 | 117 ± 18 |
| E | 10.0 × 24.0 | 960 | 18.62 | 1.05 ± 0.03 | 263 ± 39 | 136 ± 20 |
| Area | Dimensions (mm2) | Number of Pixels | Live Time (s) | Lα Intensity (104 c/s) | Surface Density (μg/cm2) | Thickness (nm) |
|---|---|---|---|---|---|---|
| A | 8.7 × 3.0 | 290 | 2.27 | 0.95 ± 0.01 | 237 ± 36 | 123 ± 18 |
| B | 4.5 × 4.2 | 210 | 1.66 | 1.88 ± 0.01 | 470 ± 71 | 244 ± 37 |
| C | 8.4 × 1.8 | 168 | 1.28 | 3.85 ± 0.02 | 961 ± 140 | 497 ± 75 |
| Area | Dimensions (mm2) | Number of Pixels | Live Time (s) | Lα Intensity (104 c/s) | Surface Density (μg/cm2) | Thickness (nm) |
|---|---|---|---|---|---|---|
| A | 15.0 × 5.7 | 950 | 3.10 | 0.90 ± 0.01 | 226 ± 34 | 118 ± 18 |
| B | 16.8 × 2.7 | 504 | 1.60 | 2.30 ± 0.01 | 574 ± 86 | 300 ± 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patakiouta, I.V.; Asvestas, A.; Tzima, A.; Danakas, S.; Mastrotheodoros, G.P.; Karydas, A.G.; Anagnostopoulos, D.F. Determining the Thickness of Gold Leaf in Post-Byzantine Religious Panel Paintings Using Imaging μ-XRF. Heritage 2025, 8, 432. https://doi.org/10.3390/heritage8100432
Patakiouta IV, Asvestas A, Tzima A, Danakas S, Mastrotheodoros GP, Karydas AG, Anagnostopoulos DF. Determining the Thickness of Gold Leaf in Post-Byzantine Religious Panel Paintings Using Imaging μ-XRF. Heritage. 2025; 8(10):432. https://doi.org/10.3390/heritage8100432
Chicago/Turabian StylePatakiouta, Ioanna Vasiliki, Anastasios Asvestas, Anastasia Tzima, Sotirios Danakas, Georgios P. Mastrotheodoros, Andreas G. Karydas, and Dimitrios F. Anagnostopoulos. 2025. "Determining the Thickness of Gold Leaf in Post-Byzantine Religious Panel Paintings Using Imaging μ-XRF" Heritage 8, no. 10: 432. https://doi.org/10.3390/heritage8100432
APA StylePatakiouta, I. V., Asvestas, A., Tzima, A., Danakas, S., Mastrotheodoros, G. P., Karydas, A. G., & Anagnostopoulos, D. F. (2025). Determining the Thickness of Gold Leaf in Post-Byzantine Religious Panel Paintings Using Imaging μ-XRF. Heritage, 8(10), 432. https://doi.org/10.3390/heritage8100432