Innovative Computational Techniques for Multi-Criteria Decision Making, in the Context of Cultural Heritage Structures’ Fire Protection: Theory

Abstract

The preservation of cultural heritage structures includes, among others, an efficient fire protection design process. This engineering design process frequently generates critical decision making issues related to conflicts that involve the buildings’ authenticity preservation, the implementation of special fire protection measures and addressing the particular needs of such structures. However, conventional approaches based on prescriptive regulations are often problematic in such cases; on the contrary, Performance-Based (PB) approaches could successfully deal with such structures to deliver designs that satisfy an acceptable fire safety level, and at the same time minimize the cost and any interventions on the building’s appearance, to the extent that authenticity is a key demand. Thus, in this study the upgrade of the fire safety level of cultural heritage structures is expressed as a Multi-Criteria Decision Making (MCDM) problem. Accordingly, the Analytic Hierarchy Process (AHP) is incorporated into a new fire protection Selection and Resource (S&R) allocation model, aiming to assess both fire safety and authenticity preservation levels with reference to the protection measures selected. Furthermore, in this study two different multi-criteria optimization approaches are applied to generate optimized solutions of the fire safety upgrading scheme. In this first part of the study, the theoretical basis of the proposed S&R allocation model that relies on a MCDM problem and how to deal with is discussed, while in the second part the implementation of the proposed model is presented for two real-world test cases. More specifically, in this study the theoretical part of the multi-objective and the multi-disciplinary problems (belonging to the MCDM type of problems) is provided with respect to the problems’ description and the methods adopted for solving the corresponding problems.

1. Introduction

Fire has been the subject of continuing research, not only regarding its potential uses for technological evolution but also regarding the protection from it and the means for extinguishing it [1]. Nevertheless, fire still constitutes a significant threat for natural and built environments, especially for cultural heritage structures, which generally incorporate special characteristics and require an enhanced approach for protection. Many times in the past invaluable damages to world cultural heritage monuments were caused by fire (e.g., historic center Chiado in Lisbon, Portugal 1988; Monastery of Simonos Petra, Mount Athos, Greece 1990; Windsor Castle, England 1992; Parliament of Brittany, Rennes, France, 1994; Notre-Dame, Paris 2019; etc.). When it comes to historic buildings, fire protection measures do not only aim at protecting the human life but should as well take care of both the building itself and, in specific cases, its contents. However, considering particular needs of such structures, such as confusing evacuation paths, combustible materials, inadequate exits, etc., it is obvious that it is difficult to meet the requirements of most current fire safety regulations. Additionally, specific fire protection techniques may not be appropriate for some building types (e.g., fire compartmentation may not be applicable in traditional wooden buildings, water suppression may not be appropriate for the case of galleries or libraries, etc.). Finally, in many cases an additional risk is linked to different uses that the historic structures have, compared to what they were initially designed for (i.e., residential buildings that now host galleries, offices, museums, etc.) [2].

Another major issue for historic structures is authenticity, expressed by particular architectural forms, materials, building technologies, special objects, historic symbolisms, etc. In many cases, preserving the authenticity of cultural heritage structures, as a whole or regarding some special features of them only, is not negotiable since it is intimately linked with priceless cultural values [3]. Authenticity demand often leads to significant increases at the fire protection upgrading cost, since it involves advanced fire protection techniques and the application of special materials, in order to maintain the cultural or historic character of the structure. Nevertheless, the available budget is not unlimited and thus must be allocated in an optimal way to maximize fire safety and minimize the building alteration when authenticity is the case. In this context and under the aforementioned restraints, the implementation of conventional approaches based on prescriptive fire safety regulations to protect such structures is problematic, e.g., they are incapable of finding solutions regarding authenticity preservation and fire protection, under strict budget constraints.

As aforementioned, cultural heritage buildings may have particular specificities and special characteristics that pose additional requirements compared to modern structures. Therefore, innovative and enhanced techniques, deriving from the Performance-Based (PB) approach, are more appropriate and efficient compared to the conventional prescriptive-based codes [4]. The selection of suitable fire protection measures alongside their implementation depends on the impact on both the overall targeted fire safety level and the designated authenticity preservation level of each building separately. All relevant decisions should consider these cause-and-effect relations, as well as possible constraints regarding the available budget. Thus, the scientific field of historic structures’ fire protection often involves unavoidable decision making challenges (e.g., selection between similar approaches or techniques, exclusion of specific fire protection measures, special care about the architectural features of the building, etc.). Generally, fire protection of such structures constitutes a Multi-Criteria Decision Making (MCDM) problem, where several and usually conflicting criteria must be integrated into the management planning process [5,6].

To evaluate fire safety and authenticity preservation levels, the Analytic Hierarchy Process (AHP) is incorporated. The AHP is a method used in many engineering problems that demand decision analysis based on multiple criteria. It was introduced by Thomas L. Saaty in 70s [7,8], and it has been widely used and further developed [9,10,11]. The AHP constitutes the tool to develop a framework for handling decision making problems formulated to embody and quantify numerous variables that are linked to the overall objectives, and eventually evaluate numerous possible solutions. In the literature there are numerous applications of the AHP for a wide range of areas [12,13,14].

The present study suggests a new approach for the preliminary fire protection design of cultural heritage buildings that incorporates into a Selection and Resource (S&R) allocation model the assessment of both fire safety and authenticity preservation levels, leading to optimized solutions concerning the proper implementation of the suitable fire protection measures to achieve certain objectives determined by the designer or designing team. The main scope is to control fire risk under certain budget restrictions while at the same time respecting the authenticity of the building. Having a formal structure of the MCDM problem regarding the fire protection of historic structures, the final step is to propose a solution scheme to optimally solve the Select and Resource (S&R) allocation model regarding the fire protection measures. This optimized decision making approach of interventions incorporates new technologies and innovative tools to deal with the budget allocation problem for protecting against fire buildings of cultural heritage. In particular, two approaches are tested in the present study; the multidisciplinary optimization approach, incorporating the Analytic Target Cascading (ATC) method and the multi-objective optimization approach, incorporating the NSGA-II algorithm (that stands for Nondominated Sorting Genetic Algorithm II), and in particular its variant that is based on evolution strategies, labelled as NSES-II algorithm. Furthermore, the efficiency of the model is presented for two cases; Villa Bianca in Thessaloniki, Greece, and the Monastery of Simonos Petra, situated in Mount Athos. The present study is structured in two parts: in the first part the theoretical basis of the proposed Selection and Resource (S&R) allocation model is described, while in the second part the results of the two aforementioned test cases are presented.

2. Literature Review

Despite the fact that the history of architectural conservation is long, fire protection of historic structures has started to be systematically studied not many decades ago. Especially the recent advances in computational techniques and algorithms have resulted in the development of new modern and effective approaches in this field, with many researchers proposing innovative methodologies to assess and control fire risk, leading to optimized solutions for specific cases. In this context, Hozjan et al. [15] presented an artificial neural network (ANN) based approach to simulate the mechanical behaviour of steel frames exposed to high temperatures reached during fires. Konoshima et al. [16] combined a spatial-dynamic optimization and a physical fire model to assist decision making regarding fuel management issues. Tavares and Galea [17] evaluated modelling analyses and incorporated numerical techniques used in the operational research field in the proposed methodology, such as design of experiments (DoE) and response surface models (RSM). Van Coile et al. [18] stressed that in fire engineering any probabilistic risk assessment should be based on hierarchies of acceptance criteria. Additionally, Lau et al. [19] assessed the fire risk of buildings adopting a scoring system applied in insurance industry and banking. Specifically, they proposed a fire risk scorecard using the AHP to weight the risk factors and treat the structures as borrowers. Van Weyenberge et al. [20] used numerical and analytical models to develop a deterministic framework and sampling techniques, response surface modelling, and limit state design to support a probabilistic framework. Then they combined these models to quantify the fire safety level through assessing the failure probability. In the same context, Sanni-Anibire and Hassanain [21] combined the results of a checklist adapted to the provisions of the International Building Code (IBC) with a simulation tool for evacuation (EVACNET4) to approach the fire safety assessment issue and used a student residence building as a case study. Kong et al. [22] presented a risk-based technique to deal with the fire safety design of buildings, using reliability theory and an optimization scheme. Furthermore, Ouache et al. [23] developed a new framework to analyse fire safety plans, both regarding protection and intervention. This framework can also predict the potential fire impact and suggest the appropriate strategy. Wang et al. [24] developed an innovative fire risk assessment methodology for large and multistorey commercial buildings in order to investigate the performance of the applied fire protection measures, facilitating the fire risk management and improving the safety of the users. For this purpose, they introduced a fire risk index scheme and used the Fuzzy Analytic Hierarchy Process (FAHP) to assess the influence of the fire-related parameters.

The difficulty in applying conventional fire protection approaches to historic structures has been recognized by several researchers. Watts [6] reviewed the activity to address such issues including a complete examination of USA fire safety codes, while Watts and Kaplan [25] defined the historic fire risk index to assess relative fire risk of historic structures, incorporating a linear additive model evaluating multiple parameters. Arborea et al. [26] extended the capabilities of the GIS platform introduced by the Italian Central Institute for Restoration (ISCR) as a tool to evaluate the level of exposure and vulnerability of cultural heritage structures, by integrating the Fire Risk Index Method for Multi-storey Apartment Buildings (FRIM-MAB) to it. Pau et al. [27] presented a PB fire protection design process of a two-storey historic structure, while Chen et al. [28] explored the minimum required distance between a historical structure and its surroundings to decrease the fire risk. Their research was based both on a literature review and on the development of a model for the fire propagation. Additionally, Vijay and Gadde [29] presented and discussed an overview of the fire-related damages in old or historic buildings with respect to the types of materials, causes of fire, history of fire accidents, fire safety codes, and fire protection measures along with visual evaluation details. Fafet and Zajmi [30] presented a qualitative analysis for assessing the vulnerability of museums and their exhibits against fire. Venegas et al. [31] examined significant fires in historic buildings between the years 1990 and 2019, highlighting some noteworthy aspects of them. Quapp and Holschemacher [32] analysed the current German regulations regarding preservation and reconstruction of heritage structures and stressed the complexity to find the right balance between protection and safety, giving useful additional information about fire protection approaches in such kind of structures.

In addition, the concern for authenticity preservation has been in focus in a number of studies but commonly in the context of a generic approach of architectural restoration [33] and concerning specific cases (i.e., during the re-use of an existing heritage building) [34,35], usually under the concept of sustainability in urban environments [36]. However, there are no significant studies connecting these two aspects of historic buildings, namely fire safety and authenticity preservation, under a common and universal numerical approach, that is considering the implementation cost as well. The present study suggests a preliminary yet comprehensive S&R allocation model to support engineers, architects, conservationists and any stakeholder through the initial phases of the fire protection design of cultural heritage buildings. It creates a “common platform” to integrate the design objectives, and merge different views to aid the decision making process through automated procedures leading to optimized solutions, which can be compared and evaluated regarding their feasibility and more detailed implementation aspects. Such a universal approach cannot be found in the relevant literature since historic buildings usually have unique characteristics and are handled individually. In this respect, the proposed model, which is explained in the next sections and successfully applied in two real case studies in the second part of the study, can significantly contribute to more efficient fire protection designs for such kind of buildings, leading to solutions that not only increase fire safety and limit costs but also preserve the authenticity, wherever this is the case and in a manner that is defined by the user and can be adapted in any case, as will be highlighted in the study.

3. Historical Background Multi-Criteria Decision Making (MCDM)—Analytic Hierarchy Process (AHP)

MCDM refers to a branch of Operations Research (OR) that is concerned with formulating and dealing with decision type of problems involving multiple criteria, often conflicting ones. Such kinds of approaches are usually convenient in engineering applications because they facilitate the solution formulation based on the engineers’ objectives. There are many such cases in the bibliography [37,38,39,40]. In a similar context, fire protection is often formulated as a multi-criteria problem, especially when historic preservation issues are involved. The purpose of this study is to support the decision making process, since for this kind of problem usually there is not a unique optimal solution and the decision maker’s preferences are essential to finding the best solutions in every case. A decision making process generally follows these steps [41,42]: (i) Problem analysis: this step includes the decomposition of the problem and the identification of the primary objective or goal of the decision making process. A careless analysis of the problem that fails to detect all its parameters and determine all the possible criteria of the deciders could result to misleading solutions, (ii) Selection of the alternative solutions: it is important for the decider to have a decent number of alternatives to choose from in order to increase the possibility of reaching an optimized solution, (iv) Evaluation of the alternative solutions and adoption of the optimum one: this step includes the selection of the weighting method to assess the importance of the criteria identified in previous steps, (v) Application and verification of the final decision: usually the final step includes the monitoring of the whole process and its success is closely related to how adequate it is.

Within this context the AHP is an extensively popular technique for addressing MCDM problems, providing a rational, structured and comprehensive framework that facilitates the efficient formulation of the decision problem, the representation and quantification of its elements, the correlation of those elements to the objectives and overall target or goal, and the evaluation of the alternative solutions that were reached through this process. The simplicity together with the effectiveness of the AHP in the fire engineering area [2,43,44,45] makes it suitable for the case examined in the present study. In Figure 1 a typical form of an AHP hierarchical tree is depicted. The hierarchical approach is originally based on the decomposition of the initial problem to discrete levels (hierarchy levels). The fire ranking incorporating the hierarchical approach was originally developed by the University of Edinburgh [46,47,48], aiming to facilitate the fire safety evaluation of the hospital. The AHP creates a framework in order to consider both subjective and objective aspects during the decision making process. The application of the AHP is based on the four following steps [49,50]:

1st Step: The first concern is to decompose the problem into its components, namely the policy or main goal, objectives, strategies and measures. This procedure is very important as it determines the basis of the decision making process, indicating the correlation between the elements of one level with those of the adjacent levels above and below. These correlations govern the whole hierarchy, succeeding in interconnecting all elements between different levels and thus forming a structured network similar to an inverted tree, where the root is the core outcome of the problem confronted and the leaves consist of the lowest level criteria, which for this work are the fire protection measures, also constituting the optimization variables for the proposed S&R allocation model. In Figure 1 a typical hierarchic structure is depicted.

2nd Step: The prioritization of the hierarchy elements of each level is the next step to determine the hierarchy interconnections. This can be done by pairwise comparisons to prioritize criteria or by using scales to score them. In the case of the proposed fire protection S&R allocation model, scaling that has been used effectively in the past [2] is more suitable for a number of reasons [50]: (a) There are more than nine alternatives (as will been shown below), a fact that would lead pairwise comparisons to three problems: they are time consuming, there are problems with consistency and there are small differences in final scores; (b) Zero has to be a choice for specific alternatives or criteria (e.g., neglect of some fire safety goals), something that is not possible in pairwise comparison, (c) The evaluators may come from different disciplines and not have a deep knowledge of every alternative, (d) Ranking gives the opportunity to add more alternatives later.

Table 1. AHP scale according to the importance of the element evaluated [43].

Importance	Weight (W)
None	0
Low	1
Moderate	2
High	3
Very high	4

contains the scale employed herein [43].

3rd Step: Having determined scaling, the normalization of weight coefficients of every element is calculated aiming to define the correlation of each element with the elements of the level above.

4th Step: The final step includes the synthesis or recomposing of the elements, based both on their normalized weight coefficients and the application grade of the fire protection measures, as will be discussed in the following sections. Given the weight coefficients, for each set of grades, a different policy or overall goal evaluation is acquired. The aforementioned steps are followed in the next sections, where the two proposed models for assessing fire safety level and authenticity preservation level are presented.

4. Fire Safety—AHP Model for Fire Safety Index (FSI)

In this section, the proposed fire safety assessment model for the case of a cultural heritage structures is presented. As aforementioned, problems referring to fire protection are complex, involving many criteria. Thus, in the aforementioned context, the AHP is incorporated to facilitate the procedure. As further discussed below, the Fire Safety Index (FSI) expresses the safety level regarding fire for a historic building. The FSI value is based on the extent of the implementation of the selected fire protection measures, while full implementation of all possible measures results to the maximum FSI. However, each fire protection measure has a different contribution to the fire safety level, depending on the AHP hierarchy selected and the weight coefficients that determine the correlation between the elements situated over and below to the AHP pyramid.

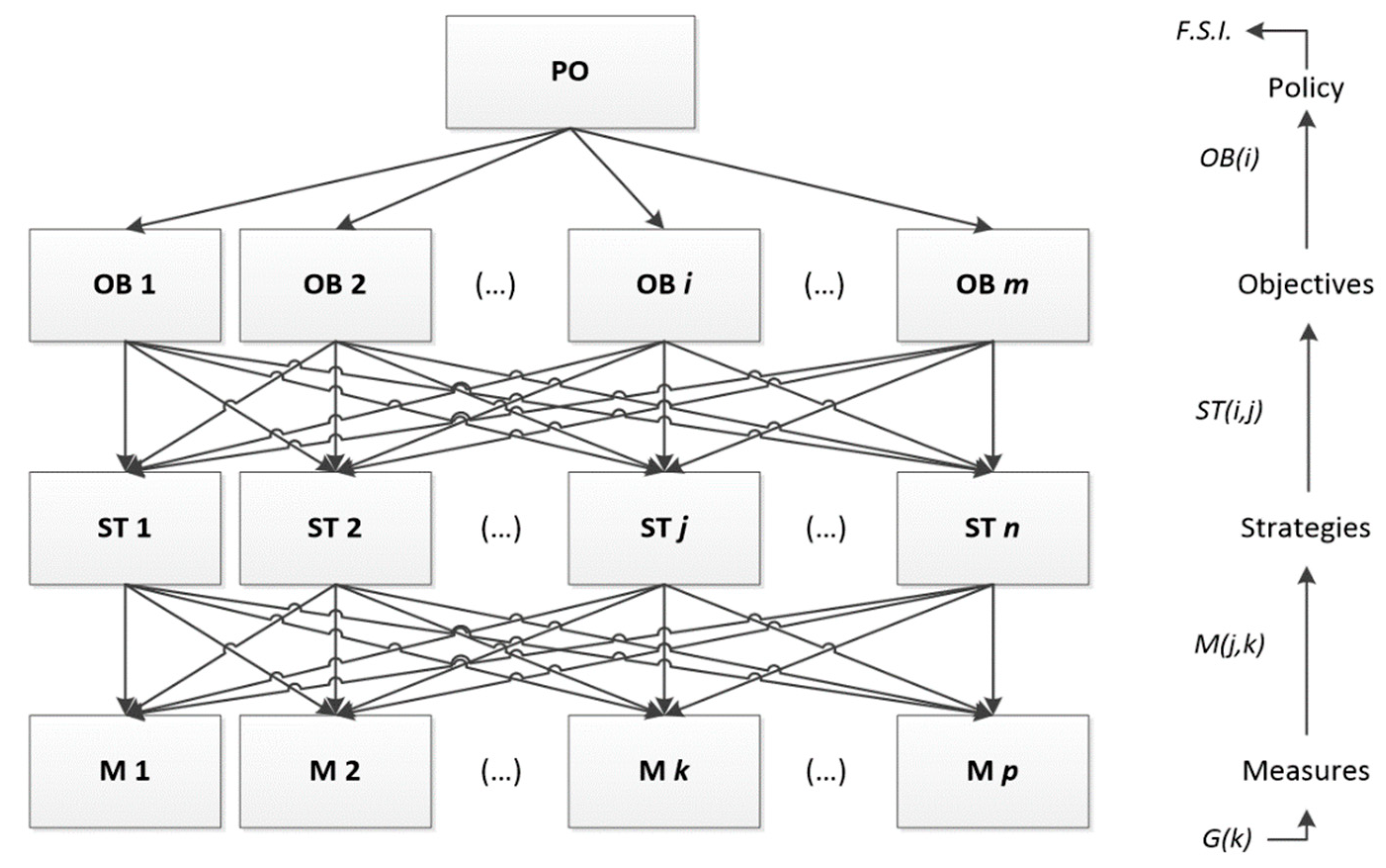
For the scope of this work, the number of the AHP levels for facilitating the decision making process is selected to be four, as depicted in Figure 2. Specifically, Policy level (PO) is situated on the top representing the main strategy regarding the fire safety level, Objectives (OB) are placed immediately below denoting more specific aspects of the fire safety strategy to be addressed, strategies (ST) occupy the third level, designating different fire protection approaches regarding available tactics, and finally Measures (M) close the base of the pyramid insofar as this level represents the final elements the implementation that determines the overall upgrading of fire safety. As will be further discussed, each one of the aforementioned elements, namely Objectives, Strategies and Measures, influence the elements above them and hence the overall policy.

Given the aforementioned hierarchy levels, the next step is to identify the criteria of the problem that represent the specific elements for each level. The criteria strongly depend on the problem and its aspects that need to be addressed and need to be carefully selected in order to describe the decision making procedure with accuracy, taking into account every significant aspect. The degree of the influence of each one of the aforementioned elements to the elements of their upper level is expressed by a weight coefficient that is determined by the designer in the first steps of the S&R allocation model application. The scale used in the present study to express these weights is presented in Table 1.

Aiming to determine the relative influence on the adjacent upper level, the weight coefficients have to be normalized for evaluating their contribution to the directly above elements. Moreover, the Measures, consisting of the elements of the bottom level of the hierarchy, are assigned with a “grade of implementation” that assesses the extent of implementation of each one, taking values between zero and monad for no or full implementation accordingly. Given all these, the FSI is calculated as the sum of the products of each element with the corresponding elements of the above level describing the fire safety level of the building under investigation, taking values between zero and monad, where bigger value denotes better performance in terms of fire safety issues. On that basis, the fire safety index, according to the AHP model described, is calculated as follows:

$$FSI={\displaystyle \sum }_{i=1}^m{\displaystyle \sum }_{j=1}^n{\displaystyle \sum }_{k=1}^{p}OB\left(i\right)\cdot ST\left(i,j\right)\cdot M\left(j,k\right)\cdot G\left(k\right)$$

(1)

where OB(i), ST(I,j) and M(j,k) represent the weight coefficients of OB_i objective in terms of the policy PO, the OB_i objective and the ST_j strategy, respectively, while G(k) expresses the grade of M_k measure implementation. The values of m, n and p denote number of Objectives, Strategies and Measures, respectively. Furthermore, the following expressions have to be fulfilled regarding the components of the calculation formula of Equation (1):

$$\begin{array}{c}{\displaystyle {\displaystyle \sum }_{i=1}^m}OB\left(i\right)=1,\hfill \\ {\displaystyle {\displaystyle \sum }_{j=1}^n}ST\left(i,j\right)=1,\forall i=1,2,\dots ,m\hfill \\ {\displaystyle {\displaystyle \sum }_{k=1}^p}M\left(j,k\right)=1,\forall j=1,2,\dots ,n\hfill \end{array}$$

(2)

Finally, the monetary value for implementing these measures is evaluated as:

$$C={\displaystyle \sum }_{k=1}^{p}G\left(k\right)\cdot C\left(k\right)\cdot A$$

(3)

where C(k) represents the cost of measure M_k (per square meter), and A represents the total building area.

5. Authenticity Preservation—AHP Model for Authenticity Preservation Index (API)

In this section, the proposed model for assessing the authenticity preservation level of a historic structure, which is upgraded concerning its fire safety level, is presented. The assessment of such a characteristic is a very challenging issue because it strongly depends on the perceptions and the pursuits of the architect, archaeologist or anyone concerned. However, there are some main principles [51,52,53,54,55,56,57,58] on which the proposed model is based on. The level of authenticity preservation for a historic structure that is upgraded regarding the fire safety measures is expressed by the Authenticity Preservation Index (API), and in the same context the AHP is incorporated into the proposed process. In accordance with the previous section, the evaluation of API is based on the extent of the implementation of the selected fire protection measures, whereas the influence of each fire protection measure individually to the overall API value depends on the AHP hierarchy and the weight coefficients chosen that determine the correlation between the elements of the adjacent levels, as described below.

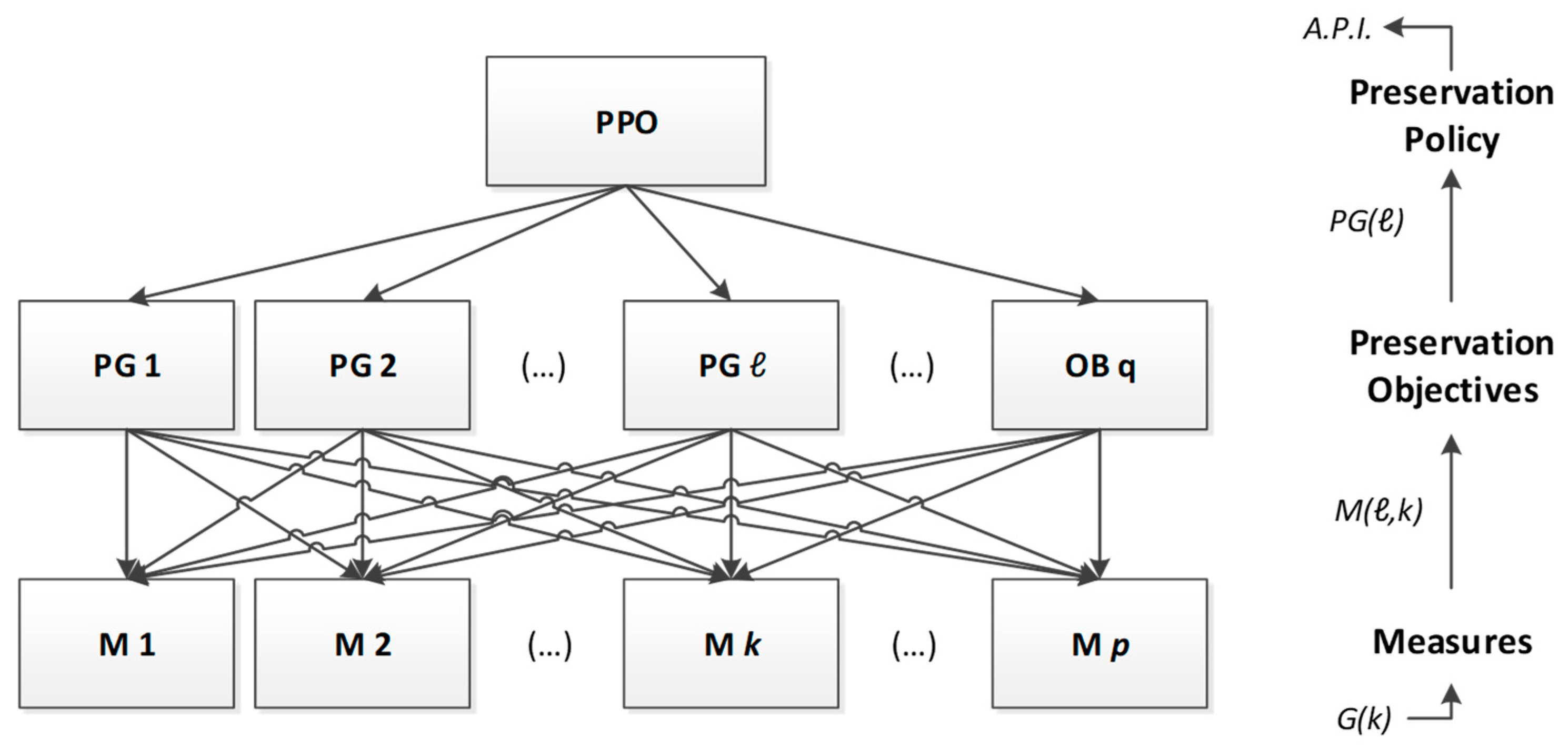
In the present study, for the evaluation of API, the number of the AHP levels for facilitating the decision making process is selected to be three (as depicted in Figure 3). Specifically, the Preservation Policy (PPO) is placed on the top representing the main strategy regarding the authenticity preservation level, Preservation Goals (PG) are placed to the intermediate level, denoting specific preservation goals to be achieved, and finally Measures (M) are completing the base of the AHP pyramid and represent, as aforementioned, the final elements whose implementation determines both the overall fire safety upgrading and the entailed authenticity alteration. It is worth mentioning that these fire protection measures are common for both the FSI and the API AHP hierarchies.

Given the aforementioned hierarchy levels, the next phase is to identify the criteria of the problem that represent the specific elements for each level. Criteria are connected to the problem and its aspects that need to be addressed, and their careful selection is crucial for describing the decision making procedure with accuracy, taking into consideration every significant aspect.

As for the case of FSI evaluation, the degree of the influence of each one of the aforementioned elements to the elements of their upper level is expressed by a weight coefficient that is determined by the designer in the first steps of the S&R allocation model application. The scale used in the present study to express these weights is presented in Table 1. Aiming to define the relative influence to the adjacent upper level’s elements, these weight coefficients have to be normalized to evaluate their relative contribution to the directly above elements.

Moreover, the measures, consisting of the elements of the bottom level of the hierarchy, are already assigned with a “grade of implementation” that assesses the extent of implementation of each one, taking values between zero and monad for no or full implementation accordingly. It is worth mentioning that these implementation grades are obviously common for FSI and API evaluation process, representing the extent of the fire safety upgrading for the case study structure. However, for API evaluation what matters is the differential implementation grade, which is given by the increase of this grade with respect to its initial value. That being said, the API is calculated as the sum of the products of each element with the corresponding elements of the above level describing the authenticity preservation level of the building under investigation, taking values between zero and monad, where a bigger value denotes a worse performance in terms of preservation issues, while the theoretical best score is calculated for each test case depending on the initial implementation grades of the fire protection measures, and represents the minimum possible value denoting the absence of any intervention or alteration works. In this context, the Authenticity Preservation Index, based on the AHP model described, is calculated as follows:

$$API\left(G\left(k\right)\right)={\displaystyle \sum }_{\ell =1}^q{\displaystyle \sum }_{k=1}^{p}PG(\ell )\cdot M\left(\ell ,k\right)\cdot \left(G\left(k\right)-G{(k)}^{init}\right)$$

(4)

where PG($\ell )$ and M($\ell$,k) represent the weight coefficients of PG$\ell$ preservation goal in terms of the preservation policy PPO and the PG$\ell$ preservation goal, respectively, while $G{(k)}^{init}$ represents the initial (before fire safety upgrade) implementation grade of M_k measure. Values of q and p represent number of Preservation Goals (or objectives) and Measures, respectively.

Furthermore, the following expressions have to be fulfilled regarding the components of the calculation formula of Equation (4):

$$\begin{array}{c}{\displaystyle {\displaystyle \sum }_{\ell =1}^q}PG(\ell )=1,\hfill \\ {\displaystyle {\displaystyle \sum }_{k=1}^p}M\left(\ell ,k\right)=1,\forall \ell =1,2,\dots ,n\hfill \end{array}$$

(5)

The cost is evaluated through Equation (3), as mentioned in the previous section.

6. Multi-Criteria Optimization—ATC & NSES-II Approaches

In the present study, two distinctive approaches to deal with the fire protection design of cultural heritage buildings optimization problem are followed, namely the multidisciplinary optimization approach, incorporating the Analytic Target Cascading (ATC) method and the multi-objective optimization approach, incorporating Nondominated Sorting Genetic Algorithm (NSGA-II). It is worth mentioning that the Differential Evolution (DE) algorithm is used for the solution of the subproblems of the ATC approach, as will be presented below.

6.1. Multidisciplinary Optimization Approach

In general, Multidisciplinary Design Optimization (MDO) comprises the use of numerical optimization techniques to solve engineering design problems involving multiple disciplines or subsystems. The main concept of MDO is based on the perception that in order to optimize a multidisciplinary system’s design, one should take full account of the way the system’s disciplines interact with each other. The problem formulation should incorporate these interactions, alongside the design variables and constraints, in a robust mathematical manner. In this study, the hierarchical ATC formulation is used for solving a single optimization problem for each subsystem of the decomposed initial problem. In this context, these solutions must be mathematically linked in order to reach the overall solution by minimizing the compatibility gap between each other. Given that, hierarchically, the solutions of the higher-level subsystems consist of the functions of the solutions of the lower-level subsystems, the ATC formulation’s objective is to minimize the gap among what the higher-level subsystems “need” and what the lower-level subsystems “offer” [59]. Therefore, the hierarchical augmented Lagrangian subproblem of ATC can be formulated as:

$$\begin{array}{c}\underset{s_{ij}}{\min /\max }{F}_{ij}\left({\overline{s}}_{ij}\right)+\phi \left(t_{ij}-r_{ij}\right)+{\displaystyle {\displaystyle \sum }_{k\in C_{ij}}}\phi \left(t_{\left(i+1\right)k}-r_{\left(i+1\right)k}\right)\\ \mathrm{subject}\mathrm{to}{g}_{ij}\left({\overline{s}}_{ij}\right)\le 0\\ \mathrm{with}{r}_{ij}=a_{ij}\left(s_{ij},r_{ij},t_{\left(i+1\right)k_1},\dots ,t_{\left(i+1\right)k_{C_{ij}}}\right)\\ {\overline{s}}_{ij}=\left[s_{ij},r_{ij},t_{\left(i+1\right)k_1},\cdots ,t_{\left(i+1\right)k_{C_{ij}}}\right].\end{array}$$

(6)

where ${\overline{s}}_{ij}$ denotes the unknowns of subproblem j at level i, $s_{ij}$ refers to the local unknowns (i.e., denote the level of implementation G(k) of M_k measures, see problem formulations in Equations (1), (2) and (4)), and $r_{ij}$ to the response variables (e.g., the level of implementation G(k) of M_k measures for the cost minimization subproblem) related to targets $t_{ij}$ (e.g., the level of implementation G(k) of M_k measures for the API minimization subproblem) calculated by the generator of subproblem j. Subproblem j calculates targets $t_{\left(i+1\right)k}$ for the set of its offspring $C_{ij}$ in turn, offspring calculate responses $r_{\left(i+1\right)k}$ and send them back to the generator. Function $F_{ij}$ is the local objective (e.g., the cost, FSI or API), and vector function $g_{ij}$ represent local inequality constraints. Functions $a_{ij}$ represent the analyses required to calculate responses $r_{ij}$. More information regarding the notations related to the heritage structures’ fire problems can be found in the second part of the study, where two real-world problems are employed for implementing the proposed models. Augmented Lagrangian function $\phi$ relaxes the consistency equality constraints $c_{ij}=t_{ij}-r_{ij}=0$ as follows:

$$\phi \left(t_{ij}-r_{ij}\right)=v_{ij}^T\left(t_{ij}-r_{ij}\right)+\Vert w_{ij}°{\left(t_{ij}-r_{ij}\right)\Vert }_2^2$$

(7)

where $v_{ij}$ and $w_{ij}$ are penalty parameters. The symbol ° represents the Hadamard product:

$$a°b={\left[a_1,\cdots ,a_n\right]}^T°{\left[b_1,\cdots ,b_n\right]}^T={\left[a_1{b}_1,\cdots ,a_n{b}_n\right]}^T$$

(8)

In the outer loop, the method of multipliers sets the penalty parameters $v^{k+1}$ for outer iteration k + 1 using the update formula [60,61]:

$$v^{k+1}=v^k+2w^k°w^k°q^k$$

(9)

where $q^k$ are the values of the extended consistency constraints at termination of the kth inner loop iteration. These are composed of the consistency constraints c and the system-wide inequality and equality constraints: $q^T=\left[c^T,{\left(g_0+s\right)}^T,h_0^T\right]$.

Large penalty weights can slow down the coordination algorithm and introduce ill-conditioning of the subproblems [62,63]. Thus, the penalty weight w is increased by a factor β only when the reduction in the extended consistency constraint value is insufficient. Formally, the penalty weight $w_i$ for the ith extended consistency constraint $q_i$ is updated by the formula [60,61]:

$$w_i^{k+1}=\{\begin{array}{c}{w}_i^k if \left|q_i^k\right|\le \gamma \left|q_i^{k-1}\right|\\ \beta w_i^k if \left|q_i^k\right|>\gamma \left|q_i^{k-1}\right|\end{array}$$

(10)

where $0<\gamma <1$ and $\beta >1$. The efficiency of coordination relies on the selection of these parameters, especially $\beta$; it is suggested [59] $\gamma =0.4$ and $\beta =2.2$.

6.2. Multiobjective Optimization Approach

In real-world technical problems, upgrading the performance of specific structural characteristics might have a negative impact on other parameters that inevitably affect their total performance. In such kinds of problems there usually exist numerous contradictory and many times incommensurable criteria that need to be dealt with in turn. Such cases impel engineers to search for a good compromise between the contradictory criteria. Such problems are also called multi-objective optimization problems that can be stated as follows:

$$\begin{array}{c}{\min }_{s\in F}{[F_1\left(s\right),F_2\left(s\right)]}^T\\ \mathrm{subject}\mathrm{to}{g}_j\left(s\right)\le 0j=1,\dots ,k\end{array}$$

(11)

where $s$ denotes the design variables vector consisting of the implementation grades of the fire protection measures considered (M_k), F stands for the feasible region where the constraint set by the designer expressed by function $g_j$ is satisfied, and $F_1$ and $F_2$ represent the objective functions that are competing. For the test case examined, which will be further analyzed in the second part of the study, the objective functions considered are the Fire Safety Index (FSI) and the Authenticity Preservation Index (API), while cost constitutes in all test cases the constraint of the problem, depending on the available budget.

Many algorithms have been presented for solving the multi-objective optimization problem [64,65]. In this study, the Nondominated Sorting Evolution Strategies II (NSES-II) algorithm [66] is employed for solving the two-objective problem at hand. The algorithm is denoted as NSES-II(μ + λ) or NSES-II(μ,λ), depending on the selection operator. In a mixed discrete and continuous optimization problem, the individuals are equipped with a set of parameters:

$$\begin{array}{c}a=\left[\left(s_d,\gamma \right),\left(s_c,\sigma ,\alpha \right)\right]\in \\ {{\rm I}}_d{=\mathrm{D}}^{n_d}\times R_{+}^{n_{\gamma }}\\ {{\rm I}}_c{=\mathrm{R}}^{n_c}\times R_{+}^{n_{\sigma }}\times {[-\pi ,\pi ]}^{n_a}\end{array}$$

(12)

Vectors $s_c$ and $s_d$ denote the continuous and discrete design variables, respectively; $\gamma$ contains the Poisson distribution variances; $\sigma \in R_{+}^{n_{\sigma }}$ contains the standard deviations (1 ≤ n_σ ≤ n_c) of the normal distribution and vector, $\alpha \in {[-\pi ,\pi ]}^{n_a}$ contains the inclination angles (n_α = (n_c − n_σ/2)(n_σ − 1)) that define the correlation of mutations for the components of $s_c$. If $B_p^{\left(g\right)}=\left\{a_1,\dots ,a_{\mu }\right\}$ refers to the gth generation’s parent population of individuals and the genetic operators are denoted by the following mappings:

$$\begin{array}{c}\mathrm{rec}: {({{\rm I}}_c)}_{\left(g\right)}^{\mu }\to {({{\rm I}}_c)}^{\lambda }\mathrm{recombination}\\ \mathrm{mut}: {({{\rm I}}_c)}^{\lambda }\to {({{\rm I}}_c)}^{\lambda }\mathrm{mutation}\\ {\mathrm{sel}}_{\mu }^k : {({{\rm I}}_c)}^k\to {({{\rm I}}_c)}_{\left(g+1\right)}^{\mu }\mathrm{selection},\mathrm{k}\in \left\{\mathsf{\lambda },\mathsf{\mu }+\mathsf{\lambda }\right\}\end{array}$$

(13)

Then an iteration is modelled by the mapping:

$${\mathrm{opt}}_{\mathrm{ES}} : {({{\rm I}}_c)}_{\left(g\right)}^{\mu }\to {({{\rm I}}_c)}_{\left(g+1\right)}^{\mu }$$

(14)

That is a step from the parent population $B_p^{\left(g\right)}$ to the next generation’s one $B_p^{\left(g+1\right)}$. Algorithms 1 depicts a pseudo code of the NSES-II(μ + λ) algorithm, while more details on its implementation can be found in [66].

Algorithms 1. Pseudo code of the NSES-II (μ + λ) optimization algorithm

1 Begin 2 $g:=0$ 3 $initialize\left({\mathit{B}}_p^{\left(0\right)}:\left\{\left({\mathit{y}}_m^{\left(0\right)},{\mathit{s}}_m^{\left(0\right)},f\left({\mathit{y}}_m^{\left(0\right)}\right)\right),m=1,2,\cdots ,\mu \right\}\right)$ 4  Repeat 5     For $l:=1$ To λ Do Begin 6      $k=random\_index\left(\mu \right)$ 7      ${\mathit{p}}_l:=SelectParent\left({\mathit{B}}_p^{\left(g\right)},k\right)$ 8      $s_l:=GetStrategy\left({\mathit{p}}_l\right)$ 9      ${\mathit{y}}_l:=GetDesign\left({\mathit{p}}_l\right)$ 10      ${\tilde{s}}_l:=s\_mutation\left(s_l\right)$ 11      ${\tilde{\mathit{y}}}_l:=y\_mutation\left({\mathit{y}}_l\right)$ 12      If ${\tilde{\mathit{y}}}_l:=is not feasible$ Go to Step 6 13    End 14    ${\mathit{B}}_o^{\left(g\right)}:\left\{\left({\mathit{y}}_l^{\left(g\right)},{\mathit{s}}_l^{\left(g\right)},f\left({\mathit{y}}_l^{\left(g\right)}\right)\right),l=1,2,\cdots ,\lambda \right\}$ 15     ${\mathit{R}}^{\left(g\right)}={\mathit{B}}_p^{\left(g\right)}{\displaystyle \cup }{\mathit{B}}_o^{\left(g\right)}$ 16    ${\mathit{S}}^{\left(g\right)}=fast-nondominated-sort\left({\mathit{R}}^{\left(g\right)}\right)$ 17    ${\mathit{B}}_p^{\left(g\right)}=\varnothing , i=1$ 18    Until $\left|{\mathit{B}}_p^{\left(g+1\right)}\right|+\left|{\mathit{S}}_i\right|\le \mu$ Do 19      $crowding-distance-assignment\left({\mathit{S}}_i\right)$ 20      ${\mathit{B}}_p^{\left(g+1\right)}={\mathit{B}}_p^{\left(g+1\right)}{{\displaystyle \cup }}^{}{\mathit{S}}_i$ 21      $i=i+1$ 22    End 23    $crowding-comparison-operator\left(S_i\right)$ 24    ${\mathit{B}}_p^{\left(g+1\right)}={\mathit{B}}_p^{\left(g+1\right)}{{\displaystyle \cup }}^{}{\mathit{S}}_i\left[1:\left(\mu -\left|{\mathit{B}}_p^{\left(g+1\right)}\right|\right)\right]$     25    $g:=g+1$ 26  Until termination_condition 27 End

7. General AHP Formulations and Parameters

Based on the AHP frameworks for fire safety and authenticity preservation, described previously, the following elements could be adopted in order to describe as accurately as possible the “dual” problem of historic structures as suggested in the present work: fire protection and authenticity preservation. The prospect is to approach both problems comprehensively, considering all possible parameters that could be involved, creating an element “pool” for the applier of the proposed S&R allocation model to facilitate the application. In this context, the fire safety level of the structure, expressed through the FSI, is placed at the top level of the proposed hierarchy, representing the main policy.

On the second level, the possible objectives are: OB1—protection of the people (occupants and visitors), OB2—protection of the building fabric, OB3—protection of the cultural contents, OB4—protection of the environment, OB5—protection of the firemen and OB6—safeguard continuity of activity. On next level, which represents the strategies, the following seven parameters were selected: ST1—reduce the probability of starting a fire, ST2—limit fire development in the fire compartment, ST3—limit fire propagation out of the fire compartment, ST4—facilitate egress, ST5—facilitate fire-fighting and rescue operations, ST6—limit the effects of fire products, ST7—protection from forest fires.

On the bottom level of the proposed hierarchy, the 16 measures that are incorporated into the proposed model in order to cover all available management and technological tools against fire are: Μ1—compartmentation, Μ2—fire resistance of structural elements, Μ3—control of fire load, Μ4—materials (reaction to fire), Μ5—control of fire spreading outside the building, Μ6—design of means of escape, Μ7—signs and safety lighting, Μ8—access of the fire brigade, Μ9—detection and alarm, Μ10—suppression and extinguishing, Μ11—smoke control systems, Μ12—training of the personnel, Μ13—fire drills and emergency planning, Μ14—management of fire safety, Μ15—maintenance of fire safety system, Μ16—salvage operation [2,43].

On the other hand, for the AHP hierarchy expressing the authenticity preservation, the preservation policy placed on top of the hierarchy could be expressed by means of the four preservation objectives chosen, namely PG1—Reversibility (the ability to reverse changes is needed to prevent problems with investigation, handling or use in the future), PG2—Discreteness (new elements must be discreet as possible, even invisible, in order not to visually alter the monument), PG3—Non-competitiveness (new elements must not dominate over authentic ones) and PG4—Distinctiveness (any new intervention must be discrete and have a definable boundary in order to be clear about which building elements are authentic), while the 16 fire protection measures remain the same as above. The weight coefficients of the above elements, required in order to formulate both AHP trees, are provided in each test case accordingly. Furthermore, it is noted that in order to assess the total cost of fire safety upgrading, the 16 fire protection measures are divided into different cost groups, in accordance with their approximate implementation cost, also provided in the second part of the study.

8. Conclusions

In the present work, we present an optimum Performance-Based (PB) fire protection design model for cultural heritage structures, expressed as a Multi-Criteria Decision Making (MCDM) problem incorporating the Analytic Hierarchy Process (AHP), which was encountered with two different approaches: (a) the multidisciplinary optimization approach, incorporating Analytic Target Cascading (ATC) method and (b) the multiobjective optimization approach, incorporating Nondominated Sorting Genetic Algorithm II (NSGA-II).

The object of the proposed framework is the upgrading of the fire safety level of an existing cultural heritage structural system through an optimized Selection and Resource Allocation (S&RA) model, taking also into account the authenticity preservation level and the cost of the fire protection measures applied. The AHP tree, which was employed for the problem of fire safety level assessment, represented by the Fire Safety Index (FSI), incorporates four hierarchy levels, namely Policy (PO), Objectives (OB) Strategies (ST) and Measures (M), while the AHP tree that was employed for the problem of assessing the alteration of the building fabric represented by Authenticity Preservation Index (API), incorporates three hierarchy levels, namely Preservation Policy (PPO), Preservation Objectives (POB) and Measures (M).

The second part of the present study presents successful applications of the proposed approach to real-world cases, demonstrating its capability of handling the fire safety issue of the historic buildings, concluding in feasible results. Specifically, Villa Bianca, a famous mansion in the city of Thessaloniki, Greece, and the Monastery of Simonos Petra located in Mount Athos, Greece, are used to demonstrate the efficiency of the proposed S&R allocation model.