A System Dynamics Framework for Market Share Forecasting in the Telecommunications Market

Highlights

What are the main findings?

• The paper introduces a data-lean system dynamics framework that represents competing providers’ market shares as interacting subscriber stocks driven by bounded churn and attraction flows, coupled with a stochastic diffusion process. Monte Carlo simulation and variance-based sensitivity analysis generate coherent probabilistic forecasts and quantify how each behavioral mechanism contributes to forecast uncertainty using only aggregate data.
• Applied to the Greek mobile telecommunications market (2006–2022), the framework reproduces the observed evolution of market shares and delivers accurate 5-year out-of-sample forecasts that outperform a reconciled ARIMA benchmark and provide well-calibrated prediction intervals. The analysis shows that outgoing churn parameters are the primary drivers of market-share variability in this mature, near-saturated oligopoly, while volatility-related parameters and exogenous noise play only a minor role.

What are the implications of the main findings?

• Operators should prioritize churn-reduction and targeted acquisition strategies, because outflow parameters account for most of the forecast uncertainty in future market shares. The model’s risk-informed forecasts and sensitivity results can be used to stress-test pricing, retention and marketing policies under alternative churn and attraction scenarios, helping firms balance growth against volatility in a disciplined way.
• Policymakers and planners can apply the framework to evaluate how regulatory changes, competitive shocks or entry/exit events would reallocate subscribers in an already saturated market, even when only aggregate data are available. By combining probabilistic forecasts with an explicit decomposition of behavioral drivers, the approach supports evidence-based decisions that sustain healthy competition, protect consumers and inform infrastructure investment.

Abstract

This paper presents a novel system dynamics-based framework for forecasting market share evolution in the telecommunications sector. The framework conceptualizes market share as flows of subscribers—driven by churn, attraction, and market growth—between interconnected compartments representing providers. It is designed to operate with limited available market data and incorporates stochastic processes to capture market uncertainty, enabling risk-informed forecasts. The framework is applied to the Greek mobile telecommunications market using historical data (2006–2022), with a 5-year hold-back period for validation. Results highlight the dominant role of churn management in market share variability, particularly for the incumbent provider Cosmote, while subscriber attraction parameters show moderate influence for alternative providers Vodafone and Wind Hellas. Sensitivity analysis confirms the model’s robustness and identifies key drivers of forecast variability. The proposed framework provides actionable insights for strategic decision-making, making it a valuable tool for providers and policymakers to address churn, optimize attraction strategies, and ensure long-term competitiveness in dynamic markets.

1. Introduction

The telecommunications industry is among the most competitive and rapidly evolving sectors globally, driven by constant technological advancements, shifting consumer demands, and intense market rivalry. With the rapid evolution of transformative technologies such as 5G, the Internet of Things (IoT), and cloud-based services, telecommunications providers face increasing pressure to innovate and deliver faster, more reliable connectivity. Simultaneously, the industry’s subscription-based revenue model intensifies competition for customer retention, as consumers can easily switch providers based on price, service quality, or promotional offers [1,2,3]. Regulatory frameworks [4], spectrum auctions [5,6,7], and the significant infrastructure costs [8,9] further complicate the competitive landscape, pushing companies to balance operational efficiency with strategic investments. This highly competitive and ever-changing environment requires providers to continuously adapt to maintain market share and ensure sustainable long-term profitability.

Market share is a measure of the proportion of total sales, revenue, or customers captured by a company within a specific market. It serves as a key indicator of a company’s competitiveness and growth potential [10,11]. Variations in market share are often influenced by factors such as overall market performance and customer churn, which refers to the loss of customers who stop purchasing from or using the services of a company [12]. Since companies have limited control over broader market performance, they typically prioritize strategies to manage churn effectively [13]. These strategies are critical because retaining existing customers is generally more cost-efficient than acquiring new ones [14].

In telecommunications, market share reflects a provider’s percentage of subscribers or revenue relative to the entire sector. Similarly to other industries, shifts in market share are primarily driven by customer churn and market trends. Churn, a significant challenge in this field, occurs when subscribers discontinue service with one provider and switch to another, often due to dissatisfaction with pricing, service quality, or promotional incentives [15,16]. To mitigate this, providers engage in competitive practices to retain current subscribers and attract new ones, as retaining customers tends to be less expensive than onboarding new ones [17,18]. This is more important in the current saturated telecommunications market landscape [19], where customer acquisition is increasingly competitive. The success of these efforts depends not only on the provider’s internal strategies but also on competitor performance and market dynamics. This interconnected market dynamic means that even a thriving market may result in individual providers losing ground if competitors outperform them [20].

Building upon this understanding, forecasting market share in the telecommunications sector is a critical tool for strategic decision-making, enabling providers to anticipate customer behavior, market trends, and competitor actions. Accurate forecasts help address challenges like churn by identifying at-risk customers and customizing retention strategies to maintain market share [21,22,23,24,25]. They also guide resource allocation toward initiatives such as pricing strategies, service enhancements, and promotional campaigns [26,27,28]. Moreover, market share forecasting is equally vital for long-term investments, such as network expansions, or adopting new technologies like 5G [29]. By understanding future trends, providers can assess the return on investment in underserved regions and emerging markets. Furthermore, forecasting highlights the interplay between internal performance and external factors, such as economic conditions and competitor activity [30,31]. For instance, the rollout of 5G networks presents a window for market share gains as customers switch providers to access enhanced connectivity services. Market share forecasting enables companies to identify such opportunities and allocate resources effectively to strengthen their competitive position. Therefore, accurate models that account for these variables are essential for telecom providers to stay competitive, adapt to industry changes, and sustain growth. Crucially, many of these decisions must be made even when only limited, aggregate market data are available, underscoring the need for data-lean forecasting approaches.

When granular, individual-level switching data are unavailable or proprietary, aggregate-level forecasting can in fact be advantageous: recent work shows that appropriate aggregation may improve prediction accuracy for items with limited histories [32], reinforcing the case for data-lean market-share models constructed from publicly available time-series.

Given the critical role of accurate market share forecasting in strategic planning, this paper aims to develop a comprehensive market share forecasting framework specifically tailored to the telecommunications industry. The proposed framework is based on systems dynamics modeling [33,34] to simulate and forecast the evolution of the telecom providers’ market share in terms of subscribers. Under this approach, market share dynamics are conceptualized as subscriber flows among providers, represented through a system of interconnected compartments. These flows are influenced by external forces, such as market trends, competition, and technological changes. Unlike approaches that rely on individual-level records, the proposed system dynamics formulation is intentionally data-lean: it uses limited, aggregate market data to estimate inter-provider flows and quantify uncertainty.

The proposed framework provides several key advantages for practitioners. One of its strengths lies in its ability to model various factors influencing subscriber preferences as distinct system functions. These factors include new subscriber attraction, subscriber churn, market effects, network effects, and the subscriber lifecycle, enabling a detailed representation of market dynamics. Additionally, the framework is highly flexible, making it adaptable to both technology-specific scenarios and the broader telecommunications market. Furthermore, it can integrate seamlessly with existing technology diffusion models used in market forecasting, to enhance its capabilities. An added benefit is its capability to incorporate uncertainty into these functions, enabling the quantification of this uncertainty’s impact on market share evolution.

The proposed framework is applied to the Greek mobile telecommunications market to evaluate its effectiveness. A 5-year hold-back testing period is employed to validate its ability to accurately forecast market share among existing active providers. Results indicate strong model performance, with an accurate central tendency and low-to-moderate variability, highlighting how market share may be affected by uncertainty and external factors. These results demonstrate the framework’s potential as a reliable and effective forecasting tool, showcasing its capacity to provide actionable, data-driven insights for the telecommunications industry.

Furthermore, to quantify the added value of this structurally grounded formulation, the framework is evaluated against a standard statistical benchmark, a coherent ARIMA-based forecasting approach with ex-post reconciliation to enforce compositional constraints. Both models are calibrated on the same training window and assessed on a 5-year hold-back period, allowing a transparent comparison of predictive accuracy and forecast uncertainty. The proposed system dynamics framework yields systematic out-of-sample gains, while delivering coherent probabilistic intervals without any reconciliation step.

By leveraging this advanced forecasting framework, telecommunication providers can enhance their understanding of market dynamics and improve their strategies for managing churn and attracting new customers. Furthermore, the framework serves as a valuable resource for analyzing competitive interactions, enabling providers to refine their decision-making processes and maintain a competitive edge in the dynamic telecommunications landscape. The data-lean nature of the approach also makes it useful for regulators and policymakers who must plan under information constraints.

The rest of this paper is organized as follows. Section 2 reviews the literature on market share forecasting in the telecommunications sector, as well as relevant research on the proposed system dynamics modeling approach. Section 3 details the proposed framework formulation, while Section 4 discusses its application. Section 5 elaborates on the application results analysis, providing a detailed evaluation of the forecasting outcomes, including the sensitivity analysis findings and their implications. Finally, Section 6 concludes the study.

The rest of this paper is organized as follows. Section 2 reviews the literature on market share forecasting in the telecommunications sector, as well as relevant research on the proposed system dynamics modeling approach and compositional forecasting as a structural alternative. Section 3 details the proposed framework formulation, while Section 4 describes its application to the Greek mobile telecommunications market. Section 5 presents the empirical analysis, providing a comparative evaluation of the proposed framework against the statistical benchmark via Monte Carlo simulation, followed by a variance-based sensitivity analysis to quantify forecast uncertainty. Section 6 discusses the broader theoretical and practical implications of the findings for industry practitioners and policymakers. Finally, Section 7 concludes the study.

2. Literature Review

2.1. Market Share Forecasting in Telecommunications

Market share forecasting is a predictive process aimed at estimating a company’s relative share of the total market, typically in comparison to its competitors within a specific industry or product category. Unlike traditional forecasting, which focuses on absolute metrics such as revenue, subscriber growth, or demand, market share forecasting places emphasis on the relative performance of a company in the competitive landscape. In the telecommunications market, where multiple service providers compete for a finite customer base, market share forecasting becomes particularly relevant for strategic planning and competitive analysis.

Research on market share forecasting has evolved significantly over the years, with approaches ranging from simulation-based methods [35] and attraction models [36] to advanced techniques such as neural networks and genetic algorithms [37]. In the telecommunications sector specifically, forecasting methodologies predominantly revolve around Markov chain models, econometric approaches, and simulation-based frameworks.

Beyond generic market-share models, research in telecommunications increasingly emphasizes churn, switching costs and network effects as the behavioral mechanisms driving competitive outcomes. Empirical studies show that customer switching decisions are governed by substantial lock-in effects. In [38], switching costs are estimated to account for roughly 70% of consumer lock-in in mobile telephony, with local network effects contributing the remaining 30%. This balance is particularly relevant in mature markets, where providers compete primarily by managing churn rather than by expanding the overall subscriber base. In parallel, analyses of European mobile oligopolies, such as in [39], document systematic asymmetries between incumbents and alternative providers, with incumbents benefiting from higher perceived switching costs and stronger network externalities, resulting in more stable subscriber bases and enhanced market power. At a more formal level, dynamic models of oligopolistic competition have begun to treat churn directly as a strategic state variable. In [40] for example, churn is incorporated in a dynamic advertising framework and demonstrate how subscriber switching alters both equilibrium strategies and long-run market configurations.

The application of Markov chain models to market share forecasting in telecommunications has been particularly prominent. These models are widely utilized for analyzing customer behavior and predicting market share transitions among competitors, based on the assumption that future states depend solely on the current state, independent of previous sequences of events. In [41] the authors introduced the use of Markov chains for market share modeling in telecommunications, demonstrating that the transition matrix of time-homogeneous Markov chains possesses descriptive properties linked to marketing variables. Building on this, in [42] a diffusion growth model was integrated into the Markov framework to forecast market share changes corresponding to different product life cycle phases, using examples from the telecommunications industry.

Subsequent studies further expanded the applicability of Markov models. In [43,44,45], Markov chains were utilized to model the market share dynamics of mobile operators. In [46] the authors emphasized the relevance of Markov chains for illustrating modern subscription-based markets, positioning them as an educational tool. In [46], a non-homogeneous Markov model was employed, incorporating non-stationary transition probability matrices to reflect external actions, such as marketing activities by service providers. In [47] a comparative analysis of four mathematical models was provided for market share forecasting, offering guidance on model selection based on problem-specific assumptions and characteristics. Most recently, in [48] the authors applied Markov Prediction Chains to assess consumer brand preferences in SIM card purchases, highlighting the dominance of private-sector providers over public-sector players. Collectively, these studies demonstrate that Markov chain models are instrumental in capturing customer switching behavior and market share transitions, where state vectors represent proportions of market share among sellers.

An alternative to Markov models involves econometric approaches, such as time-series analysis, panel data regression, and multiple linear regression models. These methods quantify relationships between market share and its determinants, such as pricing, marketing efforts, and macroeconomic indicators. In [49] a comprehensive review of econometric models for market share forecasting across industries is provided, including telecommunications. Their work highlights the strengths and limitations of methodologies like ARIMA and multiple linear regression, emphasizing the critical role of accurate data and appropriate model selection for reliable forecasts.

Simulation-based methods offer another robust approach for market share forecasting, especially in scenarios involving uncertainties and competitive interactions. Techniques like Monte Carlo simulations are particularly valuable for assessing the impact of stochastic variables on market dynamics. In [50] this approach is exemplified by employing Monte Carlo simulations to analyze competitive interactions among telecommunications providers in Slovakia. By using a mean-field approach, they modeled the behavior of new market entrants challenging incumbents, exploring diverse competitive scenarios. Their findings offer actionable insights for both new entrants and established players on effective market positioning and strategy.

Innovative approaches, such as those grounded in population biology, have also been applied to market share forecasting. In [51] concepts from population biology were utilized to predict market concentration and competition levels in telecommunications, offering novel methodologies to analyze structural shifts and market dominance.

Concluding, the forecasting of market share in telecommunications integrates diverse methodological approaches, including Markov chains, econometric models, simulation frameworks, and population biology concepts. Careful selection and application of these models are essential to account for the unique characteristics of target markets and ensure accurate, actionable forecasts.

A related strand of work focuses on diffusion and saturation dynamics in telecommunications markets. Early system dynamics and diffusion models, such as in [52], used multilevel substitution structures to capture technological replacement processes. More recent telecom applications compare alternative S-curve specifications—logistic, Gompertz, Bass and competitive Lotka–Volterra models—for mobile and broadband adoption. For example, the authors of [53] evaluate the extended Bass and Lotka–Volterra models in the mature Korean mobile market, while in [54] the logistic, Gompertz and Bass curves for broadband diffusion in Thailand are systematically compared, concluding that simple logistic specifications can provide adequate fit when the emphasis is on saturation rather than early-stage innovation effects. In a similar spirit, in [55] compartmental diffusion models are applied to 5G penetration in saturated telecom markets, showing that once aggregate adoption stabilizes, competitive dynamics shift from growth-driven acquisition to redistribution-driven churn. These findings motivate the use of a logistic S-curve for aggregate market evolution in the present framework, combined with flow-based modeling of churn and attraction to capture redistributive competition among providers.

2.2. System Dynamics Approaches to Market Competition

In this paper, the proposed framework utilizes system dynamics modeling to forecast the evolution of telecom providers’ market share in terms of subscribers. System dynamics offers an integrated approach to market share forecasting by incorporating feedback loops, competitive behaviors, and dynamic changes. These models are particularly effective for industries like telecommunications, where structural changes and technological progress play a central role.

System dynamics has been successfully applied in various industries to model market competition and technological substitution. The authors of [52] demonstrated the utility of system dynamics in predicting technological substitution and its impact on market share, showing how feedback loops and technological advancements drive market evolution. Similarly, in [56] the use of system dynamics to simulate market competition and forecast structural changes is explored, including applications in the telecommunications sector.

Further research highlights the adaptability of system dynamics across domains. For example, in [57] a system dynamics framework is developed to forecast demand and competition in the aviation industry, a methodology that can be directly applicable to telecommunications markets. More recently, the authors of [58] combined system dynamics with scenario-based models to predict market demand and competition, showcasing its versatility in capturing dynamic market behaviors.

Under the proposed approach, market share competition is conceptualized as flows of subscribers among telecom providers. These flows are represented through a system of interconnected compartments, where subscriber transitions are influenced by external forces such as market trends, competitive actions, and technological advancements. This representation allows for a comprehensive analysis of market dynamics and provides insights into how providers can adapt their strategies to capture and retain market share.

2.3. Compositional Forecasting and Hierarchical Reconciliation

It is noted that the problem addressed by this framework belongs to the specialized field of compositional or constrained forecasting, where components (individual market shares) form a defined aggregate (total market size) and are subject to the coherence constraint that component forecasts must sum to the forecast of the aggregate. This setting is not unique to telecommunications and appears in applications such as vote shares, brand shares and financial portfolios. A large body of work in hierarchical and grouped time-series addresses this coherence requirement through forecast reconciliation techniques. In [59] an optimal reconciliation is proposed based on trace minimization of the forecast-error covariance matrix (the MinT approach), and recent reviews [60] survey bottom-up, top-down, optimal-combination and related methods, highlighting the trade-offs between local and aggregate accuracy. Extensions to probabilistic forecasting have introduced the notion of stochastic coherency, recognizing that reconciliation affects not only point forecasts but also prediction intervals and full forecast distributions; the authors of [61] show that traditional reconciliation may inflate uncertainty by propagating base-forecast errors through the reconciliation matrix. Traditional univariate or multivariate statistical models (e.g., ARIMA or VAR) typically generate incoherent base forecasts for each component and then apply such reconciliation methods ex post. The present study follows this paradigm when constructing a reconciled ARIMA benchmark using the minimum-variance combination rule of [62], but contrasts it with a system dynamics formulation in which coherence is enforced by construction through structurally constrained subscriber flows between compartments.

Beyond the minimum-variance rule adopted in this study [62], other reconciliation strategies exist that trade off bias and variance under different error structures and hierarchies. The current benchmark was chosen for parsimony and transparency in a three-series composition; exploring alternative reconciliation schemes is left for future extensions.

2.4. Summary and Contribution of the Present Study

In summary, existing research on market-share forecasting in telecommunications is fragmented across several methodological traditions. Markov chain models and related stochastic processes provide a natural description of switching behavior between providers, but they typically abstract from explicit representations of market growth and feedback mechanisms, and they offer limited structural insight into how churn-management actions translate into long-run market configurations [41,42,43,44,45,46,47,48]. Econometric approaches, such as ARIMA, panel regression, and multivariate time-series models, are powerful for statistical inference and hypothesis testing [49], yet they treat market shares as generic time-series and usually require ex-post reconciliation techniques to enforce compositional coherence. Simulation-based methods, including Monte Carlo and mean-field approaches [35,50,51], are better suited to exploring competitive scenarios and uncertainty, but they often lack an explicit flow-based structure grounded in system dynamics.

The framework proposed in this paper contributes to this literature by combining a system dynamics representation of subscriber flows with stochastic diffusion modeling and coherent compositional forecasting. Building on earlier applications of system dynamics to technology substitution and market competition [55,56,57,58], the model treats churn and attraction as structurally constrained flows between provider compartments, while aggregate market evolution is governed by a calibrated diffusion process. In line with [56], who argues that system dynamics models gain their forecasting power by explicitly representing feedback structures and managerial decision rules, the present framework embeds provider churn-management and subscriber-attraction behaviors directly in the flow equations, rather than treating market shares as generic time-series patterns. In contrast to purely statistical benchmarks, the framework produces coherent forecasts by construction, explicitly decomposes market-share changes into churn and attraction components, and quantifies forecast uncertainty through Monte Carlo simulation. At the same time, by relying only on aggregate market data and by benchmarking against a reconciled ARIMA specification [49,62], the approach remains comparable to established forecasting practices and situates the model within a well-defined scientific environment.

To the best of our knowledge, no existing study combines a compartmental system dynamics representation of subscriber churn and attraction with stochastic diffusion of the aggregate market and coherent compositional forecasting, nor evaluates such a framework against a reconciled ARIMA benchmark in a mature telecommunications oligopoly.

3. Framework Formulation

The market share, defined as the number of subscribers held by a telecommunications provider, is determined by its ability to attract new subscriptions and retain existing ones, irrespective of the overall telecommunications market performance. Over a given time period, the number of subscribers a provider has at the end of this period can be estimated using the following equation:

$${SB}_t={SB}_{t-1}+\left({Cp}_t-{Cn}_t\right)+\left({Mp}_t-{Mn}_t\right)$$

(1)

where

-

SB_t: The number of subscribers to the provider at the end of the time period

-

SB_t−1: The number of subscribers to the provider at the beginning of the time period

-

Cp_t: The number of subscribers attracted from competitors (positive churn) over the time period

-

Cn_t: The number of subscribers leaving the provider for competitors (negative churn) over the time period

-

Mp_t: The number of new-to-market subscribers acquired during the time period

-

Mn_t: The number of subscribers exiting the market during the time period

In this formulation, parameters Cp_t and Cn_t capture the effects of churn on a provider’s market share, reflecting both the gains and losses of subscribers due to competition. Meanwhile, parameters Mp_t and Mn_t account for the effects of overall market performance by representing new subscriptions and market exits, respectively. Additionally, the combination of Cp_t and Mp_t represents incoming subscribers, while Cn_t and Mn_t together express the subscribers leaving the provider.

Using this approach (Equation (1)) to model the time evolution of a provider’s market share, the primary risks associated with poor performance can be attributed to three key factors:

• Poor performance in managing churn effectively.
• Superior performance of competitors’ churn management strategies.
• The overall market performance, including growth or contraction trends.

At any given time step, these risk factors drive the flows of subscribers, influencing a provider’s market share dynamics.

The proposed framework leverages system dynamics modeling to forecast the evolution of telecom providers’ market share in terms of subscribers. System dynamics is a simulation-based methodology grounded in feedback systems theory, which describes the temporal behavior of complex systems. In this approach, a complex system is conceptualized as a set of interconnected compartments containing specific contents, with flows of contents between compartments regulated by internal and external forces, as well as feedback loops that influence these flows [63,64].

In the context of market share forecasting, subscriber competition is represented as flows of subscribers among compartments, where each compartment corresponds to a specific provider. Given that the number of providers may vary across different markets, the following steps outline the proposed modeling approach to build a system model:

• Determine the governing flows: As established earlier (Equation (1)), these flows include churn, market trends, and subscriber attraction.
• Identify external forces: Assess how external forces and other influencing factors affect the determination of flow parameters. Examples include market conditions, competitive actions, and technological advancements.

By building upon these elements, a comprehensive market model can be developed that is tailored to the specific characteristics of the target market.

The derived market model can then be applied to forecast the providers’ market share over time. Standard deterministic system dynamics practices involve the use of simulation to provide fixed forecasts. The proposed modeling approach uses Monte Carlo simulation [65] to incorporate uncertainty into the forecast, resulting in a risk-informed forecast. In this setting, Monte Carlo methods transform deterministic model outputs into probability distributions by repeatedly sampling from specified input distributions, thereby quantifying not only expected outcomes but also the range and likelihood of alternative scenarios [66]. This approach is preferred as it accounts for inherent uncertainties in the market, such as market performance and subscriber preferences, which introduce variability in the flow parameters.

3.1. Churn Modeling

As suggested in [67], subscriber churn is the primary factor influencing a provider’s market share. Churn occurs when subscribers discontinue service with one provider and switch to another, often driven by factors such as dissatisfaction with pricing, service quality, or promotional incentives [15,16]. Consequently, churn can be viewed as the cumulative outcome of active subscribers’ decision-making processes at each time step.

At each time step, an active subscriber may choose to obtain service from any one of the providers. Simultaneously, each provider operates as an independent decision-maker with its own set of allowable actions—churn management strategies—that influence subscriber retention and acquisition. Providers independently decide whether to implement competitive churn management actions during each time step. The combined effect of all providers’ actions is manifested as changes in their respective market shares at the end of the time step, which then serves as the starting point for the next time step.

Given this framework, the number of outgoing subscribers for a provider due to churn is simulated at each time step. The net change in a provider’s market share reflects the cumulative result of its competitive churn management actions over the period under study. Since the outgoing subscribers due to churn are reallocated to competitive providers, they are accounted for as successfully attracted customers by those providers.

From the perspective of an individual provider, this flow of subscribers during a given time step is described mathematically as follows:

$$X_t=X_{t-1}-{Cn}_t+{Cp}_t$$

(2)

where

-

X_t: The provider’s market share at the end of the time step

-

X_t−1: The provider’s market share at the beginning of the time step

-

Cn_t: The number of outgoing subscribers due to churn

-

Cp_t: The number of incoming subscribers due to churn.

By considering outgoing subscribers as the reference churn action, for a market consisting of j active firms, Equation (2) can be rewritten for firm i as follows:

$$X_t^i=X_{t-1}^i-{Cn}_t^i+\sum _{j\ne i}{p}_{ij}·{Cn}_t^j$$

(3)

where

-

X_tⁱ: Market share of provider i at the end of the time step.

-

X_t−1ⁱ: Market share of provider i at the beginning of the time step.

-

Cn_tⁱ: Number of subscribers leaving provider i due to churn.

-

p_ij: The proportion of subscribers leaving firm j that switch to provider i.

In Equation (3), the incoming subscribers for provider i are expressed as the sum of the proportions of outgoing subscribers (churned customers) from all other active firms j who choose to switch to provider i.

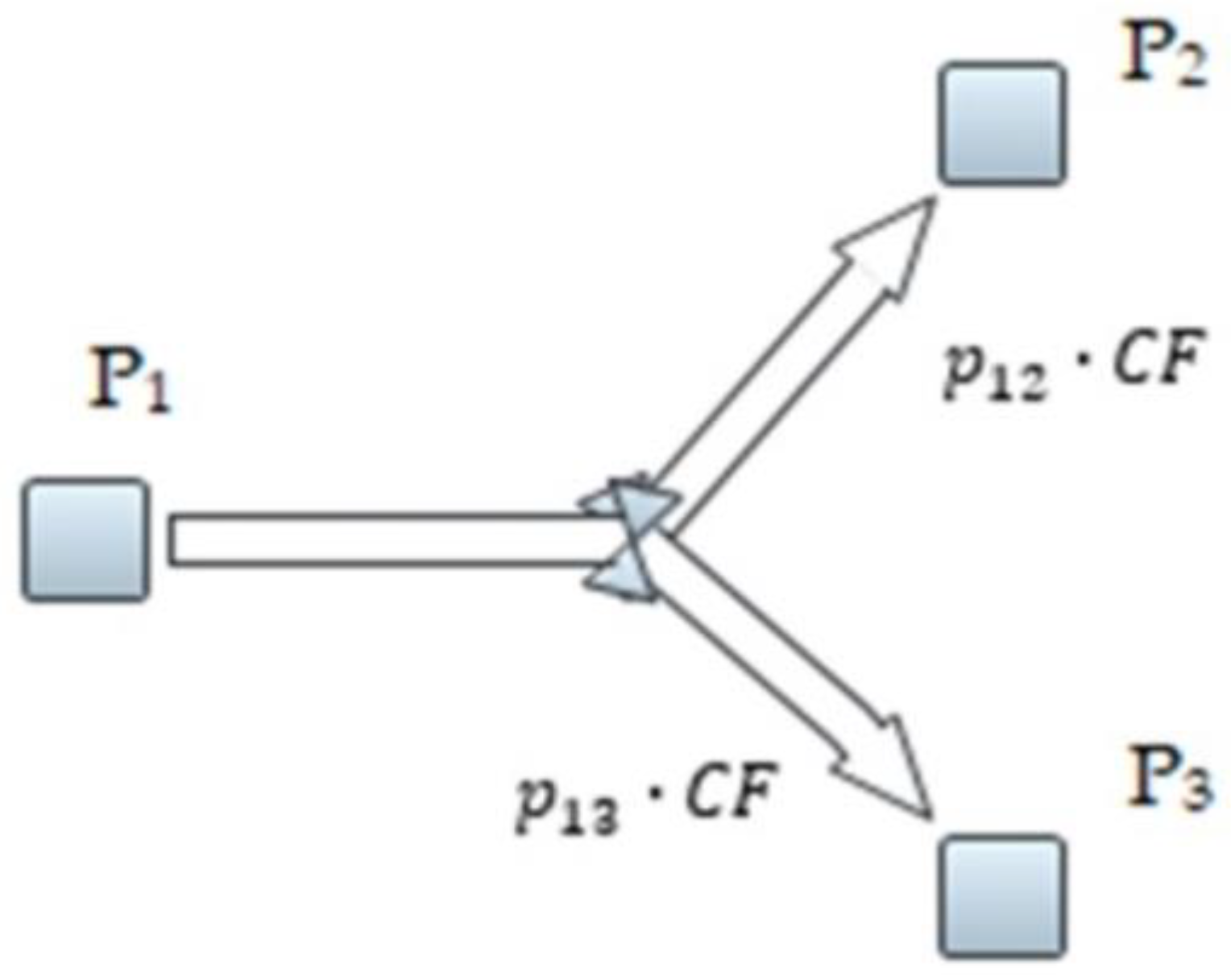
Based on the system dynamics modeling framework, the outgoing churn flow from Provider 1 (P₁) in a market with three competing firms is illustrated in Figure 1. The outgoing churn flow from Provider 1 is defined as $CF=a·P_1$, where α is the Outgoing Churn Rate.

Although Figure 1 illustrates the churn structure for Provider 1 only, the formulation is symmetric for all providers in the market. In the full three-provider system, the outgoing churn flow for each provider $i\in \{\mathrm{1,2},3\}$ is given by

$$C{F}_i\left(t\right)=a_i·X_{t-1}^i$$

(4)

where $X_{t-1}^i$ denotes the market share of provider $i$ at the beginning of the period and $a_i$ is its churn rate.

3.2. Market Performance and Subscriber Attraction Modeling

Based on the problem formulation in Equation (1), a provider’s ability to attract new subscribers directly impacts its market share. More specifically, in the real world, the overall market size is defined as the sum of the market shares of all active providers at a given time t. Mathematically, this relationship can be expressed as:

$$M_t=\sum X_t^i$$

(5)

where

-

M_t: Overall market size at time step t

-

X_tⁱ: Market share of provider i at time step t

Under this approach, any changes in the overall market performance are directly linked to fluctuations in the providers’ subscriber bases. These changes result from two key processes: the inflow of new market entrants (new subscribers entering the market) and the outflow of subscribers leaving the market. Notably, these flows occur simultaneously but remain independent of churn flows, which represent the redistribution of subscribers among existing providers.

With the framework’s goal being to analyze the impact of subscriber flows on providers’ market share, a top-down modeling approach is essential. This process begins by modeling changes at the overall market level, which are then diffused to individual providers.

Subsequently, in the proposed system dynamics modeling framework, provider attraction flows are conceptualized as flows originating from a compartment M, representing the overall market size or market saturation point, toward the compartments corresponding to individual providers. These flows can be positive (outflows from M) or negative (inflows to M), indicating either a growth or reduction in a provider’s subscriber base due to market evolution at a specific time step.

This process is mathematically described by Equation (6):

$${\Delta X}_t^i=q_i·{\Delta M}_t|\sum q_i=1$$

(6)

where

-

ΔM_t: Change in overall market size at time step t

-

ΔX_tⁱ: Change in the i-th provider’s market share at time step t

-

q_i: A coefficient indicating the relationship between changes in the overall market size and changes in provider i’s market share at time step t. It can take a positive value to represent market share growth or a negative value for market share reduction.

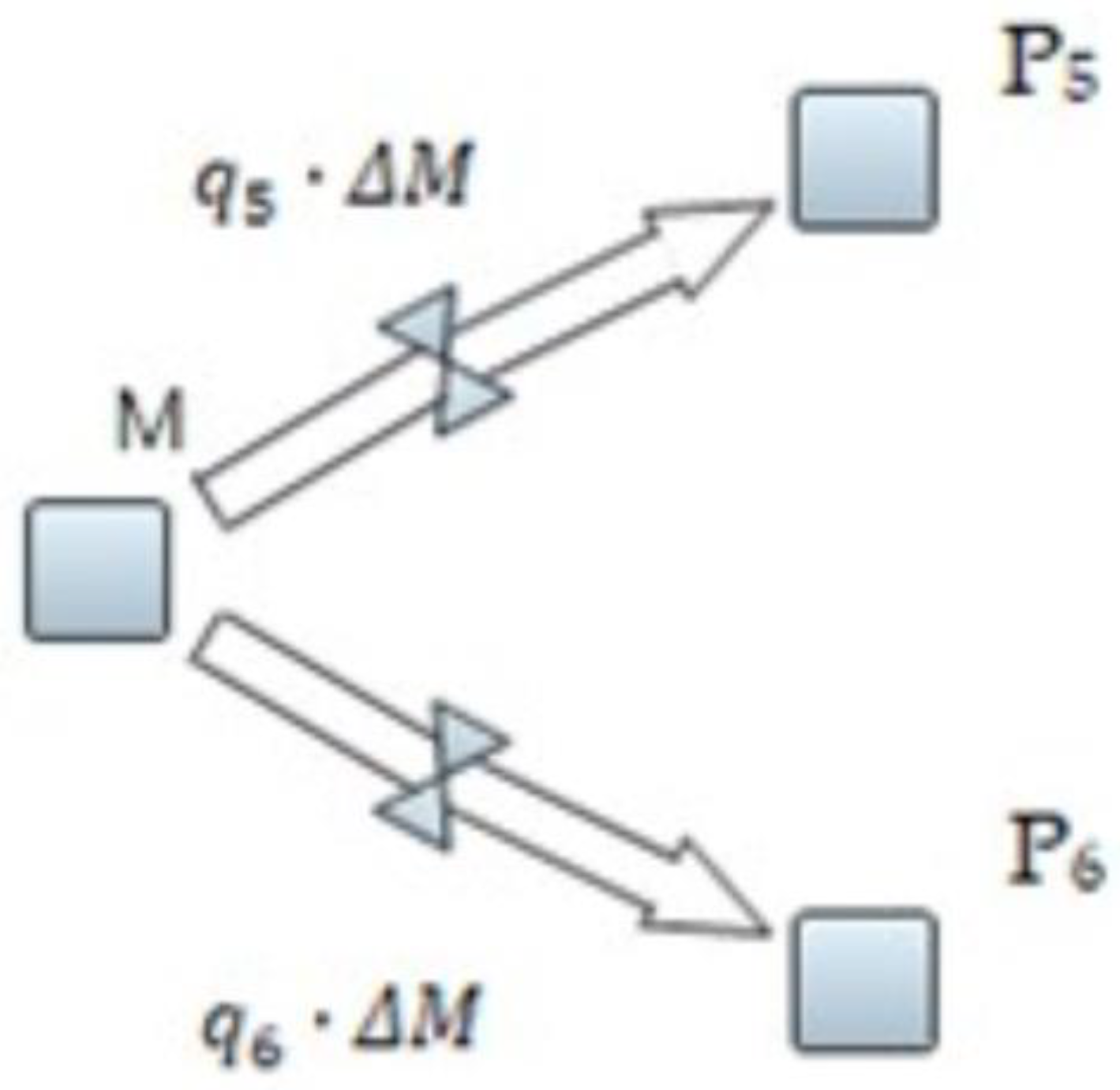
Based on Equation (6), Figure 2 depicts the generic attraction-flow structure for two representative providers, labeled P₅ and P₆, where q₅ and q₆ denote the corresponding attraction coefficients: ${\Delta {\rm X}}_5=q_5·\Delta {\rm M}$ and ${\Delta {\rm X}}_6=q_6·\Delta {\rm M}$.

3.3. Flow Parameter Determination

Building upon the definition of basic flows, the next step in completing the system’s structure is to identify and incorporate the factors that influence flow values. These factors, which may include external forces such as market trends, competitive actions, and technological advancements, must be carefully analyzed and integrated into the system dynamics framework. By explicitly defining these influences, the model becomes more robust and capable of accurately representing the dynamic interactions within the market.

Traditional system dynamics suggests that adoption flows follow the “decay equation”, described as:

$${\displaystyle \frac{dP}{dt}}=-\lambda P$$

(7)

where the rate of change in the population P over time is proportional to the current population. Here, λ is a constant that represents the adoption rate, under the assumption that the population is a homogeneous group with uniform, average behavior, resulting in a constant adoption rate over time.

However, this principle does not hold in all cases. In reality, the adoption rate may vary over time due to factors such as external influences, market conditions, or differing individual behaviors. This perspective aligns with the diffusion of innovations models, which are widely applied in technology diffusion forecasting and account for varying adoption dynamics over time [68].

Consequently, λ can be allowed to vary over time by incorporating feedback loops or predefined value series, depending on the modeling requirements. This flexibility enables the adoption flow to reflect more realistic dynamics. Additionally, the evolution of adoption flows can be modeled to vary pseudo-randomly by drawing values from selected probability distributions, such as normal, uniform, or exponential distributions. Introducing such variability adds uncertainty to the diffusion estimation. In these scenarios, Monte Carlo simulation becomes essential for obtaining results, as the adoption flow values change with each iteration, providing a range of possible outcomes, offering a risk-informed forecast.

Furthermore, λ can be modeled to exhibit behavioral changes during the simulation in response to triggering events from the system’s external environment. For example, the launch of a marketing campaign, the deployment of a novel technology or service by one firm or market entry or exit of a provider may significantly influence subscriber behavior, including churn and adoption dynamics. This event-driven approach ensures the model captures the impact of external forces on adoption and churn rates, offering a more robust and adaptive representation of market behavior.

A comprehensive analysis of how system dynamics flow parameters may determined can be found in [69,70].

3.4. Model Application

As discussed above, the main purpose of the proposed approach is to forecast the market share of active firms in a target market at a specific time. Under this approach, the outputs of the proposed market share modeling system depend on the selected methods for modeling flows and external forces. If flow rates and external forces are assumed constant throughout the simulation period, the results provide a numerical estimation of each provider’s market share at every simulation time step. Conversely, when uncertainty or time variation is introduced into the flow parameters—either directly or through external forces—the model produces a risk-informed forecast of providers’ market share. This is achieved through Monte Carlo simulation, where multiple iterations account for variability in the system.

The proposed modeling framework leverages a comprehensive analysis of uncertainty factors influencing the target telecommunications market to generate risk-informed forecasts using Monte Carlo simulation. This approach is particularly suited to the dynamic nature of the telecommunications market, characterized by intense competition and rapid changes in the services provided.

Modeling results can be further refined through a variance-based sensitivity analysis, which determines the relative impact of each parameter on the forecast results. This enhances the robustness and interpretability of the model’s outputs.

Consequently, the proposed framework is implemented through a four-step process:

• System Structure Definition: Specify the system’s structure by defining the number of compartments (providers) and the attraction and churn flows between them.
• Market Performance Modeling: Establish the overall market performance dynamics, including trends, growth rates, and competitive influences.
• Flow Parameter Determination: Define the process for flow parameter selection by identifying the key factors influencing flow values.
• Result Derivation: Generate simulation results based on the selected market structure and chosen simulation methodology (e.g., deterministic or stochastic approaches).

It is important to note that the application of the proposed approach is not limited to forecasting alone.

For established markets where time-series data on providers’ performance is available, the process can be reversed. At a specific time step, market share data can be used to calibrate the model’s parameters through data fitting techniques. This enables providers to evaluate the actual impact of their competitive strategies and assess their resilience against market competition. Such insights are valuable for informing adjustments to existing strategies or developing new competitive approaches. This is a vital step in the flow parameter determination process described above.

The proposed framework also supports the analysis of market entry and exit scenarios. At any time step, a decision variable can be introduced to simulate the entry of a new provider into the market. This variable can be case-specific, for example, linked to overall market performance, or defined arbitrarily. The framework also allows for the modeling of multiple provider entries simultaneously. Additionally, the model can impose restrictions that trigger a provider’s exit from the market. For instance, if a provider’s market share falls below a predefined threshold, exit conditions can be activated. This logic can be extended to all active providers, enabling the simulation of multiple exits. Decision variables and restrictions must be carefully designed according to the user’s specific requirements and assumptions to accurately simulate the resulting subscriber flows during such events.

By incorporating these features, the proposed system dynamics framework can be applied for long-term market structure modeling and forecasting, in conjunction with market share analysis. This comprehensive approach enables providers to anticipate market changes, analyze competitive interactions, and develop informed strategies to maintain their competitive edge in dynamic telecommunications markets.

4. Example Application

To illustrate the dynamics of the proposed system dynamics modeling approach, it is applied to the Greek mobile telecommunications market.

The Greek mobile market consists of three active providers: the incumbent provider Cosmote and the alternative providers Vodafone and Wind Hellas. These providers offer homogeneous mobile services to their subscribers, including 2G/2.5G, 3G, 4G, 5G, and VoLTE services.

The Greek mobile telecommunications market is particularly suitable for validating this data-lean system dynamics framework for three key methodological reasons:

• The market has consistently maintained a highly stable three-firm competitive structure (Cosmote, Vodafone, Wind Hellas) over the entire 17-year analysis period (2006–2022). This stability minimizes the need to model complex, external events like new market entry or exit, allowing the focus to remain squarely on inter-provider subscriber flows (churn and attraction), which is the core mechanism of the proposed framework.
• The market reached maturity and saturation by the end of the training period (2017), as confirmed by the S-curve modeling. This provides a rigorous test case for the framework’s ability to accurately forecast redistribution dynamics where competition is fierce, rather than simple market growth.
• The availability of long-term, aggregate, publicly sourced data allows the demonstration a core advantage of our framework: its ability to produce robust, risk-informed forecasts without relying on proprietary, granular, individual-level customer data, proving its utility in data-constrained settings.

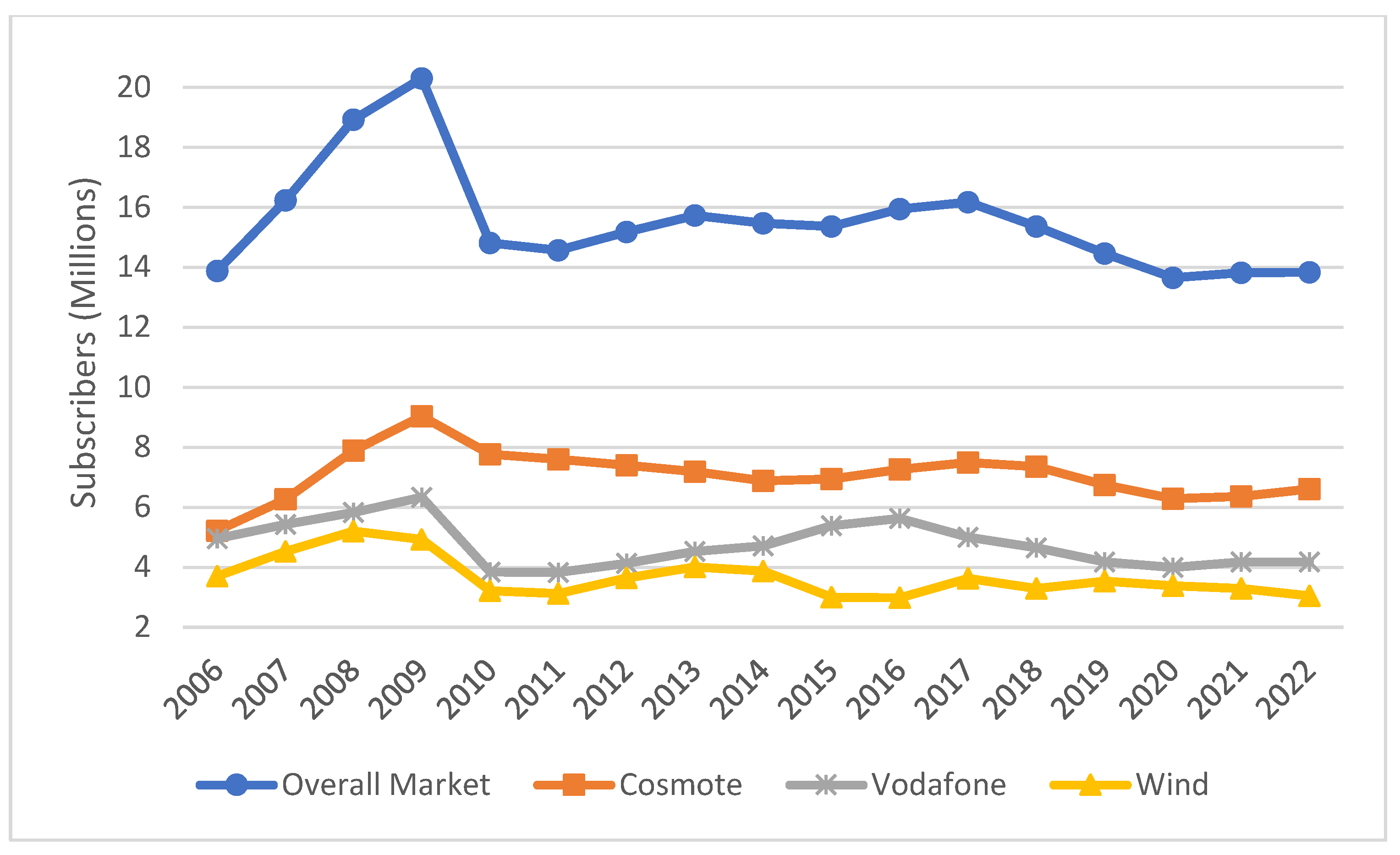
Market data include the total number of mobile subscribers and the respective market shares of the three providers from 2006 to 2022 (

Table 1. Greek Mobile Telecommunications Market Data.

Year	Market Data		Provider Market Share
	Subscriber Base	Market Change	Cosmote	Vodafone	Wind
2006	13,874,674	-	37.6%	35.7%	26.7%
2007	16,226,675	16.952%	38.6%	33.5%	27.9%
2008	18,918,092	16.586%	41.7%	30.8%	27.5%
2009	20,298,102	7.295%	44.5%	31.2%	24.3%
2010	14,815,705	−27.009%	52.4%	25.9%	21.7%
2011	14,557,672	−1.742%	52.2%	26.3%	21.5%
2012	15,176,344	4.250%	48.8%	27.2%	24.0%
2013	15,722,476	3.599%	45.7%	28.8%	25.5%
2014	15,473,683	−1.582%	44.5%	30.4%	25.0%
2015	15,353,553	−0.776%	45.2%	35.1%	19.5%
2016	15,934,294	3.782%	45.6%	35.3%	18.7%
2017	16,167,273	1.462%	46.3%	30.9%	22.4%
2018	15,354,388	−5.028%	47.9%	30.3%	21.4%
2019	14,458,145	−5.837%	46.6%	28.9%	24.5%
2020	13,650,884	−5.583%	46.0%	29.2%	24.8%
2021	13,813,026	1.188%	46.0%	30.2%	23.8%
2022	13,826,201	0.095%	47.8%	30.2%	22.0%

Source: eett.gr.

), which constitute the most recent publicly available series. These data are published annually by the Hellenic Telecommunications and Post Commission (EETT), the Greek National Regulatory Authority (NRA) [www.eett.gr (accessed on 15 Aug 2025)]. The availability of long-term data spanning almost two decades allows for a detailed examination of market trends, competitive dynamics, and subscriber flows over time. Given the annual data frequency, the time step (Δt) for the simulation is set to one year.

Figure 3 presents the time evolution of the subscriber base and market shares over the entire analysis period (2006–2022). A structural break in 2010, associated with the SIM registration policy shock, is clearly visible in the subscriber base dynamics, while the market shares exhibit more gradual but non-trivial adjustments over time. The figure confirms that the market share series are not merely smooth deterministic trends but display meaningful competitive dynamics and redistribution patterns even in the mature phase of the market, thereby justifying the use of both a structurally rich system dynamics framework and a statistical benchmark for forecasting.

The overall application is divided into two phases to ensure methodological rigor:

• Calibration (2006–2017): Flow parameters and model volatility are determined and fitted to the historical data, specifically using the 2007–2017 period for parameter fitting to stabilize the initial volatile years.
• Validation/Forecasting (2018–2022): A 5-year hold-back period is utilized. The resulting stochastic forecasts are compared against the actual observed market data to assess the model’s predictive accuracy and robustness, based on predefined validation criteria. It is noted that the 5-year hold-out matches medium-term planning horizons and provides a meaningful out-of-sample test of share forecasts.

The specific calibration windows used for the diffusion, churn/attraction flows and volatility parameters are summarized in Section 4.1, which also explains how the 2010 policy-induced structural break is treated in the analysis.

The four-step process outlined above—system structure definition, market performance modeling, flow parameter determination, and result derivation—is applied to the Greek telecommunications market case study. By evaluating both historical performance and projected trends, this analysis offers insights into the competitive dynamics of the market, the impact of churn and subscriber attraction strategies, and the overall market evolution.

4.1. Data Pre-Processing and Reliability Checks

To ensure the rigor and reliability of the data utilized for calibration and validation, the raw market share and subscriber base time-series data from the EETT underwent specific pre-processing and checks:

• Data Reliability: As the data is sourced annually from the Greek NRA, it is considered highly reliable and does not contain missing values in the primary variables (Subscriber Base, Market Share) for the analysis period (2006–2022).
• Missing Data Treatment: No imputation for missing data was required as the time-series is complete.
• Adjustment for Structural Breaks/Policy Shocks: The historical data exhibits a significant drop in subscriber numbers in 2010 due to a policy shock (regulatory changes related to SIM card registration). This non-market driven event constitutes a structural break. Therefore, whereas the entire 2006–2022 period is used for overview and historical context, for parameter calibration (fitting the Logistic S-Curve, determining churn/attraction rates, and volatility analysis), the 2007–2017 period is used, and the volatility analysis specifically excludes the immediate pre- and post-shock years by focusing on 2011–2017. This strategic selection minimizes the influence of the regulatory shock on model parameters, ensuring they reflect competitive dynamics rather than exogenous policy disturbances.
• Market Structure Check: Throughout the analysis period, the market was checked for structural changes; the stable presence of three active providers (Cosmote, Vodafone, Wind Hellas) was confirmed, meaning no adjustments for market entry or exit were necessary.

4.2. Step 1: System Structure Definition

Based on the churn and subscriber attraction flow determination presented in the previous section, the overall market structure is presented in

Table 2. Proposed System Model Structure and Parameters.

System Component	Change	Remarks
Compartment M	${\displaystyle \frac{dM}{dt}}=+dG$
Flow G	$dG=\mu \left(t\right)dt+b\left(x,t\right)dz$	Overall market growth
Compartment P1	${\displaystyle \frac{d{P}_1}{dt}}=+{\Delta {\rm X}}_1-{CF}_1+\left(p_{21}·{CF}_2\right)+\left(p_{31}·{CF}_3\right)$
Compartment P2	${\displaystyle \frac{d{P}_2}{dt}}=+{\Delta {\rm X}}_2-{CF}_2+\left(p_{12}·{CF}_1\right)+\left(p_{32}·{CF}_3\right)$
Compartment P3	${\displaystyle \frac{d{P}_3}{dt}}=+{\Delta {\rm X}}_3-{CF}_3+\left(p_{23}·{CF}_2\right)+\left(p_{13}·{CF}_1\right)$
Attraction Flow ΔΧ1	${\Delta {\rm X}}_1=q_1·\Delta M$
Attraction Flow ΔΧ2	${\Delta {\rm X}}_2=q_2·\Delta M$
Attraction Flow ΔΧ3	${\Delta {\rm X}}_3=q_3·\Delta M$
q1	$N\left(\mu ,{\sigma }^2\right)$	Provider P1 Attraction Rate
q2	$N\left(\mu ,{\sigma }^2\right)$	Provider P2 Attraction Rate
q3	$1-q_1-q_2$	Provider P3 Attraction Rate
Churn Flow CF1	${CF}_1=a_1·P_1$	Outgoing churn flow from provider P1
Churn Flow CF2	${CF}_2=a_2·P_2$	Outgoing churn flow from provider P2
Churn Flow CF3	${CF}_3=a_3·P_3$	Outgoing churn flow from provider P3
p12	${\displaystyle \frac{q_1}{q_1+q_2}}$
p13	${\displaystyle \frac{q_1}{q_1+q_3}}$
p21	${\displaystyle \frac{q_2}{q_2+q_1}}$
p23	${\displaystyle \frac{q_2}{q_2+q_3}}$
p31	${\displaystyle \frac{q_3}{q_3+q_1}}$
p32	${\displaystyle \frac{q_3}{q_3+q_2}}$
a1	$N\left(\mu ,{\sigma }^2\right)$	Provider P1 Churn Rate
a2	$N\left(\mu ,{\sigma }^2\right)$	Provider P2 Churn Rate
a3	$N\left(\mu ,{\sigma }^2\right)$	Provider P3 Churn Rate

.

The system utilizes four compartments. Compartment M represents the overall market and compartments P₁, P₂ and P₃ correspond to the three providers, Cosmote, Vodafone and Wind, respectively.

The attraction and churn flows between these compartments follow the notation provided in Section 3. Outgoing churn flows are used as the reference flows within the system.

Additionally, an overall market growth function G is integrated into the system structure. This function simulates the stochastic evolution of the overall market size over time. It reflects variability in market expansion due to factors such as economic conditions, technological advancements, and demand growth.

Furthermore, the following assumptions are incorporated into the system structure:

(a)

Providers are assumed to offer homogeneous mobile services to their subscribers throughout both the analysis and forecasting periods.

(b)

Under the NRA’s regulatory oversight, no instances of abuse of dominant position, predatory pricing, or other deceptive, disruptive, or anti-competitive practices are considered.

These assumptions simplify the analysis and focus the model on subscriber flows driven by market dynamics rather than external regulatory disturbances. As a result, no additional triggering events or external forces are incorporated into the market model. Instead, competitive behavior is captured through the market share uncertainty during the forecasting period.

To complete the system’s structure, parameters p_ij and q_i need to be established. These can be treated either separately, assuming they do not affect each other or cumulatively, implying a connection between a provider’s ability to attract both new and active subscribers.

For the purposes of the example analysis, the cumulative case is considered. This is achieved by expressing p_ij parameters in terms of q_i, establishing a direct connection between the attraction flows and a provider’s subscriber acquisition dynamics.

The complete analysis of the model structure is provided below:

4.3. Step 2: Market Performance

As shown in Table 1, the Greek mobile telecommunications market experienced a growth phase up to 2009, reaching a peak of approximately 20.3 million subscribers. In 2010, a sharp decline in subscriber numbers occurred, primarily due to regulatory changes related to SIM card registration. This event constitutes a structural break in the time-series not related to competitive dynamics. Following this shock, the market exhibited a period of recovery, with subscriber numbers increasing until 2017 to over 16.1 million subscribers. However, after 2018, a gradual decline was observed, with the total number of subscribers reducing to less than 14 million by the end of 2022.

While the specific reasons behind these fluctuations are beyond the scope of this study, they provide an opportunity to demonstrate the proposed framework’s performance in markets exhibiting changing behavior patterns. Notably, during the analysis period (2006–2022), the number of active subscribers remained relatively stable, fluctuating between 11.3 million in 2022 and 13.8 million in 2008.

The market share distribution highlights the dominance of the incumbent operator Cosmote, which consistently captures approximately 50% of the market. The remaining 50% is shared between the alternative operators, Vodafone and Wind Hellas.

To capture market performance and uncertainty for the stochastic model application during the forecasting period, the calibrated Itô stochastic process approach presented in [69] is selected. This method integrates the diffusion of innovations theory with stochastic processes, enabling the incorporation of diffusion uncertainty into long-term forecasting.

The calibrated Itô stochastic process is presented in Equation (8):

$$dx=\mu \left(t\right)dt+b\left(x,t\right)dz$$

(8)

where

-

dz is the increment of a Wiener process

-

The coefficient µ(t) corresponds to the calibrated diffusion growth rate defined in Equation (9)

-

Parameter b(x,t) reflects the volatility exhibited by the data, as a result of uncertainty.

$$\mu \left(t\right)={\displaystyle \frac{{\sum }_0^{t}N\left(t\right)-{\sum }_0^{t-1}N(t-1)}{{\sum }_0^{t-1}N(t-1)}}={\displaystyle \frac{N\left(t\right)}{{\sum }_0^{t-1}N(t-1)}}$$

(9)

It is noted that in the absence of volatility [b(x,t) = 0], Equation (8) converges to the S-shaped diffusion model that best-fits the market data.

Following the proposed market modeling approach, the logistic s-curve was selected to model the market growth rate over the time period under consideration (2006–2017), as it provided the best statistical fit to the observed data. The Logistic model is expressed as:

$$Y\left(t\right)={\displaystyle \frac{S}{1+b·e^{\left(-c·t\right)}}}$$

(10)

The parameters for the logistic S-curve and volatility are summarized in

Table 3. Market Performance Parameters.

Greek Mobile Market Modeling
S-curve Logistic	c	0.4519
	b	1.4870
	S	16,290,206
Volatility	σ	0.023

:

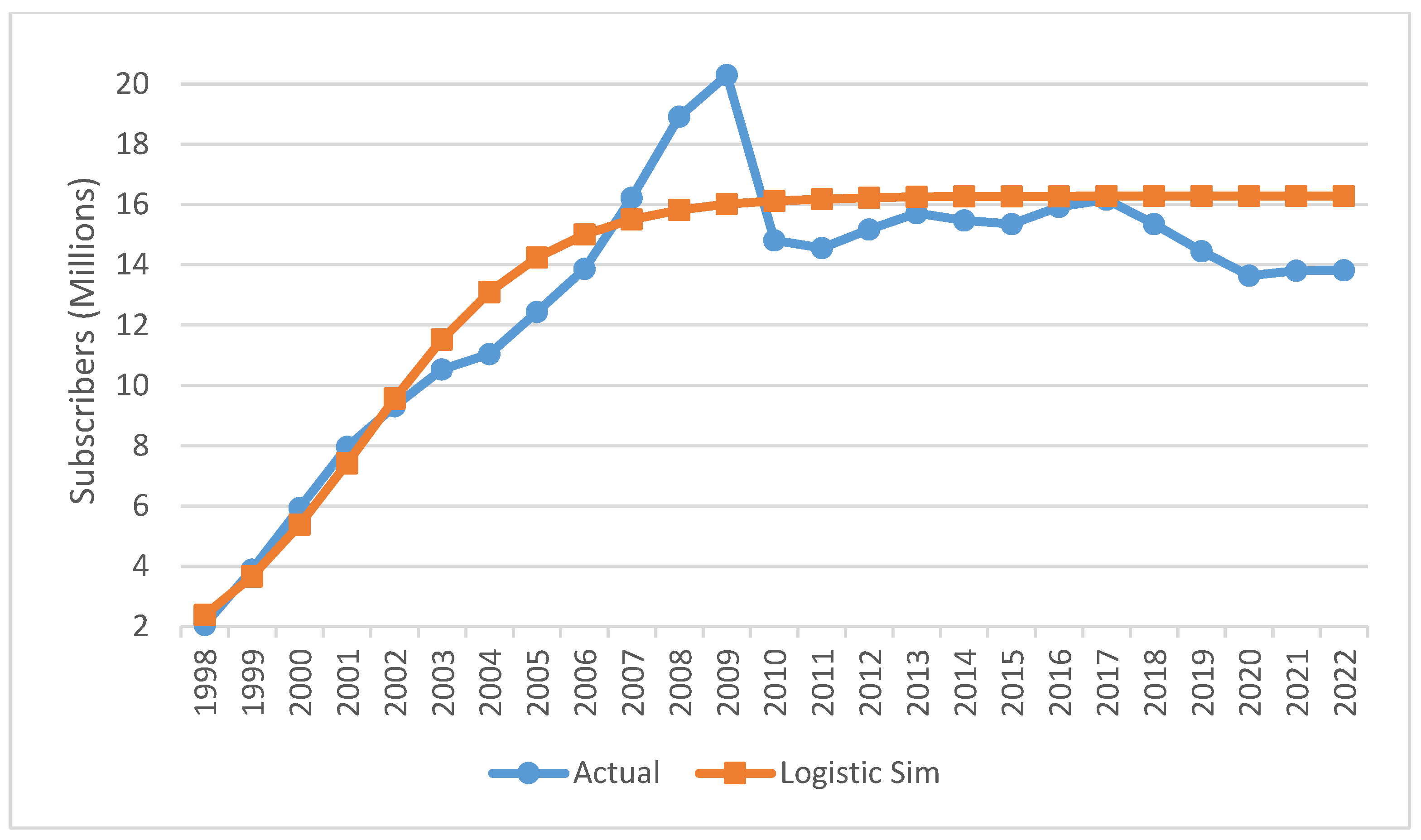
The calibrated diffusion model based on Equations (8)–(10) is presented in Figure 4 in order to focus on the goodness of fit of the aggregate market process. It is noted that, for the full span 1998–2022, the logistic fit yields MAE ≈ 0.56 million, RMSE ≈ 0.69 million, MAPE ≈ 6.0% (≈3–6% of the market level). This is adequate for the study’s purpose—The diffusion/logistic component for M_t serves only to provide a parsimonious driver for ΔM_t; its standalone level fit is informative but not decisive for the quality of share forecasts.

To continue with the calibrated Itô stochastic process calculations, the residuals for the years 2011–2017 (training period) were analyzed, as this period avoids the regulatory disruptions that occurred before 2011. The residuals were found to follow a normal distribution, with a volatility coefficient of 2.3%, reflecting the underlying uncertainty in market performance.

The choice of 2011–2017 as the training window for the stochastic component is intentional and serves two purposes. First, it excludes the 2010 policy shock and its immediate aftermath, ensuring that the diffusion and volatility parameters reflect competitive dynamics rather than regulatory-induced structural breaks. Second, although annual data on subscribers and market shares are available up to 2022 (Table 1), the years 2018–2022 are deliberately withheld as a 5-year out-of-sample hold-back period for forecast validation. This design mimics a realistic ex-ante forecasting exercise in which model parameters are estimated using information available up to the end of 2017, and subsequent years are reserved solely for evaluating predictive performance. Extending the calibration window beyond 2017 would contaminate the hold-out evaluation and lead to overly optimistic accuracy assessments, undermining the purpose of the validation exercise.

The stochastic modeling results demonstrate that by the end of the training period (2017), the Greek mobile market has reached saturation. Therefore, any changes observed after this period can be considered random and driven by external forces.

The fitted stochastic process constitutes the market growth function G within the Greek mobile market system model, which is applied during the forecasting period. In the system dynamics implementation, Equation (8) is used exclusively to generate the stochastic path of the aggregate subscriber base M_t, i.e., the stock of compartment M in Table 2. At each simulation step, the realized increment ΔM_t implied by Equation (8) is translated into attraction flows from M to the provider compartments via Equation (5) and the coefficients q_i. These attraction flows are combined with the outgoing churn flows $C{F}_i\left(t\right)$ defined in Section 3.1 and Equation (3) to update each provider’s market share. In this way, the calibrated Itô diffusion governs the total market size, while the flow-based system dynamics structure determines how this aggregate evolution is redistributed among competing providers. This information can be further applied to formulate a market growth strategy for deterministic analysis, based on expected market performance and the required sensitivity analysis.

It is important to note that while the calibrated Itô stochastic process was selected in this analysis, alternative approaches may also be employed for the forecasting period, depending on the specific requirements and assumptions of the user.

4.4. Step 3: Flow Parameter Determination

Following the market performance determination and the proposed system model structure (Table 2), the next crucial step is the explicit determination and calibration of churn and attraction flow parameters (a₁, a₂, a₃ for churn and q₁, q₂, q₃ for attraction). The calibration is performed using the training period data (2007–2017).

4.4.1. Attraction Parameter Calibration

For the training period, attraction parameters (q_i) are assumed to be proportional to the providers’ average market share. This assumption is made due to the absence of detailed individual-level attraction data for the Greek mobile market and is grounded in the network effects that govern the telecommunications sector.

The mean values are calculated from the historical data (2007–2017):

• Cosmote, the incumbent provider, demonstrates the highest average attraction rate at approximately 46%.
• Vodafone follows with an average attraction rate of 30%,
• Wind Hellas ranks third with an average attraction rate of 22.5%.

4.4.2. Churn Parameter Calibration

Once the attraction parameters are defined, the churn parameters (a₁, a₂, a₃) are determined through a parameter fitting process. Specifically, a Goal-Seek Analysis (minimizing the Root Mean Square Error, RMSE) is applied to align the calculated churn rates with the observed market share behavior during the training period (2007–2017). This ensures the model accurately replicates the actual subscriber redistribution dynamics before forecasting. The resulting churn flow parameters are summarized in

Table 4. Greek Mobile Telecommunications Providers’ Estimated Churn Rates.

Year	Cosmote	Vodafone	Wind
2007	26.763%	32.210%	30.700%
2008	19.442%	29.947%	28.411%
2009	19.631%	26.592%	35.189%
2010	26.904%	51.387%	52.482%
2011	19.020%	28.468%	31.492%
2012	23.594%	29.377%	27.071%
2013	24.340%	26.783%	27.863%
2014	22.746%	25.074%	30.217%
2015	20.561%	18.807%	41.533%
2016	20.790%	24.851%	32.865%
2017	22.355%	34.327%	24.222%
Mean	22.377%	29.802%	32.913%
St.Dev	2.67%	7.87%	7.58%

.

The findings presented in Table 4 align with those of [67], who reported that annual churn rates in telecommunications typically range between 20% and 40%.

Key observations include:

• The incumbent provider Cosmote maintains a lower churn rate (approximately 22%) compared to the alternative operators, whose churn rates are closer to 30%.
• The variability (standard deviation) in churn rates for Vodafone and Wind Hellas is significantly higher than for Cosmote, suggesting greater instability in their subscriber bases.

These insights are valuable for analyzing the effectiveness of past competitive strategies employed by providers. Understanding churn variability and attraction rates allows providers to assess their relative performance and identify areas for improvement. This step is a crucial component of the proposed methodology.

4.4.3. Stochastic Parameterization for Forecasting

For the forecasting period (2018–2022), both churn and attraction flow parameters are modeled using a Bounded Random Distribution (Normal) to incorporate uncertainty. The Normal distribution was selected because the historical residuals of the market performance (Section 4.3) approximated a normal distribution, and the resulting historical churn and attraction rates (Table 4) exhibit central tendencies appropriate for Normal fitting.

• The mean and standard deviation for these distributions are set equal to the calculated historical mean and standard deviation values from the 2007–2017 training period.
• The distributions are bounded, reflecting the historical minimum and maximum churn levels achieved by each provider from the perspective of subscriber behavior, preventing unrealistic scenario generation

The use of random bounded distributions to model customer attraction and churn strategies aligns with existing literature on churn and attraction flow estimation. For instance, [71] highlights the importance of using dynamic, uncertain variables rather than static averages to improve forecast accuracy. Similarly, [72] emphasizes that churn and attraction parameters are often provided as time-series data, enabling the tracking of changes and the fitting of appropriate distributions.

Furthermore, the inclusion of Monte Carlo simulation provides additional flexibility by allowing the model to utilize uncertain variables as inputs rather than static average values. This approach ensures that the forecasts account for variability and randomness, leading to more realistic and robust results. In the baseline implementation, the stochastic innovations to churn and attraction flows are assumed independent across providers and years, conditional on their historical means and standard deviations. Extending the framework to allow for correlated shocks—for example, via multivariate Normal draws for flows related to the same period or provider pairs—is conceptually straightforward and represents a natural direction for future research.

In summary, for all Monte Carlo experiments the only distributional assumption imposed at the input level is the bounded Normal specification for the churn and attraction flow parameters described above. The alternative families mentioned later in Section 5.2 (Normal, Lognormal, Beta) are used solely as ex-post parametric approximations to the simulated market-share distributions and do not affect the generation of scenarios. This distinction ensures that the stochastic structure of the input flows is driven directly by historical data, while distributional labels assigned to the simulated market shares serve only to summarize the emergent output behavior. The adequacy of these distributional choices is validated in three ways:

• the residuals of the aggregate market diffusion process (Section 4.3) are approximately Normal, supporting the Normal specification for the flow parameters;
• the simulated mean and median market shares over the 2018–2022 hold-back period closely match the realized values, with absolute errors typically well below one percentage point (

  Table 5. Simulation Results (Year 2022).

  Statistics	Cosmote	Vodafone	Wind
  Trials	10,000
  Mean	47.23%	30.26%	22.53%
  Median	47.19%	30.09%	22.43%
  St. Deviation	3.56%	3.49%	2.69%
  Variance	0.13%	0.12%	0.07%
  Coeff. Of Variation	0.0754	0.1154	0.1192
  Minimum	34.57%	18.99%	12.91%
  Maximum	61.63%	44.98%	35.13%
  Fit Distribution	Lognormal	Beta	Lognormal
  Actual Market Share	47.8%	30.2%	22.0%

  and

  Table 6. Comparative out-of-sample forecast accuracy of the proposed system dynamics framework and the reconciled ARIMA benchmark for the final validation year (2022).

  Provider	Actual Market Share 2022 (%)	System Dynamics Mean Forecast 2022 (%)	Absolute Error— System Dynamics (pp)	ARIMA + Reconciliation Forecast 2022 (%)	Absolute Error—ARIMA + Reconciliation (pp)
  Cosmote	47.8	47.23	0.57	44.88	2.92
  Vodafone	30.2	30.26	0.06	31.83	1.63
  Wind	22.0	22.53	0.53	23.28	1.28
  MAE	-	-	0.39	-	1.94

  (pp = percentage points).

  ); and
• the system dynamics framework systematically outperforms a coherent ARIMA benchmark under standard forecast-accuracy metrics (MAE, RMSE, MAPE) (

  Table 7. Forecast accuracy statistics over the 5-year validation period (2018–2022) for the proposed system dynamics framework and the reconciled ARIMA benchmark.

  Provider	Model	MAE (pp)	RMSE (pp)	MAPE (%)
  Cosmote	System Dynamics	0.87	0.94	1.86
  	ARIMA + Reconciliation	2.39	2.55	5.07
  Vodafone	System Dynamics	0.66	0.91	2.27
  	ARIMA + Reconciliation	1.35	1.45	4.54
  Wind	System Dynamics	1.45	1.57	6.14
  	ARIMA + Reconciliation	1.62	2.15	7.25
  Overall	System Dynamics	1.00	1.18	3.42
  	ARIMA + Reconciliation	1.79	2.10	5.62

  (pp = percentage points).

  ), indicating that the stochastic specification leads to empirically reliable forecasts.

All stochastic scenarios are simulated with annual steps; churn uses beginning-of-year shares $X_{i,t-1}$, attraction maps the within-year ΔM_t, and no further lags are assumed.

4.5. Benchmark Model Formulation

To quantify the contribution of the proposed framework, its performance was benchmarked against a widely used statistical approach: the Autoregressive Integrated Moving Average (ARIMA) model, combined with a constrained reconciliation technique based on the minimum-error variance combination rule of Guerrero and Peña [62]. This benchmark represents a standard, data-driven time-series formulation that is adapted to the compositional nature of market-share data by enforcing coherence ex post.

The benchmark model was structured as a Bottom-Up reconciliation approach. First, three separate best-fit ARIMA models were calibrated on the 2007–2017 training period to forecast the market share of each provider (Cosmote, Vodafone, Wind Hellas) over the 5-year validation period (2018–2022). For each provider i, an ARIMA $(p_i,d_i,q_i)$ specification with intercept was estimated, and the orders $(p_i,d_i,q_i)$ were selected by minimizing the Akaike Information Criterion (AIC) over a grid of low-order candidates, subject to standard identification diagnostics. This procedure yielded parsimonious models that capture the short-memory dynamics of each individual market-share series.

The resulting ARIMA components produce, for each validation year $t$, a vector of base market-share forecasts $f_t=(f_{1t},f_{2t},f_{3t}{)}^{\mathrm{\top }}$. Because these forecasts are obtained independently, their sum does not necessarily equal unity, and therefore they may violate the compositional coherence constraint. To restore coherence while preserving as much of the statistical information as possible, the base forecasts are adjusted using the combination rule of Guerrero and Peña. Specifically, let Σ denote the 3 × 3 covariance matrix of one-step-ahead forecast errors from the ARIMA models, estimated on the 2007–2017 training period, and let 1 denote a three-dimensional vector of ones. For each year t, the reconciled forecast vector g_t is obtained as

$$g_t=f_t-\Sigma 1{\left(1^{\top }\Sigma 1\right)}^{-1}(1^{\top }{f}_t-1)$$

(11)

which solves the minimum-variance problem of finding the coherent vector g_t satisfying ${\mathbf{1}}^{\mathrm{\top }}{g}_t=1$ that is closest to f_t in the quadratic form induced by ${\mathsf{\Sigma }}^{-1}$. In other words, the adjustment redistributes the incoherence ${\mathbf{1}}^{\mathrm{\top }}{f}_t-1$ across providers in proportion to their estimated forecast-error covariance structure, yielding a set of market-share forecasts that is both coherent and optimally combined under the assumed error variance.

Finally, the reconciled share forecasts g_t are converted into subscriber counts by multiplying with the observed total market size (aggregate subscriber base) in each year of the validation period. This ensures that the benchmark is evaluated on the same scale as the proposed system dynamics framework, while explicitly constraining the allocation across providers to match the realized aggregate size. In this way, the ARIMA benchmark provides a transparent, statistically rigorous comparison against which the added value of the structurally grounded system dynamics formulation can be assessed.

5. Result Analysis

To account for the uncertainty incorporated into the market performance, attraction, and churn flow parameters, Monte Carlo simulation was employed to generate a risk-informed forecast for each of the active providers—Cosmote, Vodafone, and Wind Hellas—over the forecasting period. A total of 10,000 simulation trials were conducted to ensure statistical robustness and achieve convergence of the key statistics (mean, standard deviation) for the forecasted market share distributions.

Numerically, the continuous-time relationships described in Section 3 and Section 4 are implemented as a discrete-time simulation with an annual time step Δt = 1, matching the frequency of the available data. In each Monte Carlo replication and for each year t in the forecasting horizon (2018–2022), the algorithm proceeds as follows:

• The aggregate subscriber base M_t is updated using a first-order Euler–Maruyama discretization of the Itô diffusion in Equation (8), so that the deterministic logistic component in Equation (9) governs the drift and the calibrated volatility parameter σ governs the random innovation.
• The resulting change in total market size $\mathsf{\Delta }{M}_t$ is mapped into provider-specific attraction flows via Equation (6) and the coefficients q_i, and
• Provider-level market shares X_tⁱ are updated by combining these attraction flows with the outgoing churn flows $C{F}_i\left(t\right)$ defined in Section 3.1, using Equation (3) and the calibrated churn rates α, b and c.

Because the simulation time step coincides with the observation interval of the data and no additional numerical interpolation is required, truncation error from the discretization is negligible; the dominant source of uncertainty is stochastic and is controlled by the large number of Monte Carlo replications discussed below.

The adequacy of this number of trials can be assessed by considering the Monte Carlo standard error of the simulated means. For the most volatile provider (Cosmote), the simulated standard deviation of market share in 2022 is approximately 3.56 percentage points (Table 5). With 10,000 trials, the corresponding standard error of the mean is $\sigma /\sqrt{N}\approx 0.036$ percentage points, yielding an approximate 95% confidence interval for the simulated mean of ±0.07 percentage points. This Monte Carlo noise is an order of magnitude smaller than the typical forecast errors observed in the validation period (≈0.4–1.5 percentage points), and is therefore negligible from a forecasting perspective. Inverting this relationship shows that roughly 4870 trials would already suffice to achieve a 95% confidence band of ±0.1 percentage points for the simulated means; the choice of 10,000 trials is thus deliberately conservative and ensures that additional iterations would not significantly alter the primary forecast results.

The validation of the framework’s predictive capability against the 5-year hold-back period is assessed based on three primary criteria:

• Central Tendency Accuracy: The mean and median of the stochastic forecast distribution must closely align with the actual market share observed during the hold-back period.
• Model Robustness: The model must demonstrate reliable behavior, characterized by low-to-moderate variability in the forecast outputs (Standard Deviation, Coefficient of Variation) and confirmed stability through a Sensitivity Analysis that shows negligible influence from volatility-related input parameters.
• Forecast Accuracy Statistics: Standard forecast accuracy metrics—Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE)—are computed over the 5-year validation horizon (2018–2022) for each provider and in aggregate, for both the proposed system dynamics framework and the reconciled ARIMA benchmark. These metrics provide an objective, quantitative comparison of the predictive performance of the competing approaches.

The results, summarized in Table 5, provide detailed insights into the forecasted market share distributions and their statistical properties, including measures of central tendency, dispersion, and variability, for year 2022.

5.1. Comparative Benchmark Analysis

To further evaluate the performance of the proposed framework, its forecasts were compared against those of the reconciled ARIMA benchmark described in Section 4.5. Both approaches were calibrated on the 2007–2017 training period and validated against the 5-year hold-back period 2018–2022. Whereas the system dynamics model generates risk-informed forecasts through Monte Carlo simulation of subscriber flows, the benchmark produces point forecasts and associated prediction intervals for each provider’s market share, which are subsequently reconciled to satisfy the compositional constraint.

For each provider, a grid search over ARIMA $(p,d,q)$ models with $p\in \{\mathrm{0,1},\mathrm{2,3}\}$, $d\in \{\mathrm{0,1},2\}$, and $q\in \{\mathrm{0,1},\mathrm{2,3}\}$ (excluding the trivial $(\mathrm{0,0},0)$) was conducted, and the specification with the lowest Akaike Information Criterion (AIC) was selected. This yielded ARIMA(2,0,1) for Cosmote (AIC ≈ −44.70; $c\approx 0.4665$, ${\varphi }_1\approx 1.2929$, ${\varphi }_2\approx -0.9061$, ${\theta }_1\approx -0.9721$, ${\sigma }^2\approx 2.54\times {10}^{-4}$); ARIMA(2,0,1) for Vodafone (AIC ≈ −46.02; $c\approx 0.2986$, ${\varphi }_1\approx 1.3391$, ${\varphi }_2\approx -0.8480$, ${\theta }_1\approx -0.9641$, ${\sigma }^2\approx 2.50\times {10}^{-4}$); and ARIMA(2,0,0) for Wind (AIC ≈ −52.29; $c\approx 0.2353$, ${\varphi }_1\approx 0.9042$, ${\varphi }_2\approx -0.8726$, ${\sigma }^2\approx 1.83\times {10}^{-4}$). All three series are adequately modeled without differencing ($d=0$), which is consistent with bounded market shares that show short-memory dynamics over 2007–2017.

Subsequently, for each validation year $\mathrm{t}\in \{2018,\dots ,2022\}$, the base share forecasts ${\mathrm{f}}_{\mathrm{t}}=({\mathrm{f}}_{\mathrm{Cos}\mathrm{mote},\mathrm{t}},{\mathrm{f}}_{\mathrm{Vodafone},\mathrm{t}},{\mathrm{f}}_{\mathrm{Wind},\mathrm{t}}{)}^{\mathrm{\top }}$ from the ARIMA benchmark were computed and the minimum-variance reconciliation of Guerrero and Peña was applied (Equation (11)). The reconciled shares obtained are: 2018 $g_{2018}=(0.444452,0.299172,0.256376)$(sum = 1.000000) and 2022 $g_{2022}=(0.448829,0.318342,0.232829)$(sum = 1.000000); analogous results hold for 2019–2021. These shares were converted to subscriber counts by multiplying by the observed total subscriber base in each year.

Table 6 summarizes the out-of-sample accuracy of the two approaches, focusing on the final validation year 2022 for which the system dynamics distributions in Table 5 are reported. For all three providers, the mean forecast of the proposed framework lies very close to the realized 2022 market-share values, with absolute errors well below one percentage point. By contrast, the reconciled ARIMA benchmark exhibits larger deviations, with absolute errors typically in the range of approximately one-and-a-half to three percentage points for the individual providers. These results indicate that, in this application, the system dynamics formulation delivers a substantially more accurate central tendency than a conventional time-series benchmark, despite relying on the same aggregate historical data. Absolute errors reported in Table 6 are expressed in percentage points (pp).

In addition to point accuracy, the empirical coverage of the forecast distributions was examined. The actual 2022 market shares fall comfortably within the simulated distributions generated by the system dynamics model, consistent with the moderate standard deviations and coefficients of variation reported in Table 5. Over the entire 2018–2022 hold-back period, the realized market shares for all providers lie within the approximate 95% prediction intervals implied by the simulated distributions (mean ± 1.96 × standard deviation), indicating that the stochastic forecasts are probabilistically well calibrated. For the ARIMA benchmark, the realized market shares lie within the corresponding 95% prediction intervals for the two larger providers across the validation horizon and mostly within the bands for the smaller provider, with only small deviations in some years. Such deviations are not unexpected given the nominal coverage level and the relatively short sample used to estimate the models. Overall, the comparison suggests that while the reconciled ARIMA benchmark provides a reasonable statistical description of the data, the proposed system dynamics framework exhibits superior forecast calibration and accuracy, particularly at the end of the hold-back period.

To provide a more rigorous evaluation of out-of-sample performance over the entire hold-back period, standard forecast accuracy statistics were also computed for both models. For each provider, the Root Mean Square Error (RMSE), Mean Absolute Error (MAE) and Mean Absolute Percentage Error (MAPE) were calculated over the 5-year horizon 2018–2022. For the proposed system dynamics framework, the forecasted values (${\widehat{y}}_t$) are taken as the mean of the simulated market-share distribution for each provider and year. For the reconciled ARIMA benchmark, the forecasted values correspond to the point forecast produced by the ARIMA specification after minimum-variance reconciliation, ensuring compositional coherence.

The resulting statistics are reported in Table 7 for each provider, together with an overall line aggregating all three providers across the five validation years. The system dynamics framework achieves consistently lower RMSE, MAE and MAPE values than the reconciled ARIMA benchmark. In aggregate, the overall MAE is reduced from 1.79 percentage points for the benchmark to 1.00 percentage point for the system dynamics model, while the overall RMSE decreases from 2.10 to 1.18 percentage points and the overall MAPE from 5.62% to 3.42%. Similar improvements are observed at the provider level: for example, Cosmote’s MAE falls from 2.39 pp (ARIMA) to 0.87 pp (system dynamics), and Vodafone’s from 1.35 pp to 0.66 pp. These results confirm that the structurally grounded flow-based formulation not only reproduces the observed final-year market shares with small absolute errors but also delivers superior predictive accuracy across the entire hold-back period when compared with a coherent statistical time-series benchmark.

Importantly, the benchmark also highlights the methodological advantages of the system dynamics approach. The ARIMA specification requires an explicit ex-post reconciliation step to enforce the compositional constraint, whereas the system dynamics model satisfies the aggregation rule by construction, through its compartmental representation of subscriber flows. As a result, the proposed framework simultaneously delivers coherent forecasts and rich structural insights into the drivers of market-share dynamics, while outperforming a coherent statistical benchmark in out-of-sample accuracy according to both distributional and standard forecast-error criteria.

5.2. Analysis of Stochastic Dynamics and Model Robustness

In line with the evidence presented in Table 5 and Table 6, the simulation results confirm that the mean and median market-share forecasts closely track the realized values for all three providers over the hold-back period, thereby validating the accuracy of the calibrated flow parameters and the stochastic specification.

An analysis of market share variability provides further insights into the competitive dynamics of the market. Cosmote demonstrates the largest standard deviation of 3.56% and a range spanning from 34.57% to 61.63%, reflecting both its significant market dominance and its exposure to market uncertainties. Vodafone, with a standard deviation of 3.49%, shows moderate variability, with market share values ranging between 18.99% and 44.98%. In contrast, Wind Hellas, the smallest of the three providers, has the lowest standard deviation at 2.69%, indicating greater stability in its market share but also a more constrained competitive scope. The coefficient of variation (CV) further refines this picture: Cosmote shows the lowest CV at 0.0754, indicating lower relative variability around its mean market share despite its larger absolute standard deviation. By contrast, Vodafone and Wind Hellas exhibit higher CV values of 0.1154 and 0.1192, respectively, consistent with relatively more volatile market-share trajectories given their smaller average shares.

The results also highlight differences in the distributional characteristics of market share for each provider. To identify suitable parametric forms for the simulated market-share distributions, several candidate families (Normal, Lognormal, Beta) were fitted to the Monte Carlo output for each provider. The market share distributions for Cosmote and Wind Hellas were found to follow a lognormal distribution, while Vodafone’s market share aligns with a beta distribution. Importantly, these parametric forms characterize the emergent distributions of the simulated market shares; they are not imposed as prior assumptions on the input flows, which are modeled at the churn and attraction level using bounded Normal distributions derived from historical data.

This outcome is not an input assumption but a result of the model’s structure and constraints. The preference for the Lognormal distribution for Cosmote (dominant incumbent) and Wind Hellas (smaller player) is consistent with competitive dynamics where market share changes are multiplicative and bounded by zero, leading to a natural skewness. The Beta distribution for Vodafone is typically observed in models where the outcome is constrained within defined maximum and minimum limits (0% to 100% market share) and is indicative of moderate competitive pressure and constrained variability. These findings are consistent with the nature of subscriber dynamics in competitive telecommunications markets, where churn and attraction rates often exhibit skewness due to network effects and competitive strategies [73].

The bounded random methodology applied to simulate attraction and churn flows, combined with Monte Carlo simulation, ensures that the forecasts incorporate both historical performance and market uncertainty. By accounting for randomness and variability, the model provides a robust and realistic representation of the competitive environment. The alignment of simulated forecasts with actual market share values further confirms the validity of the proposed methodology.

Furthermore, a sensitivity analysis was conducted to assess the performance, robustness, and reliability of the proposed market share forecasting model. Given the dynamic and uncertain nature of the telecommunications market, where subscriber churn rates, attraction flows, and market performance are subject to variability, it was essential to evaluate how changes in these input parameters influence the model’s outputs. By systematically varying key input parameters—such as churn rates, attraction rates, and market uncertainty—within a uniform distribution range of ±20%, the analysis highlights the relative influence of these parameters on the forecasted market share outcomes for each provider. By repeatedly drawing parameter vectors from independent uniform distributions defined on a ±20% interval around the baseline calibration and, for each draw, running the full Monte Carlo simulation described in Section 5, the analysis highlights the relative influence of these parameters on the forecasted market-share outcomes for each provider. The variance shares summarized in

Table 8. Sensitivity Analysis Results Comparative Summary.

Factor	Cosmote	Vodafone	Wind Hellas
Top Influencing Factor	Cosmote Out-Churn (78.2%)	Vodafone Out-Churn (47.8%)	Wind Out-Churn (43.1%)
Competitor Churn Impact	Moderate (Vodafone and Wind)	Significant (Cosmote)	Significant (Cosmote)
Attraction Sensitivity	Low (2.9%)	Moderate (4.5%)	Moderate (5.3%)
Volatility Impact	Negligible	Negligible	Negligible
Market Position	Dominant, stable	Mid-tier, growth-focused	Smaller, reliant on competitor churn

are empirical decompositions of the resulting ensemble, analogous in spirit to variance-based global sensitivity measures such as Sobol first-order and total indices, but computed from the uniform perturbation design rather than from an exact Sobol sequence (see, for example, [74]).

A comparative summary of the variance-based sensitivity analysis results for Cosmote, Vodafone, and Wind Hellas is presented in Table 8 below. The table highlights the top contributing parameters to market share variability, the relative influence of churn and attraction flows, and each provider’s sensitivity to market dynamics.

The results demonstrate that the Outgoing Churn parameters are the dominant drivers of market share variability across all providers, particularly for the incumbent provider Cosmote, where churn contributes up to 78.2% of the variance. This strong influence underscores the model’s ability to capture real-world market dynamics, where subscriber churn is widely recognized as a primary determinant of market performance in competitive telecommunications markets. Similarly, competitor churn rates—particularly from Cosmote—emerge as significant drivers for alternative providers, such as Vodafone and Wind Hellas, highlighting the interconnected nature of subscriber redistribution.

The sensitivity analysis further establishes that market attraction parameters, while less influential than churn, provide additional insights into subscriber acquisition dynamics. For alternative providers like Vodafone and Wind, improvements in attraction rates contribute moderately to market share gains, demonstrating the model’s capability to account for the effects of competitive targeting and promotional strategies. This reinforces the framework’s applicability to both retention-focused strategies (through churn management) and acquisition-focused strategies (through attraction flows).

The empirically confirmed dominant role of churn variability (up to 78.2% of variance for the incumbent Cosmote) carries significant theoretical implications for market competition in oligopolies. This finding strongly suggests that provider strategies and subscriber decisions are governed by dynamics related to customer switching costs and the residual effect of regulatory influence. First, the lower and more stable churn rate observed for Cosmote, combined with its high influence on overall variability, reflects the practical reality of high perceived switching costs. These costs (e.g., inertia, network effects) create an environment where the incumbent’s primary challenge is self-preservation, while alternative providers must overcome these barriers, aligning with theories of asymmetric competitive response. Second, the model’s results, which reflect competitive behavior after the structural break adjustment, imply that while regulation sets the competitive field (e.g., enabling number portability), the market dynamics are largely driven by providers’ reactionary churn management strategies. The high variability among alternative providers (Vodafone and Wind Hellas) suggests their market share is susceptible to competitor churn, forcing them into tactical competition consistent with models of intensive price/service rivalry in mature oligopolies.

Moreover, the negligible contribution of volatility-related parameters (e.g., standard deviations of attraction rates) to forecast variability highlights the model’s stability under varying assumptions. This result is particularly significant as it confirms that the forecasting outcomes are robust to changes in market share uncertainty, further validating the reliability of the proposed framework under real-world conditions.

By identifying and quantifying the contributions of key parameters, the sensitivity analysis confirms that the proposed model performs well under varying assumptions and effectively captures the complex interplay of churn, attraction, and market dynamics. This strengthens the model’s suitability as a decision-support tool for forecasting and strategic planning in competitive telecommunications markets, providing both accurate predictions and actionable insights for providers.

5.3. Innovation and Comparative Advantages of the Proposed Framework

The comparative analysis against the reconciled ARIMA benchmark highlights three distinct areas of innovation where the proposed system dynamics framework advances the state of the art in market-share forecasting, particularly for saturated oligopolies.

First, the framework ensures structural compositional coherence by construction. Traditional time-series approaches, including the ARIMA benchmark used in this study, treat market shares as independent series that must be forced to sum to unity through ex-post reconciliation techniques (e.g., [62]). While statistically valid, this approach decouples the forecasting mechanism from the physical reality of subscriber redistribution. In contrast, the proposed framework enforces coherence through conservation of flow: a subscriber lost by one provider is mathematically required to be gained by another or to exit the market. As a result, forecasts remain logically consistent at every simulation step without requiring external adjustments, providing a more natural representation of competitive reallocation in mature markets.

Second, the model provides behavioral causality and interpretability. Statistical benchmarks such as ARIMA rely on latent patterns in historical data (autocorrelation and moving-average structure) but offer limited insight into why changes occur. The proposed framework decomposes market-share evolution into explicit competitive mechanisms—outgoing churn (retention failure) and attraction (acquisition success)—that correspond to identifiable managerial levers. Moreover, uncertainty is introduced directly at this behavioral-mechanism level by modeling churn and attraction parameters as bounded random variables derived from historical data, rather than as undifferentiated residual noise. The resulting variance-based sensitivity assessment (Table 8) therefore attributes forecast risk to specific drivers; for example, the incumbent’s variability is explained primarily by outgoing churn (78.2%), whereas alternative providers are influenced strongly by competitor churn. This level of actionable granularity—distinguishing whether a market-share decline is driven by retention weakness or by competitor poaching—cannot be recovered from standard univariate time-series models.

Third, the framework offers data-lean stochastic depth suited to saturated markets. Many forecasting approaches face a trade-off between structural realism and data requirements: agent-based or micro-simulation models typically require individual-level switching or call detail records (CDR) data that are proprietary and rarely available. The proposed model innovates by producing probabilistic, risk-informed forecasts using only publicly available aggregate series. Aggregate market evolution is represented through a calibrated stochastic diffusion process around a logistic saturation path (Equations (8)–(10)), and its realized increments are mapped into provider-level attraction flows via the system dynamics structure (Equations (5)–(6)). This coupling allows the model to capture mature-market conditions in which total demand fluctuates stochastically around saturation while competitive redistribution continues through churn. Monte Carlo simulation of the bounded flow parameters yields coherent prediction intervals and empirically improves out-of-sample accuracy relative to reconciled ARIMA (reducing overall MAE from 1.79 pp to 1.00 pp). Hence, high-fidelity competitive forecasting and uncertainty quantification are achievable even in data-constrained regulatory environments.

6. Discussion

The empirical results obtained for the Greek mobile telecommunications market highlight several features of market-share dynamics that are consistent with, and extend, previous findings in the literature on churn, diffusion, and competition in subscription-based markets [19,35,36,37,41,42,43,44,45,46,47,48,50,51]. The analysis confirms that in a mature, highly penetrated environment such as Greece, competitive outcomes are driven primarily by subscriber redistribution rather than by sustained aggregate growth, and that structurally grounded, flow-based models can exploit limited aggregate data to deliver accurate, risk-informed forecasts.

First, the dominance of churn-related parameters in explaining forecast variance—particularly for the incumbent provider Cosmote—confirms the central role of subscriber switching behavior in mature subscription-based markets, as reported in earlier telecommunications churn studies [67,72] and in empirical analyses of switching costs and local network effects in mobile markets [38]. The finding that outgoing churn from the incumbent (Cosmote) is the primary driver of forecast variance, while competitor churn from Cosmote is a key source of gains for Vodafone and Wind Hellas, is in line with previous evidence that incumbents in saturated markets are more exposed to competitive poaching, whereas smaller providers rely heavily on capturing disaffected customers from the market leader [15,16,17,18,43,48]. At the same time, the moderate but non-negligible contribution of attraction parameters—particularly for Vodafone and Wind—suggests that acquisition strategies, such as promotional campaigns or differentiated service bundles, remain an important complementary lever for market-share growth [26,27,28,29]. From the perspective of the working hypotheses, these results support the expectation that churn management would emerge as the primary driver of market-share variability, with attraction effects playing a secondary but still meaningful role.

Second, the saturation of the aggregate subscriber base by the end of the calibration period, captured through the logistic diffusion specification, aligns with diffusion-of-innovation models that document S-shaped adoption and eventual maturity in telecommunications and related network industries [55,68], and is consistent with empirical comparisons of diffusion and S-curve models in saturated mobile and broadband markets [52,53,54]. In this context, the Itô diffusion process used to model aggregate market performance can be viewed as a stochastic extension of classical diffusion models, allowing for volatility around the deterministic S-curve. The finding that volatility contributes relatively little to forecast variance compared with churn parameters suggests that, in this market, structural competitive mechanisms dominate over purely exogenous market shocks—a result that echoes conclusions reached in simulation-based analyses of telecom competition [50,51]. This aligns with the broader diffusion and competition literature, where mature markets are often characterized by low residual growth and by dynamics that are increasingly governed by switching costs, customer lock-in, and network effects rather than by macroeconomic shocks.

The stochastic analysis of the simulated market-share distributions further illuminates the competitive risk profile of each provider. Cosmote exhibits the largest simulated standard deviation and widest range of market-share outcomes, reflecting the combination of dominant scale and heightened exposure to competitive pressure. By contrast, Wind Hellas displays the smallest dispersion, indicating a more constrained but comparatively stable competitive position, while Vodafone occupies an intermediate profile. At a distributional level, the emergent lognormal shapes for Cosmote and Wind Hellas, and the beta-shaped distribution for Vodafone, suggest that market-share changes are multiplicative and bounded, with natural skewness arising from asymmetric competitive opportunities and network effects. These patterns are consistent with the notion that dominant incumbents face “downside” risk from coordinated poaching, whereas smaller providers experience bounded upside potential; they also resonate with empirical evidence that subscriber flows in competitive telecom markets are often skewed by promotional campaigns, quality perceptions, and peer-to-peer influence [73].

Third, when benchmarked against a reconciled ARIMA specification, the system dynamics framework yields smaller forecast errors and better-calibrated prediction intervals over the 2018–2022 hold-back period. This supports the working hypothesis that a structurally grounded, flow-based representation of subscriber dynamics can outperform purely statistical time-series models in settings where market-share coherence and churn-driven redistribution are central [49,62]. While the ARIMA benchmark provides a reasonable statistical description of the historical market-share series, its reliance on ex-post reconciliation to enforce compositional constraints contrasts with the inherent coherence of the system dynamics formulation, in which subscriber flows between compartments ensure that shares sum to the aggregate by construction. Importantly, the comparison in this specific setting does not imply universal dominance of the system dynamics approach over all time-series models; rather, it illustrates that under the conditions of a mature oligopolistic mobile market with limited aggregate data, a structurally grounded flow-based model can deliver superior predictive accuracy and richer interpretability than a coherent statistical benchmark.

Beyond the empirical comparison, the benchmark analysis highlights key methodological implications for the broader forecasting literature. Traditional univariate or multivariate statistical models, even when adapted to compositional data through reconciliation, treat market shares as generic time-series and only impose coherence ex post. The system dynamics framework, by contrast, embeds the compositional constraint directly in the compartmental structure and models uncertainty at the level of churn and attraction flows. This combination of structural coherence and stochastic simulation bridges system dynamics and compositional forecasting traditions, showing how data-lean models can still provide probabilistically well-calibrated forecasts and transparent decomposition of uncertainty across behavioral mechanisms.

From a practical standpoint, the results imply that providers operating in saturated mobile markets should prioritize churn management as the primary lever for influencing long-run market-share trajectories. For the incumbent, this means maintaining low churn to protect its installed base, whereas for alternative providers, strategic emphasis on capturing churned subscribers from the incumbent may be more effective than aggressive attempts to stimulate aggregate market growth. At the same time, the moderate but non-negligible role of attraction parameters indicates that acquisition strategies—such as targeted promotions, differentiated service bundles, or quality improvements—remain important complementary tools, especially for smaller providers seeking incremental gains in share. The stochastic results further suggest that incumbents must manage not only average churn levels but also the variability of churn over time, since larger dispersion in outcomes translates into greater strategic risk for dominant firms.

For regulators and policymakers, the model’s ability to disentangle the effects of churn, attraction, and market growth provides a useful lens for monitoring competitive conditions and assessing whether observed market-share dynamics are driven by healthy competition or by structural barriers to switching. The relatively limited impact of the volatility component in this case suggests that, once major regulatory shocks (such as SIM registration policies) are accounted for, the residual uncertainty in aggregate demand does not undermine the stability of market shares. This reinforces the view that regulatory interventions should focus on lowering switching costs, ensuring transparency, enforcing number-portability and contract-termination rules, and preventing anti-competitive practices, rather than attempting to micro-manage short-term demand fluctuations. In addition, the framework’s ability to generate risk-informed forecasts makes it a potentially valuable tool for ex-ante assessment of regulatory proposals under different churn and attraction scenarios.

The discussion of generalizability is particularly important given that the framework is intentionally data-lean. Conceptually, the proposed system dynamics methodology is applicable to a wide range of subscription-based markets characterized by oligopolistic structure and limited time-series data. In saturated or mature markets with stable provider counts—similar to the Greek case—the framework can be used to study how small changes in churn and attraction policies propagate into long-run redistributions of share. In emerging markets, calibrating the market-performance component to early-stage diffusion S-curves allows the model to capture initial growth while focusing on the distribution of new subscribers across competing providers. In markets with varying regulatory environments (e.g., the presence of MVNOs, infrastructure-sharing obligations, or asymmetric spectrum assignments), the modular compartmental structure facilitates the addition of new provider types or flows, making it possible to examine how different regulatory regimes shape competitive outcomes.

At the same time, the empirical application highlights several limitations that qualify the scope of inference. The current formulation is less suitable for markets with rapid, unstable entry and exit, where frequent structural changes would require repeated re-design and re-calibration of the system structure. Likewise, markets characterized by highly differentiated products (for example, providers specializing entirely in B2B vs. B2C segments) may violate the assumption of homogeneous services and the linear relationship between attraction flows and aggregate market growth; in such cases, attraction coefficients would need to be replaced by multivariate functions incorporating explicit product and segment heterogeneity. Finally, the relatively short annual time-series available for calibration and validation constrain the use of more complex statistical benchmarks and imply that the reported forecast errors—although favorable—should be interpreted with appropriate caution. These limitations suggest that the framework is best viewed as a flexible, structurally grounded starting point that can be adapted or extended as richer data become available.

Looking ahead, the findings open several avenues for future research that build on both the system dynamics and forecasting literature. One avenue is to extend the framework to multi-market contexts (e.g., combined fixed and mobile services, converged bundles, or overlapping national and regional markets), where cross-market interactions and convergence effects may play a significant role. Another is to integrate richer behavioral mechanisms into the flow parameters, for example by linking churn and attraction rates to service-quality indicators, pricing strategies, or marketing expenditures when such data are available. Methodologically, comparing the system dynamics framework with alternative coherent forecasting approaches—such as hierarchical reconciliation methods or Bayesian state-space models—would help delineate the conditions under which structurally grounded flow-based models provide the greatest advantage. In addition, refining the estimation of flow parameters using advanced data-analytic techniques, such as machine learning or other predictive modeling approaches, could further improve the precision and robustness of the forecasts. Finally, Monte Carlo experiments using synthetic data generated under controlled data-generating processes could be used to systematically explore the robustness of the framework under varying levels of volatility, competition intensity, and market structure, thereby clarifying how far the present conclusions can be generalized beyond the specific Greek application.

7. Conclusions

This paper developed a system dynamics framework for forecasting market share evolution in subscription-based telecommunications markets, conceptualizing competition as flows of subscribers—churn, attraction, and aggregate market growth—between structurally constrained provider compartments. The framework is intentionally data-lean: it operates on aggregate time-series indicators while embedding uncertainty at the level of churn and attraction mechanisms, and uses stochastic diffusion and Monte Carlo simulation to generate coherent, risk-informed forecasts of provider market shares.

The framework was applied to the Greek mobile telecommunications market, a mature, highly penetrated, three-operator environment that provides a stringent testbed for churn-driven competition. Using historical data for 2006–2022 with a five-year hold-back period (2018–2022), the model produced accurate forecasts characterized by low-to-moderate variability. The simulated market-share distributions closely matched the realized shares, and their emergent lognormal and beta shapes reflected bounded, multiplicative competitive dynamics rather than arbitrary distributional assumptions. Compared with a reconciled ARIMA benchmark tailored to the compositional nature of market-share data, the system dynamics formulation systematically achieved smaller forecast errors and better-calibrated prediction intervals over the full validation horizon, as confirmed by standard accuracy metrics such as MAE, RMSE and MAPE. This demonstrates that, under the conditions of a mature oligopolistic mobile market with limited data, a structurally grounded flow-based model can outperform a coherent statistical time-series benchmark.

The empirical findings emphasize the dominant role of churn management in shaping long-run market-share trajectories, particularly for the incumbent operator, while attraction parameters play a secondary but non-negligible role for alternative providers. Volatility-related inputs contribute only marginally to forecast variance, indicating that the main sources of uncertainty are structural and competitive rather than purely random. For managers, this implies that in saturated mobile markets, strategic attention should focus primarily on controlling outgoing churn, designing effective mechanisms to capture churned subscribers from competitors, and complementing these efforts with targeted acquisition policies. For regulators and policymakers, the model’s ability to disentangle the effects of churn, attraction and aggregate market growth provides a practical tool for diagnosing competitive conditions, identifying barriers to switching, and assessing ex ante how different regulatory interventions are likely to redistribute market share.

Beyond the specific Greek case, the modeling steps are generic and can be adapted to other subscription-based oligopolies where only aggregate time-series data are available, such as pay-TV, fixed broadband and other telecom segments. At the same time, the empirical assessment rests on a single national market with relatively short annual time-series, and on a setting with a stable provider structure and largely redistributive competition. A further simplifying assumption of the cumulative case specification is that the probabilities with which churned subscribers are reallocated across providers are proportional to the respective attraction rates for new subscribers, which reduces the number of free parameters but may be restrictive in markets where poaching capabilities and general-market acquisition are driven by different mechanisms. Applications to markets with rapid entry and exit, strong product differentiation, or multi-service bundling will require re-specification of the system structure and re-calibration of the flow parameters. Future research could extend the framework to multi-market contexts (e.g., combined fixed and mobile services or converged bundles) and integrate richer behavioral drivers—such as service quality, pricing and marketing expenditure—into the flow parameters, and compare performance against alternative coherent forecasting approaches, including hierarchical reconciliation and Bayesian state-space models. Monte Carlo experiments with synthetic data under controlled data-generating processes would further clarify the conditions under which the proposed system dynamics framework provides the greatest advantage over traditional forecasting models. Together, these extensions can refine the framework’s external validity while preserving its core strengths of structural interpretability, compositional coherence and probabilistic forecasting capability.