Cross-Regional Deep Learning for Air Quality Forecasting: A Comparative Study of CO, NO2, O3, PM2.5, and PM10
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
3.1. Datasets
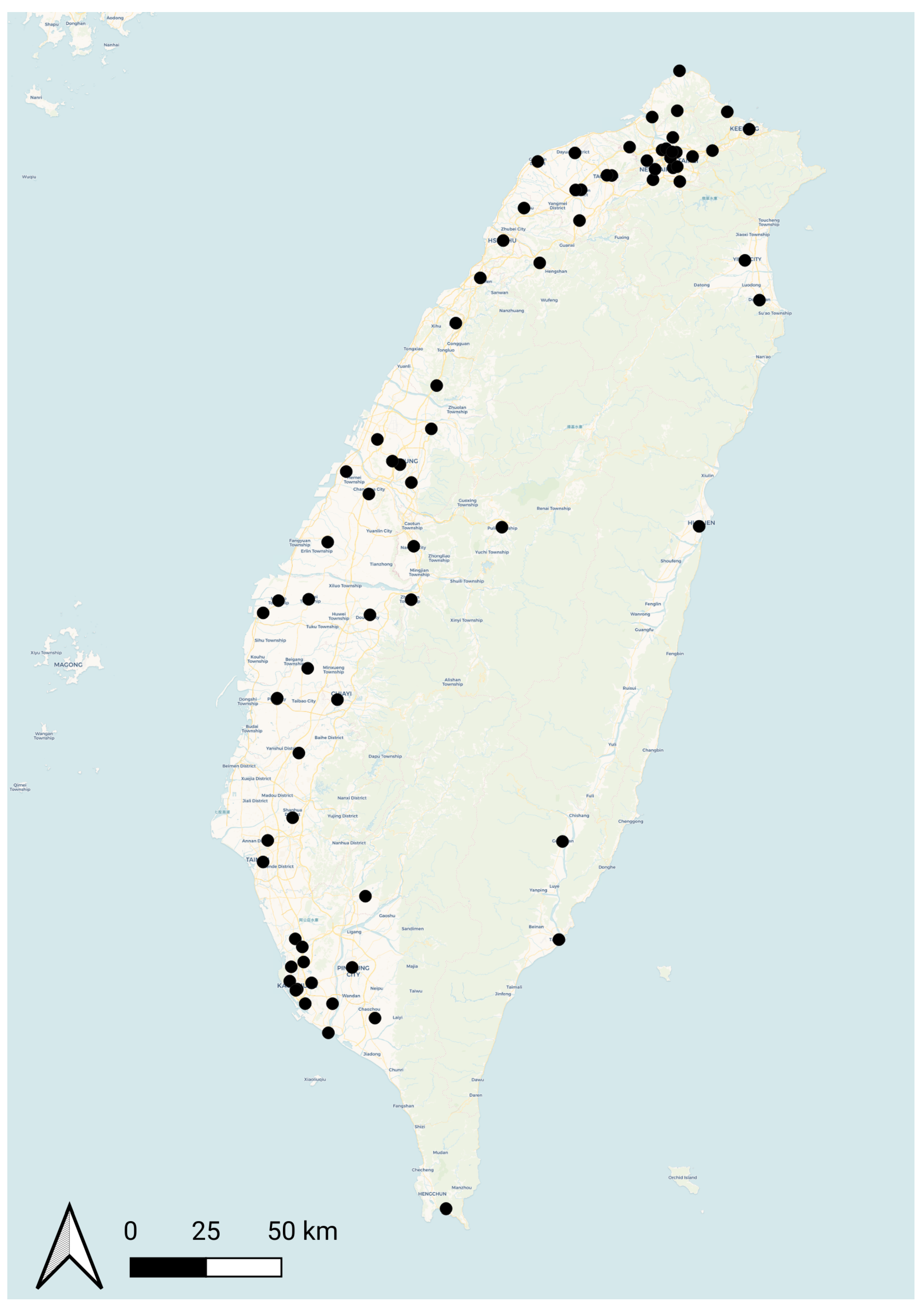
3.1.1. Taiwan Dataset
3.1.2. Beijing Dataset
3.1.3. Newcastle upon Tyne Dataset
3.1.4. Data Pre-Processing
3.2. Model Descriptions
Feedforward Neural Network
3.3. Long-Short Term Recurrent Neural Network
3.3.1. DeepAR
3.3.2. Temporal Fusion Transformer
3.4. Experimental Setup
3.4.1. Hyperparameter Tuning and Feature Selection
3.4.2. Training and Evaluation
4. Results
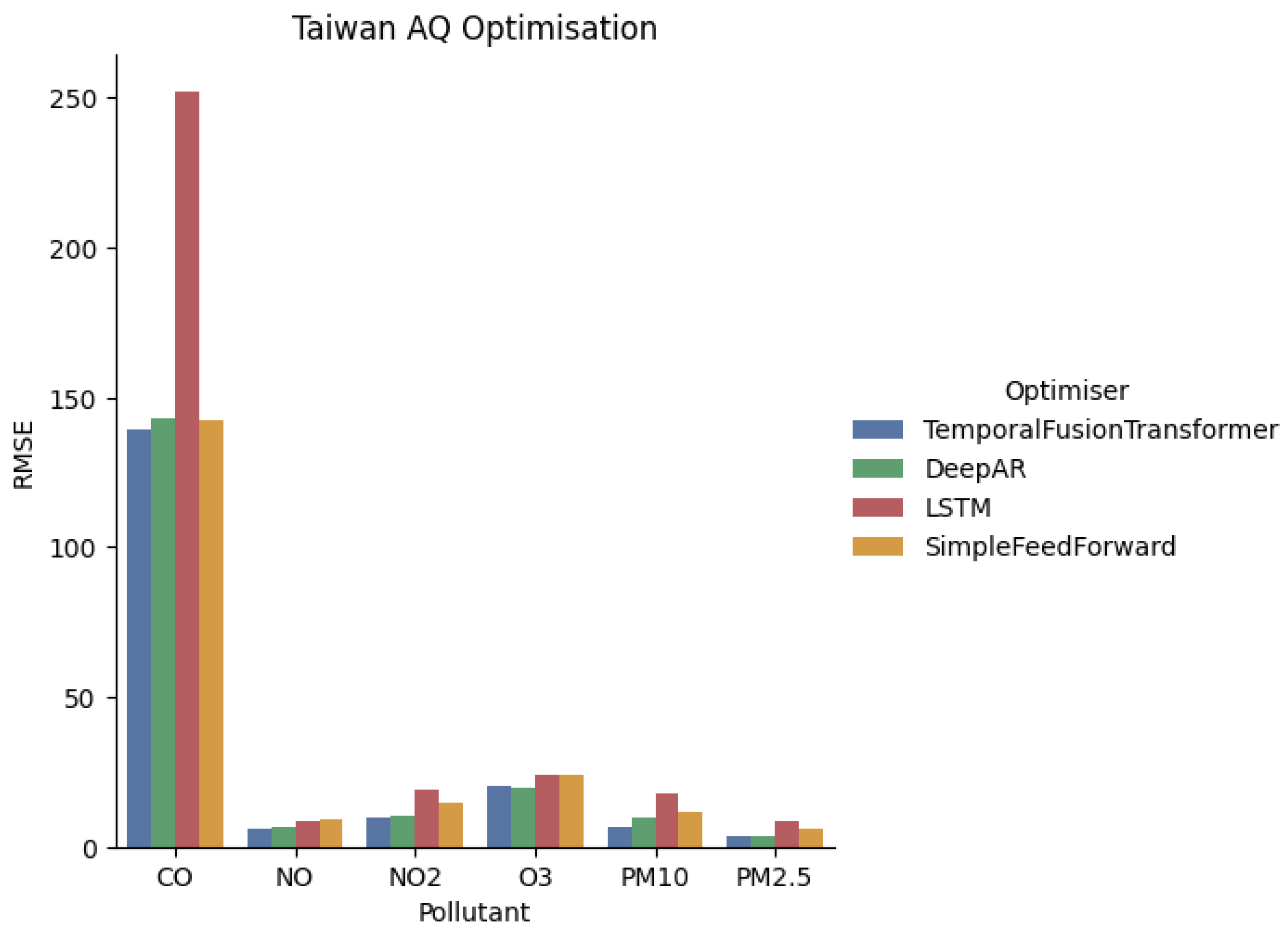
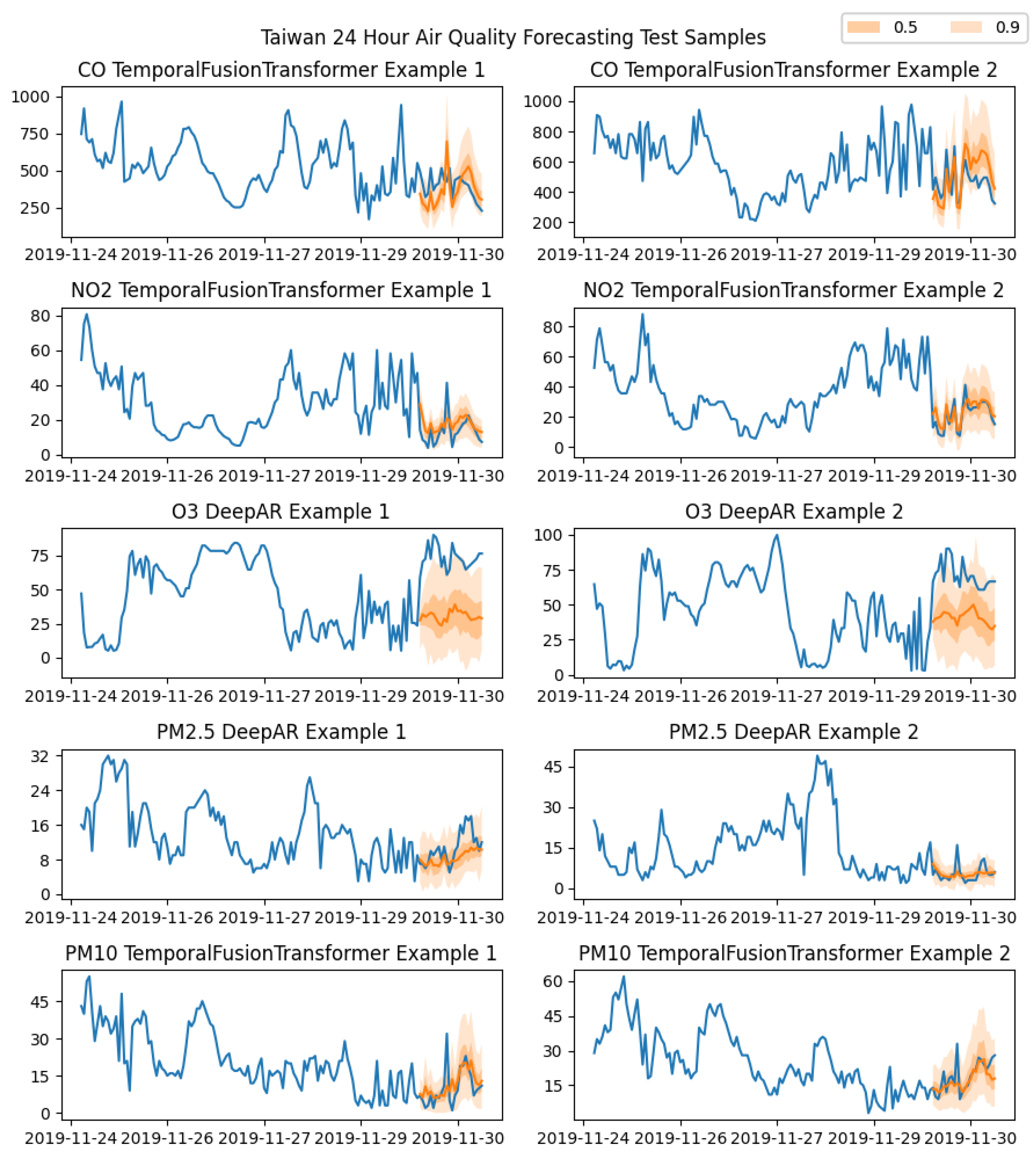
4.1. Taiwan
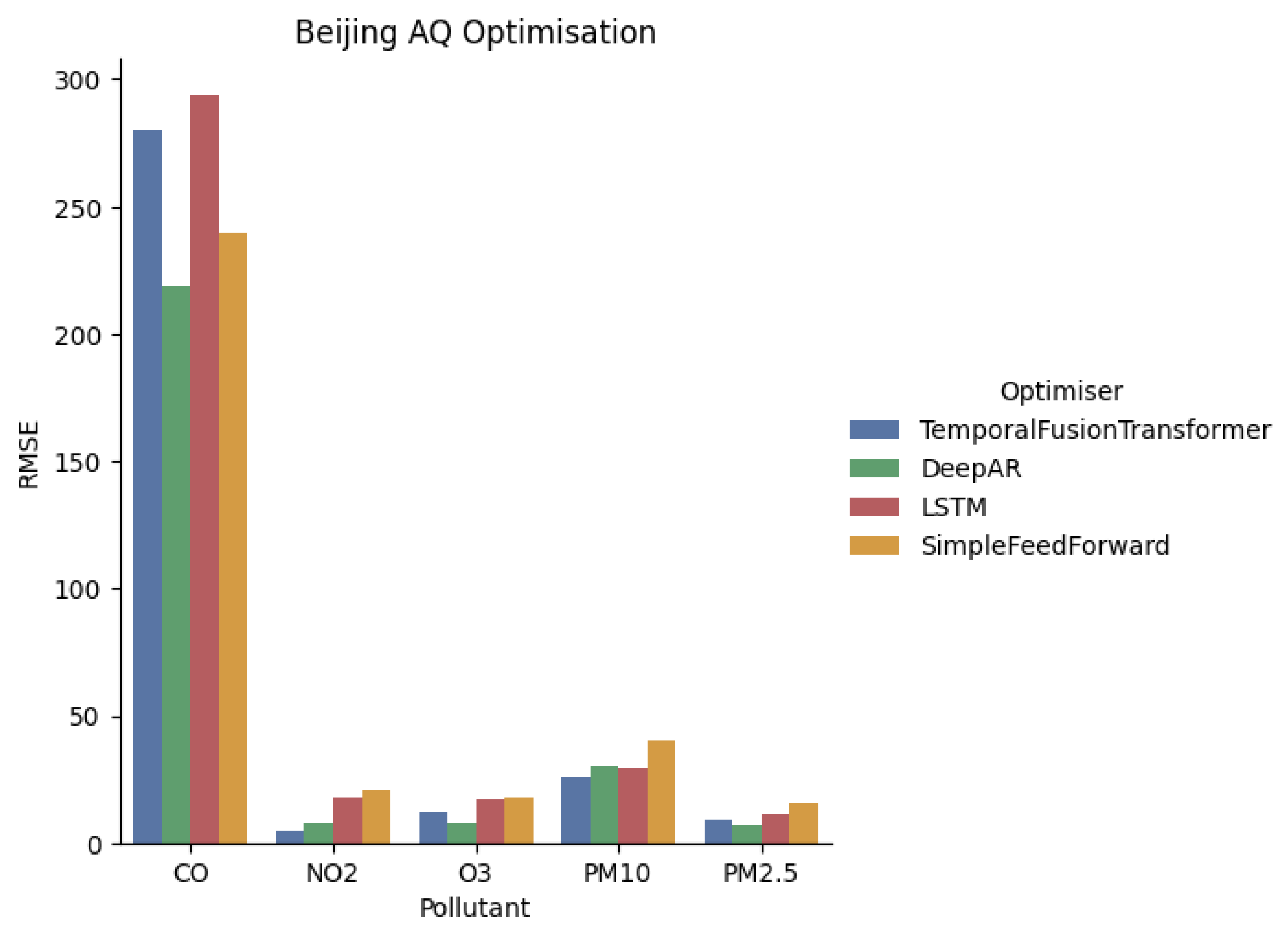
4.2. Beijing
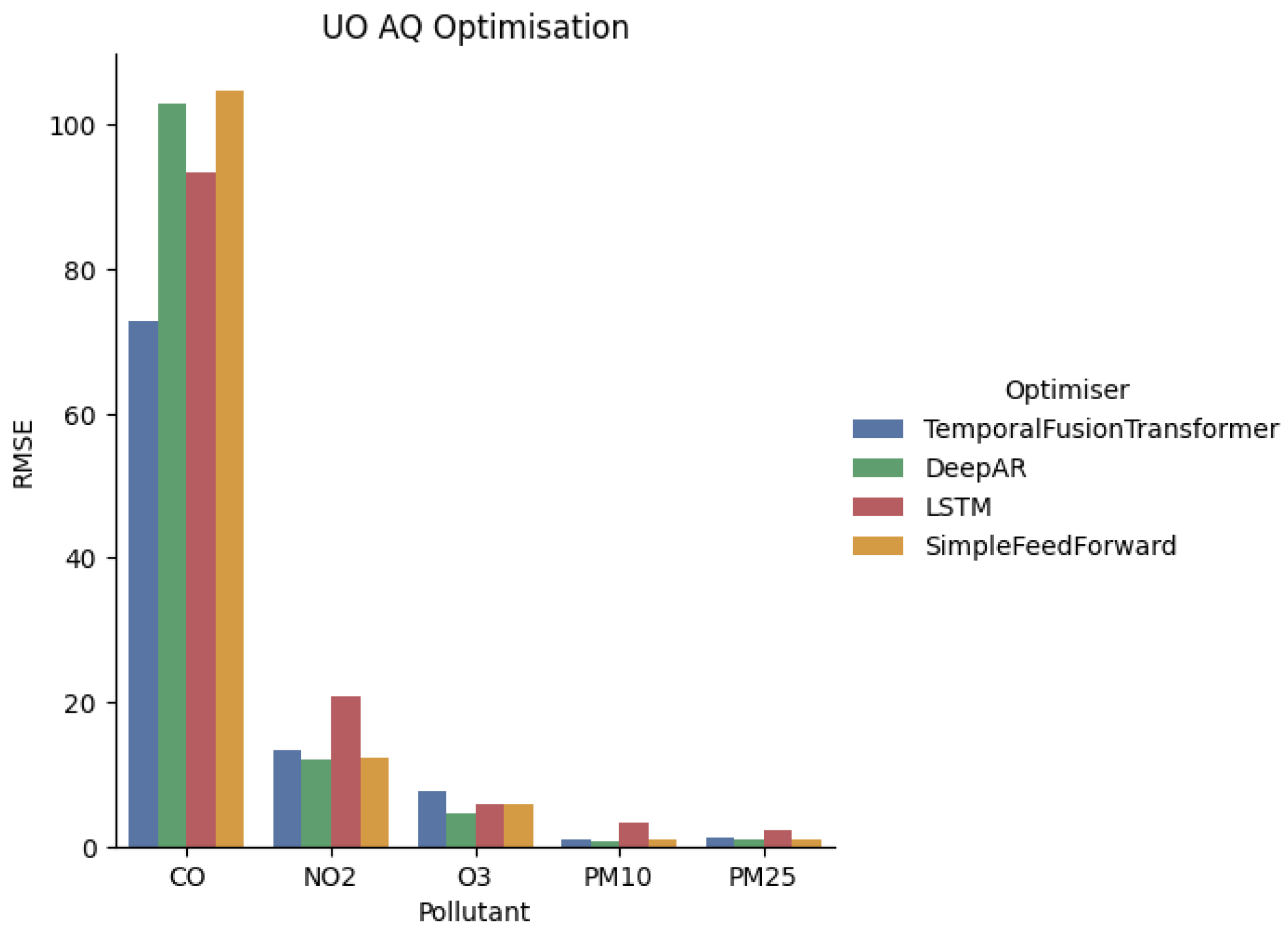
4.3. Urban Observatory
5. Discussion
5.1. Model Selection
5.2. Covariate Selection
5.3. Applications to Sensor Networks
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Health Impacts: Types of Pollutants. 2024. Available online: https://www.who.int/teams/environment-climate-change-and-health/air-quality-and-health/health-impacts/types-of-pollutants (accessed on 10 June 2024).
- Liu, N.M.; Grigg, J. Diesel, children and respiratory disease. BMJ Paediatr. Open 2018, 2, e000210. [Google Scholar] [CrossRef] [PubMed]
- Polezer, G.; Tadano, Y.S.; Siqueira, H.V.; Godoi, A.F.; Yamamoto, C.I.; de André, P.A.; Pauliquevis, T.; Andrade, M.d.F.; Oliveira, A.; Saldiva, P.H.; et al. Assessing the impact of PM2.5 on respiratory disease using artificial neural networks. Environ. Pollut. 2018, 235, 394–403. [Google Scholar] [CrossRef] [PubMed]
- Mo, Z.; Fu, Q.; Zhang, L.; Lyu, D.; Mao, G.; Wu, L.; Xu, P.; Wang, Z.; Pan, X.; Chen, Z.; et al. Acute effects of air pollution on respiratory disease mortalities and outpatients in Southeastern China. Sci. Rep. 2018, 8, 3461. [Google Scholar] [CrossRef] [PubMed]
- Slama, A.; Śliwczyński, A.; Woźnica, J.; Zdrolik, M.; Wiśnicki, B.; Kubajek, J.; Turżańska-Wieczorek, O.; Gozdowski, D.; Wierzba, W.; Franek, E. Impact of air pollution on hospital admissions with a focus on respiratory diseases: A time-series multi-city analysis. Environ. Sci. Pollut. Res. 2019, 26, 16998–17009. [Google Scholar] [CrossRef]
- Hayes, R.B.; Lim, C.; Zhang, Y.; Cromar, K.; Shao, Y.; Reynolds, H.R.; Silverman, D.T.; Jones, R.R.; Park, Y.; Jerrett, M.; et al. PM2.5 air pollution and cause-specific cardiovascular disease mortality. Int. J. Epidemiol. 2020, 49, 25–35. [Google Scholar] [CrossRef]
- Kim, J.B.; Prunicki, M.; Haddad, F.; Dant, C.; Sampath, V.; Patel, R.; Smith, E.; Akdis, C.; Balmes, J.; Snyder, M.P.; et al. Cumulative lifetime burden of cardiovascular disease from early exposure to air pollution. J. Am. Heart Assoc. 2020, 9, 14944. [Google Scholar] [CrossRef]
- Mannucci, P.M.; Harari, S.; Franchini, M. Novel evidence for a greater burden of ambient air pollution on cardiovascular disease. Haematologica 2019, 104, 2349–2357. [Google Scholar] [CrossRef]
- Lelieveld, J.; Klingmüller, K.; Pozzer, A.; Pöschl, U.; Fnais, M.; Daiber, A.; Münzel, T. Cardiovascular disease burden from ambient air pollution in Europe reassessed using novel hazard ratio functions. Eur. Heart J. 2019, 40, 1590–1596. [Google Scholar] [CrossRef]
- Wang, N.; Mengersen, K.; Tong, S.; Kimlin, M.; Zhou, M.; Wang, L.; Yin, P.; Xu, Z.; Cheng, J.; Zhang, Y.; et al. Short-term association between ambient air pollution and lung cancer mortality. Environ. Res. 2019, 179, 108748. [Google Scholar] [CrossRef]
- Bai, L.; Shin, S.; Burnett, R.T.; Kwong, J.C.; Hystad, P.; van Donkelaar, A.; Goldberg, M.S.; Lavigne, E.; Weichenthal, S.; Martin, R.V.; et al. Exposure to ambient air pollution and the incidence of lung cancer and breast cancer in the Ontario Population Health and Environment Cohort. Int. J. Cancer 2020, 146, 2450–2459. [Google Scholar] [CrossRef]
- Tseng, C.H.; Tsuang, B.J.; Chiang, C.J.; Ku, K.C.; Tseng, J.S.; Yang, T.Y.; Hsu, K.H.; Chen, K.C.; Yu, S.L.; Lee, W.C.; et al. The Relationship Between Air Pollution and Lung Cancer in Nonsmokers in Taiwan. J. Thorac. Oncol. 2019, 14, 784–792. [Google Scholar] [CrossRef] [PubMed]
- Turner, M.C.; Andersen, Z.J.; Baccarelli, A.; Diver, W.R.; Gapstur, S.M.; Pope, C.A.; Prada, D.; Samet, J.; Thurston, G.; Cohen, A. Outdoor air pollution and cancer: An overview of the current evidence and public health recommendations. CA Cancer J. Clin. 2020, 70, 460–479. [Google Scholar] [CrossRef] [PubMed]
- Liao, Q.; Zhu, M.; Wu, L.; Pan, X.; Tang, X.; Wang, Z. Deep learning for air quality forecasts: A review. Curr. Pollut. Rep. 2020, 6, 399–409. [Google Scholar] [CrossRef]
- Zaini, N.; Ean, L.W.; Ahmed, A.N.; Malek, M.A. A systematic literature review of deep learning neural network for time series air quality forecasting. Environ. Sci. Pollut. Res. 2022, 29, 4958–4990. [Google Scholar] [CrossRef]
- Zhang, Y.; Bocquet, M.; Mallet, V.; Seigneur, C.; Baklanov, A. Real-time air quality forecasting, part I: History, techniques, and current status. Atmos. Environ. 2012, 60, 632–655. [Google Scholar] [CrossRef]
- Ren, X.; Mi, Z.; Georgopoulos, P.G. Comparison of Machine Learning and Land Use Regression for fine scale spatiotemporal estimation of ambient air pollution: Modeling ozone concentrations across the contiguous United States. Environ. Int. 2020, 142, 105827. [Google Scholar] [CrossRef]
- Wang, S.; McGibbon, J.; Zhang, Y. Predicting high-resolution air quality using machine learning: Integration of large eddy simulation and urban morphology data. Environ. Pollut. 2024, 344, 123371. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Zhao, F. Important meteorological variables for statistical long-term air quality prediction in eastern China. Theor. Appl. Climatol. 2018, 134, 25–36. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Gao, M.; Ma, Q.; Zhao, J.; Zhang, R.; Wang, Q.; Huang, L. A Predictive Data Feature Exploration-Based Air Quality Prediction Approach. IEEE Access 2019, 7, 30732–30743. [Google Scholar] [CrossRef]
- Agirre-Basurko, E.; Ibarra-Berastegi, G.; Madariaga, I. Regression and multilayer perceptron-based models to forecast hourly O3 and NO2 levels in the Bilbao area. Environ. Model. Softw. 2006, 21, 430–446. [Google Scholar] [CrossRef]
- Corani, G. Air quality prediction in Milan: Feed-forward neural networks, pruned neural networks and lazy learning. Ecol. Model. 2005, 185, 513–529. [Google Scholar] [CrossRef]
- Cabaneros, S.M.S.; Calautit, J.K.S.; Hughes, B.R. Hybrid artificial neural network models for effective prediction and mitigation of urban roadside NO2 pollution. Energy Procedia 2017, 142, 3524–3530. [Google Scholar] [CrossRef]
- Caselli, M.; Trizio, L.; De Gennaro, G.; Ielpo, P. A simple feedforward neural network for the PM 10 forecasting: Comparison with a radial basis function network and a multivariate linear regression model. Water Air Soil Pollut. 2009, 201, 365–377. [Google Scholar] [CrossRef]
- Cordova, C.H.; Portocarrero, M.N.L.; Salas, R.; Torres, R.; Rodrigues, P.C.; López-Gonzales, J.L. Air quality assessment and pollution forecasting using artificial neural networks in Metropolitan Lima-Peru. Sci. Rep. 2021, 11, 24232. [Google Scholar] [CrossRef]
- Das, B.; Dursun, Ö.O.; Toraman, S. Prediction of air pollutants for air quality using deep learning methods in a metropolitan city. Urban Clim. 2022, 46, 101291. [Google Scholar] [CrossRef]
- Shahriar, S.A.; Choi, Y.; Islam, R.; Zanganeh Kia, H.; Salman, A.K. Evaluating the Efficacy of Deep Learning and Hybrid Models in Forecasting PM2.5 Concentrations in Texas: A 7-Day Predictive Analysis. 2024. Available online: https://ssrn.com/abstract=4709966 (accessed on 15 March 2024).
- Jiang, F.; Han, X.; Zhang, W.; Chen, G. Atmospheric PM2.5 prediction using DeepAR optimized by sparrow search algorithm with opposition-based and fitness-based learning. Atmosphere 2021, 12, 894. [Google Scholar] [CrossRef]
- Bahdanau, D. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Vaswani, A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017. [Google Scholar]
- Zhu, C.; Tang, Y. An Empirical Analysis of the Long Short Term Memory and Temporal Fusion Transformer Models on Regional Air Quality Forecast. In Proceedings of the 2023 International Conference on Cyber-Physical Social Intelligence (ICCSI), Xi’an, China, 20–23 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 497–502. [Google Scholar]
- Zhang, Z.; Zhang, S. Modeling air quality PM2.5 forecasting using deep sparse attention-based transformer networks. Int. J. Environ. Sci. Technol. 2023, 20, 13535–13550. [Google Scholar] [CrossRef]
- Zhao, S.; Yu, Y.; Yin, D.; He, J.; Liu, N.; Qu, J.; Xiao, J. Annual and diurnal variations of gaseous and particulate pollutants in 31 provincial capital cities based on in situ air quality monitoring data from China National Environmental Monitoring Center. Environ. Int. 2016, 86, 92–106. [Google Scholar] [CrossRef]
- Alexandrino, K.; Zalakeviciute, R.; Viteri, F. Seasonal variation of the criteria air pollutants concentration in an urban area of a high-altitude city. Int. J. Environ. Sci. Technol. 2021, 18, 1167–1180. [Google Scholar] [CrossRef]
- James, P.; Smith, L.; Jonczyk, J.; Harris, N.; Komar, T.; Puussaar, A.; Clement, M.; Dawson, R. Urban Observatory Data Newcastle (Version 4). Newcastle University. 2020. Available online: https://doi.org/10.25405/data.ncl.c.5059913.v4 (accessed on 15 March 2024).
- Hochreiter, S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, Q.; Li, V.O.; Lam, J.C. Deep-AIR: A hybrid CNN-LSTM framework for air quality modeling in metropolitan cities. arXiv 2021, arXiv:2103.14587. [Google Scholar]
- Le, V.D.; Bui, T.C.; Cha, S.K. Spatiotemporal deep learning model for citywide air pollution interpolation and prediction. In Proceedings of the 2020 IEEE International Conference on Big Data and Smart Computing (BigComp), Busan, Republic of Korea, 19–22 February 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 55–62. [Google Scholar]


| Location | Start Date | End Date | Sensors | Area km2 | Density |
|---|---|---|---|---|---|
| Taiwan | 01-01-2019 | 31-12-2019 | 69 | 33,254 | 0.002 |
| Beijing | 01-01-2017 | 31-12-2017 | 35 | 8167 | 0.004 |
| Newcastle | 01-01-2022 | 31-12-2022 | 25 | 87 | 0.29 |
| Location | CO (, ) | NO2 (, ) | O3 (, ) | PM2.5 (, ) | PM10 (, ) |
|---|---|---|---|---|---|
| Taiwan | 397.94, 192.33 | 22.55, 15.72 | 60.32, 37.20 | 18.08, 12.84 | 36.08, 23.59 |
| Beijing | 968.66, 1068.31 | 45.91, 32.23 | 56.21, 54.17 | 57.57, 60.46 | 81.30, 61.33 |
| Newcastle | 276.47, 109.29 | 32.60, 18.01 | 26.77, 24.46 | 5.02, 7.97 | 7.44, 8.93 |
| Variable | Algorithm | RMSE | CL | Lat | Lon | CO | NO | NO2 | O3 | PM10 | PM2.5 | Wind Direction | Wind Speed |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CO | TFT | 0.15 | 65 | - | - | - | Y | Y | - | - | Y | - | Y |
| DeepAR | 0.16 | 54 | Y | - | - | Y | - | - | Y | - | - | - | |
| SFF | 0.19 | 72 | - | - | - | - | - | - | - | Y | - | Y | |
| LSTM | 0.25 | 27 | - | Y | - | Y | Y | - | - | Y | Y | Y | |
| NO | TFT | 6.08 | 71 | - | Y | - | - | - | Y | Y | Y | - | - |
| DeepAR | 7.24 | 67 | Y | Y | - | - | - | Y | - | Y | - | Y | |
| LSTM | 8.37 | 51 | Y | Y | Y | - | - | - | - | - | Y | - | |
| SFF | 9.35 | 17 | - | Y | - | - | Y | Y | - | Y | - | Y | |
| NO2 | TFT | 9.92 | 72 | Y | - | Y | - | - | Y | - | Y | Y | Y |
| DeepAR | 9.99 | 69 | - | - | Y | Y | - | - | Y | Y | - | - | |
| SFF | 14.44 | 69 | - | Y | - | Y | - | - | Y | - | Y | Y | |
| LSTM | 19.10 | 40 | Y | Y | Y | - | - | - | Y | Y | Y | - | |
| O3 | TFT | 16.12 | 63 | - | Y | Y | Y | Y | - | - | Y | - | Y |
| DeepAR | 19.81 | 62 | - | Y | Y | Y | Y | - | Y | - | - | Y | |
| SFF | 24.23 | 71 | - | Y | Y | - | - | - | - | Y | - | - | |
| LSTM | 24.24 | 53 | Y | - | Y | Y | - | - | - | Y | - | - | |
| PM10 | TFT | 6.55 | 72 | - | Y | - | Y | - | - | - | Y | - | - |
| DeepAR | 8.79 | 14 | - | Y | - | - | - | - | Y | - | - | - | |
| SFF | 11.91 | 72 | - | - | - | Y | - | Y | - | - | Y | Y | |
| LSTM | 17.83 | 67 | Y | - | Y | - | Y | - | - | - | - | - | |
| PM2.5 | DeepAR | 3.38 | 72 | - | Y | Y | - | - | - | - | Y | - | - |
| TFT | 3.53 | 72 | - | - | - | Y | - | Y | - | Y | - | - | |
| SFF | 5.95 | 68 | Y | - | Y | Y | Y | - | - | Y | Y | - | |
| LSTM | 8.67 | 54 | - | Y | - | Y | - | Y | - | - | Y | - |
| Include Feature | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable | Algorithm | RMSE | CL | Lat | Lon | CO | NO2 | O3 | PM2.5 | PM10 | Humidity | Air Pressure | Temperature | Wind Direction | Wind Speed |
| CO | TFT | 0.13 | 16 | Y | - | - | Y | Y | - | Y | - | Y | - | Y | Y |
| DeepAR | 0.14 | 28 | - | - | - | Y | Y | - | Y | - | - | - | - | - | |
| SFF | 0.25 | 36 | - | Y | - | - | Y | - | - | - | - | Y | Y | - | |
| LSTM | 0.33 | 30 | - | Y | - | - | Y | Y | Y | Y | Y | - | - | Y | |
| NO2 | TFT | 4.77 | 56 | - | - | Y | - | Y | Y | Y | - | - | - | Y | Y |
| DeepAR | 7.46 | 20 | Y | - | - | - | Y | Y | - | - | - | - | - | Y | |
| LSTM | 17.58 | 66 | - | Y | - | - | - | - | - | - | - | - | - | - | |
| SFF | 21.02 | 28 | Y | - | - | - | - | Y | Y | - | Y | - | - | - | |
| O3 | DeepAR | 7.42 | 69 | - | - | Y | Y | - | Y | Y | - | Y | - | Y | - |
| TFT | 11.89 | 41 | Y | Y | Y | Y | - | Y | - | - | - | Y | - | - | |
| LSTM | 16.88 | 72 | - | - | - | - | - | - | Y | Y | - | - | - | Y | |
| SFF | 18.08 | 28 | Y | - | - | - | - | - | - | - | Y | Y | - | Y | |
| PM10 | TFT | 25.51 | 53 | Y | - | Y | - | - | Y | - | - | - | Y | - | - |
| LSTM | 29.46 | 47 | Y | Y | Y | Y | - | - | - | Y | Y | Y | - | - | |
| DeepAR | 30.22 | 59 | - | - | - | Y | - | Y | - | - | - | Y | Y | Y | |
| SFF | 40.19 | 59 | - | Y | Y | - | - | Y | - | - | Y | - | - | - | |
| PM2.5 | DeepAR | 7.35 | 13 | Y | Y | - | Y | Y | - | - | - | - | - | - | - |
| TFT | 9.45 | 28 | - | - | Y | - | Y | - | Y | - | Y | Y | - | - | |
| LSTM | 11.09 | 38 | Y | Y | - | - | Y | - | Y | - | Y | Y | Y | - | |
| SFF | 15.45 | 52 | - | - | Y | - | Y | - | Y | Y | Y | - | - | Y | |
| Variable | Algorithm | RMSE | CL | Lat | Lon | CO | NO2 | O3 | PM2.5 | PM10 | Humidity | Air Pressure | Temperature |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CO | TFT | 72.89 | 66 | Y | - | - | Y | Y | - | Y | - | - | Y |
| LSTM | 93.40 | 56 | Y | Y | - | - | - | Y | - | Y | Y | - | |
| DeepAR | 102.83 | 15 | Y | Y | - | Y | Y | - | Y | Y | - | Y | |
| SFF | 104.66 | 15 | Y | Y | - | Y | Y | - | - | - | - | Y | |
| NO2 | DeepAR | 12.12 | 12 | - | Y | Y | - | - | Y | Y | Y | - | Y |
| SFF | 12.34 | 67 | Y | Y | Y | - | Y | Y | - | Y | Y | - | |
| TFT | 13.24 | 65 | Y | - | Y | - | - | Y | - | - | - | Y | |
| LSTM | 20.83 | 49 | - | Y | - | - | - | Y | - | Y | Y | - | |
| O3 | DeepAR | 4.67 | 27 | - | - | - | Y | - | - | - | - | - | - |
| SFF | 5.75 | 71 | Y | Y | Y | - | - | - | - | Y | - | - | |
| LSTM | 5.79 | 57 | Y | - | - | - | - | Y | - | Y | - | Y | |
| TFT | 7.60 | 14 | - | Y | - | Y | - | Y | - | - | Y | Y | |
| PM10 | DeepAR | 0.82 | 62 | - | - | - | - | Y | Y | - | - | - | - |
| TFT | 1.04 | 26 | - | Y | Y | Y | Y | Y | - | Y | - | - | |
| SFF | 1.04 | 38 | - | - | Y | - | - | Y | - | - | Y | Y | |
| LSTM | 3.26 | 39 | - | - | - | - | Y | - | - | Y | Y | Y | |
| PM2.5 | DeepAR | 0.95 | 20 | - | Y | - | Y | Y | - | - | Y | - | Y |
| SFF | 0.99 | 34 | - | Y | - | Y | - | - | Y | - | - | Y | |
| TFT | 1.10 | 25 | Y | - | Y | - | Y | - | - | Y | - | - | |
| LSTM | 2.35 | 46 | - | Y | - | Y | Y | - | Y | Y | Y | Y |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Booth, A.; James, P.; McGough, S.; Solaiman, E. Cross-Regional Deep Learning for Air Quality Forecasting: A Comparative Study of CO, NO2, O3, PM2.5, and PM10. Forecasting 2025, 7, 66. https://doi.org/10.3390/forecast7040066
Booth A, James P, McGough S, Solaiman E. Cross-Regional Deep Learning for Air Quality Forecasting: A Comparative Study of CO, NO2, O3, PM2.5, and PM10. Forecasting. 2025; 7(4):66. https://doi.org/10.3390/forecast7040066
Chicago/Turabian StyleBooth, Adam, Philip James, Stephen McGough, and Ellis Solaiman. 2025. "Cross-Regional Deep Learning for Air Quality Forecasting: A Comparative Study of CO, NO2, O3, PM2.5, and PM10" Forecasting 7, no. 4: 66. https://doi.org/10.3390/forecast7040066
APA StyleBooth, A., James, P., McGough, S., & Solaiman, E. (2025). Cross-Regional Deep Learning for Air Quality Forecasting: A Comparative Study of CO, NO2, O3, PM2.5, and PM10. Forecasting, 7(4), 66. https://doi.org/10.3390/forecast7040066





