From Market Volatility to Predictive Insight: An Adaptive Transformer–RL Framework for Sentiment-Driven Financial Time-Series Forecasting
Abstract
1. Introduction
2. Literature Review
2.1. Traditional Financial Forecasting Models
2.2. Basic Deep Learning Models
2.3. Deep Learning Models with Advanced Techniques
2.4. Hybrid Deep Learning Models
2.5. Sentiment Analysis
2.6. Limitations of Existing Research and Our Contributions
- Conventional deep learning approaches fail in handling complexity: Basic deep learning approaches struggle with nonlinear, complex price movements. Even with advanced methods, such as signal decomposition methods and optimization algorithms [15,20,21,22,23], deep learning approaches still face challenges in modeling nonlinear, sentiment-driven price movements, limiting predictive accuracy.
- Inability to adapt to different market regimes: Static ensembling approaches, such as arithmetic mean and even-weighted average, fail to adjust to varying market conditions, making them impractical for real-time financial forecasting. Models are static and have fixed weights after training and fail to adapt in real time to sudden market volatility, reducing their effectiveness in dynamic environments.
- Limited generalization in existing sentiment models: Existing sentiment-based methods [32,33,34,35,36,37] are tailored to specific financial market assets. For example, Twitter sentiment was extracted in [32,33] for crude oil price forecasting, with commodity-specific features and stock movement prediction with domain-specific preprocessing, respectively, as described. Refs. [35,36,37], respectively, focused on sentiment analysis for US stock price prediction and the S&P 500 Index only. They restricted their applicability and lacked generalization across diverse financial assets.
- Domain-specific financial sentiment dictionary construction: By leveraging SnowNLP [39] and Word2Vec [40,44], we propose a financial sentiment dictionary specifically tailored for investor forum data, containing 16,673 entries. This dictionary achieves up to 97.35% classification accuracy by capturing domain-specific terminology and nuanced sentiment expressions unique to financial discussions. Our domain-specific approach addresses this gap by including sentimental features, which are critical for modeling investor behavior and market sentiment, which cannot be solely modeled by financial price data.
- Heterogeneous model framework integration: As aforementioned, existing single-model approaches often fail to comprehensively capture both linear and nonlinear dynamics, limiting their predictive capacity. We designed a hybrid framework combining Support Vector Regression (SVR) [41] to effectively capture linear trends with three Transformer variants [12] to model complex nonlinear dependencies inherent in financial time series. Our heterogeneous integration ensures diverse market patterns and sentiment impacts are better represented, enhancing robustness and accuracy in forecasting across different assets.
- DQN-driven dynamic ensembling strategy: Traditional ensembling or static-weighting approaches lack the flexibility to adjust to rapidly changing market regimes, leading to deteriorated performance during market shifts. Inspired by [45], which used deep reinforcement learning (DRL) for dynamic portfolio management, the Deep Q-Network (DQN) [42,43] enables adaptive ensembling by learning nonlinear, volatility-adaptive weights over multiple model predictions during training, reducing the average RMSE across different assets. Our DQN-driven strategy addresses this by continuously learning optimal weighting policies corresponding to evolving volatility, which forms our proposed DQN–Hybrid Transformer–SVR Ensemble Framework (DQN-HTS-EF), maintaining strong forecasting performance in dynamic financial environments.
- Multi-market generalization evaluation: Finally, comprehensive experiments were performed to validate the performance of our DQN-HTS-EF across a diverse set of financial datasets, including the China United Network Communications (China Unicom) stock, the CSI 100 index, the Amazon (AMZN) stock, and corn futures. This multi-asset selection—covering RMB-denominated equities, USD-denominated tech stocks, and agricultural commodities—facilitates a rigorous assessment of the framework’s ability to generalize across different market regimes and various asset classes.
3. Materials and Methods
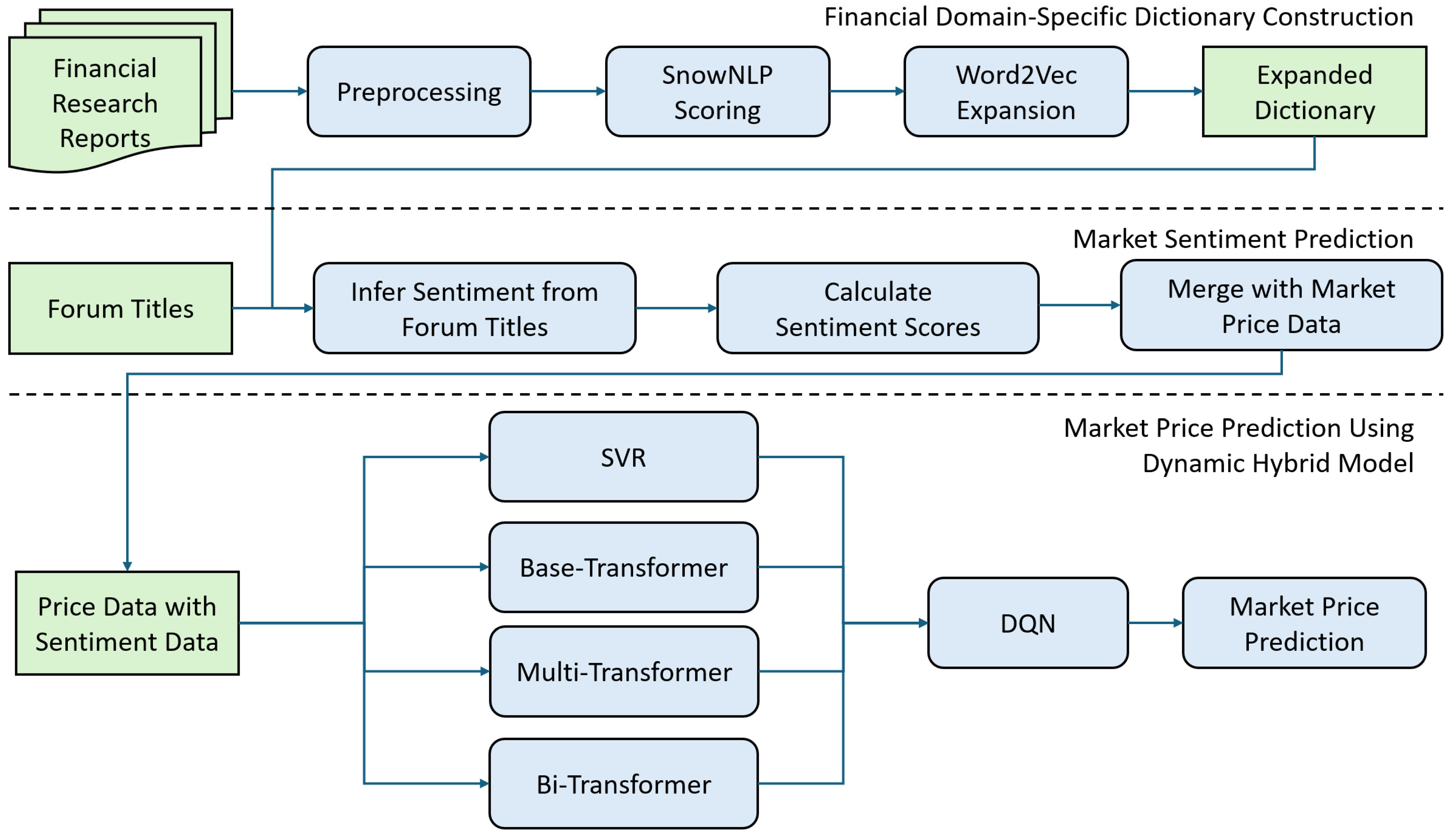
3.1. Framework Overview
- Domain-Specific Sentiment Dictionary Construction
- 2.
- Sentiment Feature Extraction for Forum Titles
- 3.
- Dynamic Model Ensembling via DRL
3.2. Data Acquisition and Data Preprocessing
3.2.1. Financial Trading Data
3.2.2. Textual Sentiment Data
3.3. Financial Domain-Specific Sentiment Dictionary Construction
3.3.1. Dictionary Construction Using Sentiment Analysis
3.3.2. Dictionary Expansion Using Word Embedding
3.4. Market and Sentiment Data Fusion for Model Prediction
3.5. Proposed DQN-HTS-EF Model Architectures
3.5.1. SVR Model for Stable Market
3.5.2. Transformer Models for Moderate-to-Volatile Market
3.5.3. DQN for Adaptive Prediction Selection
4. Results
4.1. Experimental Datasets and Setup
4.1.1. Dataset Information
4.1.2. Experimental Setup
4.2. Performance Validation of Sentiment Scoring
4.2.1. Evaluation Metrics and Results
4.2.2. Sentiment Scoring Comparison and Examples
4.2.3. Multi-Market Sentimental Scoring Validation
4.2.4. Regression Analysis of the Sentiment Score—Closing Price Relationship
4.3. Model Performance and Comparison
4.3.1. Evaluation Metrics
4.3.2. Performance Evaluation on CSI 100 Index
4.3.3. Performance Evaluation on Corn Futures
4.3.4. Performance Evaluation on China Unicom Stock
4.3.5. Performance Evaluation on Amazon Stock
4.4. Forecasting Performance Across Time
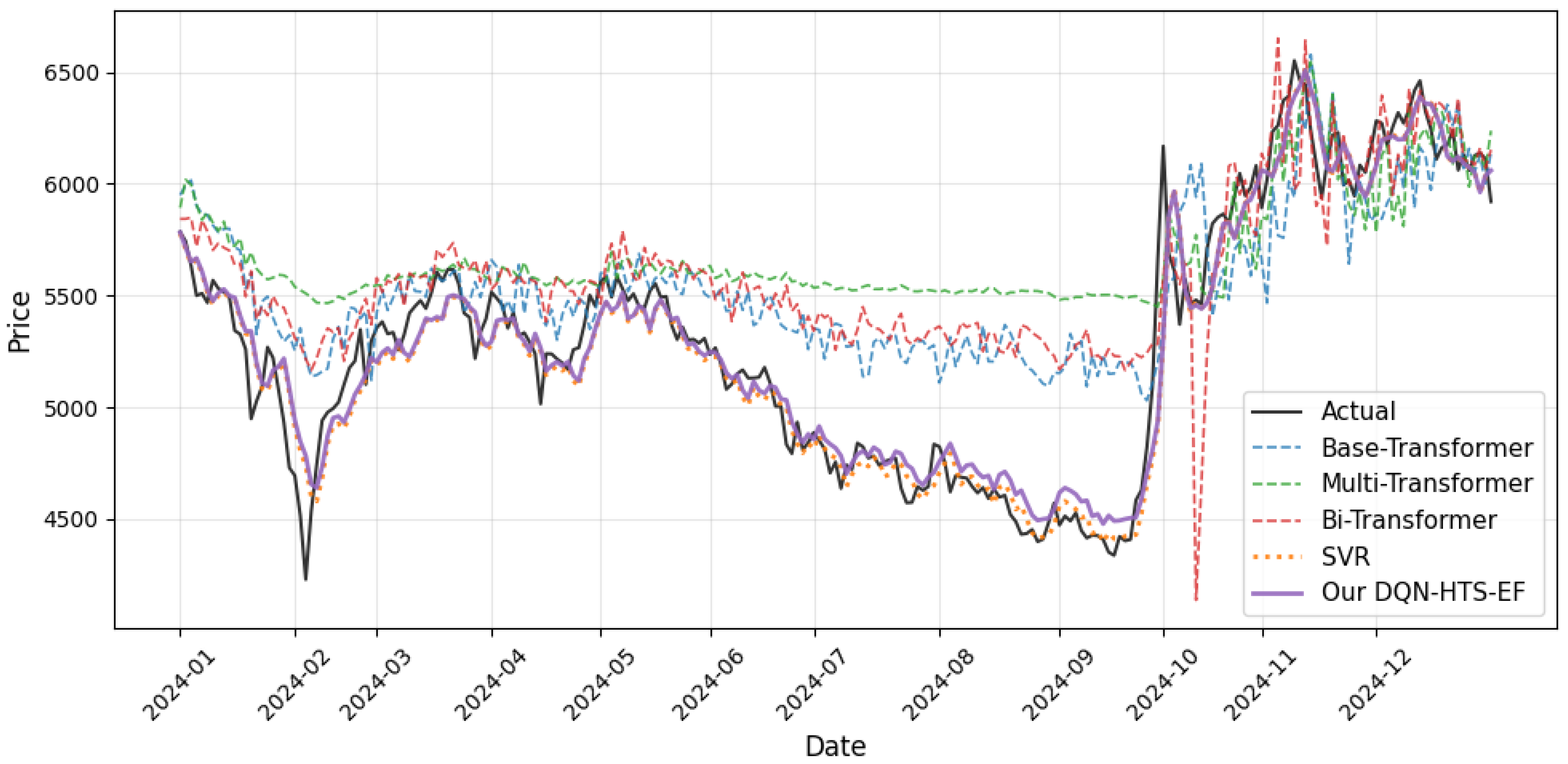
4.4.1. Prediction Across Time on CSI 100 Index
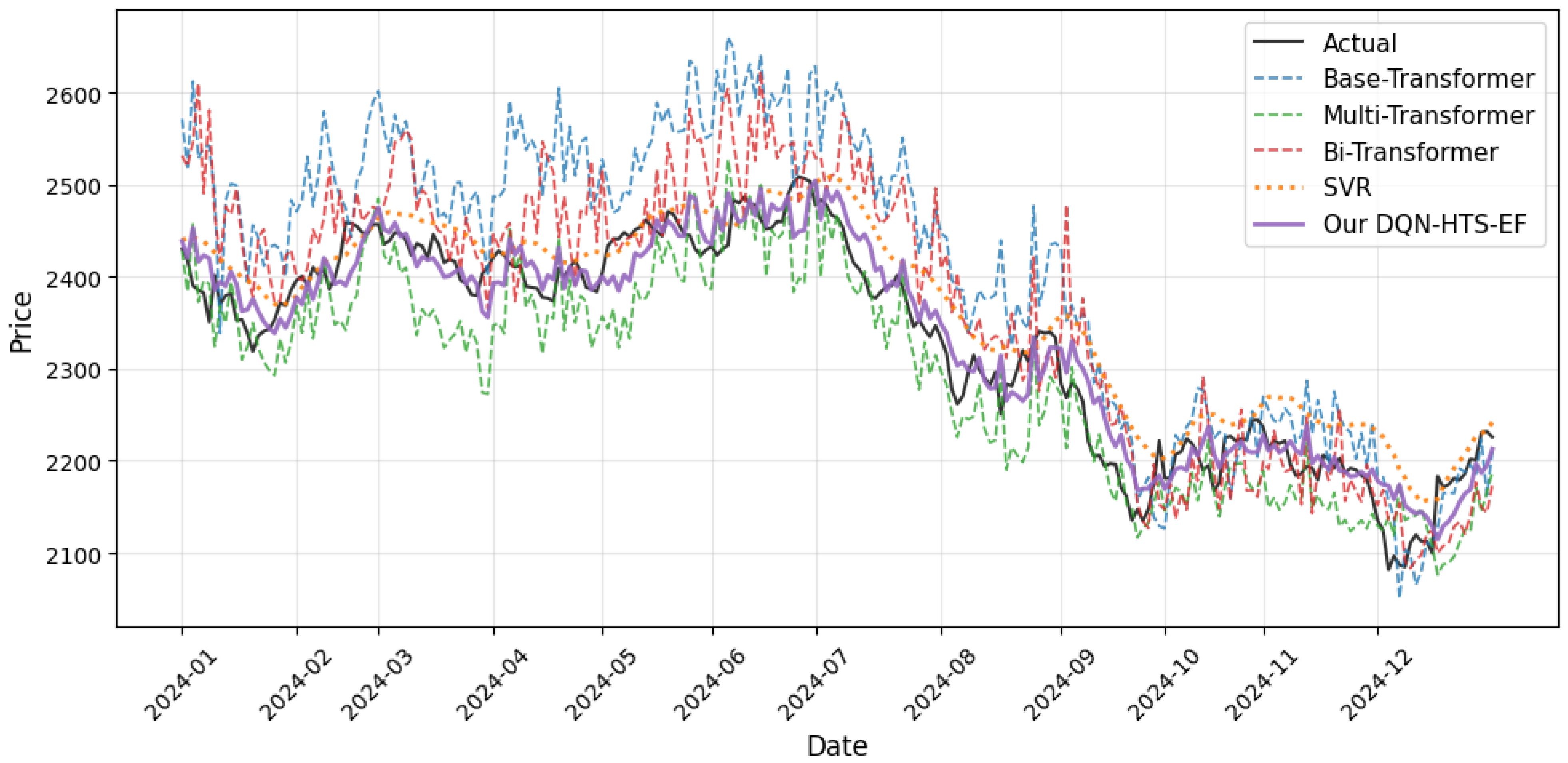
4.4.2. Prediction Across Time on Corn Futures
4.4.3. Prediction Across Time on China Unicom Stock
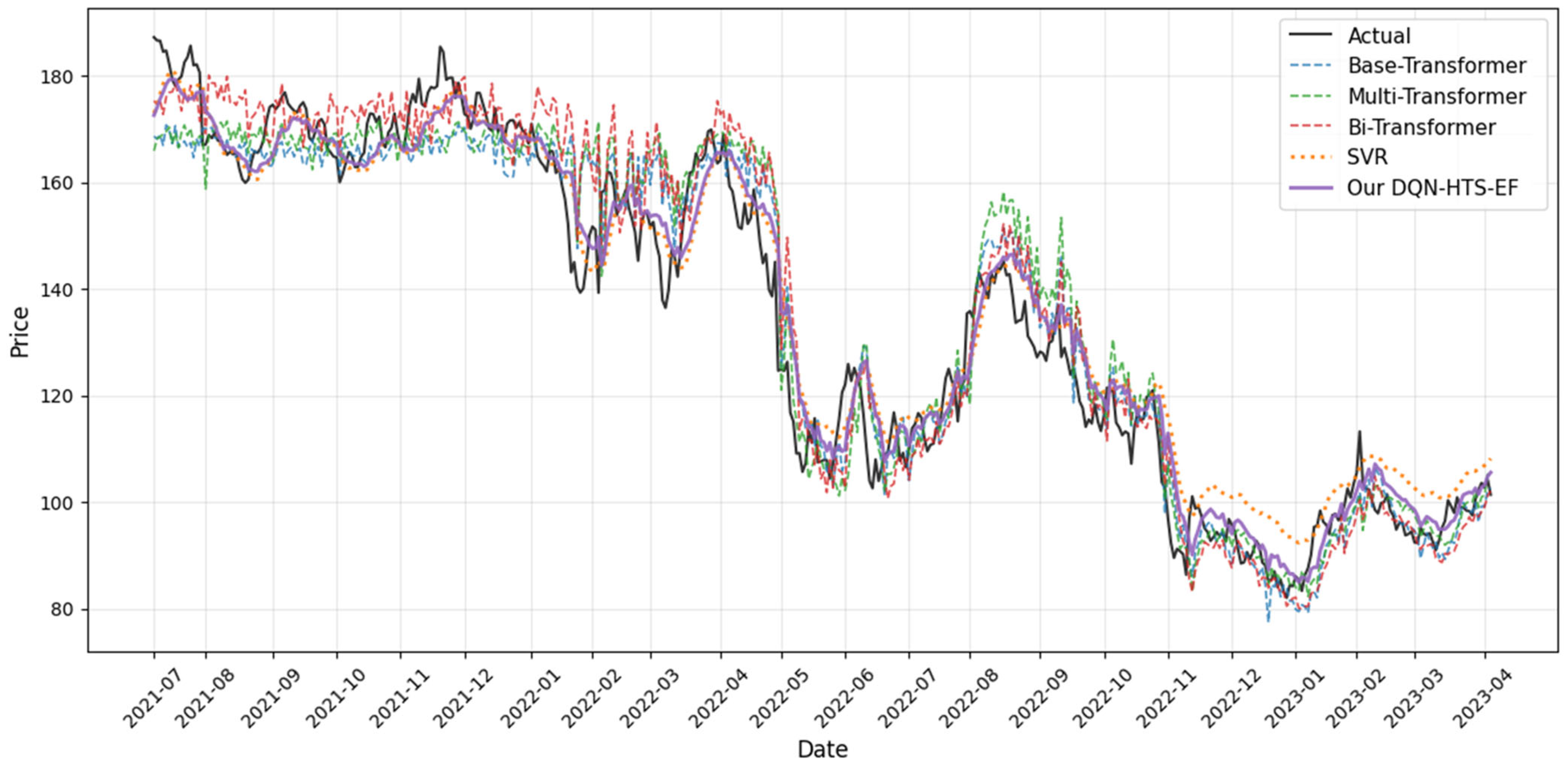
4.4.4. Prediction Across Time on Amazon Stock
4.4.5. Statistical Validation
- Bias reduction: Bias is reduced through context-specific model selection. For example, it prioritizes SVR (approximately 58%) in stable, trend-dominated markets (e.g., corn) to capture smooth price movements, while emphasizing the Base-Transformer (42%) in volatile environments (e.g., CSI 100) that exhibit relatively abrupt changes.
- Variance reduction: By not overly relying on a single model architecture, the approach lowers variance. For example, on the China Unicom stock, DQN-HTS-EF achieved an MSE of 0.012, which was 14.8% lower than SVR’s value of 0.0141 and 67.5% lower than the bidirectional Transformer’s value of 0.0369.
4.5. Further Analysis
4.5.1. SHAP Analysis Sentiment Scores and Model Predictions
4.5.2. Effects of Different Training Data Portions
4.5.3. Comparison with Alternative Ensemble Strategies
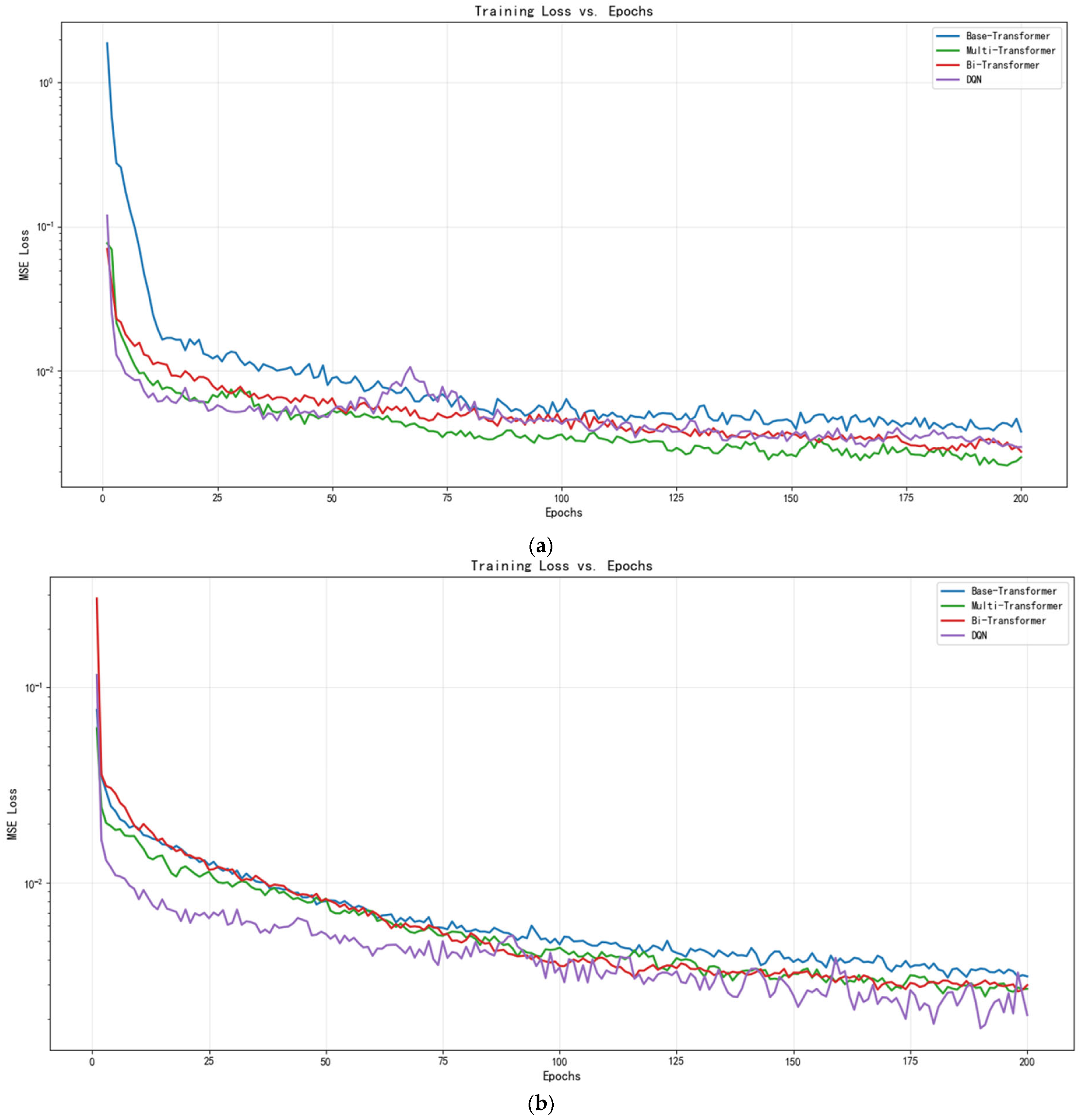
4.5.4. Convergence Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMZN | Amazon |
| ARIMA | Autoregressive Integrated Moving Average |
| BERT | Bidirectional Encoder Representations from Transformers |
| BiGRU | Bidirectional Gated Recurrent Unit |
| BiLSTM | Bidirectional Long Short-Term Memory |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| CNN | Convolutional Neural Network |
| CSI | China Securities Index |
| CST | China Standard Time |
| DRL | Deep Reinforcement Learning |
| DQN | Deep Q-Network |
| DQN-HTS-EF | DQN–Hybrid Transformer–SVR Ensemble Framework |
| ECA | Efficient Channel Attention |
| EMD | Empirical Mode Decomposition |
| ERNIE | Enhanced Representation from Knowledge Integration |
| FinBERT | Financial Bidirectional Encoder Representations from Transformers |
| FIVMD | Fast Iterative Variational Mode Decomposition |
| FN | False Negative |
| FP | False Positive |
| GARCH | Generalized Autoregressive Conditional Heteroskedasticity |
| GC-CNN | Graph Convolutional Neural Network |
| GRU | Gated Recurrent Unit |
| GWO | Grey Wolf Optimizer |
| LSTM | Long Short-Term Memory |
| MA | Moving Average |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MCS | Model Confidence Set |
| MLP | Multilayer Perceptron |
| MSE | Mean-Squared Error |
| NMSE | Negative Mean-Squared Error |
| NLP | Natural Language Processing |
| PPO | Proximal Policy Optimization |
| regex | Regular Expression |
| RL | Reinforcement Learning |
| RMB | Renminbi Currency |
| RMSE | Root-Mean-Squared Error |
| RNN | Recurrent Neural Network |
| SHAP | Shapley Additive Explanations |
| SOTA | State-of-the-Art |
| SSA | Sparrow Search Algorithm |
| SSA-BiGRU | Sparrow Search Algorithm–Bidirectional Gated Recurrent Unit |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| SWA | Sliding-Window Weighted Average |
| TP | True Positive |
| USD | US Dollar |
| VMD-SE-GRU | Variational Mode Decomposition–Squeeze-and-Excitation–Gated Recurrent Unit |
References
- Tetlock, P.C. Giving Content to Investor Sentiment: The Role of Media in Stock Markets. J. Financ. 2007, 62, 1139–1168. [Google Scholar] [CrossRef]
- Lu, Y. Investor Sentiment and Stock Price Change: Evidence from CSI 500 Index. E-Commer. Lett. 2025, 14, 836–846. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, 1st ed.; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Bollerslev, T. Generalized Autoregressive Conditional Heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Lauriola, I.; Lavelli, A.; Aiolli, F. An introduction to Deep Learning in Natural Language Processing: Models, techniques, and tools. Neurocomputing 2022, 470, 443–456. [Google Scholar] [CrossRef]
- Casolaro, A.; Capone, V.; Iannuzzo, G.; Camastra, F. Deep Learning for Time Series Forecasting: Advances and Open Problems. Information 2023, 14, 598. [Google Scholar] [CrossRef]
- Connor, J.; Martin, R.; Atlas, L. Recurrent Neural Networks and Robust Time Series Prediction. IEEE Trans. Neural Netw. 1994, 5, 240–254. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise Phoneme Classification with Bidirectional LSTM and Other Neural Network Archi-tectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 5998–6008. [Google Scholar] [CrossRef]
- Nayak, G.H.H.; Patra, M.R.; Swain, R.K. Transformer-Based Deep Learning Architecture for Time Series Forecasting. Softw. Impacts 2024, 22, 100716. [Google Scholar] [CrossRef]
- Li, Z.Q.; Li, D.S.; Sun, T.S. A Transformer-Based Bridge Structural Response Prediction Framework. Sensors 2022, 22, 3100. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Jiang, W. An Enhanced Interval-Valued Decomposition Integration Model for Stock Price Prediction Based on Comprehensive Feature Extraction and Optimized Deep Learning. Expert Syst. Appl. 2023, 243, 122891. [Google Scholar] [CrossRef]
- Nelson, D.M.Q.; Pereira, A.C.M.; de Oliveira, R.A. Stock Market’s Price Movement Prediction with LSTM Neural Networks. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: New York, NY, USA, 2017; pp. 1419–1426. [Google Scholar] [CrossRef]
- Xu, Y.; Chhim, L.; Zheng, B.; Nojima, Y. Stacked Deep Learning Structure with Bidirectional Long-Short Term Memory for Stock Market Prediction. In Proceedings of the Neural Computing for Advanced Applications, Kyoto, Japan, 12–14 October 2020; Springer: Cham, Switzerland, 2020; pp. 33–44. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Q.; Hu, Y.; Liu, H. A Study of Futures Price Forecasting with a Focus on the Role of Different Economic Markets. Information 2024, 15, 817. [Google Scholar] [CrossRef]
- Chen, W.; Jiang, M.; Zhang, W.-G.; Chen, Z. A Novel Graph Convolutional Feature Based Convolutional Neural Network for Stock Trend Prediction. Inf. Sci. 2021, 556, 67–94. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Nejati, H.R.; Mohammadi, M.; Ibrahim, H.H.; Rashidi, S.; Rashid, T.A. Forecasting Tunnel Boring Machine Penetration Rate Using LSTM Deep Neural Network Optimized by Grey Wolf Optimization Algorithm. Expert Syst. Appl. 2022, 209, 118303. [Google Scholar] [CrossRef]
- Lin, Y.; Lin, Z.; Liao, Y.; Li, Y.; Xu, J.; Yan, Y. Forecasting the Realized Volatility of Stock Price Index: A Hybrid Model Integrating CEEMDAN and LSTM. Expert Syst. Appl. 2022, 206, 117736. [Google Scholar] [CrossRef]
- Li, X.; Ma, X.; Xiao, F.; Xiao, C.; Wang, F.; Zhang, S. Time-series production forecasting method based on the integration of Bidirectional Gated Recurrent Unit (Bi-GRU) network and Sparrow Search Algorithm (SSA). J. Pet. Sci. Eng. 2022, 208 Pt A, 109309. [Google Scholar] [CrossRef]
- Zhang, S.; Luo, J.; Wang, S.; Liu, F. Oil Price Forecasting: A Hybrid GRU Neural Network Based on Decomposition–Reconstruction Methods. Expert Syst. Appl. 2023, 218, 119617. [Google Scholar] [CrossRef]
- Chen, Y.; Fang, R.; Liang, T.; Sha, Z.; Li, S.; Yi, Y.; Zhou, W.; Song, H. Stock Price Forecast Based on CNN-BiLSTM-ECA Model. Sci. Program. 2021, 2021, 2446543. [Google Scholar] [CrossRef]
- Kabir, M.R.; Bhadra, D.; Ridoy, M.; Milanova, M. LSTM–Transformer-Based Robust Hybrid Deep Learning Model for Financial Time Series Forecasting. Sci 2025, 7, 7. [Google Scholar] [CrossRef]
- Hansen, P.R.; Lunde, A.; Nason, J.M. The Model Confidence Set. Econometrica 2011, 79, 453–497. Available online: https://www.jstor.org/stable/41057463 (accessed on 2 September 2025). [CrossRef]
- Zeng, L.; Hu, H.; Song, Q.; Zhang, B.; Lin, R.; Zhang, D. A drift-aware dynamic ensemble model with two-stage member selection for carbon price forecasting. J. Energy 2024, 313, 133699. [Google Scholar] [CrossRef]
- Ghosh, I.; Chaudhuri, T.D.; Isskandarani, L.; Abedin, M.Z. Predicting financial cycles with dynamic ensemble selection frameworks using leading, coincident and lagging indicators. Res. Int. Bus. Financ. 2025, 80, 103114. [Google Scholar] [CrossRef]
- Omoware, J.M.; Abiodun, O.J.; Wreford, A.I. Predicting Stock Series of Amazon and Google Using Long Short-Term Memory (LSTM). Asian Res. J. Curr. Sci. 2023, 5, 205–217. Available online: https://jofscience.com/index.php/ARJOCS/article/view/17 (accessed on 2 September 2025).
- Hu, J.; Cen, Y.; Wu, C. Automatic Construction of Domain Sentiment Dictionary Based on Deep Learning: A Case Study of Financial Domain. Data Anal. Knowl. Discov. 2018, 2, 95–102. [Google Scholar] [CrossRef]
- Loughran, T.; McDonald, B. When Is a Liability Not a Liability? Textual Analysis, Dictionaries, and 10-Ks. J. Financ. 2011, 66, 35–68. [Google Scholar] [CrossRef]
- Li, J.; Qian, S.; Li, L.; Guo, Y.; Wu, J.; Tang, L. A Novel Secondary Decomposition Method for Forecasting Crude Oil Price with Twitter Sentiment. Energy 2024, 290, 129954. [Google Scholar] [CrossRef]
- Xu, Y.; Cohen, S.B. Stock Movement Prediction from Tweets and Historical Prices. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Melbourne, Australia, 15–20 July 2018; Association for Computational Linguistics: Stroudsburg, PA, USA, 2018; pp. 1970–1979. [Google Scholar] [CrossRef]
- Gui, J.; Naktnasukanjn, N.; Yu, X.; Ramasamy, S.S. Research on the Impact of Economic Policy Uncertainty and Investor Sentiment on the Growth Enterprise Market Return in China—An Empirical Study Based on TVP-SV-VAR Model. Int. J. Financ. Stud. 2024, 12, 108. [Google Scholar] [CrossRef]
- Fu, K.; Zhang, Y. Incorporating Multi-Source Market Sentiment and Price Data for Stock Price Prediction. Mathematics 2024, 12, 1572. [Google Scholar] [CrossRef]
- Smatov, N.; Kalashnikov, R.; Kartbayev, A. Development of Context-Based Sentiment Classification for Intelligent Stock Market Prediction. Big Data Cogn. Comput. 2024, 8, 51. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.-S.; Choi, S.-Y. Forecasting the S&P 500 Index Using Mathematical-Based Sentiment Analysis and Deep Learning Models: A FinBERT Transformer Model and LSTM. Axioms 2023, 12, 835. [Google Scholar] [CrossRef]
- Umer, M.; Awais, M.; Muzammul, M. Stock Market Prediction Using Machine Learning (ML) Algorithms. ADCAIJ Adv. Distrib. Comput. Artif. Intell. J. 2019, 8, 97–116. [Google Scholar] [CrossRef]
- Sun, F.; Belatreche, A.; Coleman, S.; McGinnity, T.M. Pre-Processing Online Financial Text for Sentiment Classification: A Natural Language Processing Approach. In Proceedings of the IEEE Computational Intelligence for Financial Engineering and Economics 2014, London, UK, 21–23 April 2014; IEEE: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. In Proceedings of the International Conference on Learning Representations, Scottsdale, AZ, USA, 2–4 May 2013; pp. 1–12. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Neural Inf. Process. Syst. 1996, 9, 155–161. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Z.; Hu, R.; Li, W.; Liu, T.; Du, X. Analogical Reasoning on Chinese Morphological and Semantic Relations. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers) 2018, Melbourne, Australia, 15–20 July 2018; Association for Computational Linguistics: Stroudsburg, PA, USA, 2018; Volume 2, pp. 138–143. [Google Scholar] [CrossRef]
- Liu, Y.; Mikriukov, D.; Tjahyadi, O.C.; Li, G.; Payne, T.R.; Yue, Y.; Siddique, K.; Man, K.L. Revolutionising Financial Portfolio Management: The Non-Stationary Transformer’s Fusion of Macroeconomic Indicators and Sentiment Analysis in a Deep Reinforcement Learning Framework. Appl. Sci. 2024, 14, 274. [Google Scholar] [CrossRef]
- Digquant Financial Database. Available online: https://digquant.com/ (accessed on 2 September 2025).
- Yahoo Finance. Available online: https://finance.yahoo.com/ (accessed on 2 September 2025).
- Eastmoney Stock Bar. Available online: https://guba.eastmoney.com/ (accessed on 19 June 2025).
- Jieba Documentation. Available online: https://github.com/fxsjy/jieba (accessed on 19 June 2025).
- Sen, D.; Deora, B.S.; Vaishnav, A. Explainable Deep Learning for Time Series Analysis: Integrating SHAP and LIME in LSTM-Based Models. J. Inf. Syst. Eng. Manag. 2025, 10, 412–423. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. Available online: https://dl.acm.org/doi/10.5555/2627435.2670313 (accessed on 2 September 2025).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar] [CrossRef]


| Assets | Related Works for Dataset | Start Date and End Date | Train–Test Split Ratio | Test Data Duration | Important Global Events During Test Period |
|---|---|---|---|---|---|
| CSI 100 stock index | [15] | 01.01.2020– 31.12.2024 | 80%:20% (969:243) | 02.01.2024– 31.12.2024 | Russia–Ukraine war |
| Corn futures | [18] | ||||
| China Unicom stock | [25] | ||||
| AMZN stock | [25] | 25.05.2017– 05.04.2023 | 70%:30% (1034:442) | 06.07.2021– 05.04.2023 | COVID-19 pandemic |
| Assets | Number of Forum Titles | Number of Positive Labels (%) | Number of Negative Labels (%) | SnowNLP Thresholds () | Overall Accuracy (%) |
|---|---|---|---|---|---|
| CSI 100 stock index | 92,184 | 52.57 (48,459) | 9.52 (8774) | (0.7, 0.3) | 97.00 |
| (0.8, 0.2) | 92.84 | ||||
| (0.9, 0.1) | 96.75 | ||||
| Corn futures | 135,110 | 42.23 (57,055) | 15.75 (21,285) | (0.7, 0.3) | 97.35 |
| (0.8, 0.2) | 95.94 | ||||
| (0.9, 0.1) | 97.28 | ||||
| China Unicom stock | 153,023 | 53.91 (82,491) | 11.12 (16,857) | (0.7, 0.3) | 97.16 |
| (0.8, 0.2) | 96.28 | ||||
| (0.9, 0.1) | 95.88 | ||||
| AMZN stock | 7382 | 77.43 (5716) | 6.18 (456) | (0.7, 0.3) | 90.53 |
| (0.8, 0.2) | 86.88 | ||||
| (0.9, 0.1) | 81.79 |
| Cosine Similarity Threshold | CSI 100 Stock Index (%) | Corn Futures (%) | China Unicom Stock (%) | AMZN Stock (%) | Overall Accuracy (%) |
|---|---|---|---|---|---|
| 0.7 | 96.07 | 97.23 | 96.21 | 82.33 | 92.96 |
| 0.8 | 97.00 | 97.35 | 97.16 | 90.53 | 95.51 |
| 0.9 | 93.62 | 96.93 | 95.68 | 83.95 | 92.55 |
| Assets | Regression Coefficient (Constant) | Regression Coefficient (Sentiment Score) | t-Value (Constant) | t-Value (Sentiment Score) | R2 Value |
|---|---|---|---|---|---|
| CSI 100 stock index | 6382.353 | 26.888 | 59.624 | 0.105 | 0.9395 |
| Corn futures | 2631.048 | −327.564 | 132.487 | −4.703 | 0.9270 |
| China Unicom stock | 4.541 | −0.488 | 53.235 | −2.450 | 0.8889 |
| AMZN stock | 98.443 | 26.526 | 59.057 | 9.910 | 0.9489 |
| Model | MAPE | RMSE | MAE |
|---|---|---|---|
| SVR [15] | 10.993 | 469.617 | 393.234 |
| GRU [15] | 7.887 | 415.654 | 353.276 |
| LSTM [15] | 7.054 | 382.569 | 313.854 |
| FIVMD-LSTM [15] | 2.772 | 154.603 | 116.563 |
| GWO-LSTM [20] | 6.083 | 326.457 | 265.384 |
| CEEMDAN-LSTM [21] | 5.249 | 296.312 | 233.445 |
| SSA-BIGRU [22] | 13.688 | 545.211 | 501.139 |
| VMD-SE-GRU [23] | 3.316 | 192.817 | 148.918 |
| MCS [26] | 1.798 | 146.625 | 113.614 |
| FinBERT [37] | 2.273 | 186.770 | 139.047 |
| Proposed DQN-HTS-EF | 2.027 | 148.796 | 106.937 |
| Model | MAPE | RMSE | MAE |
|---|---|---|---|
| TCN [18] | 2.532 | 85.720 | 70.128 |
| GRU [18] | 2.347 | 78.946 | 65.015 |
| LSTM [18] | 2.093 | 74.215 | 59.657 |
| SCINet [18] | 1.634 | 55.404 | 45.190 |
| MCS [26] | 1.588 | 51.845 | 41.808 |
| FinBERT [37] | 1.379 | 34.976 | 28.542 |
| Proposed DQN-HTS-EF | 1.075 | 30.835 | 24.826 |
| Model | MSE | RMSE | MAE |
|---|---|---|---|
| CNN [19] | 0.037 | 0.193 | 0.134 |
| LSTM [9] | 0.036 | 0.189 | 0.128 |
| BiLSTM [11] | 0.035 | 0.189 | 0.132 |
| CNN-LSTM [24] | 0.030 | 0.174 | 0.110 |
| CNN-BiLSTM [24] | 0.029 | 0.170 | 0.110 |
| BiLSTM-ECA [24] | 0.039 | 0.198 | 0.142 |
| CNN-LSTM-ECA [24] | 0.032 | 0.180 | 0.127 |
| CNN-BiLSTM-ECA [24] | 0.028 | 0.167 | 0.103 |
| LSTM-mTrans-MLP [25] | 0.018 | 0.133 | 0.092 |
| MCS [26] | 0.029 | 0.170 | 0.143 |
| FinBERT [37] | 0.024 | 0.154 | 0.107 |
| Proposed DQN-HTS-EF | 0.012 | 0.108 | 0.075 |
| Model | MAE | MSE | RMSE |
|---|---|---|---|
| Linear regression [38] | 72.47 | 7231.59 | 85.04 |
| Exponential smoothing [33] | 16.62 | 363.83 | 19.074 |
| LSTM [29] | 14.97 | 418.97 | 20.468 |
| CNN-BiLSTM [24] | 4.518 | 28.478 | 5.336 |
| MCS [26] | 23.729 | 841.835 | 29.014 |
| FinBERT [37] | 6.420 | 66.731 | 8.169 |
| Proposed DQN-HTS-EF | 4.335 | 28.018 | 5.293 |
| Assets | Sentiment Score SHAP Importance | Dominant Model (Highest SHAP Importance) | Dominant Model SHAP Importance |
|---|---|---|---|
| CSI 100 stock index | 0.0378 | Multi-Transformer | 0.1687 |
| Corn futures | 0.003 | Bi-Transformer | 0.2289 |
| China Unicom stock | 0.0088 | SVR | 0.1186 |
| AMZN stock | 0.0367 | Multi-Transformer and SVR (tied) | 1.5589/1.5510 |
| Assets | Train–Test (60:20) | Train–Test (70:20) | Train–Test (80:20) | ||||||
| MAPE | RMSE | MAE | MAPE | RMSE | MAE | MAPE | RMSE | MAE | |
| CSI 100 stock index | 1.872 | 151.025 | 117.695 | 1.868 | 150.448 | 117.449 | 2.027 | 148.796 | 106.937 |
| Corn futures | 1.547 | 52.184 | 41.307 | 1.287 | 43.128 | 34.042 | 1.075 | 30.835 | 24.826 |
| MSE | RMSE | MAE | MSE | RMSE | MAE | MSE | RMSE | MAE | |
| China Unicom stock | 0.028 | 0.167 | 0.138 | 0.029 | 0.172 | 0.144 | 0.012 | 0.108 | 0.075 |
| Train–Test (50:30) | Train–Test (60:30) | Train–Test (70:30) | |||||||
| MAE | MSE | RMSE | MAE | MSE | RMSE | MAE | MSE | RMSE | |
| AMZN stock | 29.787 | 1212.208 | 34.817 | 28.811 | 1164.353 | 34.123 | 4.335 | 28.018 | 5.293 |
| Assets | Proposed DQN-HTS-EF | Arithmetic Mean | Weighted Average | Directional Voting |
|---|---|---|---|---|
| CSI 100 stock index | 0.0015 | 0.0087 | 0.0020 | 0.0140 |
| Corn futures | 0.0008 | 0.0018 | 0.0011 | 0.0036 |
| China Unicom stock | 0.0117 | 0.0196 | 0.0146 | 0.0287 |
| AMZN stock | 0.0018 | 0.0025 | 0.0024 | 0.0033 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Tsang, H.S.-H.; Hsung, R.T.-C.; Zhu, Y.; Lo, W.-L. From Market Volatility to Predictive Insight: An Adaptive Transformer–RL Framework for Sentiment-Driven Financial Time-Series Forecasting. Forecasting 2025, 7, 55. https://doi.org/10.3390/forecast7040055
Song Z, Tsang HS-H, Hsung RT-C, Zhu Y, Lo W-L. From Market Volatility to Predictive Insight: An Adaptive Transformer–RL Framework for Sentiment-Driven Financial Time-Series Forecasting. Forecasting. 2025; 7(4):55. https://doi.org/10.3390/forecast7040055
Chicago/Turabian StyleSong, Zhicong, Harris Sik-Ho Tsang, Richard Tai-Chiu Hsung, Yulin Zhu, and Wai-Lun Lo. 2025. "From Market Volatility to Predictive Insight: An Adaptive Transformer–RL Framework for Sentiment-Driven Financial Time-Series Forecasting" Forecasting 7, no. 4: 55. https://doi.org/10.3390/forecast7040055
APA StyleSong, Z., Tsang, H. S.-H., Hsung, R. T.-C., Zhu, Y., & Lo, W.-L. (2025). From Market Volatility to Predictive Insight: An Adaptive Transformer–RL Framework for Sentiment-Driven Financial Time-Series Forecasting. Forecasting, 7(4), 55. https://doi.org/10.3390/forecast7040055







