Integration of LSTM Networks in Random Forest Algorithms for Stock Market Trading Predictions
Abstract
1. Introduction
1.1. Objectives
- (a)
- Fundamental models rely on key company financial data, e.g., earnings per share (EPS), operating cash flow, and market capitalization (fundamental variables). Using advanced decision tree algorithms such as random forest and gradient boosting, these models analyze a wide range of fundamental variables to predict the future behavior of assets. With a sufficiently large number of assets, these models offer a comprehensive view of the market and can identify significant patterns and trends influencing stock prices.
- (b)
- Technical models focus on stock price patterns and trading volumes (technical variables). Using deep learning techniques such as long short-term memory (LSTM) networks, these models incorporate a wide range of technical indicators such as the relative strength index (RSI), moving average convergence divergence (MACD), and Bollinger bands. By processing these technical signals, LSTM networks can capture complex patterns in stock prices and provide accurate predictions about their evolution.
- (c)
- Models that combine fundamental and technical variables will be referred to as hybrid models. In our approach, individual LSTM nets are built for each asset, using both price data and technical indicators. The output of these nets is then fed as an additional variable into an algorithm such as random forest. This approach allows for the capture of both long-term trends based on fundamentals and short-term patterns based on technical analysis, thus providing a more comprehensive view of the market and increasing prediction accuracy.
1.2. Related Work
1.3. Contents
2. Variables
2.1. Fundamental Variables
- Profitability Ratios
- (a)
- Div Yld Y0 Year Ended, Div Yld Y1 Current Year, Div Yld Y2, Div Yld Y3: Dividend Yield for the year ended (Y0) and the following three years (Y1, Y2, Y3). It represents the ratio of dividends paid per share to the share price.
- (b)
- Margin Ebitda % Y0 Year Ended, Margin Ebitda % Y1 Current Year, Margin Ebitda % Y2, Margin Ebitda % Y3: EBITDA Margin for the year ended (Y0) and the following three years (Y1, Y2, Y3). It represents the ratio of EBITDA to total revenue, indicating profitability before interest, taxes, depreciation, and amortization [18],
- (c)
- ROE Y1 Current Year: Return on Equity for the current year, representing the ratio of net income to shareholders’ equity,
- (d)
- Div Payout Y0 Year Ended, Div Payout Y1 Current Year, Div Payout Y2, Div Payout Y3: Dividend payout ratio for the year ended (Y0) and the following three years (Y1, Y2, Y3). It measures the percentage of earnings paid out to shareholders as dividends.
- (e)
- EPS +1E 3Meses, EPS +1E Actual, var % EPS +1E 3Meses: next-quarter estimated EPS, actual EPS, and percentage change in estimated EPS,
- (f)
- EBIT +1E 3Meses, EBIT +1E Actual, var % EBIT +1E 3Meses: next-quarter estimated EBIT, actual EBIT, and percentage change in estimated EBIT.
- (g)
- Sales +1E 3Months, Sales +1E Current, var % Sales +1E 3Months: next-quarter estimated sales, actual sales, and percentage change in estimated sales.
- Valuation Ratios
- (a)
- PER Y0 Year Ended, PER Y1 Current Year, PER Y2, PER Y3: The price-to-earnings ratio (PER) for the year ended (Y0) and the following three years (Y1, Y2, Y3). It measures the ratio of a company’s share price to its earnings per share [19],
- (b)
- EV EBITDA Y0 Year Ended, EV EBITDA Y1 Current Year, EV EBITDA Y2, EV EBITDA Y3: Enterprise value to earnings before interest, taxes, depreciation, and amortization (EV/EBITDA) multiple for the year that has ended (Y0) and the following three years (Y1, Y2, Y3). It indicates the valuation of a company relative to its operational cash flow [20],
- (c)
- Price to Book Value Y0 Year Ended, Price to Book Value Y1 Current Year, Price to Book Value Y2, Price to Book Value Y3: The price-to-book value ratio for the year that has ended (Y0) and the following three years (Y1, Y2, Y3). It compares a company’s market value to its book value [21],
- (d)
- Price CF Y0 Year Ended, Price CF Y1 Current Year, Price CF Y2, Price CF Y3: The price-to-cash flow ratio for the year that has ended (Y0) and the following three years (Y1, Y2, Y3). It compares the market value of a company to its operating cash flow [22],
- (e)
- FCF/EV (%) Y0 Year Ended, FCF/EV (%) Y1 Current Year, FCF/EV (%) Y2, FCF/EV (%) Y3: The free cash flow-to-enterprise value ratio for the year that has ended (Y0) and the following three years (Y1, Y2, Y3). It measures the percentage of free cash flow to the enterprise value [23],
- (f)
- FCF YLD (%) Y0 Year Ended, FCF YLD (%) Y1 Current Year, FCF YLD (%) Y2, FCF YLD (%) Y3: The free cash flow yield for the year ended (Y0) and the following three years (Y1, Y2, Y3). It represents the ratio of free cash flow per share to the share price [24],
- (g)
- PEG FY1, PEG FY2: The price/earnings-to-growth ratio for the next year (FY1) and the following year (FY2). It relates the P/E ratio to the anticipated future earnings growth rate [25],
- (h)
- Objective Price 12 months, Potential Objective Price %: the 12-month price target and percentage potential for the price target. The “Potential Objective Price”, also known as “Target Price” or “Target Price Potential”, is an estimation of the future value of a financial asset, typically a stock. This calculation is based on various factors, such as earnings forecasts, industry trends, market conditions, and other relevant information. Analysts and financial institutions often use different methodologies to derive target prices, including fundamental analysis, technical analysis, and valuation models [26],
- (i)
- Target Price 3Months, var % PO 3Months: 3-month price target and percentage change in the price target.
- (j)
- Long term growth %: Long-term growth percentage. It is a financial metric used in financial analysis and company valuation to estimate the expected growth rate of a company’s revenues, earnings, or other financial indicators in the future. This percentage represents the projected annual growth rate over an extended period, typically spanning several years.
- Leverage Ratios
- (a)
- The net debt to EBITDA ratio for the year ended that has (Y0) and the following three years (Y1, Y2, Y3). It measures a company’s ability to pay off its debts using its earnings [27],
- Market and Trading Data
- (a)
- Market Value EUR millions: the total market value of a company’s outstanding shares, expressed in millions of euros.
- (b)
- Float Pct Total Outstdg: the percentage of total outstanding shares that are available for trading in the open market.
- (c)
- Free-float EUR millions: the market capitalization of a company adjusted for the proportion of shares available for public trading, expressed in millions of euros.
- (d)
- Recommendation and numerical recommendation for the stock: The recommendation and numerical recommendation for the stock. This indicator is obtained based on the analysis carried out by many traders and analysts manually.
- (e)
- 12 months %, YTD %: percentage change over the last 12 months and year-to-date, respectively.
- (f)
- Last 52 Weeks Low Price and Last 52 Wks High Price: the lowest and highest prices over the last 52 weeks.
- (g)
- % From lows 1 year, % from highs 1 year: the percentage change from 1-year lows and highs, respectively.
- (h)
- 3y Price Volatility: three-year price volatility.
- (i)
- Issue Common Shares Outstdg, Average Daily Volume: the number of common shares outstanding and average daily trading volume, respectively.
- (j)
- Volume/shares %: volume per share percentage.
- (k)
- 3y BETA Rel to Loc Idx: the three-year beta relative to the local index.
- (l)
- % Capital contracted daily: the percentage of capital traded daily.
- (m)
- Diff % Mean 200, diff % Mean 50, diff % Mean 25, Mean 50/200: the percentage difference from the 200 moving average daily timeframe.
- (n)
- ECA Num EPS, ECA Num EBIT, EC Reco Total, EC Reco Up, EC Reco Down, EC Reco Unchng, % mod recom Positivas/Total, EC Reco Pos, EC Reco Neg, EC Reco Total.1, Positivas/Total (%): various parameters related to earnings per share (EPS), earnings before interest and taxes (EBIT), and recommendations.
2.2. Technical Variables
- Trend Indicators
- (a)
- Simple moving average (SMA) [28]. The formula is given bywhere n is the size of the time window (number of periods in the window), and is the closing price on the i-th day of the window. was calculated for .
- (b)
- Exponential moving average (EMA) [29]. The formula is given recurrently bywhere n is the EMA span (lookback period), and is the closing price at the last day of the period. was calculated for .
- (c)
- The Ichimoku cloud [30] is defined by the formulasThe “Tenkan Sen” line is called the conversion line, the “Kijun Sen” line is called the base line, the “Senkou Span A” line is called leading span A, and the “Senkou Span B” line is called leading span B, and the “Chikou Span” line is called the lagging span. High and low refer to the highest and lowest prices in the corresponding time window. We used the standard parametric values: , , and .
- (d)
- The average directional index (ADX) [31] is calculated using the loopwhere n is the time window, ,andwhere (resp., ) is the highest (resp., lowest) price at period t. As usual, we set .
- Momentum Oscillators
- (a)
- Here, is the average gain over the last n days, and is the average loss over the last n days. The RSI was calculated for .
- (b)
- The moving average convergence divergence (MACD) [33] is defined by the formulaswhere n is the size of the time window for the shorter EMA, m is size of the time window for the longer EMA (), p is the number of periods of the EMA signal line, is the exponential moving average of the closing prices in the window of size n, is the MACD histogram, and is the MACD signal line. We used the standard parametric values: , , and .
- (c)
- The Williams %R [34] is given bywhere is the highest price over the last n periods, is the lowest price over the last n periods, and Close is the closing price (at the last period). We used the standard value, .
- (d)
- The stochastic oscillator (KDJ) [32] is an indicator that measures the current price of an asset in relation to its range over a time interval. It is defined aswhere Close is the current closing price, is the asset’s lowest price over the last n periods, and is the highest price over the same n periods. We used the standard parametric values: the calculation time interval for %K = 14, and %D smoothing window size = 3.
- (e)
- Squeeze momentum (SQZ) [35] is a volatility indicator defined aswhere n is the size of the time window for the shorter mean (usually ranging from 5 to 20), m is the size of the time window for the longer mean (usually between 20 and 50), p is the size of the time window for the comparison mean, q is a multiplier (typically 2 or 3), and is the simple average of the closing prices in the window of size n. We use the following parametric values: , , , and .
- Volatility Indicators
- (a)
- Bollinger bands [36] are envelopes plotted at a standard deviation level above and below a simple moving average of the price. They are defined by the formulaswhere n is the size of the time window, k is the number of standard deviations of the data in the window (StdDev), Close is the closing price, is the standard deviation of the closing prices over the window, and is the simple moving average of the closing prices over the window. The parameter n determines the sensitivity of the bands to changes in prices. The parameter k determines the distance between the bands and the moving average. We used the standard parametric values: and .
- (b)
- The average true range (ATR) [37] is a price volatility indicator defined aswhere n is the size of the time window, is the highest price in the periods , is the lowest price in the periods , and is the closing price at period . We used the standard value, .
- Trend indicators (SMA, EMA, Ichimoku, ADX) identify market direction;
- Momentum oscillators (RSI, MACD, Williams %R, KDJ, SQZ) measure price velocity and reversal points;
- Volatility indicators quantify price fluctuation intensity, specifically, and Bollinger bands measure volatility through band width (BBB) and the band percentage (BBP), while ATR measures average trading range, regardless of the direction.
2.3. Target
3. Methodology
- (M1)
- Fundamental models, which are machine learning algorithms based on decision trees and fed only with fundamental variables.
- (M2)
- Technical models (one per asset), which are LSTM networks trained only with technical variables.
- (M3)
- Hybrid models, which are models built on both fundamental and technical models.
- (i)
- Area under the ROC curve (AUC).
- (ii)
- Accuracy (ACC).
- (iii)
- Recall (sensitivity).
- (iv)
- Specificity.
- (v)
- Precision.
- (vi)
- F1-score.
- (vii)
- Type I error (false positive rate).
- (viii)
- Type II error (false negative rate).
4. Models and Performances
4.1. Data Pre-Processing
4.1.1. Fundamental Variables
- Due to the lack of sufficient data, the following columns were entirely removed:
- –
- capitalization_millions
- –
- float_pct_total_outstdg
- –
- free_float_eur_millions
- For records with missing values:
- –
- In the column representing the numerical analyst recommendation, missing values were replaced with a value of 1, as it represents a neutral or average recommendation.
- –
- In all other cases, missing values were replaced with 0. This imputation was applied to variables such as EBITDA, the P/E ratio, and the price-to-book ratio.
4.1.2. Technical Variables
4.2. Fundamental Models
- Random Forest (RF): Implemented with Scikit-learn’s RandomForestClassifier, the best model was obtained with the following parameters: bootstrap=True, max_depth=5, max_samples=0.4,max_features=“sqrt”, min_samples_leaf=13, min_ samples_split=20, n_estimators=170, and class_weight=“balanced_subsample”. This configuration achieved a Test AUC of 0.563 and a Test ACC of 0.543.
- Gradient Boosting (GB): The model was implemented using Scikit-learn’s Gradient- BoostingClassifier, which is a standard implementation of gradient boosting with decision trees. We did not use optimized variants such as LightGBM or XGBoost. The optimal configuration was as follows: learning_rate=0.001, sub_sample=0.4, max_depth=3, max_features=“sqrt”, min_samples_leaf=8, min_samples_split=12, and n_esti- mators=130. This model achieved a test AUC of 0.559 and a test ACC of 0.560.
- Neural Network (NN): Built using Keras and TensorFlow, the model consists of an input layer with one neuron per input feature and ReLU activation, followed by two hidden layers. The first hidden layer contains neurons (with n being the number of input features), the second contains 256 neurons; both use ReLU activations and are regularized with Dropout (dropout rate = 0.3). The output layer has a single neuron with a sigmoid activation function for binary classification. The model was trained using the Adam optimizer with a learning rate of 0.01 and binary cross-entropy loss. The best configuration resulted in a test AUC of 0.544 and a test ACC of 0.534.
- Class imbalance naturally penalizes specificity. The scarcity of negative cases (losses) limits the model’s ability to generalize on their patterns.
- Higher false positives are operationally tolerable if the core objective remains maximizing upside participation (as evidenced by recall stability: 62.0% on the test set, 53.0% on the validation set)
4.3. Technical Models
- Epochs: 20, 40, 60, 100.
- Layers: 1, 4, 8.
- Window: 10, 20, 30.
4.4. A Hybrid Model
- (i)
- Test AUC
- (ii)
- The pondered (or weighted) probability, Pond Prob. This probability is calculated according to the formulawhere Prob is the probability that the price of the given asset will increase in 10 days, and (resp., ) is the minimum (resp., maximum) probability obtained in the test predictions.
- (iii)
- Diff AUC (Equation (3)).
4.5. An Improved Hybrid Model
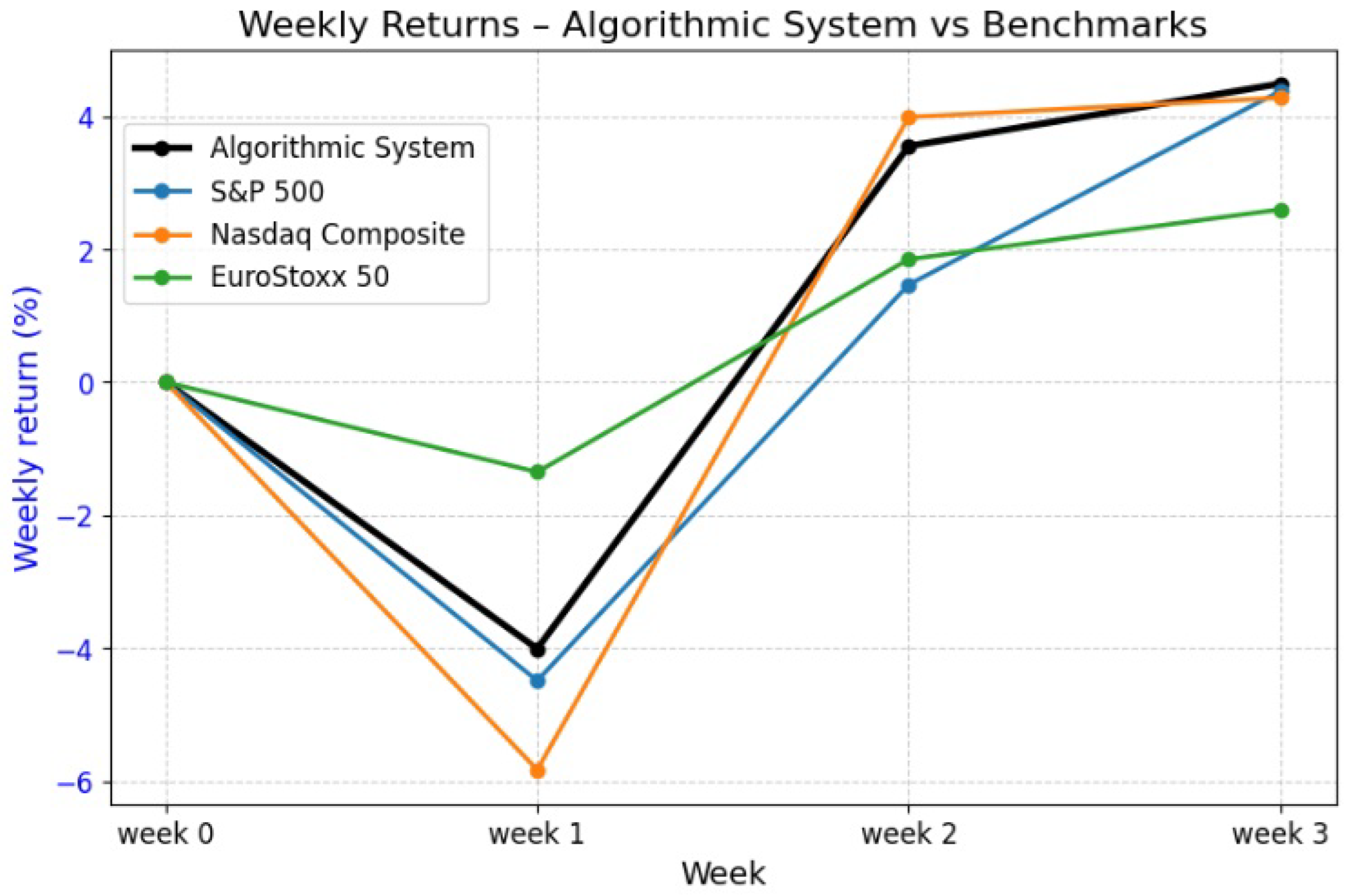
5. Simulation Results
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- King, J.C.; Dale, R.; Amigó, J.M. Blockchain metrics and indicators in cryptocurrency trading. Chaos Solitons Fractals 2024, 178, 114305. [Google Scholar] [CrossRef]
- Chen, J.; Haboub, A.; Khan, A.; Mahmud, S. Investor clientele and intraday patterns in the cross section of stock returns. Rev. Quant. Financ. Account. 2025, 64, 757–797. [Google Scholar] [CrossRef]
- Hendershott, T.; Riordan, R. Algorithmic trading and the market for liquidity. J. Financ. Quant. Anal. 2013, 48, 1001–1024. [Google Scholar] [CrossRef]
- Lei, Y.; Peng, Q.; Shen, Y. Deep learning for algorithmic trading: Enhancing macd strategy. In Proceedings of the 6th International Conference on Computing and Artificial Intelligence, Hohhot, China, 17–20 July 2020; pp. 51–57. [Google Scholar]
- Mahajan, Y. Optimization of macd and rsi indicators: An empirical study of indian equity market for profitable investment decisions. Asian J. Res. Bank. Financ. 2015, 5, 13–25. [Google Scholar] [CrossRef]
- Prasetijo, A.B.; Saputro, T.A.; Windasari, I.P.; Windarto, Y.E. Buy/sell signal detection in stock trading with bollinger bands and parabolic sar: With web application for proofing trading strategy. In Proceedings of the 2017 4th International Conference on Information Technology, Computer, and Electrical Engineering (ICITACEE), Semarang, Indonesia, 18–19 October 2017; pp. 41–44. [Google Scholar]
- Patell, J.M. Corporate forecasts of earnings per share and stock price behavior: Empirical test. J. Account. Res. 1976, 1, 246–276. [Google Scholar] [CrossRef]
- Chan, E.P. Quantitative Trading: How to Build Your Own Algorithmic Trading Business; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Namdari, A.; Li, Z.S. Integrating fundamental and technical analysis of stock market through multi-layer perceptron. In Proceedings of the 2018 IEEE Technology and Engineering Management Conference (TEMSCON), Evanston, IL, USA, 28 June–1 July 2018; pp. 1–6. [Google Scholar]
- Lazcano, A.; Herrera, P.J.; Monge, M. A combined model based on recurrent neural networks and graph convolutional networks for financial time series forecasting. Mathematics 2023, 11, 224. [Google Scholar] [CrossRef]
- Nobre, J.; Neves, R.F. Combining principal component analysis, discrete wavelet transform and XGBoost to trade in the financial markets. Expert Syst. Appl. 2019, 125, 181–194. [Google Scholar] [CrossRef]
- Lv, P.; Wu, Q.; Xu, J.; Shu, Y. Stock index prediction based on time series decomposition and hybrid model. Entropy 2022, 24, 146. [Google Scholar] [CrossRef]
- Pang, X.; Zhou, Y.; Wang, P.; Lin, W.; Chang, V. An innovative neural network approach for stock market prediction. J. Supercomput. 2020, 76, 2098–2118. [Google Scholar] [CrossRef]
- Yoon, Y.; Guimaraes, T.; Swales, G. Integrating artificial neural networks with rule-based expert systems. Decis. Support Syst. 1994, 11, 497–507. [Google Scholar] [CrossRef]
- Damodaran, A. Equity Risk Premiums: Determinants, Estimation and Implications, 2020th ed.; NYU Stern School of Business: New York, NY, USA, 2020. [Google Scholar]
- Data, Computer Codes, and List of 482 Companies. Available online: https://github.com/JuanCarlosKing/StockmarketAlgoritmicTrading (accessed on 21 February 2025).
- Ng, S.L.; Rabhi, F. A data analytics architecture for the exploratory analysis of high-frequency market data. In Proceedings of the 11th International Workshop on Enterprise Applications, Markets and Services in the Finance Industry 2022, Lecture Notes in Business Information Processing (LNBIP), Twente, The Netherlands, 23–24 August 2022; Springer: Cham, Switzerland, 2023; Volume 467, pp. 1–16. [Google Scholar]
- Okeke, C.M.G. Evaluating company performance: The role of EBITDA as a key financial metric. Int. J. Comput. Appl. Technol. Res. 2020, 9, 336–349. [Google Scholar]
- Ghaeli, M.R. Price-to-earnings ratio: A state-of-art review. Accounting 2016, 3, 131–136. [Google Scholar] [CrossRef]
- Zelmanovich, B.; Hansen, C.M. The basics of ebitda. Am. Bankruptcy Inst. J. 2017, 36, 36–37. [Google Scholar]
- Budianto, E.W.H.; Dewi, N. The influence of book value per share (BVS) on Islamic and conventional financial institutions: A bibliometric study using VOSviewer and literature review. Islam. Econ. Bus. Rev. 2023, 2, 139–147. [Google Scholar]
- Akhtar, T.; Rashid, K. The relationship between portfolio returns and market multiples: A case study of Pakistan. Oecon. Knowl. 2015, 7, 2–28. [Google Scholar]
- Toumeh, A.A.; Yahya, S.; Amran, A. Surplus free cash flow, stock market segmentations and earnings management: The moderating role of independent audit committee. Glob. Bus. Rev. 2023, 24, 1353–1382. [Google Scholar] [CrossRef]
- Purohit, S.; Agarwal, B.; Kanoujiya, J.; Rastogi, S. Impact of shareholder yield on financial distress: Using competition and firm size as moderators. J. Econ. Adm. Sci. 2025. [Google Scholar] [CrossRef]
- Babii, A.; Ball, R.T.; Ghysels, E.; Striaukas, J. Panel data nowcasting: The case of price–earnings ratios. J. Appl. Econom. 2024, 39, 292–307. [Google Scholar] [CrossRef]
- Damodaran, A. Investment Valuation: Tools and Techniques for Determining the Value of Any Asset; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-1118011522. [Google Scholar]
- Bouwens, J.; De Kok, T.; Verriest, A. The prevalence and validity of EBITDA as a performance measure. Comptabilité-Contrôle-Audit 2019, 25, 55–105. [Google Scholar] [CrossRef]
- Huang, X.D.; Qiu, X.X.; Wang, H.J.; Jin, X.F.; Xiao, F. A prospective randomized double-blind study comparing the dose-response curves of epidural ropivacaine for labor analgesia initiation between parturients with and without obesity. Front. Pharmacol. 2024, 15, 1348700. [Google Scholar] [CrossRef]
- Formis, G.; Scanzio, S.; Cena, G.; Valenzano, A. Linear Combination of Exponential Moving Averages for Wireless Channel Prediction. In Proceedings of the 2023 IEEE 21st International Conference on Industrial Informatics (INDIN), Lemgo, Germany, 18–20 July 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Lutey, M.; Rayome, D. Ichimoku cloud forecasting returns in the US. Glob. Bus. Financ. Rev. 2022, 27, 17–26. [Google Scholar] [CrossRef]
- Salkar, T.; Shinde, A.; Tamhankar, N.; Bhagat, N. Algorithmic trading using technical indicators. In Proceedings of the 2021 International Conference on Communication information and Computing Technology (ICCICT), Mumbai, India, 25–27 June 2021; pp. 1–6. [Google Scholar]
- Wu, M.; Diao, X. Technical analysis of three stock oscillators testing macd, rsi and kdj rules in sh & sz stock markets. In Proceedings of the 2015 4th International Conference on Computer Science and Network Technology (ICCSNT), Harbin, China, 19–20 December 2015; Volume 1, pp. 320–323. [Google Scholar]
- Kang, B.K. Optimal and Non-Optimal MACD Parameter Values and Their Ranges for Stock-Index Futures: A Comparative Study of Nikkei, Dow Jones, and Nasdaq. J. Risk Financ. Manag. 2023, 16, 508. [Google Scholar] [CrossRef]
- Steele, R.; Esmahi, L. Technical indicators as predictors of position outcome for technical 665 trading. In Proceedings of the International Conference on e-Learning, e-Business, Enterprise Information Systems, and e-Government (EEE), Las Vegas, NV, USA, 27–30 July 2015; p. 3. [Google Scholar]
- Alostad, H.; Davulcu, H. Directional prediction of stock prices using breaking news on Twitter. In Proceedings of the 2015 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology (WI-IAT), Singapore, 6–9 December 2015; pp. 523–530. [Google Scholar]
- Su, G. Analysis of the Bollinger Band Mean Regression Trading Strategy, Proceedings of the 3rd International Conference on Economic Development and Business Culture (ICEDBC 2023), Dali, China, 30 June–2 July 2023; Atlantis Press: Dordrecht, The Netherlands, 2023. [Google Scholar]
- Panapongpakorn, T.; Banjerdpongchai, D. Short-term load forecast for energy management systems using time series analysis and neural network method with average true range. In Proceedings of the 2019 First International Symposium on Instrumentation, Control, Artificial Intelligence, and Robotics (ICA-SYMP), Bangkok, Thailand, 16–18 January 2019; pp. 86–89. [Google Scholar]
- Aronson, D.; Masters, T. Evidence of technical analysis profitability in the foreign exchange market. J. Financ. Data Sci. 2019, 5, 279–297. [Google Scholar]
- Breitung, C. Automated stock picking using random forests. J. Empir. Financ. 2023, 72, 532–556. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Wang, X.; Hong, L.J.; Jiang, Z.; Shen, H. Gaussian process-based random search for continuous optimization via simulation. Oper. Res. 2025, 73, 385–407. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (rnn) and long short-term memory (lstm) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- García, A. Greedy algorithms: A review and open problems. J. Inequal. Appl. 2025, 2025, 11. [Google Scholar] [CrossRef]
- Kasyanov, R.A.; Vladislav, A.; Kachalyan, V.A. Evolution of the Legal Framework for UCITS Funds in the European Union (1985–2023). Kutafin Law Rev. 2024, 11, 325–369. [Google Scholar] [CrossRef]
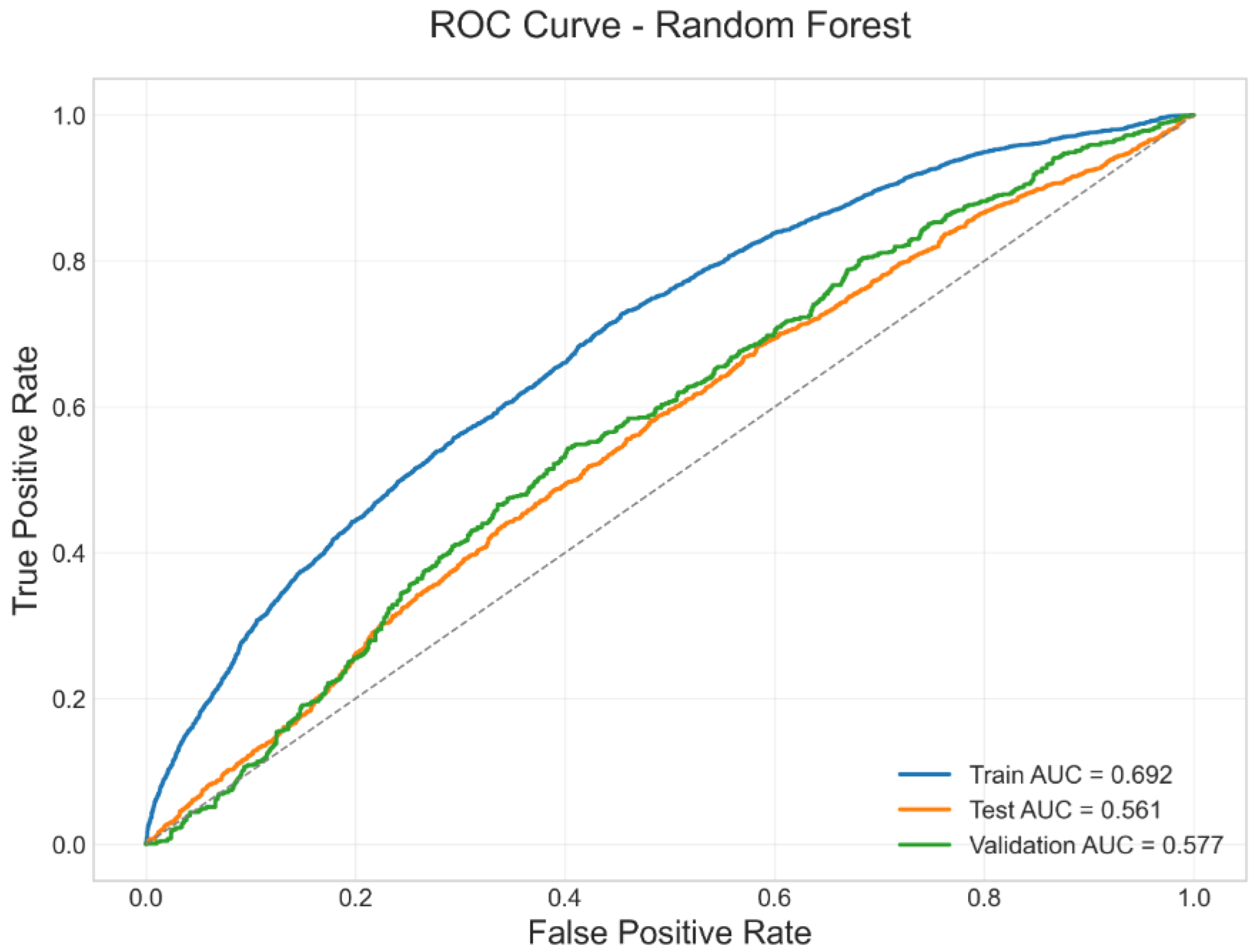
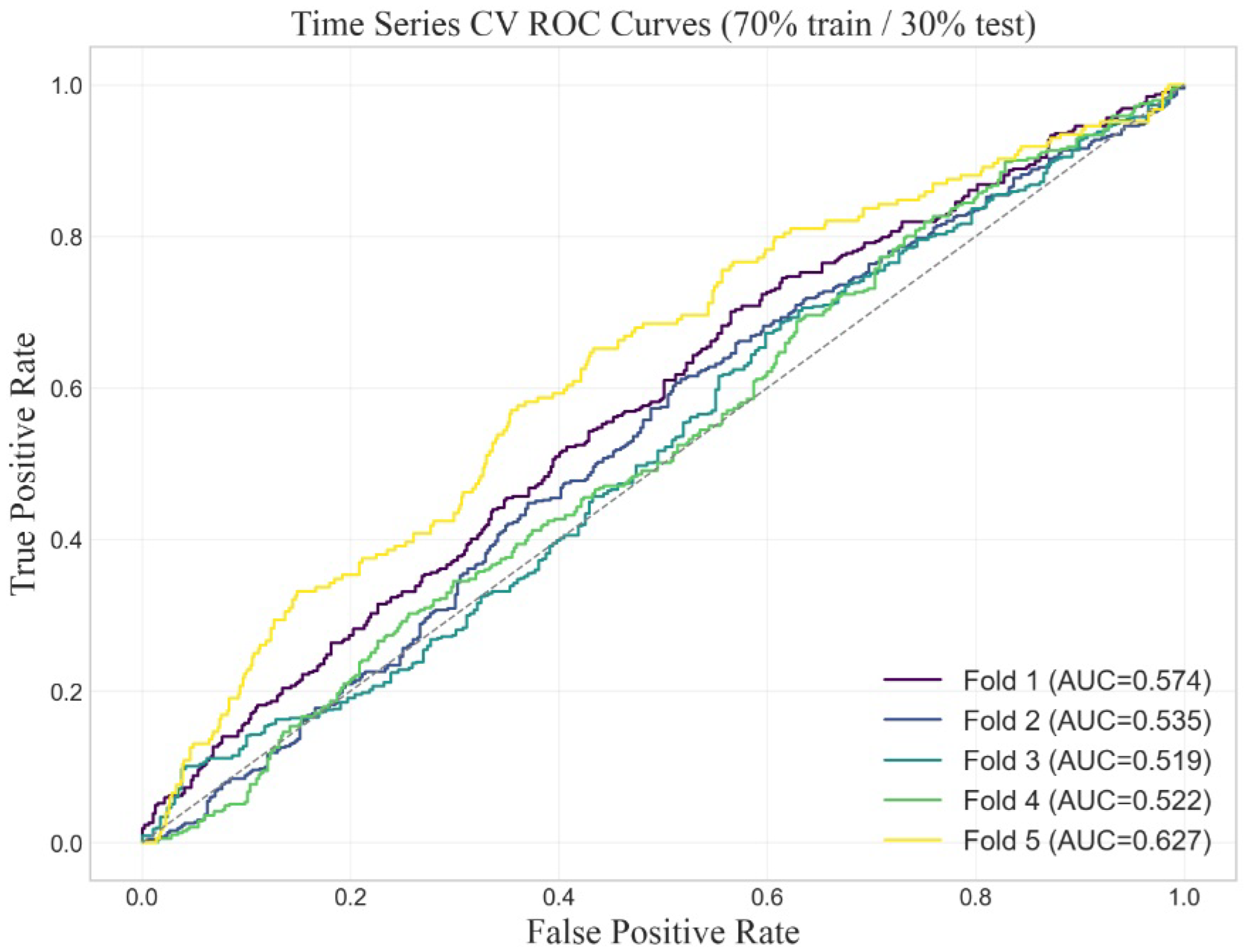
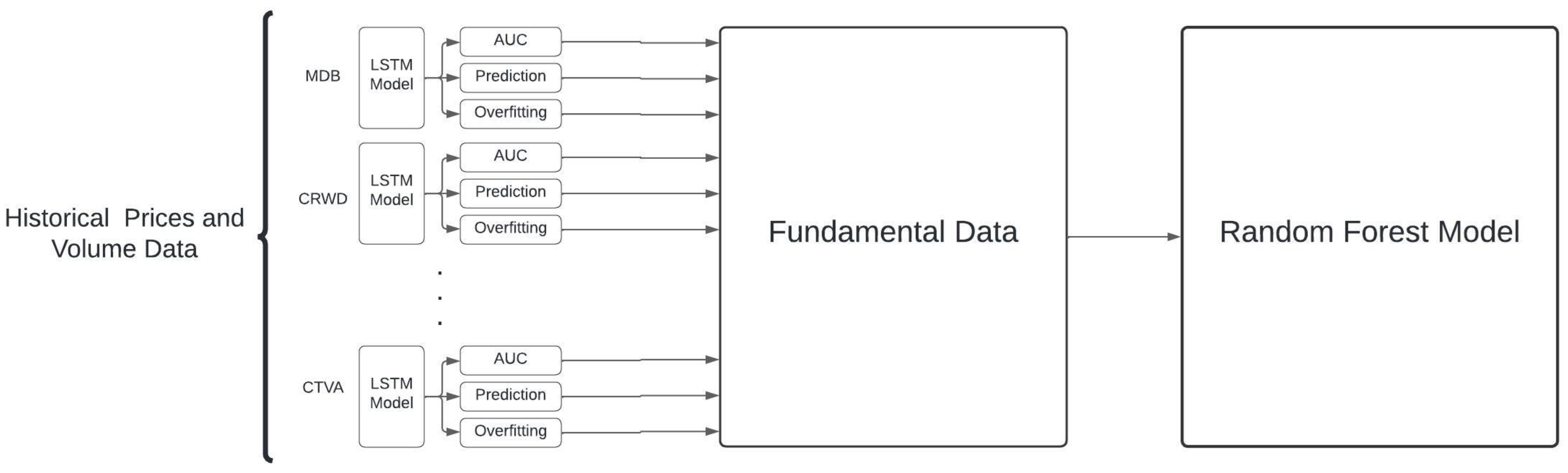

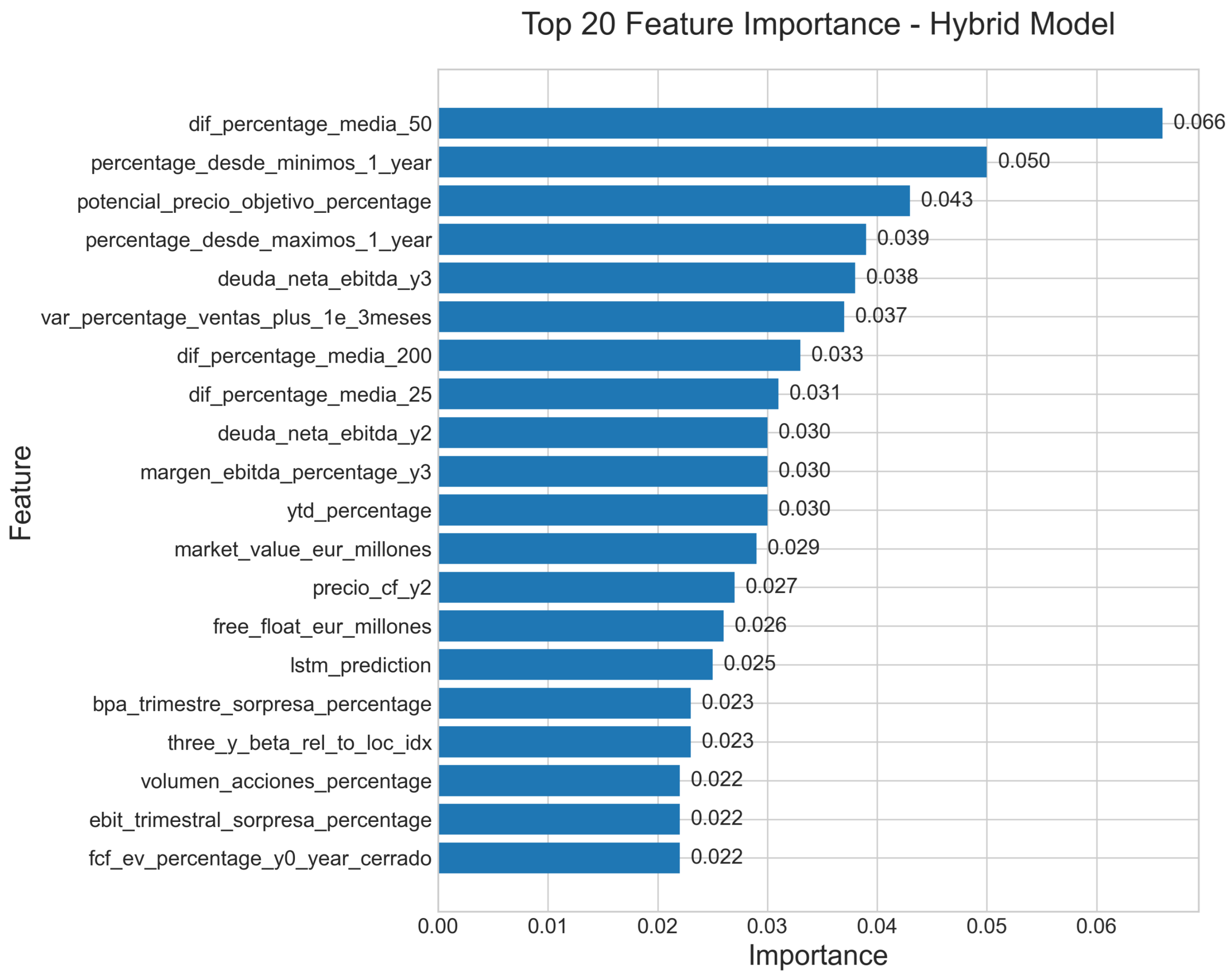
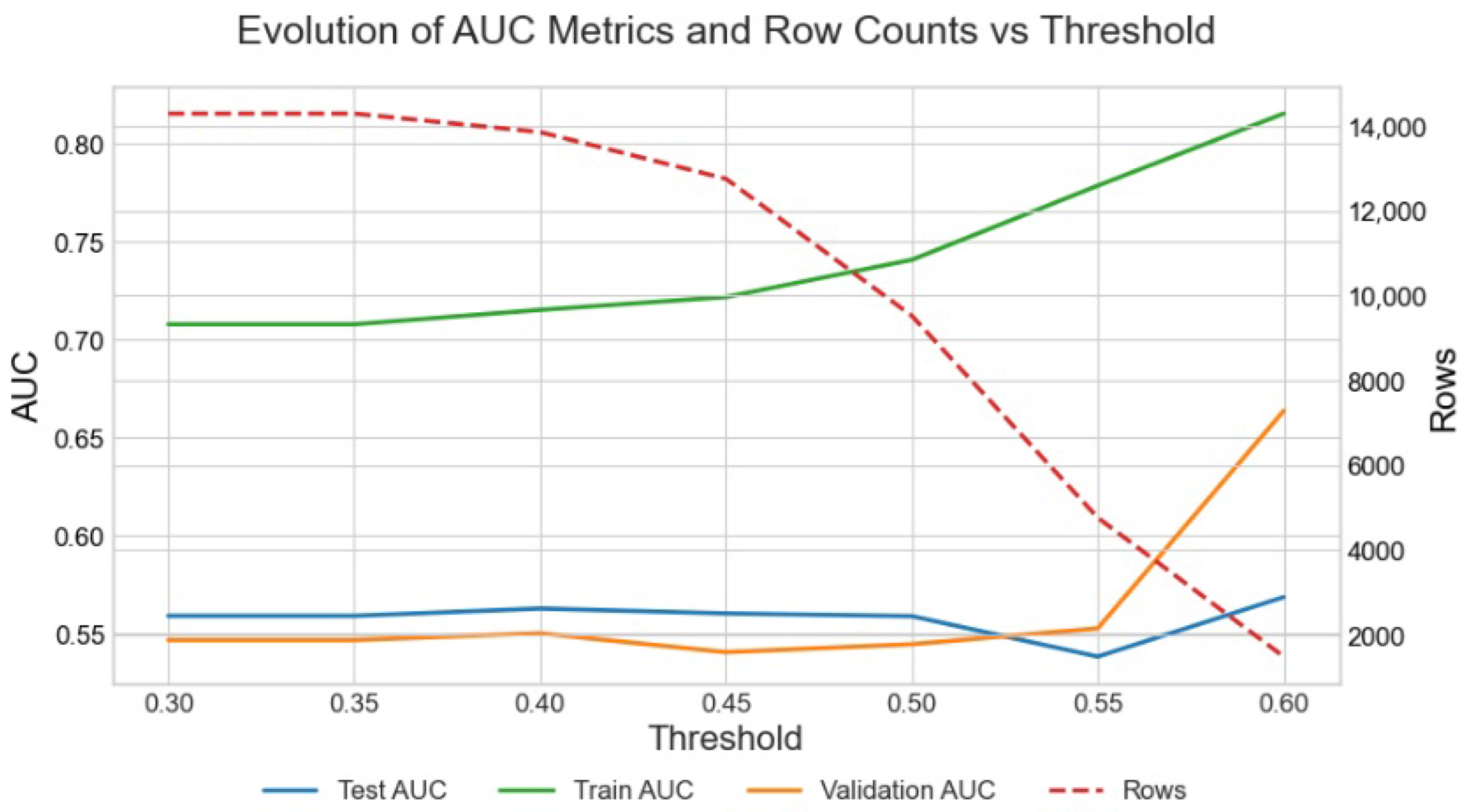

| Train | Test | Validation | |
|---|---|---|---|
| AUC | 0.690 | 0.563 | 0.575 |
| ACC (Accuracy) | 0.633 | 0.543 | 0.560 |
| Recall (Sensitivity) | 0.591 | 0.620 | 0.530 |
| Specificity | 0.673 | 0.483 | 0.588 |
| Precision | 0.634 | 0.482 | 0.552 |
| F1-Score | 0.612 | 0.543 | 0.541 |
| Type I Error | 0.327 | 0.517 | 0.412 |
| Type II Error | 0.409 | 0.380 | 0.470 |
| Metric | Av. Ag. Value |
|---|---|
| Train AUC | 0.631 |
| Test AUC | 0.527 |
| Train ACC | 0.578 |
| Test ACC | 0.524 |
| Diff AUC | 0.104 |
| Diff ACC | 0.053 |
| Model | Train AUC | Test AUC | Test AUC Sign. | 95% CI |
|---|---|---|---|---|
| Fundamental | 0.690 | 0.563 | 0.563 | [0.548, 0.578] |
| Technical | 0.631 | 0.527 | 0.493 | [−0.296, 1.282] |
| Hybrid | 0.686 | 0.566 | 0.566 | [0.550, 0.581] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
King, J.C.; Amigó, J.M. Integration of LSTM Networks in Random Forest Algorithms for Stock Market Trading Predictions. Forecasting 2025, 7, 49. https://doi.org/10.3390/forecast7030049
King JC, Amigó JM. Integration of LSTM Networks in Random Forest Algorithms for Stock Market Trading Predictions. Forecasting. 2025; 7(3):49. https://doi.org/10.3390/forecast7030049
Chicago/Turabian StyleKing, Juan C., and José M. Amigó. 2025. "Integration of LSTM Networks in Random Forest Algorithms for Stock Market Trading Predictions" Forecasting 7, no. 3: 49. https://doi.org/10.3390/forecast7030049
APA StyleKing, J. C., & Amigó, J. M. (2025). Integration of LSTM Networks in Random Forest Algorithms for Stock Market Trading Predictions. Forecasting, 7(3), 49. https://doi.org/10.3390/forecast7030049







