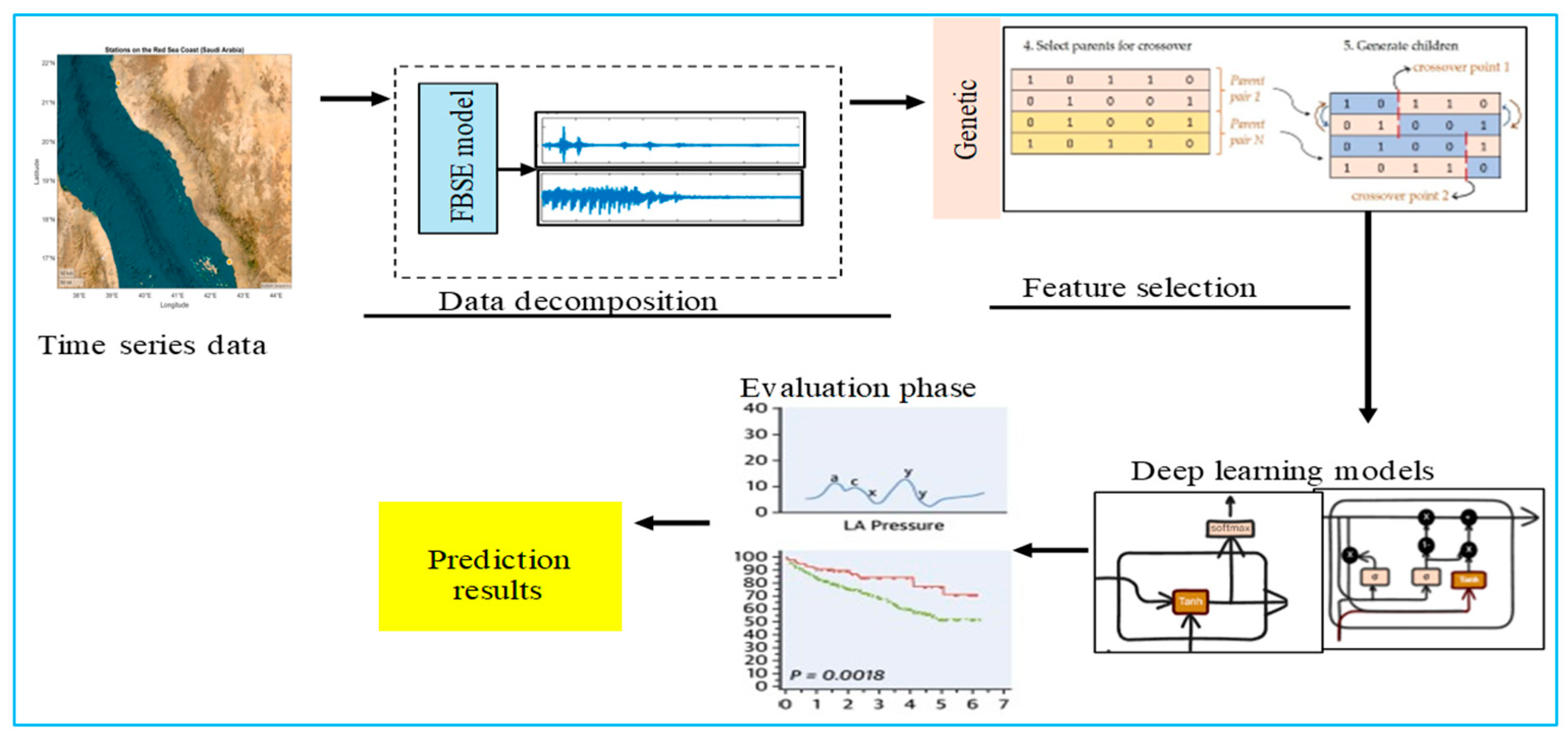
1. Introduction
The dry-bulb temperature (DBT) is a critical weather parameter which is used as a representative of temperature for many applications such as environmental monitoring of industrial and agricultural processes. It is the temperature of the air as measured by a thermometer freely exposed to the air but shielded from radiation and moisture. The accurate prediction of DBT is important in several domains such as weather forecasting, the analysis of climate change, and the management of renewable energy, and precision agriculture DBT predictions contribute to energy optimisation, building climate control as well as natural disaster preparations [
1,
2].
In the literature, DBT estimations have been traditionally based on the numerical weather prediction (NWP) model and statistical methodologies, for example on autoregressive integrated moving averages (ARIMA) or regression methods [
3]. Although these are widely applied techniques, it is frequently difficult for these techniques to effectively represent non-linear, highly complex, and dynamically interacting influences on meteorological variables [
4]. This limitation has led to the investigation and application of advanced artificial intelligence (AI) and machine learning (ML) tools to improve the accuracy of predictions [
5,
6].
Significant recent advances in deep learning (DL) have made DBT prediction more accurate through big data solutions to recognise the highly complex patterns of atmosphere behaviour. In the last few years, there has been an increasing use of machine learning (ML) for DBT prediction, especially since the conventional statistical methods have shortcomings in dealing with nonlinear relationships between input–output variables, and the temporal relationships between the variables in climatic time series.
Among these models, artificial neural networks (ANNs), the convolutional neural network (CNN), recurrent neural networks (RNNs), and long short-term memory (LSTM) have demonstrated a lot of potential. ANNs have been heavily utilised in DBT prediction because of their capacity to model complex, nonlinear relationships. For example, Gündoğdu and Elbir [
7] used a feedforward ANN to forecast maximum daily temperatures and better results were obtained compared to regression-based approaches. Similarly, Tehrani et al., [
8] used ANN models to predict hourly temperatures in urban areas, obtaining high accuracy in the representation of short-term DBT variability. Currently LSTM networks (an RNN variant that captures long-term dependencies) have been established as being some of the best methods for DBT prediction. Hasan et al., [
9] used LSTM models with features including humidity, solar radiation, and wind speed to forecast the daily DBT with substantial enhancements in the accuracy of prediction. Huang et al., [
10] found that LSTM models could successfully manage nonstationary temperature patterns to be applicable in long-term climate interpretation. Yet independent ML and DL models can be ineffective toward noisy imaging data because they are restricted by their own model capacity, and they may not entirely represent subtle nuances in DBT [
11].
In order to overcome these issues, hybrid modelling paradigms have been considered as the more promising alternative. In recent works, excellent results have been achieved by coupling signal processing methods such as multivariate variational mode decomposition (MVMD), with state-of-the-art neural network designs such as the bidirectional long short-term memory (BiLSTM) networks. To improve the accuracy of temperature prediction, in recent years, some signal decomposition methods have been widely used for preprocessing the nonstationary and nonlinear time series data inputs for the machine learning or deep learning models in the era of signal processing and data science technology. Decomposition methods aim at decomposing complex climate signals into simpler sub-structures which have more stable statistical properties to facilitate the physical interpretation of a model prediction. Empirical mode decomposition (EMD) is one of the early adaptive decomposition techniques used in this regard. It is a versatile instrument to perform signal decomposition into the IMFs without a predetermined set of basis functions [
12]. However, mode mixing and noise degradation are two drawbacks of EMD. Ensemble empirical mode decomposition (EEMD) was proposed to solve these problems, which adds white noises to cut down the mode mixing and improve stability [
13]. Further developments, such as the improvement based on the complete ensemble empirical mode decomposition with adaptive noise [
14], have enhanced the robustness and the accuracy of the decomposition of signals. Wavelet transform (WT) and discrete wavelet transform (DWT) are other methods that have been extensively used for predicting DBT. These models decompose a time series into multiple time resolutions based on fixed basis functions and are well suited to capturing localised features in non-stationary data [
15]. However, unlike EMD-based approaches, wavelet techniques necessitate a priori choice of the wavelet basis and this can be too restrictive for real-time implementations, as new wavelet representations are to be selected each time new segments of the learning data are processed.
More recently, variational mode decomposition (VMD) and its multivariate extension MVMD has been presented to accomplish this task. VMD formulates the decomposition as an optimisation problem, thereby improving the mode mixing and ensuring a compacted and band-limited modes [
16]. An extension of MVMD allows joint decomposition of the multivariate signals, retaining the inter-channel dependencies and gaining improved performance in multi-sensor and multivariate problem predictions [
17]. Multivariate empirical mode decomposition (MEMD) is another approach to process multichannel data with shared modes among the signals, to increase interpretability in multivariate systems [
18]. These approaches of decomposition together with the advanced deep learning models like BiLSTM, have shown to be successful in improving prediction performance. For instance, Tang et al., [
19] utilised VMD with BiLSTM for the hourly temperature forecast and demonstrated great improvement on the forecasting accuracy compared with raw-data-based models. Similarly, Ahmed et al., [
20] also suggested EEMD-BiLSTM for air temperature forecasting and demonstrated that hybrid decomposition and deep learning models were able to handle both seasonal patterns and non-linear relations. These findings highlight the importance of decomposition methods as a pre-processing stage for modern temperature predictors in which the deep learning models can work over thousands of more regularised and interpretable signals. These hybrid methods provide further improvement in the forecasting accuracy since complex signals can be effectively decomposed by those methods, noise is reduced, and critical temperature patterns are preserved [
21,
22]. Through this comparison, it was shown that the hybrid models that combine the ML and DL models performed the best for DBT prediction. For example, Zhou et al., [
23] developed an HBA-optimised hybrid ANN model which is denoted as HBA-ANN. They compared HBA-ANN model with the classical ANN and gene expression programming (GEP) models to predict DBT in extreme regions, the Furnace Creek Death Valley, USA, and Vostok Station, Antarctica. Within the prediction horizons of 1–3 months, the HBA-ANN model performed better than the benchmark models. Comparison on the performance of this approach versus their counterparts’ classical artificial neural networks (ANN) and RNN were performed. They employed a genetic algorithm (GA) for meta-learning to optimise abstract network architecture selection as well. They confirmed that the GA–LSTM hybrid model was better than the ML and DL models. One such contemporary hybrid model is the combination of CNN and LSTM, termed as CNN-LSTM. This is to take advantage of the CNN’s property to process low dimensional time series data and the LSTM’s ability to learn long distance relationships to capture temporal patterns present in wide datasets (i.e., large temperature datasets). In [
24], authors showed that CNN-LSTM outperformed CNN and LSTM for daily DBT forecast at the John F. Kennedy International Airport (New York). Similarly, Hou et al., [
25], using CNN-LSTM tightening methods, presented a better hourly DBT forecasting accuracy in Yinchuan, China. The superiority of hybrid deep learning models is justified also by the integration of pre-processing methods to enhance the model performance [
26]. In this paper, we attempt to construct an accurate prediction model for the DBT prediction problem and exploit the combination of the hybrid models derived from the FBSE, genetic algorithm (GA), and long short-term memory (LSTM) networks. We investigate the performance of the hybrid model FBSE-GA-LSTM and other deep learning model structures in the context of DBT prediction at various horizon lengths (i.e., one hourly/monthly/weekly ahead horizon) [
27]. The performances of the proposed FBSE-GA-BLSTM models were tested across various evaluation metrics such as root mean square error (RMSE), mean absolute error (MAE), correlation coefficient (R), linear model efficiency (LME), and relative percentage error (RPE) to critically measure the correctness of predictions from different perspectives.
Previous studies have demonstrated the potential of hybrid models for improving weather prediction accuracy; however, many have been limited by suboptimal noise handling, inadequate feature selection, or insufficient evaluation against naïve benchmarks. The proposed FBSE-GA-LSTM framework addresses these gaps by integrating Fourier–Bessel series expansion (FBSE) for effective noise reduction and extraction of dominant predictive patterns, genetic algorithm (GA) for optimal feature selection and dimensionality reduction, and long short-term memory (LSTM) networks for capturing temporal dependencies in the data. Unlike earlier approaches, the present model has been systematically compared with both advanced deep learning hybrids (FBSE-GA-BiLSTM, FBSE-GA-GRU) and simple baseline predictors (persistence and climatic average), demonstrating superior predictive performance across two distinct climatic regions. This design not only enhances accuracy but also provides robustness in forecasting highly repetitive variables such as the dry-bulb temperature.
3. Experimental Results
This section reports the results of the dry-bulb air temperature prediction based on the proposed model for the two regions in Saudia Arabia. This study evaluated the performance of the proposed model, which integrated FBSE, GA, and LSTM techniques to predict one-day, one-week, and one-month dry-bulb air temperatures. For the one-day-ahead prediction, we used the time series data from a single day (t − 1) as the input to forecast the next day (t). For the one-week-ahead prediction, we used the complete preceding week of the time series data (t − 7 to t − 1) to forecast the aggregated value for the following week. Similarly, for the one-month-ahead prediction, we used the preceding month of the time series data (t − 30 to t − 1) to predict the aggregated value for the following month. The dataset was segmented chronologically into 60% training, 20% validation, and 20% testing sets respectively. No random sampling was applied. The FBSE decomposition was applied exclusively to the training data.
3.1. Evaluation Metrics
The test set was utilised to evaluate the performance of the completed model. Several metrics were used to measure this performance, and
Table 2 summarises all the metrics applied in the evaluation of the proposed model [
35,
36,
37,
38].
3.2. Benchmark Models
In this paper, the proposed FBSE-GA was hybridised with several benchmark models: GRU, BiGRU, LSTM, and BiLSTM. The following section provides a brief description of these models.
Table 3 lists all the hyperparameters of the proposed models.
GRU: GRU was utilised as a foundational model to benchmark the performance of the hybrid approach for temperature prediction. A hybrid approach can significantly enhance the accuracy of dry-bulb air temperature predictions. This model can leverage various components.
BiGRU: Incorporating the bidirectional gated recurrent unit (BiGRU) effectively captures bidirectional dependencies within the data, leading to improved prediction accuracy.
BiLSTM: Employing bidirectional long short-term memory (BiLSTM) as an alternative to standard LSTM can reveal its advantages in recognising complex patterns within the dataset.
While the hybrid model harnesses the strengths of its components, it may demand substantial computational resources, especially when processing large datasets. Furthermore, the model’s performance can be sensitive to the choice of hyperparameters, requiring meticulous tuning and optimisation.
The complexity of the models and techniques involved may create challenges in interpreting results and understanding the underlying relationships within the data. By exploring the integration of FBSE with GRU, BiGRU, and BiLSTM in a hybrid framework, a more accurate and robust model for predicting the dry-bulb air temperature can be developed.
5. Discussion
The findings highlight the importance of integrating the decomposition model with deep learning architectures for achieving accurate predictions. The article “Hybrid Model of Feature-Based Selection and Extraction and Genetic Algorithms GA for Optimizing the Prediction of Complex and Non-Stationary Time Series” was submitted for hybrid models to predict nonstationary and complex time series data, which extended the concept of hybrid models by integrating feature-based selection and extraction (FBSE) and genetic algorithms (GA), that optimised model parameters, performed data decomposition with selected features, and eliminated the abnormal values of selecting features. This complementary relationship enabled us to seek out significant patterns from complex data and to optimise model parameters for accurate forecast. Combining these methods enabled us to handle the difficulty of nonlinearity, non-stationarity, and noise in time series data, thus improving the prediction accuracy. In addition, the FBSE-based GA demonstrated a strong performance in analysing the nonstationary and complex time series data. The relationship between the novelty of the decomposition model, feature selection, and deep learning models became clear in cases where the datasets did not necessarily satisfy the independent and identically distributed requirement. In our work to tackle these problems in DBT prediction, we introduced a hybrid model of FBSE, GA, and BiLSTM. The main discovery is described in this section.
- 1.
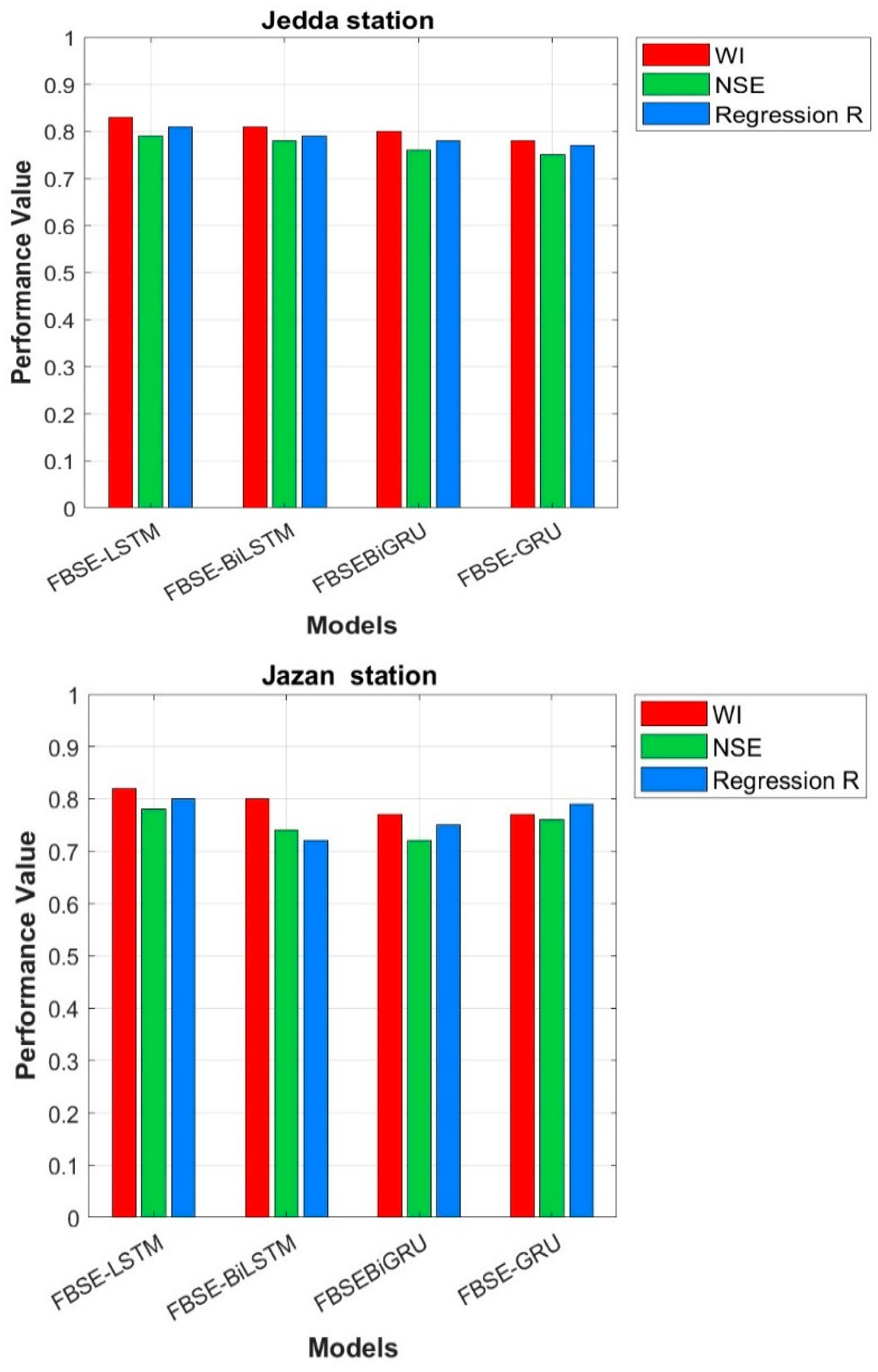
Figure 11 reports the results using Taylor diagrams. From the results, we can observe that all hybrid models were close to actual values. The proposed FBSE-GA coupled with LSTM, GRU, BiLSTM, and BiGRU models scored the highest R values for the two (Jeddah and Jazan) stations. The values generated by the individual LSTM, GRU, BiLSTM, and BiGRU models differed significantly from those generated by the actual model. For weekly and monthly air temperature predictions, it can be observed the proposed FBSE-GA-LSTM outperformed all hybrid and individual models.
- 2.
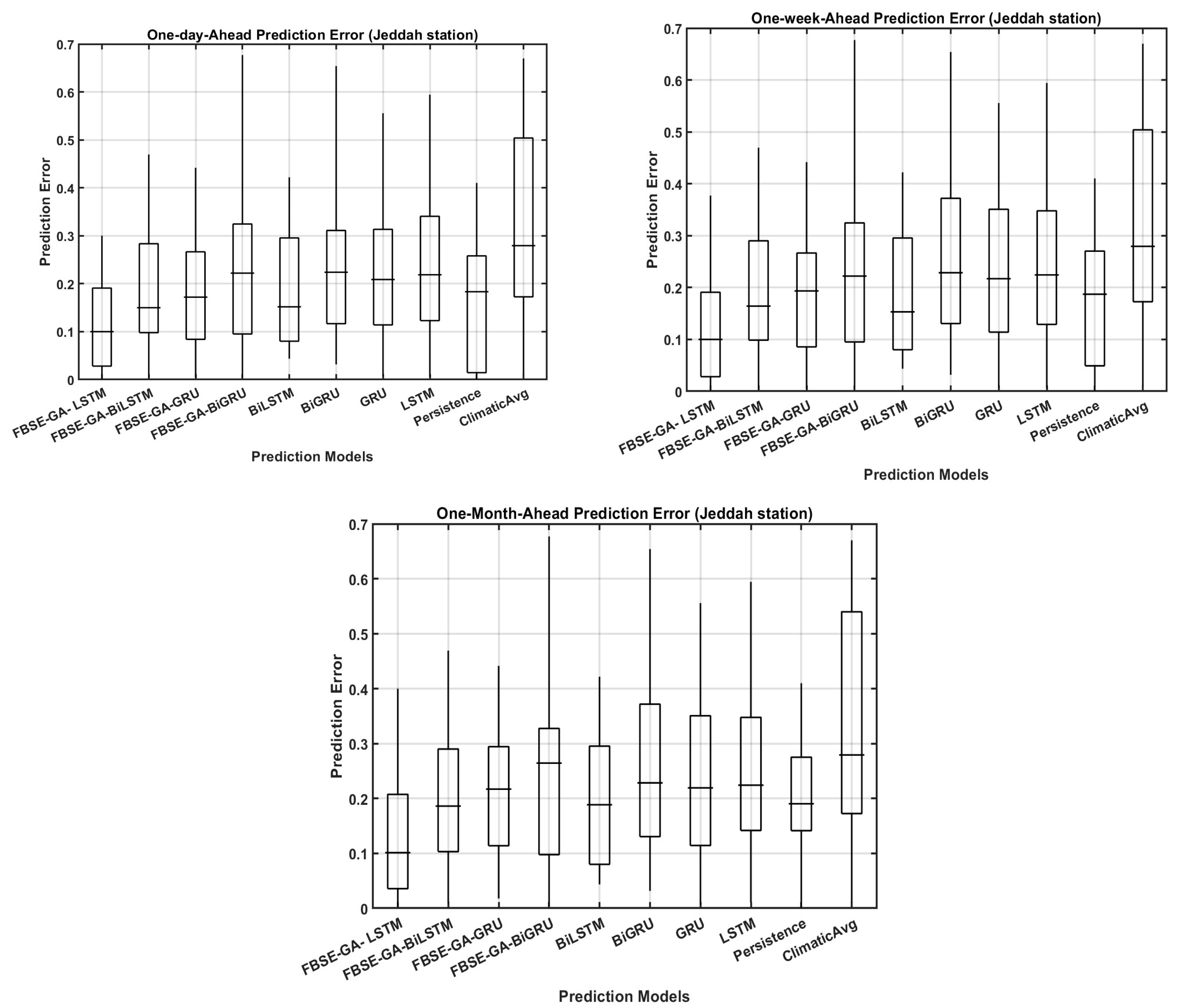
Figure 12 reports the prediction error (FE) boxplots for the daily, weekly, and monthly dry-bulb air temperature predictions for all hybrid models using the Jazan station data. The results revealed that with monthly dry-bulb air temperature prediction, all models exhibited low error forecasting accuracy across the two regions compared to the daily and weekly predictions. For the daily prediction, all hybrid models showed lower FE, while the individual models exhibited high FE. These findings indicated the ability of integrating FBSE-GA with deep learning models to improve dry-bulb air temperature prediction.
- 3.
To validate the efficiency of the proposed model, FBSE-GA-LSTM, it was compared with the classic decomposition models fast Fourier transform (FFT) and discrete wavelet transform (DWT). Comparisons with DWT and Fourier transform (FF) were also conducted. In this experiment, FFT and DWT were integrated with GA and LSTM for fair comparison.
Table 7 reports the comparison results. It was observed that FBSE outperformed FFT and DWT in terms of R and WI. In addition, the FBSE was faster, and utilised less computation time compared with FFT and DWT.
- 4.
This study also examined the effect of GA on the prediction rate.
Figure 13 shows the performance of all hybrid models without GA. The FBSE coefficients were sent directly to all models without GA. The results showed that all models’ performance was degraded and poor. The results confirmed that the combination of FBSE and GA improved the predictive accuracy of all models.
- 5.
The computational cost of the proposed FBSE-GA-LSTM and the state-of-the-art models were evaluated in terms of complexity time. Based on the results, the statistical model’s persistence and climatic average scored the lowest computational times, with training times below 16 s, reflecting their simplicity and absence of model parameter optimisation. In contrast, most of the deep learning models, particularly the proposed models, exhibited longer training times due to the additional cost associated with the GA-based feature selection phase. For example, FBSE-GA-LSTM scored approximately 320 s to train, compared to 180 s for the LSTM, exhibiting the added optimisation overhead. Overall, these results demonstrated that the proposed models offer a favourable trade-off between improved accuracy and acceptable computational overhead, especially in applications where training is performed offline, as shown in
Figure 14.
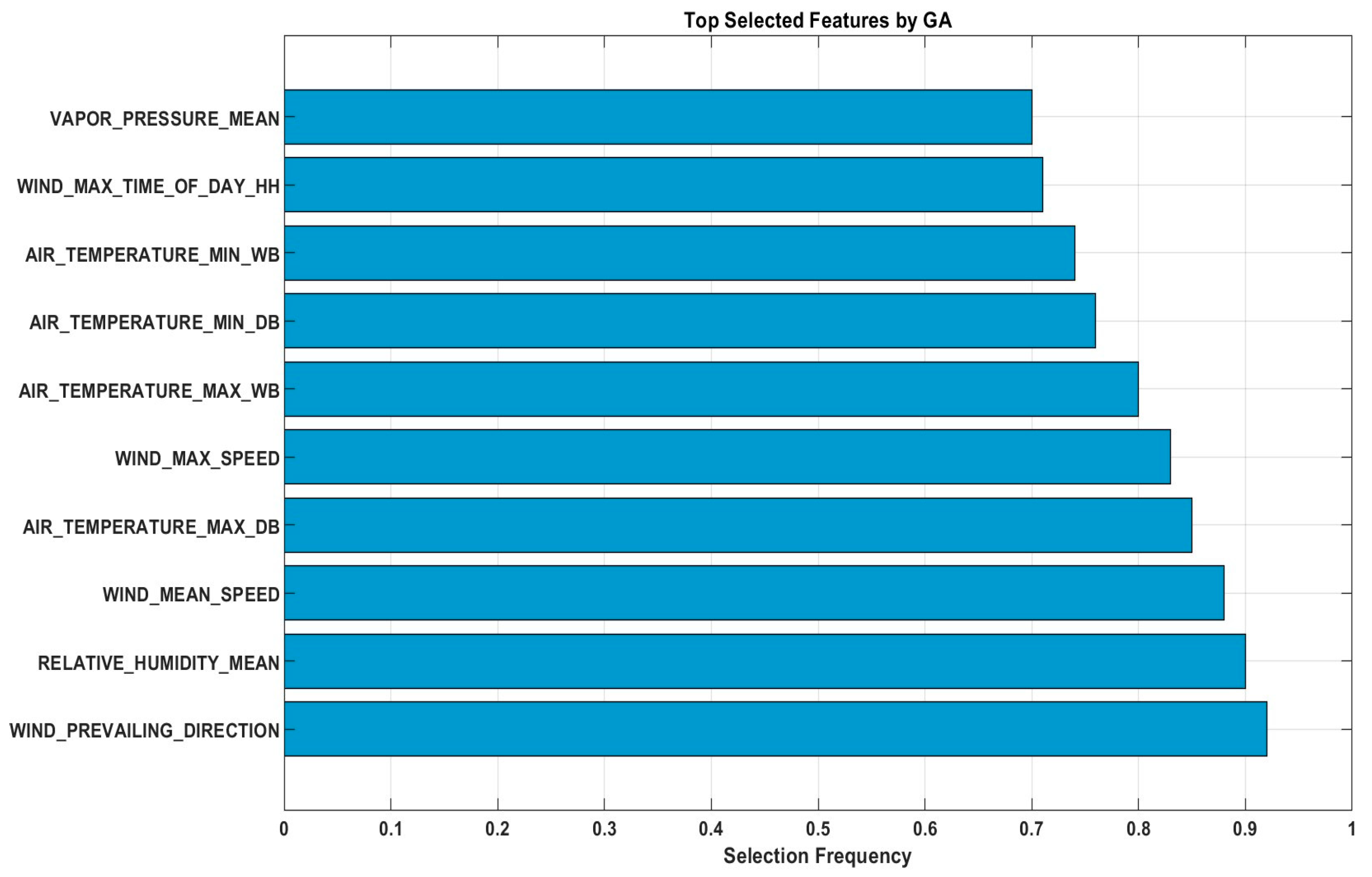
To enhance the interpretability of the proposed model, we conducted a feature analysis to show which features were selected by the GA across 100 optimisation runs. The results showed that WIND_MEAN_SPEED, RELATIVE_HUMIDITY_MEAN, AIR_TEMPERATURE_MAX_DB, WIND_PREVAILING_DIRECTION, WIND_MAX_SPEED, AIR_TEMPERATURE_MAX_WB, AIR_TEMPERATURE_MIN_DB, AIR_TEMPERATURE_MIN_W, WIND_MAX_TIME_OF_DAY_HH, and VAPOR_PRESSURE_MEAN were the top ten features, each with a selection frequency exceeding 75%. Based on our findings these features capture influential meteorological conditions influencing temperature dynamics, such as wind patterns, humidity, and temperature extremes.
Figure 15 presents a bar chart of the selection frequencies, which demonstrated that the GA effectively identifies the most relevant inputs, thereby enhancing model efficiency and reducing redundancy without compromising predictive performance. The feature wind direction had the most significant influence on DBT because it directly affects heat advection and air mass movement in the study area. Certain wind directions are associated with the transport of warmer or cooler air masses, which can substantially alter the local dry-bulb temperature. This relationship reflects the climatological patterns of the region, where prevailing winds often coincide with the specific thermal characteristics of incoming air.
The integration of decomposition models with deep learning architectures has shown promise in enhancing the predictive accuracy of hybrid models for nonstationary and complex time series data. Nevertheless, there are still restrictions, and future prospects should be considered to achieve more perfection on these models. The challenges are largely related to the integration of models, computational constraints, and the handling of more diverse datasets. The work presented here could be extended to better models for such issues and other approaches for better accuracy and performance. One of our future works is that the proposed model will be applied to predict other variables such as the relative humidity and wind speed as it was designed to work on multivariate time series data.