An Extension of Laor Weight Initialization for Deep Time-Series Forecasting: Evidence from Thai Equity Risk Prediction
Abstract
1. Introduction
2. Background and Related Works
2.1. Forecasting Models and Their Challenges
2.2. Conventional Weight Initialization Methods
2.3. Data-Driven Initialization Approaches and Limitations
2.4. Toward Optimization-Aware and Architecture-Agnostic Initialization
2.5. Relevance to Forecasting: A Case Study in the Thai Equity Market
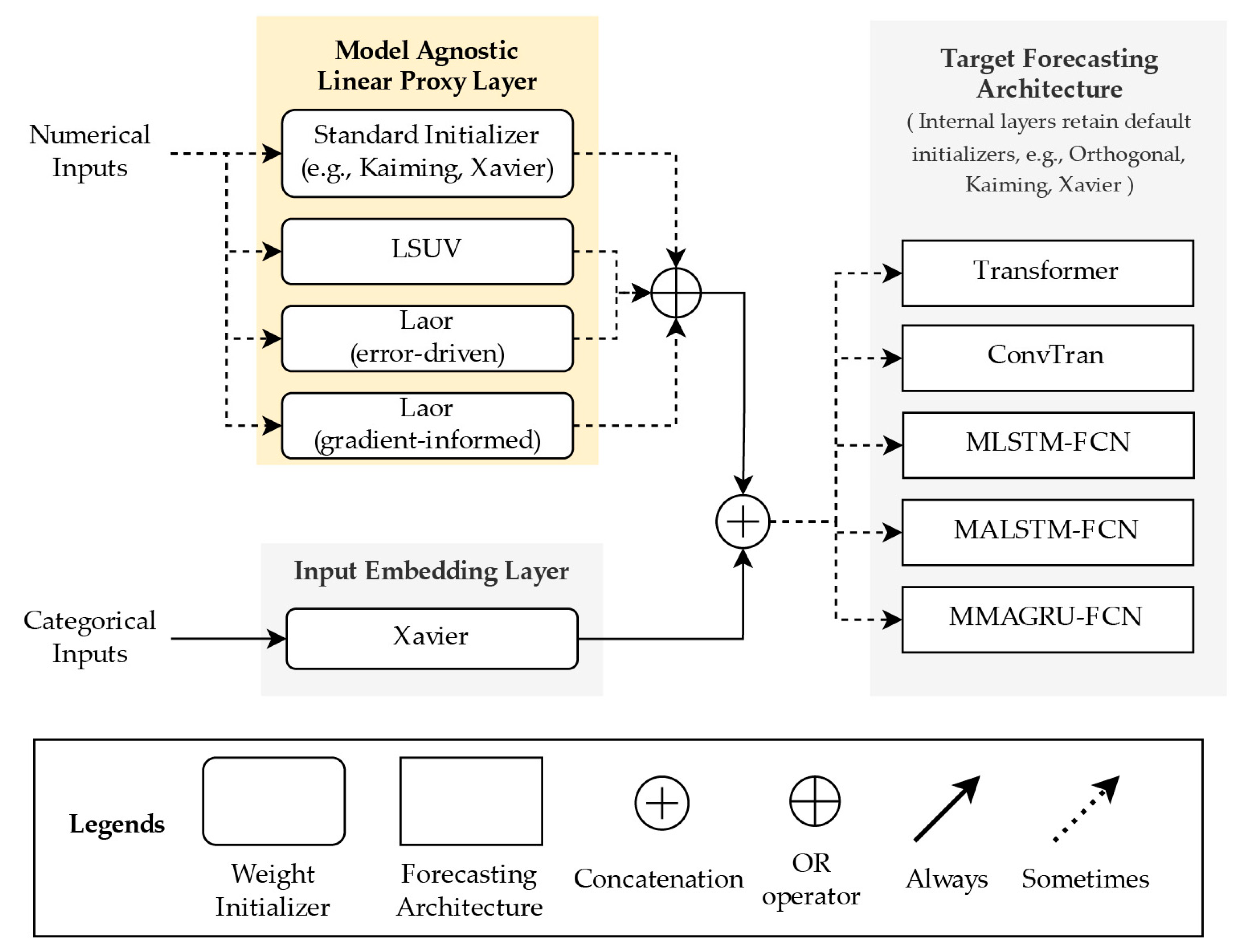
3. A Hybrid Weight Initialization Framework
3.1. Proxy Model
3.2. Gradient-Informed Evaluation
| Algorithm 1 Laor-ori (error-driven via proxy) |
|
| Algorithm 2 Laor (gradient-informed via proxy) |
|
- The key distinction between approaches lies in their selection criteria:
- Laor-ori (Algorithm 1). Selects candidates by Smaller loss values indicate lower initial misfit but do not guarantee faster optimization.
- Laor (Algorithm 2). Selects candidates by Larger gradient norms imply greater reduction potential per update step, aligning initialization with optimization dynamics rather than only initial fit quality.
- Laor-n/Laor-u: Laor with normal/uniform distribution sampling;
- Laor-kn/Laor-ku: Laor with Kaiming Normal/Kaiming Uniform sampling;
- Laor-xn/Laor-xu: Laor with Xavier Normal/Xavier Uniform sampling;
- Laor-o: Laor with orthogonal matrix sampling.
3.3. Experimental Setup
3.3.1. Inherited Setup from Prior Work
- Dataset: Daily end-of-day (EOD) stock trading data and Market Surveillance Measure List (MSML) labels were obtained from the SET Market Analysis and Reporting Tool (SETSMART) platform [39], covering the period from 16 November 2012 to 15 June 2024. The dataset includes adjusted closing prices, trading volumes, valuation ratios (P/E, P/BV), and derived technical and sentiment indicators. Each record is associated with a binary label indicating whether the corresponding equity appears on the MSML;
- Preprocessing Steps: Temporal alignment was strictly maintained by using predictors at time exclusively derived from historical observations up to . Forecasting labels were forward-shifted according to the forecasting horizon. Numerical features underwent standardization and precision rounding to six decimal places to enhance training stability. Missing trading values for suspended stocks were explicitly imputed with zeros, indicating absence of trading activity;
- Rolling Window Training Strategy: A rolling window methodology was used to handle temporal non-stationarity, employing a training window of 1260 trading days (~5 years), a validation window of 60 trading days (~1 quarter), and a rolling step size of 60 days. This strategy resulted in 26 training-validation cycles for each experimental iteration;
- Class Imbalance Handling: Given the significant minority class imbalance (~3.6% positive samples), Synthetic Minority Oversampling Technique (SMOTE) was applied within each rolling training window, doubling minority instances via interpolation with 5-nearest neighbors;
- Computational Environment: Experiments were executed using PyTorch version 2.3.0 on an NVIDIA RTX 3090 GPU (NVIDIA Corporation, Santa Clara, CA, USA), Intel i7-13700KF CPU (Intel Corporation, Santa Clara, CA, USA), and 32 GB RAM, with CUDA version 12.3, ensuring reproducibility and computational efficiency;
- Evaluation Metrics: The primary evaluation metric was Matthews Correlation Coefficient (MCC), complemented by supplementary metrics including F1 score, Recall, Precision, Accuracy, and Cross-Entropy Loss. Computational efficiency metrics encompassed training time per epoch, total wall-clock time, and epochs to convergence;
- Model Architectures: Five deep learning models are used, spanning a range of structural patterns from fully attention-based to recurrent-convolutional hybrids as in Table 2.
- Hyperparameters: Training configurations were inherited directly from prior work and remained fixed across all initialization experiments. These hyperparameters, summarized in Table 3, were tuned previously and reused to ensure a controlled evaluation setting.
3.3.2. Novel Experimental Components
- Initialization Strategies Compared: Seventeen initialization strategies were evaluated at the numerical input layer, grouped into four categories (A comparative summary is provided in Table 4):
- Traditional data-agnostic methods: Xavier (Uniform, Normal), Kaiming (Uniform, Normal), Random (Uniform, Normal), and Orthogonal.
- Variance-based method: Layer-Sequential Unit Variance (LSUV).
- Error-driven method: Original Laor Initialization, using clustering on forward-pass loss values.
- Gradient-informed variants (proposed): Laor, Laor-Normal (Laor-n), Laor-Uniform (Laor-u), Laor-Kaiming-Normal (Laor-kn), Laor-Kaiming-Uniform (Laor-ku), Laor-Xavier-Normal (Laor-xn), Laor-Xavier-Uniform (Laor-xu), Laor-Orthogonal (Laor-o). All use the same gradient-norm clustering scheme and differ only in the randomization method used to generate candidate weights.
- Proxy-Layer and Clustering Procedure: Each strategy is evaluated through the same proxy model described in Section 3.1 and 3.2. For gradient-informed variants, weight candidates are generated using the assigned randomizer, evaluated by gradient norm, and clustered using k-means with . The choice of follows the established methodology from the original Laor initialization paper, ensuring methodological consistency and comparability with prior work. The parameter aligns with the binary classification structure of our forecasting task (flagged vs. not flagged stocks), providing a natural clustering framework for candidate selection. The final weight is computed by averaging the members of the lowest-gradient cluster. The same clustering process is used for the error-driven variant, except based on forward-pass loss. All candidates are evaluated under identical proxy conditions to ensure fair comparison.
- Statistical Robustness Checks: To assess the robustness of each strategy, every experimental configuration was repeated 20 times with independent random seeds. Aggregate statistics, including mean performance, standard deviation, and training time, were reported for each model-initializer combination, allowing for comprehensive comparison of predictive accuracy and convergence efficiency.
3.4. Experiment Summary
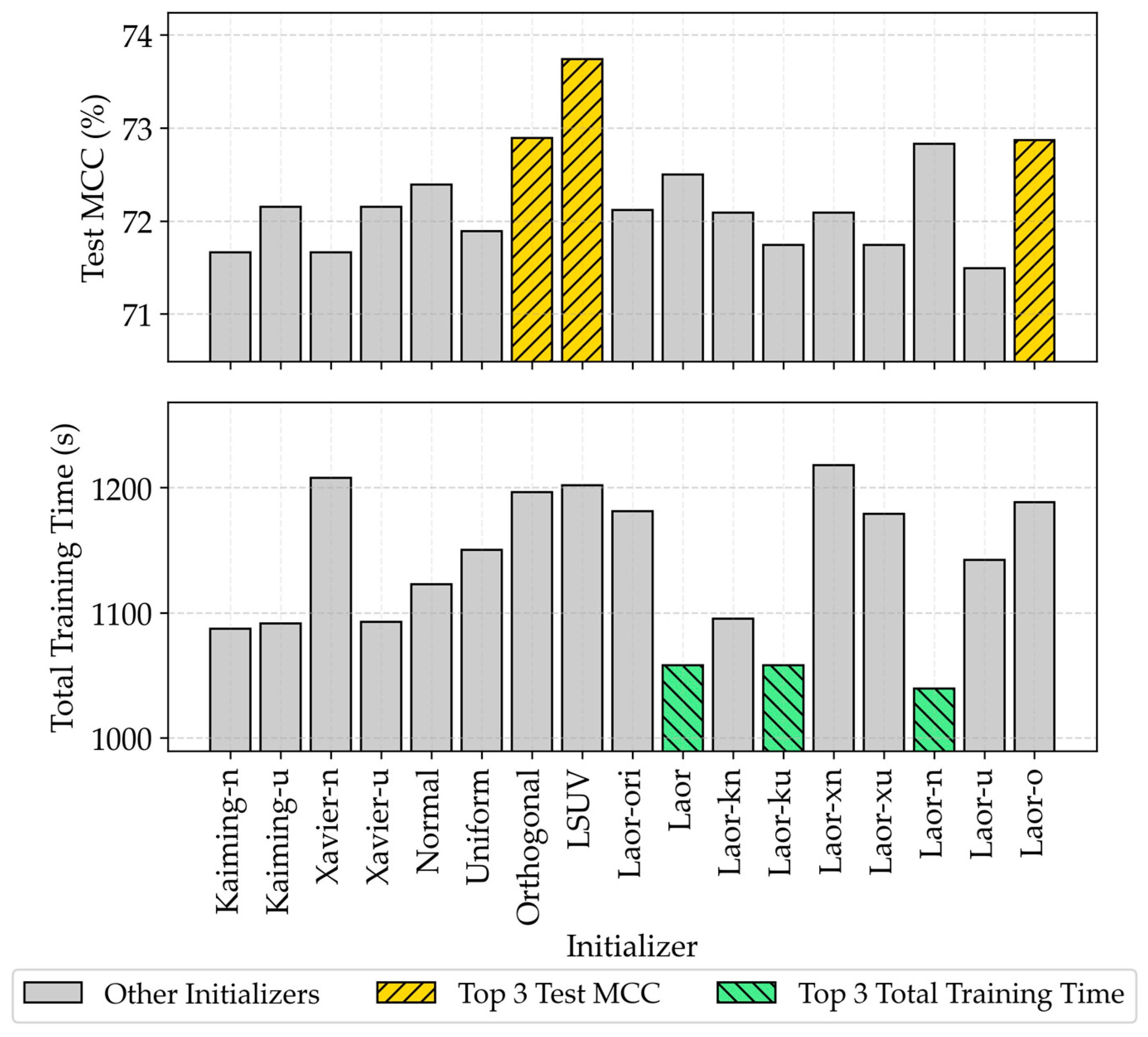
4. Results
4.1. Baseline Performance Comparison
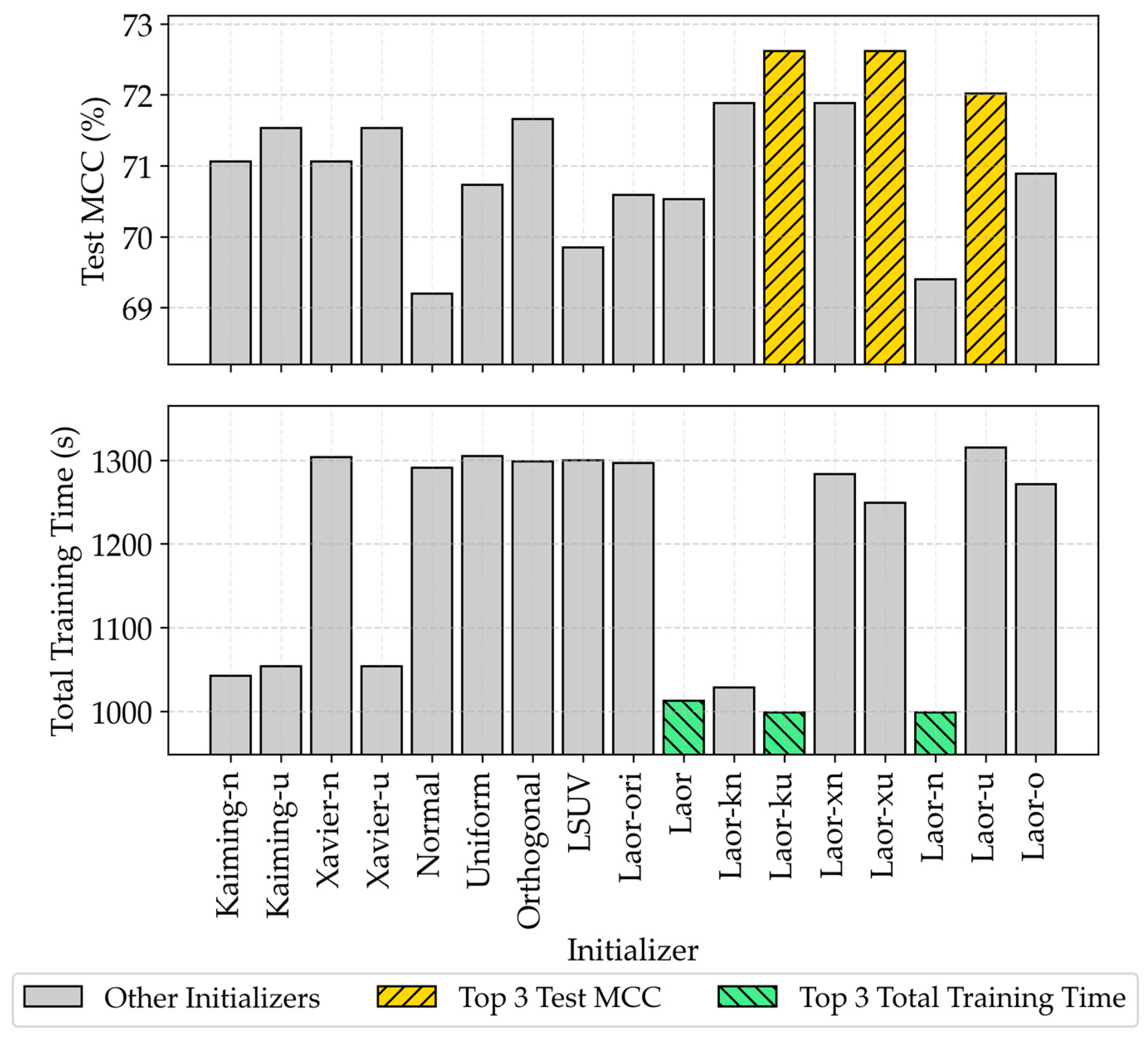
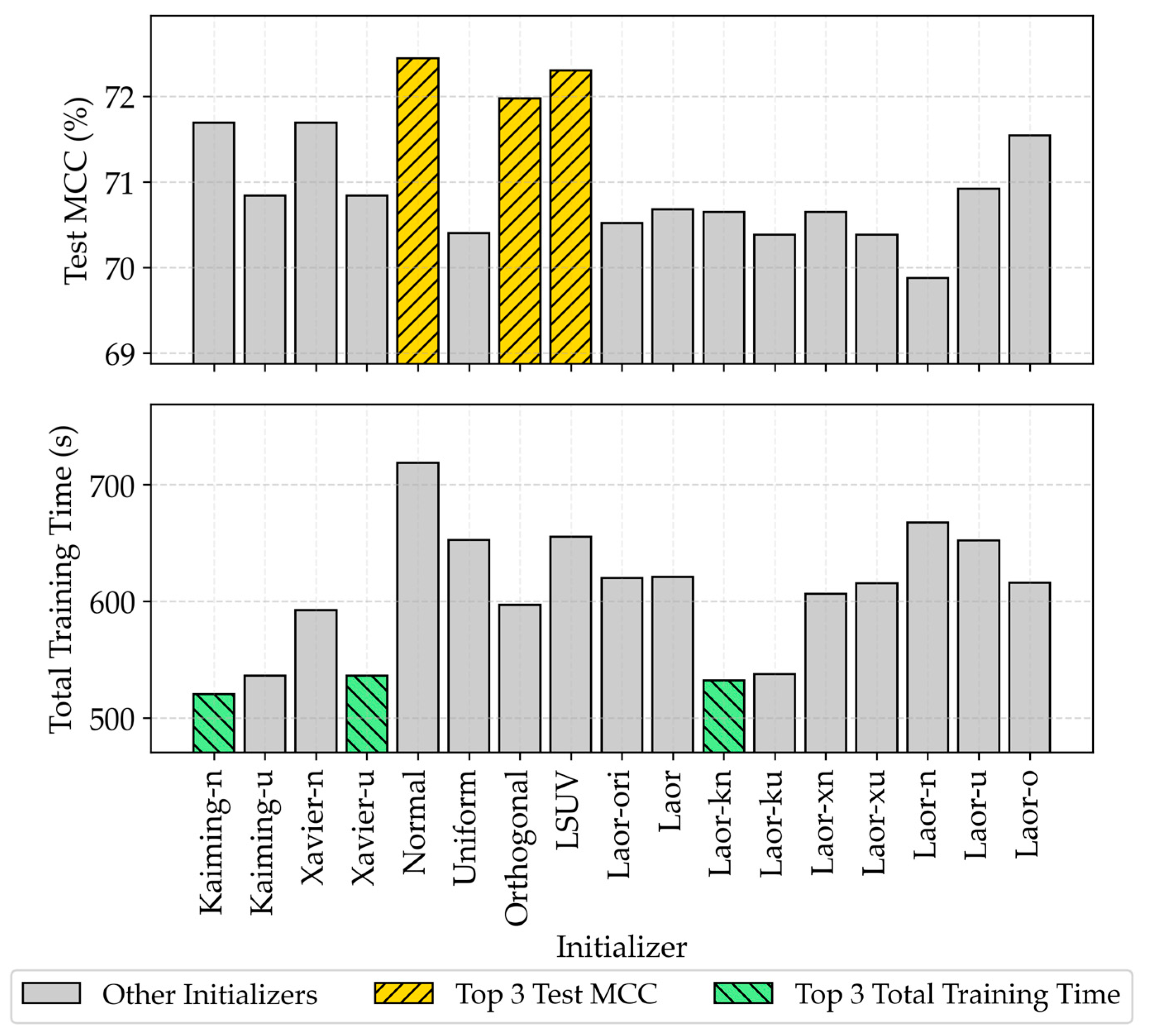
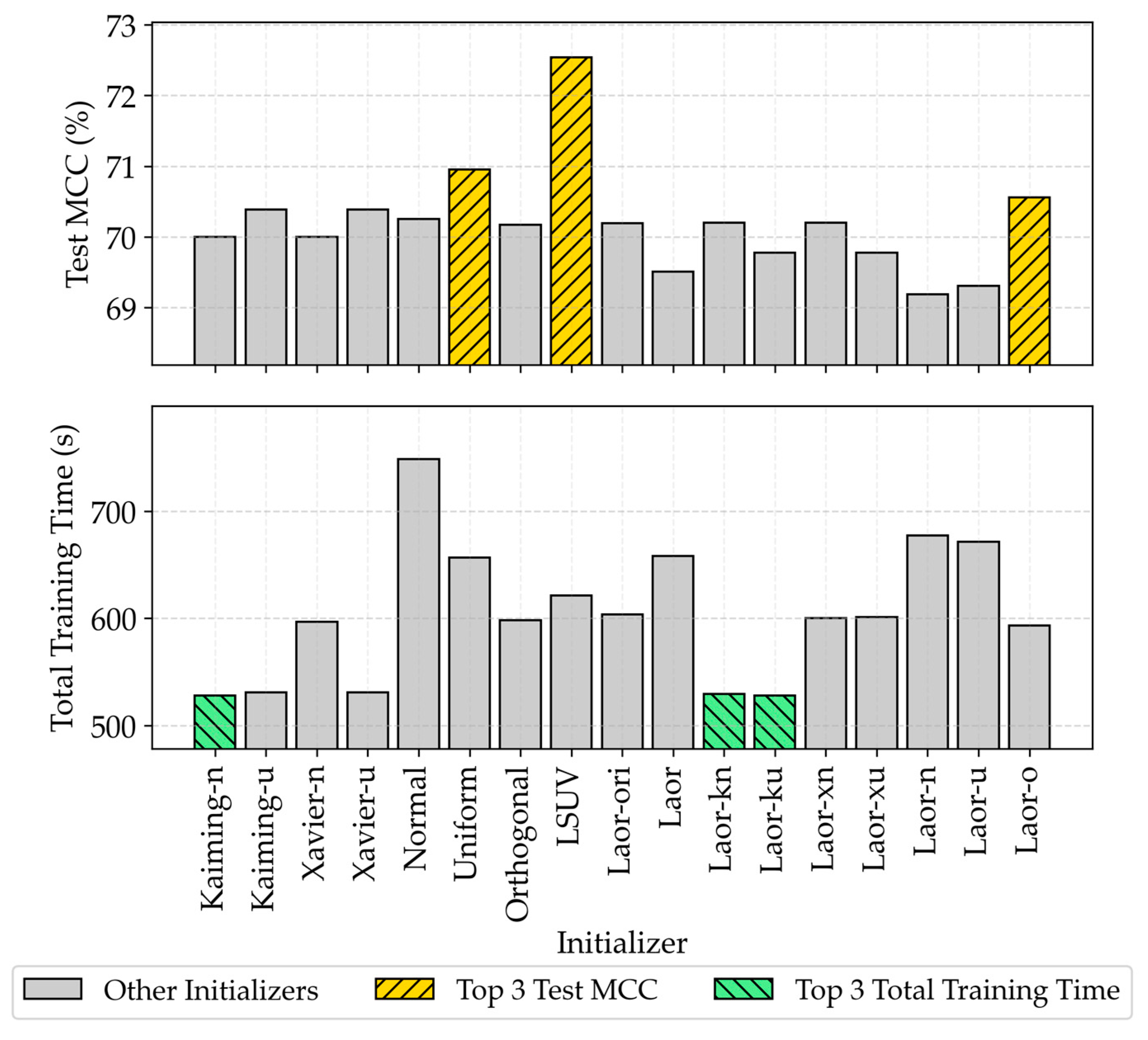
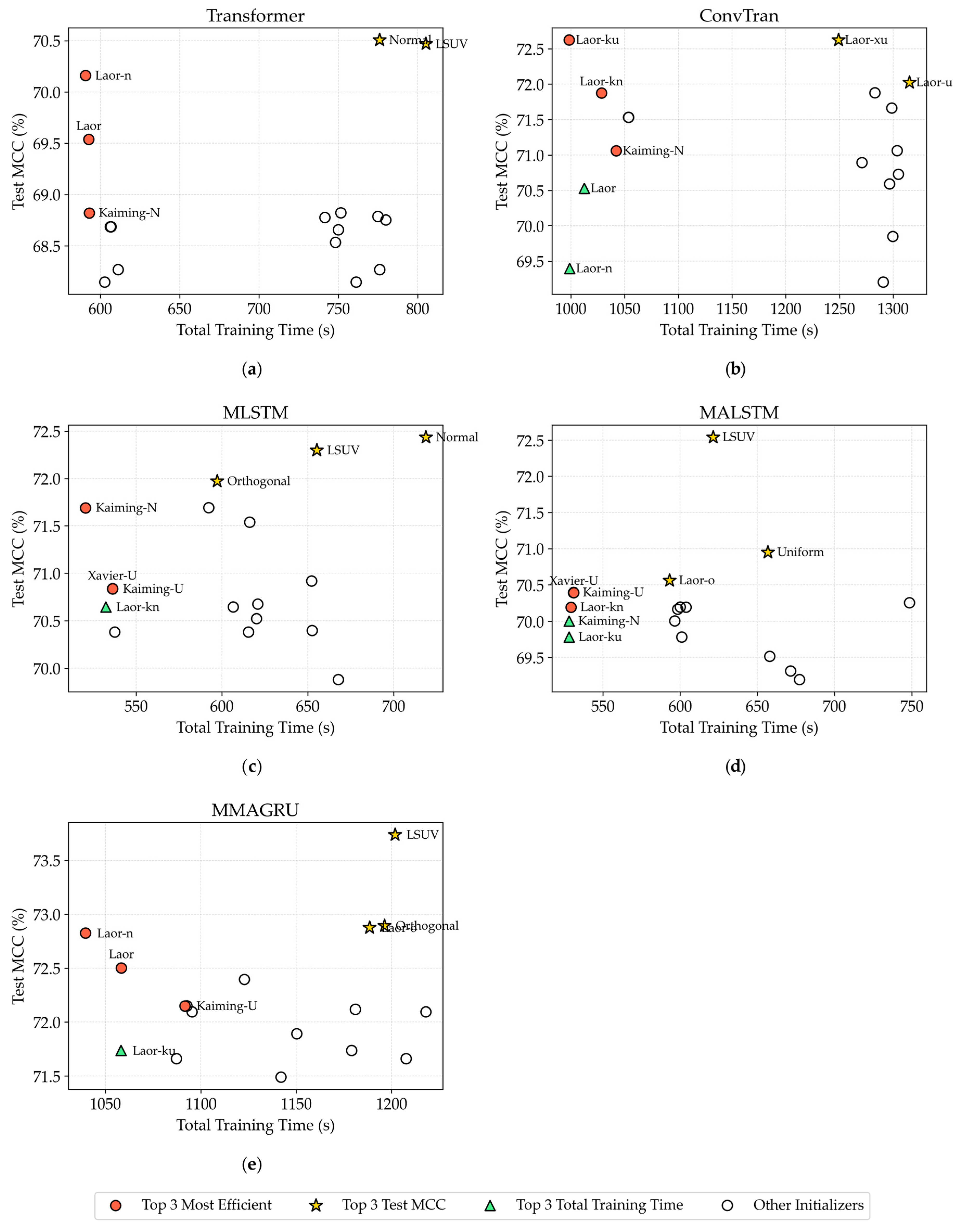
4.2. Generalizability of Weight Initializers Across Architectures
4.3. Cross-Architecture Comparison and Performance-Efficiency Trade-Offs
4.4. Computational Overhead Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNNs | Convolutional Neural Networks |
| EOD | End-of-Day |
| GRUs | Gated Recurrent Units |
| Kaiming-n | Kaiming Normal initialization |
| Kaiming-u | Kaiming Uniform initialization |
| KMITL | King Mongkut’s Institute of Technology Ladkrabang |
| Laor | Gradient-Informed Laor Initialization |
| Laor-kn | Gradient-Informed Laor Initialization with Kaiming Normal initialization |
| Laor-ku | Gradient-Informed Laor Initialization with Kaiming Uniform initialization |
| Laor-n | Gradient-Informed Laor Initialization with Normal initialization |
| Laor-o | Gradient-Informed Laor Initialization with Orthogonal initialization |
| Laor-ori | Original Laor Initialization |
| Laor-u | Gradient-Informed Laor Initialization with Uniform initialization |
| Laor-xn | Gradient-Informed Laor Initialization with Xavier Normal initialization |
| Laor-xu | Gradient-Informed Laor Initialization with Xavier Uniform initialization |
| LSTM | Long Short-Term Memory |
| LSUV | Layer-Sequential Unit-Variance |
| MCC | Matthews Correlation Coefficient |
| MSE | Mean Squared Error |
| MSML | Market Surveillance Measure List |
| MTSC | Multivariate Time-Series Classification |
| NSRF | National Science, Research and Innovation Fund |
| ReLU | Rectified Linear Units |
| RNNs | Recurrent Neural Networks |
| SET | The Stock Exchange of Thailand |
| SETSMART | SET Market Analysis and Reporting Tool |
| SMOTE | Synthetic Minority Over-sampling Technique |
| Xavier-n | Xavier Normal initialization |
| Xavier-u | Xavier Uniform initialization |
Appendix A
| Group | Weight Initializer | Test Accuracy (%) | Test Precision (%) | Test Recall (%) | Test F1 Score (%) | Test MCC (%) |
|---|---|---|---|---|---|---|
| Traditional | Kaiming-Normal | 84.30 ± 0.55 | 81.84 ± 0.82 | 88.39 ± 0.97 | 84.98 ± 0.52 | 68.82 ± 1.09 |
| (Data-agnostic baseline) | Kaiming-Uniform | 84.23 ± 0.69 | 81.77 ± 0.90 | 88.33 ± 1.11 | 84.92 ± 0.66 | 68.69 ± 1.39 |
| Xavier-Normal | 84.30 ± 0.55 | 81.84 ± 0.82 | 88.39 ± 0.97 | 84.98 ± 0.52 | 68.82 ± 1.09 | |
| Xavier-Uniform | 84.23 ± 0.69 | 81.77 ± 0.90 | 88.33 ± 1.11 | 84.92 ± 0.66 | 68.69 ± 1.39 | |
| Normal | 85.22 ± 0.50 | 84.02 ± 0.58 | 87.19 ± 1.28 | 85.57 ± 0.57 | 70.51 ± 1.02 | |
| Uniform | 84.33 ± 0.45 | 82.61 ± 0.70 | 87.19 ± 1.31 | 84.83 ± 0.51 | 68.77 ± 0.94 | |
| Orthogonal | 84.25 ± 0.58 | 81.70 ± 1.06 | 88.52 ± 0.95 | 84.96 ± 0.48 | 68.75 ± 1.08 | |
| Data-driven method | ||||||
| Variance-based | LSUV | 85.20 ± 0.39 | 84.11 ± 0.90 | 87.02 ± 1.44 | 85.53 ± 0.45 | 70.47 ± 0.80 |
| Error-driven (original Laor) | Laor-ori | 84.14 ± 0.55 | 81.49 ± 0.86 | 88.56 ± 0.92 | 84.88 ± 0.50 | 68.53 ± 1.07 |
| Gradient-informed | Laor | 84.71 ± 0.69 | 83.69 ± 1.77 | 86.54 ± 2.33 | 85.05 ± 0.69 | 69.54 ± 1.31 |
| (Laor variants) | Laor-kn | 84.04 ± 0.58 | 81.96 ± 1.27 | 87.55 ± 1.88 | 84.64 ± 0.61 | 68.27 ± 1.16 |
| Laor-ku | 83.97 ± 0.62 | 81.52 ± 0.68 | 88.06 ± 0.95 | 84.66 ± 0.61 | 68.15 ± 1.26 | |
| Laor-xn | 84.04 ± 0.58 | 81.96 ± 1.27 | 87.55 ± 1.88 | 84.64 ± 0.61 | 68.27 ± 1.16 | |
| Laor-xu | 83.97 ± 0.62 | 81.52 ± 0.68 | 88.06 ± 0.95 | 84.66 ± 0.61 | 68.15 ± 1.26 | |
| Laor-n | 85.05 ± 0.44 | 84.22 ± 1.09 | 86.49 ± 1.95 | 85.32 ± 0.58 | 70.16 ± 0.90 | |
| Laor-u | 84.28 ± 0.44 | 82.70 ± 0.41 | 86.91 ± 1.01 | 84.75 ± 0.49 | 68.66 ± 0.91 | |
| Laor-o | 84.29 ± 0.48 | 81.95 ± 0.99 | 88.18 ± 1.24 | 84.94 ± 0.44 | 68.79 ± 0.93 |
| Group | Weight Initializer | Training Time per Epoch (s) | Number of Epochs | Weight Initial Time (s) | Total Training Time (s) |
|---|---|---|---|---|---|
| Traditional | Kaiming-Normal | 7.505 ± 0.044 | 79.0 ± 5.7 | 0.101 ± 0.012 | 592.965 ± 0.250 |
| (Data-agnostic baseline) | Kaiming-Uniform | 7.508 ± 0.038 | 80.8 ± 8.1 | 0.115 ± 0.012 | 606.364 ± 0.312 |
| Xavier-Normal | 9.513 ± 0.175 | 79.0 ± 5.7 | 0.097 ± 0.016 | 751.601 ± 0.990 | |
| Xavier-Uniform | 7.514 ± 0.039 | 80.8 ± 8.1 | 0.098 ± 0.013 | 606.819 ± 0.313 | |
| Normal | 9.521 ± 0.175 | 81.5 ± 6.6 | 0.080 ± 0.016 | 776.008 ± 1.158 | |
| Uniform | 9.529 ± 0.186 | 77.8 ± 6.7 | 0.105 ± 0.013 | 741.499 ± 1.240 | |
| Orthogonal | 9.581 ± 0.164 | 81.4 ± 8.0 | 0.080 ± 0.013 | 779.953 ± 1.305 | |
| Data-driven method | |||||
| Variance-based | LSUV | 9.504 ± 0.159 | 84.7 ± 7.1 | 0.134 ± 0.014 | 805.164 ± 1.130 |
| Error-driven (original Laor) | Laor-ori | 9.536 ± 0.175 | 78.5 ± 5.7 | 0.120 ± 0.005 | 748.190 ± 0.994 |
| Gradient-informed | Laor | 7.463 ± 0.074 | 79.4 ± 8.4 | 0.121 ± 0.007 | 592.715 ± 0.624 |
| (Laor variants) | Laor-kn | 7.508 ± 0.041 | 81.4 ± 5.3 | 0.124 ± 0.010 | 611.257 ± 0.218 |
| Laor-ku | 7.515 ± 0.033 | 80.2 ± 4.3 | 0.118 ± 0.014 | 602.799 ± 0.144 | |
| Laor-xn | 9.533 ± 0.191 | 81.4 ± 5.3 | 0.120 ± 0.014 | 776.073 ± 1.010 | |
| Laor-xu | 9.490 ± 0.209 | 80.2 ± 4.3 | 0.134 ± 0.012 | 761.259 ± 0.897 | |
| Laor-n | 7.513 ± 0.037 | 78.6 ± 9.6 | 0.121 ± 0.016 | 590.652 ± 0.353 | |
| Laor-u | 9.510 ± 0.152 | 78.9 ± 7.2 | 0.123 ± 0.013 | 749.999 ± 1.095 | |
| Laor-o | 9.530 ± 0.163 | 81.3 ± 7.3 | 0.150 ± 0.014 | 774.926 ± 1.182 |
| Group | Weight Initializer | Test Accuracy (%) | Test Precision (%) | Test Recall (%) | Test F1 Score (%) | Test MCC (%) |
|---|---|---|---|---|---|---|
| Traditional | Kaiming-Normal | 85.43 ± 1.52 | 86.42 ± 1.72 | 84.57 ± 4.91 | 85.37 ± 2.04 | 71.06 ± 2.81 |
| (Data-agnostic baseline) | Kaiming-Uniform | 85.68 ± 1.73 | 86.47 ± 1.67 | 85.06 ± 4.94 | 85.65 ± 2.22 | 71.53 ± 3.29 |
| Xavier-Normal | 85.43 ± 1.52 | 86.42 ± 1.72 | 84.57 ± 4.91 | 85.37 ± 2.04 | 71.06 ± 2.81 | |
| Xavier-Uniform | 85.68 ± 1.73 | 86.47 ± 1.67 | 85.06 ± 4.94 | 85.65 ± 2.22 | 71.53 ± 3.29 | |
| Normal | 84.49 ± 0.86 | 85.08 ± 2.43 | 84.29 ± 4.65 | 84.55 ± 1.32 | 69.20 ± 1.69 | |
| Uniform | 85.23 ± 1.74 | 86.14 ± 2.07 | 84.54 ± 5.87 | 85.17 ± 2.41 | 70.73 ± 3.15 | |
| Orthogonal | 85.76 ± 0.84 | 86.81 ± 1.71 | 84.81 ± 3.48 | 85.73 ± 1.17 | 71.66 ± 1.59 | |
| Data-driven method | ||||||
| Variance-based | LSUV | 84.80 ± 1.08 | 86.30 ± 2.20 | 83.32 ± 4.60 | 84.66 ± 1.56 | 69.85 ± 2.03 |
| Error-driven (original Laor) | Laor-ori | 85.21 ± 1.18 | 86.82 ± 1.55 | 83.47 ± 3.80 | 85.04 ± 1.54 | 70.59 ± 2.24 |
| Gradient-informed | Laor | 85.21 ± 1.37 | 85.01 ± 2.01 | 85.98 ± 3.43 | 85.43 ± 1.54 | 70.53 ± 2.70 |
| (Laor variants) | Laor-kn | 85.88 ± 1.21 | 85.83 ± 1.57 | 86.41 ± 3.80 | 86.05 ± 1.58 | 71.88 ± 2.23 |
| Laor-ku | 86.27 ± 0.99 | 85.92 ± 1.38 | 87.17 ± 3.28 | 86.48 ± 1.26 | 72.62 ± 1.95 | |
| Laor-xn | 85.88 ± 1.21 | 85.83 ± 1.57 | 86.41 ± 3.80 | 86.05 ± 1.58 | 71.88 ± 2.23 | |
| Laor-xu | 86.27 ± 0.99 | 85.92 ± 1.38 | 87.17 ± 3.28 | 86.48 ± 1.26 | 72.62 ± 1.95 | |
| Laor-n | 84.64 ± 1.06 | 84.45 ± 1.93 | 85.44 ± 3.37 | 84.87 ± 1.27 | 69.40 ± 2.10 | |
| Laor-u | 85.92 ± 0.94 | 85.57 ± 2.17 | 86.96 ± 4.08 | 86.16 ± 1.30 | 72.02 ± 1.74 | |
| Laor-o | 85.34 ± 1.49 | 86.95 ± 1.43 | 83.63 ± 4.72 | 85.16 ± 2.00 | 70.89 ± 2.77 |
| Group | Weight Initializer | Training Time per Epoch (s) | Number of Epochs | Weight Initial Time (s) | Total Training Time (s) |
|---|---|---|---|---|---|
| Traditional | Kaiming-Normal | 13.747 ± 0.065 | 75.8 ± 10.2 | 0.147 ± 0.017 | 1042.183 ± 0.663 |
| (Data-agnostic baseline) | Kaiming-Uniform | 13.744 ± 0.050 | 76.7 ± 7.6 | 0.117 ± 0.014 | 1053.605 ± 0.379 |
| Xavier-Normal | 17.198 ± 0.131 | 75.8 ± 10.2 | 0.114 ± 0.014 | 1303.742 ± 1.334 | |
| Xavier-Uniform | 13.747 ± 0.051 | 76.7 ± 7.6 | 0.116 ± 0.009 | 1053.805 ± 0.385 | |
| Normal | 17.186 ± 0.135 | 75.1 ± 6.2 | 0.098 ± 0.014 | 1290.779 ± 0.841 | |
| Uniform | 17.169 ± 0.125 | 76.0 ± 7.1 | 0.097 ± 0.014 | 1304.916 ± 0.887 | |
| Orthogonal | 17.144 ± 0.060 | 75.8 ± 10.8 | 0.101 ± 0.017 | 1298.746 ± 0.650 | |
| Data-driven method | |||||
| Variance-based | LSUV | 17.134 ± 0.102 | 75.9 ± 7.1 | 0.112 ± 0.016 | 1299.713 ± 0.724 |
| Error-driven (original Laor) | Laor-ori | 17.161 ± 0.077 | 75.6 ± 9.2 | 0.135 ± 0.013 | 1296.674 ± 0.710 |
| Gradient-informed | Laor | 13.743 ± 0.047 | 73.7 ± 7.7 | 0.152 ± 0.013 | 1012.328 ± 0.363 |
| (Laor variants) | Laor-kn | 13.766 ± 0.051 | 74.7 ± 9.8 | 0.134 ± 0.012 | 1028.431 ± 0.500 |
| Laor-ku | 13.758 ± 0.043 | 72.6 ± 7.8 | 0.135 ± 0.012 | 998.282 ± 0.335 | |
| Laor-xn | 17.173 ± 0.100 | 74.7 ± 9.8 | 0.176 ± 0.012 | 1283.035 ± 0.971 | |
| Laor-xu | 17.214 ± 0.128 | 72.6 ± 7.8 | 0.136 ± 0.013 | 1249.016 ± 1.003 | |
| Laor-n | 13.764 ± 0.048 | 72.6 ± 5.9 | 0.139 ± 0.012 | 998.713 ± 0.285 | |
| Laor-u | 17.180 ± 0.112 | 76.6 ± 8.1 | 0.137 ± 0.012 | 1315.229 ± 0.908 | |
| Laor-o | 17.174 ± 0.085 | 74.0 ± 5.9 | 0.132 ± 0.011 | 1270.980 ± 0.500 |
| Group | Weight Initializer | Test Accuracy (%) | Test Precision (%) | Test Recall (%) | Test F1 Score (%) | Test MCC (%) |
|---|---|---|---|---|---|---|
| Traditional | Kaiming-Normal | 85.83 ± 1.03 | 86.20 ± 0.73 | 85.42 ± 2.02 | 85.80 ± 1.16 | 71.69 ± 2.04 |
| (Data-agnostic baseline) | Kaiming-Uniform | 85.35 ± 1.46 | 86.53 ± 1.02 | 83.88 ± 4.22 | 85.11 ± 1.92 | 70.84 ± 2.75 |
| Xavier-Normal | 85.83 ± 1.03 | 86.20 ± 0.73 | 85.42 ± 2.02 | 85.80 ± 1.16 | 71.69 ± 2.04 | |
| Xavier-Uniform | 85.35 ± 1.46 | 86.53 ± 1.02 | 83.88 ± 4.22 | 85.11 ± 1.92 | 70.84 ± 2.75 | |
| Normal | 86.16 ± 1.03 | 87.81 ± 1.05 | 84.10 ± 2.80 | 85.88 ± 1.29 | 72.44 ± 1.94 | |
| Uniform | 85.06 ± 1.43 | 87.81 ± 0.97 | 81.57 ± 4.15 | 84.50 ± 1.90 | 70.40 ± 2.63 | |
| Orthogonal | 85.97 ± 1.19 | 86.46 ± 1.04 | 85.40 ± 2.41 | 85.90 ± 1.35 | 71.97 ± 2.36 | |
| Data-driven method | ||||||
| Variance-based | LSUV | 86.10 ± 1.14 | 87.61 ± 1.19 | 84.21 ± 2.66 | 85.85 ± 1.35 | 72.30 ± 2.20 |
| Error-driven (original Laor) | Laor-ori | 85.20 ± 1.49 | 86.26 ± 1.21 | 83.89 ± 3.89 | 85.00 ± 1.85 | 70.52 ± 2.87 |
| Gradient-informed | Laor | 85.22 ± 1.22 | 87.76 ± 1.24 | 82.00 ± 3.62 | 84.73 ± 1.61 | 70.68 ± 2.25 |
| (Laor variants) | Laor-kn | 85.26 ± 1.35 | 86.71 ± 1.07 | 83.41 ± 3.47 | 84.99 ± 1.68 | 70.65 ± 2.58 |
| Laor-ku | 85.13 ± 1.12 | 86.50 ± 1.05 | 83.41 ± 3.25 | 84.88 ± 1.46 | 70.38 ± 2.09 | |
| Laor-xn | 85.26 ± 1.35 | 86.71 ± 1.07 | 83.41 ± 3.47 | 84.99 ± 1.68 | 70.65 ± 2.58 | |
| Laor-xu | 85.13 ± 1.12 | 86.50 ± 1.05 | 83.41 ± 3.25 | 84.88 ± 1.46 | 70.38 ± 2.09 | |
| Laor-n | 84.74 ± 1.90 | 88.18 ± 1.20 | 80.39 ± 4.98 | 84.00 ± 2.56 | 69.88 ± 3.39 | |
| Laor-u | 85.37 ± 1.35 | 87.47 ± 0.77 | 82.69 ± 3.66 | 84.96 ± 1.74 | 70.92 ± 2.53 | |
| Laor-o | 85.72 ± 1.23 | 86.62 ± 0.99 | 84.62 ± 3.71 | 85.55 ± 1.60 | 71.54 ± 2.36 |
| Group | Weight Initializer | Training Time per Epoch (s) | Number of Epochs | Weight Initial Time (s) | Total Training Time (s) |
|---|---|---|---|---|---|
| Traditional | Kaiming-Normal | 7.033 ± 0.045 | 74.0 ± 6.1 | 0.101 ± 0.013 | 520.549 ± 0.276 |
| (Data-agnostic baseline) | Kaiming-Uniform | 7.042 ± 0.054 | 76.2 ± 9.9 | 0.129 ± 0.011 | 536.354 ± 0.533 |
| Xavier-Normal | 8.003 ± 0.172 | 74.0 ± 6.1 | 0.110 ± 0.009 | 592.341 ± 1.052 | |
| Xavier-Uniform | 7.041 ± 0.052 | 76.2 ± 9.9 | 0.098 ± 0.010 | 536.285 ± 0.516 | |
| Normal | 7.915 ± 0.127 | 90.8 ± 6.0 | 0.096 ± 0.014 | 718.800 ± 0.771 | |
| Uniform | 7.957 ± 0.161 | 82.0 ± 9.6 | 0.096 ± 0.014 | 652.558 ± 1.555 | |
| Orthogonal | 8.009 ± 0.168 | 74.6 ± 7.3 | 0.099 ± 0.015 | 597.152 ± 1.223 | |
| Data-driven method | |||||
| Variance-based | LSUV | 7.916 ± 0.137 | 82.8 ± 7.8 | 0.086 ± 0.009 | 655.152 ± 1.072 |
| Error-driven (original Laor) | Laor-ori | 8.053 ± 0.163 | 77.0 ± 6.9 | 0.122 ± 0.011 | 620.208 ± 1.115 |
| Gradient-informed | Laor | 6.960 ± 0.053 | 89.2 ± 12.4 | 0.111 ± 0.014 | 620.899 ± 0.657 |
| (Laor variants) | Laor-kn | 7.036 ± 0.052 | 75.7 ± 8.1 | 0.120 ± 0.012 | 532.368 ± 0.419 |
| Laor-ku | 7.017 ± 0.053 | 76.6 ± 7.6 | 0.149 ± 0.015 | 537.645 ± 0.408 | |
| Laor-xn | 8.017 ± 0.135 | 75.7 ± 8.1 | 0.119 ± 0.014 | 606.597 ± 1.093 | |
| Laor-xu | 8.033 ± 0.160 | 76.6 ± 7.6 | 0.123 ± 0.012 | 615.483 ± 1.217 | |
| Laor-n | 6.976 ± 0.064 | 95.7 ± 7.2 | 0.148 ± 0.014 | 667.793 ± 0.462 | |
| Laor-u | 7.948 ± 0.147 | 82.1 ± 6.8 | 0.118 ± 0.013 | 652.262 ± 0.996 | |
| Laor-o | 8.053 ± 0.150 | 76.5 ± 7.6 | 0.137 ± 0.013 | 616.200 ± 1.146 |
| Group | Weight Initializer | Test Accuracy (%) | Test Precision (%) | Test Recall (%) | Test F1 Score (%) | Test MCC (%) |
|---|---|---|---|---|---|---|
| Traditional | Kaiming-Normal | 84.88 ± 2.26 | 84.74 ± 1.64 | 85.34 ± 6.55 | 84.86 ± 3.35 | 70.00 ± 3.89 |
| (Data-agnostic baseline) | Kaiming-Uniform | 85.08 ± 2.10 | 84.60 ± 1.76 | 86.05 ± 6.24 | 85.14 ± 3.11 | 70.39 ± 3.58 |
| Xavier-Normal | 84.88 ± 2.26 | 84.74 ± 1.64 | 85.34 ± 6.55 | 84.86 ± 3.35 | 70.00 ± 3.89 | |
| Xavier-Uniform | 85.08 ± 2.10 | 84.60 ± 1.76 | 86.05 ± 6.24 | 85.14 ± 3.11 | 70.39 ± 3.58 | |
| Normal | 84.97 ± 1.65 | 87.59 ± 1.70 | 81.69 ± 4.94 | 84.43 ± 2.23 | 70.25 ± 2.99 | |
| Uniform | 85.36 ± 1.85 | 86.66 ± 1.29 | 83.80 ± 5.70 | 85.07 ± 2.59 | 70.95 ± 3.31 | |
| Orthogonal | 84.99 ± 1.84 | 84.72 ± 1.45 | 85.60 ± 5.55 | 85.02 ± 2.67 | 70.17 ± 3.23 | |
| Data-driven method | ||||||
| Variance-based | LSUV | 86.19 ± 1.23 | 86.06 ± 1.61 | 86.59 ± 4.50 | 86.23 ± 1.73 | 72.54 ± 2.29 |
| Error-driven (original Laor) | Laor-ori | 85.02 ± 1.47 | 84.62 ± 1.73 | 85.82 ± 4.50 | 85.12 ± 1.98 | 70.19 ± 2.72 |
| Gradient-informed | Laor | 84.60 ± 1.52 | 86.60 ± 2.03 | 82.16 ± 5.66 | 84.16 ± 2.23 | 69.51 ± 2.72 |
| (Laor variants) | Laor-kn | 85.01 ± 1.70 | 84.33 ± 1.65 | 86.22 ± 5.06 | 85.15 ± 2.33 | 70.20 ± 3.13 |
| Laor-ku | 84.76 ± 2.21 | 84.53 ± 1.70 | 85.38 ± 6.61 | 84.76 ± 3.23 | 69.78 ± 3.89 | |
| Laor-xn | 85.01 ± 1.70 | 84.33 ± 1.65 | 86.22 ± 5.06 | 85.15 ± 2.33 | 70.20 ± 3.13 | |
| Laor-xu | 84.76 ± 2.21 | 84.53 ± 1.70 | 85.38 ± 6.61 | 84.76 ± 3.23 | 69.78 ± 3.89 | |
| Laor-n | 84.41 ± 1.80 | 87.34 ± 1.42 | 80.69 ± 5.43 | 83.76 ± 2.47 | 69.19 ± 3.25 | |
| Laor-u | 84.43 ± 2.73 | 87.06 ± 1.53 | 81.14 ± 7.75 | 83.74 ± 3.88 | 69.31 ± 4.76 | |
| Laor-o | 85.12 ± 2.73 | 84.26 ± 1.51 | 86.63 ± 7.72 | 85.18 ± 4.12 | 70.56 ± 4.70 |
| Group | Weight Initializer | Training Time per Epoch (s) | Number of Epochs | Weight Initial Time (s) | Total Training Time (s) |
|---|---|---|---|---|---|
| Traditional | Kaiming-Normal | 7.363 ± 0.095 | 71.7 ± 6.5 | 0.104 ± 0.013 | 528.049 ± 0.623 |
| (Data-agnostic baseline) | Kaiming-Uniform | 7.398 ± 0.081 | 71.8 ± 6.8 | 0.097 ± 0.009 | 530.897 ± 0.555 |
| Xavier-Normal | 8.318 ± 0.192 | 71.7 ± 6.5 | 0.099 ± 0.017 | 596.533 ± 1.258 | |
| Xavier-Uniform | 7.400 ± 0.082 | 71.8 ± 6.8 | 0.111 ± 0.011 | 531.044 ± 0.557 | |
| Normal | 8.377 ± 0.181 | 89.4 ± 7.8 | 0.096 ± 0.011 | 748.587 ± 1.408 | |
| Uniform | 8.265 ± 0.223 | 79.5 ± 13.7 | 0.095 ± 0.010 | 656.733 ± 3.060 | |
| Orthogonal | 8.316 ± 0.197 | 72.0 ± 6.2 | 0.126 ± 0.011 | 598.442 ± 1.210 | |
| Data-driven method | |||||
| Variance-based | LSUV | 8.271 ± 0.194 | 75.1 ± 9.5 | 0.104 ± 0.012 | 621.266 ± 1.838 |
| Error-driven (original Laor) | Laor-ori | 8.293 ± 0.225 | 72.8 ± 8.0 | 0.134 ± 0.010 | 603.850 ± 1.803 |
| Gradient-informed | Laor | 7.360 ± 0.077 | 89.4 ± 16.5 | 0.120 ± 0.016 | 658.065 ± 1.266 |
| (Laor variants) | Laor-kn | 7.360 ± 0.067 | 71.9 ± 7.6 | 0.121 ± 0.011 | 529.312 ± 0.510 |
| Laor-ku | 7.353 ± 0.076 | 71.8 ± 7.7 | 0.119 ± 0.010 | 528.090 ± 0.581 | |
| Laor-xn | 8.344 ± 0.154 | 71.9 ± 7.6 | 0.149 ± 0.015 | 600.093 ± 1.173 | |
| Laor-xu | 8.370 ± 0.187 | 71.8 ± 7.7 | 0.117 ± 0.014 | 601.082 ± 1.430 | |
| Laor-n | 7.361 ± 0.074 | 92.0 ± 13.9 | 0.120 ± 0.015 | 677.343 ± 1.033 | |
| Laor-u | 8.300 ± 0.197 | 80.9 ± 14.5 | 0.147 ± 0.012 | 671.585 ± 2.866 | |
| Laor-o | 8.387 ± 0.188 | 70.7 ± 7.5 | 0.125 ± 0.007 | 593.112 ± 1.408 |
| Group | Weight Initializer | Test Accuracy (%) | Test Precision (%) | Test Recall (%) | Test F1 Score (%) | Test MCC (%) |
|---|---|---|---|---|---|---|
| Traditional | Kaiming-Normal | 85.81 ± 0.41 | 86.57 ± 0.63 | 84.84 ± 1.46 | 85.68 ± 0.54 | 71.66 ± 0.81 |
| (Data-agnostic baseline) | Kaiming-Uniform | 86.07 ± 0.46 | 86.46 ± 0.60 | 85.58 ± 1.14 | 86.01 ± 0.53 | 72.15 ± 0.90 |
| Xavier-Normal | 85.81 ± 0.41 | 86.57 ± 0.63 | 84.84 ± 1.46 | 85.68 ± 0.54 | 71.66 ± 0.81 | |
| Xavier-Uniform | 86.07 ± 0.46 | 86.46 ± 0.60 | 85.58 ± 1.14 | 86.01 ± 0.53 | 72.15 ± 0.90 | |
| Normal | 86.19 ± 0.43 | 86.84 ± 0.52 | 85.35 ± 1.30 | 86.08 ± 0.54 | 72.39 ± 0.84 | |
| Uniform | 85.93 ± 0.53 | 86.82 ± 0.55 | 84.77 ± 1.43 | 85.77 ± 0.65 | 71.89 ± 1.03 | |
| Orthogonal | 86.44 ± 0.33 | 86.73 ± 0.52 | 86.10 ± 1.16 | 86.40 ± 0.43 | 72.89 ± 0.65 | |
| Data-driven method | ||||||
| Variance-based | LSUV | 86.86 ± 0.35 | 86.93 ± 0.40 | 86.82 ± 1.10 | 86.87 ± 0.43 | 73.74 ± 0.69 |
| Error-driven (original Laor) | Laor-ori | 86.05 ± 0.43 | 86.44 ± 0.55 | 85.57 ± 1.23 | 86.00 ± 0.52 | 72.12 ± 0.84 |
| Gradient-informed | Laor | 86.24 ± 0.49 | 86.80 ± 0.59 | 85.53 ± 1.40 | 86.15 ± 0.60 | 72.50 ± 0.96 |
| (Laor variants) | Laor-kn | 86.04 ± 0.47 | 86.52 ± 0.64 | 85.42 ± 1.47 | 85.96 ± 0.59 | 72.09 ± 0.92 |
| Laor-ku | 85.85 ± 0.55 | 86.63 ± 0.69 | 84.84 ± 1.82 | 85.71 ± 0.73 | 71.74 ± 1.04 | |
| Laor-xn | 86.04 ± 0.47 | 86.52 ± 0.64 | 85.42 ± 1.47 | 85.96 ± 0.59 | 72.09 ± 0.92 | |
| Laor-xu | 85.85 ± 0.55 | 86.63 ± 0.69 | 84.84 ± 1.82 | 85.71 ± 0.73 | 71.74 ± 1.04 | |
| Laor-n | 86.40 ± 0.44 | 87.08 ± 0.57 | 85.53 ± 1.19 | 86.29 ± 0.52 | 72.83 ± 0.86 | |
| Laor-u | 85.72 ± 0.65 | 86.92 ± 0.54 | 84.14 ± 1.86 | 85.49 ± 0.84 | 71.49 ± 1.23 | |
| Laor-o | 86.43 ± 0.33 | 86.78 ± 0.48 | 86.00 ± 1.08 | 86.38 ± 0.41 | 72.87 ± 0.65 |
| Group | Weight Initializer | Training Time per Epoch (s) | Number of Epochs | Weight Initial Time (s) | Total Training Time (s) |
|---|---|---|---|---|---|
| Traditional | Kaiming-Normal | 14.691 ± 0.113 | 74.0 ± 6.4 | 0.095 ± 0.012 | 1087.222 ± 0.724 |
| (Data-agnostic baseline) | Kaiming-Uniform | 14.681 ± 0.147 | 74.4 ± 6.1 | 0.090 ± 0.013 | 1091.627 ± 0.896 |
| Xavier-Normal | 16.319 ± 0.197 | 74.0 ± 6.4 | 0.082 ± 0.008 | 1207.720 ± 1.260 | |
| Xavier-Uniform | 14.695 ± 0.147 | 74.4 ± 6.1 | 0.084 ± 0.010 | 1092.692 ± 0.895 | |
| Normal | 16.224 ± 0.200 | 69.2 ± 4.5 | 0.127 ± 0.016 | 1122.856 ± 0.893 | |
| Uniform | 16.281 ± 0.203 | 70.7 ± 6.1 | 0.084 ± 0.010 | 1150.324 ± 1.245 | |
| Orthogonal | 16.352 ± 0.224 | 73.2 ± 5.3 | 0.079 ± 0.008 | 1196.220 ± 1.195 | |
| Data-driven method | |||||
| Variance-based | LSUV | 16.262 ± 0.210 | 73.9 ± 6.3 | 0.064 ± 0.013 | 1201.796 ± 1.316 |
| Error-driven (original Laor) | Laor-ori | 16.312 ± 0.221 | 72.4 ± 6.6 | 0.100 ± 0.009 | 1181.097 ± 1.447 |
| Gradient-informed | Laor | 14.564 ± 0.140 | 72.7 ± 4.9 | 0.102 ± 0.015 | 1058.180 ± 0.693 |
| (Laor variants) | Laor-kn | 14.712 ± 0.118 | 74.5 ± 5.6 | 0.127 ± 0.012 | 1095.417 ± 0.665 |
| Laor-ku | 14.684 ± 0.137 | 72.1 ± 5.4 | 0.103 ± 0.012 | 1058.094 ± 0.742 | |
| Laor-xn | 16.359 ± 0.226 | 74.5 ± 5.6 | 0.108 ± 0.011 | 1218.062 ± 1.271 | |
| Laor-xu | 16.363 ± 0.214 | 72.1 ± 5.4 | 0.124 ± 0.008 | 1179.093 ± 1.164 | |
| Laor-n | 14.629 ± 0.146 | 71.1 ± 5.3 | 0.105 ± 0.013 | 1039.461 ± 0.766 | |
| Laor-u | 16.302 ± 0.231 | 70.1 ± 5.0 | 0.102 ± 0.008 | 1142.087 ± 1.147 | |
| Laor-o | 16.379 ± 0.235 | 72.6 ± 6.5 | 0.135 ± 0.009 | 1188.419 ± 1.537 |
References
- Ensafi, Y.; Amin, S.H.; Zhang, G.; Shah, B. Time-Series Forecasting of Seasonal Items Sales Using Machine Learning—A Comparative Analysis. Int. J. Inf. Manag. Data Insights 2022, 2, 100058. [Google Scholar] [CrossRef]
- Luiz, L.E.; Fialho, G.; Teixeira, J.P. Is Football Unpredictable? Predicting Matches Using Neural Networks. Forecasting 2024, 6, 1152–1168. [Google Scholar] [CrossRef]
- Wei, L.; Yu, Z.; Jin, Z.; Xie, L.; Huang, J.; Cai, D.; He, X.; Hua, X.S. Dual Graph for Traffic Forecasting. IEEE Access 2024, 13, 122285–122293. [Google Scholar] [CrossRef]
- Skorski, M.; Temperoni, A.; Theobald, M. Revisiting Weight Initialization of Deep Neural Networks. In Proceedings of the 13th Asian Conference on Machine Learning, Virtual, 17–19 November 2021; Balasubramanian, V.N., Tsang, I., Eds.; PMLR: Cambridge, MA, USA, 2021; Volume 157, pp. 1192–1207. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. J. Mach. Learn. Res. 2010, 9, 249–256. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Saxe, A.M.; McClelland, J.L.; Ganguli, S. Exact Solutions to the Nonlinear Dynamics of Learning in Deep Linear Neural Networks. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014—Conference Track Proceedings, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Narkhede, M.V.; Bartakke, P.P.; Sutaone, M.S. A Review on Weight Initialization Strategies for Neural Networks. Artif. Intell. Rev. 2022, 55, 291–322. [Google Scholar] [CrossRef]
- Mishkin, D.; Matas, J. All You Need Is a Good Init. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016—Conference Track Proceedings, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Boongasame, L.; Muangprathub, J.; Thammarak, K. Laor Initialization: A New Weight Initialization Method for the Backpropagation of Deep Learning. Big Data Cogn. Comput. 2025, 9, 181. [Google Scholar] [CrossRef]
- Securities Met Market Surveillance Criteria. Available online: https://www.set.or.th/en/market/news-and-alert/surveillance-c-sign-temporary-trading/market-surveillance-measure-list (accessed on 5 July 2025).
- SEC Fines IFEC Execs for Insider Trades. Available online: https://www.bangkokpost.com/business/general/1527334/sec-fines-ifec-execs-for-insider-trades (accessed on 18 September 2024).
- Court Accepts Class-Action Suit Against Stark Auditors. Available online: https://www.bangkokpost.com/business/general/2839118/court-accepts-class-action-suit-against-stark-auditors (accessed on 18 September 2024).
- JKN Founder Admits to “Forced Selling” of Shares. Available online: https://www.bangkokpost.com/business/general/2643514/jkn-founder-admits-to-forced-selling-of-shares (accessed on 18 September 2024).
- An Expensive Lesson. Available online: https://www.bangkokpost.com/business/general/1872004/an-expensive-lesson (accessed on 18 September 2024).
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Foumani, N.M.; Tan, C.W.; Webb, G.I.; Salehi, M. Improving Position Encoding of Transformers for Multivariate Time Series Classification. Data Min. Knowl. Discov. 2024, 38, 22–48. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Harford, S. Multivariate LSTM-FCNs for Time Series Classification. Neural Netw. 2019, 116, 237–245. [Google Scholar] [CrossRef]
- Yuan, J.; Wu, F.; Wu, H. Multivariate Time-Series Classification Using Memory and Attention for Long and Short-Term Dependence ⋆. Appl. Intell. 2023, 53, 29677–29692. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Bollerslev, T. Generalized Autoregressive Conditional Heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Gated Recurrent Units. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP); Alessandro Moschitti, Q.C.R.I., Bo Pang, G., Walter Daelemans, U.A., Eds.; Association for Computational Linguistics: Washington, CO, USA, 2014; pp. 1724–1734. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zivot, E.; Wang, J. Modeling Financial Time Series with S-PLUS®; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Chauhan, A.; Prasad, A.; Gupta, P.; Prashanth Reddy, A.; Kumar Saini, S. Time Series Forecasting for Cold-Start Items by Learning from Related Items Using Memory Networks. In Proceedings of the Web Conference 2020—Companion of the World Wide Web Conference, WWW 2020, Taipei, China, 20–24 April 2020. [Google Scholar]
- Petchpol, K.; Boongasame, L. Enhancing Predictive Capabilities for Identifying At-Risk Stocks Using Multivariate Time-Series Classification: A Case Study of the Thai Stock Market. Appl. Comput. Intell. Soft Comput. 2025, 2025, 3874667. [Google Scholar] [CrossRef]
- Zivot, E.; Wang, J. Rolling Analysis of Time Series. In Modeling Financial Time Series with S-Plus®; Springer: New York, NY, USA, 2003. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority over-Sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; OTexts: Melbourne, Australia, 2015. [Google Scholar]
- Nguyen, D.; Widrow, B. Improving the Learning Speed of 2-Layer Neural Networks by Choosing Initial Values of the Adaptive Weights. In Proceedings of the IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990. [Google Scholar]
- Sreekumar, G.; Martin, J.P.; Raghavan, S.; Joseph, C.T.; Raja, S.P. Transformer-Based Forecasting for Sustainable Energy Consumption Toward Improving Socioeconomic Living: AI-Enabled Energy Consumption Forecasting. IEEE Syst. Man Cybern. Mag. 2024, 10, 52–60. [Google Scholar] [CrossRef]
- La Gatta, V.; Moscato, V.; Postiglione, M.; Sperlí, G. An Epidemiological Neural Network Exploiting Dynamic Graph Structured Data Applied to the COVID-19 Outbreak. IEEE Trans. Big Data 2021, 7, 45–55. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep Learning in Environmental Remote Sensing: Achievements and Challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- SETSMART. Available online: https://www.set.or.th/en/services/connectivity-and-data/data/web-based (accessed on 7 March 2025).


| Layer Type | Typical Usage | Initialization Method | Rationale |
|---|---|---|---|
| Numerical input layer | Input embedding for continuous features | Gradient-Informed (Proposed) | Sensitive to input scale; proxy-based optimization-aware selection |
| Category embedding layer | Discrete feature embedding (e.g., symbols) | Xavier | Symmetric activation; standard for embedding weights |
| Linear layers | Attention, classifiers, residual paths | Xavier or Kaiming (depending on activation) | Preserves variance across layers |
| ReLU-activated convolutional layers | Temporal/spatial convolutions | Kaiming | Designed for ReLU; prevents vanishing gradients |
| GRU/LSTM input weights | Input-to-hidden recurrence | Xavier | Balanced signal propagation |
| GRU/LSTM recurrent weights | Hidden-to-hidden recurrence | Orthogonal | Preserves long-term dependencies across time steps |
| Bias terms | All layers with bias | Zeros | Ensures no unintended initial activation bias |
| Model | Description |
|---|---|
| Transformer | Attention-only architecture [16] |
| ConvTran | CNN-Transformer hybrid [17] |
| MLSTM-FCN | Multivariate LSTM with fully convolutional classifier [18] |
| MALSTM-FCN | Attention-augmented MLSTM-FCN |
| MMAGRU-FCN | Memory–attention–GRU hybrid with CNN feature extractor [19] |
| Model | Learning Rate | Dropout | Weight Decay | Sequence Length | Hidden Dim | FF Dim | Heads | Emb. Dim | Layers | CNN Dim |
|---|---|---|---|---|---|---|---|---|---|---|
| Transformer | 0.0001 | 0.5 | 0.01 | 28 | – | 32 | 2 | 4 | 1 | – |
| ConvTran | 0.0001 | 0.7 | 0.001 | 56 | – | 4 | 2 | 4 | 1 | 8 |
| MLSTM-FCN | 0.0001 | 0.8 | 0.001 | 14 | 32 | – | – | – | 1 | 8 |
| MALSTM-FCN | 0.0001 | 0.8 | 0.01 | 14 | 32 | – | – | – | 1 | 16 |
| MMAGRU-FCN | 0.00001 | 0.5 | 0.001 | 7 | 64 | – | – | – | 3 | 64 |
| Group | Initializers | Description |
|---|---|---|
| Data-agnostic baseline | Xavier-Normal/Uniform, Kaiming-Normal/Uniform, Normal, Uniform, Orthogonal | Commonly used baselines relying only on fan-in/out and variance scaling without data or label information |
| Data-driven method | ||
| Variance-based | LSUV | Initialization based on layer-sequential unit variance using activation statistics |
| Error-driven (original Laor) | Laor-ori | Reimplementation of the original Laor method using k-means clustering on forward-pass loss values |
| Gradient-informed (Laor variants) | Laor, Laor-n, Laor-u, Laor-kn, Laor-ku, Laor-xn, Laor-xu, Laor-o | Variants of Laor Initialization using gradient norms during clustering, evaluated through a proxy layer and fixed across training |
| Group | Weight Initializer | Test MCC (%) | Weight Initial Time (s) | Total Training Time (s) |
|---|---|---|---|---|
| Traditional | Kaiming-Normal | 68.82 ± 1.09 | 0.101 ± 0.012 | 592.965 ± 0.250 |
| (Data-agnostic baseline) | Kaiming-Uniform | 68.69 ± 1.39 | 0.115 ± 0.012 | 606.364 ± 0.312 |
| Xavier-Normal | 68.82 ± 1.09 | 0.097 ± 0.016 | 751.601 ± 0.990 | |
| Xavier-Uniform | 68.69 ± 1.39 | 0.098 ± 0.013 | 606.819 ± 0.313 | |
| Normal | 70.51 ± 1.02 | 0.080 ± 0.016 | 776.008 ± 1.158 | |
| Uniform | 68.77 ± 0.94 | 0.105 ± 0.013 | 741.499 ± 1.240 | |
| Orthogonal | 68.75 ± 1.08 | 0.080 ± 0.013 | 779.953 ± 1.305 | |
| Data-driven method | ||||
| Variance- based | LSUV | 70.47 ± 0.80 | 0.134 ± 0.014 | 805.164 ± 1.130 |
| Error-driven (original Laor) | Laor-ori | 68.53 ± 1.07 | 0.120 ± 0.005 | 748.190 ± 0.994 |
| Gradient-informed | Laor | 69.54 ± 1.31 | 0.121 ± 0.007 | 592.715 ± 0.624 |
| (Laor variants) | Laor-kn | 68.27 ± 1.16 | 0.124 ± 0.010 | 611.257 ± 0.218 |
| Laor-ku | 68.15 ± 1.26 | 0.118 ± 0.014 | 602.799 ± 0.144 | |
| Laor-xn | 68.27 ± 1.16 | 0.120 ± 0.014 | 776.073 ± 1.010 | |
| Laor-xu | 68.15 ± 1.26 | 0.134 ± 0.012 | 761.259 ± 0.897 | |
| Laor-n | 70.16 ± 0.90 | 0.121 ± 0.016 | 590.652 ± 0.353 | |
| Laor-u | 68.66 ± 0.91 | 0.123 ± 0.013 | 749.999 ± 1.095 | |
| Laor-o | 68.79 ± 0.93 | 0.150 ± 0.014 | 774.926 ± 1.182 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petchpol, K.; Boongasame, L. An Extension of Laor Weight Initialization for Deep Time-Series Forecasting: Evidence from Thai Equity Risk Prediction. Forecasting 2025, 7, 47. https://doi.org/10.3390/forecast7030047
Petchpol K, Boongasame L. An Extension of Laor Weight Initialization for Deep Time-Series Forecasting: Evidence from Thai Equity Risk Prediction. Forecasting. 2025; 7(3):47. https://doi.org/10.3390/forecast7030047
Chicago/Turabian StylePetchpol, Katsamapol, and Laor Boongasame. 2025. "An Extension of Laor Weight Initialization for Deep Time-Series Forecasting: Evidence from Thai Equity Risk Prediction" Forecasting 7, no. 3: 47. https://doi.org/10.3390/forecast7030047
APA StylePetchpol, K., & Boongasame, L. (2025). An Extension of Laor Weight Initialization for Deep Time-Series Forecasting: Evidence from Thai Equity Risk Prediction. Forecasting, 7(3), 47. https://doi.org/10.3390/forecast7030047






