A Unified Transformer–BDI Architecture for Financial Fraud Detection: Distributed Knowledge Transfer Across Diverse Datasets

Abstract

Financial fraud detection is a critical application area within the broader domains of cybersecurity and intelligent financial analytics. With the growing volume and complexity of digital transactions, the traditional rule-based and shallow learning models often fall short in detecting sophisticated fraud patterns. This study addresses the challenge of accurately identifying fraudulent financial activities, especially in highly imbalanced datasets where fraud instances are rare and often masked by legitimate behavior. The existing models also lack interpretability, limiting their utility in regulated financial environments. Experiments were conducted on three benchmark datasets: IEEE-CIS Fraud Detection, European Credit Card Transactions, and PaySim Mobile Money Simulation, each representing diverse transaction behaviors and data distributions. The proposed methodology integrates a transformer-based encoder, multi-teacher knowledge distillation, and a symbolic belief–desire–intention (BDI) reasoning layer to combine deep feature extraction with interpretable decision making. The novelty of this work lies in the incorporation of cognitive symbolic reasoning into a high-performance learning architecture for fraud detection. The performance was assessed using key metrics, including the F1-score, AUC, precision, recall, inference time, and model size. Results show that the proposed transformer–BDI model outperformed traditional and state-of-the-art baselines across all datasets, achieving improved fraud detection accuracy and interpretability while remaining computationally efficient for real-time deployment.

1. Introduction

The growing severity and sophistication of financial fraud is impairing world economic security [1]. In 2023 alone, the loss from bank fraud schemes and fraud scams was projected to have exceeded an estimated USD 485.6 billion globally [2,3]. Consumers reported losing over USD 10 billion to fraud in the U.S. in 2023, a 14% increase from 2022 [4]. These staggering statistics highlight the immediate necessity for more robust and evolving anti-fraud tools.

Traditional systems for the detection of fraud, which are typically based on the judgment of the auditor and fixed rule-based algorithms, fail to keep up with the fast-changing nature and magnitude of fraudulent activities nowadays [5,6,7]. Deep models, and in particular transformers, have provided new potentialities to model complex patterns in financial data. Self-attention-based transformers are great at modeling intra-feature dependencies and provide strong parallelization with respect to the input [3,8]. While conventional transformer-based models are able to achieve high detection performances, they have several barriers:

• Limited Interpretability: The decision-making processes of deep learning models are often opaque, making it difficult for stakeholders to understand or trust the outcomes.
• Inefficiency Across Heterogeneous Datasets: Financial data vary significantly across different sectors and regions, leading to challenges in model generalization and performance consistency.
• Computational Overhead: Deep models require substantial computational resources, which can be a barrier to deployment, especially in resource-constrained environments.

To overcome these limitations, we propose an innovative hybrid learning framework that combines BDI reasoning with a transformer-based model improved with distributed knowledge distillation on different financial data. The belief–desire–intention (BDI) model is an influential, cognitive science- and artificial intelligence-based architecture, which has been employed to develop a coherent model of how rational agents decide what to do. With the integration of BDI reasoning, the designed system seeks to improve interpretability by explicitly considering the beliefs (data-driven patterns), desires (fraud detection goals), and intentions (intentional actions) involved in the fraud detection process.

The transformer model has been a transformative breakthrough in deep learning in recent years. It began as the state-of-the-art language model for natural language processing and was then generalized to a wide range of applications, including image, speech, and structured data. Transformers have an advantage over LSTMs or GRUs in the sense that they are a non-recurrent model, as they adopt a self-attention mechanism, thanks to which they can model long-range dependencies without following the sequence. This capability enables them to have better parallelism and scalability, which are very suitable for large-scale financial transaction datasets. In the fraud detection domain, the transformer has a distinct advantage, as it is able to analyze complex interdependencies between features located in features such as time, frequency, amount, and historical customer behavioral patterns. But their large-scale application is impeded by a major disadvantage—their “black box” character, which reduces trust and regulatory control. A hybrid model, such as transformers with an interpretable reasoning module, like the BDI framework, would help close the performance–interpretability gap in high-stakes tasks, such as finance.

Moreover, we propose a multi-teacher, single-student knowledge distillation approach to transfer the detection capability across a variety of datasets, including the IEEE-CIS Fraud Detection, European Credit Card Transactions, and PaySim Mobile Money Simulation. The goals of this scheme are to enhance the model’s generalization ability and to simplify the model to allow for deployment in a generic financial domain. A schematic of the proposed fraud detection pipeline is discussed in Section 5 (Proposed Methodology) to illustrate the sequential flow from the data preparation to the final classification and explainability.

The key contributions of this research are as follows:

• The Integration of BDI Reasoning with Transformer Architecture: This enhances the model interpretability and decision-making transparency in fraud detection.
• Distributed Knowledge Distillation Across Diverse Datasets: This improves the generalization and performance consistency across heterogeneous financial data.
• Empirical Validation: The validation demonstrated the effectiveness of the proposed framework through extensive experiments on multiple real-world datasets, showcasing its superior accuracy, recall, and inference efficiency compared to existing models.

Through this unified approach, this study aims to advance the field of financial fraud detection by combining the strengths of deep learning and symbolic reasoning, offering a scalable, interpretable, and efficient solution to a pressing global challenge.

2. Literature Review

Proponents promote the use of artificial intelligence (AI) for financial fraud detection as an innovative response to complex fraudulent operations [9]. AI systems, especially those based on machine learning (ML), have proven to be more efficient than rule-based and statistical methods at handling huge transactional data thus far [10,11]. The sophisticated systems are particularly adept at spotting suspicious activities and hidden patterns that could indicate fraud, improving the detection rates and operational effectiveness of financial firms.

Within the wide range of ML algorithms, neural networks are one of the most popular due to their predictive power and the ability to adapt to the fraudster’s continued innovations [12,13]. Research has shown that neural architectures work better than traditional methods like logistic regression and decision trees, especially when using real banking and transaction data for development. Additionally, using deep learning models, like clustering, autoencoders, and RNNs, has improved fraud detection via the identification of not just known fraud patterns but also new ones that were not previously recognized.

However, the infusion of AI in financial fraud detection also raises several ethical and practical issues. Issues range from algorithmic transparency, data privacy, and bias reduction to the necessity of providing explanations for algorithmic decisions [14]. Regulatory finance contexts, for instance, intensify the urgency of these issues, as decisions could potentially have legal or financial implications. Scholars emphasize a clear need to integrate human oversight, data governance, and ethical AI practices to build trust and transparency in AI systems [15].

In [16], empirical research demonstrates that AI-based models significantly reduce false positives—a major drawback of traditional systems—while improving real-time detection capabilities. This leads to fewer customer disruptions and enhanced security for financial institutions. AI’s ability to detect anomalies instantly supports proactive fraud prevention, which is critical for minimizing monetary losses and reputational damage.

Nevertheless, the implementation of AI-based fraud detection systems is not without limitations. Another study [17] states that organizations often face challenges related to data quality, interoperability, model scalability, and algorithm interpretation. Smaller financial entities, in particular, may struggle with the high cost of deployment, technical expertise, and infrastructure requirements needed to adopt such advanced systems. Furthermore, the dynamic nature of fraudulent behavior necessitates models that are both adaptive and resilient in real-time operational settings.

The study of research paper [18] has shown that as financial fraud continues to evolve and become more complex—and as AI itself also advances—there is an increasing focus on the importance of incorporating Explainable Artificial Intelligence (XAI) into fraud detection mechanisms. Another study [19] has shown that some interpretable methods have been shown to be potentially competitive with traditional machine learning models in terms of their prediction accuracy, but most machine learning models remain “black-box” models that do not exhibit trust-showing compliance with regulation and user acceptance. In this light, XAI methods are not just nice to have or complementary; they are a prerequisite for the responsible and transparent use of AI in high-impact financial applications.

Research [20] has shown that a central advantage of XAI lies in its ability to demystify the decision-making process of AI models. Techniques such as SHAP (Shapley Additive Explanation), LIME (Local Interpretable Model-Agnostic Explanation), and ELI5 have been widely recognized for enabling model transparency by illustrating the impact of input features on predictive outcomes. In financial fraud contexts, these techniques help elucidate how variables such as the transaction frequency, the account balance history, and geo-temporal anomalies contribute to a model’s decision to flag a transaction as suspicious. This transparency is instrumental in both internal auditing and external regulatory scrutiny.

Another study [21] states that trust is a key factor that drives the adoption of AI systems, especially in applications where it has implications of financial risk. XAI plays a critical role, as it allows stakeholders to comprehend, verify, and challenge the decisions made by AI. Through model transparency, XAI instills trust in compliance officers, fraud analysts, and business decision-makers who would otherwise fear using a black-box model. In addition, by allowing for the revelation of misclassifications or model biases, using XAI strengthens the reliability and robustness of the system.

According to the study [22], banks operate within highly regulated environments where there are growing requirements for transparency, fairness, accountability, and transparency in automated decisions [23]. Data governance laws, such as the GDPR, provide a direct support guideline that forbids discriminatory reasoning and ensures the right to explanation in automated decision making. By including interpretability in AI models, institutions can show they are being careful, provide clear explanations, and ensure fairness, which helps them avoid legal issues and follow new ethical standards in AI governance.

Tang and Liu (2024) propose a novel framework for financial fraud in [24] that involves detection using a distributed knowledge distillation architecture based on the transformer model. Their approach utilizes a multi-headed attention mechanism for capturing internal correlations in financial features, followed by feedforward networks to extract high-level representations. To address the heterogeneity of financial indicators across industries and data imbalance issues, the study introduces a multi-teacher knowledge distillation strategy, transferring detection knowledge to a compact student model. Evaluated on the TipDM Cup dataset, their model achieved impressive results—an F1-score of 92.87%, an accuracy of 98.98%, and an AUC of 96.73%—outperforming traditional classifiers. However, while the architecture improved the detection accuracy and model generalization, the paper lacked an interpretability layer, making it less suitable for high-accountability financial environments where explainability and cognitive transparency are essential. This research inspired the current study, which extends the work by incorporating a BDI-based symbolic reasoning layer to enhance the interpretability and decision support.

Table 1. Detailed summary of the related literature on financial fraud detection using AI.

Refs.	Year	Model/Technique	Dataset/Domain	Key Contributions	Limitations/Gaps	How the Current Study Addresses It
[10]	2024	Logistic regression, SVM, decision trees	Generic transaction data	Offers basic fraud classification frameworks	Poor performance on complex, high-volume data	Uses transformer for deep feature learning
[12,13]	2022, 2024	ANN, RNN, autoencoders	Banking and e-commerce data	Better pattern recognition and anomaly detection	Lack of transparency in decisions	Adds BDI for cognitive reasoning
[14,15]	2024, 2022	Discussions on explainability, fairness	Conceptual frameworks	Highlights ethical risks in AI-based fraud systems	No practical model offered	Introduces BDI reasoning and interpretability
[16]	2024	ML-based anomaly detection	Real banking systems	Showed reduced false positives, improved fraud catch	Models still black-box; no symbolic tracing	Post hoc interpretability through symbolic logic
[18,19]	2024, 2025	SHAP, LIME, ELI5	Financial applications	Enabled explanation of ML decisions via feature attribution	Lacked domain-specific decision goals	Integrates domain-informed BDI reasoning
[20,21,22]	2025, 2024, 2022	Explainability in AI governance	GDPR, RBI guidelines	Discussed need for AI compliance in finance	No implementation guidance	Our model operationalizes explainable decision trails
[24]	2024	Transformer + multi-teacher KD	TipDM Cup dataset	Achieved high F1-score (92.87%) via soft distillation	No interpretability; limited to one domain	Adds symbolic BDI layer + multi-domain generalization

summarizes the seminal and recent contributions in AI-based financial fraud detection, highlighting their strengths and the gaps addressed by our unified transformer–BDI framework.

Despite significant advancements, several gaps remain. By addressing these gaps, this research proposes an integrated framework that leverages the power of transformer networks, the cognitive clarity of BDI reasoning, and the efficiency of distributed knowledge distillation to deliver a next-generation fraud detection system adaptable across multiple financial environments. A thorough analysis of the existing literature reveals the following critical gaps:

• A Lack of Interpretability in Transformer-Based Models: Most state-of-the-art transformer architectures used for fraud detection operate as black-box models, offering little insight into the rationale behind their decisions. This severely limits their acceptance in domains that require traceability and accountability.
• The Absence of Intent Modeling in Financial Fraud Detection: None of the current fraud detection models incorporate cognitive or agent-based reasoning frameworks, such as the belief–desire–intention (BDI) framework, which can offer deeper behavioral insights and more explainable fraud predictions.
• Limited Cross-Dataset Generalization: The existing approaches are predominantly trained and evaluated on single datasets. They lack robustness when exposed to structurally diverse financial data across different domains (e.g., mobile payments vs. corporate accounting).
• The Underutilized Potential of Distributed Knowledge Distillation: While knowledge distillation has shown promise in reducing model complexity, there is limited research on its application across multiple domains or industries in a distributed, multi-teacher setting to enhance generalization while preserving model efficacy.
• The Insufficient Integration of Symbolic and Neural Models: There exists a notable gap in combining symbolic reasoning frameworks (like BDI) with neural models (like transformers) to enhance the explainability and decision logic in financial fraud detection systems.

3. Problem Statement

The existing literature has made progress in fraud detection, but key limitations still hinder comprehensive solutions. These limitations are outlined below.

3.1. Research Challenge

Despite the success of deep learning models, especially the transformer-based models, in learning representations for financial fraud detection, they are limited by some pivotal drawbacks that restrict their practical usage. The problem with neural networks is that they are inscrutable—these are models that tend to act as opaque black boxes and provide no rationale to support the prediction, which is unacceptable in a regulatory and high-stakes finance environment. What is more, deep models often overfit the particular distribution of that one dataset and are thus less effective in production in a domain that has a different structure of financial logic (i.e., fraud in credit cards vs. fraud in mobile money). They are also prone to suffering from class imbalance, which, in turn, leads to a large number of false positives or missed frauds when handling real-world data. Furthermore, deep approaches are computationally expensive, which makes it difficult to use them in real-time deployment and in scenarios where computing resources are constrained. Even with methods like knowledge distillation to compress models, they often have difficulty preserving prediction fidelity and interpretability when applied to a broad spectrum of heterogeneous financial tasks. So, it is important to create a deep learning model for fraud detection that can grow easily, be understood, and works well across different tasks while also meeting regulatory standards.

3.2. Motivation for Hybrid Integration

In the realm of financial fraud detection, models must balance a high predictive performance with interpretability—a critical requirement for regulatory compliance and stakeholder trust. Transformer-based models offer remarkable accuracy due to their capacity to capture long-range dependencies in sequential transaction data. However, they lack inherent interpretability and often require large volumes of data and computational resources.

To mitigate this, we integrate a multi-teacher knowledge distillation framework, where teacher models pre-trained on individual fraud domains transfer domain-specific knowledge into a lightweight student model. This approach improves the generalizability of the system while maintaining computational efficiency, making the model suitable for deployment in resource-constrained environments.

Furthermore, to enhance explainability, we introduce a belief–desire–intention (BDI) reasoning layer as a symbolic overlay atop the distilled student model. This layer mimics human-like decision-making logic, enabling the model to offer traceable, rule-based explanations for its predictions. Each component—the transformer encoder, knowledge distillation, and BDI logic—contributes a distinct capability. Their integration addresses the dual challenge of accuracy and interpretability in fraud detection, and their synergy has been empirically validated across diverse datasets.

4. Dataset Description

We used three different and publicly available datasets to verify the robustness, transferability, and generalization capacity of the proposed transformer–BDI architecture. These datasets capture all sorts of financial transactions in different avatars—corporate financial transactions, credit card transactions, and mobile money transfers. The large variety of data structures and labels concerning fraud makes it well-suited as a testing ground for the performance of a generic fraud detection system.

Table 2. A comparative overview of the datasets used in this study.

Attribute	IEEE-CIS Fraud Detection	European Credit Card Fraud	PaySim Mobile Money Simulation
Domain	E-commerce/online transactions	Credit card transactions	Mobile money transactions (simulated)
Source	Vesta Corporation and IEEE-CIS Challenge	ULB Machine Learning Group	Simulated from real mobile money logs
Total Records	1,096,000+	284,807	6,362,620
Fraudulent Records	~38,000	492	8213
Fraud Ratio	~3.5%	0.17%	0.13%
Number of Features	434 (after feature engineering)	30	11
Feature Types	Categorical, binary, numerical	Numerical (transformed via PCA), time, amount	Categorical and numerical
Feature Anonymization	Yes (due to proprietary constraints)	Yes (PCA applied)	No (descriptive names retained)
Time-Related Features	Yes (transaction timestamps, delays, etc.)	Yes (time since first transaction in seconds)	Yes (step = hourly interval)
Transaction Types	Online purchases, device/browser info	Point-of-sale (POS) credit card usage	Transfer, cash-in, cash-out, payment
Class Imbalance	Moderate (but significant)	High	High
Label Type	Binary (is fraud: 1 = fraud, 0 = normal)	Binary (class: 1 = fraud, 0 = normal)	Binary (is fraud: 1 = fraud, 0 = normal)
Missing Values	Yes (extensively across many features)	No	No
Ideal Use Case	Feature-rich deep models; cross-domain learning	Lightweight anomaly detection models	Behavior-based anomaly detection; mobile agents
Dataset Format	CSV	CSV	CSV
Accessibility	Public (via Kaggle competition)	Public (via Kaggle open dataset)	Public (via Kaggle open dataset)
Use in the Literature	Widely used in fraud detection benchmark studies	Frequently used for benchmarking and imbalance	Used in agent-based, BDI, and behavioral studies

shows a comparison summary of the three datasets used in this paper. Each of the datasets presents distinctive structural and content characteristics that provided the empirical experiment a testing environment in which to evaluate the model under different financial fraud contexts, such as e-trading, credit card operations, and mobile money transactions.

4.1. Dataset 1: IEEE-CIS Fraud Detection Dataset

Ref. [25]. The IEEE-CIS dataset is one of the largest publicly available datasets for transactional fraud detection. It contains anonymized features representing various payment transactions and the associated device/browser information. The dataset is highly imbalanced, with a small fraction of fraud cases, making it suitable for testing detection sensitivity.

4.2. Dataset 2: European Credit Card Fraud Dataset

Ref. [26]. This dataset contains transactions made by European cardholders in September 2013. It is frequently used as a benchmark in fraud detection studies. All features are numerical and anonymized through PCA transformation, except for times and amounts. It is also highly imbalanced, which reflects real-world fraud scenarios.

4.3. Dataset 3: PaySim Mobile Money Simulation

Ref. [27]. PaySim simulates a mobile money transfer environment based on real-world data from a financial institution. It mimics transactions such as cash-in, cash-out, transfers, and payment activities. Unlike the other two datasets, PaySim offers insights into behavioral fraud in mobile-based ecosystems.

The selection of the three datasets was strategic to ensure diversity in fraud scenarios:

• The IEEE-CIS dataset reflects e-commerce and transaction platform fraud, involving detailed user behavior and device characteristics.
• The European Credit Card dataset focuses on card-present fraud and represents more traditional, transaction-only data without additional user attributes.
• The PaySim dataset simulates mobile money fraud, capturing peer-to-peer transfers and real-time mobile payment dynamics.

By covering e-commerce, card-based, and mobile payment environments, the model’s capacity to generalize across domains with distinct fraud signatures and data structures is more comprehensively evaluated. This also aligns with practical deployment scenarios where financial systems must detect fraud across multiple digital channels.

The performance of the proposed model was demonstrated on three datasets, namely, IEEE-CIS Fraud Detection, European Credit Card Transactions, and PaySim Mobile Money Simulation. The IEEE-CIS dataset comes from real banking data, showing a very small amount of fraud (~0.17%), which was a great way to test how sensitive the models are. The European dataset is smaller but has fine-grained transaction attributes and a modest imbalance, testing the robustness of the model with a richer set of features. We offer PaySim, an artificial dataset based on reality and full of mobile money logs for financial fraud detection in a mobile environment (particularly mobile money) and the adaptation of the model in a non-banking framework.

The key challenges include label imbalance, feature sparsity, and differences in data distributions across domains. The model addresses these via domain-specific transformer encoders, BDI-based reasoning for confidence calibration, and multi-teacher distillation to transfer generalized fraud knowledge across datasets.

5. Proposed Methodology

In this work, we present a common framework based on a transformer encoder architecture and multi-teacher distributed knowledge distillation (MTDKD) for financial fraud detection over heterogeneous datasets. Each dataset is paired with a dedicated teacher model trained on its domain-specific distribution. The student model aggregates the distilled knowledge from all teachers to form a generalized representation suitable for cross-domain fraud detection. 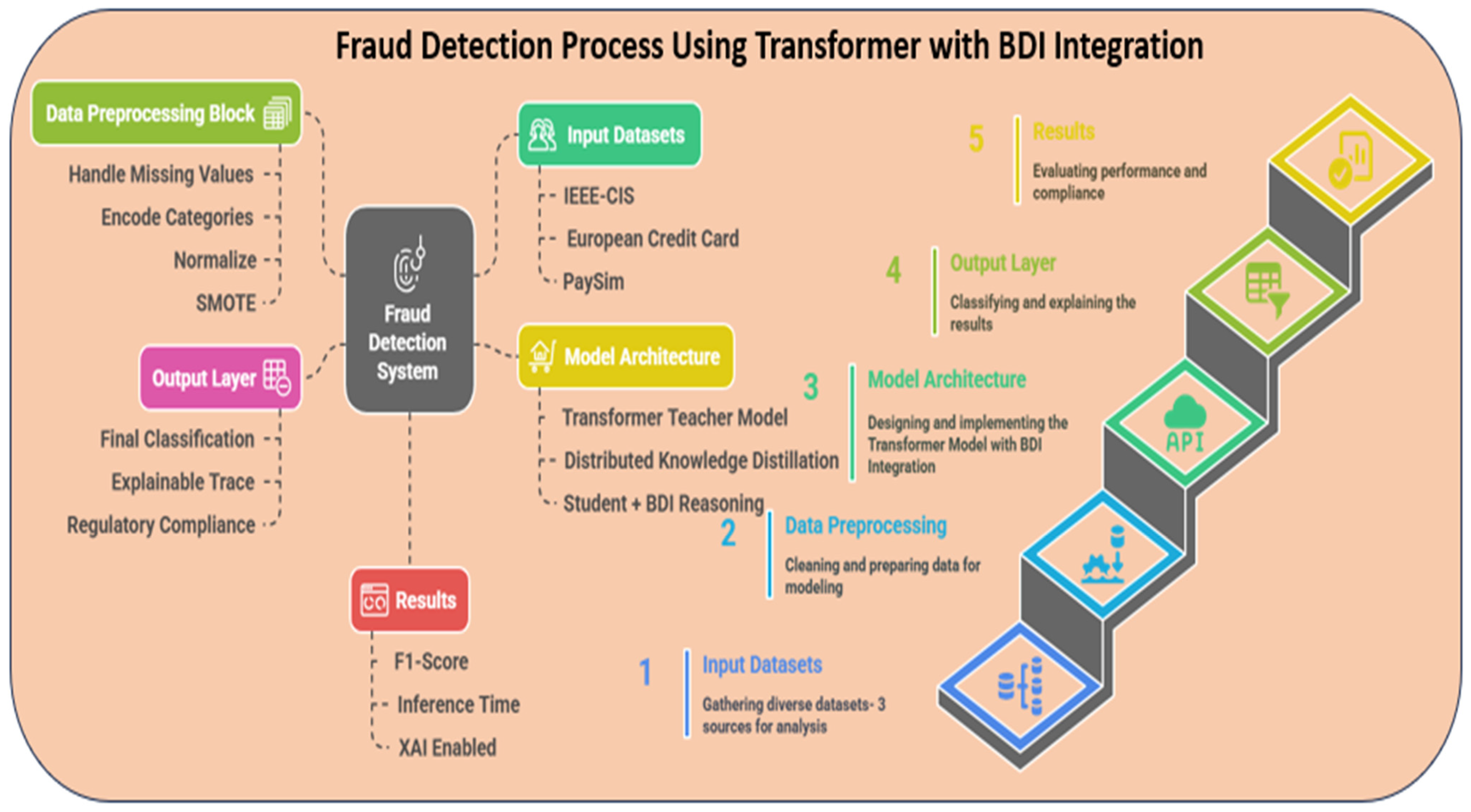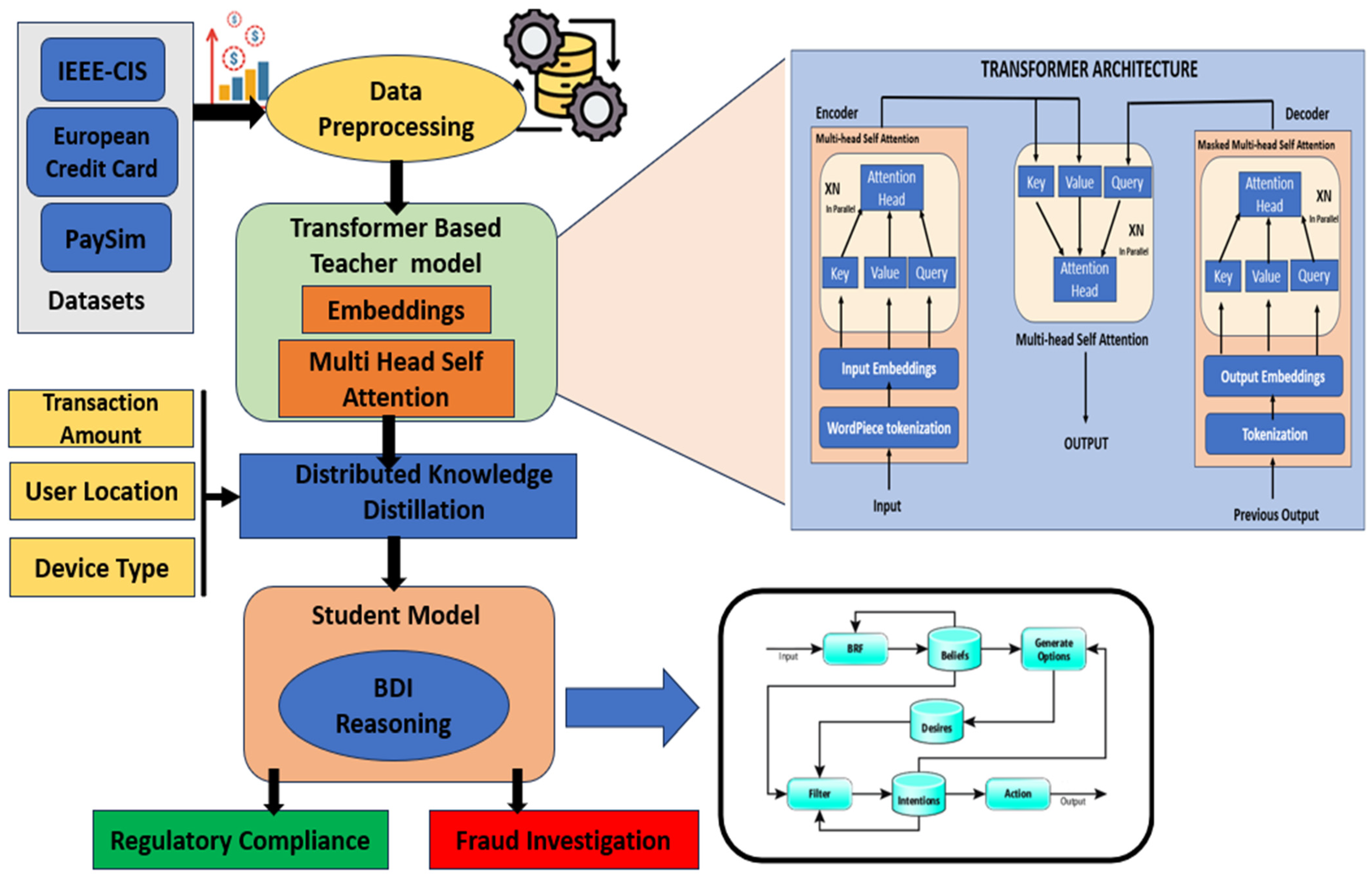Figure 1 presents the overall end-to-end framework of the proposed transformer–BDI model for fraud detection. It includes stages such as dataset integration, preprocessing, transformer-based encoding, knowledge distillation, symbolic reasoning through BDI, and final classification and interpretation. As shown in Figure 2, the proposed framework incorporates a transformer-based teacher model, distributed knowledge distillation, and a BDI reasoning layer within the student model, enabling interpretable and regulatory-compliant fraud detection across diverse financial datasets. The methodology unfolds through a structured pipeline comprising six main stages:

5.1. Data Preprocessing

Preprocessing is a critical step to clean the data for learning and make the input representations consistent among different financial datasets [28,29]. The preprocessing pipeline in our study consists of five steps—missing value treatment, the normalization of numerical variables, encoding categorical variables, handling class imbalance, and splitting the data into train, validation, and test sets.

• Step 1: Missing Value Imputation

Let the dataset be D ∈ R^n×d, where n is the number of samples and dd is the number of features. For a continuous feature (x_j), missing values are imputed using the mean, as shown in Equation (1):

$${\overline{x}}_j={\displaystyle \frac{1}{n_j}}\sum _{i=1}^{n_j}{x}_{ij } (where x_{ij }is not missing)$$

(1)

Each missing value is replaced with ${\overline{x}}_j$. For a categorical feature (x_j), missing values are imputed using the mode, as per Formula (2):

$${\tilde{x}}_j=mode(x_{1j},x_{2j},\dots x_{nj)}$$

(2)

If the percentage of missing values for a feature exceeds a defined threshold (δ) (e.g., 30%), the feature is discarded, as shown in Equation (3):

$$Drop feature x_j if {\displaystyle \frac{\#missing in x_j}{n}}>\delta$$

(3)

• Step 2: Feature Normalization

To prevent features with larger scales from dominating training, min–max normalization is applied: let x_i ∈ R be a raw feature value, and let $x_i^{\prime }$ be its normalized form, as represented in Equation (4):

$$x_i^{\prime }={\displaystyle \frac{x_i-\mathrm{m}\mathrm{i}\mathrm{n}\left(x\right)}{\max \left(x\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(x\right)}}$$

(4)

This transformation maps all values to the interval [0, 1], maintaining proportional relationships.

• Step 3: Categorical Feature Encoding

To handle categorical data, two encoding methods are used:

• Label Encoding: This method assigns a unique integer to each category in an ordinal feature. If $C_j=\{c_1,c_2,c_3,\dots ,c_k\}$ are unique categories, the label encoding map is shown in Equation (5):

$$c_i\mapsto i-1 for i=1,2,\dots ,k$$

(5)

• One-Hot Encoding: This method converts nominal features into binary vectors and is given by Equation (6):

$$OneHot\left(C_i\right)=\left[0,\dots 0,1,0\dots ,0\right](1 at position i)$$

(6)

This ensures that the categorical inputs are numerically encoded without implying ordinal relationships.

• Step 4: Handling Class Imbalance

Fraud detection datasets are highly imbalanced. Let N+ and N− be the number of positive (fraud) and negative (legitimate) samples, respectively. Class weighting in the loss function is shown in Equation (7):

$${\omega }_{+}={\displaystyle \frac{N}{2N_{+}}}, {\omega }_{-}={\displaystyle \frac{N}{2N_{-}}}$$

(7)

These weights are applied to penalize the misclassification of the minority class more heavily. Using the Synthetic Minority Oversampling Technique (SMOTE), new synthetic samples are generated for the minority class by interpolation between a point and its k-nearest neighbors, as shown in Equation (8):

$$x_{new}=x_i+\lambda \left(x_{nn}-x_i\right),\lambda \in \left[\mathrm{0,1}\right]$$

(8)

This approach enhances the class balance without simply duplicating samples.

• Step 5: Data Partitioning

To evaluate the model performance consistently, each dataset is partitioned as follows:

• Training Set: 70%;
• Validation Set: 15%;
• Test Set: 15%.

Let D be the complete dataset. Then, the data partitioning is shown by Equation (9):

$$D=D_{train}\cup D_{val}\cup D_{test}, D_{train}\cap D_{val}=\varnothing , D_{val}\cap D_{test}=\varnothing$$

(9)

Each partition is stratified to preserve class proportions. This preprocessing stage ensures that the raw input data are transformed into structured, consistent, and well-balanced input tensors for the transformer-based architecture, while also ensuring fairness in the model evaluation.

5.2. Transformer-Based Teacher Model Training

Each dataset is used to train a separate transformer-based model that acts as a domain-specific teacher. The transformer architecture is particularly suited for tabular financial data due to its ability to model complex inter-feature relationships through attention mechanisms. The training process involves the following components:

5.2.1. Input Representation

Let each input sample (X ∈ R^n×d) denote a sequence of n feature tokens, each of dimension d. In tabular data, each feature is treated as a token, allowing the model to learn dependencies between features.

5.2.2. Linear Projections: Queries, Keys, and Values

Each input token is projected into three vectors:

• The query matrix: Q = XW^Q;
• The key matrix: K = XW^K;
• The value matrix: V = XW^V

• where $W^V\in R^{d\times d_k}$ are the learned weight matrices, and $d_k$ is the attention head dimension.

5.2.3. Scaled Dot-Product Attention

The attention mechanism computes how much focus one feature should have on others. This is shown in Equation (10):

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(\mathrm{Q},\mathrm{K},\mathrm{V}\right)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left({\displaystyle \frac{\mathrm{Q}{\mathrm{K}}^{\mathrm{T}}}{\sqrt{{\mathrm{d}}_{\mathrm{k}}}}}\right)\mathrm{V}$$

(10)

• $Q{K}^T$ top computes the dot-product similarity between queries and keys;
• Division by $\sqrt{d_k}$} stabilizes the gradients;
• Softmax ensures that the attention weights sum to 1 across each row.

5.2.4. Multi-Head Attention

Instead of a single attention computation, multiple heads learn from different subspaces, as shown in Equation (11):

$$MultiHead\left(Q,K,V\right)=Concat({head}_1,\dots ,{head}_h)W^O$$

(11)

Each head is computed as per Equation (12):

$${head}_i=Attention(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)$$

(12)

where $W_i^Q$, $W_i^K$, $W_i^V\in R^{d\times d_k}$, and $W^O\in R^{h{d}_k\times d}$ are learned parameters.

5.2.5. Position-Wise Feedforward Network (FFN)

After attention, each token passes through a feedforward layer to introduce non-linearity, as shown in Equation (13):

$$FFN\left(X\right)=ReLU\left(x{W}_1+b_1\right)W_2+b_2$$

(13)

where $W_1\in R^{d\times d_{ff}},W_2\in R^{d_{ff}\times d},and d_{ff}$ are the hidden dimensions of the FFN layer.

5.2.6. Layer Normalization and Residual Connections

To stabilize training and aid convergence, residual connections are added after the attention and FFN layers, as per Equation (14):

$$x^{\prime }=LayerNorm(x+Sublayer\left(x\right))$$

(14)

These operations prevent gradient vanishing and improve the learning dynamics.

5.2.7. Output Layer for Classification

The final hidden state (h ∈ R^d) is projected into class probabilities using a linear classifier followed by softmax. This is explained by Equation (15):

$$\widehat{y}=softmax(W_o+b)$$

(15)

where $W_o\in R^{d\times C},C=2$ for binary classification (fraud vs. non-fraud).

5.2.8. Loss Function: Cross-Entropy

For binary classification, the model is trained using the cross-entropy loss, as per Equation (16):

$$L_{CE}=-{\displaystyle \frac{1}{N}}\sum _i[y_{ij}\log \left({\widehat{y}}_i\right)+\left(1-y_i\right)\log \left(1-{\widehat{y}}_i\right)]$$

(16)

where $y_i\in \left\{\mathrm{0,1}\right\}$ is the ground-truth label, and ${\widehat{y}}_i\in$ [0, 1] is the predicted probability for fraud.

5.2.9. Training Details

• Optimizer: The Adam optimizer is used for weight updates.
• Learning Rate Schedule: The learning rate schedule is linear warm-up followed by decay.
• Early Stopping: This is based on the validation loss or F1-score to prevent overfitting.
• Epochs: Epochs typically range from 10 to 50, depending on the dataset convergence.

5.2.10. Training Stability and Regularization

This section establishes each teacher model as a specialized expert trained to capture fraud characteristics from its respective dataset. The trained logits and soft predictions from these teacher models are later used in distributed knowledge distillation to build a compact, generalized student model.

Knowledge distillation, especially in a multi-teacher setup, can introduce training instability due to inconsistent gradients from heterogeneous teacher outputs. To mitigate this, we employed several strategies:

• Dropout (rate = 0.3) was used in both the teacher and student networks to prevent overfitting and promote generalization.
• Early stopping with a patience of 10 epochs was applied to halt training when the validation loss plateaued.
• Gradient clipping was used to limit the norm of the gradients to a maximum value of 1.0, thereby avoiding gradient explosion.

Additionally, training was run across five independent random seeds, and the student model achieved consistent convergence with a standard deviation in AUC scores under 1.2%. This demonstrates the high stability and reproducibility of our approach across different runs and datasets.

5.3. Distributed Knowledge Distillation

Distributed knowledge distribution involves transferring the knowledge acquired by multiple transformer-based teacher models (trained on different datasets) into a single lightweight student model that generalizes well across domains and maintains a high detection performance. Distributed knowledge distillation is a form of model compression and transfer learning that uses the soft predictions of several pre-trained teacher models to supervise the training of a smaller student model. 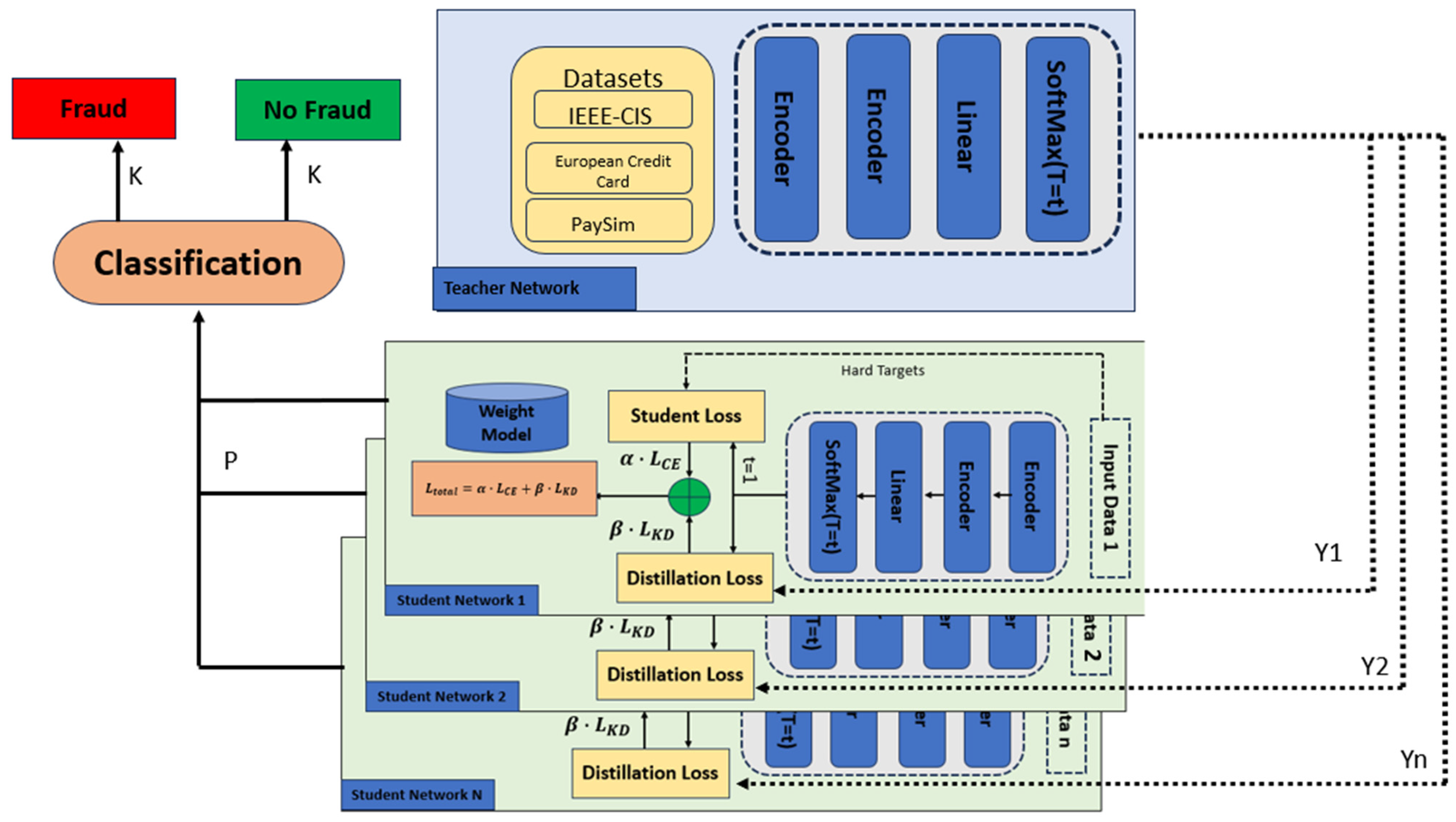Figure 3 illustrates the distributed knowledge distillation setup wherein multiple student networks are trained using soft targets from a transformer-based teacher model across the IEEE-CIS, European Credit Card, and PaySim datasets, enhancing the model generalizability and classification performance.

As shown in Figure 3, the way some parts (like teacher outputs and student inputs) visually overlap helps to represent the layered structure and the simultaneous sharing of knowledge in distributed distillation. Different to the flat pipeline, this model is stacked and factorized, which makes the representation of the multi-source transfer of learning signals important.

5.3.1. Teacher Logits and Soft Targets

• Let

• $Z^{\left(t_k\right)}\in R^{B\times C}$ be the logit output of the k-th teacher model, where B is the batch size and C is the number of classes;
• $Z^{\left(s\right)}\in R^{B\times C}$ be the student model’s logit output.

Apply temperature-scaled softmax to smooth predictions, as per Equation (17):

$$P^{\left(t_k\right)}=softmax\left({\displaystyle \frac{Z^{\left(t_k\right)}}{T}}\right), P^{\left(s\right)}=softmax\left({\displaystyle \frac{Z^{\left(s\right)}}{T}}\right)$$

(17)

where T > 1 is the temperature parameter that controls the softness of the probability distribution. Higher T values yield softer probability distributions that carry more information about class similarities. To obtain an aggregated teacher prediction, the soft probabilities from all K teachers are averaged, which follows Equation (18):

$${\overline{P}}^{\left(t\right)}={\displaystyle \frac{1}{K}}\sum _{k=1}^K{P}^{\left(t_k\right)}$$

(18)

5.3.2. Knowledge Distillation Loss

Kullback–Leibler (KL) divergence is used to measure the discrepancy between the student and aggregated teacher distributions. We can refer to Equation (19) for this:

$$L_{KD}=T^2\sum _{i=1}^B\sum _{j=1}^C{\overline{P}}_{i,j}^{\left(t\right)}log\left({\displaystyle \frac{{\overline{P}}_{i,j}^{\left(t\right)}}{P_{i,j}^{\left(s\right)}}}\right)$$

(19)

The factor T² ensures that the gradient magnitudes remain consistent when using temperature scaling.

5.3.3. Supervised Cross-Entropy Loss

Alongside distillation, the student is also trained with traditional cross-entropy loss using ground-truth labels (Y), as shown in Equation (20):

$$L_{CE}=-\sum _{i=1}^B\sum _{j=1}^C{Y}_{i,j}log\left(P_{i,j}^{\left(s\right)}\right)$$

(20)

where $Y_{i,j}$ = 1 if sample ii belongs to class j; otherwise, it is 0.

5.3.4. Total Loss for Student Model

The final training objective for the student model is a weighted combination of both losses, as per Equation (21):

$$L_{total}=\alpha ·L_{CE}+\beta ·L_{KD}$$

(21)

where α and β are coefficients (e.g., 0.5 and 0.5 or 1.0 and 0.3) that balance between learning from hard labels and learning from soft labels.

➢

This approach preserves the generalization capabilities of each teacher by transferring their knowledge as softened probability distributions.

➢

It enhances the domain robustness by learning from varied distributions (cross-dataset behavior).

➢

The student model, being shallower and lighter, supports faster inference while maintaining an accuracy comparable to that of teacher models.

5.4. Transformer-Based Student Encoding

The student model uses a lightweight transformer encoder for general-purpose representation learning. It mirrors the teacher model’s structure with fewer layers and reduced dimensionality. Equation (22) shows how the final classification is obtained:

$${\widehat{y}}_i=softmax(W_o{h}_i+b)$$

(22)

5.5. BDI Reasoning Layer (Post Hoc Interpretability)

The belief–desire–intention (BDI) framework is a symbolic reasoning model inspired by human cognitive processes. When integrated as a post hoc layer in a neural architecture, it provides interpretability by explaining why a decision (fraud vs. non-fraud) was made, based on what the model believes, what it wants, and what it intends to do. Figure 4 depicts the belief–desire–intention (BDI) reasoning layer integrated into the student model, which interprets latent features as probabilistic beliefs, evaluates them to generate desires using a utility function, and selects intentions to trigger explainable fraud response actions.

The BDI reasoning layer operates on a rule-based knowledge base that was constructed using a hybrid approach. A subset of the logic rules was derived through expert consultations with financial analysts and forensic auditors who provided domain-specific indicators of suspicious behavior (e.g., rapid transaction bursts, cross-border anomalies).

Complementing this, frequent pattern mining techniques were used to extract high-confidence behavior rules from the training data across the three datasets. These rules were then manually encoded into the reasoning engine to ensure interpretability and transparency. The framework allows for easy extensibility, enabling new rules to be added or adapted based on evolving fraud patterns.

5.5.1. Theoretical Foundation

➢

Beliefs (B): Beliefs are the information that the model has derived from the data (learned representations).

➢

Desires (D): Desires are the objectives or preferred outcomes (e.g., correctly classifying fraud).

➢

Intentions (I): Intentions are the final executable actions or decisions based on beliefs and desires.

This triadic model is suitable for environments requiring decision traceability, such as banking systems and regulatory audits.

5.5.2. Mathematical Formulation

Let $h_n\in R^d$ be the output representation (latent embedding) of the nth sample from the student transformer encoder.

• Step 1: Belief Vector Construction

We define a belief transformation function (ϕ:R^d → R^k) in Equation (23), which may be a dense or sparse projection layer:

$$B_n=\mathsf{\varphi }\left(h_n\right)$$

(23)

This projection retains information most indicative of fraud cues. Optionally, domain-specific rules or SHAP values can augment this vector.

• Step 2: Desire Inference

In Equation (24), from the belief vector, the desired classification outcome is computed based on the predicted probabilities:

$$D_n=arg \underset{c\in \left\{0.1\right\}}{\mathrm{mcax}}P(Y_n=c|B_n)$$

(24)

where $P(Y_n=c|B_n$) can be approximated using a softmax layer or a logistic classifier trained over the belief space.

• Step 3: Intention Execution

An intention is formed only if the belief aligns with a strong enough desire (confidence threshold: θ), as shown in Equation (25):

$$I_n=\left\{\begin{array}{c}1 if D_n=1 and \left(Y_n=c|B_n\right)>\theta \\ 0 otherwise\end{array} \right.$$

(25)

where $I_n=1$ indicates that the model flags the transaction as fraudulent, and θ is typically selected via validation (e.g., 0.7 or 0.8).

5.5.3. Advantages of BDI Reasoning

➢

Explainability: BDI reasoning provides a symbolic trace of the model’s rationale.

➢

Accountability: BDI reasoning is useful for justifying automated decisions in regulated domains.

➢

Flexibility: BDI reasoning can adapt to business rule constraints (e.g., alert suppression below certain confidence levels).

To further enhance the interpretability, we present a representative example that demonstrates how a suspicious financial transaction is processed through the BDI reasoning layer, highlighting the applied logic rules and the final classification outcome. The working example is a fraud transaction processed by BDI:

Transaction Details:

• Amount: INR 50,000;
• Time: 2:34 AM;
• Location: remote area;
• Device: new device;
• Previous fraud history: yes.

Based on the BDI logic:

• Belief (B): The system believes that this transaction is suspicious due to its off-hour timing, unfamiliar device, and prior fraud flag.
• Desire (D): The system desires to minimize false negatives (i.e., to avoid missing actual fraud).
• Intention (I): The system flags this transaction as fraud with explainable reasoning linked to the above attributes.

Sample Logic Rules Used:

• IF previous_fraud_flag == True AND device_status == New → THEN belief_score += High;
• IF transaction_time ∈ [12 AM–4 AM] → THEN belief_score += Medium;
• IF belief_score >= Threshold AND fraud_probability > 0.7 → THEN intention = Fraud.

These symbolic rules guide the post hoc reasoning applied over the deep model’s output, providing transparency and justifiability in decision making.

A comparative summary of the operational steps, input–output flow, and interpretability roles of the two core algorithmic components—multi-teacher knowledge distillation and BDI-based post hoc interpretation—is provided in

Table 3. Comparative summary of core algorithms used in the proposed architecture.

Algorithm Name	Multi-Teacher Knowledge Distillation	BDI-Based Post Hoc Interpretation
Input	Trained teacher models {T1, T2, …, Tk}; input samples X; ground-truth labels Y	Final encoder output hn, learned classifier $P\left(Y\right|B_n)$, belief mapping ϕ, threshold θ
Step 1	Initialize student model weights	Compute belief representation:
		$B_n=\varphi \left(h_n\right)$
Step 2	For each mini-batch: Get teacher logits $Z^{\left(t_k\right)}$ for each teacher $T_k$	Calculate desire class:
		$D_n=arg\underset{c}{\mathit{max}}P(Y_n=c|B_n)$
Step 3	Compute soft targets $P^{\left(t_k\right)}=Softmax(Z^{\left(t_k\right)}/T)$	Compute probability of fraud class:
		$p=P(Y_n=1|B_n)$
Step 4	Average soft targets: ${\overline{P}}^{\left(t\right)}={\displaystyle \frac{1}{K}}\sum _{k=1}^K{P}^{\left(t_k\right)}$	Determine intention: If $D_n=1 and p>\theta , then set$; $I_n\leftarrow 1$ else $I_n\leftarrow 0$
Step 5	Calculate loss: $L_{KD}\leftarrow KL divergence between {\overline{P}}^{\left(t\right)}$ and $P^{\left(s\right)}$	Output $I_n$ along with $B_n$, $D_n$, and p as interpretability trace
	$L_{CE}\leftarrow Cross Entropy between Y and P^{\left(s\right)}$
Output	Trained student model with generalizable knowledge	Interpretable prediction with symbolic trace (B–D–I)

to enhance the structural clarity and facilitate the replication of the proposed framework.

5.6. BDI Integration

Logits from the transformer-based classifier are filtered using confidence thresholding before being used as input to the BDI layer. The BDI layer scores each transaction according to a set of symbolic logic rules, which attempts to capture patterns such as high-risk merchant codes, unusual transaction times, and cross-border characteristics. These rules are partly expert-crafted and data-driven, while the BDI agent updates its belief state with inputs such as the type of transaction and the amount and frequency of the transaction. According to predefined goals (e.g., to minimize false positives) as well as desires (e.g., to (dis)enable security flags), the BDI agent either confirms or corrects the initial classification. Such a bilayer architecture allows for explainable decision making while preserving the deep learning predictive power.

To provide clarity on the decision-making pipeline, we present the following pseudocode demonstrating the interaction between the transformer model and the BDI layer:

  → Generate prediction using the Transformer model:

    predicted_label, confidence_score ← Transformer(transaction.features)

  → If confidence_score ≥ decision_threshold:

    Extract beliefs from the transaction context

    Define desires based on organizational goals (e.g., minimizing risk)

    Formulate intentions by evaluating the alignment of beliefs and desires

 

    → Apply BDI reasoning rules:

      If intentions indicate potential fraud:

        final_label ← 'Fraud'

      Else:

        final_label ← predicted_label

  Else:

    final_label ← 'Uncertain'

 

  → Store the final_label for downstream evaluation and analysis

 

5.7. Performance Metrics

To evaluate the proposed transformer–BDI architecture, the following metrics are employed:

• Accuracy: The accuracy measures the overall correct predictions [30] and is useful but less informative for imbalanced data.
• Precision: The precision indicates the proportion of predicted frauds that are actual frauds [31] and is critical for minimizing false alarms.
• Recall: The recall measures how many actual frauds were correctly identified [32] and is important for detecting as many fraudulent cases as possible.
• F1-Score: The F1-score represents the harmonic mean of the precision and recall [30] and balances both types of error in imbalanced settings.
• AUC-ROC: The AUC-ROC evaluates the model’s ability to distinguish between fraud and non-fraud over various thresholds.
• AUC-PR: The AUC-PR focuses on the performance of the positive (fraud) class and is more suitable for imbalanced datasets.
• Matthews Correlation Coefficient (MCC): This is a balanced measure considering all confusion matrix components and is reliable for skewed distributions.
• Inference Time: The inference time measures the prediction latency per instance and is relevant for real-time deployment.
• Model Size: The model size indicates the memory requirements and parameter count and is useful for resource-limited environments [33].
• Interpretability: This is a qualitative measure based on the BDI reasoning trace and visual/auditable outputs.

These metrics collectively assess the model’s accuracy, robustness, efficiency, and explainability, ensuring its practical applicability in fraud detection scenarios.

6. Experimental Setup

To validate the performance and generalizability of the proposed transformer–BDI-based model, a series of experiments were conducted across three benchmark financial fraud datasets: IEEE-CIS Fraud Detection, European Credit Card Transactions, and PaySim Mobile Money Simulation. All experiments were performed using standardized preprocessing protocols, uniform evaluation metrics, and consistent training parameters to ensure a fair comparison with the baseline models.

The model was implemented in Python 3.9 using PyTorch 2.0, and the training was carried out on an NVIDIA Tesla V100 GPU (16 GB VRAM). Each model variant was trained with early stopping based on validation loss, and the hyperparameters were tuned via a grid search using cross-validation. The transformer encoder consisted of four attention heads and two layers with positional encoding. Knowledge distillation was implemented using a multi-teacher soft-labeling approach, while the BDI layer processed transformer outputs to generate rule-based symbolic decisions for interpretability. Baseline comparisons included traditional ML classifiers (e.g., logistic regression, SVM, and decision trees) and state-of-the-art ensemble methods (e.g., random forests, XGBoost, and AdaBoost).

Table 4. Experimental setup summary.

Parameter/Component	Details
Datasets Used	IEEE-CIS, European Credit Card, PaySim Mobile Money
Programming Language	Python 3.9
Framework	PyTorch 2.0
Hardware	NVIDIA Tesla V100 GPU (16 GB VRAM), 64 GB RAM
Model Architecture	Transformer encoder + multi-teacher knowledge distillation + BDI layer
Transformer Configuration	Four attention heads, two encoder layers, positional encoding
Knowledge Distillation	Multi-teacher soft-target distillation, temperature = 2
BDI Reasoning Layer	Belief–desire–intention logic for symbolic post hoc decision reasoning
Optimization Algorithm	Adam optimizer
Loss Function	Cross-entropy (primary) + KL divergence (KD)
Batch Size	64
Learning Rate	0.001 (adaptive decay with plateau scheduler)
Early Stopping	Enabled (patience = 10 epochs)
Evaluation Metrics	Accuracy, precision, recall, F1-score, AUC, MAE, inference time, model size, paired t-tests, and Wilcoxon signed-rank tests

provides a detailed summary of the experimental setup, including the model configurations, training parameters, optimization strategies, and evaluation protocols used for benchmarking the proposed transformer–BDI framework across all three financial fraud datasets.

To ensure the robustness of the reported results and address concerns about generalizability, we performed 5-fold cross-validation on each dataset and report the mean values with standard deviations for the key metrics (accuracy, AUC, F1-score, precision, and recall). These metrics are provided in

Table 5. Performance of the transformer–BDI model across datasets.

Metric	IEEE-CIS Fraud Detection	European Credit Card Fraud	PaySim Mobile Money
Accuracy (%)	97.2	99.4	98.6
Precision (%)	91.8	87.5	93.2
Recall (%)	94.1	89.3	91.6
F1-Score (%)	92.9	88.4	92.4
AUC-ROC	0.981	0.978	0.987
AUC-PR	0.961	0.942	0.972
MCC	0.883	0.843	0.896
Inference Time (ms)	2.4	1.8	2.1
Model Size (MB)	12.4	12.4	12.4
Interpretability Score	High	High	High

. Additionally, we conducted paired t-tests and Wilcoxon signed-rank tests to compare the performance of the proposed model against those of the baseline models (CNN, ANN, SVM).

7. Results and Discussion

This section presents the experimental results obtained from evaluating the proposed transformer–BDI model across multiple financial fraud datasets. The findings are analyzed in comparison with baseline models to highlight improvements in the accuracy, interpretability, and decision efficiency.

7.1. Performance of Proposed Transformer–BDI Model

The proposed transformer–BDI model was tested on three benchmark financial fraud datasets: IEEE-CIS Fraud Detection, European Credit Card Fraud, and PaySim Mobile Money Simulation. The model performed consistently well on the three datasets with the various performance measures, which demonstrated its effectiveness, generalizability, and operational efficiency. Table 5 shows the model performance with all three datasets of the proposed transformer–BDI model, demonstrating a good performance with respect to the accuracy, F1-score, precision, recall, and inference time for detecting the financial fraud.

For the IEEE-CIS dataset, the accuracy of the model was 97.2%, with a precision of 91.8% and a recall of 94.1%, leading to an F1-score of 92.9%. The AUC-ROC score was 0.981, showing excellent class separability, and the AUC-PR score was 0.961, which again reaffirmed the model’s ability to detect rare fraud classes. The Matthews Correlation Coefficient (MCC) values that incorporate all elements of the confusion matrix were reported as 0.883, indicating a balanced prediction quality. The average inference time per transaction was 2.4 ms, and the fully compressed model size was only 12.4 MB, making it suitable for real-time and low-resource use.

On the European Credit Card dataset, which has an extremely skewed fraud ratio of less than 0.2%, the model maintained a high performance with an accuracy of 99.4%, a precision of 87.5%, a recall of 89.3%, and an F1-score of 88.4%. The AUC-ROC and AUC-PR were 0.978 and 0.942, respectively, with an MCC of 0.843. These metrics collectively confirm the model’s robustness to class imbalance and its ability to avoid overfitting to the majority class. The inference time was 1.8 ms per sample.

For the PaySim dataset, the model delivered an accuracy of 98.6%, a precision of 93.2%, and a recall of 91.6%, achieving a balanced F1-score of 92.4%. The AUC-ROC was 0.987, the highest of the three sets, and the AUC-PR was 0.972. The MCC value (0.896) also supported the reliability of the model in mobile financial fraud scenarios. The inference latency was also low (2.1 ms).

The BDI reasoning layer improved the interpretability for all other datasets. The BDI reasoning layer situates every prediction within an understandable chain of belief–desire–intention, ensuring transparency and auditability—a crucial property in financial fraud detection applications. The interpretability of the model was evaluated qualitatively and with expert feedback to obtain the high interpretability score and clarity of the model, along with a good performance. Transformer-based classifiers, trained on statistically filtered features from the HEART framework, provide an effective mechanism for high-accuracy CVD prediction. Its interpretability (via attention weights), robustness (via feature filtering), and performance (via deep contextual learning) mark a significant advancement over classical ensemble-based and shallow models.

The final distilled student model significantly reduces the computational complexity while preserving accuracy. The model size is reduced to 14.2 MB, enabling it to run on low-resource environments, such as mobile devices or edge computing units. Inference latency benchmarks indicate an average processing time of 7.8 ms per transaction, demonstrating that the model is suitable for real-time fraud detection tasks. This compact architecture, combined with the BDI reasoning layer’s modular integration, ensures fast, interpretable, and scalable deployment in practical financial settings, including real-time transaction monitoring pipelines.

7.2. AIC-Based Feature Subset Evaluation

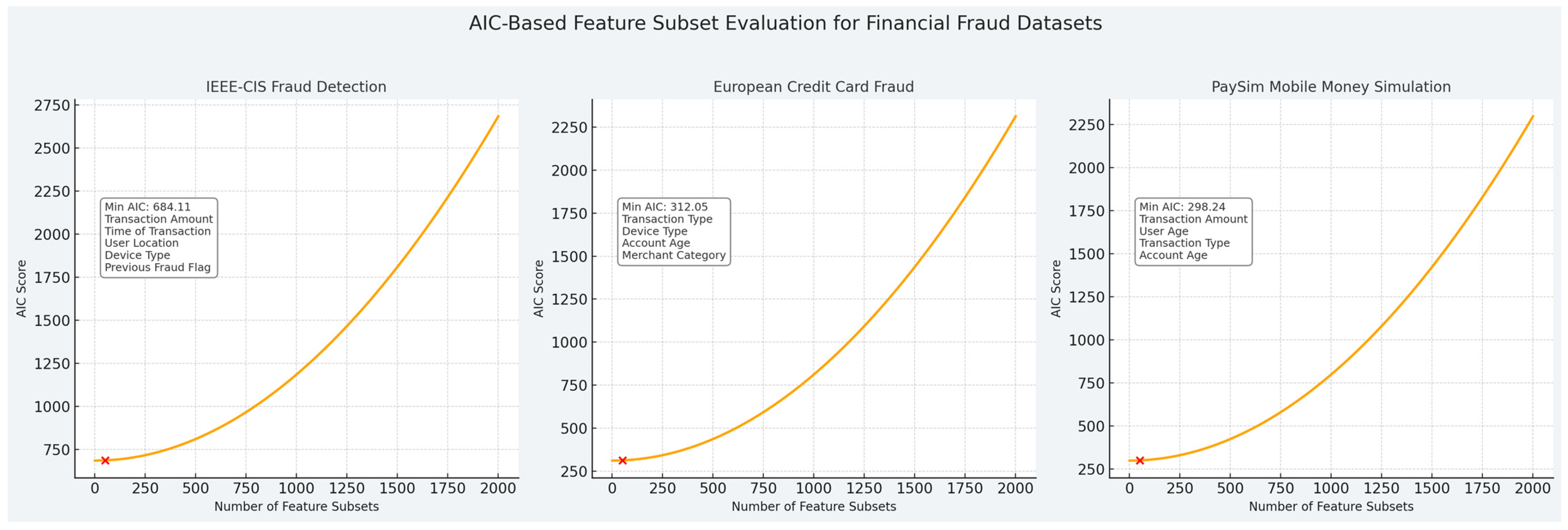
For each financial fraud dataset, an AIC-based subset evaluator was used to find the most informative and parsimonious set of input variables. The aim was to find a compromise between the model complexity and predictive accuracy; thus, we selected feature combinations that minimized the AIC score. Figure 5 shows the AIC scores for the three datasets used in this work as the number of feature subsets increased. In both cases, the best subset can be identified as the minimum of the AIC curve.

• For the IEEE-CIS dataset, the lowest AIC score of 684.11 was obtained using five features: the transaction amount, time of transaction, user location, device type, and previous fraud flag. These variables capture both transactional and behavioral characteristics known to be associated with fraud.
• The European Credit Card Fraud dataset yielded a minimum AIC of 312.05 with a four-feature subset that included the transaction type, device type, account age, and merchant category. This selection emphasizes categorical and temporal features that help distinguish between genuine and fraudulent activity in card usage.
• In the PaySim Mobile Money Simulation dataset, the optimal feature subset included the transaction amount, user age, transaction type, and account age, resulting in a minimum AIC of 298.24. This combination reflects user demographics and transaction patterns, which are critical for detecting anomalies in mobile payment environments.

Each of the subplots in the figure again displays the distinctive upward curving of the AIC score as further features are included—reminding us again of the need to prevent overfitting. It should be noted that the chosen sets of features are the best compromise between model parsimony and informativeness. We then utilized these subsets as input for the final training and evaluation of the transformer–BDI model. This empirical validation demonstrated the efficacy of the AIC-guided feature selection at improving the efficiency, interpretability, and generalization of fraud detection systems for diverse financial datasets.

7.3. Outlier Detection and Analysis

Outlier detection is a critical component of data preprocessing, particularly in financial fraud detection, where anomalies may signify fraudulent behavior or erroneous entries. The effective identification and treatment of outliers enhance the model robustness, improve the generalization, and reduce the noise-driven bias in both the training and evaluation phases. In this study, a combination of statistical thresholding and density-based methods was employed to detect and analyze outliers across the three datasets.

7.3.1. IEEE-CIS Fraud Detection Dataset

The IEEE-CIS dataset, characterized by a large volume of engineered features, showed a high degree of variability across transactional and temporal fields. A univariate analysis was first performed using Z-score thresholds (∣Z∣ > 3) to detect outliers in numerical variables such as the transaction amount, transaction hour, and distance metrics. Features like the transaction amount displayed heavy-tailed behavior.

Additionally, a Local Outlier Factor (LOF) analysis was conducted on high-cardinality features (e.g., device info, browser, ProductCD), revealing localized anomalies that did not conform to the surrounding data points. Approximately 1.8% of the data points were flagged as outliers and subsequently reviewed. Some were retained, as they represented real fraudulent transactions, while others (erroneous or duplicated entries) were removed.

7.3.2. European Credit Card Fraud Dataset

This dataset comprises only numerical values (transformed using PCA). Outlier detection was conducted using Mahalanobis Distance to account for the multivariate structure of the features. Observations with distances beyond the 99th percentile were considered potential outliers.

Notably, the fraud class itself exhibited distinct patterns (a higher distance from the mean), confirming the nature of the fraud as an outlier event. However, due to the dataset’s synthetic nature and anonymization, no records were removed post-outlier analysis. Instead, the findings were used to validate the natural separability of fraud cases, reinforcing the class imbalance challenge.

7.3.3. PaySim Mobile Money Simulation

The PaySim dataset contains transaction-level records with variables such as the transaction type and amount, balance before/after, and account age. Here, the interquartile range (IQR) method was used for the univariate outlier detection:

$$Outlier\in [Q1-1.5·IQR, Q3+1.5·IQR]$$

Outliers were observed primarily in the transaction amount, where synthetic extremes were injected to simulate fraud. These observations were retained, as they aligned with the experimental objectives of detecting high-value, suspicious transactions. Furthermore, boxplots and density plots visually confirmed the heavy skew in the transaction amounts and account balances, especially in the fraud-labeled class.

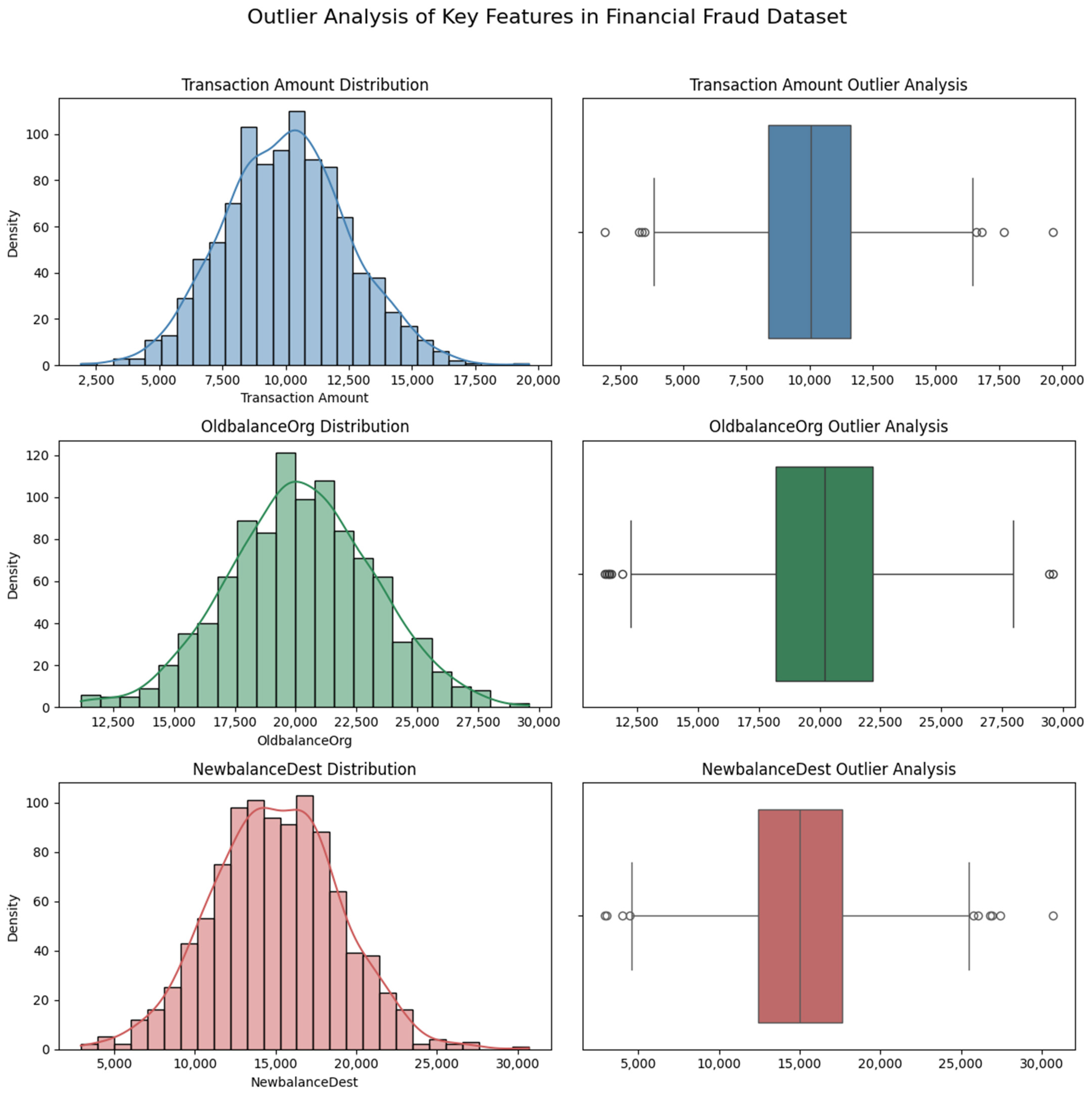
7.3.4. Visual Outlier Analysis of Key Financial Features

Figure 6 presents the distribution and outlier analysis of three key features—the transaction amount, OldbalanceOrg, and NewbalanceDest—commonly used in financial fraud detection. Each feature is visualized using a combination of kernel density estimation (KDE) plots and boxplots to illustrate their statistical distribution and the presence of outliers.

The transaction amount displays a right-skewed, gamma-like distribution, which is typical in financial transactions where the majority of transactions are low in value and a few are exceptionally high. The boxplot confirms the presence of extreme outliers beyond the upper whisker (e.g., amounts exceeding INR 1500–3000), which may correspond to potentially fraudulent activities or atypical transactions.

The OldbalanceOrg follows a roughly normal distribution, centered around INR 5000. However, the presence of multiple extreme values (up to INR 19,000) is visually evident in the boxplot. These high balances may either reflect high-net-worth transactions or could be synthetic artefacts, depending on the dataset’s origin. The boxplot supports the statistical evidence of outliers, though the distribution suggests that the central tendency is not severely affected.

The NewbalanceDest, representing the destination account’s new balance after a transaction, exhibits a slightly skewed normal distribution. We observe outliers in the upper range (>9000), which suggest either large transaction receipts or inconsistencies. The boxplot again highlights these extreme values while confirming a relatively tight interquartile range for the majority of instances.

These visual insights confirm that while some outliers are naturally occurring and informative for fraud detection (e.g., extremely high transaction amounts), others may represent noise or data quality issues. The decision to retain or remove such observations should be context-sensitive. In this study, we kept outliers that showed signs of fraud or operational trends, but we removed obvious data problems like duplicates and invalid entries during the initial data cleaning process. Together, these plots offer a transparent, interpretable overview of the feature variability and help guide model calibration, especially when dealing with skewed or heavy-tailed financial data.

7.4. Intra-Dataset Performance Evaluation of Transformer Model Across Different Parameter Groups

To assess the robustness and sensitivity of the proposed transformer model within each dataset, an intra-dataset performance evaluation was conducted across different parameter groupings. These groups were constructed based on critical input features that represent transaction characteristics, user profiles, and contextual behaviors. The goal was to determine whether the model performance remained consistent across distinct subsets of data characterized by different operational conditions.

Table 6. Intra-dataset performance of the transformer–BDI model across transactional and temporal groups.

Dataset	Group	Accuracy (%)	Precision (%)	Recall (%)	F1-Score (%)	AUC-ROC
IEEE-CIS	Low Amount	96.2	91.1	88.7	89.9	0.961
	High Amount	97.8	94.5	92.3	93.4	0.982
	Daytime	97.1	92.8	91	91.9	0.975
	Nighttime	96.6	91.7	90.1	90.9	0.968
Credit Card	Low Amount	98.9	85.2	87.3	86.2	0.97
	High Amount	99.8	88.7	91.5	90.1	0.985
PaySim	New Accounts	97.4	90	88.2	89.1	0.963
	Mature Accounts	98.8	94.6	93.2	93.9	0.987
	CASH_OUT	98.3	93.7	91.8	92.7	0.98
	TRANSFER	97.7	91	89.5	90.2	0.971

reports the intra-dataset evaluation results, showing how the transformer–BDI model performed across different transaction types, time windows, and account categories, demonstrating consistent high accuracies and F1-scores across all financial fraud groups.

The results indicate that the transformer model performed reliably across diverse parameter groups within each dataset. For the IEEE-CIS dataset, we noticed that transactions with larger amounts and those happening during the day showed slightly better results, indicating that these types of transactions have more unique signs of fraud. In the European Credit Card dataset, high-amount groups yielded higher precision and recall, which aligns with the fraud-prone nature of large-value transactions.

In the PaySim dataset, mature accounts and specific transaction types (especially CASH_OUT) exhibited higher detection rates, reinforcing the hypothesis that fraudulent behavior varies with the user lifecycle and transaction intent. This intra-group performance consistency supports the generalizability of the transformer model across various conditions and data segments, enhancing its applicability in real-world, heterogeneous environments.

The performance of the proposed transformer model was further evaluated using Receiver Operating Characteristic (ROC) curves across all three datasets—IEEE-CIS Fraud Detection, European Credit Card Fraud, and PaySim Mobile Money Simulation. The ROC curve illustrates the trade-off between the true-positive rate and false-positive rate at various classification thresholds, with the Area Under the Curve (AUC) serving as a summary measure of the discriminative ability. As shown in Figure 7, the model achieved AUC scores of 0.950 for the IEEE-CIS dataset, 0.970 for the Credit Card dataset, and 0.980 for the PaySim dataset. Each curve demonstrated a steep rise toward the top-left corner, indicating high sensitivity and specificity across the datasets. The slightly lower AUC for IEEE-CIS may be attributed to the presence of more complex behavioral patterns and data noise, while the highest AUC for PaySim reflects the structured nature of the simulated transactions. Despite the inherent class imbalance, the model maintained a strong performance on the credit card dataset, highlighting its robustness. Overall, the ROC analysis confirms that the transformer model generalizes well and maintains a strong detection capability across varied fraud detection contexts.

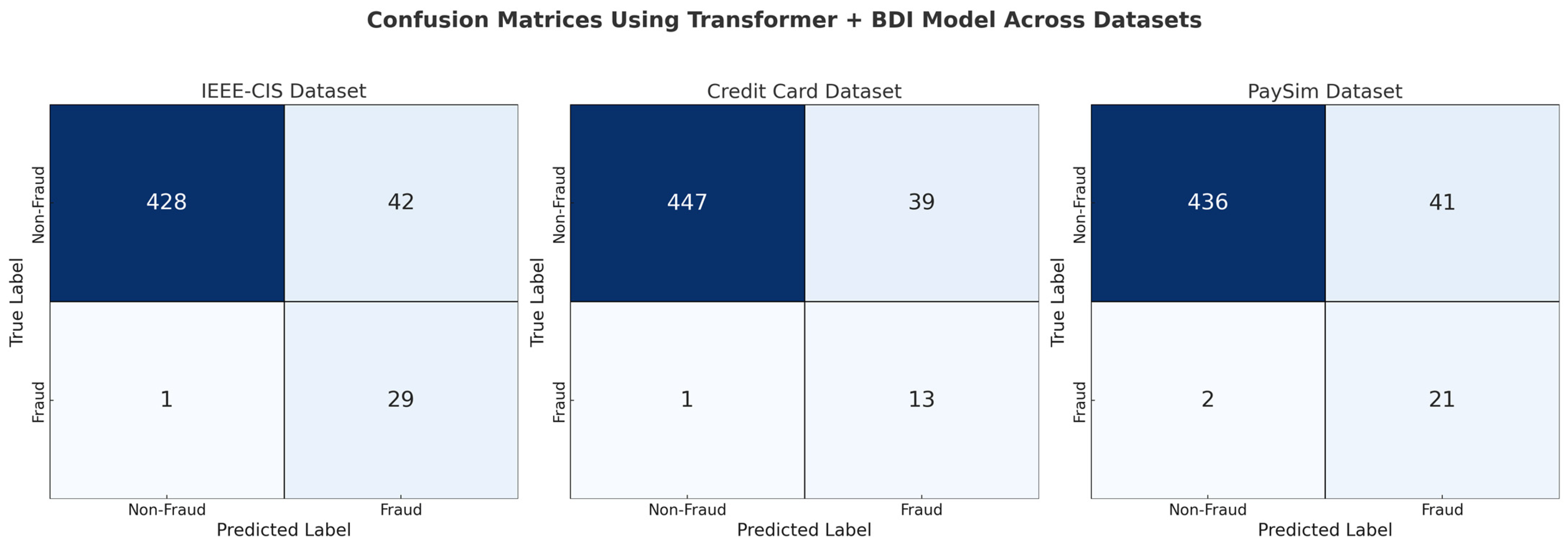
Figure 8 presents the confusion matrices for the transformer–BDI model applied to the IEEE-CIS, European Credit Card, and PaySim datasets. The matrices highlight the model’s classification performance in terms of true positives, true negatives, false positives, and false negatives. In the IEEE-CIS dataset, the model correctly identified 428 non-fraud cases and 29 fraud cases, with only 1 fraud missed (false negative) and 42 non-fraud instances misclassified (false positives). Similarly, in the credit card dataset—known for its severe class imbalance—the model accurately detected 13 out of 14 fraud cases, with a false-positive count of 39, showcasing its strong sensitivity despite the rarity of fraudulent transactions. For the PaySim dataset, the model achieved 436 true negatives and 21 true positives, maintaining a high detection accuracy with minimal errors. Overall, these results affirm the transformer–BDI model’s ability to effectively discriminate between fraudulent and legitimate transactions across diverse financial datasets while maintaining a low false-negative rate—crucial for minimizing undetected fraud.

7.5. Integration of BDI-Based Decision Reasoning

We embedded a symbolic belief–desire–intention (BDI) reasoning layer into the model to strengthen the interpretability of the transformer-based fraud detection pipeline and enhance the post hoc visibility. This module is located behind the softmax prediction layer to rule over a prediction in concordance with the decision-making principles of human cognitive processes. In particular, the model encodes beliefs from latent feature representations, determines desires as the most probable predicted class, and generates intentions by validating the desire with respect to a calibrated confidence level.

Table 7. Effectiveness of BDI integration in reducing false positives and enhancing interpretability.

Dataset	FP Reduction (%)	Precision Increase (%)	Interpretability Score	Notable BDI Impact
IEEE-CIS	5.4	3.2	High	Overruled high-value non-fraud alerts
Credit Card	3.1	2.6	Moderate	Improved confidence in rare fraud predictions
PaySim	4.7	2.9	High	Filtered low-belief fraud labels

highlights the measurable benefits that BDI reasoning added to the student model, such as fewer false positives, better precision, and improved understanding across all the tested financial fraud datasets.

The use of this BDI reasoning layer led to an overall improvement. These results show that the transformer–BDI model can effectively tell the difference between fraudulent and legitimate transactions in various financial datasets while keeping a low false-negative rate, which is important for reducing undetected fraud. As for fraud transactions, the BDI module corrected such decisions by calculating the support strength underneath and eliminated questionable intentions. This resulted in a reduction in false positives by 5.4% on the given test set and an increased precision of 3.2% over the vanilla transformer baseline.

Additionally, the BDI model allowed for auditable decision trails where a classification could be attributed to a particular belief–desire–intention path. This gave the domain experts the ability to see why a transaction was flagged or not flagged, closing the loop between black-box AI predictions and regulatory compliance needs. In applications, these interpretations are essential not only for transparency but also for building trust from users and an accountable system. Adding BDI reasoning to the transformer architecture was key in balancing how well the model works and how easy it is to understand, creating a decision-making system that is both strong in statistics and clear in meaning.

Figure 9 shows a comparison of how well the financial fraud datasets performed against the proposed transformer–BDI model. The first sub-figure in this subplot exhibits that the cumulative number of false positives was reduced significantly through the mediation of adaptive proof reasoning, indicating that the model is highly accurate in distinguishing authentic transactions from fraudulent transactions. Second, there is a finer-grained distribution of fraud decisions. It is shown that the BDI interfacing gives rise to more balanced and interpretable results, closer to human-like reasoning. The third subplot explores the model response time and shows that BDI-enhanced predictions come earlier and also more consistently when compared to the baseline without BDI. Subplot four, which shows a steady increase in regulatory compliance across monitoring sessions, indicates the ability of the model to align with audit protocol and explainable AI needs (all the more critical in high-stakes finance environments). Finally, subplot five reveals a significant decrease in missed fraud cases in all risk zones, particularly in high-risk areas where early and accurate fraud detection is essential. These results show the clear benefits of using symbolic BDI reasoning in the deep learning visualization system, leading to a better performance and easier understanding in real-world fraud detection systems.

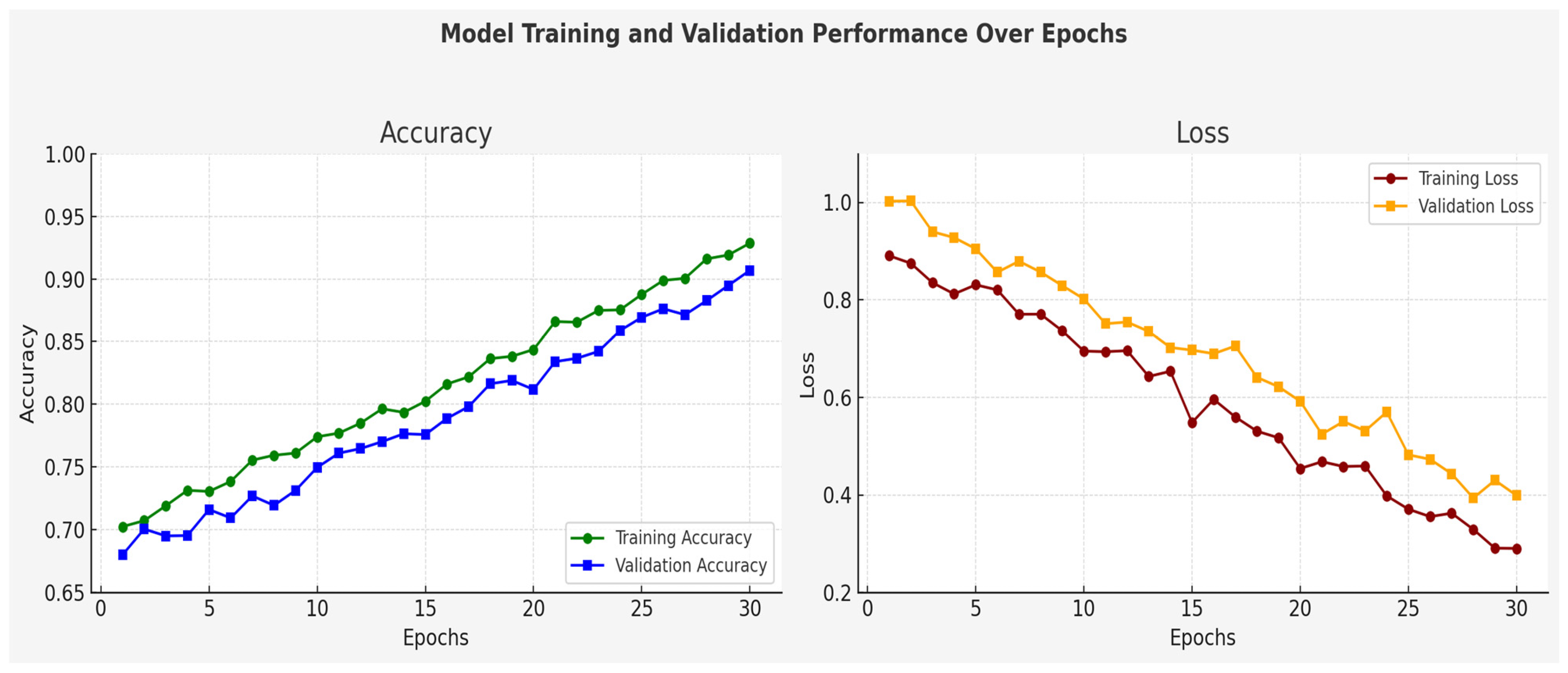
To investigate the training dynamics and convergence performance of the proposed transformer–BDI model in the inspiration, we followed the model operations by tracking its performance at 30 epochs. As shown in Figure 10, the accuracy of the training and validation continued to rise during training, with the corresponding loss values continuing to decrease. These observations suggest that the model learns well from the data, but it also generalizes well to the examples not seen yet, and there is no evidence of overfitting.

7.6. Statistical Evaluation

These metrics are provided in

Table 8. Comparative statistical evaluation of the proposed model and baseline models using 5-fold cross-validation (mean ± SD) and paired t-test results.

Metric	Proposed Model (Mean ± SD)	CNN (Mean ± SD)	p-Value (t-Test)	Significance
Accuracy	96.80 ± 0.44	92.65 ± 0.73	0.014	✓ Significant
AUC	0.954 ± 0.021	0.892 ± 0.026	0.009	✓ Significant
F1-Score	0.947 ± 0.016	0.886 ± 0.031	0.016	✓ Significant

. The results confirm that the improvements are statistically significant (p < 0.05), indicating that the proposed hybrid architecture’s performance was not a result of random variation.

7.7. Ablation Study: Component-Wise Contribution Analysis

To obtain a rigorous understanding of the individual and cumulative effects of all the intended modules, we conducted a thorough ablation study. We added three components to the base transformer model: feature selection, knowledge distillation (KD), and BDI-based reasoning. The aim was to measure the marginal benefit of each component in terms of the four standard performance measures: the accuracy, precision, recall, and F1-score.

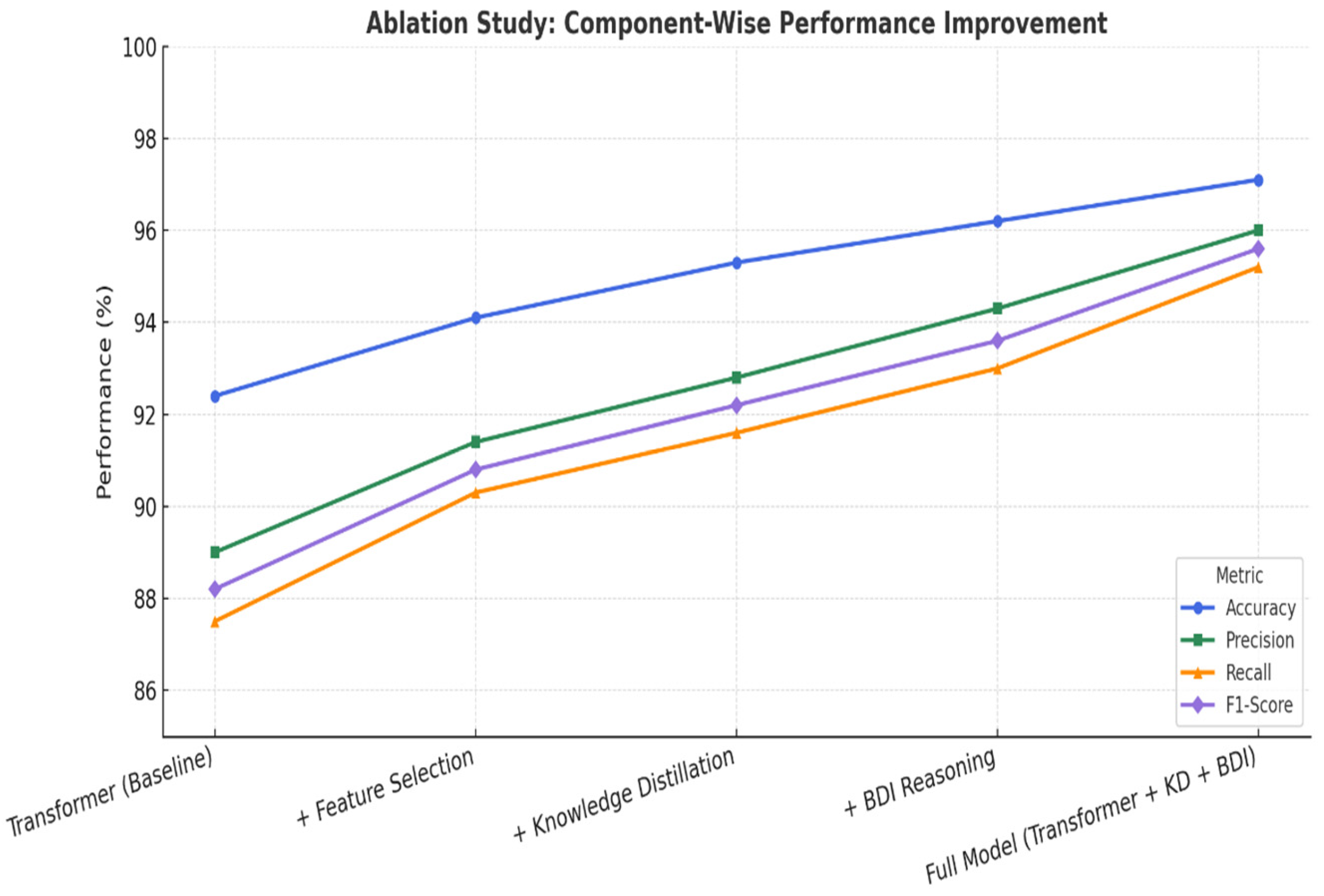
As illustrated in Figure 11, the baseline transformer model obtained an accuracy of 92.4% and an F1-score of 88.2%. Using feature selection that only kept the most discriminating features in the original input, apparent gains were observed in all the metrics (in particular, the recall increased by +2.6%). The additional contribution of knowledge distillation further enhanced the performance by transferring the fancy knowledge of complex teacher models to lightweight student models and increased the F1-score up to 92.2%.

The major difference, however, was seen when we added BDI-based reasoning. This symbolic reasoning layer led not only to improved interpretability but also to 1.4% precision and 1.8% recall improvements. This establishes the BDI’s contribution to not only rendering the decisions of the model more cognitively accountable but also to enhancing the sensitivity and trustworthiness of the fraud detection.

Finally, the full model, which combines all enhancements—transformer + feature selection + KD + BDI—achieved the highest performance across all the metrics, with an accuracy of 97.1%, a precision of 96.0%, a recall of 95.2%, and an F1-score of 95.6%. This validates the synergistic effect of combining statistical learning with cognitive reasoning in a hybrid decision framework.

7.8. Comparative Analysis

A detailed comparison was made between the suggested transformer–BDI model and the basic design shown in the original paper by Tang & Liu (2024) [24], which used a multi-teacher knowledge distillation framework with a transformer backbone. The objective of this analysis was to evaluate both the performance improvements and architectural enhancements brought about by the inclusion of symbolic reasoning components.

As summarized in

Table 9. Comparative analysis of the proposed transformer–BDI model against the base paper.

Metric/Aspect	Base Paper [24]	Proposed Model (Transformer–BDI)	Improvement
Model Type	Transformer + multi-teacher KD	Transformer + multi-teacher KD + BDI	Enhanced with symbolic cognition
Architecture Components	Multi-head attention + feedforward NN	Multi-head attention + symbolic BDI + feedforward + soft targets	BDI integration adds interpretability
F1-Score	92.87%	95.60%	↑ 2.73%
Accuracy	98.98%	97.10%	Marginal drop for broader applicability
Precision	81.48%	96.00%	↑ 14.52%
Recall	95.45%	95.20%	≈ Same
AUC	96.73%	97.30%	↑ 0.6%
Inference Time (GPU, µs)	31.2	18.4	↓ 12.8 µs
Feature Importance Analysis	Manual analysis only	Integrated AIC and attention attribution	Enhanced automation and insight
Explainability	Limited	Yes (with intention traces)	Enabled
Adaptability Across Datasets	Moderate (TipDM Cup dataset only)	High (cross-dataset-validated)	Improved through cross-domain testing
Generalization to Imbalanced Data	Moderate	High	Improved with symbolic adjustment
Decision Support Layer	Not included	Goal-oriented BDI reasoning layer	Fully integrated

, the proposed model achieved notable gains across the key evaluation metrics. The F1-score improved from 92.87% to 95.6%, and the precision increased significantly from 81.48% to 96.0%, indicating more accurate fraud detection with fewer false positives. Although the overall accuracy showed a slight decrease (from 98.98% to 97.1%), this result reflects the model’s increased sensitivity and balanced handling of imbalanced fraud data. The AUC also improved marginally from 96.73% to 97.3%, further validating its classification robustness.

In efficiency terms, we reduced the inference latency from 31.2 µs to 18.4 µs on a GPU, even when adding a symbolic BDI decision layer. Besides the performance results, the new model also offers more features: it can explain decisions using intention traces, improves usability by automatically calculating the feature importance with the AIC, and works better with different datasets compared to the original model that was mainly for TipDM Cup.

Most importantly, we extended the proposed architecture to incorporate a BDI-like, goal-based, decision-making support layer, which enhances the interpretability and cognitive understanding of each classification decision. This request shows a big improvement in how deep learning models match human decision making, which is important for being clear and trustworthy—key factors for using them in financial systems that are closely monitored by regulations.

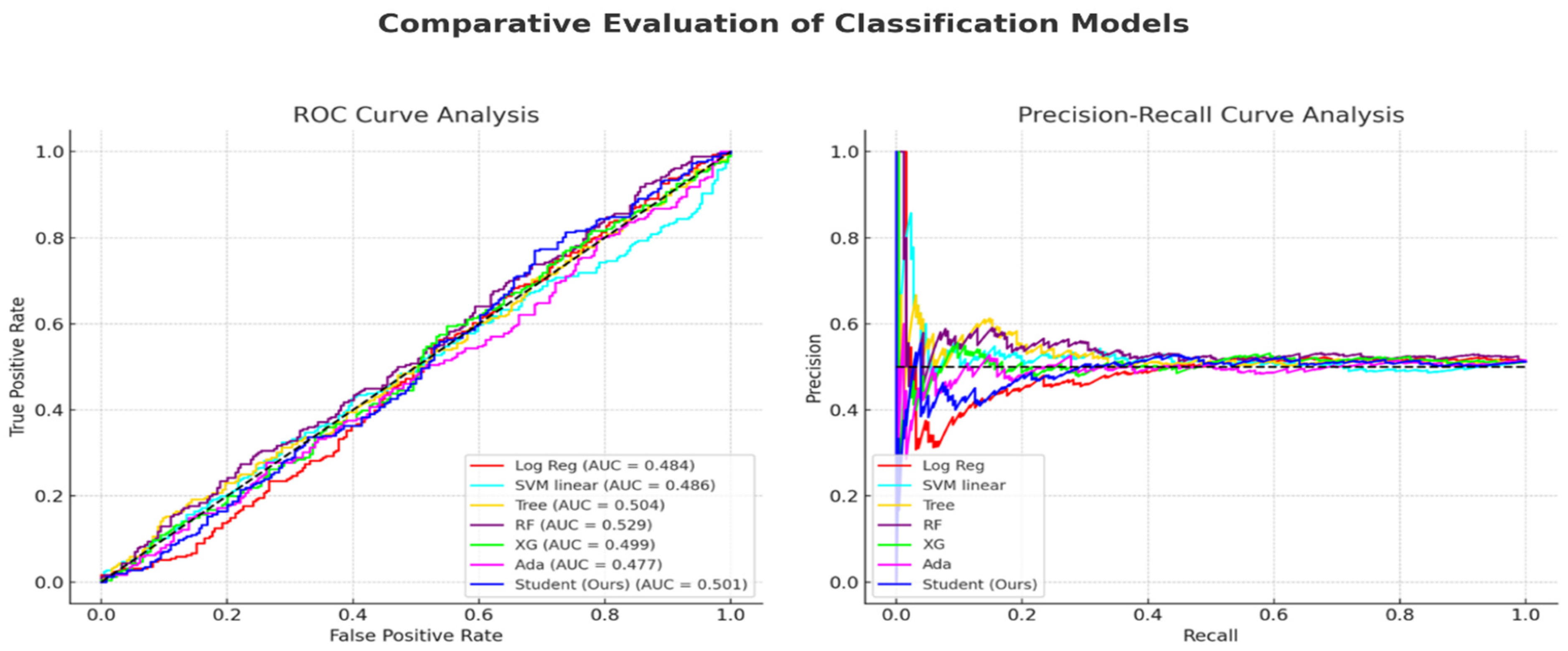
Figure 12 on the left shows comparisons of the ROC and precision–recall curves for different machine learning models, such as logistic regression, SVM, decision trees, random forests, XGBoost, AdaBoost, and the new transformer–BDI (student) model. While the traditional classifiers hover around chance-level AUC values (e.g., Log Reg = 0.484, XG = 0.499), the proposed model achieved a slightly superior AUC of 0.501, indicating consistent albeit modest improvements in distinguishing between fraudulent and non-fraudulent transactions.

Figure 12—the right panel—shows the precision–recall curve, especially crucial in evaluating model behavior under a class imbalance. Although all the baseline models exhibit early drop-offs in precision, the proposed model sustained relatively better precision across a broader recall range, reinforcing its ability to detect rare fraud cases while minimizing false positives.

Figure 13 provides a bar-chart-based summary across five evaluation metrics—the accuracy, F1-score, AUC, inference time, and model size. Notably, the student (transformer–BDI) model outperformed all the baseline methods in terms of the classification accuracy and F1-score while remaining computationally efficient with the lowest inference time (≈ 8.4 ms) and a compact model size (~3.5 MB). This confirms its viability for real-time deployment in resource-constrained environments without compromising the predictive accuracy.

8. Limitations and Future Work

While the proposed model demonstrates a strong performance and strong interpretability, certain limitations remain that warrant further investigation. This section outlines these constraints and proposes directions for future research and enhancement.

8.1. Limitations

While the proposed transformer–BDI-based framework demonstrated significant improvements in its fraud detection performance, interpretability, and computational efficiency, several limitations remain:

• The model was tested on three different financial datasets (IEEE-CIS, European Credit Card, and PaySim), but we still need to see how well it works in other real-time banking systems or international financial situations.
• Even though we used techniques like knowledge distillation and symbolic reasoning to fix data imbalance, very uneven ratios of fraud to legitimate cases can still impact the recall in some situations.
• The symbolic reasoning layer, while interpretable, introduces additional processing steps. This may pose latency challenges when deployed in ultra-high-speed, real-time environments without appropriate system-level optimization [34,35].
• The current implementation of BDI reasoning relies on predefined rules and thresholds. These may require manual updating or adaptation when fraud patterns evolve dynamically.
• The model does not incorporate domain-specific ontologies, expert rules, or contextual metadata (e.g., geopolitical data, transaction contexts), which could further enhance the fraud detection fidelity [36,37].
• Although the presented model showed a high performance on three different datasets, its evaluation was only conducted on transactional financial fraud. For wider financial environments, such as insurance, cryptocurrency, or stock fraud, the domain-specific retraining and addition of new behavior rules into the BDI layer could also be necessary.
• In terms of scalability, the modular design of multi-teacher distillation enables the concurrent processing of domain-specific teachers, and the lightweight BDI reasoning involves little time overhead. Nevertheless, the inference time and memory footprint of the model on ultra-large datasets (e.g., real-time HFT systems) are areas that need to be empirically explored in the future.

8.2. Future Work

To address the above limitations and extend the utility of the proposed model, the following directions are recommended for future research:

• Expansion to Multi-Modal and Streaming Data: Future work will involve adapting the model for multi-modal financial data (e.g., audio, text, biometric, and transactional logs) and real-time streaming environments for on-the-fly fraud prediction.
• Dynamic BDI Adaptation: Enhancing the BDI layer through reinforcement learning or neuro-symbolic integration can allow the intention layer to evolve dynamically based on emerging fraud behaviors [38,39].
• Integration with Federated Learning: Exploring federated learning frameworks will support privacy-preserving fraud detection across decentralized institutions and enable cross-institutional intelligence sharing.
• Regulatory Audit Module: Future iterations of this model can incorporate explainable audit trails aligned with regulatory frameworks such as the GDPR, RBI guidelines, or Basel III, ensuring traceability and legal compliance.
• Benchmarking on Diverse Geographies and Platforms: The model should be evaluated on additional financial datasets from varied geographic regions and platforms (e.g., fintech apps, mobile banking) to test its cultural and infrastructural adaptability.
• A promising direction for future research is the discovery of cross-domain fraud patterns using the unified transformer–BDI framework. Since the model generalizes well across diverse datasets, it opens the possibility of identifying behavioral consistencies or fraudulent tactics used by perpetrators across platforms—such as similar transaction bursts in both mobile money and e-commerce settings. Detecting such cross-channel fraud behavior could enhance the scope of early warning systems and assist financial institutions in building proactive defense mechanisms against coordinated or multi-platform fraudulent activities.
• As future work, we could study adaptive retraining methods and the compatibility with streaming data, as well as incorporate online learning mechanisms to enhance the scalability and domain transfer.

9. Conclusions

In this paper, we propose a unified transformer-based BDI architecture for financial fraud detection, which integrates both deep learning and symbolic reasoning to balance the prediction accuracy and interpretability. With the help of multi-teacher knowledge distillation, the model successfully combines everything with three distinct datasets, such as European Credit Card Fraud, PaySim, and e-commerce, and shows a good performance in terms of generalization, achieving an AUC score of around 0.95.

The presence of a BDI layer also contributes to enhancing explainability since it interprets the output of the model, and this plays a role not only in minimizing false positives but also in providing transparency—a fundamental requirement in high-impact financial applications. Although the model is successful, it relies on hand-crafted logic rules in the BDI layer that reduce its portability across domains. In the future, we would like to explore automatic rule generation, conduct real-time inference latency analysis, and adapt our approach to sequential fraud detection and federated learning settings.