A Set of New Tools to Measure the Effective Value of Probabilistic Forecasts of Continuous Variables
Abstract
:1. Introduction
2. The Value of Probabilistic Forecasts of Binary Events
2.1. The Cost–Loss Situation
2.2. Benchmarking with Climatology
3. The Value of Probabilistic Forecasts of Continuous Variables: Theory and Hypothesis
3.1. The Underlying Decision-Making Process and the Importance of Cost Modeling
3.2. The Link with the Quantile Score
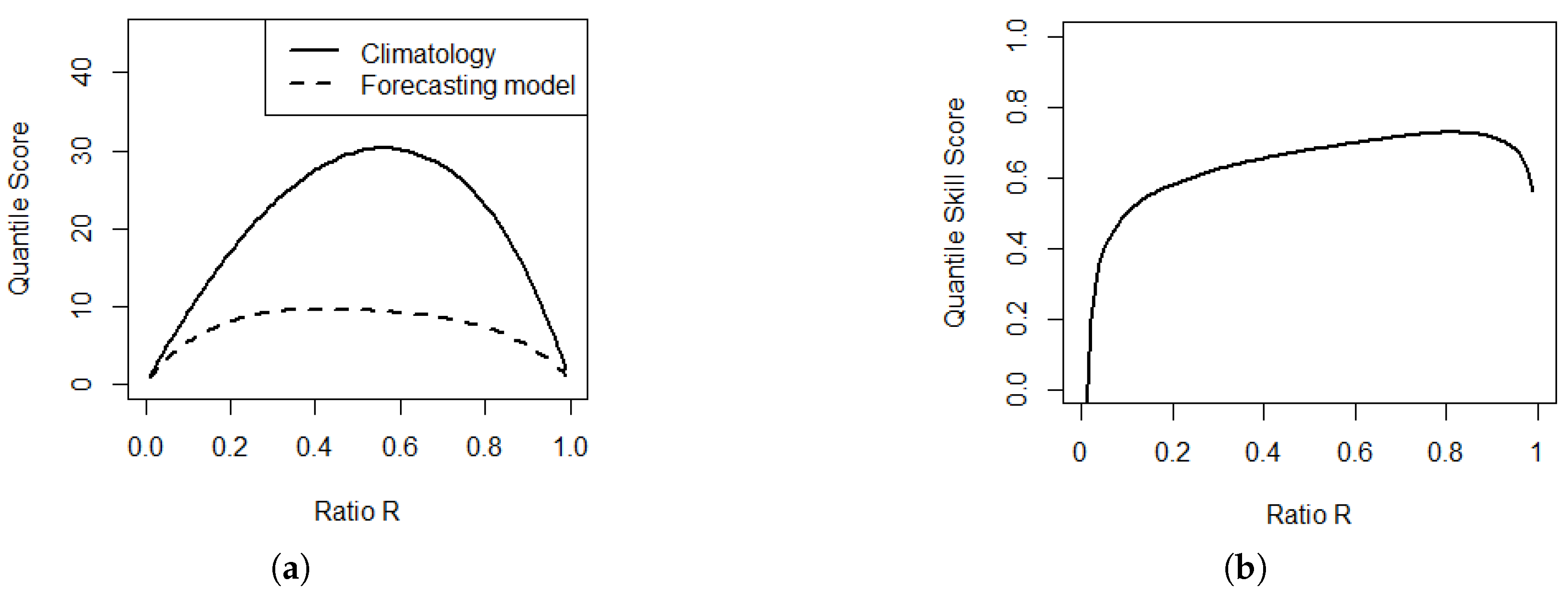
4. A New Diagnostic Tool to Assess the Value of Forecasts of Continuous Variables in Real Cases: The EVC
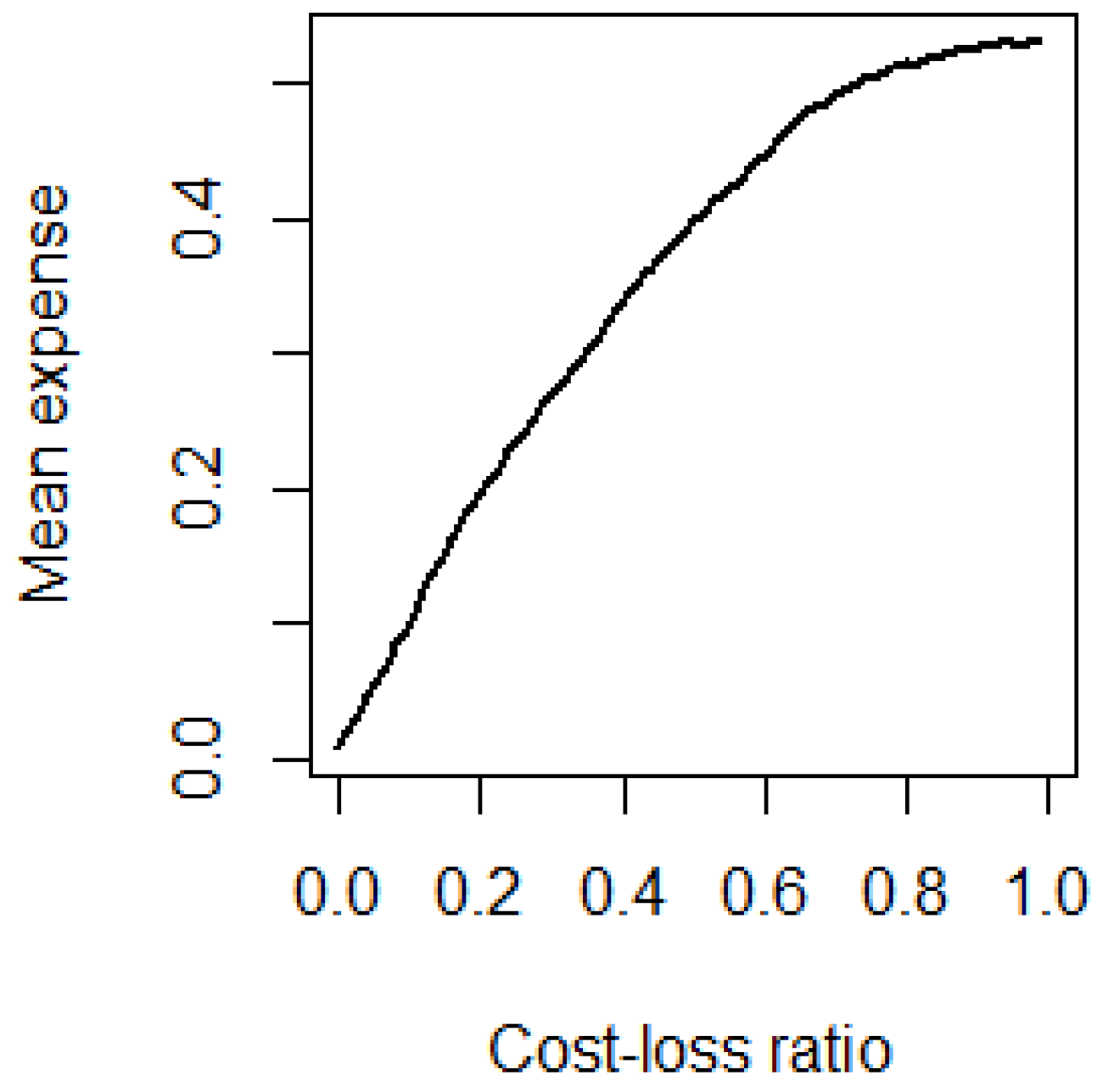
4.1. The Potential Economic Value of Forecasts of Continuous Variables
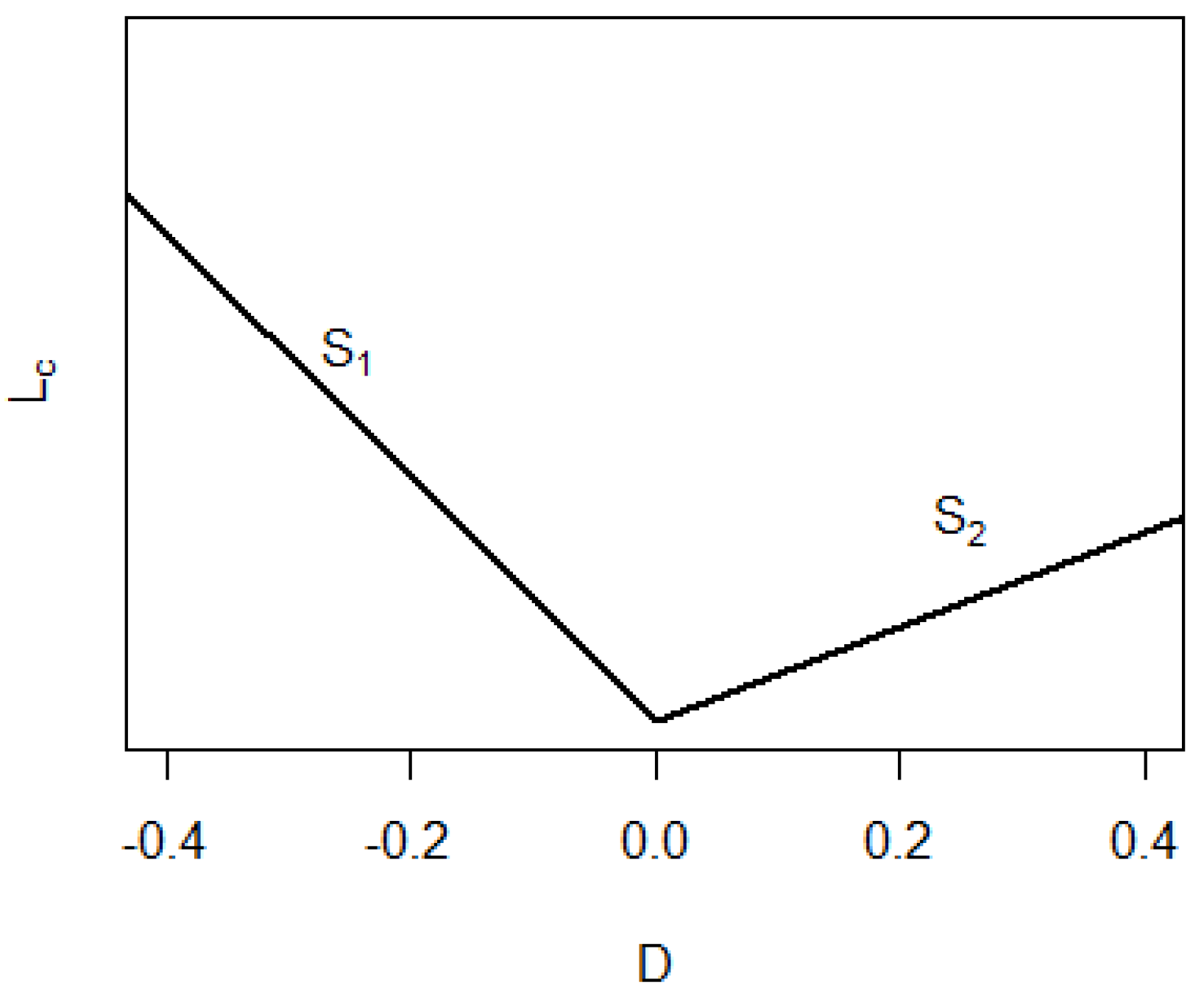
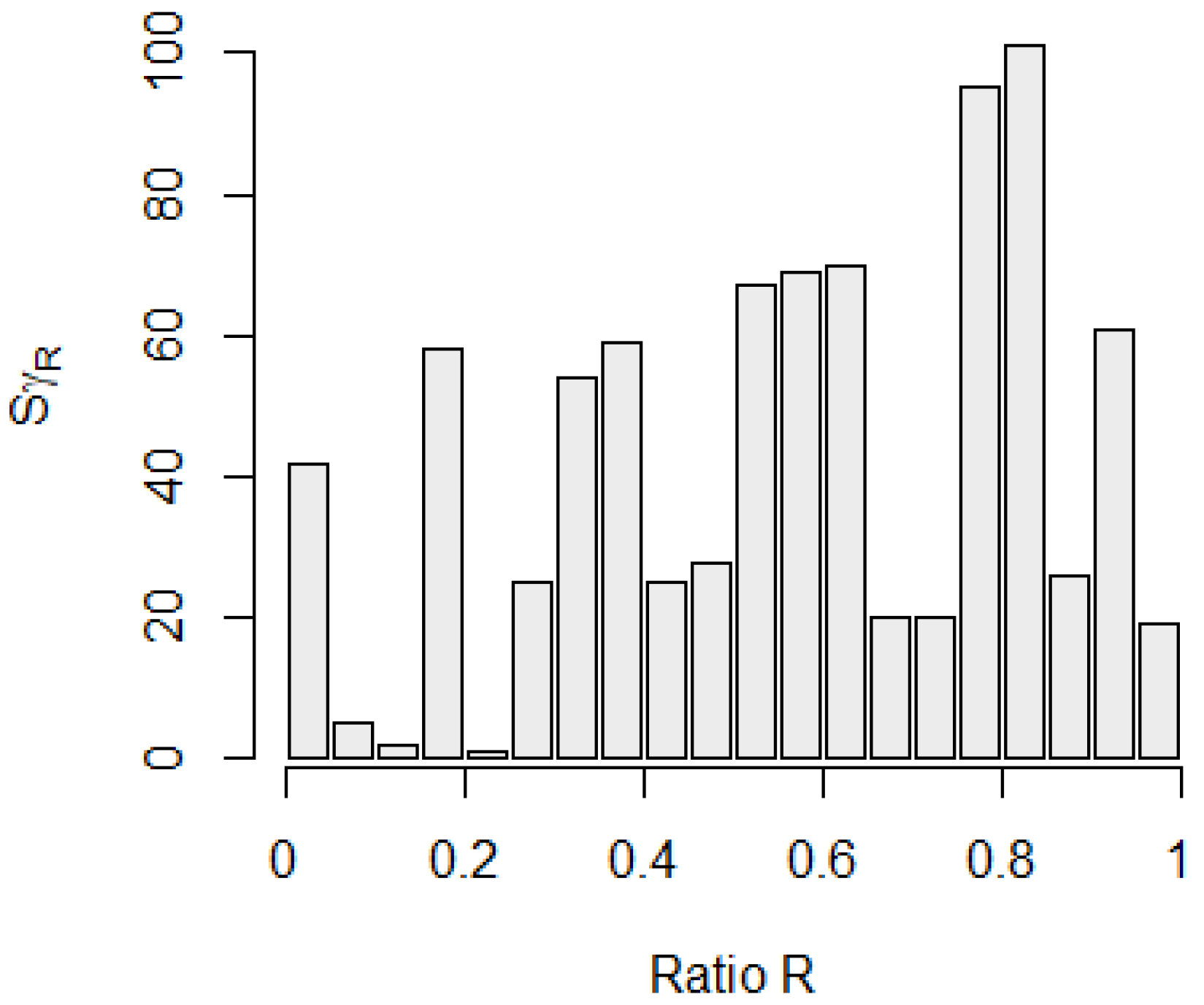
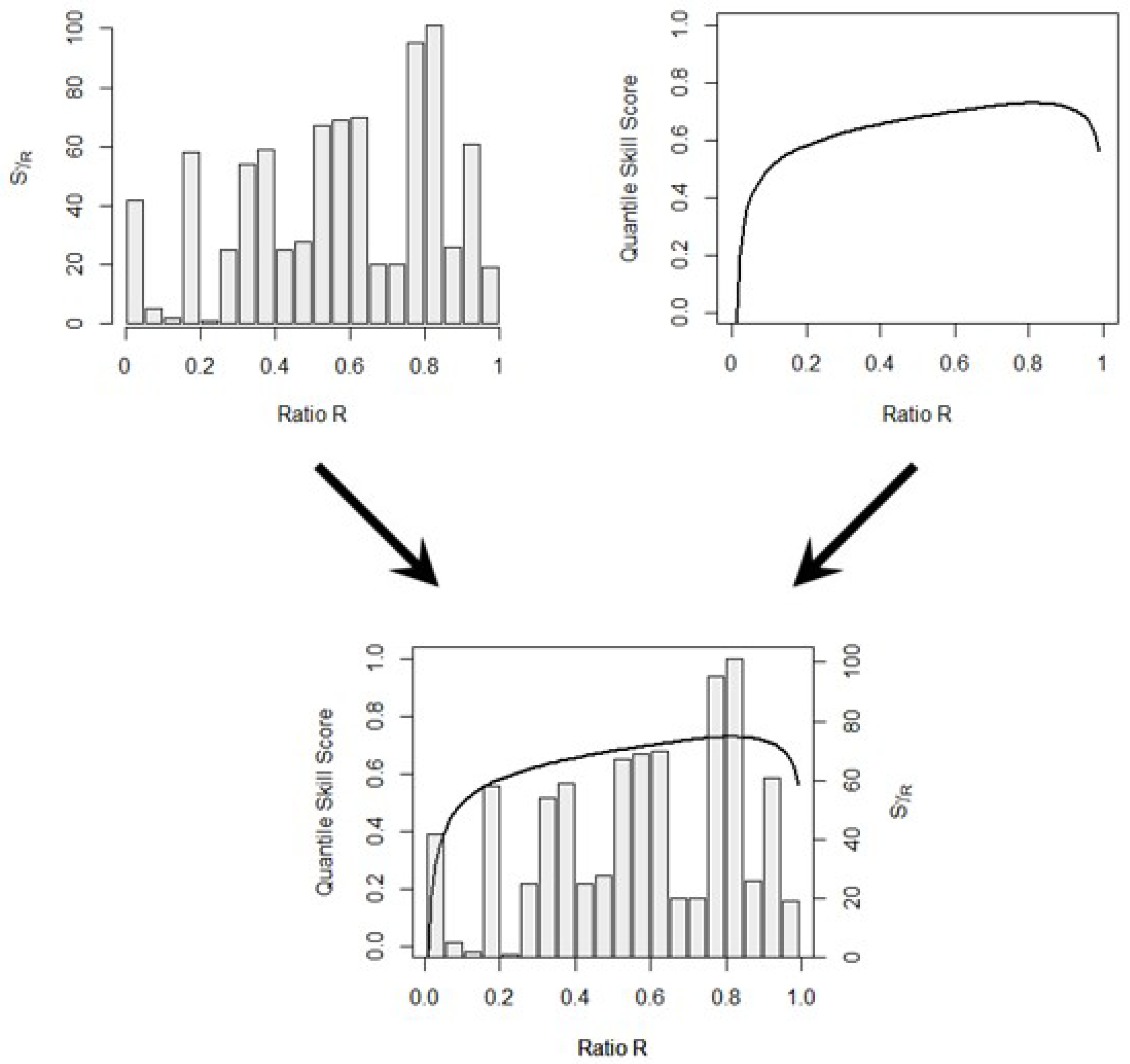
4.2. The Risk Distribution Diagram
4.3. The Effective Economic Value of Forecasts of Continuous Variables in Practical Cases
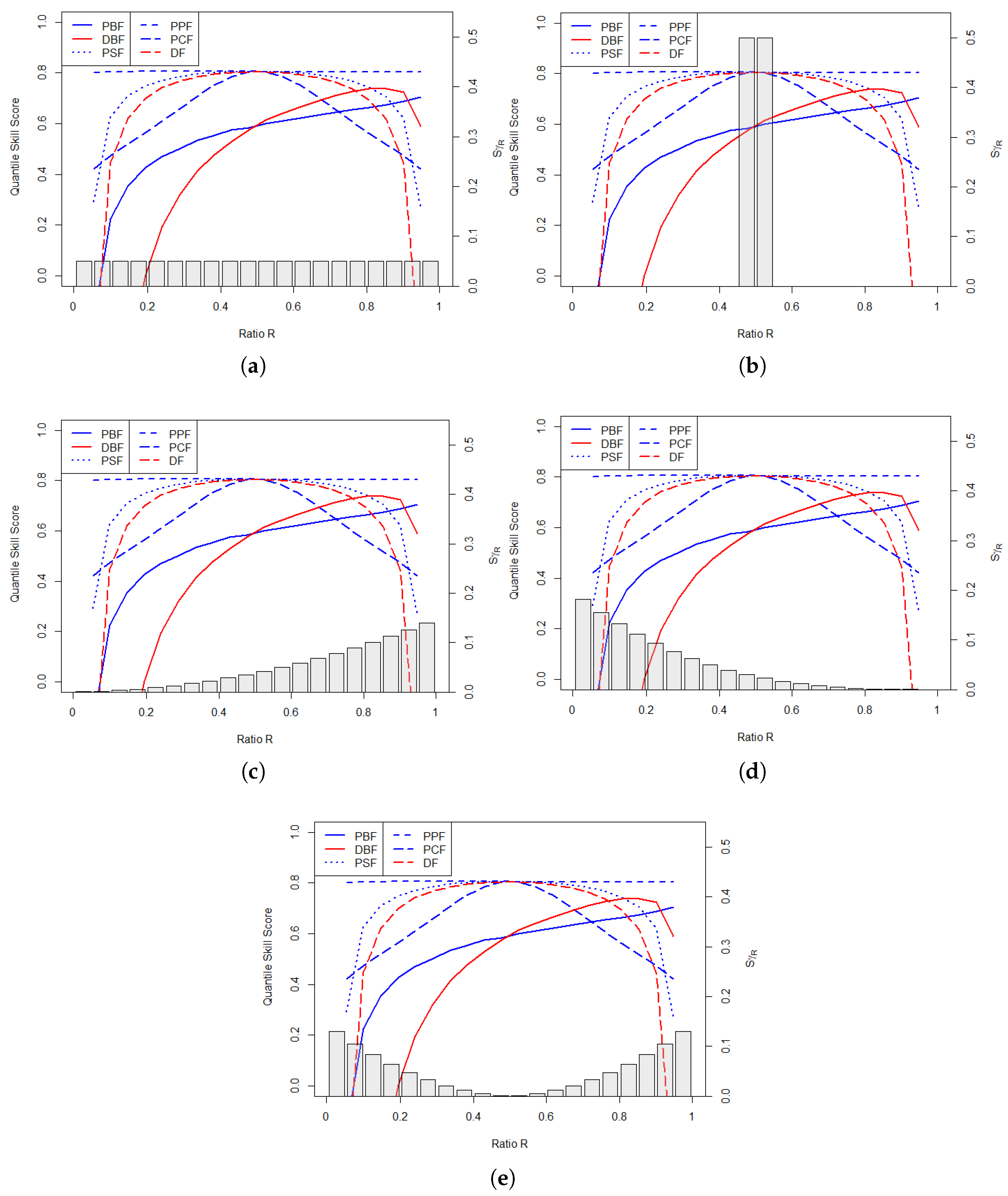
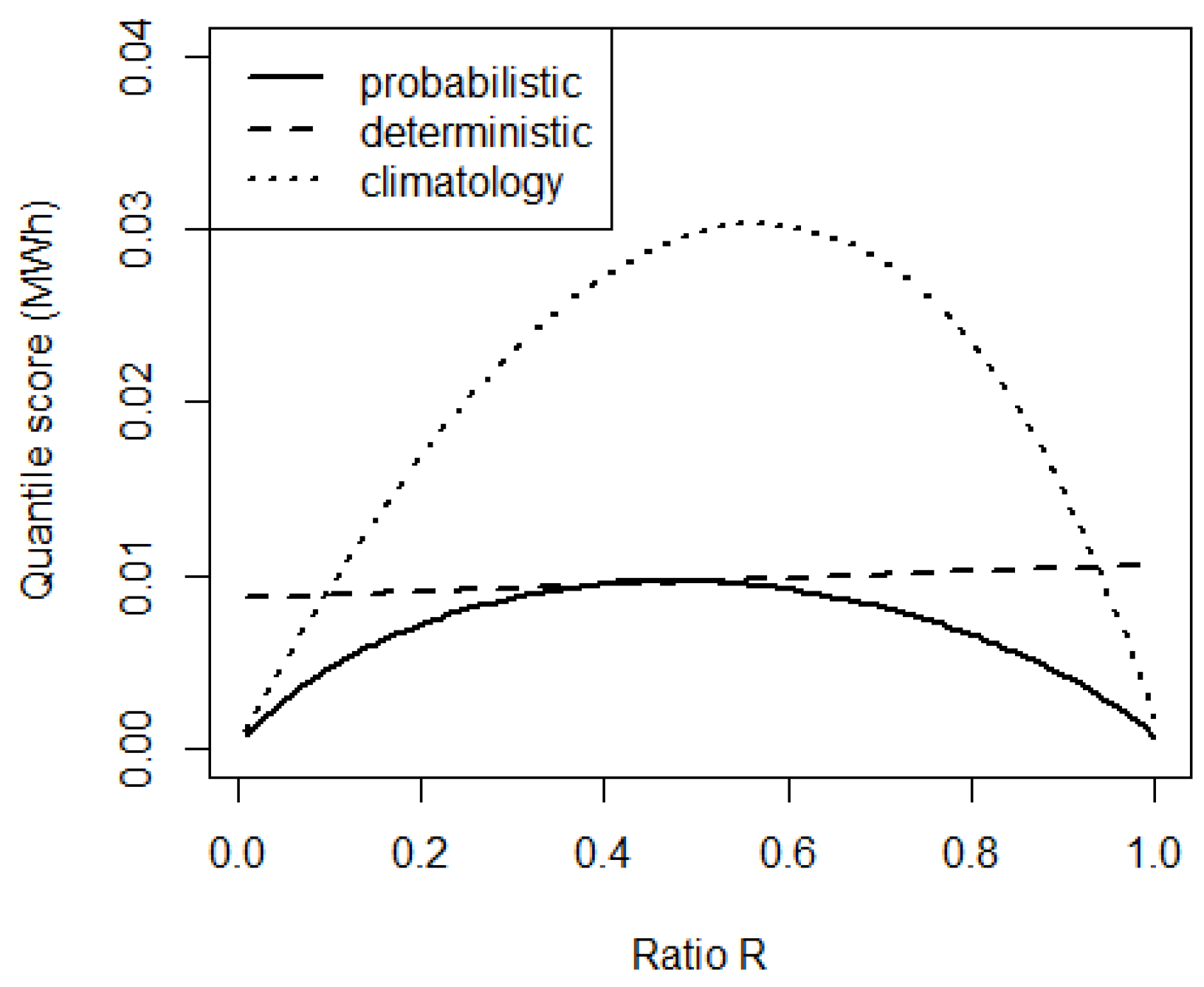
5. The Value of Probabilistic and Deterministic Approaches
- A climatological model following the global distribution is implemented;
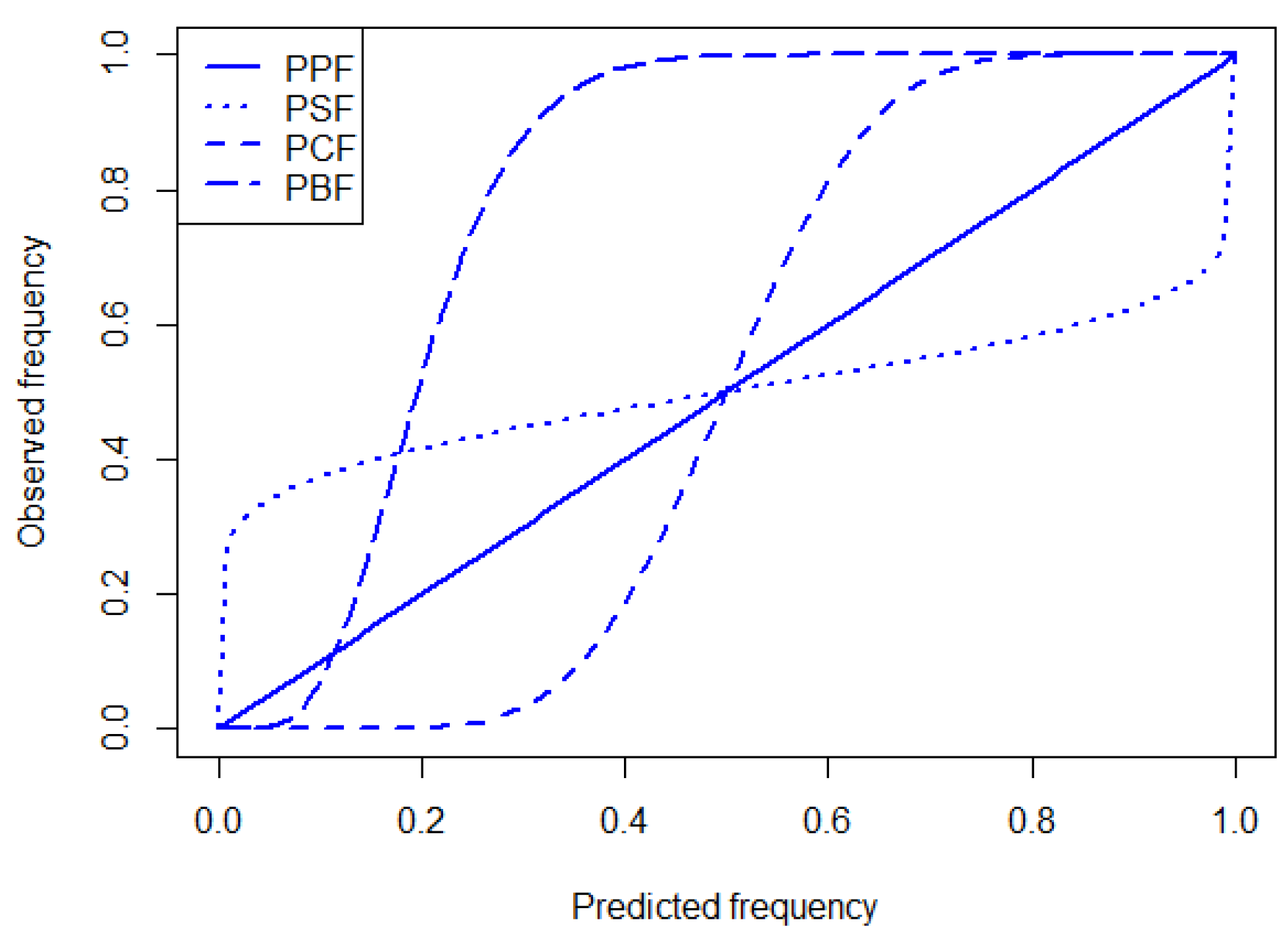
- A statistically consistent probabilistic forecast named “PPF” predicts ;
- A probabilistic sharp forecast named “PSF” predicts ;
- A probabilistic coarse forecast named “PCF” predicts ;
- A probabilistic unreliable (and biased) forecast named “PBF” predicts , where is uniform distribution;
- A deterministic unbiased forecast named “DF” predicts X;
- A deterministic biased forecast named “DBF” predicts .
- The “Flat” distribution has uniform risks;
- The “Centered” distribution has only almost-symmetric ratios (close to 0.5);
- The “Right-Quad” distribution exhibits a prominence of high ratios;
- The “Left-Quad” distribution exhibits a prominence of small ratios;
- The “Ext-Quad” distribution avoids centered ratios.
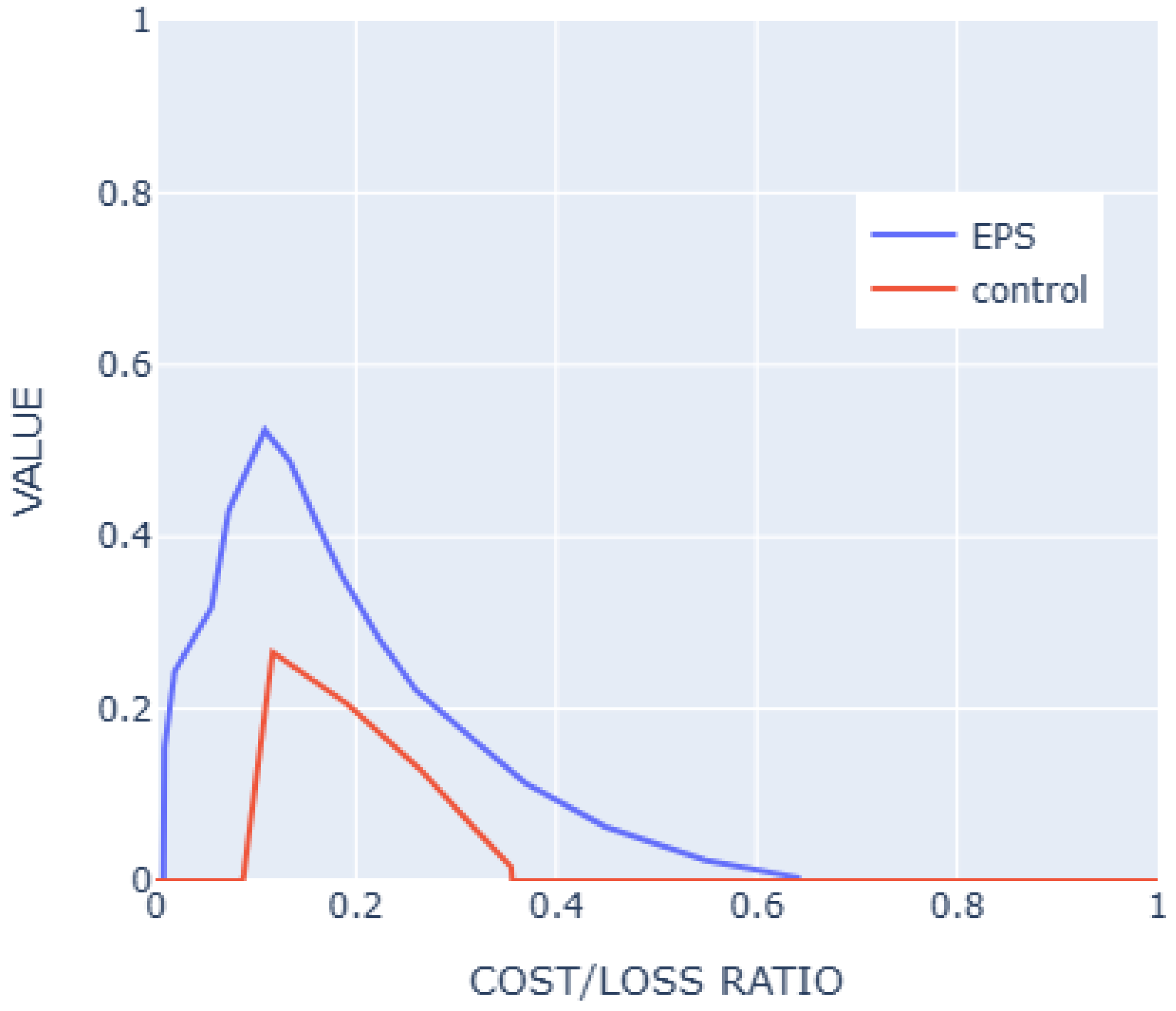
6. Application to the Energy Market
6.1. Presentation of the Case Study
6.2. Using the EVC Methodology
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Quality of the Six Simulated Forecasts
| PPF | PSF | PCF | PBF | DF | DBF | |
|---|---|---|---|---|---|---|
| Bias | 0 | 0 | 0 | +60 | 0 | +60 |
| Sharpness | 27 | 7 | 94 | 27 | - | - |
References
- Clemen, R.T. Making Hard Decisions. Technometrics 2002, 44, 199–200. [Google Scholar] [CrossRef]
- Thompson, J.C. On the Operational Deficiences in Categorical Weather Forecasts. Bull. Am. Meteorol. Soc. 1952, 33, 223–226. [Google Scholar] [CrossRef]
- Sims, C. A Nine-Variable Probabilistic Macroeconomic Forecasting Model. In Business Cycles, Indicators, and Forecasting; National Bureau of Economic Research, Inc.: Cambridge, MA, USA, 1993; pp. 179–212. [Google Scholar]
- Garratt, A.; Lee, K.; Pesaran, M.H.; Shin, Y. Forecast Uncertainties in Macroeconomic Modeling: An Application to the U.K. Economy. J. Am. Stat. Assoc. 2003, 98, 829–838. [Google Scholar] [CrossRef]
- Chen, Z.; Iqbal, A.; Lai, H. Forecasting the probability of US recessions: A Probit and dynamic factor modelling approach. Can. J. Econ./Rev. Can. D’Econ. 2011, 44, 651–672. [Google Scholar] [CrossRef]
- Forrest, D.; Simmons, R. Forecasting sport: The behaviour and performance of football tipsters. Int. J. Forecast. 2000, 16, 317–331. [Google Scholar] [CrossRef]
- Bartos, J.A. The Assessment of Probability Distributions for Future Security Prices. Ph.D. Thesis, Indiana University, Bloomington, IN, USA, 1969. [Google Scholar]
- Önkal, D.; Muradoglu, G. Effects of task format on probabilistic forecasting of stock prices. Int. J. Forecast. 1996, 12, 9–24. [Google Scholar] [CrossRef]
- Adolfson, M.; Andersson, M.; Lindé, J.; Villani, M.; Vredin, A. Modern Forecasting Models in Action: Improving Macroeconomic Analyses at Central Banks. SSRN Electron. J. 2007, 829–838. [Google Scholar] [CrossRef]
- Garratt, A.; Koop, G.; Mise, E.; Vahey, S.P. Real-Time Prediction With U.K. Monetary Aggregates in the Presence of Model Uncertainty. J. Bus. Econ. Stat. 2009, 27, 480–491. [Google Scholar] [CrossRef]
- Schueller, G.I.; Gumbel, E.; Panggabean, H. Probabilistic determination of design wind velocity in Germany. Proc. Inst. Civ. Eng. 1976, 61, 673–683. [Google Scholar] [CrossRef]
- Gel, Y.; Raftery, A.E.; Gneiting, T.; Tebaldi, C.; Nychka, D.; Briggs, W.; Roulston, M.S.; Berrocal, V.J. Calibrated Probabilistic Mesoscale Weather Field Forecasting: The Geostatistical Output Perturbation Method [with Comments, Rejoinder]. J. Am. Stat. Assoc. 2004, 99, 575–590. [Google Scholar] [CrossRef]
- Gneiting, T.; Larson, K.; Westrick, K.; Genton, M.; Aldrich, E. Calibrated Probabilistic Forecasting at the Stateline Wind Energy Center: The Regime-Switching SpaceTime Method. J. Am. Stat. Assoc. 2006, 101, 968–979. [Google Scholar] [CrossRef]
- Murphy, A.H.; Winkler, R.L. Probability Forecasting in Meterology. J. Am. Stat. Assoc. 1984, 79, 489–500. [Google Scholar] [CrossRef]
- Sloughter, J.M.; Gneiting, T.; Raftery, A. Probabilistic Wind Speed Forecasting Using Ensembles and Bayesian Model Averaging. J. Am. Stat. Assoc. 2010, 105, 25–35. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Strictly Proper Scoring Rules, Prediction, and Estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Roulston, M.S.; Smith, L.A. Evaluating Probabilistic Forecasts Using Information Theory. Mon. Weather Rev. 2002, 130, 1653–1660. [Google Scholar] [CrossRef]
- Murphy, A.H. What Is a Good Forecast? An Essay on the Nature of Goodness in Weather Forecasting. Weather Forecast. 1993, 8, 281–293. [Google Scholar] [CrossRef]
- Zhu, Y.; Toth, Z.; Wobus, R.; Richardson, D.; Mylne, K. The economic value of ensemble-based weather forecasts. Bull. Am. Meteorol. Soc. 2002, 83, 73–83. [Google Scholar] [CrossRef]
- Wilks, D.S.; Hamill, T.M. Potential Economic Value of Ensemble-Based Surface Weather Forecasts. Mon. Weather Rev. 1995, 123, 3565–3575. [Google Scholar] [CrossRef]
- Gneiting, T.; Katzfuss, M. Probabilistic Forecasting. Annu. Rev. Stat. Its Appl. 2014, 1, 125–151. [Google Scholar] [CrossRef]
- Thompson, J.C.; Brier, G.W. The economic utility of weather forecasts. Mon. Weather Rev. 1955, 83, 249–253. [Google Scholar] [CrossRef]
- Murphy, A.H. A Note on the Utility of Probabilistic Predictions and the Probability Score in the Cost-Loss Ratio Decision Situation. J. Appl. Meteorol. Climatol. 1966, 5, 534–537. [Google Scholar] [CrossRef]
- Murphy, A.H. The Value of Climatological, Categorical and Probabilistic Forecasts in the Cost-Loss Ratio Situation. Mon. Weather Rev. 1977, 105, 803–816. [Google Scholar] [CrossRef]
- Murphy, A.H. Hedging and the Mode of Expression of Weather Forecasts. Bull. Am. Meteorol. Soc. 1978, 59, 371–373. [Google Scholar] [CrossRef]
- Thornes, J.; Stephenson, D. How to judge the quality and value of weather forecast products. Meteorol. Appl. 2001, 8, 307–314. [Google Scholar] [CrossRef]
- Wilks, D.S. A skill score based on economic value for probability forecasts. Meteorol. Appl. 2001, 8, 209–219. [Google Scholar] [CrossRef]
- Buizza, R. The value of probabilistic prediction. Atmos. Sci. Lett. 2008, 9, 36–42. [Google Scholar] [CrossRef]
- Richardson, D.S. Skill and relative economic value of the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 2000, 126, 649–667. [Google Scholar] [CrossRef]
- Mylne, K.R. Decision-making from probability forecasts based on forecast value. Meteorol. Appl. 2002, 9, 307–315. [Google Scholar] [CrossRef]
- Smith, L.; S., R.M.; von Hardenbergm, J. End to End Ensemble Forecasting: Towards Evaluating the Economic Value of the Ensemble Prediction System; Technical Memorandum; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2001. [Google Scholar]
- Roulston, M.S.; Kaplan, D.T.; von Hardenberg, J.; Smith, L.A. Using medium-range weather forcasts to improve the value of wind energy production. Renew. Energy 2003, 28, 585–602. [Google Scholar] [CrossRef]
- Pinson, P.; Chevallier, C.; Kariniotakis, G. Optimizing Benefits from wind power participation in electricity market using advanced tools for wind power forecasting and uncertainty assessment. In Proceedings of the EWEC 2004, London, UK, 22–25 November 2004. [Google Scholar]
- Murphy, A.H.; Katz, R.W.; Winkler, R.L.; Hsu, W. Repetitive decision making and the value of forecasts in the cost-loss ratio situation: A dynamic model. Mon. Weather Rev. 1985, 113, 801–813. [Google Scholar] [CrossRef]
- Buizza, R. Accuracy and Potential Economic Value of Categorical and Probabilistic Forecasts of Discrete Events. Mon. Weather Rev. 2001, 129, 2329–2345. [Google Scholar] [CrossRef]
- Doubleday, K.; Van Scyoc Hernandez, V.; Hodge, B. Benchmark probabilistic solar forecasts: Characteristics and recommendations. Sol. Energy 2020, 206, 52–67. [Google Scholar] [CrossRef]
- Le Gal La Salle, J.; David, M.; Lauret, P. A new climatology reference model to benchmark probabilistic solar forecasts. Sol. Energy 2021, 223, 398–414. [Google Scholar] [CrossRef]
- Wilks, D. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Ramahatana, F.; David, M. Economic optimization of micro-grid operations by dynamic programming with real energy forecast. J. Phys. Conf. Ser. 2019, 1343, 012067. [Google Scholar] [CrossRef]
- Holttinen, H. Optimal electricity market for wind power. Energy Policy 2005, 33, 2052–2063. [Google Scholar] [CrossRef]
- Linnet, U. Tools Supporting Wind Energy Trade in Deregulated Markets. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2005. [Google Scholar]
- Pinson, P.; Chevallier, C.; Kariniotakis, G. Trading Wind Generation from Short-Term Probabilistic Forecasts of Wind Power. IEEE Trans. Power Syst. 2007, 22, 1148–1156. [Google Scholar] [CrossRef]
- Lauret, P.; David, M.; Pinson, P. Verification of solar irradiance probabilistic forecasts. Sol. Energy 2019, 194, 254–271. [Google Scholar] [CrossRef]
- Benedetti, R. Scoring Rules for Forecast Verification. Mon. Weather Rev. 2010, 138, 203–211. [Google Scholar] [CrossRef]
- Selten, R. Axiomatic Characterization of the Quadratic Scoring Rule. Exp. Econ. 1998, 1, 43–61. [Google Scholar] [CrossRef]
- Bentzien, S.; Friederichs, P. Decomposition and graphical portrayal of the quantile score: Quantile Score Decomposition and Portrayal. Q. J. R. Meteorol. Soc. 2014, 140, 1924–1934. [Google Scholar] [CrossRef]
- Ben Bouallègue, Z.; Pinson, P.; Friederichs, P. Quantile forecast discrimination ability and value. Q. J. R. Meteorol. Soc. 2015, 141, 3415–3424. [Google Scholar] [CrossRef]
- Gneiting, T.; Ranjan, R. Comparing Density Forecasts Using Threshold- and Quantile-Weighted Scoring Rules. J. Bus. Econ. Stat. 2011, 29, 411–422. [Google Scholar] [CrossRef]
- Lipiecki, A.; Uniejewski, B.; Weron, R. Postprocessing of Point Predictions for Probabilistic Forecasting of Day-Ahead Electricity Prices: The Benefits of Using Isotonic Distributional Regression. Energy Econ. 2024, 139, 107934. [Google Scholar] [CrossRef]
- Luque, A.; Hegedus, S. Handbook of Photovoltaic Science and Engineering; Wiley: Chichester, UK, 2011. [Google Scholar]
- Alessandrini, S.; Sperati, S.; Pinson, P. A comparison between the ECMWF and COSMO Ensemble Prediction Systems applied to short-term wind power forecasting on real data. Appl. Energy 2013, 107, 271–280. [Google Scholar] [CrossRef]
- ENTSO-E. Transparency Platform. Available online: https://transparency.entsoe.eu (accessed on 1 April 2025).
- Sivle, A.D.; Agersten, S.; Schmid, F.; Simon, A. Use and perception of weather forecast information across Europe. Meteorol. Appl. 2022, 29, e2053. [Google Scholar] [CrossRef]
- van der Bles, A.M.; van der Linden, S.; Freeman, A.; Mitchell, J.; Galvao, A.; Zaval, L.; Spiegelhalter, D. Communicating uncertainty about facts, numbers and science. R. Soc. Open Sci. 2019, 6, 181870. [Google Scholar] [CrossRef] [PubMed]
- Spiegelhalter, D. Risk and uncertainty communication. Annu. Rev. Stat. Its Appl. 2017, 4, 31–60. [Google Scholar] [CrossRef]
- Bröcker, J.; Smith, L.A. Increasing the Reliability of Reliability Diagrams. Weather Forecast. 2007, 22, 651–661. [Google Scholar] [CrossRef]


| Outcome | |||
|---|---|---|---|
| Yes | No | ||
| Protection | Yes | Hit | False alarm |
| C | C | ||
| No | Miss | Correct rejection | |
| L | 0 | ||
| Risk Distribution | |||||
|---|---|---|---|---|---|
| Flat | Centered | Right-Quad | Left-Quad | Ext-Quad | |
| PPF | 80.4% | 80.5% | 80.4% | 80.5% | 80.4% |
| PSF | 71.1% | 80.5% | 68.2% | 68.7% | 60.2% |
| PCF | 62.9% | 80.3% | 60.3% | 60.4% | 52.4% |
| PBF | 53.6% | 59.2% | 64.5% | 39.9% | 47.8% |
| DF | 64.5% | 80.5% | 59.9% | 60.3% | 46.6% |
| DBF | 46.7% | 59.4% | 65.4% | 23.9% | 38.2% |
| Case | ||||
|---|---|---|---|---|
| France | Portugal | Switzerland | ||
| Forecast | Deterministic | 4.7% | 67.4% | 55.0% |
| Probabilistic | 68.9% | 69.7% | 67.0% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Gal La Salle, J.; David, M.; Lauret, P. A Set of New Tools to Measure the Effective Value of Probabilistic Forecasts of Continuous Variables. Forecasting 2025, 7, 30. https://doi.org/10.3390/forecast7020030
Le Gal La Salle J, David M, Lauret P. A Set of New Tools to Measure the Effective Value of Probabilistic Forecasts of Continuous Variables. Forecasting. 2025; 7(2):30. https://doi.org/10.3390/forecast7020030
Chicago/Turabian StyleLe Gal La Salle, Josselin, Mathieu David, and Philippe Lauret. 2025. "A Set of New Tools to Measure the Effective Value of Probabilistic Forecasts of Continuous Variables" Forecasting 7, no. 2: 30. https://doi.org/10.3390/forecast7020030
APA StyleLe Gal La Salle, J., David, M., & Lauret, P. (2025). A Set of New Tools to Measure the Effective Value of Probabilistic Forecasts of Continuous Variables. Forecasting, 7(2), 30. https://doi.org/10.3390/forecast7020030








