Testing for Bias in Forecasts for Independent Multinomial Outcomes
Abstract
1. Introduction and Motivation
2. The Main Idea
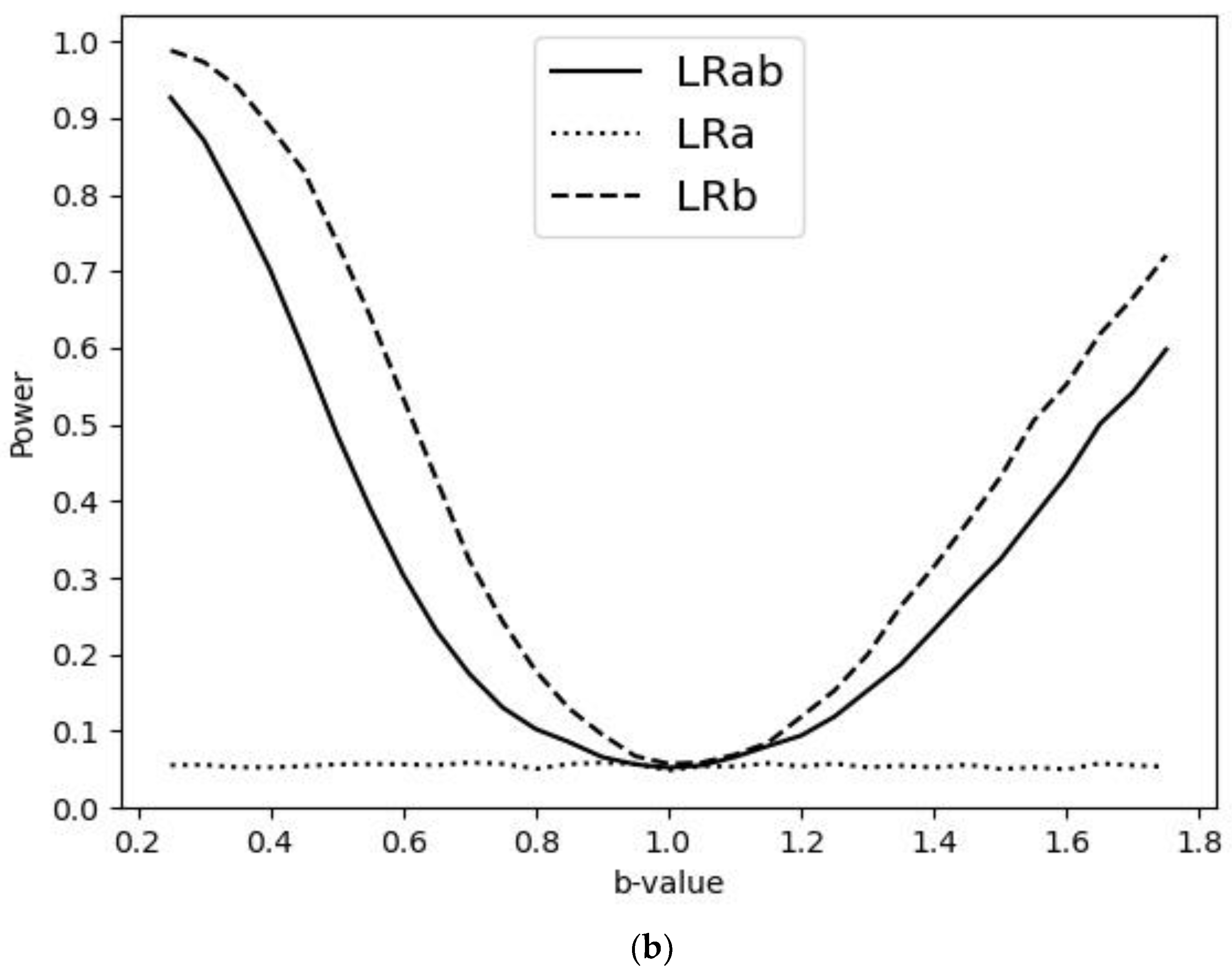
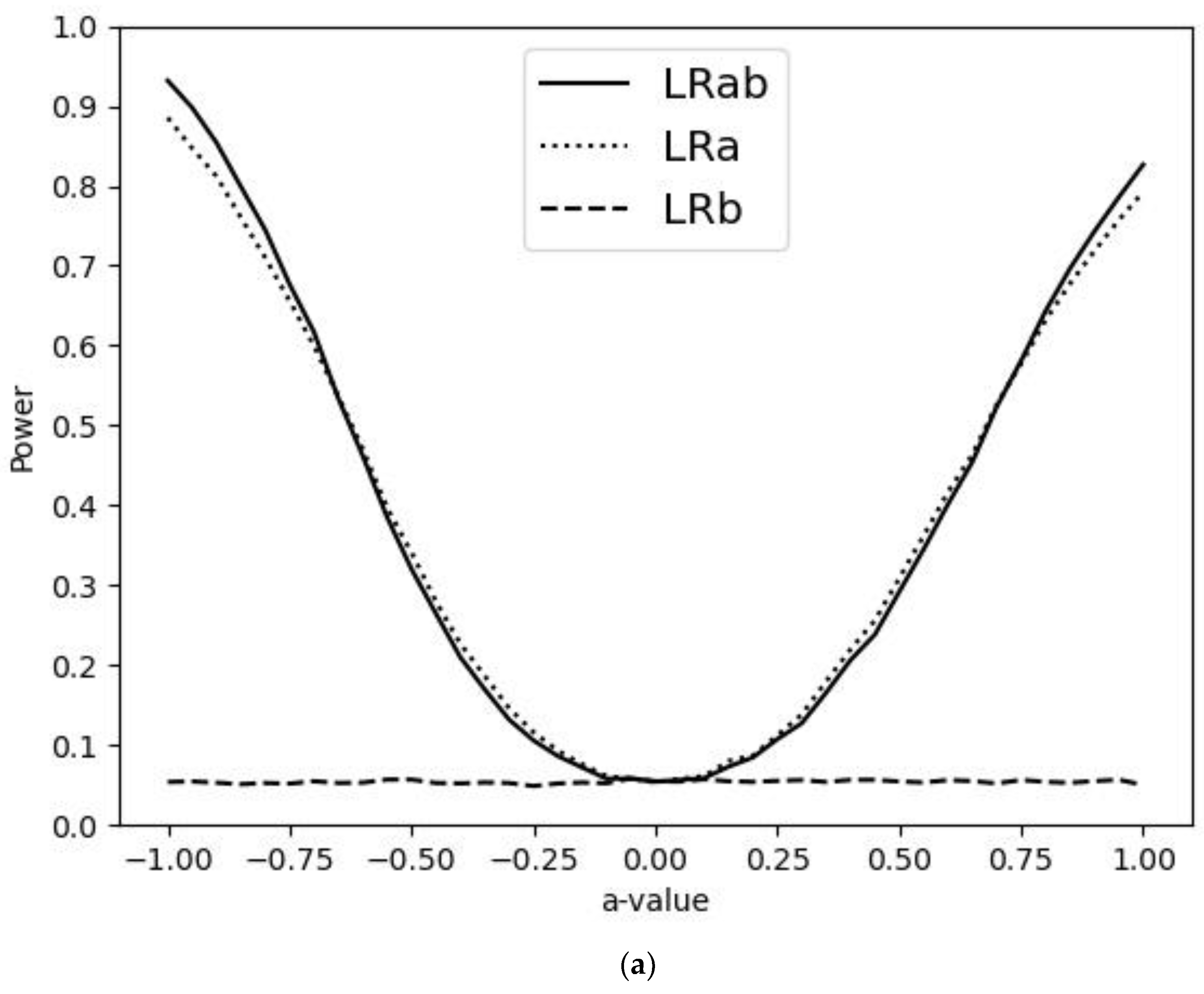
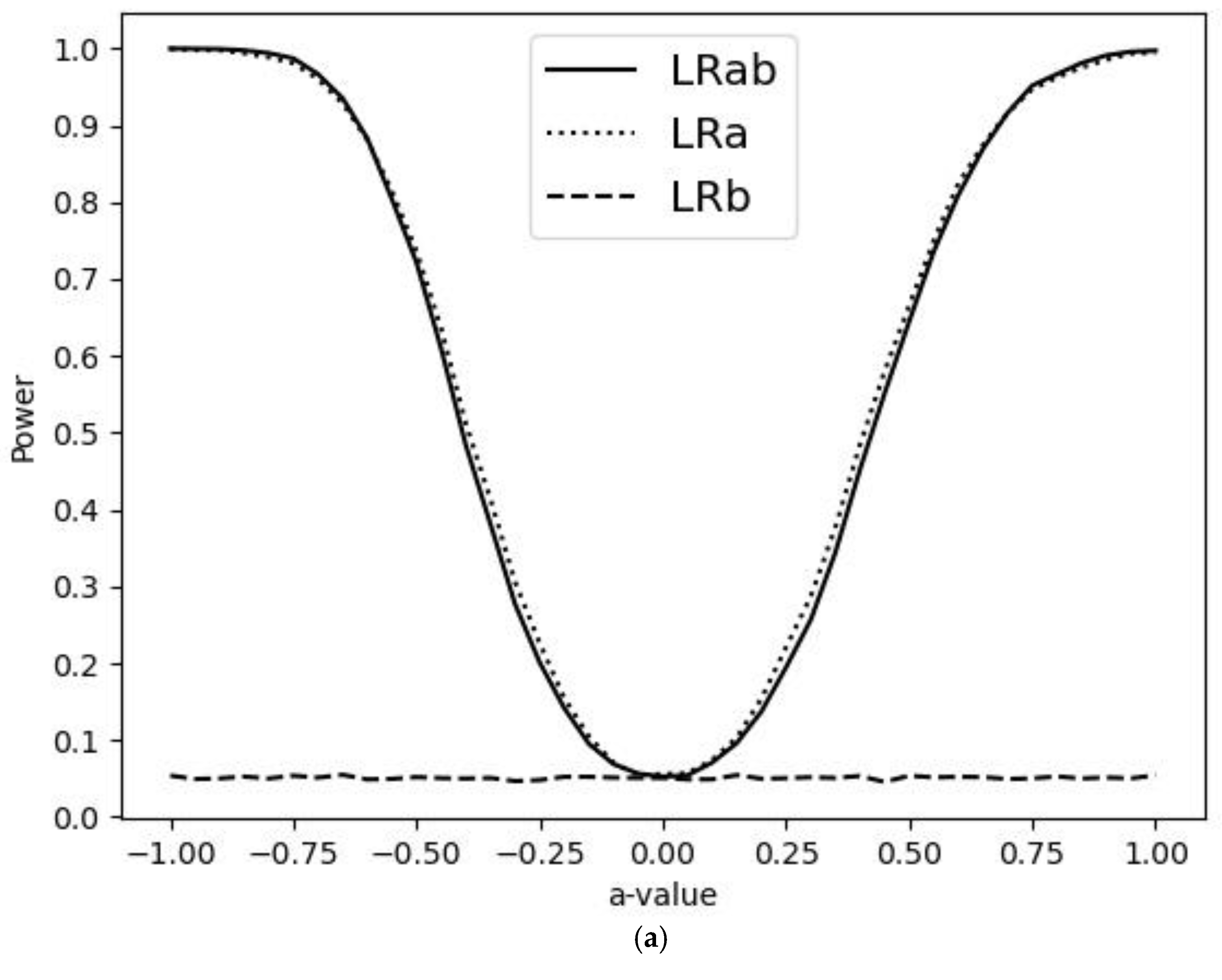
3. Simulations
4. Illustration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- de Jong, V.M.T.; Eijkemans, M.J.C.; van Calster, B.; Timmerman, D.; Moons, K.G.M.; Steyerberg, E.W.; van Smeden, M. Sample size consideration and predictive performance of multinomial logistic prediction models. Stat. Med. 2019, 38, 1601–1619. [Google Scholar] [CrossRef] [PubMed]
- Mincer, J.; Zarnowitz, V. The evaluation of economic forecasts. In Economic Forecasts and Expectations; Mincer, J., Ed.; National Bureau of Economic Research: New York, NY, USA, 1969. [Google Scholar]
- Franses, P.H. Testing for bias in forecasts for independent binary outcomes. Appl. Econ. Lett. 2021, 28, 1336–1338. [Google Scholar] [CrossRef]
- Franses, P.H.; Paap, R. Quantitative Models in Marketing Research; Cambridge University Press (CUP): Cambridge, UK, 2001. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franses, P.H.; Paap, R. Testing for Bias in Forecasts for Independent Multinomial Outcomes. Forecasting 2025, 7, 4. https://doi.org/10.3390/forecast7010004
Franses PH, Paap R. Testing for Bias in Forecasts for Independent Multinomial Outcomes. Forecasting. 2025; 7(1):4. https://doi.org/10.3390/forecast7010004
Chicago/Turabian StyleFranses, Philip Hans, and Richard Paap. 2025. "Testing for Bias in Forecasts for Independent Multinomial Outcomes" Forecasting 7, no. 1: 4. https://doi.org/10.3390/forecast7010004
APA StyleFranses, P. H., & Paap, R. (2025). Testing for Bias in Forecasts for Independent Multinomial Outcomes. Forecasting, 7(1), 4. https://doi.org/10.3390/forecast7010004






