Evaluating the Potential of Copulas for Modeling Correlated Scenarios for Hydro, Wind, and Solar Energy
Abstract
1. Introduction
- How effectively can copula-based methods model the complex dependency structures (including correlations and complementarities) between hydro, wind, and solar renewable energy resources in the context of the Brazilian energy system?
- To what extent do the joint scenarios for monthly natural energy inflows, wind speed, and solar radiation generated using a copula-based approach accurately reproduce the statistical properties (including extreme events and variability) of historical data?
- How robust are copula-based models for representing the interdependencies between hydro, wind, and solar resources across different regions within Brazil with varying climatological characteristics?
- How do we construct a link between the inflows scenarios, generated by official dispatch models from the existing Brazilian Electricity Market framework, and the scenarios for wind and solar power plants generated by the proposed copula-based model?
2. Methodological Approach
2.1. Copulas—Brief Introduction
- CDFs are always increasing, is increasing in each component ;
- The marginal in component i is obtained by setting for all and it must be uniformly distributed ;
- For , the probability must be non-negative, which leads to the so-called, where and .
- Empirical Approach: pairwise dependence is measured by Kendall’s tau or Spearman’s rho between all variables (Kendall’s and Spearman’s are both examples of rank correlations. As rank correlations, they possess several advantageous properties compared to linear correlation: (i) independence from marginal distributions; (ii) invariance to strictly increasing non-linear transformations; (iii) always defined; and (iv) bounded range [−1, 1]. They can also be expressed in terms of copulas). The variable exhibiting the strongest overall dependence on others is a potential candidate for the dominant position.
- Model Selection Criteria: information criteria (e.g., Akaike information criterion (AIC), Bayesian information criterion (BIC))are employed to compare different C-vine models, each with a different variable chosen as dominant. The model with the best fit (lowest AIC/BIC) often points to a suitable dominant variable.
- Starting in Tree 1: dominant variable connections.
- Specify a candidate set of copula families.
- Estimate the parameters: for each candidate copula, estimate its parameters using the maximum likelihood estimation (MLE) on the data for that pair.
- Evaluate goodness of fit: employ a model selection criterion, typically AIC or BIC, to compare the fit of the candidate copulas. Lower AIC/BIC values indicate a better fit.
- Select the best copula: select the copula family with the lowest AIC/BIC for that particular edge.
- Subsequent Trees: conditional dependencies.
- Move to the next tree, modeling the dependence between two variables conditional on the variable(s) connecting them in the previous tree.
- For each edge in the trees, carry out the following:
- ‐
- Specify a candidate set of copula families.
- ‐
- Conditional estimation: estimate the copula parameters using MLE. This step requires conditioning the variables linking the pair in the previous tree.
- ‐
- Goodness of fit and selection: as executed for Tree 1, AIC/BIC is used to compare the fit of the candidate copulas and select the copula that presents a better fit.
- Iterate through trees: this process of copula family selection is replicated for each edge in each subsequent tree of the C-vine structure.
2.2. Proposed Framework
3. Case Study
3.1. Case Study Data
- Hydropower Dominance: Brazil heavily relies on hydroelectric power plants for about 65% of its electricity generation. This makes it one of the world’s leaders in hydroelectric energy.
- Diverse Geography: Hydroelectric plants are spread across the country.
- Large-Scale Plants: like Itaipu (the second largest in the world shared with Paraguay), Tucuruí, and Belo Monte.
- Growing Renewable Sources: While hydropower dominates, Brazil has increasingly incorporated wind power, biomass, and solar energy into its mix. The wind and solar power plants reached 30% of Brazil installed capacity in 2023 [7].
- Vast Transmission Network and Interconnected System: Due to the large distances between some generation centers (like the Amazon basin) and major consumption centers (Southeast), it enables the sharing of energy resources between different regions. The main transmission system, called the basic grid, operating transmission lines from 230 kV to 800 kV, reached 171.640 km in 2023 (source: Brazilian National System Operator (ONS) website).
- Energy Equivalent Reservoir (EER) [31]: Hydropower reservoirs are aggregated, allowing the official model (NEWAVE) to represent the hydropower plants. Currently, there are 12 EERs in the official model used by the Brazilian Operator System (ONS) and Energy Trading Chamber (CCEE).
- Price Zones: the system is divided into 4 subsystems (price zones) South, Southeast/Midwest, Northeast, and North.
3.2. Historical Data Analysis
4. Results
4.1. Estimated Model
4.1.1. Marginal Distribution Estimation
4.1.2. C-Vine Structure Assessment
- The C-vine structure was defined without the energy inflow variable, using the VineCopula Package in R [30], where the root nodes are selected by identifying the node with the strongest dependencies on all other nodes. In other words, given the empirical Kendall’s matrix, the node corresponding to the column that presents the maximum sum is selected. This step is important to model the variables’ relationship from the second level of the C-vine structure and on.
- The energy inflow is set as a dominant variable in the C-vine structure defined in the preceding step, adding a first level to the C-vine structure defined in the previous step.
4.1.3. Copula Family Selection
4.2. Analysis of Simulated Scenarios
4.2.1. Correlation and Complementarity Between Variables
4.2.2. Jointly Simulated Scenarios
4.2.3. Cross-Correlation Between Variables
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VRE | variable renewable energy |
| PV | solar photovoltaic |
| ESG | Environmental, Social and Governance |
| IEA | International Energy Agency |
| PAR(p) | periodic autoregressive |
| Probability Density Function | |
| CDF | Cumulative Density Function |
| PV | photovoltaic |
| RMSE | Root Mean Square Error |
| ONS | Operador Nacional do Sistema |
| ANEEL | Agência Nacional de Energia Elétrica |
| CCEE | Câmara de Comercialização de Energia Elétrica |
| MME | Ministério de Minas e Energia |
| PCC | pair-copula construction |
| EER | Energy Equivalent Reservoir |
| GHI | Global Horizontal Solar Irradiation |
| ENSO | El Niño–Southern Oscillation |
References
- Brouwer, A.S.; van den Broek, M.; Seebregts, A.; Faaij, A. Impacts of large-scale Intermittent Renewable Energy Sources on electricity systems, and how these can be modeled. Renew. Sustain. Energy Rev. 2014, 33, 443–466. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Renewable Energy Market Update—June 2023; IEA: Paris, France, 2023. [Google Scholar]
- de Queiroz, A.R. Stochastic hydro-thermal scheduling optimization: An overview. Renew. Sustain. Energy Rev. 2016, 62, 382–395. [Google Scholar] [CrossRef]
- Souza, R.C.; Marcato, A.L.M.; Dias, B.H.; Oliveira, F.L.C. Optimal operation of hydrothermal systems with Hydrological Scenario Generation through Bootstrap and Periodic Autoregressive Models. Eur. J. Oper. Res. 2012, 222, 606–615. [Google Scholar] [CrossRef]
- Oliveira, F.L.C.; Souza, R.C.; Marcato, A.L.M. A time series model for building scenarios trees applied to stochastic optimisation. Int. J. Electr. Power Energy Syst. 2015, 67, 315–323. [Google Scholar] [CrossRef]
- de Castro, C.M.; Marcato, A.L.; Souza, R.C.; Junior, I.C.S.; Oliveira, F.L.C.; Pulinho, T. The generation of synthetic inflows via bootstrap to increase the energy efficiency of long-term hydrothermal dispatches. Electr. Power Syst. Res. 2015, 124, 33–46. [Google Scholar] [CrossRef]
- EPE. Balanço Energético Nacional. 2024. Available online: https://www.epe.gov.br/pt/publicacoes-dados-abertos/publicacoes/balanco-energetico-nacional-ben (accessed on 10 June 2024).
- Iung, A.M.; Cyrino Oliveira, F.L.; Marcato, A.L.M. A review on modeling variable renewable energy: Complementarity and spatial–temporal dependence. Energies 2023, 16, 1013. [Google Scholar] [CrossRef]
- CEPEL NEWAVE—Manual do Usuário. 2022. Available online: https://www.cepel.br/wp-content/uploads/2024/10/ManualUsuario-2.pdf (accessed on 10 June 2024).
- Baboli, P.T.; Brand, M.; Lehnhoff, S. Stochastic Correlation Modelling of Renewable Energy Sources for Provision of Ancillary Services using Multi-dimensional Copula Functions. In Proceedings of the 2021 11th Smart Grid Conference (SGC), Tabriz, Iran, 7–9 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Papaefthymiou, G.; Kurowicka, D. Using Copulas for Modeling Stochastic Dependence in Power System Uncertainty Analysis. IEEE Trans. Power Syst. 2009, 24, 40–49. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, Y.; Wang, X.; Chang, J.; Zhou, Y.; Liu, T. Modeling and simulation of large-scale wind power base output considering the clustering characteristics and correlation of wind farms. Front. Energy Res. 2022, 10, 810082. [Google Scholar] [CrossRef]
- de Almeida Pereira, G.A.; Veiga, Á. Periodic Copula Autoregressive Model Designed to Multivariate Streamflow Time Series Modelling. Water Resour. Manag. 2019, 33, 3417–3431. [Google Scholar] [CrossRef]
- de Almeida Pereira, G.A.; Veiga, Á. PAR(p)-vine copula based model for stochastic streamflow scenario generation. Stoch. Environ. Res. Risk Assess. 2018, 32, 833–842. [Google Scholar] [CrossRef]
- Denault, M.; Dupuis, D.; Couture-Cardinal, S. Complementarity of hydro and wind power: Improving the risk profile of energy inflows. Energy Policy 2009, 37, 5376–5384. [Google Scholar] [CrossRef]
- Ávila R., L.; Mine, M.R.; Kaviski, E.; Detzel, D.H.; Fill, H.D.; Bessa, M.R.; Pereira, G.A. Complementarity modeling of monthly streamflow and wind speed regimes based on a copula-entropy approach: A Brazilian case study. Appl. Energy 2020, 259, 114127. [Google Scholar] [CrossRef]
- Ávila, L.; Mine, M.R.; Kaviski, E.; Detzel, D.H. Evaluation of hydro-wind complementarity in the medium-term planning of electrical power systems by joint simulation of periodic streamflow and wind speed time series: A Brazilian case study. Renew. Energy 2021, 167, 685–699. [Google Scholar] [CrossRef]
- de Andrade Melo, G.; Oliveira, F.L.C.; Maçaira, P.M.; Meira, E. Exploring complementary effects of solar and wind power generation. Renew. Sustain. Energy Rev. 2025, 209, 115139. [Google Scholar] [CrossRef]
- Melo, G.; Barcellos, T.; Ribeiro, R.; Couto, R.; Gusmão, B.; Oliveira, F.L.C.; Maçaira, P.; Fanzeres, B.; Souza, R.C.; Bet, O. Renewable energy sources spatio-temporal scenarios simulation under influence of climatic phenomena. Electr. Power Syst. Res. 2024, 235, 110725. [Google Scholar] [CrossRef]
- Huang, X.; Maçaira, P.M.; Hassani, H.; Cyrino Oliveira, F.L.; Dhesi, G. Hydrological natural inflow and climate variables: Time and frequency causality analysis. Phys. A Stat. Mech. Appl. 2019, 516, 480–495. [Google Scholar] [CrossRef]
- McNeil, A.J.; Frey, R.; Embrechts, P. Quantitative Risk Management: Concepts, Techniques and Tools-Revised Edition; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Jaworski, P.; Durante, F.; Hardle, W.K.; Rychlik, T. Copula Theory and Its Applications; Springer: Berlin/Heidelberg, Germany, 2010; Volume 198. [Google Scholar]
- Charpentier, A.; Fermanian, J.D.; Scaillet, O. The estimation of copulas: Theory and practice. Copulas Theory Appl. Financ. 2007, 35. [Google Scholar]
- Xu, H.; Chen, J.; Lin, H.; Yu, P. Unraveling Financial Interconnections: A Methodical Investigation into the Application of Copula Theory in Modeling Asset Dependence. Eur. Acad. J. 2024, 1. [Google Scholar]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Bedford, T.; Cooke, R.M. Vines—A new graphical model for dependent random variables. Ann. Stat. 2002, 30, 1031–1068. [Google Scholar] [CrossRef]
- Bedford, T.; Cooke, R.M. Probability density decomposition for conditionally dependent random variables modeled by vines. Ann. Math. Artif. Intell. 2001, 32, 245–268. [Google Scholar] [CrossRef]
- Kurowicka, D.; Cooke, R. Distribution-free continuous Bayesian belief. Mod. Stat. Math. Methods Reliab. 2005, 10, 309. [Google Scholar]
- Kurowicka, D.; Cooke, R.M. Uncertainty Analysis with High Dimensional Dependence Modelling; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Nagler, T.; Schepsmeier, U.; Stoeber, J.; Brechmann, E.C.; Graeler, B.; Erhardt, T.; Almeida, C.; Min, A.; Czado, C.; Hofmann, M.; et al. Vinecopula: Statistical Inference of Vine Copulas. 2023. Available online: https://cran.r-project.org/web/packages/VineCopula/VineCopula.pdf (accessed on 10 June 2024).
- Arvanitidits, N.V.; Rosing, J. Composite Representation of a Multireservoir Hydroelectric Power System. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 319–326. [Google Scholar] [CrossRef]
- Agência Nacional de Energia Elétrica—ANEEL. 2023. Available online: https://www.gov.br/aneel/pt-br (accessed on 10 June 2024).
- Staffell, I.; Pfenninger, S. Renewables.Ninja. 2016. Available online: https://www.renewables.ninja (accessed on 5 October 2018).
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K.; et al. MERRA: NASA’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Müller, R.; Pfeifroth, U.; Träger-Chatterjee, C.; Trentmann, J.; Cremer, R. Digging the METEOSAT Treasure—3 Decades of Solar Surface Radiation. Remote Sens. 2015, 7, 8067–8101. [Google Scholar] [CrossRef]
- Müller, R.; Pfeifroth, U.; Träger-Chatterjee, C.; Cremer, R.; Trentmann, J.; Hollmann, R. Surface Solar Radiation Data Set—Heliosat (SARAH). 2015. Available online: https://www.cmsaf.eu/en/products/radiation/surface_solar_radiation/sarah_v2/index.html (accessed on 10 June 2024).
- Jung, C.; Schindler, D. Wind speed distribution selection—A review of recent development and progress. Renew. Sustain. Energy Rev. 2019, 114, 109290. [Google Scholar] [CrossRef]
- Peruchena, C.M.F.; Ramírez, L.; Silva-Pérez, M.A.; Lara, V.; Bermejo, D.; Gastón, M.; Moreno-Tejera, S.; Pulgar, J.; Liria, J.; Macías, S.; et al. A statistical characterization of the long-term solar resource: Towards risk assessment for solar power projects. Sol. Energy 2016, 123, 29–39. [Google Scholar] [CrossRef]



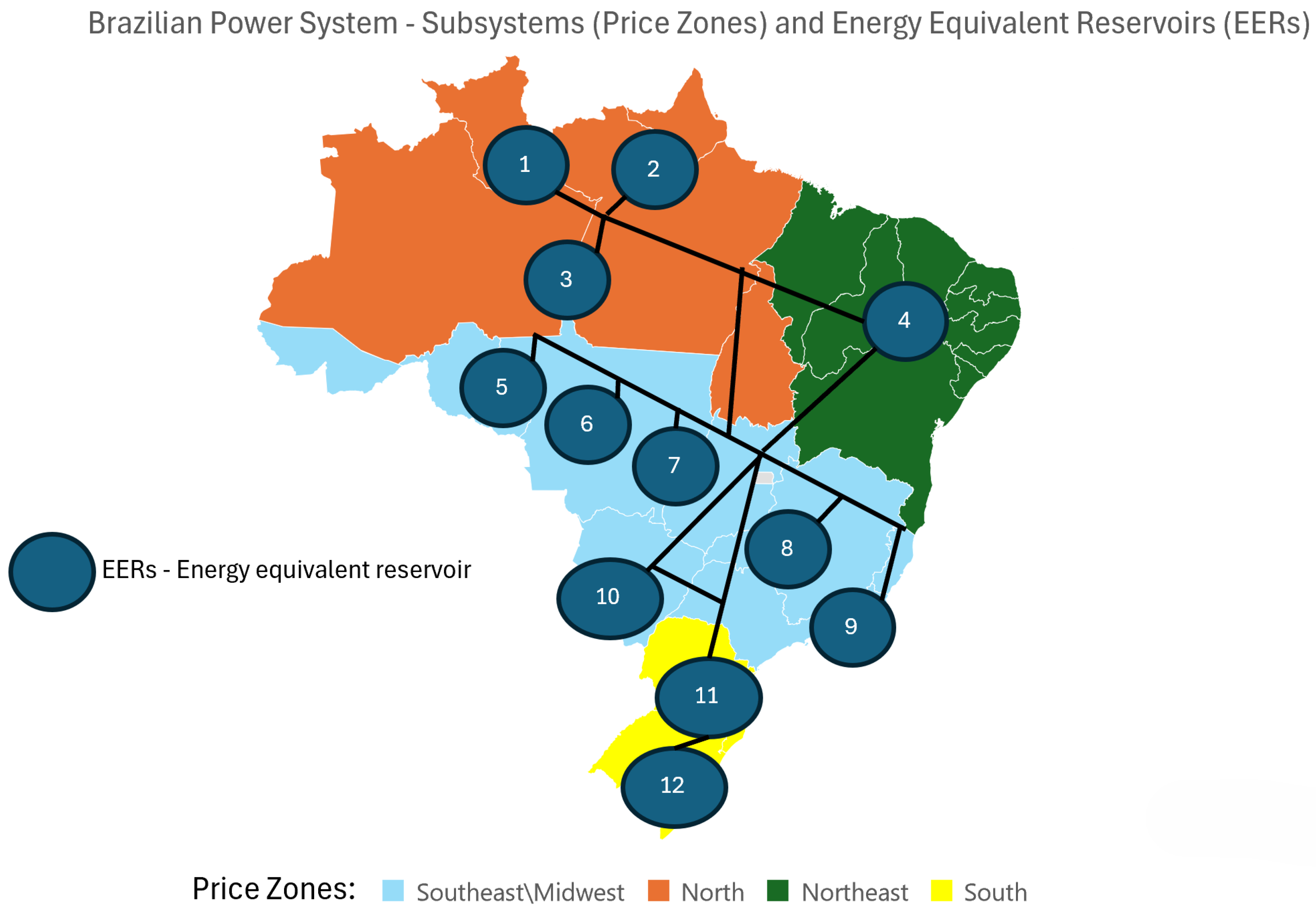
















| Number | Energy Equivalent Reservoir (ERR) |
|---|---|
| 1 | Manaus |
| 2 | Norte |
| 3 | Belo Monte |
| 4 | Nordeste |
| 5 | Madeira |
| 6 | Teles Pires |
| 7 | Sudeste |
| 8 | Paranapanema |
| 9 | Paraná |
| 10 | Itaipu |
| 11 | Sul |
| 12 | Iguaçu |
| Number | Variable |
|---|---|
| 1 | Wind Speed—Bahia |
| 2 | Wind Speed—Piauí |
| 3 | Wind Speed—Rio Grande do Norte |
| 4 | Solar Irradiance—Bahia |
| 5 | Solar Irradiance—Minas Gerais |
| 6 | Solar Irradiance—Piauí |
| 7 | Natural Energy Inflow—Southeast |
| T | T_90 | T_180 | T_270 | T2 | T2_90 | T2_180 |
| 1.2% | 4.8% | 3.2% | 2.0% | 2.8% | 3.6% | 2.4% |
| T2_270 | C | C_90 | C_270 | SC | J | J_90 |
| 6.7% | 2.8% | 3.2% | 3.6% | 3.2% | 4.8% | 3.6% |
| J_270 | SJ | G | G_90 | G_270 | SG | F |
| 1.6% | 2.8% | 4.8% | 2.0% | 0.8% | 4.4% | 9.1% |
| N | t | BB7 | BB7_270 | SBB7 | BB8_270 | SBB8 |
| 7.1% | 2.8% | 0.8% | 0.4% | 0.4% | 0.4% | 0.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iung, A.M.; Cyrino Oliveira, F.L.; Marcato, A.L.M.; Pereira, G.A.A. Evaluating the Potential of Copulas for Modeling Correlated Scenarios for Hydro, Wind, and Solar Energy. Forecasting 2025, 7, 7. https://doi.org/10.3390/forecast7010007
Iung AM, Cyrino Oliveira FL, Marcato ALM, Pereira GAA. Evaluating the Potential of Copulas for Modeling Correlated Scenarios for Hydro, Wind, and Solar Energy. Forecasting. 2025; 7(1):7. https://doi.org/10.3390/forecast7010007
Chicago/Turabian StyleIung, Anderson M., Fernando L. Cyrino Oliveira, Andre L. M. Marcato, and Guilherme A. A. Pereira. 2025. "Evaluating the Potential of Copulas for Modeling Correlated Scenarios for Hydro, Wind, and Solar Energy" Forecasting 7, no. 1: 7. https://doi.org/10.3390/forecast7010007
APA StyleIung, A. M., Cyrino Oliveira, F. L., Marcato, A. L. M., & Pereira, G. A. A. (2025). Evaluating the Potential of Copulas for Modeling Correlated Scenarios for Hydro, Wind, and Solar Energy. Forecasting, 7(1), 7. https://doi.org/10.3390/forecast7010007








