Dynamic Bayesian Network Model for Overhead Power Lines Affected by Hurricanes
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Paper Contribution
1.4. Paper Organization
2. Overhead Line Failure Model
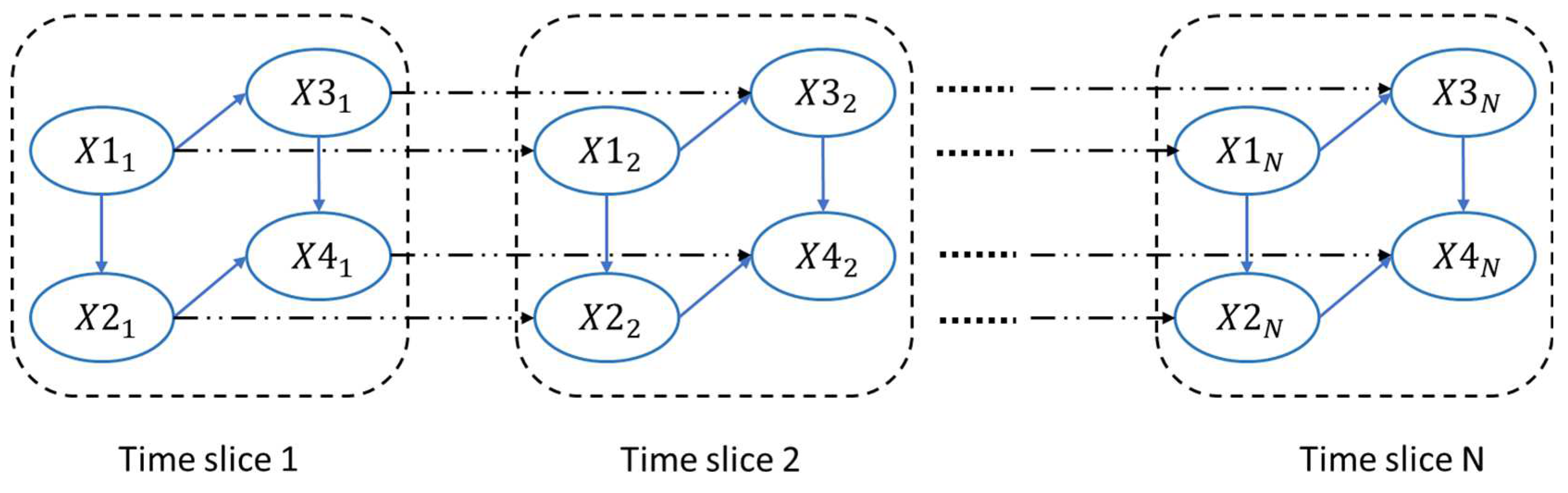
2.1. Dynamic Bayesian Network (DBN)
2.2. Uncertainty Modeling
2.2.1. Scenario-Based Approach
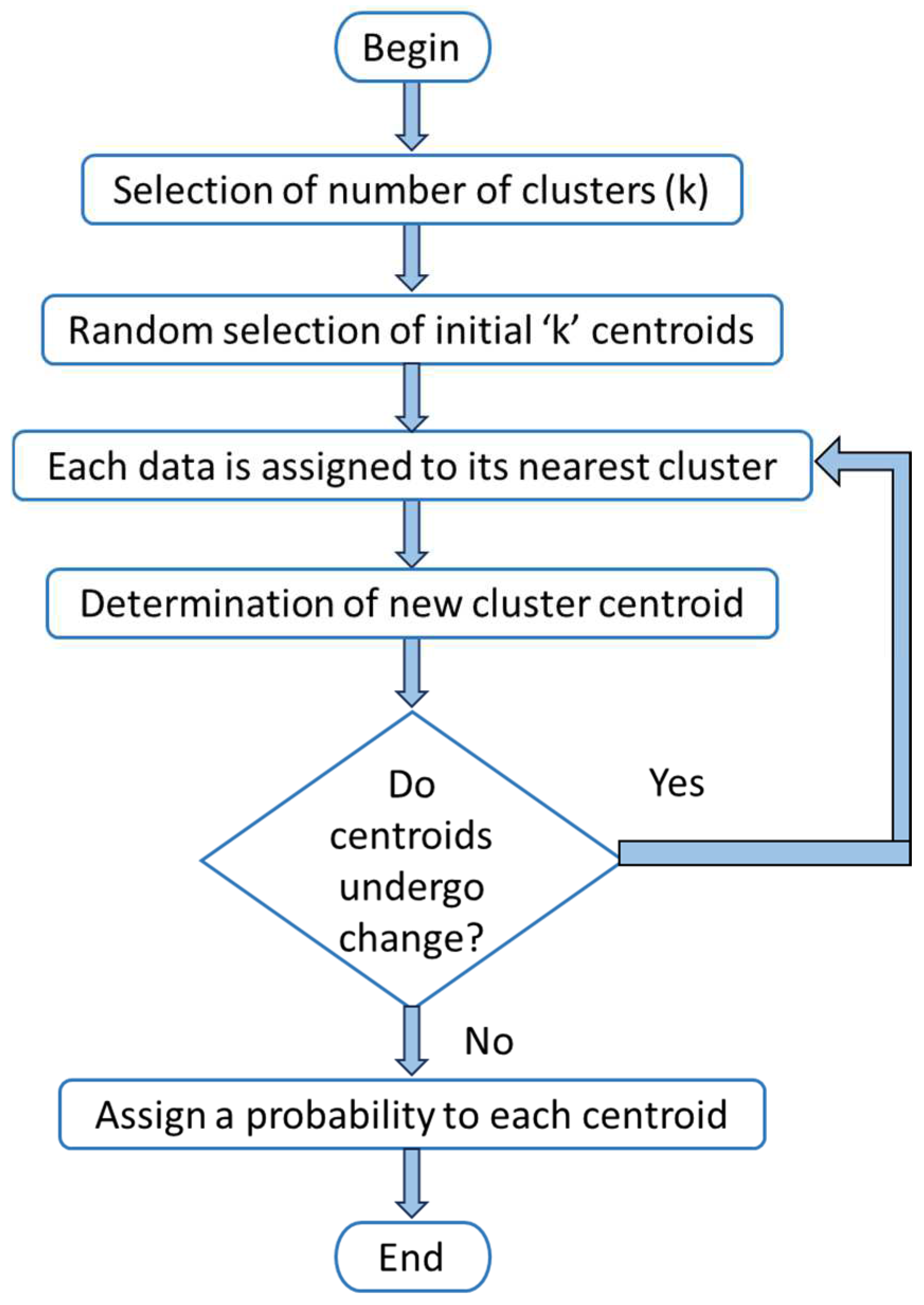
2.2.2. K-Means Technique
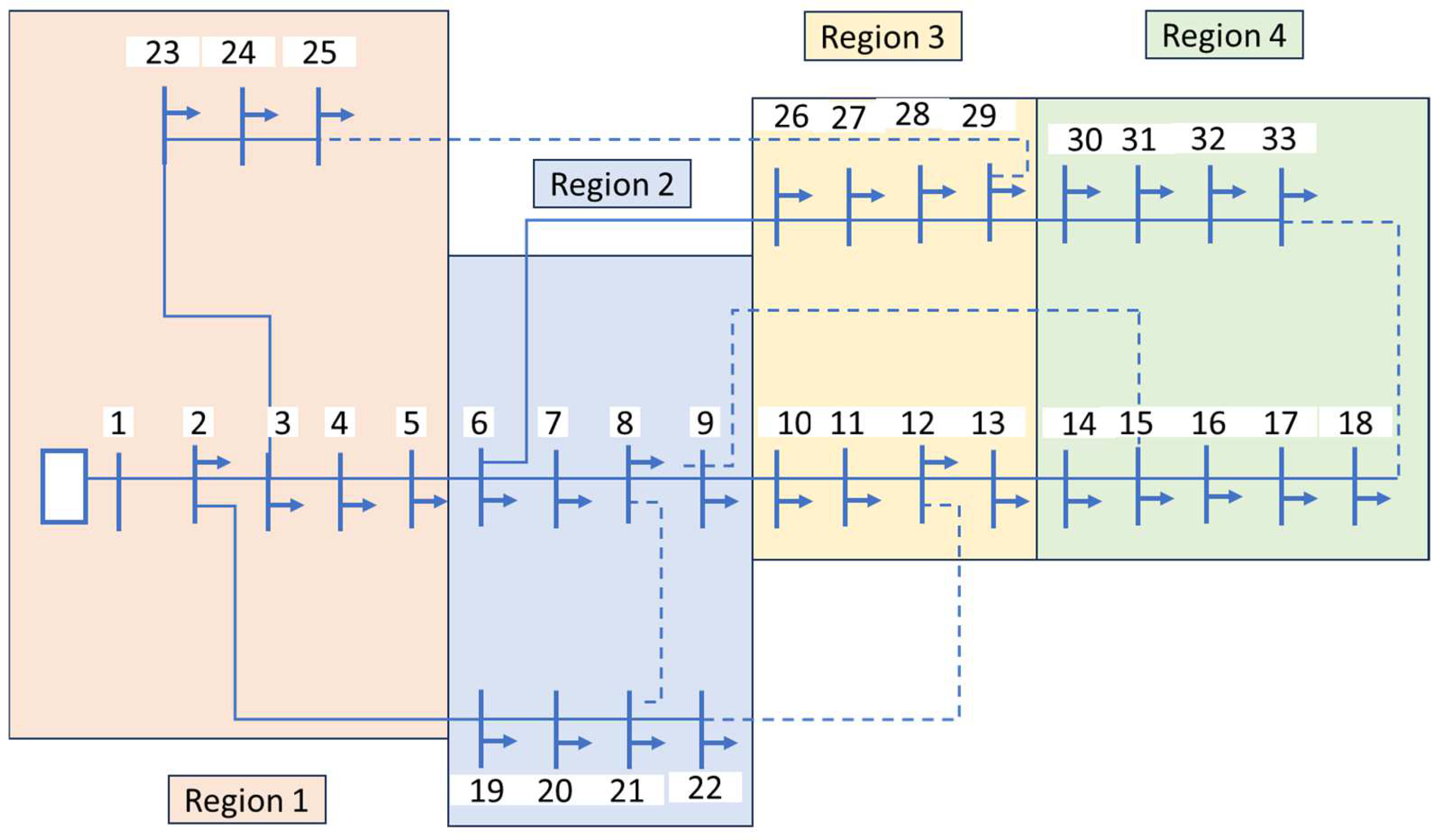
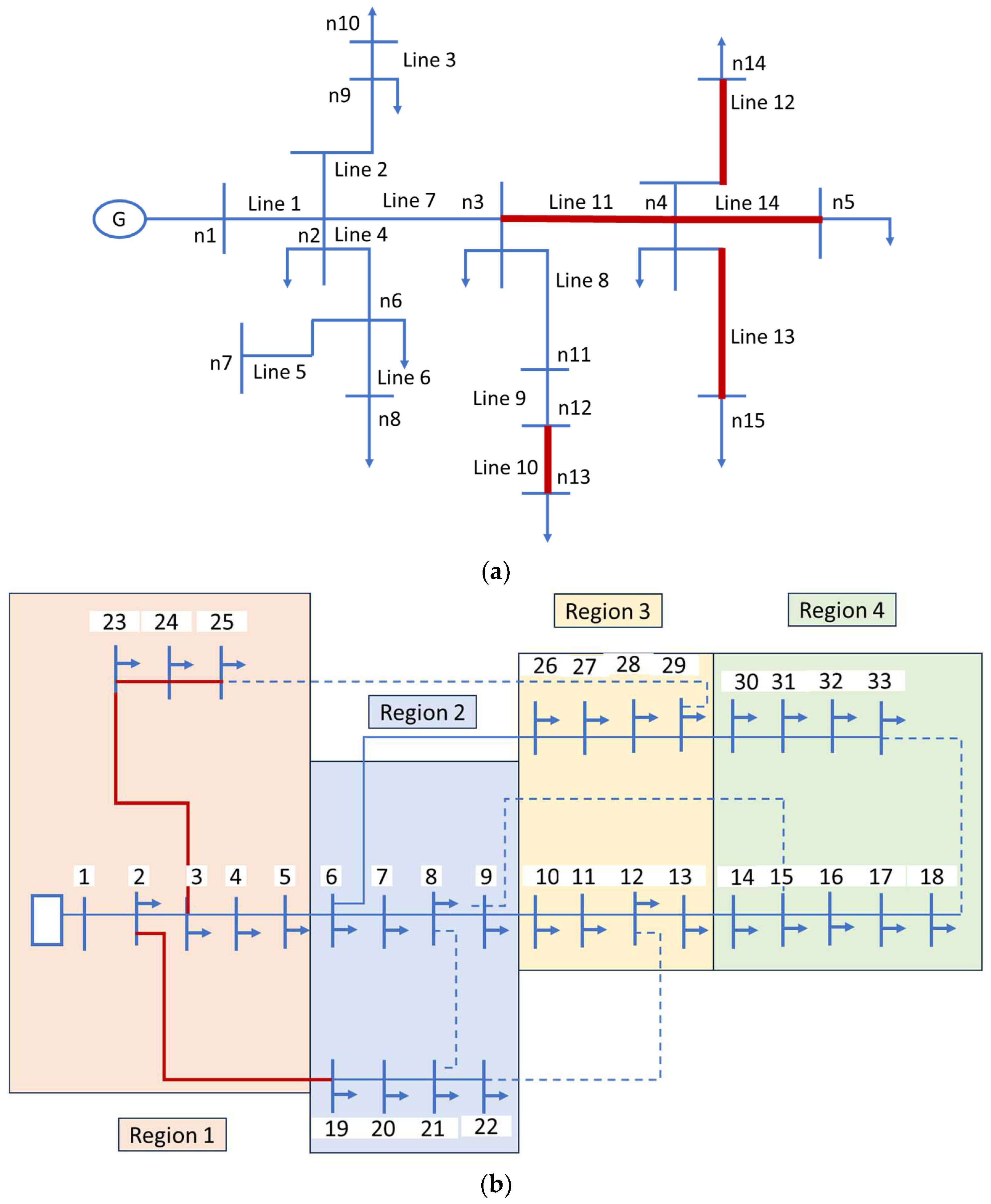
3. The Applications of DBN—IEEE 15 Bus System and IEEE 33 Bus System as Case Study
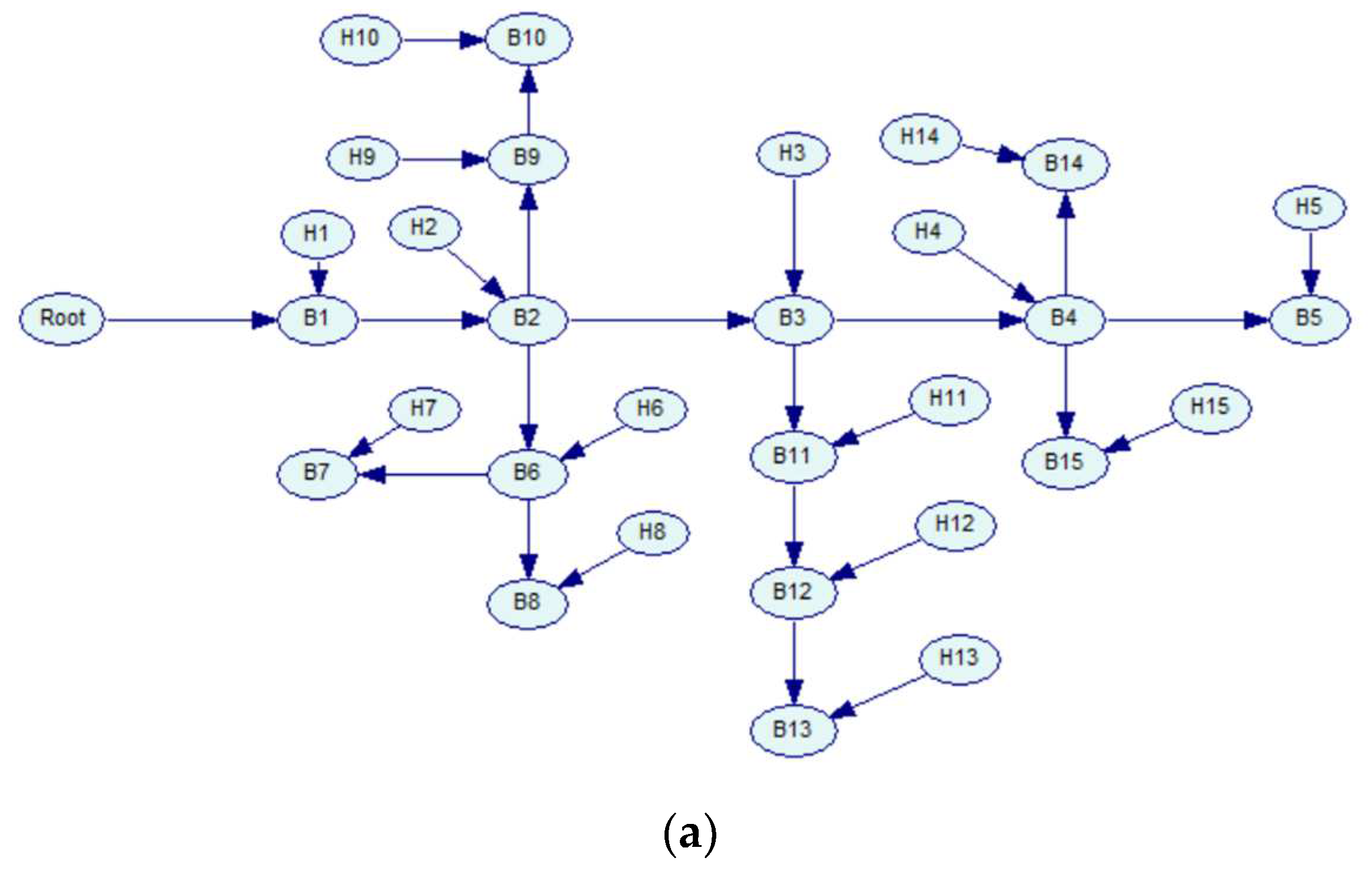
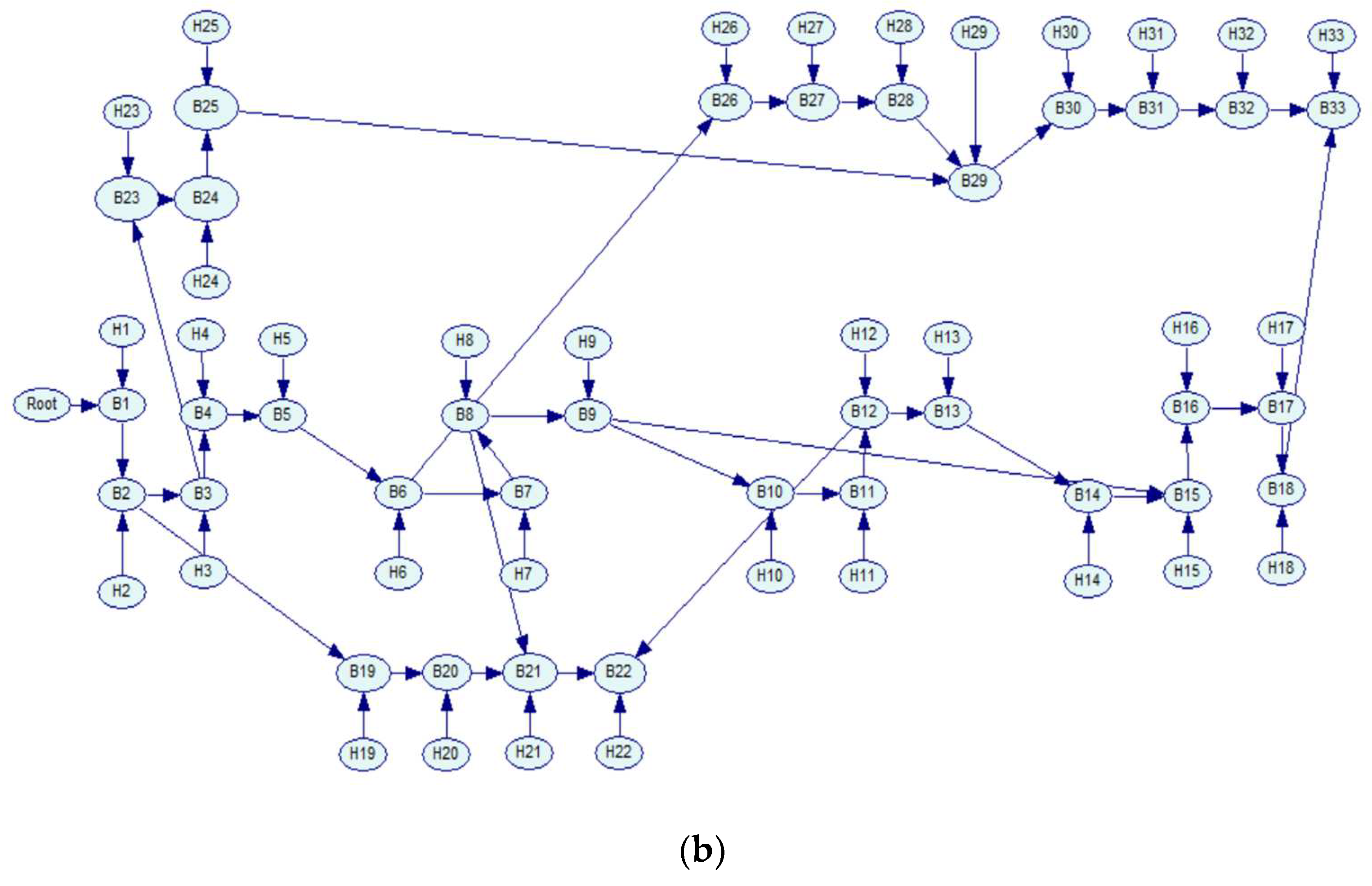
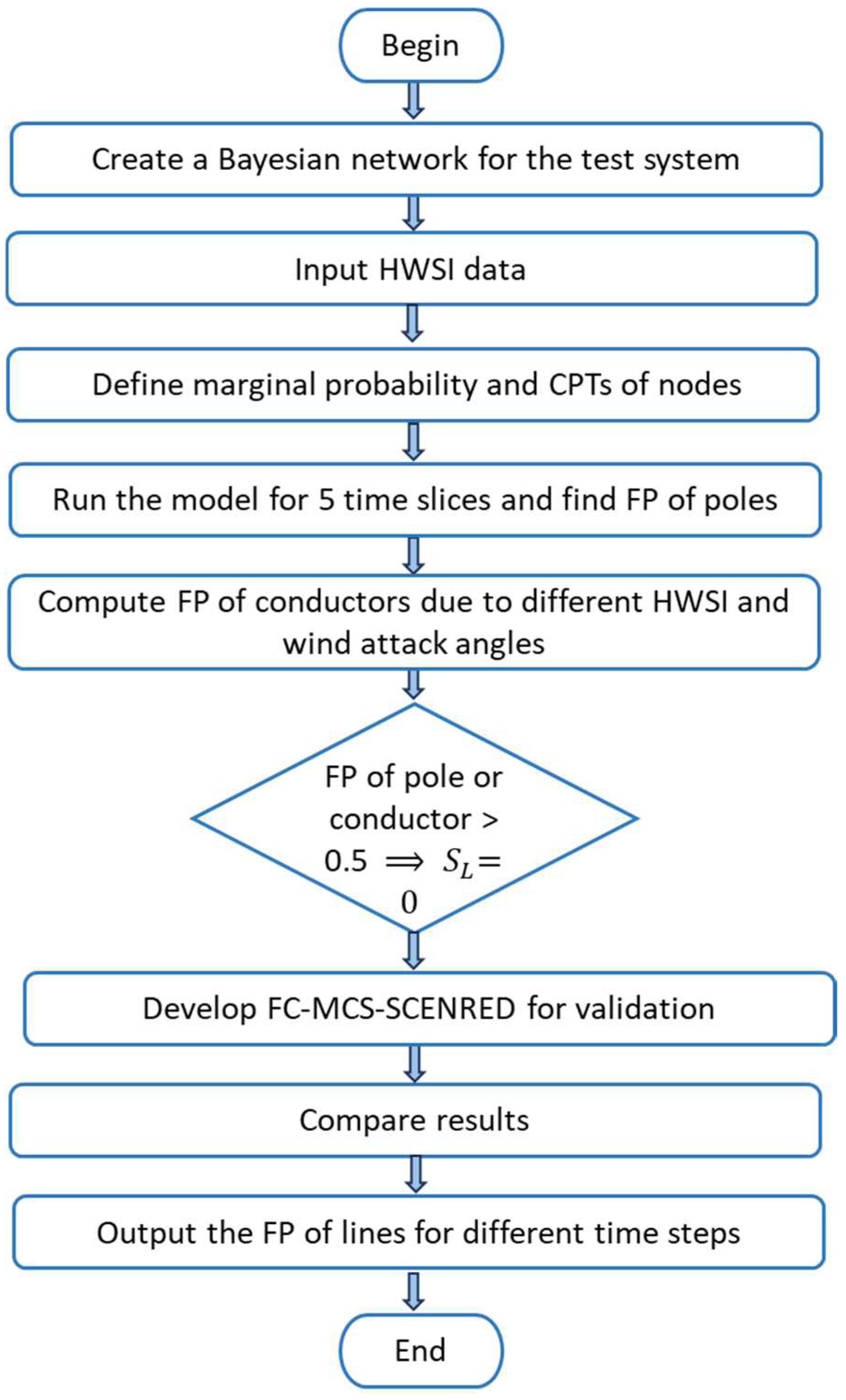
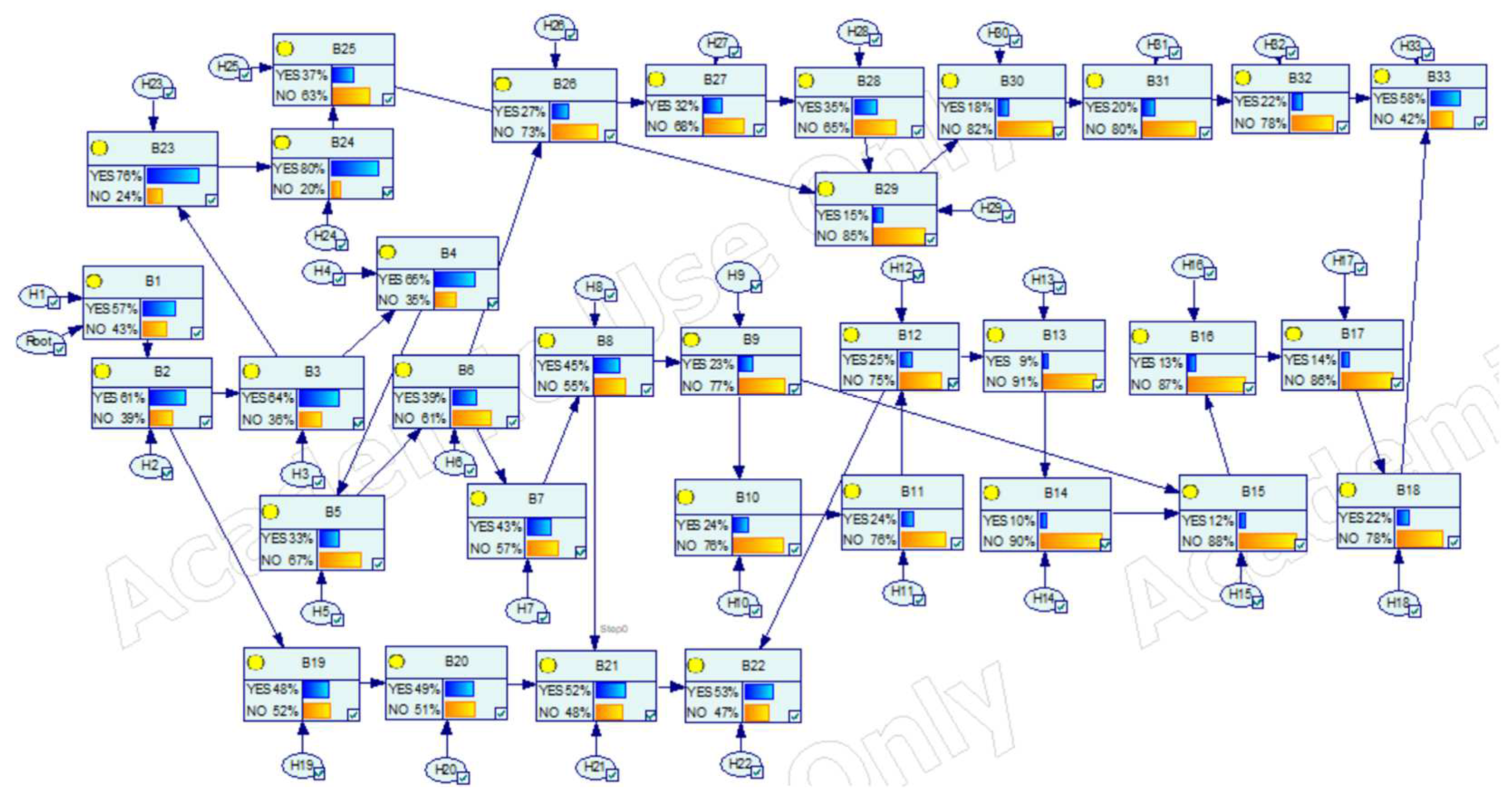
3.1. Step I: Creating a Bayesian Network (BN)
3.2. Step II: Dynamic Framework for Overhead Lines
3.3. III: Bayesian Inference
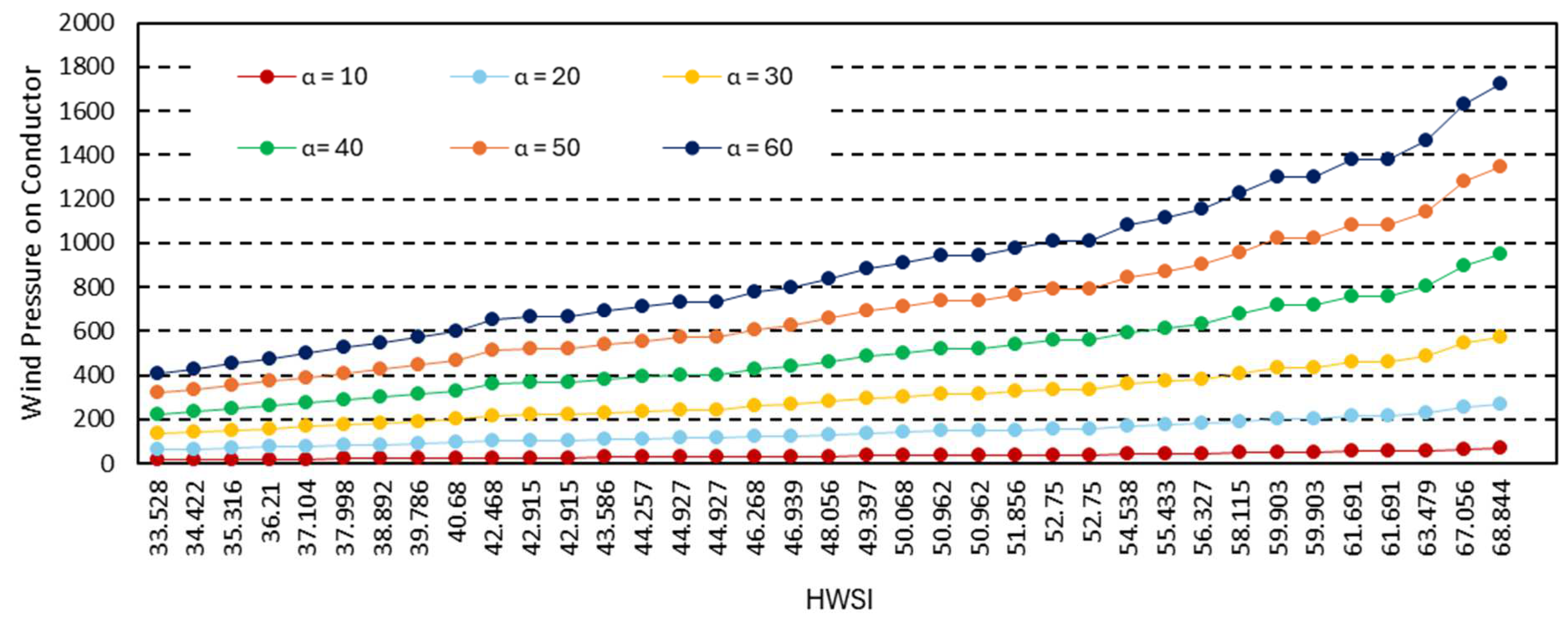
3.4. Step IV: Validation Using FC-MCS-SCENRED Model
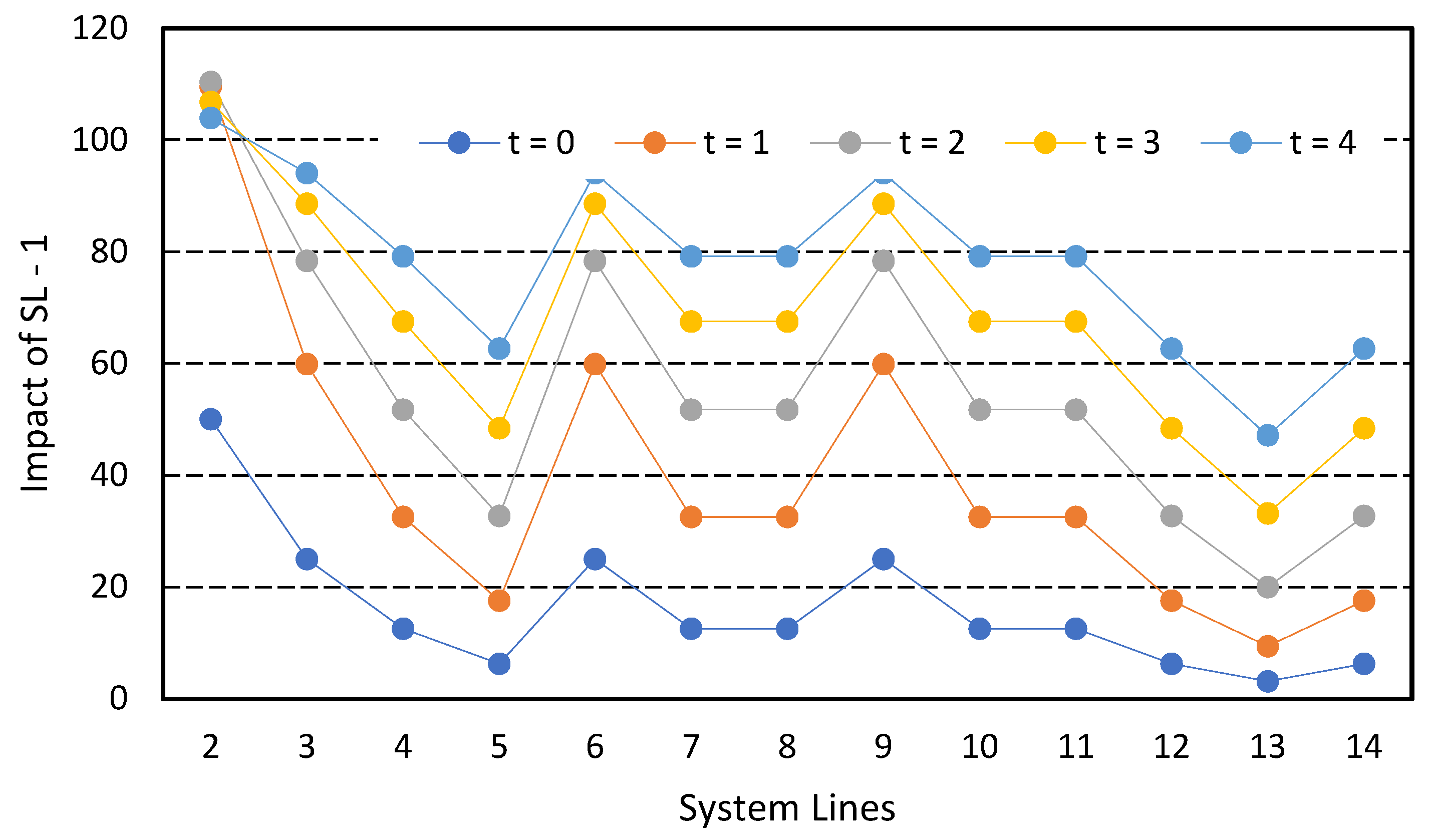
4. Results and Discussion
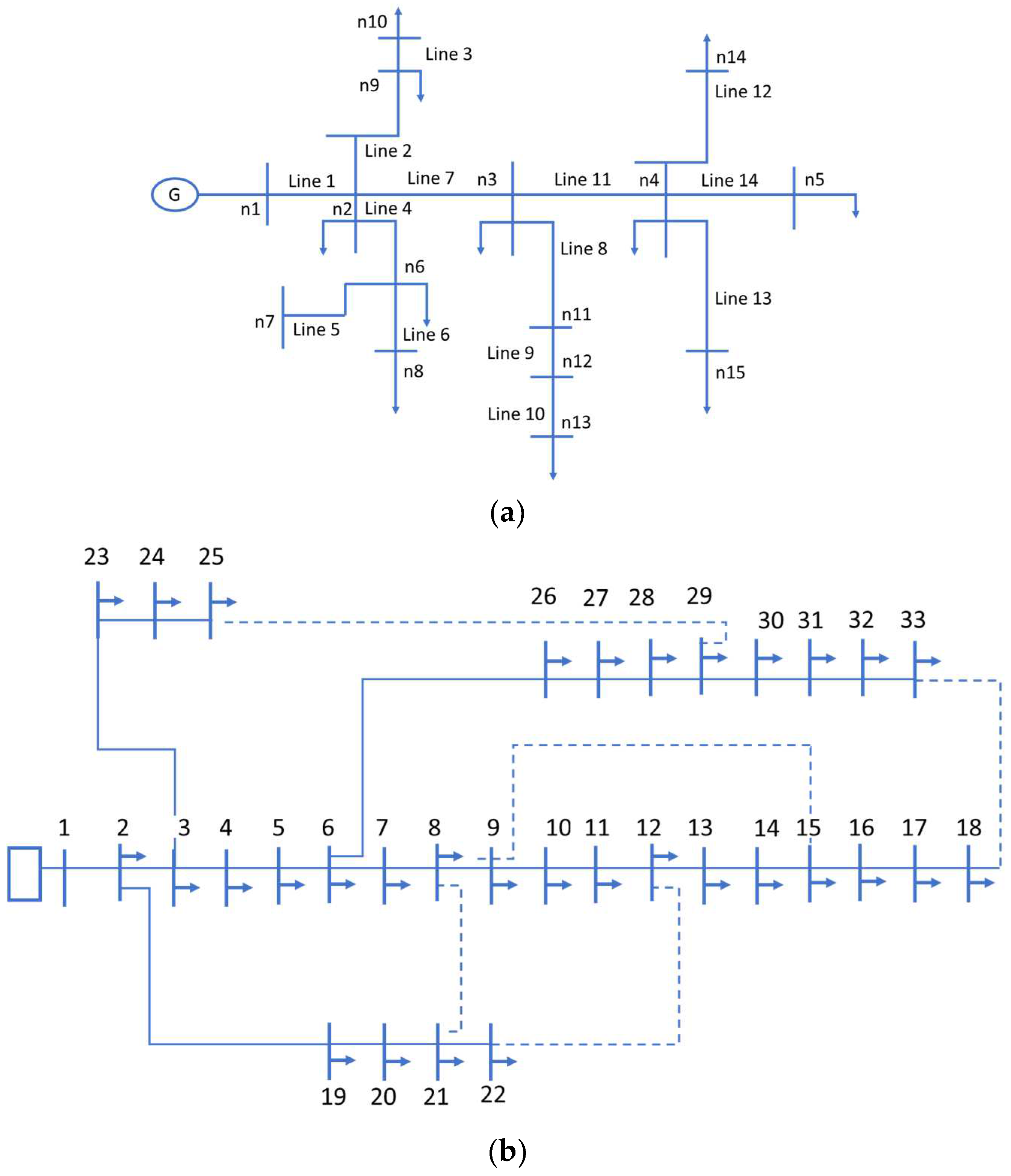
4.1. IEEE 15 Bus Test System
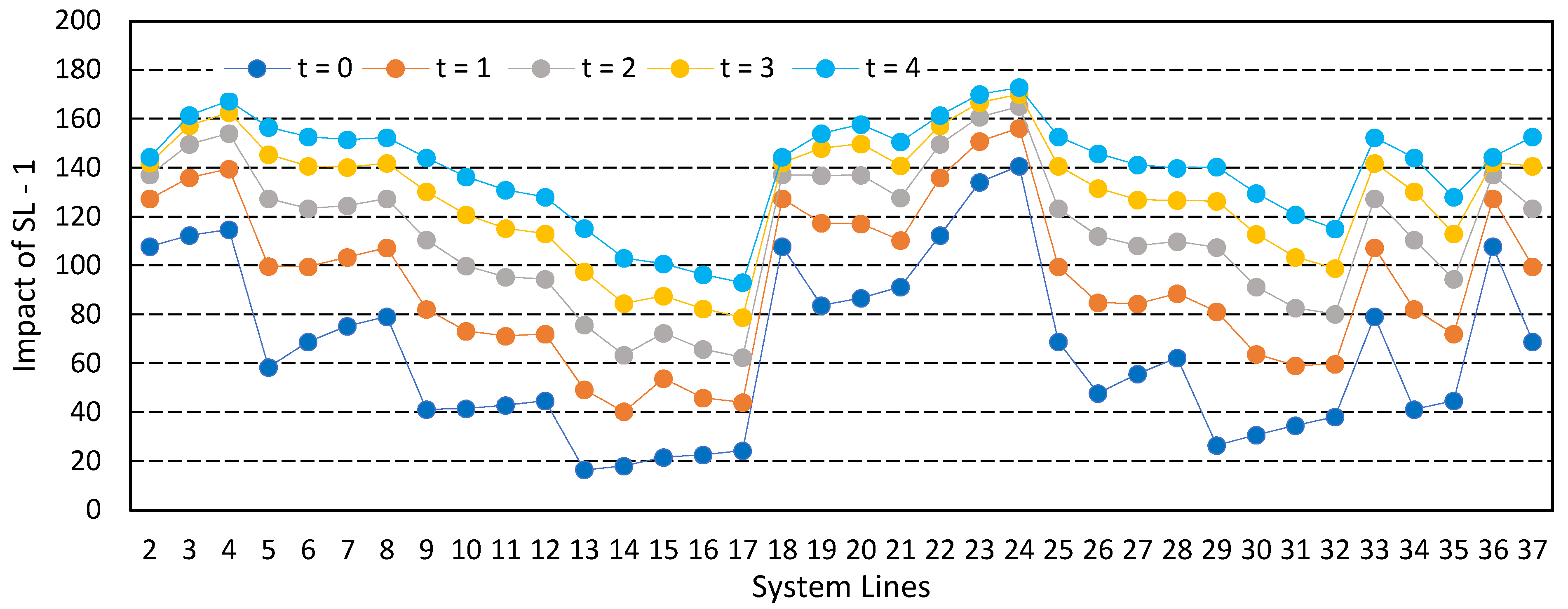
4.2. IEEE 33 Bus Test System
5. Model Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BN | Bayesian Network |
| CPTs | Conditional Probability Tables |
| DBN | Dynamic Bayesian Network |
| FP | Failure Probability |
| FC | Fragility Curves |
| HIF | Hurricane Induced Failure |
| HWSI | Hurricane Wind Speed Intensity |
| MCS | Monte Carlo Simulation |
| FC-MCS-SCENRED | Monte Carlo Simulation Based on Fragility Curves Scenario Reduction Algorithm |
| PDSs | Power Distribution Systems |
| PS | Power System |
| Probability Distribution Function | |
| PDS | Probable Damage Scenarios |
| SCENRED | Scenario Reduction |
| SL | System Line |
References
- Stürmer, J.; Plietzsch, A.; Vogt, T.; Hellmann, F.; Kurths, J.; Otto, C.; Frieler, K.; Anvari, M. Protecting the Texas Power Grid from Tropical Cyclones: Increasing Resilience by Protecting Critical Lines. arXiv 2023, arXiv:2301.13793. [Google Scholar]
- Daeli, A.; Mohagheghi, S. Power Grid Infrastructural Resilience against Extreme Events. Energies 2023, 16, 64. [Google Scholar] [CrossRef]
- Liu, X.; Xie, Q.; Liang, H.; Zhang, X. Post-Earthquake Recover Strategy for Substations Based on Seismic Resilience Evaluation. Eng. Struct. 2023, 279, 115583. [Google Scholar] [CrossRef]
- Salman, A.M.; Li, Y.; Stewart, M.G. Evaluating System Reliability and Targeted Hardening Strategies of Power Distribution Systems Subjected to Hurricanes. Reliab. Eng. Syst. Saf. 2015, 144, 319–333. [Google Scholar] [CrossRef]
- Zhai, C.; Chen, T.Y.; White, A.G.; Guikema, S.D. Power Outage Prediction for Natural Hazards Using Synthetic Power Distribution Systems. Reliab. Eng. Syst. Saf. 2021, 208, 107348. [Google Scholar] [CrossRef]
- Martinez-Amaya, J.; Radin, C.; Nieves, V. Advanced Machine Learning Methods for Major Hurricane Forecasting. Remote Sens. 2023, 15, 119. [Google Scholar] [CrossRef]
- Klauberg, C.; Vogel, J.; Dalagnol, R.; Ferreira, M.P.; Hamamura, C.; Broadbent, E.; Silva, C.A. Post-Hurricane Damage Severity Classification at the Individual Tree Level Using Terrestrial Laser Scanning and Deep Learning. Remote Sens. 2023, 15, 1165. [Google Scholar] [CrossRef]
- Cheng, P.-H.; Lin, C.C.-H.; Morton, Y.T.J.; Yang, S.-C.; Liu, J.-Y. A Bagged-Tree Machine Learning Model for High and Low Wind Speed Ocean Wind Retrieval From CYGNSS Measurements. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–10. [Google Scholar] [CrossRef]
- Moeini, M.; Memari, A.M. Hurricane-Induced Failure Mechanisms in Low-Rise Residential Buildings and Future Research Directions. Nat. Hazards Rev. 2023, 24, 03123001. [Google Scholar] [CrossRef]
- Faramarzi, D.; Rastegar, H.; Riahy, G.H.; Doagou-Mojarrad, H. A Three-Stage Hybrid Stochastic/IGDT Framework for Resilience-Oriented Distribution Network Planning. Int. J. Electr. Power Energy Syst. 2023, 146, 108738. [Google Scholar] [CrossRef]
- McCann, Z.H.; Szaflarski, M. Differences in County-Level Cardiovascular Disease Mortality Rates Due to Damage Caused by Hurricane Matthew and the Moderating Effect of Social Capital: A Natural Experiment. BMC Public Health 2023, 23, 60. [Google Scholar] [CrossRef] [PubMed]
- Liang, D.; Ewing, B.; Cardella, E.; Song, L. Probabilistic Modeling of Small Business Recovery after a Hurricane: A Case Study of 2017 Hurricane Harvey. Nat. Hazards Rev. 2023, 24, 05022012. [Google Scholar] [CrossRef]
- Friedman, E.; Solecki, W.; Troxler, T.G.; Paganini, Z. Linking Quality of Life and Climate Change Adaptation Through the Use of the Macro-Adaptation Resilience Toolkit. Clim. Risk Manag. 2023, 39, 100485. [Google Scholar] [CrossRef]
- Fatima, K.; Shareef, H.; Bajwa, A.A. An Insight into Power System Resilience and Its Confounding Traits. In Proceedings of the 2022 International Seminar on Application for Technology of Information and Communication (iSemantic), Semarang, Indonesia, 17–18 September 2022; pp. 226–231. [Google Scholar]
- Xu, Y.; Xing, Y.; Huang, Q.; Li, J.; Zhang, G.; Bamisile, O.; Huang, Q. A Review of Resilience Enhancement Strategies in Renewable Power System under HILP Events. Energy Rep. 2023, 9, 200–209. [Google Scholar] [CrossRef]
- Schmidt, D.H.; Garland, K.; Quebedeaux, L.K. Resilient Recovery Strategies: Lessons from the Local Nonprofit Sector Following Hurricane Ike. In Case Studies in Disaster Recovery; Elsevier: Amsterdam, The Netherlands, 2023; pp. 33–51. [Google Scholar]
- Hou, G.; Muraleetharan, K.K.; Panchalogaranjan, V.; Moses, P.; Javid, A.; Al-Dakheeli, H.; Bulut, R.; Campos, R.; Harvey, P.S.; Miller, G. Resilience Assessment and Enhancement Evaluation of Power Distribution Systems Subjected to Ice Storms. Reliab. Eng. Syst. Saf. 2023, 230, 108964. [Google Scholar] [CrossRef]
- Li, X.; Fu, D.; Nielsen-Gammon, J.; Gangrade, S.; Kao, S.C.; Chang, P.; Morales Hernández, M.; Voisin, N.; Zhang, Z.; Gao, H. Impacts of Climate Change on Future Hurricane Induced Rainfall and Flooding in a Coastal Watershed: A Case Study on Hurricane Harvey. J. Hydrol. 2023, 616, 128774. [Google Scholar] [CrossRef]
- Darestani, Y.M.; Shafieezadeh, A. Multi-Dimensional Wind Fragility Functions for Wood Utility Poles. Eng. Struct. 2019, 183, 937–948. [Google Scholar] [CrossRef]
- Panteli, M.; Mancarella, P. Influence of Extreme Weather and Climate Change on the Resilience of Power Systems: Impacts and Possible Mitigation Strategies. Electr. Power Syst. Res. 2015, 127, 259–270. [Google Scholar] [CrossRef]
- Omogoye, O.S.; Folly, K.A.; Awodele, K.O. Enhancing the Distribution Power System Resilience against Hurricane Events Using a Bayesian Network Line Outage Prediction Model. J. Eng. 2021, 2021, 731–744. [Google Scholar] [CrossRef]
- Fatima, K.; Sefid, M.; Anees, M.A.; Rihan, M. An Investigation of the Impact of Synchrophasors Measurement on Multi-Area State Estimation in Active Distribution Grids. Aust. J. Electr. Electron. Eng. 2020, 17, 122–131. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, L.; Cheng, G.; Gao, X.; Feng, T.; Zhou, Y. A Quantitative Framework for Network Resilience Evaluation Using Dynamic Bayesian Network. Comput. Commun. 2022, 194, 387–398. [Google Scholar] [CrossRef]
- Lu, Q.; Zhang, W. Integrating Dynamic Bayesian Network and Physics-Based Modeling for Risk Analysis of a Time-Dependent Power Distribution System during Hurricanes. Reliab. Eng. Syst. Saf. 2022, 220, 108290. [Google Scholar] [CrossRef]
- Shafieezadeh, A.; Onyewuchi, U.P.; Begovic, M.M.; DesRoches, R. Age-dependent fragility models of utility wood poles in power distribution networks against extreme wind hazards. IEEE Trans. Power Del. 2013, 29, 131–139. [Google Scholar]
- Winkler, J.; Duenas-Osorio, L.; Stein, R.; Subramanian, D. Performance Assessment of Topologically Diverse Power Systems Subjected to Hurricane Events. Reliab. Eng. Syst. Saf. 2010, 95, 323–336. [Google Scholar] [CrossRef]
- Ouyang, M.; Duenas-Osorio, L. Multi-Dimensional Hurricane Resilience Assessment of Electric Power Systems. Struct. Saf. 2014, 48, 15–24. [Google Scholar] [CrossRef]
- Hughes, W.; Zhang, W.; Cerrai, D.; Bagtzoglou, A.; Wanik, D.; Anagnostou, E. A Hybrid Physics-Based and Data-Driven Model for Power Distribution System Infrastructure Hardening and Outage Simulation. Reliab. Eng. Syst. Saf. 2022, 225, 108628. [Google Scholar] [CrossRef]
- Kammouh, O.; Gardoni, P.; Cimellaro, G.P. Probabilistic Framework to Evaluate the Resilience of Engineering Systems Using Bayesian and Dynamic Bayesian Networks. Reliab. Eng. Syst. Saf. 2020, 198, 106813. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, Z.; Wei, R.; Huang, Y.; Liang, Y.; Li, X. Review of Failure Risk and Outage Prediction in Power System under Wind Hazards✰. Electr. Power Syst. Res. 2022, 210, 108098. [Google Scholar] [CrossRef]
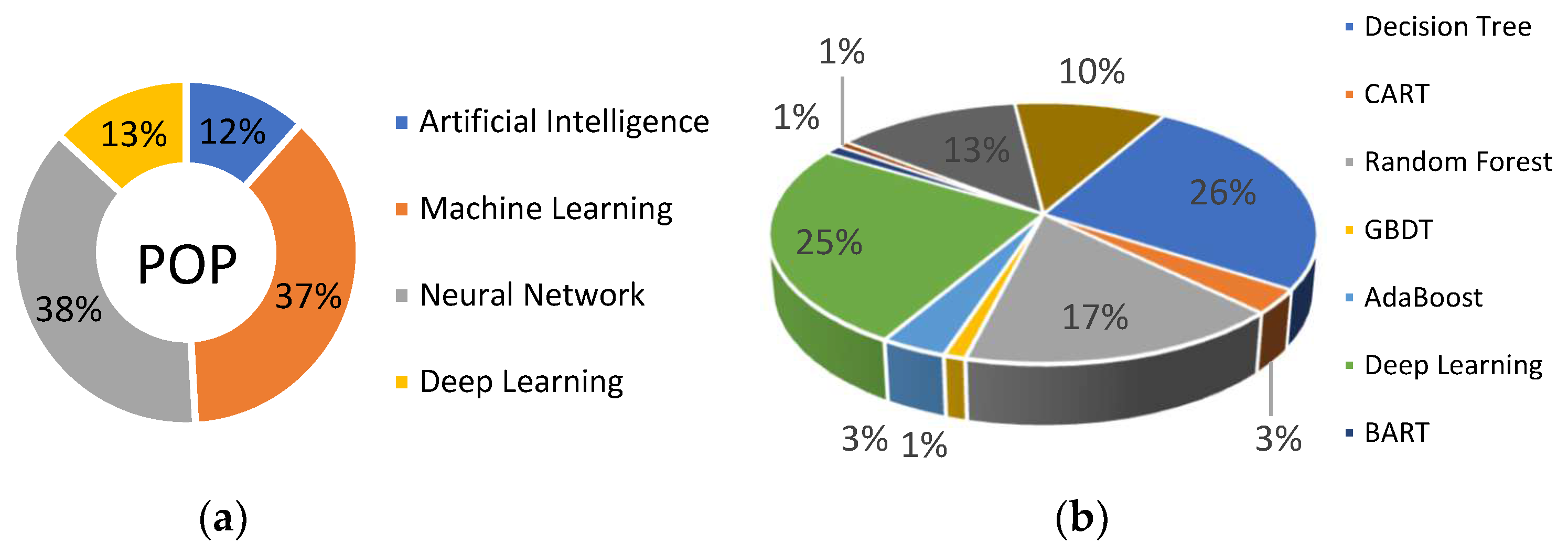
- Fatima, K.; Shareef, H.; Costa, F.B.; Bajwa, A.A.; Wong, L.A. Machine Learning for Power Outage Prediction during Hurricanes: An Extensive Review. Eng. Appl. Artif. Intell. 2024, 133, 108056. [Google Scholar] [CrossRef]
- Nateghi, R.; Guikema, S.; Quiring, S.M. Power Outage Estimation for Tropical Cyclones: Improved Accuracy with Simpler Models. Risk Anal. 2014, 34, 1069–1078. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, Z.; Yu, J.; Wei, R.; Huang, Y.; Li, X. Damage Prediction of 10 KV Power Towers in Distribution Network under Typhoon Disaster Based on Data-Driven Model. Int. J. Electr. Power Energy Syst. 2022, 142, 108307. [Google Scholar] [CrossRef]
- Kankanala, P.; Das, S.; Pahwa, A. AdaBoost+: An Ensemble Learning Approach for Estimating Weather-Related Outages in Distribution Systems. IEEE Trans. Power Syst. 2014, 29, 359–367. [Google Scholar] [CrossRef]
- Udeh, K.; Wanik, D.W.; Cerrai, D.; Aguiar, D.; Anagnostou, E. Autoregressive Modeling of Utility Customer Outages with Deep Neural Networks. In Proceedings of the 2022 IEEE 12th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 26–29 January 2022; pp. 406–414. [Google Scholar]
- Khediri, A.; Laouar, M.R. Deep-Belief Network Based Prediction Model for Power Outage in Smart Grid. In Proceedings of the 4th ACM International Conference of Computing for Engineering and Sciences, Kuala Lumpur, Malaysia, 6–8 July 2018; pp. 1–6. [Google Scholar]
- Yang, F.; Watson, P.; Koukoula, M.; Anagnostou, E.N. Enhancing Weather-Related Power Outage Prediction by Event Severity Classification. IEEE Access 2020, 8, 60029–60042. [Google Scholar] [CrossRef]
- Ryan, P.C.; Stewart, M.G.; Spencer, N.; Li, Y. Reliability Assessment of Power Pole Infrastructure Incorporating Deterioration and Network Maintenance. Reliab. Eng. Syst. Saf. 2014, 132, 261–273. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Guo, Y.; Zhong, M.; Li, Q.; Gao, C. System Operational Reliability Evaluation Based on Dynamic Bayesian Network and XGBoost. Reliab. Eng. Syst. Saf. 2022, 225, 108622. [Google Scholar] [CrossRef]
- Khomami, M.S.; Sepasian, M.S. Pre-Hurricane Optimal Placement Model of Repair Teams to Improve Distribution Network Resilience. Electr. Power Syst. Res. 2018, 165, 1–8. [Google Scholar] [CrossRef]
- Yang, Y.; Khan, F.; Thodi, P.; Abbassi, R. Corrosion Induced Failure Analysis of Subsea Pipelines. Reliab. Eng. Syst. Saf. 2017, 159, 214–222. [Google Scholar] [CrossRef]
- Sajid, Z.; Khan, F.; Zhang, Y. Integration of Interpretive Structural Modelling with Bayesian Network for Biodiesel Performance Analysis. Renew. Energy 2017, 107, 194–203. [Google Scholar] [CrossRef]
- Taleb-Berrouane, M.; Khan, F.; Hawboldt, K. Corrosion Risk Assessment Using Adaptive Bow-Tie (ABT) Analysis. Reliab. Eng. Syst. Saf. 2021, 214, 107731. [Google Scholar] [CrossRef]
- Adumene, S.; Khan, F.; Adedigba, S.; Zendehboudi, S. Offshore System Safety and Reliability Considering Microbial Influenced Multiple Failure Modes and Their Interdependencies. Reliab. Eng. Syst. Saf. 2021, 215, 107862. [Google Scholar] [CrossRef]
- Khakzad, N.; Khan, F.; Amyotte, P. Safety Analysis in Process Facilities: Comparison of Fault Tree and Bayesian Network Approaches. Reliab. Eng. Syst. Saf. 2011, 96, 925–932. [Google Scholar] [CrossRef]
- Taleb-Berrouane, M.; Khan, F.; Hawboldt, K.; Eckert, R.; Skovhus, T.L. Model for Microbiologically Influenced Corrosion Potential Assessment for the Oil and Gas Industry. Corros. Eng. Sci. Technol. 2018, 53, 378–392. [Google Scholar] [CrossRef]
- Bensi, M.; Der Kiureghian, A.; Straub, D. Efficient Bayesian Network Modeling of Systems. Reliab. Eng. Syst. Saf. 2013, 112, 200–213. [Google Scholar] [CrossRef]
- Hassan, S.; Wang, J.; Kontovas, C.; Bashir, M. An Assessment of Causes and Failure Likelihood of Cross-Country Pipelines under Uncertainty Using Bayesian Networks. Reliab. Eng. Syst. Saf. 2022, 218, 108171. [Google Scholar] [CrossRef]
- Moradi, R.; Cofre-Martel, S.; Lopez Droguett, E.; Modarres, M.; Groth, K.M. Integration of Deep Learning and Bayesian Networks for Condition and Operation Risk Monitoring of Complex Engineering Systems. Reliab. Eng. Syst. Saf. 2022, 222, 108433. [Google Scholar] [CrossRef]
- Dao, U.; Sajid, Z.; Khan, F.; Zhang, Y. Dynamic Bayesian Network Model to Study Under-Deposit Corrosion. Reliab. Eng. Syst. Saf. 2023, 237, 109370. [Google Scholar] [CrossRef]
- Sajid, Z. A Dynamic Risk Assessment Model to Assess the Impact of the Coronavirus (COVID-19) on the Sustainability of the Biomass Supply Chain: A Case Study of a U.S. Biofuel Industry. Renew. Sustain. Energy Rev. 2021, 151, 111574. [Google Scholar] [CrossRef]
- Sajid, Z.; Khan, F.; Veitch, B. Dynamic Ecological Risk Modelling of Hydrocarbon Release Scenarios in Arctic Waters. Mar. Pollut. Bull. 2020, 153, 111001. [Google Scholar] [CrossRef]
- Rezaei, N.; Pezhmani, Y. Optimal Islanding Operation of Hydrogen Integrated Multi-Microgrids Considering Uncertainty and Unexpected Outages. J. Energy Storage 2022, 49, 104142. [Google Scholar] [CrossRef]
- Rezaei, N.; Pezhmani, Y.; Mohammadiani, R.P. Optimal Stochastic Self-Scheduling of a Water-Energy Virtual Power Plant Considering Data Clustering and Multiple Storage Systems. J. Energy Storage 2023, 65, 107366. [Google Scholar] [CrossRef]
- Taheri, B.; Safdarian, A.; Moeini-Aghtaie, M.; Lehtonen, M. Enhancing Resilience Level of Power Distribution Systems Using Proactive Operational Actions. IEEE Access 2019, 7, 137378–137389. [Google Scholar] [CrossRef]
- Poudel, S.; Dubey, A.; Bose, A. Risk-Based Probabilistic Quantification of Power Distribution System Operational Resilience. IEEE Syst. J. 2020, 14, 3506–3517. [Google Scholar] [CrossRef]
- Zhou, K.; Yang, S.; Shao, Z. Household Monthly Electricity Consumption Pattern Mining: A Fuzzy Clustering-Based Model and a Case Study. J. Clean. Prod. 2017, 141, 900–908. [Google Scholar] [CrossRef]
- McLoughlin, F.; Duffy, A.; Conlon, M. A Clustering Approach to Domestic Electricity Load Profile Characterisation Using Smart Metering Data. Appl. Energy 2015, 141, 190–199. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Kang, C.; Xia, Q. Clustering of Electricity Consumption Behavior Dynamics Toward Big Data Applications. IEEE Trans. Smart Grid 2016, 7, 2437–2447. [Google Scholar] [CrossRef]
- Ozawa, A.; Furusato, R.; Yoshida, Y. Determining the Relationship between a Household’s Lifestyle and Its Electricity Consumption in Japan by Analyzing Measured Electric Load Profiles. Energy Build. 2016, 119, 200–210. [Google Scholar] [CrossRef]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 1 January 1967; Volume 1, pp. 281–297. [Google Scholar]
- Galvani, S.; Rezaeian Marjani, S.; Morsali, J.; Ahmadi Jirdehi, M. A New Approach for Probabilistic Harmonic Load Flow in Distribution Systems Based on Data Clustering. Electr. Power Syst. Res. 2019, 176, 105977. [Google Scholar] [CrossRef]
- Bajwa, A.A.; Mokhlis, H.; Mekhlief, S.; Mubin, M.; Azam, M.M.; Sarwar, S. Resilience-Oriented Service Restoration Modelling Interdependent Critical Loads in Distribution Systems with Integrated Distributed Generators. IET Gener. Transm. Distrib. 2021, 15, 1257–1272. [Google Scholar] [CrossRef]
- GeNIe Modeler by BayesFusion, LLC. Available online: https://www.bayesfusion.com/genie/ (accessed on 2 February 2024).
- Yazdi, M.; Khan, F.; Abbassi, R.; Quddus, N. Resilience Assessment of a Subsea Pipeline Using Dynamic Bayesian Network. J. Pipeline Sci. Eng. 2022, 2, 100053. [Google Scholar] [CrossRef]
- Omogoye, O.S.; Folly, K.A.; Awodele, K.O. Review of Proactive Operational Measures for the Distribution Power System Resilience Enhancement Against Hurricane Events. In Proceedings of the 2021 Southern African Universities Power Engineering Conference/Robotics and Mechatronics/Pattern Recognition Association of South Africa (SAUPEC/RobMech/PRASA), Potchefstroom, South Africa, 27–29 January 2021; pp. 1–6. [Google Scholar]
- Naik, V.K.; Yadav, A. High Impedance Fault Detection and Classification on IEEE-15 Bus Radial Distribution System by Using Fuzzy Inference System. In Proceedings of the 2018 2nd International Conference on Power, Energy and Environment: Towards Smart Technology (ICEPE), Shillong, India, 1–2 June 2018; pp. 1–6. [Google Scholar]
- Hou, G.; Muraleetharan, K.K. Modeling the Resilience of Power Distribution Systems Subjected to Extreme Winds Considering Tree Failures: An Integrated Framework. Int. J. Disaster Risk Sci. 2023, 14, 194–208. [Google Scholar] [CrossRef]
- Muhammad, M.A.; Mokhlis, H.; Naidu, K.; Amin, A.; Franco, J.F.; Othman, M. Distribution Network Planning Enhancement via Network Reconfiguration and DG Integration Using Dataset Approach and Water Cycle Algorithm. J. Mod. Power Syst. Clean Energy 2020, 8, 86–93. [Google Scholar] [CrossRef]











| System Lines | From Bus—to Bus | HWSI | DBN | FC-MCS-SCENRED | ||
|---|---|---|---|---|---|---|
| (m/s) | Failure Probability | Outage Prediction | Failure Probability | Outage Prediction | ||
| 1 | 1−2 | 10.288 | 0.26 | 1 | 0 | 1 |
| 2 | 2−9 | 15.433 | 0.262 | 1 | 0.005 | 1 |
| 3 | 9−10 | 20.577 | 0.267 | 1 | 0.01 | 1 |
| 4 | 2−6 | 25.722 | 0.28 | 1 | 0.028 | 1 |
| 5 | 6−7 | 30.866 | 0.305 | 1 | 0.08 | 1 |
| 6 | 6−8 | 36.011 | 0.307 | 1 | 0.129 | 1 |
| 7 | 2−3 | 41.155 | 0.375 | 1 | 0.206 | 1 |
| 8 | 3−11 | 46.299 | 0.408 | 1 | 0.304 | 1 |
| 9 | 11−12 | 51.444 | 0.411 | 1 | 0.402 | 1 |
| 10 | 12−13 | 56.588 | 0.566 | 0 | 0.531 | 0 |
| 11 | 3−4 | 61.733 | 0.505 | 0 | 0.642 | 0 |
| 12 | 4−14 | 66.877 | 0.693 | 0 | 0.778 | 0 |
| 13 | 4−15 | 72.022 | 0.824 | 0 | 0.85 | 0 |
| 14 | 4−5 | 82.311 | 0.61 | 0 | 0.919 | 0 |
| System Lines | From Bus—to Bus | HWSI | DBN | FC-MCS-SCENRED | ||
|---|---|---|---|---|---|---|
| (m/s) | Failure Probability | Outage Prediction | Failure Probability | Outage Prediction | ||
| 1 | 1−2 | 58.115 | 0.569 | 0 | 0.597 | 0 |
| 2 | 2−3 | 59.903 | 0.613 | 0 | 0.573 | 0 |
| 3 | 3−4 | 61.691 | 0.639 | 0 | 0.653 | 0 |
| 4 | 4−5 | 63.479 | 0.653 | 0 | 0.655 | 0 |
| 5 | 5−6 | 50.068 | 0.332 | 1 | 0.383 | 1 |
| 6 | 6−7 | 50.962 | 0.391 | 1 | 0.397 | 1 |
| 7 | 7−8 | 51.856 | 0.428 | 1 | 0.416 | 1 |
| 8 | 8−9 | 52.750 | 0.450 | 1 | 0.434 | 1 |
| 9 | 9−10 | 42.915 | 0.234 | 1 | 0.206 | 1 |
| 10 | 10−11 | 43.586 | 0.236 | 1 | 0.234 | 1 |
| 11 | 11−12 | 44.257 | 0.244 | 1 | 0.241 | 1 |
| 12 | 12−13 | 44.927 | 0.254 | 1 | 0.250 | 1 |
| 13 | 13−14 | 33.528 | 0.093 | 1 | 0.108 | 1 |
| 14 | 14−15 | 34.422 | 0.103 | 1 | 0.091 | 1 |
| 15 | 15−16 | 35.316 | 0.122 | 1 | 0.101 | 1 |
| 16 | 16−17 | 36.210 | 0.129 | 1 | 0.120 | 1 |
| 17 | 17−18 | 37.104 | 0.138 | 1 | 0.145 | 1 |
| 18 | 2−19 | 59.903 | 0.613 | 0 | 0.629 | 0 |
| 19 | 19−20 | 54.538 | 0.476 | 1 | 0.484 | 1 |
| 20 | 20−21 | 55.433 | 0.494 | 1 | 0.46 | 1 |
| 21 | 21−22 | 56.327 | 0.519 | 0 | 0.486 | 0 |
| 22 | 3−23 | 61.691 | 0.639 | 0 | 0.631 | 0 |
| 23 | 23−24 | 67.056 | 0.763 | 0 | 0.760 | 0 |
| 24 | 24−25 | 68.844 | 0.801 | 0 | 0.814 | 0 |
| 25 | 6−26 | 50.962 | 0.391 | 1 | 0.405 | 1 |
| 26 | 26−27 | 46.268 | 0.271 | 1 | 0.305 | 1 |
| 27 | 27−28 | 46.939 | 0.316 | 1 | 0.315 | 1 |
| 28 | 28−29 | 48.056 | 0.354 | 1 | 0.347 | 1 |
| 29 | 29−30 | 37.998 | 0.151 | 1 | 0.154 | 1 |
| 30 | 30−31 | 38.892 | 0.175 | 1 | 0.163 | 1 |
| 31 | 31−32 | 39.786 | 0.196 | 1 | 0.162 | 1 |
| 32 | 32−33 | 40.680 | 0.216 | 1 | 0.175 | 1 |
| 33 | 8−21 | 52.750 | 0.450 | 1 | 0.434 | 1 |
| 34 | 9−15 | 42.915 | 0.234 | 1 | 0.197 | 1 |
| 35 | 12−22 | 44.927 | 0.254 | 1 | 0.275 | 1 |
| 36 | 18−33 | 42.468 | 0.221 | 1 | 0.204 | 1 |
| 37 | 25−29 | 49.397 | 0.374 | 1 | 0.399 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatima, K.; Shareef, H. Dynamic Bayesian Network Model for Overhead Power Lines Affected by Hurricanes. Forecasting 2025, 7, 11. https://doi.org/10.3390/forecast7010011
Fatima K, Shareef H. Dynamic Bayesian Network Model for Overhead Power Lines Affected by Hurricanes. Forecasting. 2025; 7(1):11. https://doi.org/10.3390/forecast7010011
Chicago/Turabian StyleFatima, Kehkashan, and Hussain Shareef. 2025. "Dynamic Bayesian Network Model for Overhead Power Lines Affected by Hurricanes" Forecasting 7, no. 1: 11. https://doi.org/10.3390/forecast7010011
APA StyleFatima, K., & Shareef, H. (2025). Dynamic Bayesian Network Model for Overhead Power Lines Affected by Hurricanes. Forecasting, 7(1), 11. https://doi.org/10.3390/forecast7010011






