Comparison of ARIMA, SutteARIMA, and Holt-Winters, and NNAR Models to Predict Food Grain in India
Abstract
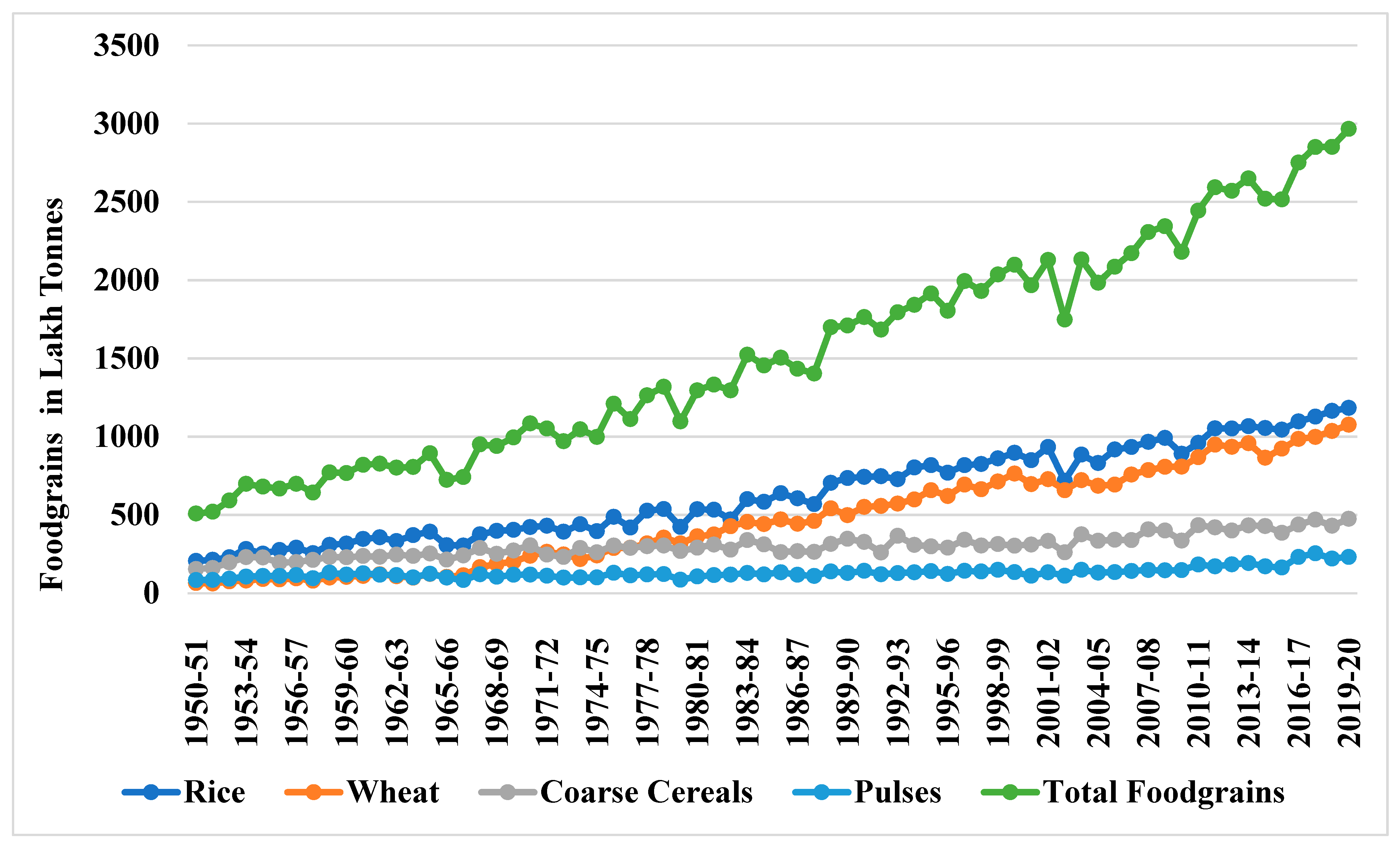
1. Overview of the Study
Research Gap
2. Model
2.1. ARIMA
2.2. α-Sutte Indicator
2.3. SutteARIMA
2.4. Holt-Winters
2.5. Neural Network Auto-Regressive (NNAR)
3. Methodology
4. Experimental Results and Discussion
4.1. Result of ARIMA Model
4.2. Result of SutteARIMA Model
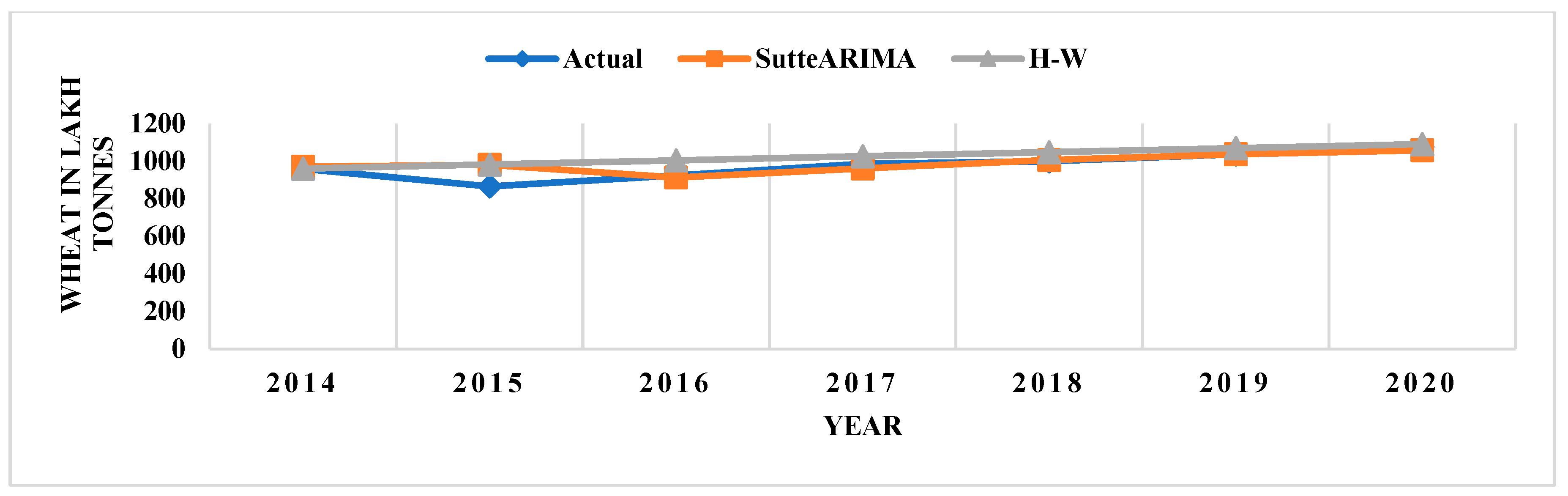
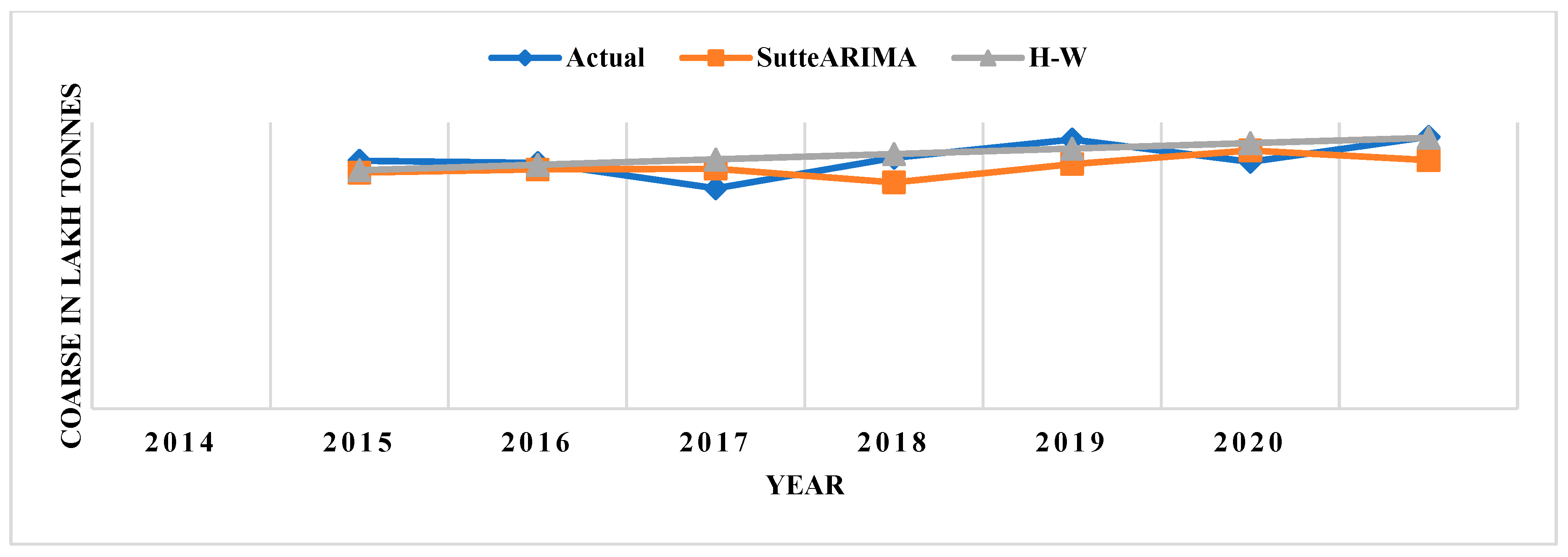
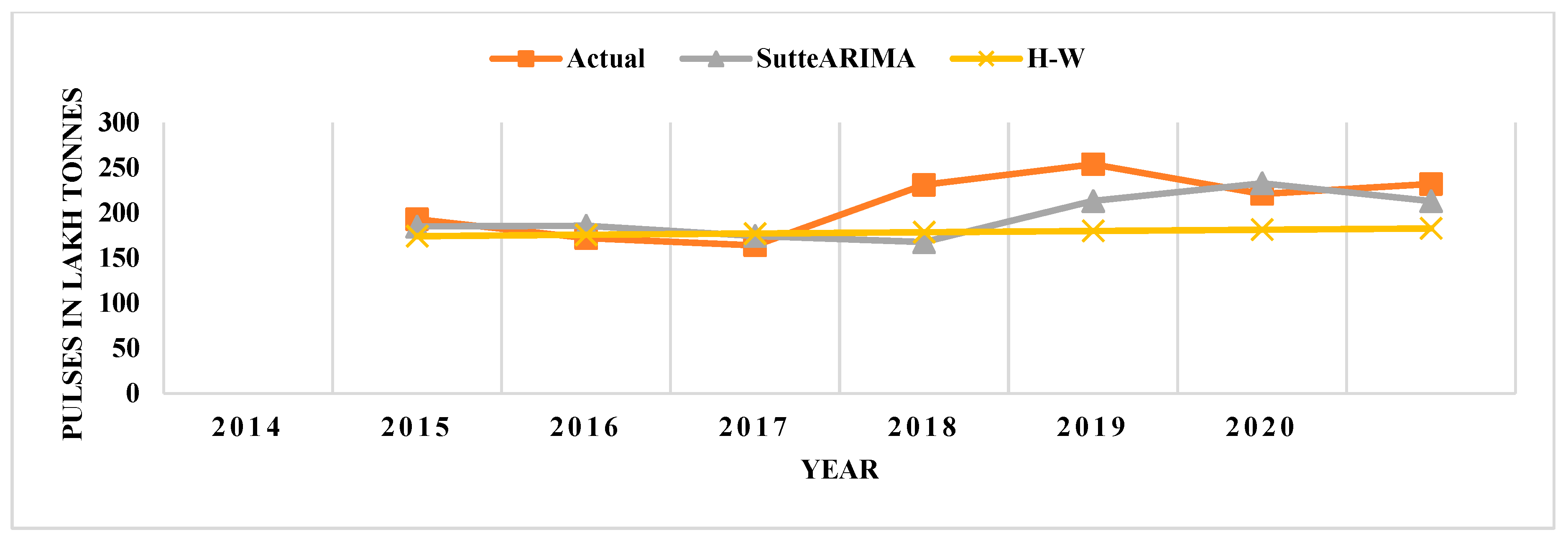
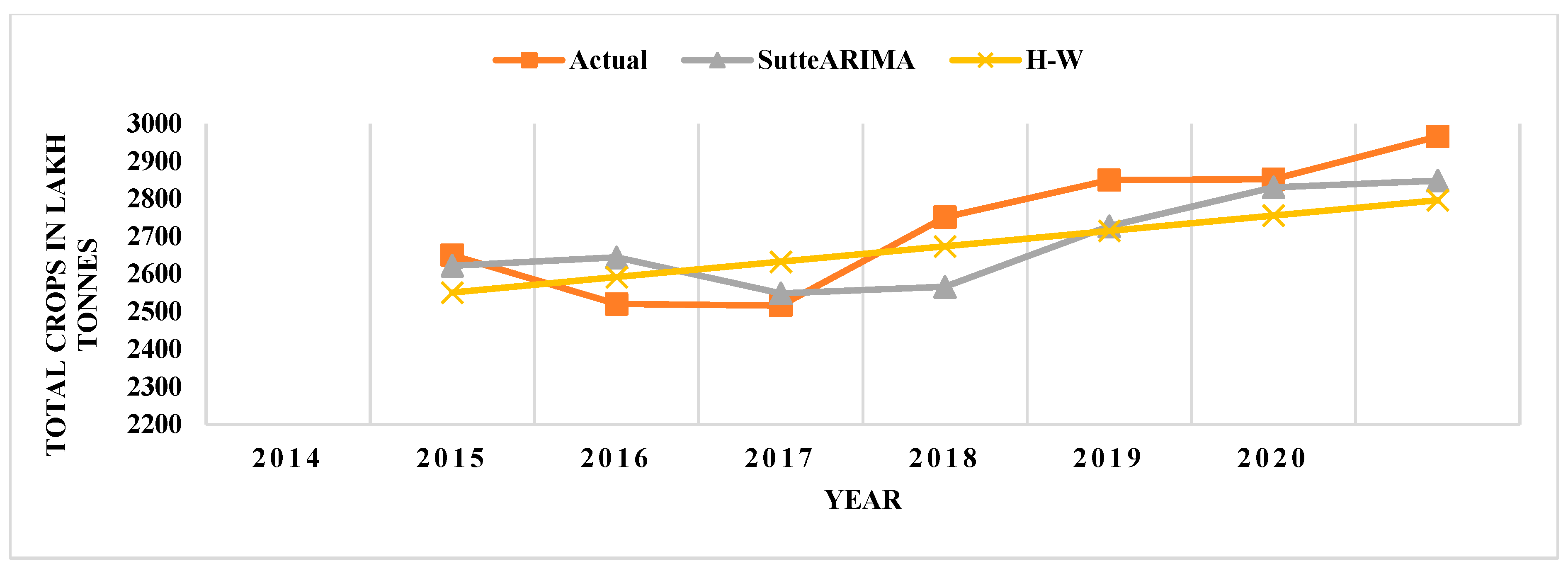
4.3. Comparison of SutteARIMA and Holt-Winters (H-W)
4.4. Result of NNAR Model
5. Conclusions
6. Policy Implication and Further Suggestion for Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, J.; Pray, C.; Rozelle, S. Enhancing the Crops to Feed the Poor. Nature 2002, 418, 678–684. [Google Scholar] [CrossRef] [PubMed]
- Ray, D.K.; Ramankutty, N.; Mueller, N.D.; West, P.C.; Foley, J.A. Recent Patterns of Crop Yield Growth and Stagnation. Nat. Commun. 2012, 3, 1293. [Google Scholar] [CrossRef]
- von Braun, J. Food Insecurity, Hunger and Malnutrition: Necessary Policy and Technology Changes. New Biotechnol. 2010, 27, 449–452. [Google Scholar] [CrossRef] [PubMed]
- Pathak, P.K.; Singh, A. Trends in Malnutrition among Children in India: Growing Inequalities across Different Economic Groups. Soc. Sci. Med. 2011, 73, 576–585. [Google Scholar] [CrossRef]
- Chatterjee, N.; Fernandes, G.; Hernandez, M. Food Insecurity in Urban Poor Households in Mumbai, India. Food Secur. 2012, 4, 619–632. [Google Scholar] [CrossRef]
- FAO. Food and Agriculture Organization of the United Nations. Available online: http://www.fao.org/home/en/ (accessed on 31 May 2021).
- Le Mouël, C.; Forslund, A. How Can We Feed the World in 2050? A Review of the Responses from Global Scenario Studies. Eur. Rev. Agric. Econ. 2017, 44, 541–591. [Google Scholar] [CrossRef]
- Pingali, P.; Aiyar, A.; Abraham, M.; Rahman, A. Indian Food Systems towards 2050: Challenges and Opportunities. In Transforming Food Systems for a Rising India; Palgrave Studies in Agricultural Economics and Food Policy; Pingali, P., Aiyar, A., Abraham, M., Rahman, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 1–14. ISBN 978-3-030-14409-8. [Google Scholar]
- van Klompenburg, T.; Kassahun, A.; Catal, C. Crop Yield Prediction Using Machine Learning: A Systematic Literature Review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Guo, W.W.; Xue, H. Crop Yield Forecasting Using Artificial Neural Networks: A Comparison between Spatial and Temporal Models. Math. Probl. Eng. 2014, 2014, 857865. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef]
- Veenadhari, S.; Misra, B.; Singh, C. Machine Learning Approach for Forecasting Crop Yield Based on Climatic Parameters. In Proceedings of the 2014 International Conference on Computer Communication and Informatics, Coimbatore, India, 3–5 January 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–5. [Google Scholar]
- Paul, R.K.; Sinha, K. Forecasting Crop Yield: A Comparitve Assessment of Arimax and Narx Model. RASHI J. Soc. Appl. Stat. Agric. Allied Sci. 2016, 1, 77–85. [Google Scholar]
- Kandiannan, K.; Chandaragiri, K.K.; Sankaran, N.; Balasubramanian, T.N.; Kailasam, C. Crop-Weather Model for Turmeric Yield Forecasting for Coimbatore District, Tamil Nadu, India. Agric. For. Meteorol. 2002, 112, 133–137. [Google Scholar] [CrossRef]
- Gandhi, N.; Armstrong, L.J. Rice Crop Yield Forecasting of Tropical Wet and Dry Climatic Zone of India Using Data Mining Techniques. In Proceedings of the 2016 IEEE International Conference on Advances in Computer Applications (ICACA), Coimbatore, India, 24 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 357–363. [Google Scholar]
- Woodhouse, P. Technology, Environment and the Productivity Problem in African Agriculture: Comment on the World Development Report 2008. J. Agrar. Chang. 2009, 9, 263–276. [Google Scholar] [CrossRef]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine Learning Approaches for Crop Yield Prediction and Nitrogen Status Estimation in Precision Agriculture: A Review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Prassanna, A.S.; Harshanand, B.A.; Srishti, B.; Chaitanya, R.; Soundari, K.N.; Sriram, S.; Kumar, V.M.; Chennamsetti, V.; Venkateshwaran, G.; Maurya, P.K. Crop Value Forecasting Using Decision Tree Regressor and Models. Eur. J. Mol. Clin. Med. 2020, 7, 3702–32722. [Google Scholar]
- Sujatha, R.; Isakki, P. A Study on Crop Yield Forecasting Using Classification Techniques. In Proceedings of the 2016 International Conference on Computing Technologies and Intelligent Data Engineering (ICCTIDE’16), Kovilpatti, India, 7–9 January 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–4. [Google Scholar]
- Alhnaity, B.; Pearson, S.; Leontidis, G.; Kollias, S. Using Deep Learning to Predict Plant Growth and Yield in Greenhouse Environments. Acta Hortic. 2020, 1296, 425–432. [Google Scholar] [CrossRef]
- Banik, D. The Hungry Nation: Food Policy and Food Politics in India. Food Ethics 2016, 1, 29–45. [Google Scholar] [CrossRef]
- Sherman, T.C. From ‘Grow More Food’ to ‘Miss a Meal’: Hunger, Development and the Limits of Post-Colonial Nationalism in India, 1947–1957. South Asia J. South Asian Stud. 2013, 36, 571–588. [Google Scholar] [CrossRef]
- Hazra, K.K.; Bohra, A. Increasing Relevance of Pulse Crops to Sustainable Intensification of Indian Agriculture. Natl. Acad. Sci. Lett. 2021, 44, 1–3. [Google Scholar] [CrossRef]
- Mittal, S.; Dai, H.; Fujimori, S.; Masui, T. Bridging Greenhouse Gas Emissions and Renewable Energy Deployment Target: Comparative Assessment of China and India. Appl. Energy 2016, 166, 301–313. [Google Scholar] [CrossRef]
- Birthal, P.S.; Joshi, P.K.; Roy, D.; Thorat, A. Diversification in Indian Agriculture toward High-Value Crops: The Role of Small Farmers. Can. J. Agric. Econ. Can. Agroecon. 2013, 61, 61–91. [Google Scholar] [CrossRef]
- Thomas, K.T. Crop Prediction Using Machine Learning. Int. J. Future Gener. Commun. Netw. 2020, 13, 6. [Google Scholar]
- Kang, Y.; Ozdogan, M.; Zhu, X.; Ye, Z.; Hain, C.; Anderson, M. Comparative Assessment of Environmental Variables and Machine Learning Algorithms for Maize Yield Prediction in the US Midwest. Environ. Res. Lett. 2020, 15, 064005. [Google Scholar] [CrossRef]
- Zheng, H.; Li, W.; Jiang, J.; Liu, Y.; Cheng, T.; Tian, Y.; Zhu, Y.; Cao, W.; Zhang, Y.; Yao, X. A Comparative Assessment of Different Modeling Algorithms for Estimating Leaf Nitrogen Content in Winter Wheat Using Multispectral Images from an Unmanned Aerial Vehicle. Remote Sens. 2018, 10, 2026. [Google Scholar] [CrossRef]
- Sivanandhini, P.; Prakash, J. Crop Yield Prediction Analysis Using Feed Forward and Recurrent Neural Network. Int. J. Innov. Sci. Res. Technol. 2020, 5, 1092–1096. [Google Scholar]
- Fung, K.F.; Huang, Y.F.; Koo, C.H.; Mirzaei, M. Improved SVR Machine Learning Models for Agricultural Drought Prediction at Downstream of Langat River Basin, Malaysia. J. Water Clim. Chang. 2020, 11, 1383–1398. [Google Scholar] [CrossRef]
- Shao, Y.E.; Dai, J.-T. Integrated Feature Selection of ARIMA with Computational Intelligence Approaches for Food Crop Price Prediction. Complexity 2018, 2018, e1910520. [Google Scholar] [CrossRef]
- Zou, H.F.; Xia, G.P.; Yang, F.T.; Wang, H.Y. An Investigation and Comparison of Artificial Neural Network and Time Series Models for Chinese Food Grain Price Forecasting. Neurocomputing 2007, 70, 2913–2923. [Google Scholar] [CrossRef]
- Paidipati, K.; Banik, A. Forecasting of Rice Cultivation in India-A Comparative Analysis with ARIMA and LSTM-NN Models. ICST Trans. Scalable Inf. Syst. 2018, 7, 161409. [Google Scholar] [CrossRef]
- Maya Gopal, P.S.; Bhargavi, R. A Novel Approach for Efficient Crop Yield Prediction. Comput. Electron. Agric. 2019, 165, 104968. [Google Scholar] [CrossRef]
- Ahmar, A.S.; Boj, E. SutteARIMA: Short-Term Forecasting Method, a Case: Covid-19 and Stock Market in Spain. Sci. Total Environ. 2020, 729, 138883. [Google Scholar] [CrossRef]
- Ahmar, A.; Boj, E. Current Research in Behavioral Sciences Will COVID-19 Confirmed Cases in the USA Reach 3 Million? A Forecasting Approach by Using SutteARIMA Method. Curr. Res. Behav. Sci. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Ahmar, A.S.; Rusli, R. Will Covid-19 Cases in the World Reach 4 Million? A Forecasting Approach Using SutteARIMA. JOIV Int. J. Inform. Vis. 2020, 4, 159–161. [Google Scholar] [CrossRef]
- Trull, O.; García-Díaz, J.C.; Troncoso, A. Initialization Methods for Multiple Seasonal Holt-Winters Forecasting Models. Mathematics 2020, 8, 268. [Google Scholar] [CrossRef]
- Paraschiv, D.; Tudor, C.; Petrariu, R. The Textile Industry and Sustainable Development: A Holt-Winters Forecasting Investigation for the Eastern European Area. Sustainability 2015, 7, 1280–1291. [Google Scholar] [CrossRef]
- Kahforoushan, E.; Zarif, M.; Mashahir, E.B. Prediction of Added Value of Agricultural Subsections Using Artificial Neural Networks: Box-Jenkins and Holt-Winters Methods. J. Dev. Agric. Econ. 2010, 2, 115–121. [Google Scholar] [CrossRef]
- Michel, L.; Makowski, D. Comparison of Statistical Models for Analyzing Wheat Yield Time Series. PLoS ONE 2013, 8, e78615. [Google Scholar] [CrossRef]
- Ahmar, A.S.; Rahman, A.; Mulbar, U. α-Sutte Indicator: A New Method for Time Series Forecasting. J. Phys. Conf. Ser. 2018, 1040, 012018. [Google Scholar] [CrossRef]
- Zhang, G.; Eddy Patuwo, B.; Hu, M.Y. Forecasting with Artificial Neural Networks: The State of the Art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Reserver Bank of India. Dbie-Rbi: Database of Indian Economy. Available online: https://dbie.rbi.org.in/DBIE/dbie.rbi?site=statistics (accessed on 20 May 2021).
- Ahmar, A.S. RcmdrPlugin. SutteForecastR: An RcmdrPlugin for Forecasting Data. J. Phys. Conf. Ser. 2018, 1028, 012224. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H. A New Metric of Absolute Percentage Error for Intermittent Demand Forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Adebiyi, A.A.; Adewumi, A.O.; Ayo, C.K. Comparison of ARIMA and Artificial Neural Networks Models for Stock Price Prediction. J. Appl. Math. 2014, 2014, 614342. [Google Scholar] [CrossRef]
- Tratar, L.F.; Strmčnik, E. The Comparison of Holt-Winters Method and Multiple Regression Method: A Case Study. Energy 2016, 109, 266–276. [Google Scholar] [CrossRef]
- Maleki, A.; Nasseri, S.; Aminabad, M.S.; Hadi, M. Comparison of ARIMA and NNAR Models for Forecasting Water Treatment Plant’s Influent Characteristics. KSCE J. Civ. Eng. 2018, 22, 3233–3245. [Google Scholar] [CrossRef]
- Thoplan, R. Simple v/s Sophisticated Methods of Forecasting for Mauritius Monthly Tourist Arrival Data. Int. J. Stat. Appl. 2014, 4, 217–223. [Google Scholar]
- Davidescu, A.A.; Apostu, S.-A.; Paul, A. Comparative Analysis of Different Univariate Forecasting Methods in Modelling and Predicting the Romanian Unemployment Rate for the Period 2021-2022. Entropy 2021, 23, 325. [Google Scholar] [CrossRef]
- Chakraborty, T.; Chattopadhyay, S.; Ghosh, I. Forecasting Dengue Epidemics Using a Hybrid Methodology. Phys. Stat. Mech. Its Appl. 2019, 527, 121266. [Google Scholar] [CrossRef]

| Year | Actual | ARIMA (1,1,0) with Drift | APE | SutteARIMA | APE | H-W | APE | NNAR(1,1) | APE |
|---|---|---|---|---|---|---|---|---|---|
| 2014 | 959 | 960.08 | 0.11 | 969.68 | 1.11 | 959.96 | 0.10 | 934.12 | 2.59 |
| 2015 | 865 | 970.15 | 12.16 | 980.23 | 13.32 | 981.84 | 13.51 | 933.36 | 7.90 |
| 2016 | 923 | 985.99 | 6.82 | 912.37 | 1.15 | 1003.73 | 8.75 | 932.71 | 1.05 |
| 2017 | 985 | 999.61 | 1.48 | 960.48 | 2.49 | 1025.62 | 4.12 | 932.16 | 5.36 |
| 2018 | 999 | 1014.08 | 1.51 | 1005.33 | 0.63 | 1047.50 | 4.85 | 931.68 | 6.73 |
| 2019 | 1036 | 1028.22 | 0.75 | 1036.61 | 0.06 | 1069.39 | 3.22 | 931.26 | 10.10 |
| 2020 | 1076 | 1042.50 | 3.11 | 1058.55 | 1.62 | 1091.27 | 1.42 | 930.91 | 13.48 |
| Year | Actual | ARIMA (0,1,1) with Drift | APE | SutteARIMA | APE | H-W | APE | NNAR (1,1) | APE |
|---|---|---|---|---|---|---|---|---|---|
| 2014 | 1067 | 1034.46 | 3.05 | 1071.21 | 0.39 | 1037.96 | 2.72 | 1011.00 | 5.24 |
| 2015 | 1055 | 1047.62 | 0.70 | 1075.88 | 1.98 | 1052.62 | 0.23 | 985.60 | 6.57 |
| 2016 | 1044 | 1060.78 | 1.61 | 1058.25 | 1.37 | 1067.28 | 2.23 | 968.77 | 7.20 |
| 2017 | 1097 | 1073.93 | 2.10 | 1057.67 | 3.59 | 1081.94 | 1.37 | 957.16 | 12.74 |
| 2018 | 1128 | 1087.09 | 3.63 | 1097.28 | 2.72 | 1096.59 | 2.78 | 948.92 | 15.87 |
| 2019 | 1165 | 1100.25 | 5.56 | 1126.59 | 3.30 | 1111.25 | 4.61 | 942.96 | 19.05 |
| 2020 | 1184 | 1113.40 | 5.96 | 1159.76 | 2.05 | 1125.91 | 4.91 | 938.61 | 20.72 |
| Year | Actual | ARIMA (0,1,1) with Drift | APE | SutteARIMA | APE | H-W | APE | NNAR (2,2) | APE |
|---|---|---|---|---|---|---|---|---|---|
| 2014 | 433 | 398.64 | 7.93 | 412.19 | 4.81 | 416.32 | 3.85 | 387.98 | 10.39 |
| 2015 | 429 | 402.06 | 6.28 | 417.70 | 2.63 | 425.78 | 0.75 | 383.05 | 10.70 |
| 2016 | 385 | 405.48 | 5.32 | 419.04 | 8.84 | 435.23 | 13.05 | 380.02 | 1.29 |
| 2017 | 438 | 408.90 | 6.64 | 395.07 | 9.80 | 444.69 | 1.53 | 378.54 | 13.57 |
| 2018 | 470 | 412.31 | 12.27 | 426.96 | 9.16 | 454.15 | 3.37 | 377.66 | 19.64 |
| 2019 | 431 | 415.73 | 3.54 | 450.85 | 4.61 | 463.60 | 7.56 | 377.19 | 12.48 |
| 2020 | 475 | 419.15 | 11.76 | 433.78 | 8.68 | 473.06 | 0.41 | 376.92 | 20.64 |
| Year | Actual | ARIMA (0,1,1) with Drift | APE | SutteARIMA | APE | H-W | APE | NNAR (2,2) | APE |
|---|---|---|---|---|---|---|---|---|---|
| 2014 | 193 | 173.30 | 10.21 | 184.90 | 4.20 | 174.28 | 9.70 | 178.34 | 7.59 |
| 2015 | 172 | 174.63 | 1.53 | 185.82 | 8.03 | 175.71 | 2.16 | 178.53 | 3.80 |
| 2016 | 164 | 175.95 | 7.29 | 174.46 | 6.38 | 177.13 | 8.01 | 178.34 | 8.74 |
| 2017 | 231 | 177.28 | 23.26 | 167.75 | 27.38 | 178.56 | 22.70 | 178.33 | 22.80 |
| 2018 | 254 | 178.61 | 29.68 | 213.26 | 16.04 | 179.99 | 29.14 | 178.32 | 29.80 |
| 2019 | 221 | 179.93 | 18.58 | 232.74 | 5.31 | 181.41 | 17.91 | 178.32 | 19.31 |
| 2020 | 232 | 181.26 | 21.87 | 213.09 | 8.15 | 182.84 | 21.19 | 178.32 | 23.14 |
| Year | Actual | ARIMA (0,1,1) with Drift | APE | SutteARIMA | APE | H-W | APE | NNAR (1,1) | APE |
|---|---|---|---|---|---|---|---|---|---|
| 2014 | 2650 | 2536.40 | 4.29 | 2621.95 | 1.06 | 2550.90 | 3.74 | 2534.96 | 4.34 |
| 2015 | 2520 | 2568.49 | 1.92 | 2644.35 | 4.93 | 2591.82 | 2.85 | 2506.17 | 0.55 |
| 2016 | 2516 | 2600.57 | 3.36 | 2548.88 | 1.31 | 2632.74 | 4.64 | 2482.89 | 1.32 |
| 2017 | 2751 | 2632.66 | 4.30 | 2565.91 | 6.73 | 2673.66 | 2.81 | 2463.88 | 10.44 |
| 2018 | 2850 | 2664.74 | 6.50 | 2727.00 | 4.32 | 2714.58 | 4.75 | 2448.24 | 14.10 |
| 2019 | 2852 | 2696.83 | 5.44 | 2830.45 | 0.76 | 2755.50 | 3.38 | 2435.30 | 14.61 |
| 2020 | 2966 | 2728.91 | 7.99 | 2848.49 | 3.96 | 2796.42 | 5.72 | 2424.52 | 18.26 |
| Foodgrains | Forecasting Models | MAPE | MSE |
|---|---|---|---|
| Wheat | ARIMA (1,1,0) with drift | 3.71 | 339.78 |
| SutteARIMA | 2.91 | 294.93 | |
| Holt-Winters | 5.14 | 520.84 | |
| NNAR (1,1) | 6.74 | 912.86 | |
| Rice | ARIMA (0,1,1) with drift | 3.23 | 260.77 |
| SutteARIMA | 2.20 | 106.32 | |
| Holt-Winters | 2.69 | 180.96 | |
| NNAR (1,1) | 12.49 | 3566.22 | |
| Coarse | ARIMA (0,1,1) with drift | 7.68 | 201.08 |
| SutteARIMA | 6.93 | 153.24 | |
| Holt-Winters | 4.36 | 85.20 | |
| NNAR (2,2) | 12.67 | 586.46 | |
| Pulses | ARIMA (0,1,1) with drift | 16.06 | 272.83 |
| SutteARIMA | 10.78 | 133.09 | |
| Holt-Winters | 15.83 | 260.16 | |
| NNAR (2,2) | 16.45 | 278.95 | |
| Total Foodgrains | ARIMA (0,1,1) with drift | 4.83 | 3082.16 |
| SutteARIMA | 3.29 | 1652.90 | |
| Holt-Winters | 3.98 | 1857.13 | |
| NNAR (2,2) | 9.09 | 14,800.21 |
| Year | Wheat | Rice | Coarse | Pulses | Total Food Grain | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F * | U | L | F * | U | L | F * | U | L | F * | U | L | F * | U | L | |
| 2021 | 1072.74 | 979.80 | 1165.69 | 1174.26 | 1124.20 | 1174.26 | 446.74 | 411.37 | 482.10 | 229.08 | 180.67 | 277.50 | 2894.25 | 2698.61 | 3089.90 |
| 2022 | 1089.59 | 973.35 | 1205.83 | 1188.76 | 1118.00 | 1188.76 | 451.67 | 416.30 | 487.03 | 236.803 | 186.89 | 286.72 | 2938.14 | 2674.80 | 3201.48 |
| 2023 | 1106.44 | 970.81 | 1242.08 | 1203.27 | 1116.58 | 1203.27 | 456.60 | 421.23 | 491.96 | 244.521 | 193.14 | 295.91 | 2982.03 | 2665.03 | 3299.03 |
| 2024 | 1123.29 | 970.66 | 1275.92 | 1217.77 | 1117.64 | 1217.77 | 461.53 | 426.16 | 496.89 | 252.239 | 199.41 | 305.07 | 3025.91 | 2663.01 | 3388.83 |
| 2025 | 1140.14 | 972.19 | 1308.09 | 1232.27 | 1120.28 | 1232.27 | 466.46 | 431.09 | 501.82 | 259.95 | 205.72 | 314.20 | 3069.80 | 2666.10 | 3473.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmar, A.S.; Singh, P.K.; Ruliana, R.; Pandey, A.K.; Gupta, S. Comparison of ARIMA, SutteARIMA, and Holt-Winters, and NNAR Models to Predict Food Grain in India. Forecasting 2023, 5, 138-152. https://doi.org/10.3390/forecast5010006
Ahmar AS, Singh PK, Ruliana R, Pandey AK, Gupta S. Comparison of ARIMA, SutteARIMA, and Holt-Winters, and NNAR Models to Predict Food Grain in India. Forecasting. 2023; 5(1):138-152. https://doi.org/10.3390/forecast5010006
Chicago/Turabian StyleAhmar, Ansari Saleh, Pawan Kumar Singh, R. Ruliana, Alok Kumar Pandey, and Stuti Gupta. 2023. "Comparison of ARIMA, SutteARIMA, and Holt-Winters, and NNAR Models to Predict Food Grain in India" Forecasting 5, no. 1: 138-152. https://doi.org/10.3390/forecast5010006
APA StyleAhmar, A. S., Singh, P. K., Ruliana, R., Pandey, A. K., & Gupta, S. (2023). Comparison of ARIMA, SutteARIMA, and Holt-Winters, and NNAR Models to Predict Food Grain in India. Forecasting, 5(1), 138-152. https://doi.org/10.3390/forecast5010006








