A Day-Ahead Photovoltaic Power Prediction via Transfer Learning and Deep Neural Networks
Abstract
1. Introduction
2. Methodology
2.1. Linear Model
2.2. Feed-Forward Neural Network
2.3. Convolutional Neural Network
2.4. Long Short-Term Memory Network
2.5. Transfer Learning
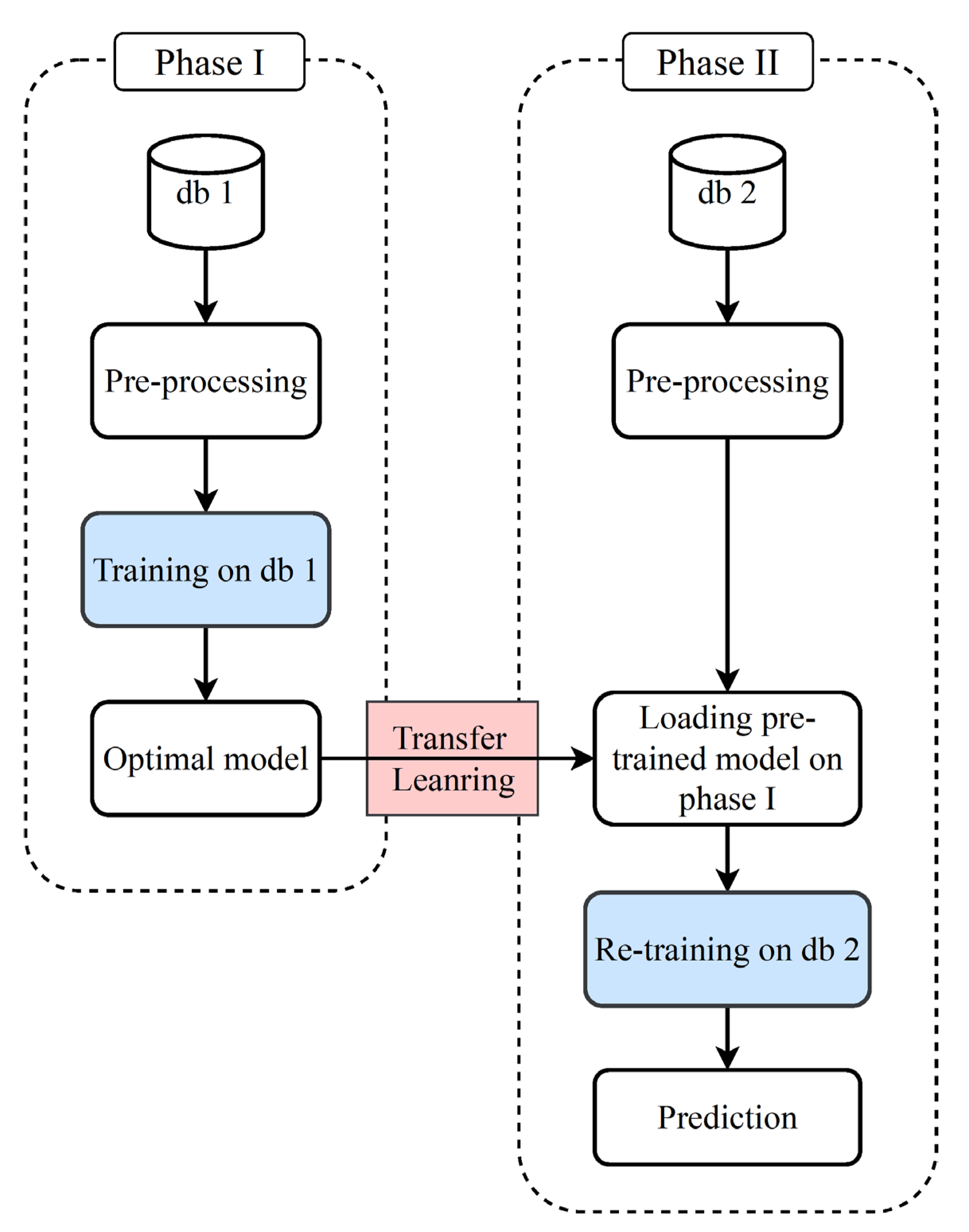
2.6. The Model Framework
3. Results and Discussion
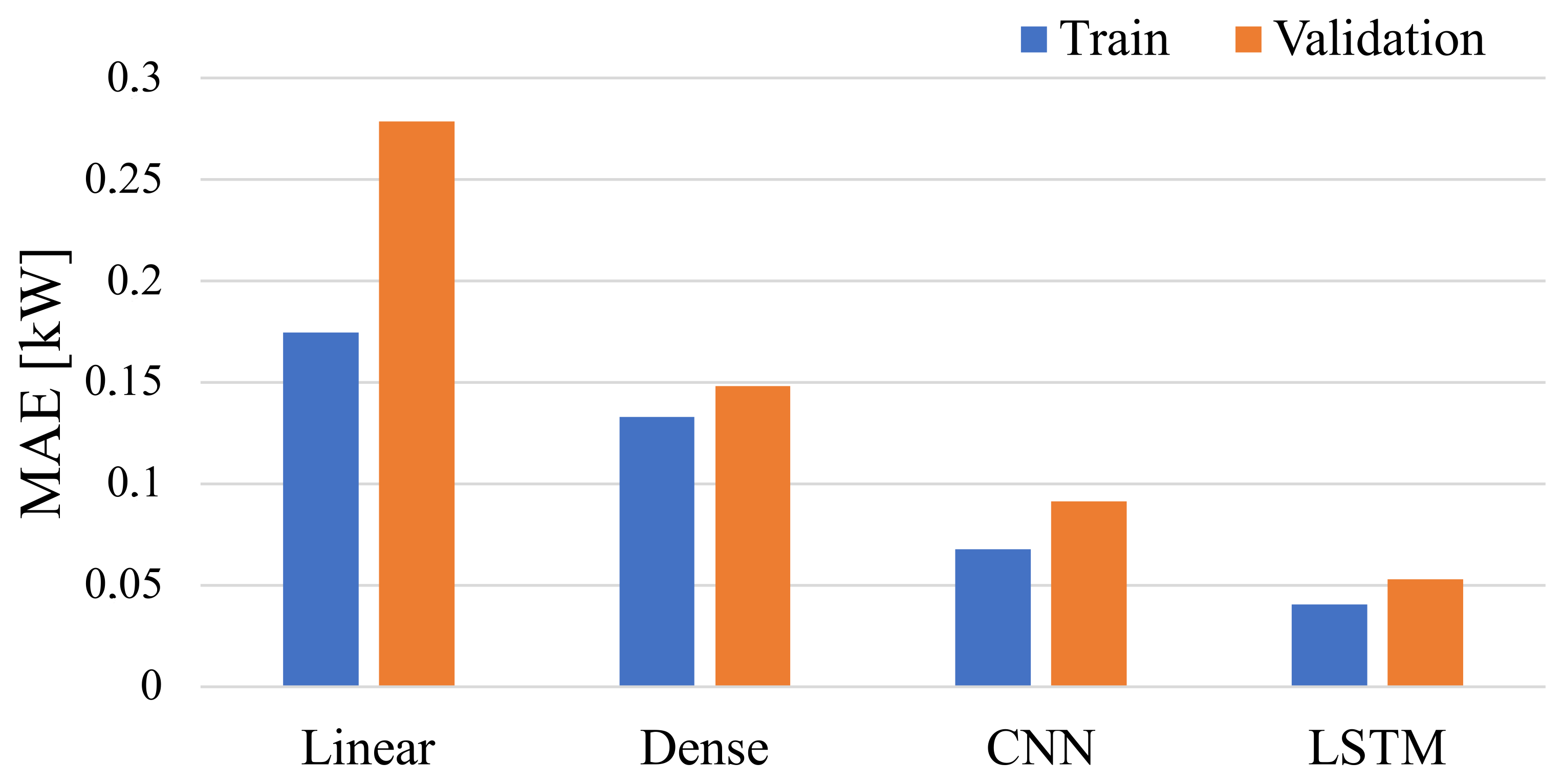
3.1. Training the Base Model
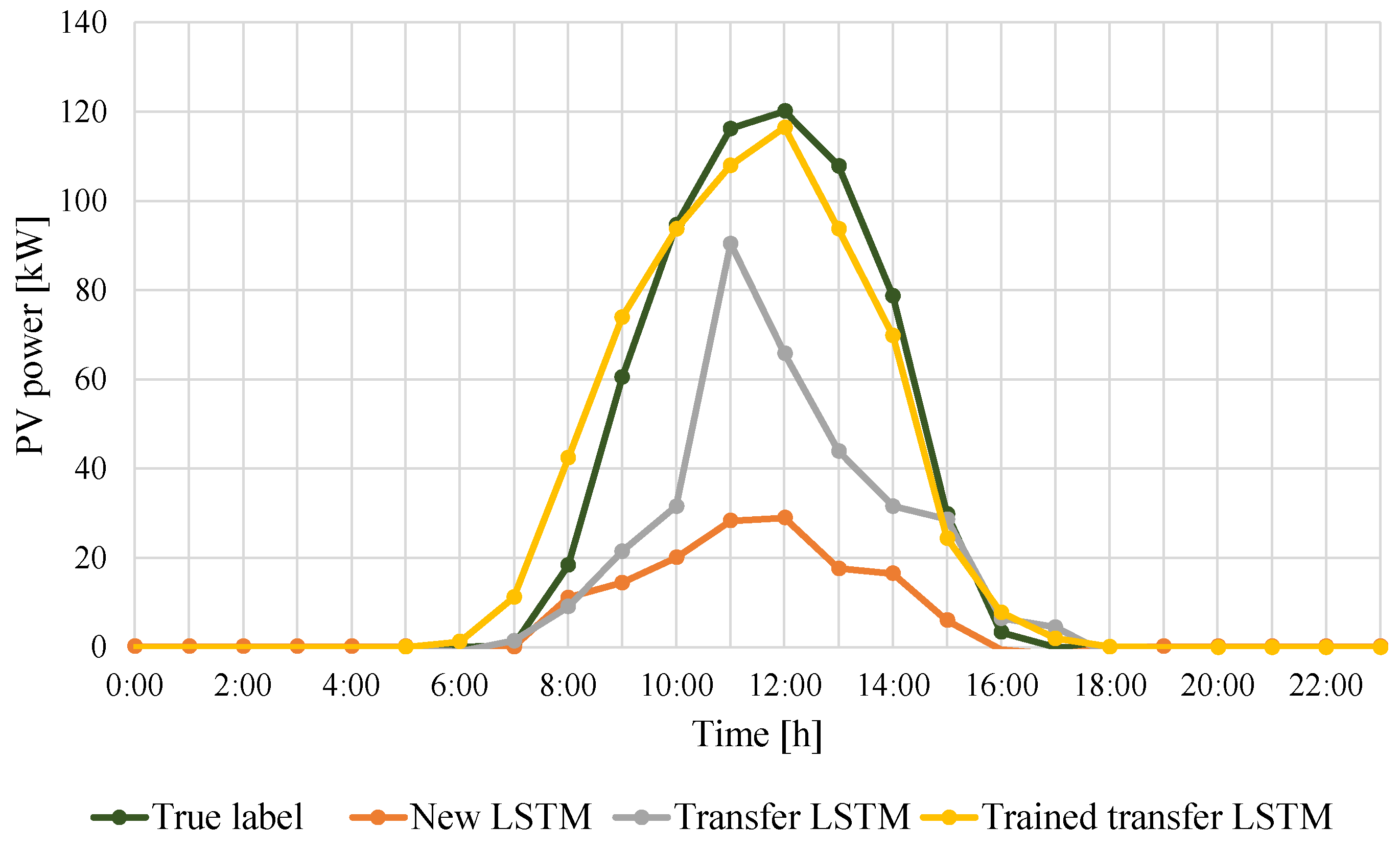
3.2. Transfer Learning
- New model: a set of new models trained by the training set of db 2. These models are developed specifically for the data and requirements of phase II.
- Transfer: a set of models transferred from phase I that have undergone minimal modifications. These models are not retrained, but rely on their preexisting knowledge and training to perform predictions in the new environment of phase II.
- Trained transfer: a set of models transferred from phase I, but have been further trained using the training set of db 2. These models benefit from the knowledge and training acquired during phase I, but also incorporate new information and adapt to the specifics of the new environment in phase II. As a result, the performance of these models may be improved compared to the transferred models.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Terminology |
| PV | Photovoltaic |
| EV | Electric vehicle |
| ML | Machine learning |
| DL | Deep learning |
| RL | Reinforcement learning |
| TL | Transfer learning |
| FNN | Feedforward neural network |
| CNN | Convolutional neural network |
| LSTM | Long short-term memory |
| ReLU | Rectified linear unit |
| RNN | Recurrent neural network |
| db # | Database number |
| μ | Mean |
| σ | Standard deviations |
| x | Input feature space |
| MAE | Mean absolute error |
| Total number in the sample | |
| MSE | Mean square error |
| MAPE | Mean absolute percentage error |
| RMSE | Root mean square error |
| wMAPE | Weighted mean absolute percentage error |
References
- García-Triviño, P.; Sarrias-Mena, R.; García-Vázquez, C.A.; Leva, S.; Fernández-Ramírez, L.M. Optimal Online Battery Power Control of Grid-Connected Energy-Stored Quasi-Impedance Source Inverter with PV System. Appl. Energy 2023, 329, 120286. [Google Scholar] [CrossRef]
- Miraftabzadeh, S.M.; Longo, M.; Foiadelli, F. Estimation Model of Total Energy Consumptions of Electrical Vehicles under Different Driving Conditions. Energies 2021, 14, 854. [Google Scholar] [CrossRef]
- Dimitropoulos, N.; Sofias, N.; Kapsalis, P.; Mylona, Z.; Marinakis, V.; Primo, N.; Doukas, H. Forecasting of Short-Term PV Production in Energy Communities through Machine Learning and Deep Learning Algorithms. In Proceedings of the 2021 12th International Conference on Information, Intelligence, Systems & Applications (IISA), Chania Crete, Greece, 12–14 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Touati, F.; Chowdhury, N.A.; Benhmed, K.; San Pedro Gonzales, A.J.R.; Al-Hitmi, M.A.; Benammar, M.; Gastli, A.; Ben-Brahim, L. Long-Term Performance Analysis and Power Prediction of PV Technology in the State of Qatar. Renew. Energy 2017, 113, 952–965. [Google Scholar] [CrossRef]
- Karabiber, A.; Alçin, Ö.F. Short Term PV Power Estimation by means of Extreme Learning Machine and Support Vector Machine. In Proceedings of the 2019 7th International Istanbul Smart Grids and Cities Congress and Fair (ICSG), Istanbul, Turkey, 25–26 April 2019; pp. 41–44. [Google Scholar] [CrossRef]
- Rana, M.; Rahman, A.; Jin, J. A Data-driven Approach for Forecasting State Level Aggregated Solar Photovoltaic Power Production. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK,, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Khandakar, A.; Chowdhury, M.E.H.; Kazi, M.K.; Benhmed, K.; Touati, F.; Al-Hitmi, M.; Gonzales, A.S.P. Machine Learning Based Photovoltaics (PV) Power Prediction Using Different Environmental Parameters of Qatar. Energies 2019, 12, 2782. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M.; Ogliari, E.; Leva, S.; Lughi, V. Advanced Methods for Photovoltaic Output Power Forecasting: A Review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef]
- Miraftabzadeh, S.M.; Longo, M.; Foiadelli, F.; Pasetti, M.; Igual, R. Advances in the Application of Machine Learning Techniques for Power System Analytics: A Survey. Energies 2021, 14, 4776. [Google Scholar] [CrossRef]
- Miraftabzadeh, S.M.; Longo, M.; Foiadelli, F. A-Day-Ahead Photovoltaic Power Prediction Based on Long Short Term Memory Algorithm. In Proceedings of the SEST 2020—3rd International Conference on Smart Energy Systems and Technologies, Istanbul, Turkey, 7–9 September 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020. [Google Scholar]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M.D. A Review and Evaluation of the State-of-the-Art in PV Solar Power Forecasting: Techniques and Optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Mohan, V.; Senthilkumar, S. IoT Based Fault Identification in Solar Photovoltaic Systems Using an Extreme Learning Machine Technique. J. Intell. Fuzzy Syst. 2022, 43, 3087–3100. [Google Scholar] [CrossRef]
- Daliento, S.; Chouder, A.; Guerriero, P.; Pavan, A.M.; Mellit, A.; Moeini, R.; Tricoli, P. Monitoring, Diagnosis, and Power Forecasting for Photovoltaic Fields: A Review. Int. J. Photoenergy 2017, 2017, 1356851. [Google Scholar] [CrossRef]
- Kong, Z.; Xia, Z.; Cui, Y.; Lv, H. Probabilistic Forecasting of Short-Term Electric Load Demand: An Integra-tion Scheme Based on Correlation Analysis and Improved Weighted Extreme Learning Machine. Appl. Sci. 2019, 9, 4215. [Google Scholar] [CrossRef]
- Dolara, A.; Leva, S.; Manzolini, G. Comparison of Different Physical Models for PV Power Output Prediction. Sol. Energy 2015, 119, 83–99. [Google Scholar] [CrossRef]
- Kaaya, I.; Ascencio-Vásquez, J. Photovoltaic Power Forecasting Methods. In Solar Radiation-Measurement, Modeling and Forecasting Techniques for Photovoltaic Solar Energy Applications; IntechOpen: London, UK, 2021. [Google Scholar]
- Zhang, Y.; Wang, J. GEFCom2014 Probabilistic Solar Power Forecasting Based on K-Nearest Neighbor and Kernel Density Estimator. In Proceedings of the IEEE Power and Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; Volume 2015. [Google Scholar]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of Photovoltaic Power Generation and Model Optimization: A Review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. A Physical Hybrid Artificial Neural Network for Short Term Forecasting of PV Plant Power Output. Energies 2015, 8, 1138–1153. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, Y.; Chang, D.; Xie, J.; Ma, Z.; Sun, Q.; Yin, H.; Wennersten, R. Prediction of Short-Term PV Power Output and Uncertainty Analysis. Appl. Energy 2018, 228, 700–711. [Google Scholar] [CrossRef]
- Lee, H.Y.; Kim, N.W.; Lee, J.G.; Lee, B.T. Uncertainty-Aware Forecast Interval for Hourly PV Power Output. IET Renew. Power Gener. 2019, 13, 2656–2664. [Google Scholar] [CrossRef]
- Netsanet, S.; Zhang, J.; Zheng, D.; Agrawal, R.K.; Muchahary, F. An Aggregative Machine Learning Approach for Output Power Prediction of Wind Turbines. In Proceedings of the 2018 IEEE Texas Power and Energy Conference, TPEC 2018, College Station, TX, USA, 8–9 February 2018; pp. 1–6. [Google Scholar]
- Mohammadi, Y.; Mahdi Miraftabzadeh, S.; Bollen, M.H.J.; Longo, M. Seeking Patterns in Rms Voltage Variations at the Sub-10-Minute Scale from Multiple Locations via Unsupervised Learning and Patterns’ Post-Processing. Int. J. Electr. Power Energy Syst. 2022, 143, b108516. [Google Scholar] [CrossRef]
- Khodayar, M.; Liu, G.; Wang, J.; Khodayar, M.E. Deep Learning in Power Systems Research: A Review. CSEE J. Power Energy Syst. 2021, 7, 209–220. [Google Scholar]
- Ozcanli, A.K.; Yaprakdal, F.; Baysal, M. Deep Learning Methods and Applications for Electrical Power Sys-tems: A Comprehensive Review. Int. J. Energy Res. 2020, 44, 7136–7157. [Google Scholar] [CrossRef]
- Miraftabzadeh, S.M.; Foiadelli, F.; Longo, M.; Pasetti, M. A Survey of Machine Learning Applications for Power System Analytics. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–5. [Google Scholar]
- Mohammadi, Y.; Miraftabzadeh, S.M.; Bollen, M.H.J.; Longo, M. Voltage-Sag Source Detection: Developing Supervised Methods and Proposing a New Unsupervised Learning. Sustain. Energy Grids Netw. 2022, 32, 100855. [Google Scholar] [CrossRef]
- Miraftabzadeh, S.M.; Longo, M.; Brenna, M.; Pasetti, M. Data-Driven Model for PV Power Generation Patterns Extraction via Unsupervised Machine Learning Methods. In Proceedings of the 2022 North American Power Symposium (NAPS), Salt Lake City, UT, USA, 9–11 October 2022; pp. 1–5. [Google Scholar]
- Mishra, M.; Nayak, J.; Naik, B.; Abraham, A. Deep Learning in Electrical Utility Industry: A Comprehensive Review of a Decade of Research. Eng. Appl. Artif. Intell. 2020, 96, 104000. [Google Scholar] [CrossRef]
- Li, B.; Delpha, C.; Diallo, D.; Migan-Dubois, A. Application of Artificial Neural Networks to Photovoltaic Fault Detection and Diagnosis: A Review. Renew. Sustain. Energy Rev. 2021, 138, 110512. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Miraftabzadeh, S.M.; Bollen, M.H.J.; Longo, M. An Unsupervised Learning Schema for Seeking Patterns in Rms Voltage Variations at the Sub-10-Minute Time Scale. Sustain. Energy Grids Netw. 2022, 31, 100773. [Google Scholar] [CrossRef]
- Berghout, T.; Benbouzid, M.; Bentrcia, T.; Ma, X.; Djurović, S.; Mouss, L.H. Machine Learning-Based Condi-tion Monitoring for Pv Systems: State of the Art and Future Prospects. Energies 2021, 14, 6316. [Google Scholar] [CrossRef]
- Aldhshan, S.R.S.; Abdul Maulud, K.N.; Wan Mohd Jaafar, W.S.; Karim, O.A.; Pradhan, B. Energy Consumption and Spatial Assessment of Renewable Energy Penetration and Building Energy Efficiency in Malaysia: A Review. Sustainability 2021, 13, 9244. [Google Scholar] [CrossRef]
- Aziz, F.; Ul Haq, A.; Ahmad, S.; Mahmoud, Y.; Jalal, M.; Ali, U. A Novel Convolutional Neural Network-Based Approach for Fault Classification in Photovoltaic Arrays. IEEE Access 2020, 8, 41889–41904. [Google Scholar] [CrossRef]
- Cheng, L.; Zang, H.; Ding, T.; Wei, Z.; Sun, G. Multi-Meteorological-Factor-Based Graph Modeling for Photovoltaic Power Forecasting. IEEE Trans. Sustain. Energy 2021, 12, 1593–1603. [Google Scholar] [CrossRef]
- Wen, S.; Zhang, C.; Lan, H.; Xu, Y.; Tang, Y.; Huang, Y. A Hybrid Ensemble Model for Interval Prediction of Solar Power Output in Ship Onboard Power Systems. IEEE Trans. Sustain. Energy 2021, 12, 14–24. [Google Scholar] [CrossRef]
- Abubakar Mas’ud, A. Comparison of Three Machine Learning Models for the Prediction of Hourly PV Out-put Power in Saudi Arabia. Ain Shams Eng. J. 2022, 13, 101648. [Google Scholar] [CrossRef]
- Benhmed, K.; Touati, F.; Al-Hitmi, M.; Chowdhury, N.A.; Gonzales, A.S.P.; Qiblawey, Y.; Benammar, M. PV Power Prediction in Qatar Based on Machine Learning Approach. In Proceedings of the 2018 6th International Renewable and Sustainable Energy Conference, IRSEC 2018, Rabat, Morocco, 5–8 December 2018. [Google Scholar]
- Cecaj, A.; Lippi, M.; Mamei, M.; Zambonelli, F. Sensing and Forecasting Crowd Distribution in Smart Cities: Potentials and Approaches. IoT 2021, 2, 33–49. [Google Scholar] [CrossRef]
- Zhao, J.; Yu, H.; Geng, G. TransOS-ELM: A Short-Term Photovoltaic Power Forecasting Method Based on Transferred Knowledge from Similar Days. In Proceedings of the 5th IEEE Conference on Energy Internet and Energy System Integration: Energy Internet for Carbon Neutrality, EI2 2021, Taiyuan, China, 22–24 October 2021; pp. 89–94. [Google Scholar]
- Jung, S.M.; Park, S.; Jung, S.W.; Hwang, E. Monthly Electric Load Forecasting Using Transfer Learning for Smart Cities. Sustainability 2020, 12, 6364. [Google Scholar] [CrossRef]
- Yu, F.; Xiu, X.; Li, Y. A Survey on Deep Transfer Learning and Beyond. Mathematics 2022, 10, 3619. [Google Scholar] [CrossRef]
- Akram, M.W.; Li, G.; Jin, Y.; Chen, X.; Zhu, C.; Ahmad, A. Automatic Detection of Photovoltaic Module De-fects in Infrared Images with Isolated and Develop-Model Transfer Deep Learning. Sol. Energy 2020, 198, 175–186. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, L.; Mao, M.; Xi, X. Transfer Learning for Photovoltaic Power Forecasting with Long Short-Term Memory Neural Network. In Proceedings of the 2020 IEEE International Confer-ence on Big Data and Smart Computing, BigComp 2020, Busan, Republic of Korea, 19–22 February 2020; pp. 125–132. [Google Scholar]



| Approach Type | Forecasting Type | Method | Utility |
|---|---|---|---|
| Phenomenological approach | Medium/long-term forecasting | Numerical weather prediction, satellite images for regional models. | Maintenance and PV plant planning. |
| Statistical approach | Short-term forecasting up to one day ahead | Include regression models, exponential smoothing, autoregressive models, autoregressive moving integrated average, time series ensemble, and probabilistic approaches. | Control of power system operation, unit commitment, and sales. |
| ML approach | From short-term forecasting up to the long-term horizon | Cross-sectoral method, which combines models and Artificial Intelligence. | Production, anomaly detection, and energy disaggregation. |
| Hybrid approach | From short-term forecasting up to the long-term horizon | Combine one of the mentioned advanced methods with one physical or statistical approach. | From short-term power production to maintenance and plant planning. |
| Probabilistic approach | From short-term forecasting up to medium-term horizon | Provide output with quantile, interval and density function. | Electric load forecasting |
| Database | Rated Power [kW] | Duration | Average of Power [kW] | Standard Deviation of Power | Location * [] |
|---|---|---|---|---|---|
| db 1 | 75 | 2015 (January)–2017 (December) | 10.05 | 16.44 | [39.1385, −77.2155] |
| db 2 | 243 | 2017 (September)–2018 (January) | 33.14 | 52.94 | [39.1319, −77.2041] |
| Model | MAE * | MSE * | MAPE | RMSE | wMAPE |
|---|---|---|---|---|---|
| Linear | 0.278 | 0.118 | 98.90 | 0.344 | 73.61 |
| Dense | 0.148 | 0.066 | 64.17 | 0.258 | 43.15 |
| CNN | 0.091 | 0.045 | 45.31 | 0.212 | 39.59 |
| LSTM | 0.052 | 0.015 | 24.00 | 0.101 | 25.05 |
| Model | MAE * | MSE * | MAPE | RMSE | wMAPE | |
|---|---|---|---|---|---|---|
| Linear | New | 7.122 | 176.42 | 5775.01 | 12.05 | 640.93 |
| Untrained transfer | 0.685 | 1.81 | 293.22 | 1.345 | 150.92 | |
| Trained transfer | 0.572 | 1.538 | 252.58 | 1.146 | 120.34 | |
| Dense | New | 1.044 | 2.67 | 466.67 | 1.636 | 170.76 |
| Untrained transfer | 0.390 | 0.346 | 268.22 | 0.589 | 98.69 | |
| Trained transfer | 0.236 | 0.246 | 198.39 | 0.496 | 33.97 | |
| CNN | New | 0.360 | 0.462 | 165.56 | 0.68 | 41.97 |
| Untrained transfer | 0.253 | 0.268 | 145.17 | 0.501 | 36.25 | |
| Trained transfer | 0.231 | 0.197 | 68.25 | 0.437 | 34.98 | |
| LSTM | New | 0.3615 | 0.55 | 109.99 | 0.745 | 47.07 |
| Untrained transfer | 0.313 | 0.387 | 97.20 | 0.622 | 45.07 | |
| Trained transfer | 0.211 | 0.168 | 74.44 | 0.403 | 32.04 | |
| Model | Phase I | Phase II | |
|---|---|---|---|
| Original | Transfer | ||
| Dense | 175 * | 44 | 23 |
| CNN | 375 | 150 | 38 |
| LSTM | 750 | 201 | 76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miraftabzadeh, S.M.; Colombo, C.G.; Longo, M.; Foiadelli, F. A Day-Ahead Photovoltaic Power Prediction via Transfer Learning and Deep Neural Networks. Forecasting 2023, 5, 213-228. https://doi.org/10.3390/forecast5010012
Miraftabzadeh SM, Colombo CG, Longo M, Foiadelli F. A Day-Ahead Photovoltaic Power Prediction via Transfer Learning and Deep Neural Networks. Forecasting. 2023; 5(1):213-228. https://doi.org/10.3390/forecast5010012
Chicago/Turabian StyleMiraftabzadeh, Seyed Mahdi, Cristian Giovanni Colombo, Michela Longo, and Federica Foiadelli. 2023. "A Day-Ahead Photovoltaic Power Prediction via Transfer Learning and Deep Neural Networks" Forecasting 5, no. 1: 213-228. https://doi.org/10.3390/forecast5010012
APA StyleMiraftabzadeh, S. M., Colombo, C. G., Longo, M., & Foiadelli, F. (2023). A Day-Ahead Photovoltaic Power Prediction via Transfer Learning and Deep Neural Networks. Forecasting, 5(1), 213-228. https://doi.org/10.3390/forecast5010012








