Evaluating State-of-the-Art, Forecasting Ensembles and Meta-Learning Strategies for Model Fusion
Abstract
:1. Introduction
1.1. Model Fusion and Meta-Learning
- Early model fusion integrates the base learners before training. The combined model is then trained as a single fused model.
- Late model fusion first trains the base learners individually. The now pretrained base learners are then integrated without further modification.
- Incremental model fusion performs model integration while training the base learners incrementally. Each combined base learner’s parameters remain fixed once trained.
- Meta-model fusion uses model-based meta-learning to perform the model integration process.
- Aggregation fusion, or just aggregation, uses a simple aggregation scheme, such as weighted averaging, to perform the model integration process.
1.2. Related Literature
1.3. Makridakis Competitions (M-Competitions)
1.4. Contributions of This Paper
- 1.
- Presenting a novel taxonomy for organising the current literature around forecasting model fusion;
- 2.
- Studying the potential improvement of the predictive power of any state-of-the-art forecasting model;
- 3.
- Contrasting the performance of multiple ensembling techniques from different architectures;
- 4.
- Delivering an equitable comparison of techniques by providing the validation results of the ensembles over five runs of ten-fold cross-validation.
2. Materials and Methods
2.1. The M4 Forecasting Competition
2.2. Statistical Base Learners
- Auto-ARIMA is a standard method for comparing forecast methods’ performances. We use the forecasts from an Auto-ARIMA method that uses maximum-likelihood estimation to approximate the parameters [43].
- Theta is the best method of the M3 competition [44]. Theta is a simple forecasting method that averages the extrapolated Theta-lines, computed from two given Theta-coefficients, applied to the second differences of the time-series.
- Comb (or COMB S-H-D) is the arithmetic average of the three exponential smoothing methods: single, Holt-Winters and damped exponential smoothing [47]. Comb was the winning approach for the M2 competition and was used as a benchmark in the M4 Competition.
2.3. ES-RNN Base Learner
2.3.1. Preprocessing
2.3.2. Forecasts by the RNN
2.3.3. The Architecture
2.3.4. Loss Function and Optimiser
2.4. Simple Model Averaging (AVG)
2.5. FFORMA
| Algorithm 1: FFORMA’s forecast combination [19] |
 |
2.6. Random Forest Feature-Based FORecast Model Selection (FFORMS-R)
2.7. Gradient Boosting Feature-Based FORecast Model Selection (FFORMS-G)
2.8. Neural Network Model Stacking (NN-STACK)
2.9. Neural Network Feature-Based FORecast Model Averaging (FFORMA-N)
2.10. N-BEATS
3. Experimental Method and Results
3.1. Hyperparameter Tuning
3.2. Detailed Results
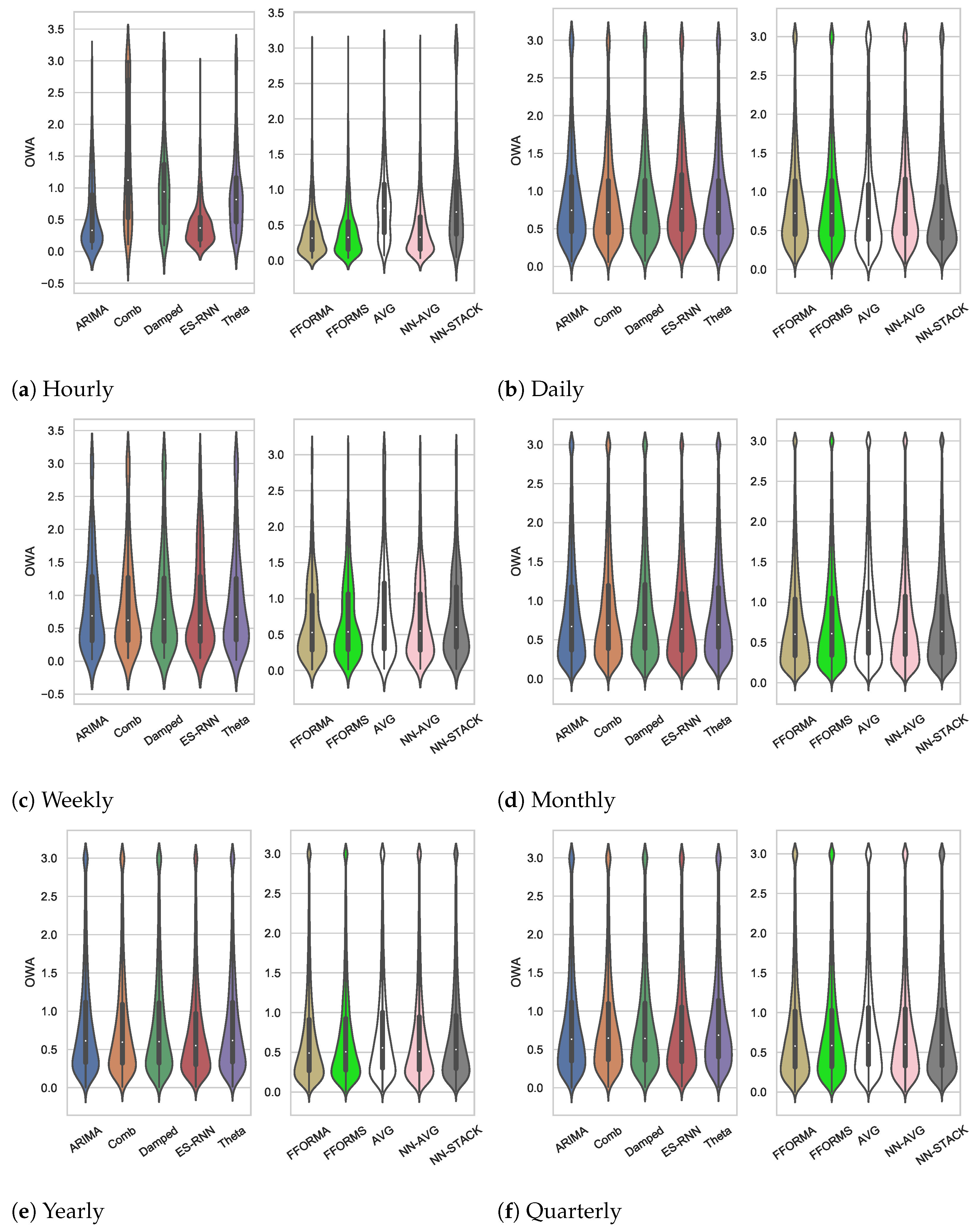
3.2.1. The Hourly Subset
3.2.2. The Daily Subset
3.2.3. The Weekly Subset
3.2.4. The Monthly Subset
3.2.5. The Yearly Subset
3.2.6. The Quarterly Subset
3.3. Overall Results
- 1.
- The performance of ensemble learning is dependent on the performances of its weak learners;
- 2.
- Ensemble learning’s performance is dependent on the diversity of the data (i.e., the similarity of the time-series from the different domains);
- 3.
- For smaller subsets, the traditional methods do better but are still outperformed by the ensemble methods and even more so for larger datasets, where more cross-learning can be exploited;
- 4.
- The ensembles of hybrids can still lead to improved performance;
- 5.
- We reaffirm that there is no free lunch concerning the selection of ensembling methods and that validation will still be required for model selection.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ARIMA | Autoregressive Integrated Moving Average |
| AVG | model averaging |
| ES | Exponential Smoothing |
| ES-RNN | Exponential Smoothing-Recurrent Neural Network |
| FFORMA | Feature-Based FORecast Model Averaging |
| FFORMA-N | Neural Network Feature-Based FORecast Model Averaging |
| FFORMS-R | Random Forest Feature-Based FORecast Model Selection |
| FFORMS-G | Gradient Boosting Feature-Based FORecast Model Selection |
| LSTM | Long Short-Term Memory |
| MASE | Mean Absolute Scaled Error |
| MLP | Multilayer Perceptron |
| N-BEATS | Neural Basis Expansion Analysis |
| NN-STACK | Neural Network Model Stacking |
| OWA | Overall Weighted Average |
| RNN | Recurrent Neural Network |
| RF | Random Forest |
| sMAPE | Symmetric Mean Absolute Percentage Error |
References
- Cawood, P.; van Zyl, T.L. Feature-weighted stacking for nonseasonal time series forecasts: A case study of the COVID-19 epidemic curves. In Proceedings of the 2021 8th International Conference on Soft Computing Machine Intelligence (ISCMI), Cario, Egypt, 26–27 November 2021; pp. 53–59. [Google Scholar]
- Makridakis, S.; Hyndman, R.J.; Petropoulos, F. Forecasting in social settings: The state of the art. Int. J. Forecast. 2020, 36, 15–28. [Google Scholar] [CrossRef]
- Atherfold, J.; Van Zyl, T. A method for dissolved gas forecasting in power transformers using ls-svm. In Proceedings of the 2020 IEEE 23rd International Conference On Information Fusion (FUSION), Rustenburg, South Africa, 6–9 July 2020; pp. 1–8. [Google Scholar]
- Mathonsi, T.; Zyl, T. Multivariate anomaly detection based on prediction intervals constructed using deep learning. In Proceedings of the Neural Computing And Applications, Jinan, China, 8–10 July 2022; pp. 1–15. [Google Scholar]
- Timilehin, O.; Zyl, T. Surrogate Parameters Optimization for Data and Model Fusion of COVID-19 Time-series Data. In Proceedings of the 2021 IEEE 24th International Conference On Information Fusion (FUSION), Sun City, South Africa, 1–4 November 2021; pp. 1–7. [Google Scholar]
- Freeborough, W.; Zyl, T. Investigating Explainability Methods in Recurrent Neural Network Architectures for Financial Time Series Data. Appl. Sci. 2022, 12, 1427. [Google Scholar] [CrossRef]
- Michelsanti, D.; Tan, Z.H.; Zhang, S.X.; Xu, Y.; Yu, M.; Yu, D.; Jensen, J. An overview of deep-learning-based audio-visual speech enhancement and separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 1368–1396. [Google Scholar] [CrossRef]
- Arinze, B. Selecting appropriate forecasting models using rule induction. Omega 1994, 22, 647–658. [Google Scholar] [CrossRef]
- Ribeiro, M.H.D.M.; Coelho, L.D.S. Ensemble approach based on bagging, boosting and stacking for short-term prediction in agribusiness time series. Appl. Soft Comput. 2020, 86, 105837. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid arima and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Reich, N.G.; Brooks, L.C.; Fox, S.J.; Kandula, S.; McGowan, C.J.; Moore, E.; Osthus, D.; Ray, E.L.; Tushar, A.; Yamana, T.K.; et al. A collaborative multiyear, multimodel assessment of seasonal influenza forecasting in the united states. Proc. Natl. Acad. Sci. USA 2019, 116, 3146–3154. [Google Scholar] [CrossRef]
- McGowan, C.J.; Biggerstaff, M.; Johansson, M.; Apfeldorf, K.M.; Ben-Nun, M.; Brooks, L.; Convertino, M.; Erraguntla, M.; Farrow, D.C.; Freeze, J.; et al. Collaborative efforts to forecast seasonal influenza in the united states, 2015–2016. Sci. Rep. 2019, 9, 683. [Google Scholar] [CrossRef]
- Johansson, M.A.; Apfeldorf, K.M.; Dobson, S.; Devita, J.; Buczak, A.L.; Baugher, B.; Moniz, L.J.; Bagley, T.; Babin, S.M.; Guven, E.; et al. An open challenge to advance probabilistic forecasting for dengue epidemics. Proc. Natl. Acad. Sci. USA 2019, 116, 24268–24274. [Google Scholar] [CrossRef]
- Raftery, A.E.; Madigan, D.; Hoeting, J.A. Bayesian model averaging for linear regression models. J. Am. Stat. Assoc. 1997, 92, 179–191. [Google Scholar] [CrossRef]
- Clarke, B. Comparing bayes model averaging and stacking when model approximation error cannot be ignored. J. Mach. Learn. Res. 2003, 4, 683–712. [Google Scholar]
- Lorena, A.C.; Maciel, A.I.; de Miranda, P.B.; Costa, I.G.; Prudêncio, R.B. Data complexity meta-features for regression problems. Mach. Learn. 2018, 107, 209–246. [Google Scholar] [CrossRef]
- Barak, S.; Nasiri, M.; Rostamzadeh, M. Time series model selection with a meta-learning approach; evidence from a pool of forecasting algorithms. arXiv 2019, arXiv:1908.08489. [Google Scholar]
- Montero-Manso, P.; Athanasopoulos, G.; Hyndman, R.J.; Talagala, T.S. Fforma: Feature-based forecast model averaging. Int. J. Forecast 2020, 36, 86–92. [Google Scholar] [CrossRef]
- Smyl, S. A hybrid method of exponential smoothing and recurrent neural networks for time series forecasting. Int. J. Forecast 2020, 36, 75–85. [Google Scholar] [CrossRef]
- Liu, N.; Tang, Q.; Zhang, J.; Fan, W.; Liu, J. A hybrid forecasting model with parameter optimization for short-term load forecasting of micro-grids. Appl. Energy 2014, 129, 336–345. [Google Scholar] [CrossRef]
- Wang, J.-Z.; Wang, Y.; Jiang, P. The study and application of a novel hybrid forecasting model—A case study of wind speed forecasting in china. Appl. Energy 2015, 143, 472–488. [Google Scholar] [CrossRef]
- Qin, Y.; Li, K.; Liang, Z.; Lee, B.; Zhang, F.; Gu, Y.; Zhang, L.; Wu, F.; Rodriguez, D. Hybrid forecasting model based on long short term memory network and deep learning neural network for wind signal. Appl. Energy 2019, 236, 262–272. [Google Scholar] [CrossRef]
- Mathonsi, T.; van Zyl, T.L. Prediction interval construction for multivariate point forecasts using deep learning. In Proceedings of the 2020 7th International Conference on Soft Computing & Machine Intelligence (ISCMI), Stockholm, Sweden, 14–15 November 2020; pp. 88–95. [Google Scholar]
- Laher, S.; Paskaramoorthy, A.; Zyl, T.L.V. Deep learning for financial time series forecast fusion and optimal portfolio rebalancing. In Proceedings of the 2021 IEEE 24th International Conference on Information Fusion (FUSION), Sun City, South Africa, 1–4 November 2021; pp. 1–8. [Google Scholar]
- Mathonsi, T.; van Zyl, T.L. A statistics and deep learning hybrid method for multivariate time series forecasting and mortality modeling. Forecasting 2022, 4, 1–25. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Aksoy, A.; Öztürk, N.; Sucky, E. Demand forecasting for apparel manufacturers by using neuro-fuzzy techniques. J. Model. Manag. 2014, 9, 918–935. [Google Scholar] [CrossRef]
- Deng, W.; Wang, G.; Zhang, X. A novel hybrid water quality time series prediction method based on cloud model and fuzzy forecasting. Chemom. Intell. Lab. Syst. 2015, 149, 39–49. [Google Scholar] [CrossRef]
- Rahmani, R.; Yusof, R.; Seyedmahmoudian, M.; Mekhilef, S. Hybrid technique of ant colony and particle swarm optimization for short term wind energy forecasting. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 163–170. [Google Scholar] [CrossRef]
- Kumar, S.; Pal, S.K.; Singh, R. A novel hybrid model based on particle swarm optimisation and extreme learning machine for short-term temperature prediction using ambient sensors. Sustain. Cities Soc. 2019, 49, 101601. [Google Scholar] [CrossRef]
- Shinde, G.R.; Kalamkar, A.B.; Mahalle, P.N.; Dey, N.; Chaki, J.; Hassanien, A.E. Forecasting models for coronavirus disease (COVID-19): A survey of the state-of-the-art. SN Comput. Sci. 2020, 1, 197. [Google Scholar] [CrossRef]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-beats: Neural basis expansion analysis for interpretable time series forecasting. arXiv 2019, arXiv:1905.10437. [Google Scholar]
- Huang, G.; Liu, Z.; Maaten, L.V.D.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The m5 competition: Background, organization, and implementation. Int. J. Forecast. 2021. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The m4 competition: 100,000 time series and 61 forecasting methods. Int. J. Forecast. 2020, 36, 54–74. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. M5 accuracy competition: Results, findings, and conclusions. Int. J. Forecast. 2022. [Google Scholar] [CrossRef]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Wu, Q. A hybrid-forecasting model based on gaussian support vector machine and chaotic particle swarm optimization. Expert Syst. Appl. 2010, 37, 2388–2394. [Google Scholar] [CrossRef]
- Khashei, M.; Bijari, M. A new class of hybrid models for time series forecasting. Expert Syst. Appl. 2012, 39, 4344–4357. [Google Scholar]
- Makridakis, S. Accuracy measures: Theoretical and practical concerns. Int. J. Forecast. 1993, 9, 527–529. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for r. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Assimakopoulos, V.; Nikolopoulos, K. The theta model: A decomposition approach to forecasting. Int. J. Forecast. 2000, 16, 521–530. [Google Scholar] [CrossRef]
- Holt, C.C. Forecasting seasonals and trends by exponentially weighted moving averages. Int. J. Forecast. 2004, 20, 5–10. [Google Scholar] [CrossRef]
- McKenzie, E.; Gardner, E.S., Jr. Damped trend exponential smoothing: A modelling viewpoint. Int. J. Forecast. 2010, 26, 661–665. [Google Scholar] [CrossRef]
- Makridakis, S.; Hibon, M. The m3-competition: Results, conclusions and implications. Int. J. Forecast. 2000, 16, 451–476. [Google Scholar] [CrossRef]
- Fathi, O. Time series forecasting using a hybrid arima and lstm model. Velv. Consult. 2019, 1–7. Available online: https://www.velvetconsulting.com/nos-publications2/time-series-forecasting-using-a-hybrid-arima-and-lstm-model/ (accessed on 7 June 2022).
- Petropoulos, F.; Hyndman, R.J.; Bergmeir, C. Exploring the sources of uncertainty: Why does bagging for time series forecasting work? Eur. J. Oper. Res. 2018, 268, 545–554. [Google Scholar] [CrossRef]
- Chan, F.; Pauwels, L.L. Some theoretical results on forecast combinations. Int. J. Forecast. 2018, 34, 64–74. [Google Scholar] [CrossRef]
- Gardner, E.S., Jr. Exponential smoothing: The state of the art. J. Forecast. 1985, 4, 1–28. [Google Scholar] [CrossRef]
- Chang, S.; Zhang, Y.; Han, W.; Yu, M.; Guo, X.; Tan, W.; Cui, X.; Witbrock, M.; Hasegawa-Johnson, M.; Huang, T.S. Dilated recurrent neural networks. arXiv 2017, arXiv:1710.02224. [Google Scholar]
- Claeskens, G.; Hjort, N.L. Model Selection and Model Averaging; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Hyndman, R.J.; Wang, E.; Laptev, N. Large-scale unusual time series detection. In Proceedings of the 2015 IEEE International Conference on Data Mining Workshop (ICDMW), Atlantic City, NJ, USA, 14–17 November 2015; pp. 1616–1619. [Google Scholar]
- Talagala, T.S.; Hyndman, R.J.; Athanasopoulos, G. Meta-learning how to forecast time series. Monash Econom. Bus. Stat. Work. Pap. 2018, 6, 18. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Agarap, A.F. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zar, J.H. Spearman rank correlation. Encycl. Biostat. 2005, 7. [Google Scholar] [CrossRef]
- Blum, L.; Blum, M.; Shub, M. A simple unpredictable pseudo-random number generator. SIAM J. Comput. 1986, 15, 364–383. [Google Scholar] [CrossRef]
- Egrioglu, E.; Fİldes, R. A note on the robustness of performance of methods and rankings for m4 competition. Turk. J. Forecast. 2020, 4, 26–32. [Google Scholar]
- Schulze, M. The Schulze method of voting. arXiv 2018, arXiv:1804.02973. [Google Scholar]


| Data Subset | Micro | Industry | Macro | Finance | Demographic | Other | Total |
|---|---|---|---|---|---|---|---|
| Yearly | 6538 | 3716 | 3903 | 6519 | 1088 | 1236 | 23,000 |
| Quarterly | 6020 | 4637 | 5315 | 5305 | 1858 | 865 | 24,000 |
| Monthly | 10,975 | 10,017 | 10,016 | 10,987 | 5728 | 277 | 48,000 |
| Weekly | 112 | 6 | 41 | 164 | 24 | 12 | 359 |
| Daily | 1476 | 422 | 127 | 1559 | 10 | 633 | 4227 |
| Hourly | 0 | 0 | 0 | 0 | 0 | 414 | 414 |
| Total | 25,121 | 18,798 | 19,402 | 24,534 | 8708 | 3437 | 100,000 |
| Hyperparameter | H | D | W | M | Y | Q |
|---|---|---|---|---|---|---|
| n-estimators | 2000 | 2000 | 2000 | 1200 | 1200 | 2000 |
| min data in leaf | 63 | 200 | 50 | 100 | 100 | 50 |
| number of leaves | 135 | 94 | 19 | 110 | 110 | 94 |
| eta | 0.61 | 0.90 | 0.46 | 0.20 | 0.10 | 0.75 |
| max depth | 61 | 9 | 17 | 28 | 28 | 43 |
| subsample | 0.49 | 0.52 | 0.49 | 0.50 | 0.50 | 0.81 |
| colsample bytree | 0.90 | 0.49 | 0.90 | 0.50 | 0.50 | 0.49 |
| H (0.4K) | D (4.2K) | W (0.4K) | M (48K) | Y (23K) | Q (24K) | M, Y and Q | |
|---|---|---|---|---|---|---|---|
| Base Learners | |||||||
| ARIMA | 0.577 | 1.047 | 0.925 | 0.903 | 0.892 | 0.898 | 0.899 |
| Comb | 1.556 | 0.981 | 0.944 | 0.920 | 0.867 | 0.890 | 0.899 |
| Damped | 1.141 | 0.999 | 0.992 | 0.924 | 0.890 | 0.893 | 0.907 |
| ES-RNN | 0.440 | 1.046 | 0.864 | 0.836 | 0.778 | 0.847 | 0.825 |
| Theta | 1.006 | 0.998 | 0.965 | 0.907 | 0.872 | 0.917 | 0.901 |
| Ensembles | |||||||
| FFORMA | 0.415 | 0.983 | 0.725 | 0.800 | 0.732 | 0.816 | 0.788 |
| FFORMS-R | 0.423 | 0.981 | 0.740 | 0.817 | 0.752 | 0.830 | 0.805 |
| FFORMS-G | 0.427 | 0.984 | 0.740 | 0.810 | 0.745 | 0.826 | 0.798 |
| AVG | 0.847 | 0.985 | 0.860 | 0.863 | 0.804 | 0.856 | 0.847 |
| FFORMA-N | 0.428 | 0.979 | 0.718 | 0.813 | 0.746 | 0.828 | 0.801 |
| NN-STACK | 1.427 | 0.927 | 0.810 | 0.833 | 0.771 | 0.838 | 0.819 |
| State of the Art | |||||||
| N-BEATS | - | - | - | 0.819 | 0.758 | 0.800 | 0.799 |
| H (0.4K) | D (4.2K) | W (0.4K) | M (48K) | Y (23K) | Q (24K) | Schulze Rank [63] | |
|---|---|---|---|---|---|---|---|
| Base Learners | |||||||
| ARIMA | 0.332 | 0.745 | 0.688 | 0.670 | 0.612 | 0.633 | 9 |
| Comb | 1.121 | 0.718 | 0.623 | 0.684 | 0.595 | 0.648 | 8 |
| Damped | 0.940 | 0.727 | 0.637 | 0.691 | 0.602 | 0.644 | 9 |
| ES-RNN | 0.370 | 0.764 | 0.546 | 0.637 | 0.550 | 0.610 | 5 |
| Theta | 0.817 | 0.723 | 0.673 | 0.692 | 0.617 | 0.686 | 11 |
| Ensembles | |||||||
| FFORMA | 0.318 | 0.723 | 0.529 | 0.602 | 0.491 | 0.580 | 1 |
| FFORMS-R | 0.311 | 0.711 | 0.552 | 0.615 | 0.511 | 0.589 | 2 |
| FFORMS-G | 0.328 | 0.722 | 0.538 | 0.610 | 0.506 | 0.596 | 2 |
| AVG | 0.738 | 0.656 | 0.632 | 0.652 | 0.557 | 0.619 | 7 |
| FFORMA-N | 0.326 | 0.720 | 0.539 | 0.614 | 0.508 | 0.594 | 2 |
| NN-STACK | 0.685 | 0.646 | 0.606 | 0.637 | 0.535 | 0.595 | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cawood, P.; Van Zyl, T. Evaluating State-of-the-Art, Forecasting Ensembles and Meta-Learning Strategies for Model Fusion. Forecasting 2022, 4, 732-751. https://doi.org/10.3390/forecast4030040
Cawood P, Van Zyl T. Evaluating State-of-the-Art, Forecasting Ensembles and Meta-Learning Strategies for Model Fusion. Forecasting. 2022; 4(3):732-751. https://doi.org/10.3390/forecast4030040
Chicago/Turabian StyleCawood, Pieter, and Terence Van Zyl. 2022. "Evaluating State-of-the-Art, Forecasting Ensembles and Meta-Learning Strategies for Model Fusion" Forecasting 4, no. 3: 732-751. https://doi.org/10.3390/forecast4030040
APA StyleCawood, P., & Van Zyl, T. (2022). Evaluating State-of-the-Art, Forecasting Ensembles and Meta-Learning Strategies for Model Fusion. Forecasting, 4(3), 732-751. https://doi.org/10.3390/forecast4030040







