Comparing Prophet and Deep Learning to ARIMA in Forecasting Wholesale Food Prices
Abstract
:1. Introduction
2. Materials and Methods
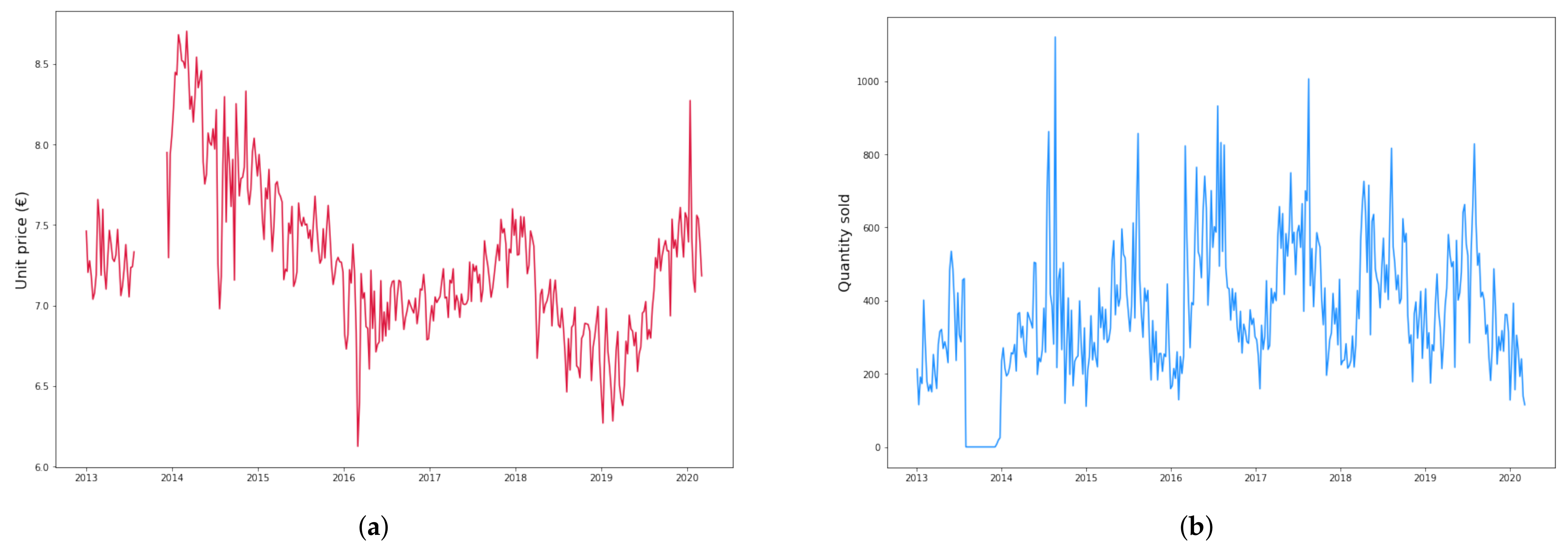
2.1. Dataset Description and Preparation
- Training dataset: years 2013–2017;
- Validation dataset: year 2018;
- Test dataset: years 2019–March 2020.
- Since the time series for all products have a long window with no data in the second half of year 2013, we do not consider this empty period and start right after it;
- When occasional weeks with no data occur, we take the average of the preceding and following week prices and interpolate.
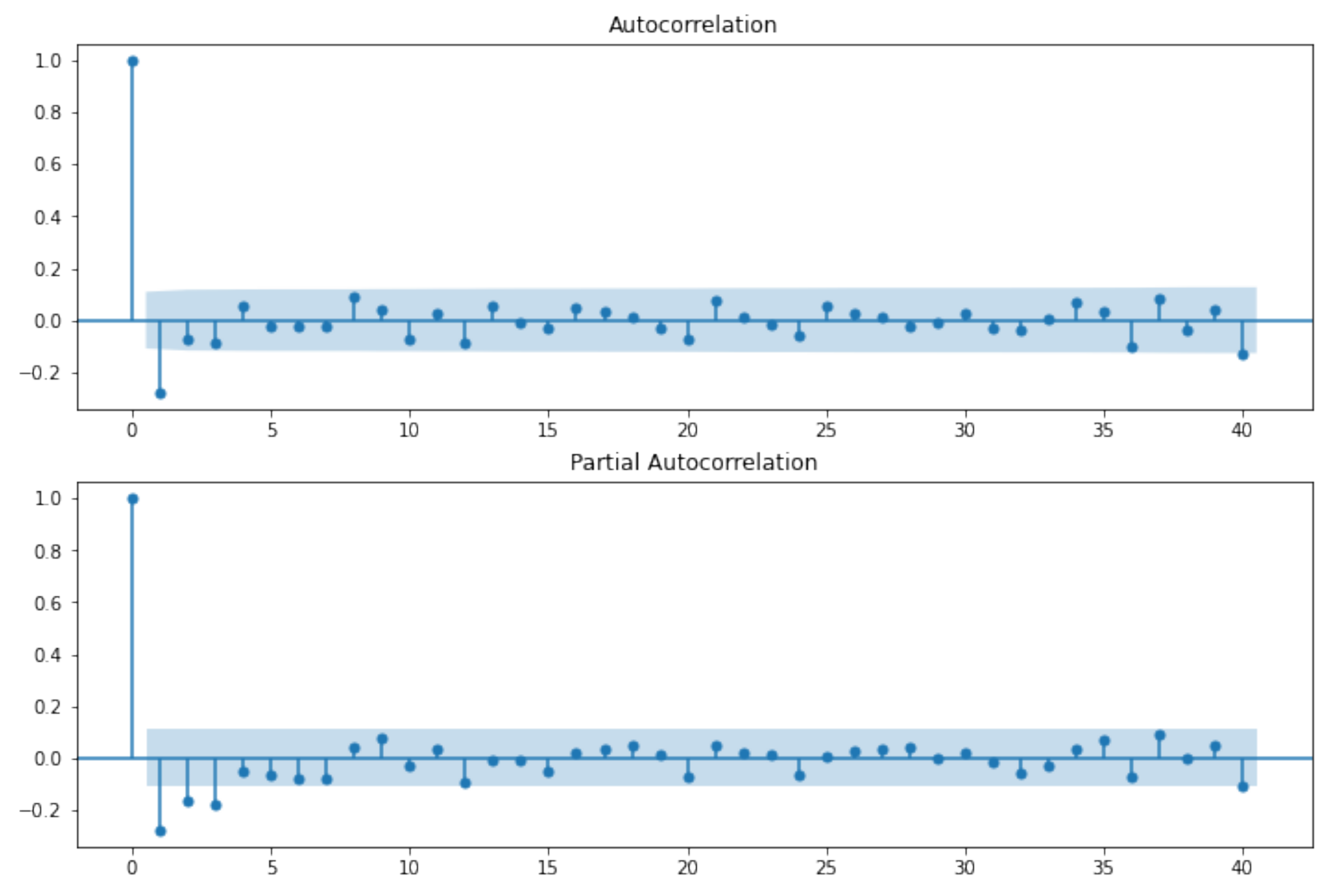
2.2. ARIMA Models
- for an exact MA(q), ACF is zero for lags larger than q;
- for an exact AR(p), PACF is zero for lags larger than p.
2.3. Prophet
2.4. Neural Networks
- reshape data so that at each time t, is a tensor containing the n last values of each time series in Table 4;
- set as the variable to be used in the cost function.
3. Results
3.1. ARIMA Results
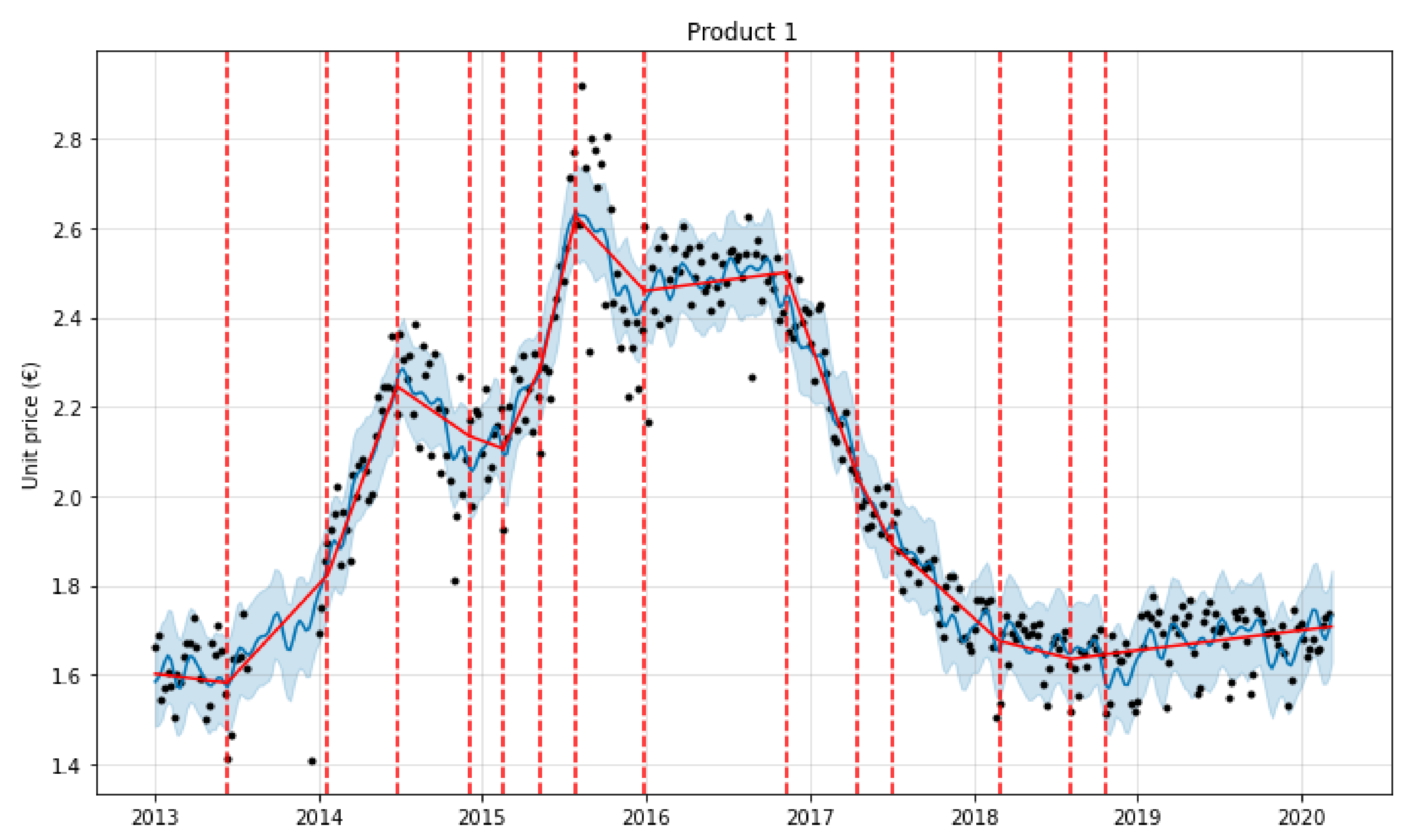
3.2. Prophet Results
3.2.1. Prophet Grid Search
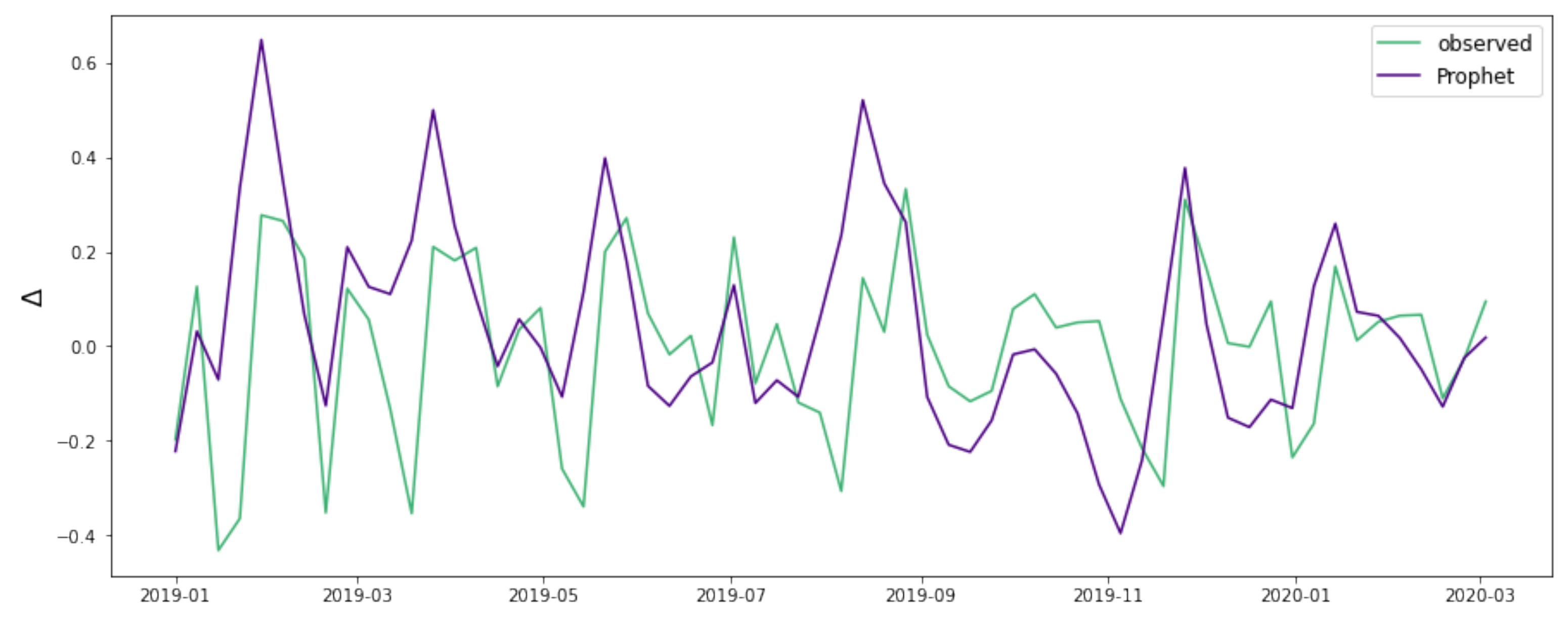
3.2.2. Prophet Forecasting
3.3. Neural Networks Results
3.3.1. NN Grid Search
- a number of LSTM layers;
- a number of LSTM neurons in every layer, with normal Glorot weight initialization [42]. Each layer has the same number of units;
- following each LSTM layer, a dropout layer with dropout rate . The dropout rate is taken to be equal for all layers;
- an output layer consisting of a single neuron with linear activation function and normal Glorot initialization;
- an early stopping procedure, monitoring the cost function on the validation set with a patience of 5 epochs, while also having an upper bound of 150 training epochs.
- two one-dimensional convolutional layers (conv1D) with output filters each, kernel size and relu (rectified linear unit) activation function. The hyperparameters were taken to be the same for both layers;
- in each of the conv1D layers, padding was set to same, causal, or no padding at all. The corresponding hyperparameters are dubbed pad, pad;
- an average pooling layer in between the convolutional layers, with pool size equal to 2 and no padding;
- following the above layers, LSTM layers are added following the same structure as for the first class of models.
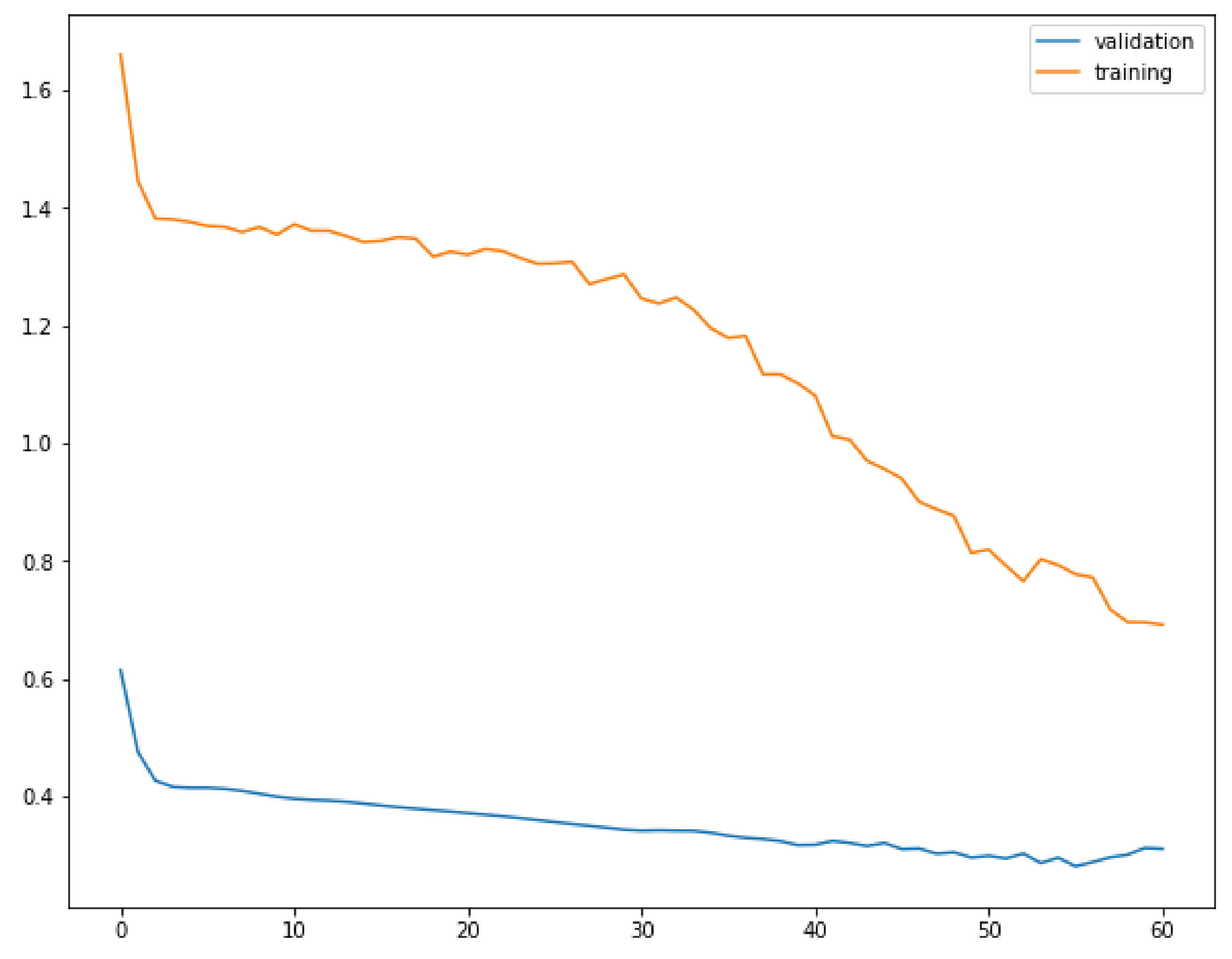
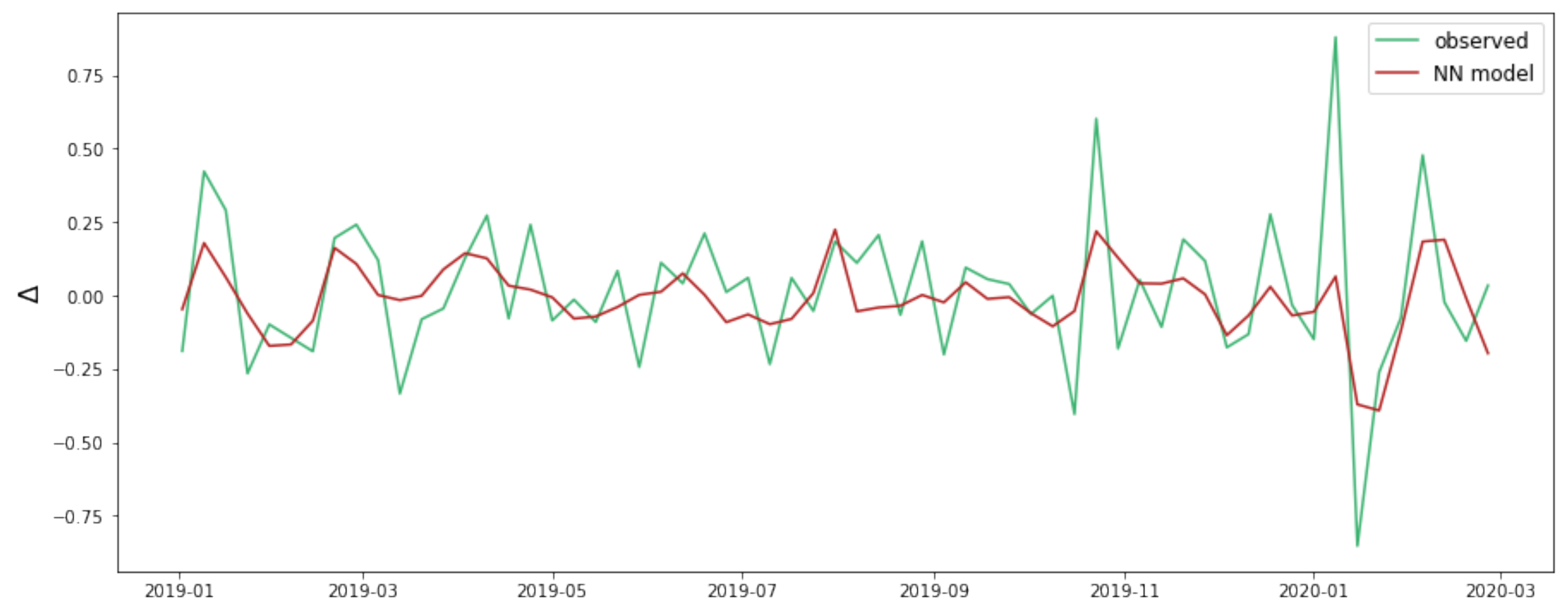
3.4. NN Forecasting
3.5. Result Comparison
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NN | Neural Network |
| LSTM | Long Short–Term Memory |
| NN | Neural Network |
| CNN | Convolutional Neural Network |
| GAM | Generalized Additive Model |
| ARIMA | Autoregressive Integrated Moving Average |
| ADF | Augmented Dikey–Fuller |
| BIC | Bayesian Information Criterion |
| ACF | Autocorrelation Function |
| PACF | Partial Autocorrelation Function |
| RMSE | Root Mean Squared Error |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percent Error |
| ME | Mean Error |
Appendix A. Univariate Deep Learning Models
| Product | l | r | Train RMSE | Valid RMSE | ||
|---|---|---|---|---|---|---|
| 1 | 2 | 96 | 0.2 | 0.001 | 0.116 | 0.0674 |
| 2 | 2 | 96 | 0.3 | 0.0005 | 0.195 | 0.183 |
| 3 | 2 | 64 | 0.3 | 0.001 | 0.224 | 0.162 |
| Product | l | r | f | pad | pad | n | Train RMSE | Valid RMSE | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 96 | 0.3 | 0.0005 | 30 | 2 | valid | same | 8 | 0.112 | 0.0600 |
| 2 | 2 | 96 | 0.1 | 0.001 | 10 | 2 | causal | causal | 12 | 0.188 | 0.179 |
| 3 | 1 | 64 | 0.2 | 0.001 | 30 | 2 | same | causal | 8 | 0.229 | 0.154 |
| Product | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| class | A | B | A | B | A | B |
| RMSE | 0.0630 | 0.0591 | 0.186 | 0.166 | 0.226 | 0.207 |
| MAE | 0.0468 | 0.0449 | 0.131 | 0.122 | 0.155 | 0.158 |
| MAPE | 0.0281 | 0.0257 | 0.0175 | 0.0163 | 0.0221 | 0.0220 |
| ME | 0.00605 | 0.00747 | −0.0981 | −0.0654 | 0.0530 | 0.0262 |
References
- Adhikari, R.; Agrawal, R.K. An Introductory Study on Time Series Modeling and Forecasting. arXiv 2013, arXiv:1302.6613. [Google Scholar]
- Petropoulos, F.; Apiletti, D.; Assimakopoulos, V.; Babai, M.Z.; Barrow, D.K.; Taieb, S.B.; Bergmeir, C.; Bessa, R.J.; Bijak, J.; Boylan, J.E.; et al. Forecasting: Theory and practice. arXiv 2021, arXiv:2012.03854. [Google Scholar]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef] [Green Version]
- Sezer, O.B.; Gudelek, M.U.; Ozbayoglu, A.M. Financial time series forecasting with deep learning: A systematic literature review: 2005–2019. Appl. Soft Comput. 2020, 90, 106181. [Google Scholar] [CrossRef] [Green Version]
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: A survey. Philos. Trans. R. Soc. A 2021, 379, 20200209. [Google Scholar] [CrossRef]
- Lara-Benítez, P.; Carranza-García, M.; Riquelme, J.C. An Experimental Review on Deep Learning Architectures for Time Series Forecasting. Int. J. Neural Syst. 2021, 31, 2130001. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. Handb. Brain Theory Neural Netw. 1995, 3361, 1995. [Google Scholar]
- Alibašić, E.; Fažo, B.; Petrović, I. A new approach to calculating electrical energy losses on power lines with a new improved three-mode method. Teh. Vjesn. 2019, 26, 405–411. [Google Scholar]
- Kolassa, S.; Siemsen, E. Demand Forecasting for Managers; Business Expert Press: New York, NY, USA, 2016. [Google Scholar]
- Taylor, J.W. Forecasting daily supermarket sales using exponentially weighted quantile regression. Eur. J. Oper. Res. 2007, 178, 154–167. [Google Scholar] [CrossRef] [Green Version]
- Hofmann, E.; Rutschmann, E. Big data analytics and demand forecasting in supply chains: A conceptual analysis. Int. J. Logist. Manag. 2018, 29, 739–766. [Google Scholar] [CrossRef]
- MOFC. The M5 Competition. Available online: https://mofc.unic.ac.cy/m5-competition/ (accessed on 2 September 2021).
- Haofei, Z.; Guoping, X.; Fangting, Y.; Han, Y. A neural network model based on the multi-stage optimization approach for short-term food price forecasting in China. Expert Syst. Appl. 2007, 33, 347–356. [Google Scholar] [CrossRef]
- Zou, H.; Xia, G.; Yang, F.; Wang, H. An investigation and comparison of artificial neural network and time series models for Chinese food grain price forecasting. Neurocomputing 2007, 70, 2913–2923. [Google Scholar] [CrossRef]
- Jha, G.K.; Sinha, K. Agricultural price forecasting using neural network model: An innovative information delivery system. Agric. Econ. Res. Rev. 2013, 26, 229–239. [Google Scholar] [CrossRef] [Green Version]
- Ahumada, H.; Cornejo, M. Forecasting food prices: The case of corn, soybeans and wheat. Int. J. Forecast. 2016, 32, 838–848. [Google Scholar] [CrossRef]
- Pavlyshenko, B.M. Machine-Learning Models for Sales Time Series Forecasting. Data 2019, 4, 15. [Google Scholar] [CrossRef] [Green Version]
- Livieris, I.E.; Pintelas, E.; Pintelas, P. A CNN–LSTM model for gold price time-series forecasting. Neural Comput. Appl. 2020, 32, 17351–17360. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, F.; Xu, B.; Chi, W.; Wang, Q.; Sun, T. Prediction of stock prices based on LM-BP neural network and the estimation of overfitting point by RDCI. Neural Comput. Appl. 2018, 30, 1425–1444. [Google Scholar] [CrossRef]
- Thakur, G.S.M.; Bhattacharyya, R.; Mondal, S.S. Artificial Neural Network Based Model for Forecasting of Inflation in India. Fuzzy Inf. Eng. 2016, 8, 87–100. [Google Scholar] [CrossRef] [Green Version]
- Paranhos, L. Predicting Inflation with Neural Networks. arXiv 2021, arXiv:2104.03757. [Google Scholar]
- Araujo, G.S.; Gaglianone, W.P. Machine Learning Methods for Inflation Forecasting in Brazil: New Contenders Versus Classical Models. Technical Report, Mimeo. 2020. Available online: https://www.cemla.org/actividades/2020-final/2020-10-xxv-meeting-cbrn/Session%202/3.%20Machine_Learning...%20Wagner%20Piazza.pdf (accessed on 10 August 2021).
- Yan, X.; Weihan, W.; Chang, M. Research on financial assets transaction prediction model based on LSTM neural network. Neural Comput. Appl. 2021, 33, 257–270. [Google Scholar] [CrossRef]
- Kamalov, F. Forecasting significant stock price changes using neural networks. Neural Comput. Appl. 2020, 32, 17655–17667. [Google Scholar] [CrossRef]
- Hao, Y.; Gao, Q. Predicting the trend of stock market index using the hybrid neural network based on multiple time scale feature learning. Appl. Sci. 2020, 10, 3961. [Google Scholar] [CrossRef]
- Xiao, Y.; Xiao, J.; Wang, S. A hybrid model for time series forecasting. Hum. Syst. Manag. 2012, 31, 133–143. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, B.; Zhou, C. Forecasting stock prices with long-short term memory neural network based on attention mechanism. PLoS ONE 2020, 15, e0227222. [Google Scholar] [CrossRef]
- Chimmula, V.K.R.; Zhang, L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 2020, 135, 109864. [Google Scholar] [CrossRef]
- Wu, N.; Green, B.; Ben, X.; O’Banion, S. Deep Transformer Models for Time Series Forecasting: The Influenza Prevalence Case. arXiv 2020, arXiv:2001.08317. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hastie, T.; Tibshirani, R. Generalized Additive Models. Stat. Sci. 1986, 1, 297–310. [Google Scholar] [CrossRef]
- Chan, W.N. Time Series Data Mining: Comparative Study of ARIMA and Prophet Methods for Forecasting Closing Prices of Myanmar Stock Exchange. J. Comput. Appl. Res. 2020, 1, 75–80. [Google Scholar]
- Yenidoğan, I.; Çayir, A.; Kozan, O.; Dağ, T.; Arslan, Ç. Bitcoin forecasting using ARIMA and prophet. In Proceedings of the 2018 3rd International Conference on Computer Science and Engineering (UBMK), Sarajevo, Bosnia and Herzegovina, 20–23 September 2018; pp. 621–624. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at Scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 28, pp. 1310–1318. [Google Scholar]
- Box, G.E.; Pierce, D.A. Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. J. Am. Stat. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- Ljung, G.M.; Box, G.E. On a measure of lack of fit in time series models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; Volume 9, pp. 249–256. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sims, C.A. Macroeconomics and reality. Econom. J. Econom. Soc. 1980, 48, 1–48. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- Mentzer, J.T.; Moon, M.A. Sales Forecasting Management: A Demand Management Approach; Sage Publications: Thousand Oaks, CA, USA, 2004. [Google Scholar]
- Zhang, G.P. Neural Networks in Business Forecasting; IGI Global: Hershey, PA, USA, 2004. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; Volume 30, pp. 5998–6008. [Google Scholar]
- Ekambaram, V.; Manglik, K.; Mukherjee, S.; Sajja, S.S.K.; Dwivedi, S.; Raykar, V. Attention based Multi-Modal New Product Sales Time-series Forecasting. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 3110–3118. [Google Scholar] [CrossRef]
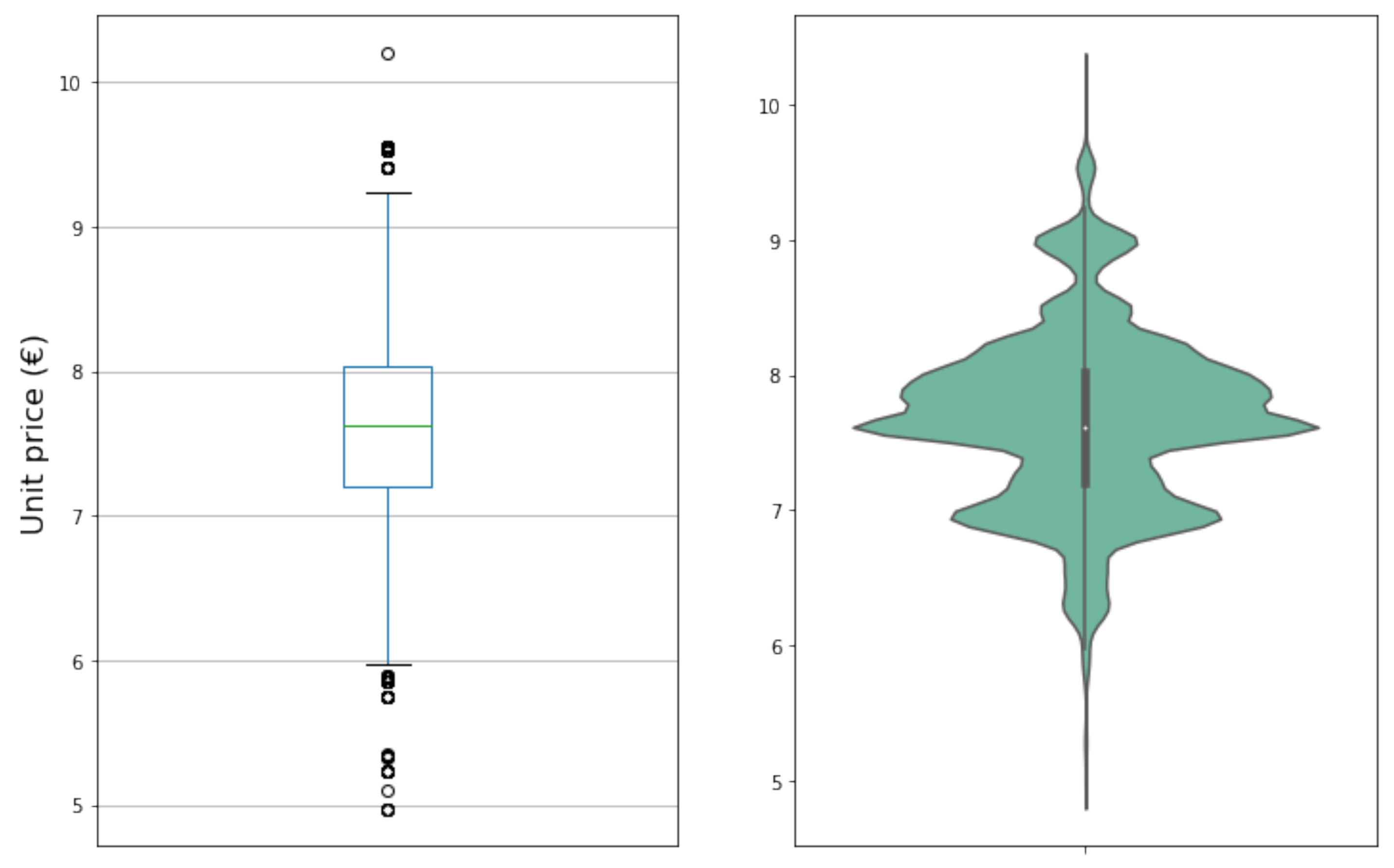
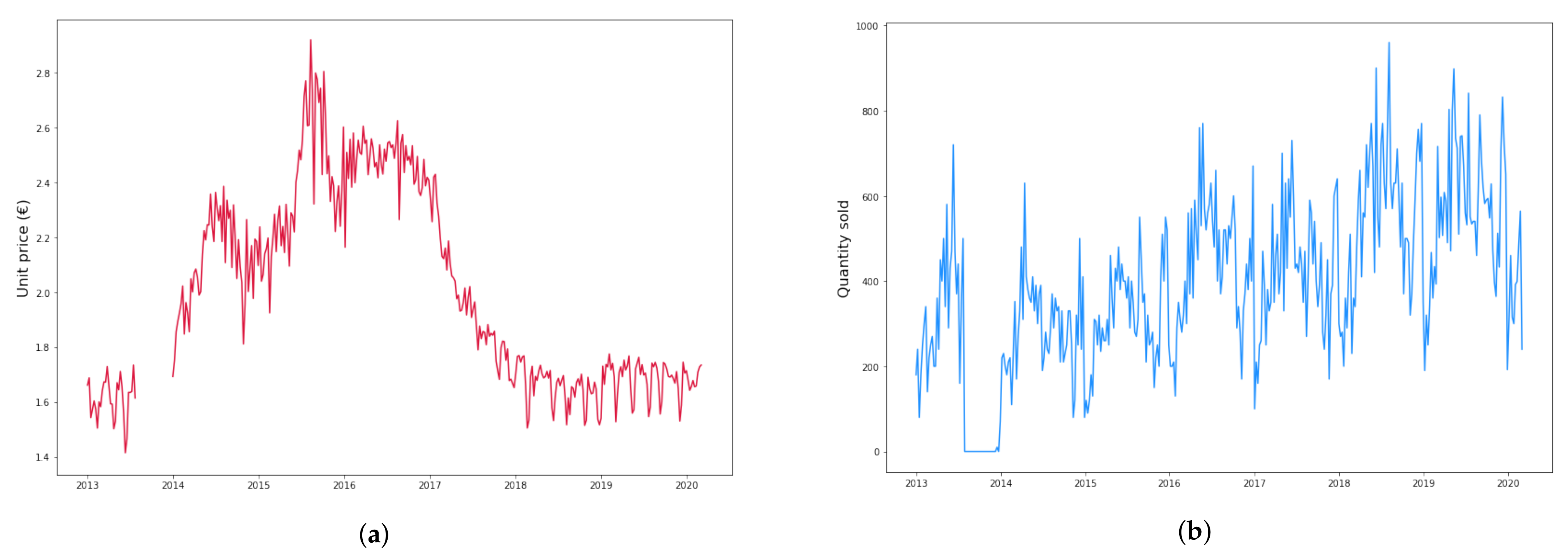
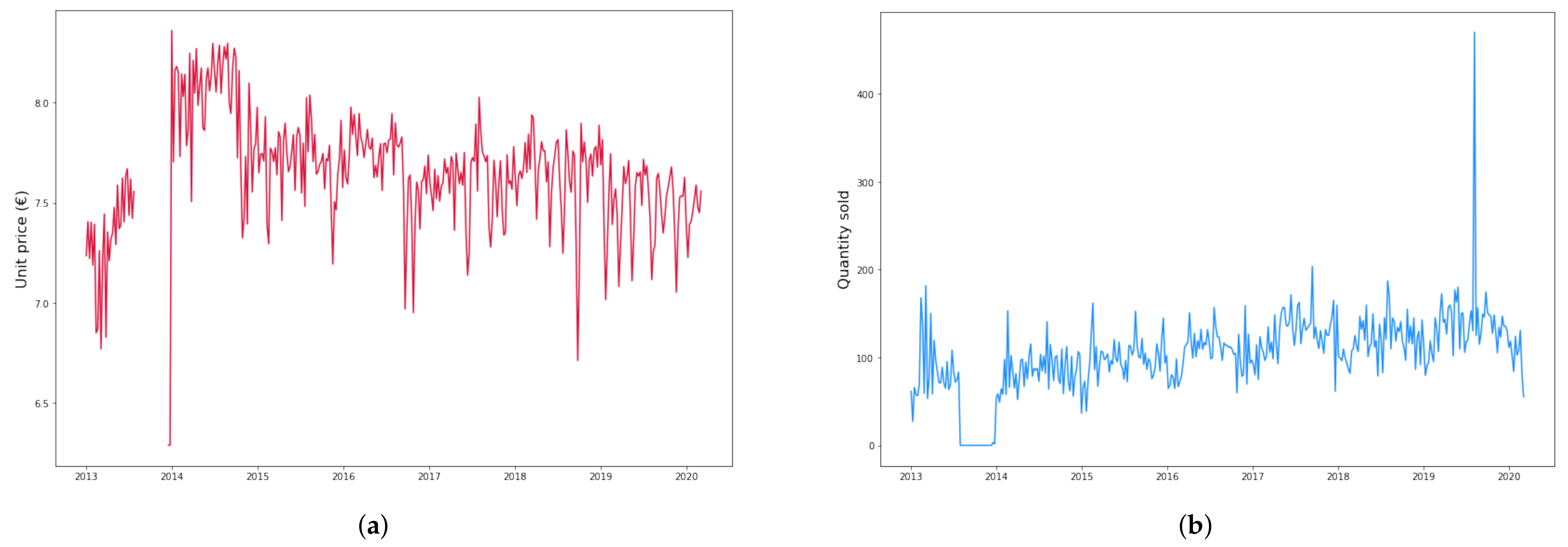
| Product | 1 | 2 | 3 |
|---|---|---|---|
| Mean (€) | 1.99 | 7.64 | 7.27 |
| Std (€) | 0.36 | 0.40 | 0.26 |
| Product | Model | Train | Valid | Test |
|---|---|---|---|---|
| 1 | Prophet | 240 | 52 | 62 |
| ARIMA & NN | 211 | |||
| 2 | Prophet | 241 | 52 | 62 |
| ARIMA & NN | 211 | |||
| 3 | Prophet | 242 | 52 | 62 |
| ARIMA & NN | 212 |
| Product | Series | ADF Test Statistics | p-Value | Lags Used |
|---|---|---|---|---|
| 1 | −1.10 | 0.713 | 4 | |
| −12.3 | 3 | |||
| 2 | −2.84 | 0.0530 | 7 | |
| −11.5 | 6 | |||
| 3 | −2.29 | 0.175 | 7 | |
| −11.5 | 6 |
| Quant | Customers | Orders | On Sale | cost_avg | w_cos | w_sin | p_std | price_avg |
|---|---|---|---|---|---|---|---|---|
| 10 | 1 | 1 | 0 | 1.40 | 0.990 | −0.141 | 0 | 1.41 |
| 0 | 0 | 0 | 0 | 1.40 | 1.000 | −0.0214 | 0 | 1.55 |
| 70 | 6 | 6 | 0 | 1.40 | 0.993 | 0.120 | 0.0690 | 1.69 |
| 220 | 17 | 18 | 0 | 1.40 | 0.971 | 0.239 | 0.0580 | 1.75 |
| 230 | 14 | 15 | 0 | 1.39 | 0.935 | 0.353 | 0.0685 | 1.86 |
| Product | Model | Train + Val RMSE | Test RMSE | Test MAE | Test MAPE | Test ME |
|---|---|---|---|---|---|---|
| 1 | ARIMA (2, 1, 0) | 0.097 | 0.0758 | 0.173 | 0.215 | 0.00521 |
| 2 | ARIMA (0, 1, 2) | 0.232 | 0.0581 | 0.132 | 0.159 | 0.0140 |
| 3 | ARIMA (3, 1, 1) | 0.211 | 0.0348 | 0.0178 | 0.0222 | 0.0507 |
| Product | Valid RMSE | Test RMSE | Test MAE | Test MAPE | Test ME | ||
|---|---|---|---|---|---|---|---|
| 1 | 0.5 | 0.01 | 0.0831 | 0.00812 | 0.0694 | 0.0414 | −0.0152 |
| 2 | 0.1 | 0.01 | 0.293 | 0.220 | 0.165 | 0.0224 | 0.0456 |
| 3 | 0.5 | 1.0 | 0.215 | 0.350 | 0.301 | 0.0424 | −0.217 |
| Product | l | r | Train RMSE | Valid RMSE | ||
|---|---|---|---|---|---|---|
| 1 | 3 | 32 | 0.1 | 0.001 | 0.0964 | 0.0612 |
| 2 | 3 | 32 | 0.1 | 0.001 | 0.157 | 0.176 |
| 3 | 1 | 64 | 0.1 | 0.001 | 0.143 | 0.148 |
| Product | l | r | f | pad | pad | n | Train RMSE | Valid RMSE | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 64 | 0.3 | 0.0005 | 20 | 2 | causal | causal | 8 | 0.0770 | 0.0553 |
| 2 | 3 | 64 | 0.1 | 0.0005 | 20 | 2 | no | same | 12 | 0.175 | 0.165 |
| 3 | 1 | 32 | 0.2 | 0.001 | 20 | 2 | same | same | 8 | 0.148 | 0.132 |
| Product | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| class | A | B | A | B | A | B |
| RMSE | 0.0617 | 0.0613 | 0.179 | 0.162 | 0.219 | 0.200 |
| MAE | 0.0498 | 0.0511 | 0.130 | 0.126 | 0.157 | 0.150 |
| MAPE | 0.0299 | 0.0305 | 0.0174 | 0.0168 | 0.0221 | 0.0212 |
| ME | 0.0138 | 0.00138 | −0.0767 | −0.0321 | −0.0260 | 0.0262 |
| Product | Metric | ARIMA | Prophet | NN-A | NN-B | No-Change |
|---|---|---|---|---|---|---|
| 1 | RMSE | 0.0758 | 0.0812 | 0.0617 | 0.0613 | 0.0972 |
| MAE | 0.0581 | 0.0694 | 0.0498 | 0.0511 | 0.0715 | |
| MAPE | 0.0348 | 0.0414 | 0.0299 | 0.0305 | 0.0429 | |
| ME | 0.00521 | −0.0152 | 0.0138 | 0.00138 | −0.0066 | |
| 2 | RMSE | 0.173 | 0.220 | 0.179 | 0.162 | 0.268 |
| MAE | 0.132 | 0.165 | 0.135 | 0.126 | 0.204 | |
| MAPE | 0.0178 | 0.0224 | 0.0181 | 0.0168 | 0.0276 | |
| ME | 0.0140 | 0.0456 | −0.0767 | −0.0321 | 0.00811 | |
| 3 | RMSE | 0.215 | 0.350 | 0.219 | 0.200 | 0.354 |
| MAE | 0.159 | 0.391 | 0.157 | 0.150 | 0.376 | |
| MAPE | 0.0222 | 0.0424 | 0.0221 | 0.0212 | 0.0425 | |
| ME | 0.0507 | −0.217 | −0.0260 | 0.0262 | −0.0211 | |
| avg MAPE | 0.0249 | 0.0354 | 0.0234 | 0.0228 | 0.0377 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menculini, L.; Marini, A.; Proietti, M.; Garinei, A.; Bozza, A.; Moretti, C.; Marconi, M. Comparing Prophet and Deep Learning to ARIMA in Forecasting Wholesale Food Prices. Forecasting 2021, 3, 644-662. https://doi.org/10.3390/forecast3030040
Menculini L, Marini A, Proietti M, Garinei A, Bozza A, Moretti C, Marconi M. Comparing Prophet and Deep Learning to ARIMA in Forecasting Wholesale Food Prices. Forecasting. 2021; 3(3):644-662. https://doi.org/10.3390/forecast3030040
Chicago/Turabian StyleMenculini, Lorenzo, Andrea Marini, Massimiliano Proietti, Alberto Garinei, Alessio Bozza, Cecilia Moretti, and Marcello Marconi. 2021. "Comparing Prophet and Deep Learning to ARIMA in Forecasting Wholesale Food Prices" Forecasting 3, no. 3: 644-662. https://doi.org/10.3390/forecast3030040
APA StyleMenculini, L., Marini, A., Proietti, M., Garinei, A., Bozza, A., Moretti, C., & Marconi, M. (2021). Comparing Prophet and Deep Learning to ARIMA in Forecasting Wholesale Food Prices. Forecasting, 3(3), 644-662. https://doi.org/10.3390/forecast3030040